Abstract
Developing an adaptation option is challenging for long-term engineering decisions due to uncertain future climatic conditions; this is especially true for urban flood risk management. This study develops a real options approach to assess adaptation options in urban surface water flood risk management under climate change. This approach is demonstrated using a case study of Waterloo in London, UK, in which three Sustainable Drainage System (SuDS) measures for surface water flood management, i.e., green roof, bio-retention and permeable pavement, are assessed. A trinomial tree model is used to represent the change in rainfall intensity over future horizons (2050 s and 2080 s) with the climate change data from UK Climate Projections 2009. A two-dimensional Cellular Automata-based model CADDIES is used to simulate surface water flooding. The results from the case study indicate that the real options approach is more cost-effective than the fixed adaptation approach. The benefit of real options adaptations is found to be higher with an increasing cost of SuDS measures compared to fixed adaptation. This study provides new evidence on the benefits of real options analysis in urban surface water flood risk management given the uncertainty associated with climate change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Urban surface water flooding, as one of the major natural hazards in both developed and developing countries, can cause great environmental and economic damage and social interruption (Zhou et al. 2012; Hirabayashi et al. 2013; Yin et al. 2015; Jenkins et al. 2017; Löwe et al. 2017). For example, the summer floods of 2007 in UK led to 55,000 properties flooded with an estimated economic loss of £3.2 billion (Pitt 2008). This situation can get worse over the next decades due to climate change and rapid urbanization (Dawson et al. 2008; Jenkins et al. 2017). The expected annual damage (EAD) from surface water flooding in England can increase by 135% by 2080 under future climate scenario (Sayers et al. 2015). Therefore, there is a need to assess the impact of climate change and develop effective adaptation measures in response to increasing flood risk (Koukoui et al. 2015; Zhang et al. 2017).
Significant efforts have been made during the last few decades to develop cost-effective, long-term adaptation measures for alleviating increased flood risk through cost–benefit analysis (Löwe et al. 2017). For example, Koukoui et al. (2015) described a tipping point-opportunity method to identify the adaptation strategy with lower costs, considering the effects of climate change. Zhou et al. (2012) developed a pluvial flood risk assessment framework to identify and access adaptation measures based on the cost–benefit process. Löwe et al. (2017) developed a new framework to assess flood risk adaptation measures by coupling a 1D–2D hydrodynamic flood model with an agent-based urban development model to consider the long-term effects of urban development and climate change.
However, there are large uncertainties in assessing the long-term performance and benefit of adaptation measures, due to multiple sources of uncertainty such as climate change and land use change (Hino and Hall 2017). Furthermore, based on the worst climate change scenario, the investments can be very large over a long-term planning horizon (e.g., 30 years); this may lead to overdesign for the uncertainty of climate change. To bridge this gap, real options analysis is introduced in this study to handle the uncertainties in future infrastructure investments and provide decision support for appropriate climate change adaptation.
The real options approach originated from the study of financial decision making (Myers 1984). The success of financial options development and application led to the award of Nobel Prize in Economic Sciences to Robert Merton and Myron Scholes in 1997. A real option means the right but not the obligation to take future actions. Thus, unlike the traditional planning approach, which considers only one-off investment option and ignores the flexibility under significant future uncertainties, real options can consider management flexibility and volatility by making changes to an investment when new information comes in the future. Many tools have been developed for the analysis of real options, and most of them are based upon the Black–Scholes model and binominal model, such as binominal and trinomial decision trees (Gersonius et al. 2013). Apart from financial option analysis, real options is also an important analytical tool that has been applied to a number of diverse fields such as management of infrastructure systems, renewable energy and water supply. For example, Zhao et al. (2004) used real options for decision making in highway development, operation, expansion and rehabilitation. Jeuland and Whittington (2014) developed a methodology for planning new water resources infrastructure investment and operating strategies considering climate change uncertainty. Kim et al. (2017b) proposed a real options-based framework to assess economic benefits of adapting hydropower plants to climate change.
In recent years, the concept of real options has been used in the flood risk management for developing cost-effective adaptation measures in order to reduce the consequences of climate change. Woodward et al. (2011) assessed a set of interventions in a flood system across a range of future climate change scenarios. Furthermore, Woodward et al. (2014) developed a new methodology by capturing the concepts of real options and multiobjective optimization to evaluate potential flood risk management opportunities. Hino and Hall (2017) analyzed real options in flood risk management by considering the joint effects of uncertainties in socioeconomic drivers and climate change. However, all these studies above focused on the design of flood defense systems (more specifically on flood walls). In urban flooding, however, there were only a few studies on the use of real options to build flexibility into urban drainage infrastructure (Gersonius et al. 2013; Kim et al. 2017a). There is a need to further develop the real options approach in urban surface water flood management and test its effectiveness in developing adaptation measures related to Sustainable Drainage Systems (SuDS).
In this paper, we aim to present a real options approach for urban surface water flood risk management under long-term climate change scenarios. The trinomial tree model is used to represent the future changes in rainfall intensity over two planning horizons in 2050 and 2080. The Cellular Automata Dual-DraInagE Simulation (CADDIES) model (Guidolin et al. 2016) is used for flood simulation. The Waterloo urban catchment in London is used as a case study to assess SuDS measures for surface water flood management including green roof, bio-retention and permeable pavement. Real options measures are compared to a fixed adaptation approach. The results obtained from the case study show the advantage of real options in urban surface water flood risk management considering future climate change.
2 Methodology
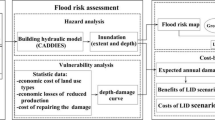
Figure 1 summarizes the real options approach used in this study. The climate change data from UKCP09 (Murphy et al. 2009) are used to generate climate change scenarios. To investigate the performance of the real options approach on flood risk reduction under future climate change, two different adaptation approaches (i.e., ‘do nothing’ baseline and fixed adaptation approach) are used for comparison with the real options approach through cost–benefit analysis. Furthermore, three kinds of SuDS measures, i.e., green roof, bio-retention and permeable pavement, are chosen to generate adaptation scenarios. The depth-damage curves combined with the inundation (extent and depth) from CADDIES flood model are used to assess flood damage. These are detailed below.
2.1 Climate change scenarios
The trinomial tree model, which is an extension of the lattice binomial model (Boyle 1988), is used to represent the uncertainty of rainfall due to climate change. This model was originally developed for real options analysis in financial investments, but has been used in many fields due to its flexibility and effectiveness, such as renewable energy and urban drainage infrastructure (Gersonius et al. 2013; Dittrich et al. 2016; Gong and Li 2016; Tang et al. 2017). In this model, the stochastic process is simplified by three jump parameters (u for moving up, d for moving down and m for remaining the same) to describe the possible changes of a system’s status with related transition probabilities (pu, pd and pm) over a time period. Meanwhile, these parameters and their corresponding probabilities can be calculated by Eqs. (1)–(6) (Zaboronski and Zhang 2008).
where r is drift rate, σ is the volatility and Δt is the length of the time period.
It is possible to estimate the change of the future rainfall intensity with u, d and m. Further, when a system’s status remains the same, i.e., the rainfall intensity won’t change over a time period, so the value of m is set as 1. For example, the rainfall intensity is denoted by S at time t0, then it will change to S*u, S*d or S for each climate change scenario at time t1. Based on the mean and standard deviation of the normal approximation of the climate change data from UKCP09, the drift rate r and volatility σ can be estimated for the change in rainfall intensity by Eqs. (7)–(8) (Gersonius et al. 2013), as below:
where μ is the mean value for normal approximation of the rainfall change of T years, and \({\sigma_s}\) is the standard deviation.
2.2 Approach for adaptation
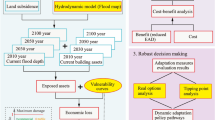
The real options approach is compared with the traditional fixed adaptation approach. In the fixed adaptation approach, as shown in Fig. 2, all adaptation measures Af are implemented at year t0 regardless of future climate predictions. For the real options approach, adaptation measures are adopted only for the scenarios in which the rainfall intensity increases. For example, adaptation measures of Ar1 will be implemented when the rainfall intensity increases following the upward path with a probability of pu at year t0, then Ar1 (with a probability of pmpu) or Ar2 (with a probability of pupu) will be implemented at year t1 depending on different scenarios of rainfall prediction at year t2.
2.3 Flood risk assessment
2.3.1 Flood modeling
In this paper, the CADDIES model was used for the surface water mapping to assess the flood risk. CADDIES is a fast 2D urban flood simulation model for high-resolution or large-scale simulations based on the principle of cellular automata (CA). This model performs a 2D pluvial flood inundation simulation using simple transition rules for modeling complex physical systems. Furthermore, the model allows each grid cell using its own roughness value or infiltration rate to represent spatial variations of land cover condition, soil infiltration and drainage capacity. This model’s effectiveness has been proven on the 2D benchmark test cases and real-world case studies (Guidolin et al. 2016).
2.3.2 Flood risk assessment
Expected annual damage (EAD) is often used to evaluate the benefits for adaptation measures in flood risk management decision making, especially for a long-term flood risk intervention strategy (Woodward et al. 2011, 2014; Zhou et al. 2012; Hino and Hall 2017; Löwe et al. 2017). EAD is the frequency weighted sum of damage for the full range of possible damaging flood events and would occur in a particular area over a very long period of time, which can be defined as below:
where D is the flood damage and p is the annual exceedance probability for a rainfall event.
In this paper, we consider the direct tangible flood damages on building to quantify the impact of flooding and the benefits of implementing different adapting strategies. The damage is determined using the flood depth information obtained from CADDIES and the depth-damage functions for different building uses. Furthermore, the trapezoidal rule (Olsen et al. 2015) is used to approximate the EAD using three events. For example, three rainfall events with the annual exceedance probability of p1, p2 and p3 are illustrated to calculate the damage in Fig. 1.
For each adaptation scenario, the total damage is calculated by integration of the flood damages over all different rainfall paths with different probabilities. So even with the same adaptation measures implemented in year 2080, the EAD will be different in the fixed and real options approaches due to the probabilities of future climate scenarios considered in Eq. (9).
2.4 Cost–benefit analysis
In order to compare the benefits of different adaptation investments with the corresponding costs, cost–benefit analysis is implemented to assess the performance of real options in flood risk reduction compared to the fixed adaptation approach and ‘do nothing’ baseline. The benefits are defined as the reduction in flood damage when the adaptation implemented compared to the baseline scenario without adaptation. The investment costs of adaptation measures can be obtained for green roof, bio-retention and permeable pavement. NPVs are calculated with a discount rate in order to convert the benefits and costs at different future horizons to their present values using the equation below:
where \({B_t}\) represents the benefits of the adaptation measure at year t, \(C{}_t\) is the cost of the adaptation measure at year t, r denotes the discount rate and T is the total number of years considered. Higher NPV values indicate that the relevant adaptation approaches are more cost-effective in alleviating the increased flood risk.
3 Case study
3.1 Study area
In this paper, the Waterloo area in the London Borough of Southwark is used as the case study. The digital elevation data (DEM) of bare terrain, obtained from Ordnance Survey, has a 5 m × 5 m resolution with the highest and lowest elevations of 115.5 m and − 6.4 m, respectively. We analyzed the terrain elevation to determine the catchment boundary of the study area, and thus the closed boundary condition was set in the flood model.
As shown in Fig. 3b, the topography data (Ordnance Survey 2015) were classified into six different land cover types, including building, green land, manmade surface, rail, road and water, to set up the infiltration rate and roughness parameters in the CADDIES flood model. The Waterloo catchment covers an area of 68.8 km2, with 81.0% developed as buildings and impervious surfaces, while 19.0% of the area remains as permeable green land.
Furthermore, this study area can also be classified into seven different land use types, including education, industrial, medical care center, office, residential, shop and non-constructed areas (Fig. 3a), for assessing direct tangible flood damages based on the depth-damage functions. The depth-damage functions are available for over 100 building types in the UK’s Multi-Coloured Manual (Penning-Rowsell et al. 2010). Figure 4 shows the depth-damage functions of the six land use types considered in this study.
3.2 Rainfall events
3.2.1 Design rainfall
In order to calculate the EAD under different adaptation scenarios, design rainfall events of three return periods (30-, 50- and 100-year events) with a duration of 2 h were simulated using the rainfall Intensity–Duration–Frequency curves from the Flood Estimation Handbook (CEH 2015), and the rainfall hyetographs are shown in Fig. 5. Furthermore, the design rainfall depths and peak rainfall intensities under different return periods are shown in Table 1.
3.2.2 Climate change
In this study, the cumulative distribution data of rainfall intensity change (London, UK) by 2080 s under high emissions were obtained from UKCP09 (UKCP09 2017), as shown in Fig. 6. Furthermore, a normal distribution (mean μ = 1.260, and standard deviation σs = 0.200) was fitted to the UKCP09 climate data. The drift rate r and volatility σ were calculated as 0.24 and 1.45% using Eqs. (7)–(8).
Furthermore, a planning horizon from 2020 to 2080 was considered, and the adaptation measures will be applied in two stages, i.e., t0 = 2020, t1 = 2050. With the interval of 30 years, three jump parameters (u, d and m) with related transition probabilities (\({p_u}\), \({p_d}\) and \({p_m}\)) are estimated as below: u = 1.12, d = 0.89, m = 1, pu= 76.9%, pm= 21.6% and pd= 1.5%. Then we can calculate rainfall for the future years of 2050 and 2080 based on the three design rainfalls with 30-, 50- and 100-year return periods.
3.3 Adaptation scenarios
SuDS is used to manage flood risk by slowing down and reducing the quantity of surface water runoff (Woods et al. 2015). Out of many different SuDS measures for surface water management, we considered three measures in this paper, i.e., green roof implemented for every grid cell of buildings, permeable pavement for every grid cell of roads, and bio-retention for every grid cell of manmade surface. However, as shown in Table 2, we have considered 7 combinations of measures for the fixed adaptation approach and 19 combinations for the real options approach.
For example, for the fixed adaptation scenario F5, green roof and permeable pavement will be adopted for every grid cell of each land cover in year t0= 2020. For real options scenario R7, adaptation measures G will be implemented in year 2020 when the rainfall intensity is predicted to increase, i.e., following the upward path with a probability of pu. Then in 2050, adaption measures will be implemented in two cases only: (1) P will be implemented when rainfall intensity is predicted to increase from S*u to S*u*u; (2) G will be implemented when rainfall intensity is predicted to increase from S to S*u. So F5 and R7 can have the same measures in 2080, but this is true only when the rainfall intensity increases from S in 2020 to S*u in 2050 and further to S*u*u in 2080. In all other climate change scenarios, F5 and R7 will have different measures implemented in 2080.
Table 3 shows the unit costs for each SuDS measures below: £50–90/m2 for green roof, £15–35/m2 for bio-retention and £20–40/m2 for permeable pavement (HaskoningDHV 2012; Environment Agency 2015). The unit cost of £70/m2, £25/m2 and £30/m2 are chosen for green roof, bio-retention and permeable pavement. The discount rate was applied according to HM Treasury guidance, i.e., 3.5% for the years between 2020 and 2050, 3.0% for the years between 2050 and 2080 (Treasury and Book 2003).
3.4 Flood simulation details
In CADDIES, different Manning’s roughness values were assigned to different land cover types: (1) 0.05 s/m1/3 for the building areas; (2) 0.03 s/m1/3 for green lands; (3) 0.025 s/m1/3 for manmade surface areas; (4) 0.05 s/m1/3 for rails; (5) 0.02 s/m1/3 for roads; and (6) 0.035 s/m1/3 for water (Environment Agency 2013).
Furthermore, different constant infiltration rates were applied to different land covers to reflect both urban drainage capacity and soil infiltration. The combined sewer drainage system was designed to accommodate a rainfall event of the 15 year return period in the London Borough of Southwark (Environment Agency 2011). A combination of infiltration rates, i.e., 35 mm/h and 25 mm/h, were set for the green land cover and other covers during the model setup process according to the drainage capacity.
Note that this study is to illustrate the performance of real options on flood damage reduction rather than produce the exact reduction of runoff. Thus, infiltration rates for the land covers of building, manmade surface and road are assumed to be increased by 12 mm/h, 5 mm/h and 8 mm/h when green roof, bio-retention and permeable pavement are adopted, respectively, according to the literature (Qin et al. 2013; Woods et al. 2015; Alizadehtazi et al. 2016; Jato-Espino et al. 2016; Bell et al. 2017; Ossa-Moreno et al. 2017; Rocheta et al. 2017).
4 Results and discussion
4.1 Expected annual damage
The maximum flood depth and damage under the design rainfall of 30-year return period are presented in Fig. 7. The damage values shown in Fig. 7b are the direct building content damage per unit area. Extensive flood is distributed over the grid cells of building, road, manmade surface and so on. For example, the inundation extent (depth > 0.1 m) would cover a total area of 2.3 km2, of which the grid cells of building account for 23%. Furthermore, the inundation depth in 130 grid cells of building is greater than 1.0 m.
The total building flood damage for the study area can be calculated based on the unit damages. The EAD is then calculated by integration of the flood damage over the three rainfall events, each with a specific probability. In this study, the EAD for 2020, 2050 and 2080 are calculated, and for other years the EAD is calculated using linear interpolation.
The EADs are simulated for the real options, the fixed adaptation and the ‘do nothing’ baseline case. Compared with EAD for 2020 under ‘do nothing’ scenario, relative values of EAD for 2020, 2050 and 2080 under different adaptation scenarios are presented in Fig. 8. The EAD of the ‘do nothing’ baseline case increases rapidly from 2020 to 2080 due to increased rainfall intensities. Specifically, EADs are £29.2 × 106, £33.4 × 106 and £37.6 × 106 for year 2020, 2050 and 2080 under the ‘do nothing’ baseline case, i.e., relative EADs are 100, 114, 129%. However, the seven fixed adaptation scenarios can effectively reduce the EAD in a range of different values. The implementation of SuDS measures is effective in reducing flood risk, even though flood risk still increases in the planning horizon as a result of increased rainfall intensities. For example, in F1, the relative EAD is reduced to 90% in 2020 when compared to 100% in the base case, due to the green roof measure adopted, but increases to 105 and 119% in 2050 and 2080, respectively. It is clear that scenario F7 is the most effective among the fixed scenarios, because all three measures are adopted at year 2020, with the smallest relative EAD for the year 2050 and 2080, i.e., 96 and 111%, respectively.
The 19 real options scenarios show a similar trend to the fixed adaptation approach between year 2020 and 2050 and the EADs are further reduced when adaptation measures are adopted at year 2050. However, when same measures are adopted, the real options approach tends to result in a slightly larger EAD than the fixed adaptation approach. This is because these adaptation measures are only implemented when the rainfall increases following the upward path. For example, relative EADs are 96 and 111% for year 2050 and 2080 under the scenario of F7, but they are 97 and 112% under the scenario of R19, though both scenarios consider three kinds of adaptation measures in the planning horizon.
4.2 Net present value
Cost–benefit analysis is conducted to compare different adaptation approaches. The benefit of an adaptation measure can be calculated as the difference between the EADs before and after the adaptation adopted.
Figure 9 shows NPVs for the 7 fixed adaptation scenarios and 19 real options scenarios. In the fixed adaptation scenarios, F7 has the smallest NPV, − £2.00 × 109, even though it has the largest benefit (reduced EAD). This is related to the high cost of F7 due to the implementation of all three kinds of adaptation measures regardless of the future climate. Furthermore, the real options approach has higher NPV than fixed adaptation approach by adopting the same measures in the planning horizon when the rainfall increases following the upward path. For example, both F7 and R19 consider the same SuDS measures, but their NPVs are − £2.00 × 109 and − £1.02 × 109, respectively. This implies that the real options approach is substantially more cost-effective than fixed adaptation approach.
The results in Fig. 9 show that all the calculated NPVs of the fixed adaptation and real options are negative. This is because only direct tangible damage to buildings is considered in this study. However, more benefits can be provided from flood reduction due to the adoption of SuDS measures. For example, economic benefits can arise from reduced road damage, basement damage, sewer damage and traffic delays. Furthermore, SuDS can also provide ecosystem service benefits (wider benefits), including mitigation of heat island effects and noise, improvements in water and air quality (Ossa-Moreno et al. 2017). Negative NPVs obtained from flood adaptation assessment are not uncommon in the literature (Zhou et al. 2012; Löwe et al. 2017), for example, Löwe et al. (2017) found that the performance of adaptation strategies strongly depended on many factors, and thus may led to negative NPVs values.
4.3 Uncertainty analysis
Uncertainties in the adaptation costs and SuDS measures drainage capacity are considered in the cost–benefit analysis and the results are analyzed below.
4.3.1 Adaptation cost uncertainty
In the analyses discussed above, the average costs shown in Table 3 are considered. The lower and upper costs were chosen for further analysis. The NPVs of 26 adaptation scenarios under low, medium and high cost scenarios are shown in Fig. 10. The 26 scenarios are divided into 7 categories according to the kind of measures adopted during the planning horizon: CG, CB and CP when only one measure is adopted, CGB, CGP and CBP when two measures adopted, and CGBP when all three measures adopted. The NPV tends to decrease as the cost of SuDS measures increases. For example, NPVs are − £0.72 × 109, − £1.00 × 109 and − £1.36 × 109 for scenario F1 under low, medium and high cost scenarios, separately. Furthermore, the difference between the fixed adaptation approach and the real options approach in each category increases as the increase of costs. The real options approach has a bigger advantage than the fixed adaptation approach when the cost increases. For example, for the category of CGBP, the differences in NPV between F7 and R18 under low, medium and high cost scenarios are £0.67 × 109, £0.98 × 109 and £1.30 × 109, respectively.
4.3.2 SuDS measures drainage capacity uncertainty
In order to study the influence of the uncertainty in drainage capacity of the SuDS measures, two scenarios of infiltration rate were set up for flood damage analysis based on the current drainage capacity (denoted by ‘S’): ‘SR’ represents a 50% reduction of the increased infiltration rate for SuDS measures of green roof, bio-retention and permeable pavement, and ‘SI’ represents a 50% increase of the increased infiltration rate for each SuDS measure. The EAD for fixed adaptation scenario F7 and real adaptation scenario R19 are shown in Fig. 11.
Figure 11 illustrates the variations in EAD during the planning horizon for the adaptation scenarios F7 and R19 under different drainage capacity scenarios. For fixed adaptation scenario F7, a big difference in flood damage is shown under the drainage capacity scenario of ‘S’, ‘SR’ and ‘SI’. That is, EAD values can be reduced when the drainage capacity is increased. However, EAD values might be higher when the drainage capacity is reduced under the scenario of ‘SR’.
The real option adaptation scenario R19 shows the similar characteristics to the fixed adaptation F7 though its flood damage is larger than that of F7. Furthermore, the difference between R19 and F7 tends to become smaller with a decrease in the drainage capacity. For example, the difference of EAD between R19 and F7 are £2.0 × 106 and £0.6 × 106 for year 2050 and 2080 under ‘SI’, while only £0.7 × 106 and £0.2 × 106 for ‘SR’.
5 Conclusions
In this paper a real options approach was developed to assess adaptation options in urban surface water flood risk management under climate change. A CA-based urban two-dimensional model was used to simulate surface water flooding. The trinomial tree model was used to calculate the transition probability of rainfall intensity change over the planning horizon with the climate change data from UKCP09. Two approaches, fixed adaptation and real options, were investigated and compared using a case study of the Waterloo catchment in London, UK. Main conclusions are drawn as below:
-
1.
The real options approach is more cost-effective compared to the fixed adaptation approach. When the same SuDS measures are adopted during the planning horizon, the real options approach can have a slightly higher EAD but have a much lower cost when compared with the fixed approach, which makes it achieve a higher NPV during the planning horizon.
-
2.
The real options approach achieves a bigger advantage than the fixed adaptation approach with an increasing cost of adaptation measures but the benefit is reduced when the drainage capacity of SuDS measures decreases.
-
3.
The results obtained from the case study indicate the real options approach is able to handle the uncertainty of climate change in assessing SuDS measures for surface water flood risk management.
This study considers three SuDS measures only in a case study of the Waterloo catchment. More SuDS measures will be further investigated in the future in order to explore the advantage of using real options on urban surface water flood risk management.
Change history
28 August 2018
The article “Assessing real options in urban surface water flood risk management under climate change”, written by Haixing Liu, Yuntao Wang, Chi Zhang, Albert S. Chen and Guangtao Fu, was originally published electronically on the publisher’s internet portal (currently SpringerLink) on 21 May 2018 without open access.
References
Agency Environment (2011) Surface water management plan-London Borough of Southwark. Bristol, UK
Agency Environment (2013) Updated Flood Map for Surface Water-National Scale Surface Water Flood Mapping Methodology. Bristol, UK
Agency Environment (2015) Cost estimation for SUDS—summary of evidence. Bristol, UK
Alizadehtazi B, DiGiovanni K, Foti R, Morin T, Shetty NH, Montalto FA, Gurian PL (2016) Comparison of Observed Infiltration Rates of Different Permeable Urban Surfaces Using a Cornell Sprinkle Infiltrometer. J Hydrol Eng 21(7):06016003
Bell S., Jones K., McIntosh A., Malki-Epshtein L. and Yao Z. (2017). Green Infrastructure for London: A review of the evidence, London
Boyle PP (1988) A lattice framework for option pricing with two state variables. Journal of Financial and Quantitative Analysis 23(1):1–12
CEH (2015). FEH Web Service. https://fehweb.ceh.ac.uk/
Dawson R, Speight L, Hall J, Djordjevic S, Savic D, Leandro J (2008) Attribution of flood risk in urban areas. Journal of Hydroinformatics 10(4):275–288
Dittrich R, Wreford A, Moran D (2016) A survey of decision-making approaches for climate change adaptation: are robust methods the way forward? Ecol Econ 122(68):79–89
Gersonius B, Ashley R, Pathirana A, Zevenbergen C (2013) Climate change uncertainty: building flexibility into water and flood risk infrastructure. Clim Change 116(2):411–423
Gong P, Li X (2016) Study on the investment value and investment opportunity of renewable energies under the carbon trading system. Chinese Journal of Population Resources and Environment 14(4):271–281
Guidolin M, Chen AS, Ghimire B, Keedwell EC, Djordjević S, Savić DA (2016) A weighted cellular automata 2D inundation model for rapid flood analysis. Environ Model Softw 84(2016):378–394
HaskoningDHV R. (2012). Costs and Benefits of Sustainable Drainage Systems, UK
Hino M, Hall JW (2017) Real Options Analysis of Adaptation to Changing Flood Risk: structural and Nonstructural Measures. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering 3(3):04017005
Hirabayashi Y, Mahendran R, Koirala S, Konoshima L, Yamazaki D, Watanabe S, Kim H, Kanae S (2013) Global flood risk under climate change. Nature climate change 3(9):816–821
Jato-Espino D, Charlesworth SM, Bayon JR, Warwick F (2016) Rainfall-Runoff Simulations to Assess the Potential of SuDS for Mitigating Flooding in Highly Urbanized Catchments. International journal of environmental research and public health 13(1):149
Jenkins K, Surminski S, Hall J, Crick F (2017) Assessing surface water flood risk and management strategies under future climate change: insights from an Agent-Based Model. Sci Total Environ 595(2017):159–168
Jeuland M, Whittington D (2014) Water resources planning under climate change: assessing the robustness of real options for the Blue Nile. Water Resour Res 50(3):2086–2107
Kim K, Ha S, Kim H (2017a) Using real options for urban infrastructure adaptation under climate change. J Clean Prod 143(2017):40–50
Kim K, Park T, Bang S, Kim H (2017b) Real Options-Based Framework for Hydropower Plant Adaptation to Climate Change. Journal of Management in Engineering 33(3):04016049
Koukoui N, Gersonius B, Schot PP, van Herk S (2015) Adaptation tipping points and opportunities for urban flood risk management. Journal of Water and Climate Change 6(4):695–710
Löwe R, Urich C, Domingo NS, Mark O, Deletic A, Arnbjerg-Nielsen K (2017) Assessment of urban pluvial flood risk and efficiency of adaptation options through simulations–A new generation of urban planning tools. J Hydrol 550(2017):355–367
Murphy JM, Sexton D, Jenkins G, Booth B, Brown C, Clark R, Collins M, Harris G, Kendon E, Betts R (2009) UK climate projections science report: climate change projections, Report 1906360022. Exeter, UK
Myers SC (1984) Finance theory and financial strategy. Interfaces 14(1):126–137
Olsen AS, Zhou Q, Linde JJ, Arnbjergnielsen K (2015) Comparing Methods of Calculating Expected Annual Damage in Urban Pluvial Flood Risk Assessments. Water 7(1):255–270
Ordnance Survey (2015). OS MasterMap Topography Layer [FileGeoDatabase geospatial data], Scale 1:1250, Tiles: GB, Updated: 11 June 2015, Ordnance Survey (GB), Using: EDINA Digimap Ordnance Survey Service, http://digimap.edina.ac.uk, Downloaded: 2016-02-02. http://digimap.edina.ac.uk
Ossa-Moreno J, Smith KM, Mijic A (2017) Economic analysis of wider benefits to facilitate SuDS uptake in London. UK. Sustainable Cities and Society 28(2017):411–419
Penning-Rowsell E, Viavattene C, Pardoe J, Chatterton J, Parker D, Morris J (2010) The Benefits of Flood and Coastal Risk Management: A Handbook of Assessment Techniques. Flood Hazard Research Centre, Middlesex University, London
Pitt M (2008) Learning lessons from the 2007 floods. Cabinet Office, London
Qin H-P, Li Z-X, Fu G (2013) The effects of low impact development on urban flooding under different rainfall characteristics. Journal of environmental management 129(2013):577–585
Rocheta VLS, Isidoro JMG, de Lima JL (2017) Infiltration of Portuguese cobblestone pavements–An exploratory assessment using a double-ring infiltrometer. Urban Water Journal 14(3):291–297
Sayers P., Horritt M., Penning-Rowsell E. and McKenzie A. (2015). Climate Change Risk Assessment 2017: Projections of future flood risk in the UK. Research undertaken by Sayers and Partners on behalf of the Committee on Climate Change. Published by Committee on Climate Change, London
Tang B-J, Zhou H-L, Chen H, Wang K, Cao H (2017) Investment opportunity in China’s overseas oil project: an empirical analysis based on real option approach. Energy Policy 105(2017):17–26
Treasury H, Book G (2003) Appraisal and Evaluation in Central Government. The Stationery Office, London
UKCP09 (2017). http://ukclimateprojections.metoffice.gov.uk/
Woods B., Wilson S., Udale-Clarke H., Illman S., Scott T., Ashley R. and Kellagher R. (2015). The SuDS Manual, C753, CIRIA, London, UK, ISBN 978-0-86017-760-9. http://www.susdrain.org/resources/SuDS_Manual.html
Woodward M, Gouldby B, Kapelan Z, Khu ST, Townend I (2011) Real options in flood risk management decision making. Journal of Flood Risk Management 4(4):339–349
Woodward M, Kapelan Z, Gouldby B (2014) Adaptive Flood Risk Management Under Climate Change Uncertainty Using Real Options and Optimization. Risk Analysis 34(1):75–92
Yin J, Ye M, Yin Z, Xu S (2015) A review of advances in urban flood risk analysis over China. Stochastic Environmental Research and Risk Assessment 29(3):1063–1070
Zaboronski P. C. O. and Zhang K. (2008). Pricing Options Using Trinomial Trees, University of Warwick
Zhang C, Wang Y, Li Y, Ding W (2017) Vulnerability Analysis of Urban Drainage Systems: tree vs Loop Networks. Sustainability 9(3):397
Zhao T, Sundararajan SK, Tseng C-L (2004) Highway development decision-making under uncertainty: a real options approach. Journal of Infrastructure Systems 10(1):23–32
Zhou Q, Mikkelsen PS, Halsnæs K, Arnbjerg-Nielsen K (2012) Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. Journal of Hydrology 414(2012):539–549
Acknowledgements
This research was partially funded by the British Council through the Global Innovation Initiative (GII206) and the UK Engineering and Physical Sciences Research Council under the Building Resilience into Risk Management project (EP/N010329/1). The corresponding author was funded by the China Scholarship Council. The authors would also like to thank Ordnance Survey for the Master Maps, and NVIDIA Corporation for the Tesla K20c GPU used in this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
About this article
Cite this article
Liu, H., Wang, Y., Zhang, C. et al. Assessing real options in urban surface water flood risk management under climate change. Nat Hazards 94, 1–18 (2018). https://doi.org/10.1007/s11069-018-3349-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-018-3349-1