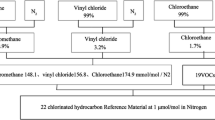
Gaseous mixtures of ethanol in nitrogen are prepared by the gravimetric method according to ISO 6142. The liquid component, ethanol, is added into the cylinder by the gas tight syringe. The exact amount of added liquid is determined by weighing the syringes. The exact amount of ethanol is calculated before starting filling the cylinder in accordance with the concentration of the final mixture. This calculated amount of liquid is filled into the syringe. The same type and volume of the empty syringe is used as a reference syringe. Before filling, the full syringe is weighed vs. the reference syringe. After filling, the empty syringe is weighed vs. the reference syringe. This procedure and the determination of the uncertainty of the weighing have a considerable influence on the certified value of the final mixture. Here, based on this simple experiment, we present the approach for uncertainty analysis used at the Slovak Institute of Metrology and compare it with different approaches, which includes the GUM uncertainty framework, the Monte Carlo method, and the characteristic function approach.
Similar content being viewed by others
1. Introduction. At the Slovak Institute of Metrology (SMU), the gaseous mixtures of ethanol in nitrogen are prepared by the standard gravimetric method. Before starting the preparation of the gaseous mixture, the exact amount of ethanol is calculated in accordance with the concentration of the final mixture. The liquid component, ethanol, is added into the cylinder by a gas-tight syringe. The exact amount of added liquid is determined by weighing the syringes. The procedure of weighing and the determination of the uncertainty of the weighing have a considerable infl uence on the certified value of the final mixture. In this experiment we present the applicability of different approaches for uncertainty analysis, such as GUM, the Monte Carlo method, and the characteristic function approach, and we compare the obtained results.
2. Description of the gravimetric method. The gravimetric method of gas mixture preparation is described in ISO 6142 [1]. At the SMU, we use 5 liter aluminum cylinders with passivated inner surface. As the matrix we use nitrogen. For preparation of gas mixtures of ethanol in nitrogen, we use two types of balances. One type – the comparator balances – is used for weighing of aluminum cylinders, and the other – the analytical balances – is used for weighing the gas-tight syringes.
At the start, we have a fully evacuated cylinder and its mass, weighed on comparator balances. This cylinder we connect to the filling station and add the weighed amount of ethanol into the cylinder. After that we add the calculated amount of nitrogen. Then we weigh the cylinder with the final mixture on comparator balances [2]. Next, we describe the process of weighing of syringes, because the concentration of ethanol in the final mixture strongly depends on the correct determination of the added amount of liquid ethanol.
3. Determination of the added amount of liquid ethanol. Ethanol is added into the cylinder in liquid form and by heating the pipes it becomes gaseous. It is necessary to calculate the maximum pressure in the cylinder to keep the ethanol in gaseous form. So, the concrete mixture with concrete concentration has its own pressure, amount of nitrogen, and amount of ethanol. These quantities are tied together and none of them can be changed. That is why we should determine the added amount of ethanol very precisely. To determinate the added amount of ethanol, we use the comparative method of weighing on analytical balances, see [2].
Step one. We determine the difference between the full syringe and reference syringe. The reference syringe is the same type of syringe and is empty. In this step we measure the weight of the full and reference syringe repeatedly 12 and 11 times, respectively. Subsequently, we calculate the mass differences based on the weighings, as indicated in Table 1. From the measurements presented in Table 1, we get the following summary statistics:
the mean value of the mass differences of the full syringe with liquid ethanol and the empty reference syringe (calculated as an average of all mass differences from Table 1);
the standard deviation of ΔmSZ.
At this moment, after taking all mass measurements of the used full syringe, we add the liquid ethanol into the cylinder.
Step two. We determine the difference between the empty syringe and reference syringe. In this step we measure the weight of the empty syringe and the reference syringe repeatedly 12 and 11 times, respectively. Subsequently, we calculate the mass differences based on the weighings. From the measurements presented in Table 2, we get the following summary statistics:
the mean value of the mass differences of the empty syringe and the empty reference syringe (calculated as an average of all mass differences from Table 2);
the standard deviation of ΔmIS.
Step three. We determine the mass of the added amount of liquid ethanol as the difference μSMU = ΔμSZ – ΔμIS between the result from step one and result from step two and its standard uncertainty. Then, the standard uncertainty of μSMU is determined as
From these calculations, we get the fi nal result of the analysis of the SMU measurement:
-
μSMU = 0.25051 g, the SMU (best) estimate of the measurand μ;
-
uSMU = 0.00010 g, the standard uncertainty of the result, set as the maximum of the calculated value [u(ΔmSZ)2 + + u(ΔmIS)2]1/2 = 0.000047 and the used minimum threshold value 0.00010;
-
USMU = 2uSMU = 2·10–4 g, the expanded uncertainty;
-
CISMU = [μSMU – USMU, μSMU + USMU] = [0.25031, 0.25071], the SMU approximate 95% coverage interval of values that could be attributed to the mass μ.
4. Alternative approaches for uncertainty analysis. In this section we present alternative approaches for uncertainty analysis based on the GUM uncertainty framework according to [3], the Monte Carlo method according to [4, 5], and the characteristic functions approach according to [6, 7]. For more details, see also [8].
The measurement model for the full syringe mass measurements (the realizations are given in Table 1) is expressed by the following measurement equations
and the measurement model for the reference syringe mass measurement is expressed by the following measurement equations:
Analogously, the measurement model of the empty syringe mass measurements (the realizations are given in Table 2) is expressed by the following measurement equations
and the measurement model for the reference syringe mass measurement is expressed by the following measurement equations
where μF, μE, μR are the true unknown masses of the full, empty, and reference syringe, respectively; \( {X}_{SZ}^{(i)},{X}_{SR}^{(i)},{X}_{IS}^{(i)},\kern0.5em \mathrm{and}\kern0.5em {X}_{IS R}^{(i)} \) are independent random variables representing our knowledge of the measurement errors, with known Gaussian distributions with zero-means and known (given) common standard uncertainty uX, i.e.,
\( {\Delta}_{dig, SZ}^{(i)},{\Delta}_{dig, SR}^{(i)},{\Delta}_{dig, IS}^{(i)},\kern0.5em \mathrm{and}\kern0.5em {\Delta}_{dig, IS R}^{(i)} \) are known applied corrections caused by the last digit changes, obtained from type B evaluations, with rectangular distribution on the interval (–0.00001, 0.00001), i.e.,
with equal standard uncertainties
\( {\Delta}_{EX, SZ}^{(i)},{\Delta}_{EX, SR}^{(i)},{\Delta}_{EX, IS}^{(i)},\kern0.5em \mathrm{and}\kern0.5em {\Delta}_{EX, IS R}^{(i)} \)are known applied corrections of eccentricity, obtained from type B evaluations, all having the same rectangular distribution, R(–0.000004\( \sqrt{3} \), 0.000004\( \sqrt{3} \)), with the same standard uncertainty uΔEX = 0.000004; \( {\Delta}_{H, SZ}^{(i)}\kern0.5em \mathrm{and}\kern0.5em {\Delta}_{H, IS}^{(i)} \) are the uncertainty contributions due to the hygroscopy of ethanol left in the syringe needle; this contribution is obtained from type B evaluations, with the rectangular distribution R(–0.0000002, 0.0000002) and the same standard uncertainty
uΔH = 0.0000002/\( \sqrt{3} \); \( {\Delta}_{T, IS}^{(i)} \) and \( {\Delta}_{E, IS}^{(i)} \) are the uncertainty contributions due to the evaporation of ethanol left in the syringe needle; this contribution is obtained from type B evaluations, with the same rectangular distribution R(–0.00004, 0.00004) and the equal standard uncertainty \( {u}_{\Delta_E}=0.00001/\sqrt{3};{\Delta}_{GC} \)
is the uncertainty contribution due to the increased temperature of the needle after emptying the syringe; this contribution is obtained from type B evaluations, having rectangular distribution R(–0.00001, 0.00001) and the standard uncertainty \( {u}_{\Delta_T}=0.00001/\sqrt{3};{\Delta}_{GC} \) is correction due to gauge calibration with known distribution obtained from type B evaluations (not specified here as it will be canceled out during the subsequent calculations); ΔB,SZ, ΔB,SR, ΔB,IS, and ΔB,SZR are corrections to buoyancy with known distributions obtained from type B evaluations (not specified here as they will be canceled out during the subsequent calculations).
All considered distributions are assumed to be mutually independent.
Now, let us denote
and further, let us denote the realizations of
by
Based on type A and type B evaluations, the squared standard uncertainty \( {u}_X^2 \)of the measurement errors is determined as
Further, we shall use the following notation:
Here we also consider that ΔB, SZ = ΔB, SR = ΔB, IS = ΔB, ISR.
Further, let us denote by μ the true (unknown) amount of liquid ethanol added into the cylinder. Here μ = (μF – μR) –– (μE – μR) = μF – μE. Based on that, we shall consider the following measurement equation:
where
Hence, based on this measurement equation and the observed value \( \overline{m} \)of \( \overline{M} \), we can specify the state-of-knowledge distribution about the possible values that can be attributed to the mass μ. It is given by the distribution of the random variable\( \tilde{\upmu} \), which is specified by
The best estimate of μ is given as the expectation of \( \tilde{\upmu} \), which is m, the realization (observed value) of \( \overline{M} \), i.e.,
with its standard uncertainty specified by
where
4.1. Solution based on the GUM uncertainty framework. By using the SMU measurements and the above measurement model and method for calculation of \( \tilde{\upmu} \) and uμ, we directly get the following result of the uncertainty analysis, based on the GUM uncertainty framework (GUF):
-
μGUF = E(\( \tilde{\upmu} \)) = 0.250508 g, the best estimate of the mass μ,
-
uGUF = u(\( \tilde{\upmu} \)) = 7.1·10–5 g, the associated measurement uncertainty,
-
UGUF = 2uGUF = 1.4·10–4 g, the expanded uncertainty,
-
CIGUF = [μGUF – UGUF, μGUF + UGUF] = [0.250367, 0.250649], the GUF approximate 95%-coverage interval of values that could be attributed to the mass μ.
4.2. Solution based on the Monte Carlo method. In general, the explicit expression for the state-of-knowledge distribution about the mass μ is difficult to derive. However, this distribution can be reasonably well approximated by numerical computer intensive methods, e.g., by using the approach based on the Monte Carlo method as proposed in GUM Supplements 1 and 2 (see [4, 5]).
The MCM approach is based on a simple concept and the required algorithms are relatively easy to implement with the standard computer programming environments for technical computing as MATLAB or R. However, when the state-of knowledge distribution is required to be evaluated with high precision the required computational burden can be substantial.
Based on the above measurement model with the specified state-of-knowledge distributions we have generated N = 106 independent realizations of the random variable \( \tilde{\upmu} \). From that, we get the following results of the uncertainty analysis based on the Monte Carlo Method (MCM):
-
μMCM = 0.250508 g, the best estimate of the mass μ,
-
uMCM = 7.1·10–5 g, the associated measurement uncertainty,
-
UMCM = 2uMCM = 1.4·10–4 g, the expanded uncertainty,
-
CIMCM = [\( \tilde{\upmu} \)MCM,0.025, \( \tilde{\upmu} \)MCM,0.975] = [0.250369, 0.250647], the MCM 95%-coverage interval of values that could be attributed to the mass μ.
4.3. Solution based on using the characteristic function approach. Based on the above measurement model with the specified state-of-knowledge distributions, we have calculated the state-of-knowledge distribution of the random variable \( \tilde{\upmu} \) by numerical inversion of its characteristic function, which is fully known based on the given measurement model and the specified state-of-knowledge distributions of the input variables. From that we get the following results of the uncertainty analysis based on the characteristic function approach (CFA):
-
μCFA = 0.250508 g, the best estimate of the mass μ,
-
uCFA = 7.1·10–5 g, the associated measurement uncertainty,
-
UCFA = 2uCFA = 1.4·10–4 g, the expanded uncertainty,
-
CICFA = [\( \tilde{\upmu} \)CFA,0.025, \( \tilde{\upmu} \)CFA,0.975] = [0.250369, 0.250647], the CFA 95%-coverage interval of values that could be attributed to the mass μ.
The MATLAB code used for computing the 95%-coverage intervals based on the CFA approach is available from the authors. A general purpose software package with MATLAB algorithms for computing the selected characteristic functions and their numerical inversion to the associated distribution functions is freely available, see [7].
4.4. Discussion of the results obtained by the alternative methods. All methods presented in this section, i.e., GUF, MCM, and CFA, give consistent results. The best estimate of the considered measurand, i.e., the mass μ, was equally evaluated as μ = 0.250508 g for each of the considered methods. Small numerical differences in the calculated standard uncertainties (not visible on the presented significant digits) are due to variability caused by simulations (in MCM) and/or the used implementation of the numerical differentiation method (in CFA the uncertainty was numerically evaluated from the used characteristic function by numerical differentiation).
The true coverage probability of the GUF coverage interval is 95.45% (slightly above 95%). This exact probability was calculated by using the characteristic function approach (CFA).
5. Conclusions. The approach for the evaluation of uncertainty used at the SMU presents a simple classical way of uncertainty evaluation, currently used in laboratory practice. This approach is based on the estimation of uncertainty components based on laboratory experience. In practice, a higher value of the uncertainty component is taken into account in order to cover all possible circumstances. The results obtained by evaluation at the SMU give higher values of uncertainties than the uncertainties evaluated by using the other presented methods (GUF, MCM, and CFA). These methods are based on detailed measurement model and uncertainty budget, and in comparison with the SMU approach are much more complex, but allow one to reduce the reported uncertainty, and hence should be used if necessary.
References
ISO 6142:2001, Gas Analysis – Preparation of Calibration Gas Mixtures – Gravimetric Method.
A. Alink and A. M. H. Van der Veen, “Uncertainty calculations for the preparation of primary gas mixtures. Part 1: Gravimetry,” Metrologia, 37, No. 6, 641–650 (2000).
JCGM 100:2008, Guide to the Expression of Uncertainty in Measurement (GUM).
JCGM 101:2008, Evaluation of Measurement Data – Suplement 1 to the Guide to the Expression of Uncertainty in Measurement – Propagation of Probability Distributions Using a Monte Carlo Method.
JCGM 102:2011, Evaluation of Measurement Data – Supplement 2 to the Guide to the Expression of Uncertainty in Measurement – Extension to Any Number of Output Quantities, Joint Committee for Guides in Metrology (ISO, BIPM, IEC, IFCC, ILAC, IUPAC, IUPAP and OIML) (2011).
V. Witkovský, “Numerical inversion of a characteristic function: An alternative tool to form the probability distribution of output quantity in linear measurement models,” Acta IMEKO, 5, No. 3, 32–44 (2016).
V. Witkovský, CharFunTool: The Characteristic Functions Toolbox (MATLAB) (2018), https://github.com/witkovsky/CharFunTool/.
V. Witkovský, G. Wimmer, Z. Ďurišová, et al., “Brief overview of methods for measurement uncertainty analysis: GUM uncertainty framework, Monte Carlo method, characteristic function approach,” in: Measurement 2017: 11th Int. Conf. on Measurement, IEEE, pp. 35–38.
Acknowledgment
The research was supported by the Slovak Research and Development Agency, projects APVV-15-0164 and APVV-15-0295, and by the Scientific Grant Agency VEGA of the Ministry of Education of the Slovak Republic and the Slovak Academy of Sciences, by the projects VEGA 2/0054/18, 1/0098/18, 1/0556/18, 1/0610/17 and 2/0011/16, and the agency KEGA projects 039STU-4/2017 and 006STU-4/2018.
Author information
Authors and Affiliations
Corresponding author
Additional information
Russian translation published in Izmeritel’naya Tekhnika, No. 4, pp. 14–18, April, 2019.
Rights and permissions
About this article
Cite this article
Ďuriš, S., Ďurišová, Z., Palenčár, J. et al. Alternative Methods for Determination of Certified Value and its Uncertainty: Case Study of Using the Gravimetric Method for Preparation of Gaseous Primary Reference Material of Ethanol in Nitrogen at the Slovak Institute of Metrology. Meas Tech 62, 312–318 (2019). https://doi.org/10.1007/s11018-019-01623-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11018-019-01623-z