Triadic Formal Concept Analysis and triclustering: searching for optimal patterns

Abstract

This paper presents several definitions of “optimal patterns” in triadic data and results of experimental comparison of five triclustering algorithms on real-world and synthetic datasets. The evaluation is carried over such criteria as resource efficiency, noise tolerance and quality scores involving cardinality, density, coverage, and diversity of the patterns. An ideal triadic pattern is a totally dense maximal cuboid (formal triconcept). Relaxations of this notion under consideration are: OAC-triclusters; triclusters optimal with respect to the least-square criterion; and graph partitions obtained by using spectral clustering. We show that searching for an optimal tricluster cover is an NP-complete problem, whereas determining the number of such covers is #P-complete. Our extensive computational experiments lead us to a clear strategy for choosing a solution at a given dataset guided by the principle of Pareto-optimality according to the proposed criteria.

1 Introduction and related work

Clustering is an activity for finding homogeneous chunks in data. In machine learning, clustering represents an important branch related to what is referred to as unsupervised learning. The most popular idea of cluster relates to instances in a feature space. A cluster in this space is of a subset of data points that are relatively close to each other and relatively far from other data points. Feature space clustering algorithms are a popular tool in marketing research, bioinformatics, banking, image analysis, web mining, etc. With the growing popularity of more recent data sources such as biomolecular techniques and Internet, other than instance-to-feature data structures attract attention of researchers. Among these data structures is data matrix in which all the entries refer to values measured in the same scale. One example is gene expression data, entries of which show levels of gene material captured in a polymerase reaction. Another example would be relational data to express presence–absence of a relation among several itemsets such as:

• Bibsonomy data from bibsonomy.org (Benz et al. 2010) capturing a ternary relation among three sets: (i) users, (ii) bookmarks, (iii) tags (topics);

• Movies database IMDb (www.imdb.com) capturing, say, a binary relation of “relevance” between a set of movies and a set keywords or a ternary relation between sets of movies, keywords and celebrities;

• job banks comprising at least four itemsets (jobs, job descriptions, job seekers, seeker skills).

Although the concept of a feature space cluster remains much relevant to such same-scale data, other cluster approaches gain popularity too. Among the latter is the concept of bicluster in a data matrix representing a relation between two itemsets (Mirkin 1996, p. 296). Rather than a single subset of entities, a bicluster comprises two subsets of different itemsets. To pick these subsets up, no concept of distance applies, but rather the data submatrix corresponding to them is taken into account. Generically, the larger the values in the submatrix, the better interconnection between the subsets, the more relevant is the corresponding bicluster. At the relational data presence–absence data represented by binary 1/0 values this criterion amounts to the proportion of unities in the submatrix, its “density”: the larger, the better. Therefore, a bicluster is an ultimate expression of the interconnection at the presence–absence data where the density is 1, that is, all the within-submatrix entries in a bicluster are unities. A bicluster of the density 1 is referred to as a formal concept if its constituent subsets cannot be increased without a drop in the density value, i.e. a maximal rectangle of 1s in the input matrix w.r.t. permutations of its rows and columns (Ganter and Wille 1999). This name relates to a specific interpretation of the itemsets: one is supposed to be a set of attributes, the other to be a set of objects; then subsets constituting a formal concept can be interpreted as the concept’s intent and extent, respectively. The intent is a set of attributes defining the concept, whereas the extent is the set of objects having all attributes from the set.

Obviously, biclusters form a set of clumps in the data so that further learning can be organized within them. The biclustering techniques and Formal Concept Analysis machinery are being developed independently in independent communities using different mathematical frameworks. Specifically, the mainstream in Formal Concept Analysis is based on order structures, lattices and semilattices (Ganter and Wille 1999; Poelmans et al. 2013a), whereas biclustering is based more on conventional optimization approaches and matrix algebra frameworks (Madeira and Oliveira 2004; Eren et al. 2013). Yet these different frameworks considerably overlap in applications. Among those: finding co-regulated genes over gene expression data (Madeira and Oliveira 2004; Besson et al. 2005; Barkow et al. 2006; Tarca et al. 2007; Hanczar and Nadif 2010; Kaytoue et al. 2011; Eren et al. 2013), prediction of biological activity of chemical compounds (Blinova et al. 2003; Kuznetsov and Samokhin 2005; DiMaggio et al. 2010; Asses et al. 2012), summarization and classification of texts (Dhillon 2001; Cimiano et al. 2005; Banerjee et al. 2007; Ignatov and Kuznetsov 2009; Carpineto et al. 2009), structuring websearch results and browsing navigation in Information Retrieval (Carpineto and Romano 2005; Koester 2006; Eklund et al. 2012; Poelmans et al. 2012), finding communities in two-mode networks in Social Network Analysis (Duquenne 1996; Freeman 1996; Latapy et al. 2008; Roth et al. 2008; Gnatyshak et al. 2012) and Recommender Systems (Boucher-Ryan and Bridge 2006; Symeonidis et al. 2008; Ignatov and Kuznetsov 2008; Nanopoulos et al. 2010; Ignatov et al. 2014).

It is worth noting that Formal Concept Analysis helped to algebraically rethink several models and methods in Machine Learning such as version spaces (Ganter and Kuznetsov 2003), learning from positive and negative examples (Blinova et al. 2003; Kuznetsov 2004), and decision trees (Kuznetsov 2004). It was also shown that concept lattice is a perfect search space for learning globally optimal decision trees (Belohlávek et al. 2009). However, since early 90s both supervised and unsupervised machine learning techniques and application based on Formal Concept Analysis were introduced in the machine learning community. For example in Carpineto and Romano (1993), Carpineto and Romano (1996) there were reported results on the concept lattice based clustering in GALOIS system that suited for information retrieval via browsing. Fu et al. (2004) performed a comparison of seven FCA-based classification algorithms. Rudolph (2007) and Tsopzé et al. (2007) propose independently to use FCA to design a neural network architecture. In Outrata (2010), Belohlávek et al. (2014) FCA was used as a data preprocessing technique to transform the attribute space to improve the results of decision tree induction. Visani et al. (2011) proposed Navigala, a navigation-based approach for supervised classification, and applied it to noisy symbol recognition. Lattice-based approaches were also successfully used for finding frequent (closed) itemsets (Pasquier et al. 1999; Kuznetsov and Obiedkov 2002; Zaki and Hsiao 2005) as well as on data with complex descriptions such as graphs or trees for classification (Kuznetsov and Samokhin 2005; Zaki and Aggarwal 2006) and sequential pattern mining (Zaki 2001; Buzmakov et al. 2013). Recent survey on theoretical advances and applications of FCA can be found in (Poelmans et al. 2013a, b).

In some applications the structure of the phenomenon under consideration can be represented only in part or represented improperly when using relations between two aspects only. For example, according to Mirkin and Kramarenko (2011) biclusters found at a dataset relating most popular movies and keywords according to Movies database are rather trivial; adding one more aspect, genre, makes the obtained clumps more sensible, see, for example, bicluster and tricluster containing movie “Twelve Angry Men” from (Mirkin and Kramarenko 2011) Table 1.

Table 1 Bicluster and tricluster from Mirkin and Kramarenko (2011)

Therefore, it can be useful to extend the concepts and techniques for bicluster and Formal Concept Analysis to data of relation among more than two datasets. A few attempts in this direction have been published in the literature. For example, Zhao and Zaki (2005) proposed Tricluster algorithm for mining biclusters extended by time dimension to real-valued gene expression data. A triclustering method was designed in Li and Tuck (2009) to mine gene expression data using black-box functions and parameters coming from the domain. In the Formal Concept Analysis framework, theoretic papers (Wille 1995; Lehmann and Wille 1995) introduced the so-called Triadic Formal Concept Analysis. In Krolak-Schwerdt et al. (1994), triadic formal concepts apply to analyze small datasets in a psychological domain. Paper (Jäschke et al. 2006) proposed rather scalable method for mining frequent triconcepts in Folksonomies. Simultaneously, a less efficient method on mining closed cubes in ternary relations was proposed by Ji et al. (2006). There are several recent efficient algorithms for mining closed ternary sets (triconcepts) and even more general algorithms than Trias. Thus, Data-Peeler (Cerf et al. 2009) is able to mine $n$-ary formal concepts and its descendant mines fault-tolerant $n$-sets (Cerf et al. 2013); the latter was compared with DCE algorithm for fault-tolerant $n$-sets mining from Georgii et al. (2011). The paper (Spyropoulou et al. 2014) generalises $n$-ary formal concept mining to multi-relational setting in databases.

The goal of this paper is to investigate the extensions of the concepts of bicluster and formal concept to the case of data representing a yes/no relation among three, rather than two, sets of entities. Specifically, in this paper we consider the case of data on yes/no relation among three sets of entities and the concepts of tricluster and formal triconcept. This allows us to bring forward both lattice-based and linear algebraic approaches, Formal Concept Analysis using lattices of closed sets (see Ganter and Wille 1999; Lehmann and Wille 1995; Jäschke et al. 2006) and density/approximation based methods from linear algebra (see Mirkin and Kramarenko 2011). The formal triconcepts refer to such subsets of each of the three sets of entities that all the within-triples are in “yes” relation, whereas the algebraic methods allow some of the triples be not related. Each of the approaches has its advantages and disadvantages, but they have never been compared experimentally.

We describe a set of triclustering techniques proposed by members of the team in different projects within Formal Concept Analysis and/or bicluster analysis perspectives (OAC-box (Ignatov et al. 2011), Tribox (Mirkin and Kramarenko 2011), SpecTric (Ignatov et al. 2013) and a novel OAC-prime algorithm. This novel algorithm, OAC-prime, overcomes computational and substantive drawbacks of the earlier formal-concept-like algorithms. In our description, we take steps to relate the formal triconcepts to the known problem of covering a graph, which allows us to prove several intractability statements for them; we also estimate the complexity of each of the algorithms under comparison. In our spectral approach (SpecTric algorithm) we rely on an extension of the well-known reformulation of a bipartite graph partitioning problem to the spectral partitioning of a graph (see, e.g. Dhillon 2001). Some authors also made attempts to extend this approach to the case of tripartite graphs (Gao et al. 2005; Liu et al. 2010; Nanopoulos et al. 2009), but not to triadic hypergraphs, so our approach bridges the gap. Then we proceed to experimental comparison of the triclustering algorithms, including the Triadic Formal Concept Analysis Trias algorithm. In this, we propose new developments in the following components of the experiment setting:

• 1. Evaluation criteria In our study we use the following six criteria: the average density, the coverage, the diversity and the number of triclusters, and the computation time and noise tolerance for the algorithms.

• 2. Benchmark datasets We use triadic datasets from publicly available internet data as well as synthetic datasets with various noise models.

A similar experimental comparison was conducted in Gnatyshak et al. (2013), yet on a much smaller scale of the experiments. Mathematical properties of the algorithms, the investigation of the optimization problem for the search of optimal patterns, NP- and #P-completeness results, and pairwise criteria graphs are reported in the current paper for the first time as well.

The remainder is organised as follows. In Sect. 2 we give main definitions of Formal Concept Analysis and describe Trias algorithm for triadic concept generation. Section 3 introduces the notion of OAC tricluster, as a relaxation of the triadic formal concept, and presents two associated OAC-triclustering methods OAC-box and OAC-prime. Section 4 introduces the notion of box tricluster based on the conventional least-squares criterion and describes the TriBox approach. In Sect. 5 we present SpecTric triclustering approach based on the adaptation of spectral clustering to the triadic setting. Section 6 describes the evaluation criteria for tricluster collections and comparison of the algorithms. It also contains results on the complexity of a related problem, the optimal tricluster cover search. Section 7 describes the datasets selected or generated for our experiments. Section 8 presents the results obtained in the experimentation section and their discussion. The last section concludes the paper and indicates some further research directions.

2 Triadic Formal Concept Analysis and TRIAS method

2.1 Binary and n-ary contexts

First, we recall some basic notions from Formal Concept Analysis (FCA) Ganter and Wille (1999). Let $G$ and $M$ be sets, called the set of objects and attributes, respectively, and let $I$ be a relation $I\subseteq G\times M$: for $g\in G, \ m\in M$, $gIm$ holds iff the object $g$ has the attribute $m$. The triple $\mathbb {K}=(G,M,I)$ is called a (formal) context.

A triadic context $\mathbb {K}=(G,M,B,Y)$ consists of sets $G$ (objects), $M$ (attributes), and $B$ (conditions), and ternary relation $Y\subseteq G \times M \times B$ (Lehmann and Wille 1995). An incidence $(g, m, b) \in Y$ shows that object $g$ has attribute $m$ under condition $b$.

An $n$ -adic context is an $(n + 1)$-tuple $\mathbb {K}= (X_1,X_2, \ldots ,X_n, Y)$, where $Y$ is an $n$-ary relation between sets $X_1, \ldots , X_n$ (Voutsadakis 2002).

2.2 Concept forming operators and formal concepts

If $A\subseteq G$, $B\subseteq M$ are arbitrary subsets, then the Galois connection between $(2^{G},\subseteq )$ and $(2^{M},\subseteq )$ is given by the following derivation (prime) operators:

$$\begin{aligned} \begin{array}{c} A' = \left\{ m\in M\mid gIm \ \mathrm{for\ all}\ g\in A\right\} , \\ B' = \left\{ g\in G\mid gIm \ \mathrm{for\ all}\ m\in B\right\} . \end{array} \end{aligned}$$

(1)

If we have several contexts, the derivative operator of a context $(G, M, I)$ is denoted by $(.)^I$.

The pair $(A,B)$, where $A\subseteq G$, $B\subseteq M$, $A' = B$, and $B' = A$ is called a (formal) concept (of the context $K$ ) with extent $A$ and intent $B$ (in this case we have also $A'' = A$ and $B'' = B$).

The concepts, ordered by $(A_1,B_1)\ge (A_2,B_2) \iff A_1\supseteq A_2$ form a complete lattice, called the concept lattice $\underline{{\mathfrak B}}(G,M,I)$.

2.3 Formal concepts in triadic and in n-ary contexts

For convenience, a triadic context is denoted by $(X_1,X_2,X_3,Y)$. A triadic context $\mathbb {K}=(X_1,X_2,X_3,Y)$ gives rise to the following diadic contexts

$\mathbb {K}^{(1)}=(X_1, X_2\times X_3, Y^{(1)})$, $\mathbb {K}^{(2)}=(X_2, X_1\times X_3, Y^{(2)})$, $\mathbb {K}^{(3)}=(X_3, X_1\times X_2, Y^{(3)})$,

where $gY^{(1)}(m,b):\Leftrightarrow mY^{(2)}(g,b):\Leftrightarrow bY^{(3)}(g,m):\Leftrightarrow (g,m,b) \in Y$. The derivation operators (primes or concept-forming operators) induced by $\mathbb {K}^{(i)}$ are denoted by $(.)^{(i)}$. For each induced dyadic context we have two kinds of such derivation operators. That is, for $\{i,j,k\}=\{1,2,3\}$ with $j<k$ and for $Z \subseteq X_i$ and $W \subseteq X_j\times X_k$, the $(i)$-derivation operators are defined by:

$$\begin{aligned} Z \mapsto Z^{(i)}= & {} \left\{ (x_j,x_k) \in X_j\times X_k| x_i, x_j, x_k \text{ are } \text{ related } \text{ by } \text{ Y } \text{ for } \text{ all } x_i \in Z\right\} ,\\ W \mapsto W^{(i)}= & {} \left\{ x_i \in X_i| x_i, x_j, x_k \text{ are } \text{ related } \text{ by } \text{ Y } \text{ for } \text{ all } (x_j,x_k) \in W\right\} . \end{aligned}$$

Formally, a triadic concept of a triadic context $\mathbb {K}=(X_1,X_2,X_3,Y)$ is a triple $(A_1,A_2,A_3)$ of $A_1 \subseteq X_1, A_2 \subseteq X_2, A_3 \subseteq X_3$, such that for every $\{i,j,k\}=\{1,2,3\}$ with $j<k$ we have $(A_j \times A_k)^{(i)}=A_i$. For a certain triadic concept $(A_1,A_2,A_3)$, the components $A_1$, $A_2$, and $A_3$ are called the extent, the intent, and the modus of $(A_1,A_2,A_3)$. It is important to note that for interpretation of $\mathbb {K}=(X_1,X_2,X_3,Y)$ as a three-dimensional cross table, according to our definition, under suitable permutations of rows, columns, and layers of the cross table, the triadic concept $(A_1,A_2,A_3)$ is interpreted as a maximal cuboid full of crosses. The set of all triadic concepts of $\mathbb {K}=(X_1,X_2,X_3,Y)$ is called the concept trilattice and is denoted by $\mathfrak {T}(X_1,X_2,X_3,Y)$. However, the concept trilattice does not form partial order by extent inclusion since it is possible for the same triconcept extent to have different combinations of intent and modus components (Wille 1995; Lehmann and Wille 1995).

One may introduce $n$-adic formal concepts without $n$-ary concept forming operators. The $n$-adic concepts of an $n$-adic context $(X_1, \ldots ,X_n, Y)$ are exactly the maximal $n$-tuples $(A_1, \ldots , A_n)$ in $2^{X_1} \times \cdots \times 2^{X_n}$ with $A_1 \times \cdots \times A_n \subseteq Y$ with respect to component-wise set inclusion (Voutsadakis 2002). The notion of $n$-adic concept lattice can be introduced in the similar way to the triadic case (Voutsadakis 2002).

2.4 NextClosure algorithm extended

Trias (Jäschke et al. 2006) is a method for finding (frequent) triadic formal concepts, that are closed 3-sets. Since we consider triadic formal concepts as starting point of our search of optimal tripatterns and absolutely dense triclusters, this method was added to the study.

Formally, Trias solves the following problem:

Problem 1

(Mining all frequent tri-concepts) Let $\mathbb {K}=(G, M,B, I )$ be a triadic context, and let $g$-minsup, $m$-minsup, $b$-minsup $\in [0, 1]$. The task of mining all frequent tri-concepts consists in determining all triconcepts $(X,Y,Z)$ of $\mathbb {K}$ with $|X| \le \tau _G$, $|Y| \le \tau _M$, and $|Z| \le \tau _B$, where $\tau _G = |G| \cdot g$-minsup, $\tau _M= |M| \cdot m$-minsup, and $\tau _B = |B| \cdot b$-minsup.

Trias is based on the NextClosure algorithm (Ganter 1987; Ganter and Wille 1999) that enumerates all formal concepts of the dyadic context in lectic order, the lexicographic order on bit vectors describing subsets of objects (attributes, respectively).

In Trias this approach is extended to the triadic case and minimal support constraints are added (triclusters with too small extent, intent or modus are skipped).

The Trias algorithm was designed to mine so-called folksonomies (Vander Wal 2007) in resource sharing systems, e.g. in social bookmarking systems like delicious and bibsonomy.

Formally, a folksonomy is a tricontext $\mathbb {F}=(U,T,R,H)$, $U \times T \times R \subseteq H$, where $U$ is a set of users, $T$ is a set of tags, and $R$ is a set of resources. A triple $(u,t,r) \in H$ means that the user $u$ assigned the tag $t$ to the resource $r$.

Trias has a precursor, Tripat algorithm (Krolak-Schwerdt et al. 1994), for analysing triadic data from psychological studies.

The pseudo-code for the TRIAS algorithm with some fixed inconsistencies is provided (Algorithm 1) below.

The Trias algorithm uses two other functions FirstFreqCon and NextFreqCon as subroutines. First it composes the new binary relation $\tilde{I}:=\{(g,(m,b)){\,|\,}(g,m,b)\in I\}$ (line 2) and then finds the first frequent concept in the corresponding formal context $(G,M\times B,\tilde{I})$ (line 3) w.r.t. lectic order on concept extents and minimal support $\tau _G$.

As the NextClosure algorithm the procedure NextFreqCon requires a total order on elements of the set of objects (or attributes), $G$ (or $M$). We then consider $G$ as a subset of natural numbers and the lectic order on sets forms a total order on it (equivalent to the lexicographic order of bit vectors representing those sets). To find the next concept we define for $A \subseteq G$ and $i \in G$ the set $A \oplus i = (A \cap \{1, \ldots , i1\}) \cup \{i\})$. By applying the closure operator $(\cdot )^{\prime \prime }$ to $A \oplus i$ the NextFreqCon computes for a given $A$ the set $C = (A \oplus i)^{\prime \prime }$. This set $C$ is the lectically next extent, in case $A <_{i} C$ holds, that is $i$ is the smallest element in which $A$ and $C$ differ, and $i \in C$. The only difference between original NextClosure and NextFreqCon is that of the latter additionally checks whether the computed extent $C$ fullfills the minimal support criterion.

The wrapper function FirstFreqCon tries to find the first frequent concept of $(G,M\times B,\tilde{I})$ as $(\emptyset ^{\prime \prime },\emptyset ^{\prime })$ and if it is not succeeded, it passes the infrequent concept $(\emptyset ^{\prime \prime },\emptyset ^{\prime })$ to NextFreqCon to check the next lectic one. If NextFreqCon returns the frequent concept $(X,J)$ of the context $(G,M\times B,\tilde{I})$ (line 3), then Trias extracts the new context $(M,B,J)$ (line 6) and search frequent concepts in it with the corresponding minimal support thresholds $\tau _M$ and $\tau _B$. In case of passing all the check the triple $((Y\times Z)^{\tilde{I}}),Y,Z)$ is the frequent triconcept of $(G,M,B,I)$ (line 10).

The main advantages of the Trias algorithm are as follows: It does not generate the same triconcept more than once and it uses the main memory space almost only for the input data storage.

Let us discuss the time complexity of the Trias algorithm. The function $NextFreqCon$ $((X,J),(G,M\times B,\tilde{I}),\tau _G=0)$ produces the set of all concepts of $\mathbb {K}_{\tilde{I}}$ in time $O(|G|^2|M||B||L_{\tilde{I}}|)$ with polynomial delay $O(|G|^2|M|)$ and $NextFreqCon((Y,Z),$ $(M,B,J),\tau _M=0)$ produces the set of all concepts of $\mathbb {K}_{J}$ in time $O(|M|^2|B||L_{J}|)$ with polynomial delay $O(|M|^2|B|)$, where $L_{\tilde{I}}$ and $L_{J}$ are the sets of all concepts of corresponding contexts $\mathbb {K}_{\tilde{I}}$ and $\mathbb {K}_{J}$ respectively. These worst-case bounds are based on those of NextClosure algorithm reported in Kuznetsov and Obiedkov (2002). Note that the upper bound values of $L_{\tilde{I}}$ and $L_{J}$ are $2^{\min \{|G|,|M||B|\}}$ and $2^{\min \{|M|,|B|\}}$ for the case where each of these lattices is isomorphic to a Boolean lattice of the corresponding size. However this case is a rare one taking into account high sparsity of real datasets.

In paper (Biedermann 1998) the upper bound size of concept trilattice $\mathfrak {T}(X,X,X,Y_X)$ is provided when $Y_X= X\times X \times X \setminus (x,x,x)$, where $x \in X$: $|\mathfrak {T}|=3^{|X|}$. Hence, the worst-case upper bound for an arbitrary tricontext $\mathbb {K}=(G, M, B, I)$ is $|\mathfrak {T}|=3^{\min \{G,M,B\}}$.

3 Relaxed object-attribute-condition patterns: OAC triclusters

Guided by the idea of finding scalable and noise-tolerant triconcepts, we had a look at triclustering paradigm in general for a triadic binary data, i.e. for tricontexts as input datasets.

3.1 Ternary patterns and their density

Let $\mathbb {K}=(G,M,B,I)$ be a triadic context, where $G$, $M$, and $B$ are sets, and $I$ is a ternary relation: $I\subseteq G\times M\times B$.

Suppose $X$, $Y$, and $Z$ are some subsets of $G$, $M$, and $B$ respectively.

Definition 1

Suppose $\mathbb {K}=(G,M,B,I)$ is a triadic context and $Z \subseteq G$, $Y \subseteq M$, $Z \subseteq B$. A triple $T=(X,Y,Z)$ is called an OAC-tricluster. Traditionally, its components are called (tricluster) extent, (tricluster) intent, and (tricluster) modus, respectively.

The density of a tricluster $T=(X,Y,Z)$ is defined as the fraction of all triples of $I$ in $X\times Y\times Z$:

$$\begin{aligned} \rho (T):=\frac{|I\cap (X\times Y\times Z)|}{|X||Y||Z|} \end{aligned}$$

(2)

Definition 2

The tricluster $T$ is called dense iff its density is not less than some predefined threshold, i.e. $\rho (T)\ge \rho _{min}$.

The collection of all triclusters for a given tricontext $\mathbb {K}$ is denoted by $\mathcal {T}$.

Since we deal with all possible cuboids in Cartesian product $G\times M\times B$, it is evident that the number of all OAC-triclusters, $|\mathcal {T}|$, is equal to $2^{|G|\cdot |M|\cdot |B|}$. However not all of them are supposed to be dense, especially for real data which are often quite sparse. Below we discuss two possible OAC-tricluster definitions, which give us an efficient way to find within polynomial time a number of (dense) triclusters not greater than the number $|I|$ of triples in the initial data.

3.2 Bounding operator box

Here let us define the box operators and describe box OAC-triclustering. We use a slightly different introduction of the main TCA notions because of their further technical usage.

Derivation (prime) operators for a triple $(\widetilde{g},\widetilde{m},\widetilde{b})\in I$ from triadic context $\mathbb {K}$ can be defined as follows:

$$\begin{aligned}&\widetilde{g}^\prime :=\left\{ \,(m,b){\,|\,}(\widetilde{g},m,b)\in I\right\} \end{aligned}$$

(3)

$$\begin{aligned}&\widetilde{m}^\prime :=\left\{ \,(g,b){\,|\,}(g,\widetilde{m},b)\in I\right\} \end{aligned}$$

(4)

$$\begin{aligned}&\widetilde{b}^\prime :=\left\{ \,(g,m){\,|\,}(g,m,\widetilde{b})\in I\right\} \end{aligned}$$

(5)

$(\widetilde{g},\widetilde{m})^\prime$, $(\widetilde{g},\widetilde{b})^\prime$, $(\widetilde{m},\widetilde{b})^\prime$ prime operators can be defined the same way.

$$\begin{aligned}&(\widetilde{g},\widetilde{m})^\prime :=\left\{ \,b{\,|\,}(\widetilde{g},\widetilde{m},b)\in I\right\} \end{aligned}$$

(6)

$$\begin{aligned}&(\widetilde{g},\widetilde{b})^\prime :=\left\{ \,m{\,|\,}(\widetilde{g},m,\widetilde{b})\in I\right\} \end{aligned}$$

(7)

$$\begin{aligned}&(\widetilde{m},\widetilde{b})^\prime :=\left\{ \,g{\,|\,}(g,\widetilde{m},\widetilde{b})\in I\right\} \end{aligned}$$

(8)

Now for a triple $(\widetilde{g},\widetilde{m},\widetilde{b})\in I$ let us define box operator $\widetilde{g}^\square$ ($\widetilde{m}^\square$ and $\widetilde{b}^\square$ are introduced in the same way):

$$\begin{aligned}&\widetilde{g}^\square :=\left\{ \,g {\,|\,}\exists m(g,m)\in \widetilde{b}^\prime \vee \exists b(g,b)\in \widetilde{m}^\prime \right\} \end{aligned}$$

(9)

$$\begin{aligned}&\widetilde{m}^\square :=\left\{ \,m{\,|\,}\exists g(g,m)\in \widetilde{b}^\prime \vee \exists b(m,b)\in \widetilde{g}^\prime \right\} \end{aligned}$$

(10)

$$\begin{aligned}&\widetilde{b}^\square :=\left\{ \,b{\,|\,}\exists g(g,b)\in \widetilde{m}^\prime \vee \exists m(m,b)\in \widetilde{g}^\prime \right\} \end{aligned}$$

(11)

Definition 3

Suppose $\mathbb {K}=(G,M,B,I)$ is a triadic context. For a triple $(g,m,b)\in I$ a triple $T=(g^\square ,m^\square ,b^\square )$ is called a box operator based OAC-tricluster. Traditionally, its components are respectively called extent, intent, and modus.

Let us elaborate on the structure of box operator based triclusters. Consider the triple $(\widetilde{g},\widetilde{m},\widetilde{b})\in I$ from $\mathbb {K}=(G,M,B,I)$. Then object $\overline{g}$ will be added to $\widetilde{g}^\square$ iff $\{(\overline{g},\widetilde{m},b){\,|\,}b\in B\wedge (\overline{g},\widetilde{m},b)\in I\}\ne \emptyset \,\vee \,\{(\overline{g},m,\widetilde{b}){\,|\,}m\in M\wedge (\overline{g},m,\widetilde{b})\in I\}\ne \emptyset$. It is clear that this condition is equivalent to the one in Eq. (9), and can be easily illustrated (Fig. 1): if at least one of the elements from “grey” cells is an element of $I$, then $\overline{g}$ is added to $\widetilde{g}^\square$.

Fig. 1

$\overline{g}$ addition condition

The proposed OAC-tricluster definition has a useful property (see Proposition 1): for every triconcept in a given tricontext there exists a tricluster of the same tricontext containing the triconcept. It means that there is no information loss, since we keep all the triconcepts in the resulting tricluster collection.

Proposition 1

(Ignatov et al. 2013) Let $\mathbb {K}=(G,M,B,Y)$ be a triadic context and $\rho _{min}=0$. For every $T_c=(A_c,B_c,C_c) \in \mathfrak {T}(G,M,B,Y)$ there exists a box OAC-tricluster $T=(A,B,C) \in \mathbf {T}_{\square }(G,M,B,Y)$ such that $A_c \subseteq A,B_c \subseteq B, C_c \subseteq C$.

3.3 Prime operator applied to pairs

The second author of the paper proposed Prime OAC-triclustering which extends the biclustering method from Ignatov et al. (2012) to the triadic case. It uses prime operators (Eq. 6) to generate triclusters.

Definition 4

Suppose $\mathbb {K}=(G,M,B,I)$ is a triadic context. For a triple $(g,m,b)\in I$ a triple $T=\left( (m,b)^\prime ,(g,b)^\prime ,(g,m)^\prime \right)$ is called a prime operator based OAC-tricluster. Its components are called respectively extent, intent, and modus.

Prime based OAC-triclusters are more dense than box operator based ones. Their structure is illustrated in Fig. 2: every element corresponding to the “grey” cell is an element of $I$. Thus, prime operator based OAC-triclusters in a three-dimensional matrix form contain an absolutely dense cross-like structure.

Fig. 2

Prime operator based tricluster structure

A similar property holds for the prime based OAC-triclusters:

Proposition 2

Let $\mathbb {K}=(G,M,B,Y)$ be a triadic context and $\rho _{min}=0$. For every $T_c=(A_c,B_c,C_c) \in \mathfrak {T}(G,M,B,Y)$ there exists a prime OAC-tricluster $T=(A,B,C) \in \mathbf {T}_{\prime }(G,M,B,Y)$ such that $A_c \subseteq A,B_c \subseteq B, C_c \subseteq C$.

3.4 Tricluster generating algorithms

3.4.1 OAC-triclustering based on box operators

The idea of box OAC-triclustering is to enumerate all triples of the ternary relation $I$ for a context $\mathbb {K}$ generating a box operator based tricluster for each. If generated tricluster $T$ was not added to the set of all triclusters $\mathcal {T}_{\Box }$ on previous steps, then $T$ is added to $\mathcal {T}_{\Box }$. It is possible to implement hash functions for triclusters in order to significantly decrease computation time by simplifying the comparison of triclusters. A minimal density threshold can be used as well.

A pseudo-code for such an algorithm can be as follows (Algorithm 4):

Proposition 3

For a given formal context $\mathbb {K}=(G,M,B,I)$ and $\rho _{min}\ge 0$ the largest number of box OAC-triclusters is equal to $|I|$; all OAC-triclusters can be generated in time $O(|I|\cdot (|M||B|+|G||B|+|G||M|))$ if $\rho _{min}= 0$ or $O(|I||G||M||B|)$ if $\rho _{min}>0$.

Note that a post-processing step of elimination of duplicate triclusters would require an additional time $|I|log(|I|)$ to be added to the time estimates in the Proposition 3.

3.4.2 OAC-triclustering based on primes of pairs

A pseudo-code for the prime OAC-triclustering algorithm is provided (Algorithm 5).

To avoid duplicate tricluster generation we suggest the usage of hash functions.

A similar property can be proved.

Proposition 4

For a given formal context $\mathbb {K}=(G,M,B,I)$ and $\rho _{min}\ge 0$ the largest number of box OAC-triclusters is equal to $|I|$; all prime OAC-triclusters can be generated in time $O(|I|\cdot (|G|+|M|+|B|))$ if $\rho _{min}= 0$ or $O(|I||G||M||B|)$ if $\rho _{min}> 0$.

So, from the time complexity point of view the prime OAC-triclustering may have an advantage in comparison with the box OAC-triclustering at $\rho _{min}=0$.

4 Approximate triclusters: TriBox method

4.1 Individual tricluster approximation model

The TriBox method (Mirkin and Kramarenko 2011) implements an optimization approach for tricluster generation. Suppose $\mathbb {K}=(G,M,B,I)$ is a triadic context. The idea is to select some triple of $I$, take it for the initial tricluster, and then to modify its extent, intent, and modus so that they covered a significant part of the context while maintaining high density. TriBox aims at finding a set of triclusters $\mathcal {T}=\{T_t=(X_t,Y_t,Z_t)\}$ that maximize criterion 12.

The resulting triclusters compose locally optimal solution for the trade-off problem between the density $\rho$ and the volume of various possible triclusters.

$$\begin{aligned} f(T)=\rho (T)^2 |X||Y||Z| \end{aligned}$$

(12)

For convenience, triadic context $\mathbb {K}$ is represented as a third order boolean tensor $\mathbf {R}$ with components:

$$\begin{aligned} r_{gmb}= {\left\{ \begin{array}{ll} 1, &{} \text { if }(g,m,b)\in I;\\ 0, &{} \text { if } (g,m,b)\not \in I. \end{array}\right. } \end{aligned}$$

(13)

A set of triclusters $\mathcal {T}=\{T_t=(X_t,Y_t,Z_t)\}$ forms the following model of data:

$$\begin{aligned} r_{gmb}=\max _{t=1,\dots ,|\mathcal {T}|}\lambda _t [(g, m, b) \in X_t \times Y_t \times Z_t] + \lambda _0 + \varepsilon _{gmb} \end{aligned}$$

(14)

where:

• 1. $\lambda _t$ is a parameter (some measure for the tricluster $\mathcal {T}_t$)

• 2. $[(g, m, b) \in X_t \times Y_t \times Z_t]$ equals to $1$, if $(g, m, b) \in X_t \times Y_t \times Z_t$ is true, and to $0$ otherwise

• 3. $\lambda _0$ is a constant, $0 \le \lambda _{0} \le 1$, plays the role of an intercept in linear data models

• 4. $\varepsilon _{g,m,b}$ is a residual

This model 14 involves the operation of maximization rather than summation. To fit 14 with a relatively small number of boxes, assume $\lambda _{0}$ to be constant and specified before the fitting of the model. Then the model can be rewritten by putting $r_{gmb}^* = r_{gmb} - \lambda _{0}$ on the left, so that $\lambda _{0}$ becomes a similarity shift value rather than an intercept.

We apply here the one-by-one fitting strategy (Mirkin 1996) so that each box tricluster $(X_{t}, Y_{t}, Z_t)$ with $\lambda _{t}$ is found as the most deviant from the “middle”, that is, minimizing the residuals in a single cluster model (with a constant $\lambda _{0}$)

$$\begin{aligned} r_{gmb}^* = r_{gmb} - \lambda _{0} = \lambda [(g, m, b) \in T] + e_{gmb} \end{aligned}$$

(15)

4.2 Equivalent criterion and parameters

Let us initially assume $\lambda _{0}=0$ so that $r_{gmb}^* = r_{gmb}$. Box cluster $(X_{t}, Y_{t}, Z_{t})$ with $\lambda _{t}$, minimizing the least squares criterion

$$\begin{aligned} L^{2} = \sum \limits _{gmb} \left( r_{gmb}^* - \lambda \left[ (g, m, b) \in T\right] \right) ^{2} \end{aligned}$$

(16)

over real $\lambda$ and binary $[(g, m, b) \in T]$, must lead to optimal $\lambda$ being equal to the within-box average:

$$\begin{aligned} \lambda = \sum \limits _{g\in X, m\in Y,b \in Z} r_{gmb}^*/|X||Y||Z| \end{aligned}$$

(17)

which is the proportion of ones within the box minus $\lambda _{0}$, and, assuming that the $\lambda$ is optimal, criterion $L^{2}$ in (16) admits the following decomposition:

$$\begin{aligned} L^{2} = \sum \limits _{gmb}r_{gmb}^{*2} - \lambda ^{2}|X|Y||Z| \end{aligned}$$

(18)

thus implying the following criterion to maximize

$$\begin{aligned} g(X,Y,Z)= \lambda ^{2}|X||Y||Z| \end{aligned}$$

(19)

According to (18), this criterion expresses the contribution of the box $(X,Y,Z)$ to the data scatter $\Sigma _{gmb}r_{gmb}^{*2}$ which is useful to watch how closely the box follows the data. On the other hand, criterion (19) combines two contrasting criteria for a box to be optimal: (a) the largest area, (b) the largest proportion of within-box unities. If restricted to a within-box non-zero option, the criterion (19) would lead to the formal concepts of the largest sizes, $|X||Y||Z|$, as the only maximizers.

Its optimization will lead to $\lambda =\rho (T) - \lambda _0$ (density of $T$ minus $\lambda _0$). Therefore, $f(T)$ in criterion (12) is a particular case of $g(T)$ when $\lambda _0=0$.

4.3 Local optimization: TriBox method

Fitting model (14) can be done by applying algorithm TriBox starting from each of the triples and retaining only different and most contributing solutions. Let us remind that the contribution of a box bicluster is but the value of criterion (19).

The value of difference $D(e^{*})=g(X',Y,Z) - g(X,Y,Z)$, where $X'$ differs from $X$ by the state of just one entity $e^{*}\in G$ so that $e^{*}$ either belongs to $X'$ if $e^{*}\notin X$ or does not, if $e^{*}\in X$, is expressed with the formula

$$\begin{aligned} D(e^{*}) = \frac{\left[ r^{2}(e^{*},Y,Z)+2z_{e^{*}}r(X,Y,Z)r(e^{*},Y,Z) - z_{e^{*}}r^{2}(X,Y,Z)/|X|\right] }{\left( (|X|+~z_{e^{*}})|Y||Z|\right) } \end{aligned}$$

(20)

Here $z_{e^{*}}=1$, if $e^{*}$ is added to $X$ and $z_{e^{*}}=-1$ otherwise, $r(X,Y,Z)$ is the sum of all the entries in $\mathbf {R}^*$ over $(g,m,b)\in X\times Y\times Z$ (i.e. $r(X,Y,Z)=|I\cap X\times Y\times Z|$ in case $\lambda _0=0$), and $r(e^{*},Y,Z)$ is the sum of all the $r_{e^{*}mb}^*$ over $m\in Y$ and $b\in Z$. A symmetric expression holds for the changes in box $(X,Y,Z)$ over $e^{*}\in Y$ or $e^{*}\in Z$. This leads to the following tricluster finding algorithm.

The pseudo-code for TriBox algorithm is given in Algorithm 6.

At $\lambda _0=0$ the value of $\lambda$ can be interpreted as a box tricluster density. The resulting box tricluster is provably rather contrast:

Proposition 5

If box tricluster $(X,Y,Z)$ is found with the TriBox algorithm then, for any entity outside the box, its average density on the two counterpart entity sets from $\{X, Y, Z\}$, is less than the half of the within-box density $\lambda$; in contrast, for any entity belonging to the box, its average density on the counterpart entity sets is greater than or equal to the half of the within-box density $\lambda$.

Proposition 6

For a given formal context $\mathbb {K}=(G,M,B,I)$ and $\lambda _0=0$ the largest number of box triclusters found by TriBox is equal to $|I|$, all box triclusters can be generated in time $O(|I|\cdot ((|G|+|M|+|B|)^2|G||M||B|))$.

Once again, by using hash functions to avoid duplicate triclusters an additional time complexity item $O(|I|log|I|)$, for the last loop, should be added.

In comparison to Trias, and box and prime OAC-triclustering, Tribox is able to work with real-valued data without sufficient modifications (one only needs to change the initialization step at line 3).

5 Spectral approach extended to triclustering: SpecTric method

5.1 Adjacency matrix and Laplace transformation for the triadic hypergraph

Spectral triclustering method (Ignatov et al. 2013) is based on the spectral graph partition approach. The idea is to represent the given triadic context as a tripartite graph and then recursively divide it into partitions minimizing some objective function through the solution of a corresponding eigenvalue problem. To find an optimal partitioning spectral clustering uses the second smallest eigenvector of the Laplacian matrix (Fiedler 1973).

Let us elaborate on this technique. Suppose $\mathbb {K}=(G,M,B,I)$ is a triadic context. First we need to transform $\mathbb {K}$ into tripartite graph $\varGamma =\langle V,E\rangle$. Since $I$ is a ternary relation it is only possible to represent $\mathbb {K}$ as a tripartite hypergraph without the information loss. The following transformation technique is considered: $V:=G\sqcup M\sqcup B$, for each triple $(g,m,b)\in I$ edges $\{g,m\}$, $\{g,b\}$ and $\{m,b\}$ are added to $E$ to form an undirected non-weighted tripartite graph with the adjacency matrix $\mathbf {A}$.

As the result some additional triples will be added to $I$ after inverse transformation. However, these triples will be added only in “dense” areas of $I$ thus possibly filling missing values and “smoothing” tricontext for methods aiming at finding formal triconcepts. Thus this technique is acceptable for the problem.

We can rearrange the rows and columns of $\mathbf {A}$ first placing object vertices, then attribute and condition vertices:

$$\begin{aligned} \mathbf {A}= \begin{pmatrix} 0 &{}\quad \mathbf {E}_{GM} &{}\quad \mathbf {E}_{GB} \\ \mathbf {E}_{MG} &{}\quad 0 &{}\quad \mathbf {E}_{MB} \\ \mathbf {E}_{BG} &{}\quad \mathbf {E}_{BM} &{}\quad 0 \\ \end{pmatrix} \end{aligned}$$

(21)

After the transformation Laplacian matrix is built for $\varGamma$:

$$\begin{aligned} L_{ij} = {\left\{ \begin{array}{ll} degree(v_i), &{} \text { if }i=j \\ -1, &{} \text { if }i\not =j \text { and }\exists \text { edge }(v_i,v_j) \\ 0, &{} \text { otherwise } \end{array}\right. } \end{aligned}$$

(22)

where $v_i$ is the $i^{th}$ vertex of V.

For the triadic context $\mathbb {K}$ Laplacian matrix will have the following form:

$$\begin{aligned} \mathbf {L}= \begin{pmatrix} \mathbf {D}_G &{}\quad -\mathbf {E}_{GM} &{}\quad -\mathbf {E}_{GB} \\ -\mathbf {E}_{MG} &{}\quad \mathbf {D}_M &{}\quad -\mathbf {E}_{MB} \\ -\mathbf {E}_{BG} &{}\quad -\mathbf {E}_{BM} &{}\quad \mathbf {D}_B \\ \end{pmatrix} \end{aligned}$$

(23)

where $\mathbf {E}$ are the adjacency submatrices, $\mathbf {D}$ are diagonal matrices containing degrees of the corresponding vertices on the main diagonal.

The second minimal eigenvector of $L$ is an optimal solution to a relaxed version of the optimal partition problem for $\varGamma$ (finding the minimal set $\tilde{E}\subseteq E$ so that the graph $\tilde{\varGamma }=(V,E\setminus \tilde{E})$ is not connected). The sign of each component of this vector indicates one of the 2 new connected components. The solution vector $v$ is used to partition the graph by placing the nodes with greater than zero $v_i$ values into one partition and those with less than zero values into another.

In order to avoid partitioning of dangling vertices or small subgraphs the generalized eigenvalue problem must be considered (Shi and Malik 2000):

$$\begin{aligned} \mathbf {L} v=\lambda \mathbf {D} v \end{aligned}$$

(24)

where $\mathbf {D}$ is a diagonal matrix containing vertices’ degrees on the main diagonal.

Every partition can then be recursively split by solving a new eigenvalue problem for the corresponding submatrix.

Also, some minimum size constraint can be used to avoid too deep partitioning. Since spectral triclustering is not able to generate the same tricluster more than once, it is not necessary to use hash functions to avoid duplicates.

5.2 The spectral triclustering algorithm

The pseudo-code for SpecTric is provided (Algorithm 7).

The possible constraints below can be introduced to select triclusters of acceptable quality.

• 1. $C_{void}$ constraint: in the tricluster $T=(X,Y,Z)$ corresponding to $\mathbf {A}$ at least one of the parts, extent, intent or modus is empty

• 2. $C_{\lnot size}$ constraint: $Size(T) < s_{min}$, where $Size(X,Y,Z)=\frac{|X|+|Y|+|Z|}{|G|+|M|+|B|}$ or the other tricluster size-related measure.

The method recursively splits the input graph (matrix, context) into two parts, checks the constraints for both parts, if one of them is false, then the previous subgraph (submatrix, subcontext) is added as a tricluster to $\mathcal {T}$ and the corresponding branch is cancelled.

The standard matrix diagonalization methods require $O(|V|^3)$ operations, where $|V|$ is the number of nodes in the graph, and impractical for large datasets. However, we can take advantage of the sparsity of the graph using iterative methods (Lanczoc or Arnoldi algorithms Golub and van Loan 1989), especially since only one vector should be computed. The complexity of Lanczos type algorithm is only $O(k |E|)$, where $|E|$ is the number of edges in the graph and $k$ is the number of iterations required for the convergence (see Shi and Malik 2000; Golub and van Loan 1989). In practice, usually $k \ll \sqrt{|V|}$.

Taking this into account, the worst case complexity of the SpecTric algorithm vary from $O(k|E||V|)$ to $O(|E||V|^3)$, or in terms of formal tricontext entities, from $O(k|I|(|G|+|M|+|B|))$ to $O(|I|(|G|+|M|+|B|)^3)$, depending on eigenvalue problem solver and data sparsity. Since we deal with a recursive partition scheme, the number of generated triclusters cannot be greater than $|I|$, however, in the worst case, the number of cuts performed is $|I|-1$ since SpecTric cannot guarantee equally sized triclusters at each split.

6 Criteria for evaluation of triclusters

6.1 Criteria for cluster sets

To evaluate the quality of the whole tricluster collection obtained by a triclustering method, we propose using the following four criteria: the number of triclusters, average density, coverage and the diversity.

Cardinality and Density For a given tricluster collection $\mathcal {T}$ cardinality is trivially the number of its members $|\mathcal {T}|$. The average collection density is $\rho _{av}(\mathcal {T})=\frac{1}{|\mathcal {T}|}\sum \nolimits _{T\in \mathcal {T}}\rho {(T)}$.

Diversity is an important measure in Information Retrieval for diversified search results and in Machine Learning for ensemble construction (Tsymbal et al. 2005).

To define diversity we use a binary function that equals to 1 if the intersection of triclusters $\mathcal {T}_i$ and $\mathcal {T}_j$ is not empty, and 0 otherwise.

$$\begin{aligned} intersect(\mathcal {T}_i,\mathcal {T}_j)= \left[ G_{\mathcal {T}_i}\cap G_{\mathcal {T}_j}\not =\emptyset \wedge M_{\mathcal {T}_i}\cap M_{\mathcal {T}_j}\not =\emptyset \wedge B_{\mathcal {T}_i}\cap B_{\mathcal {T}_j}\not =\emptyset \right] \end{aligned}$$

(25)

It is also possible to define $intersect$ for the sets of objects, attributes and conditions. For instance, $intersect_G(\mathcal {T}_i,\mathcal {T}_j)$ is equal to 1 if triclusters $\mathcal {T}_i$ and $\mathcal {T}_j$ have nonempty intersection of their extents, and 0 otherwise.

$$\begin{aligned} intersect_G(\mathcal {T}_i,\mathcal {T}_j)=\left[ G_{\mathcal {T}_i}\cap G_{\mathcal {T}_j}\not =\emptyset \right] \end{aligned}$$

(26)

Now we can define diversity of the tricluster set $\mathcal {T}$:

$$\begin{aligned} diversity(\mathcal {T}) = 1-\frac{\sum _j\sum _{i<j}intersect(\mathcal {T}_i, \mathcal {T}_j)}{\frac{|\mathcal {T}|(|\mathcal {T}|-1)}{2}} \end{aligned}$$

(27)

The diversity for the sets of objects (attributes or conditions) is similarly defined.

Coverage is defined as a fraction of the triples of the context (alternatively, objects, attributes or conditions) included in at least one of the triclusters of the resulting set.

More formally, let $\mathbb {K}=(G,M,B,I)$ be a tricontext and $\mathcal {T}$ be the associated triclustering set obtained by some triclustering method, then coverage of $\mathcal {T}$:

$$\begin{aligned} coverage(\mathcal {T})=\sum \limits _{(g,m,b)\in I} \left[ (g,m,b)\in \bigcup \limits _{(X,Y,Z)\in \mathcal {T}} X \times Y \times Z\right] /|I| \end{aligned}$$

(28)

The coverage of the object set $G$ by the tricluster collection $\mathcal {T}$ is defined as follows:

$$\begin{aligned} coverage_G(\mathcal {T})=\sum \limits _{g\in G} \left[ g\in \bigcup \limits _{(X,Y,Z)\in \mathcal {T}} X \right] /|G| \end{aligned}$$

(29)

Coverage of attribute or condition sets can be defined analogously. These measures may have sense when one of the dimensions has high importance, e.g. in case where objects are users (clients) and one does not want to miss even a few of them.

6.1.1 Complexity of an optimal tricluster set

The discrete optimization task of “finding an optimal tricluster solution” can be formalized in the following way:

For a given tricontext $\mathbb {K}=(G,M,B,I \subseteq G\times M\times B)$, minimal density $\rho _{min}\in [0,1]$ and coverage level $\alpha \in [0,1]$ find

$$\begin{aligned} \mathcal {T}_{opt}\in Arg\min \limits _{\mathcal {T}_{cov} \subseteq \mathcal {T}}(|\mathcal {T}_{cov}|, -Diversity(\mathcal {T}_{cov})) \end{aligned}$$

(30)

subject to constraints

• $(1) \quad \forall T \in \mathcal {T}_{cov}: \rho (T)\ge \rho _{min},$

• $(2) \quad \forall (g,m,b) \in I \quad \exists (X,Y,Z) \in \mathcal {T}_{cov}: (g,m,b)\in X\times Y\times Z$

• or

• $(2') \quad coverage(\mathcal {T}_{cov})\ge \alpha , \text{ where } 0 \le \alpha \le 1,$

• $(3) \quad \forall (X,Y,Z) \in \mathcal {T}_{cov}: |X|\ge minsup_{G}, |Y|\ge minsup_{M}, |Z|\ge minsup_{B}.$

Condition (1) requires all triclusters to be dense. Condition $(2')$ is a relaxed (and more general) version of (2) which requires all initial triples from $I$ to be covered. Condition (3) helps to avoid trivial triclusters of small size.

There are two possible ways to find an optimal tricluster set according to the introduced criteria:

• 1. To devise an algorithm that tries to find directly an optimal triclustering solution (w.r.t. a particular tricluster definition) for a given tricontext.

• 2. To reduce the resulting collection obtained by one of the triclustering methods to some of its subsets from the corresponding Pareto set.

Let us concentrate on the second approach, because it can help to better understand whether there is an efficient way to find a good tricluster subset among the obtained triclustering solutions.

Assume that we already have a tricluster collection $\mathcal {T}$ for a given tricontext $\mathbb {K}$ obtained by some of the discussed triclustering techniques. We can also assume that the triclusters are dense and large enough, but their collection has an excessive size because of triclusters overlapping and can be reduced without violation condition (2). For the sake of simplicity we omit the second optimized criteria, Diversity of the tricluster collection, thus coming to the problem of optimal tricluster cover, the computational complexity of which is discussed below.

Let us recall some decision problems and introduce auxiliary constructions.

A vertex cover of a graph $\varGamma =(V,E)$ is a subset of vertices $V_1 \subseteq V$ such that for every edge $(u,v) \in E$ we have $v \in V_1$ and/or $u \in V_1$.

Definition 5

For an arbitrary graph $\varGamma =(V,E)$ the associated bipartite graph is a graph $\varDelta =(X \cup Y, E_1)$, where $|X|=|V|$, vertices from $X$ are in one-to-one correspondence to vertices from $V$ and vertices from $Y$ are in one-to-one correspondence to edges from $E$; $(x_i,y_j) \in E_1$ if the vertex $v_i \in V$ is incident to the edge $e_j \in E$.

We say that in a bipartite graph $\varDelta =(X \cup Y, E)$ a set of vertices $X_1 \subseteq X$ dominates vertices from $Y_1 \subseteq Y$ if each vertex from $Y_1$ is adjacent to a vertex from $X_1$.

Lemma 1

Let $\varGamma =(V,E)$ be a graph and $\varDelta$ be its associated bipartite graph. $\varGamma$ has a vertex cover of size $k$ iff in the bipartite graph $\Delta$ there is a pair $(Z,Y)$, where $Z \subseteq X$, $Z$ dominates vertices from $Y$ and $|Z|=k$.

Proof

The proof directly follows from the construction of the graph $\varDelta$. $\square$

Definition 6

Tricluster bipartite cover graph corresponding to a bipartite graph $\varDelta =(X \cup Y, E_1)$ is the graph $\Theta (\Delta )=(\mathcal {T} \cup I,J)$, where all triclusters from $\mathcal {T}$ are in in one-to-one correspondence with vertices from $X$, all triples ($g,m,b) \in I$ are in one-to-one correspondence with vertices from $Y$ and $(T,(g,m,b)) \in J$ if $(T, y_{(g,m,b)}) \in E_1$. The internal tricluster structure $T=(G_T,M_T,B_T)$ is defined by adjacent edges in $J$, i.e. $\forall (g,m,b) \in I \exists T \in \mathcal {T}: (g,m,b) \in G_T \times M_T \times B_T$.

Without loss of generality let $\mathcal {T}=X$.

Lemma 2

Let $\varDelta$ be a bipartite graph given by Definition 6 and $\varTheta (\varDelta )$ be the corresponding tricluster bipartite cover graph. Then the following two statements are equivalent:

• 1. There is a pair $(Z,Y)$ of sets of vertices of graph $\varDelta$ such that $Z \subseteq X$ and $Z$ dominates all vertices from $Y$.

• 2. $Z$ is a tricluster cover of the tricluster bipartite cover graph $\varTheta (\varDelta )$, i.e. for every $(g,m,b)\in I$ there exist $T=(G_T,M_T,B_T)\in Z$ such that $(g,m,b) \in G_T\times M_T\times B_T$.

Proof

The proof directly follows from the construction of the graph $\varTheta (\varDelta )$. $\square$

Theorem 1

The following “minimal tricluster cover” problem is NP-complete.

• Instance: Triadic context $\mathbb {K}=(G,M,B,I)$, tricluster bipartite cover graph $\varTheta =(\mathcal {T},I,J)$, and positive integer $k$.

• Question: Does there exist a tricluster cover $\mathcal {T}_{cov}\subseteq \mathcal {T}$ such that $|\mathcal {T}_{cov}|\le k$?

Proof

The problem obviously belongs to NP. For each potential solution, i.e., a subset of triclusters $S\subseteq \mathcal {T}$, one needs to check whether each $(g,m,b)$ from $I$ belongs to at least one tricluster $T$ from $\mathcal {T}$ and the size of $\mathcal {T}$ is less or equal to $k$. The first condition can be verified within $O(|I|\cdot |\mathcal {T}| \cdot (|G|+ |M|+ |B|))$ using tricontext or within $O(|I|\cdot |\mathcal {T}|)$ using $\varTheta$.

Now we reduce the problem of minimal vertex cover from Garey and Johnson (1979) to that of ours.

• Instance: Graph $\varGamma =(G,V)$, positive integer $k \le |V|$

• Question: Does there exist a set $W\subseteq V$ such that $|W|\le k$ and $v \in W$ or $u \in W$ for each $e=(u,v)) \in E$?

Applying Definition 5, we construct a bipartite graph $\varDelta$ associated with $\varGamma$. By Lemma 1 a vertex cover of size $k$ of graph $\varGamma$ corresponds, in graph $\varDelta$, to a pair $(Z,Y)$ such that $|Z|=k$ and $Z$ dominates the set $Y$. By Lemma 2, this pair corresponds to a tricluster cover of $\varTheta (\varDelta )$ with the number of triclusters $k$ formed by $k$ vertices of the first part of $\varDelta$, $X$, by Definition 6. The reduction is realized within $O(E)$ time. $\square$

Theorem 2

The following problem “the number of all minimal tricluster covers” is #P-complete.

Proof

We reduce the #P-complete problem of determining the number of inclusion-minimal vertex covers (Valiant 1979) to our problem.

• Input: Graph $\varGamma =(V,E)$.

• Output: $\#\{W \in V{\,|\,}((u,v) \in E))\rightarrow (u \in A) \vee (v \in A)) \text{ holds } \text{ for } A= W \text{ but } \text{ not } \text{ for } \text{ any } A \subset W\}.$

By construction of Lemma 1, an inclusion-minimal vertex cover in graph $\varGamma$ corresponds to a pair $(Z,Y)$ of subsets of vertices of the bipartite graph $\varDelta$ associated with $\varGamma$ and $Z$ is an inclusion-minimal set of vertices from $X$ that dominates $Y$. Conversely, each pair of this form corresponds to an inclusion-minimal vertex cover in graph $\varGamma$. By Lemma 2 the pairs of this form are in one-to-one correspondence with tricluster covers of a tricontext cover graph corresponding to the bipartite graph $\varDelta$. The inclusion minimality of the set of vertices $Z$ corresponds to the minimality of the tricluster cover. $\square$

6.2 Criteria for algorithms

Noise tolerance The noise tolerance of an algorithm has been defined as the ability to build triclusters similar to initial cuboids. We used the Jaccard similarity coefficient to find the most similar tricluster $t$ for the given cuboid $c$ and their similarity. Total similarity has been defined as follows:

$$\begin{aligned} \sigma (\mathcal {C},\mathcal {T})=\frac{1}{|\mathcal {C}|}\sum _{c=c_1}^{c_C}\max _{t=t_1,\dots ,t_T} \frac{|G_c\cap G_t|}{|G_c\cup G_t|}\frac{|M_c\cap M_t|}{|M_c\cup M_t|}\frac{|B_c\cap B_t|}{|B_c\cup B_t|} \end{aligned}$$

(31)

Speed Although the computation time is not of prime importance for us, we provide the computation time for each algorithm on different analyzed datasets.

Complexity In Table 2 we summarize time complexities of the considered algorithms.

Table 2 Time complexity of the algorithms

7 Selection of triadic datasets for experiments

The experiments on the computation time, cardinality, coverage, density, and diversity is conducted on both real and synthetic datasets (Table 3) including the series of experiments on noise tolerance for the latter ones (Sect. 7.2).

Table 3 Contexts for the experiments with 5 chosen evaluation measures

7.1 Real datasets

Mobile operators We select 16 mobile operators with maximal revenue¹. As attributes we consider countries where a particular mobile operator acts. A network type (technology) is chosen as a condition. Thus, each triple in the dataset has the following structure: “operator”, “country”, “technology”.

Movies We compose a context of top 250 popular movies from www.imdb.com, objects are movie titles, attributes are tags, whereas conditions are genres.

Bibsonomy We selected a random sample of 3000 of the first 100,000 triples of the bibsonomy.org dataset, objects are users, attributes are tags, and conditions are bookmark names. The Bibsonomy resource sharing system was developed for collecting, organising, and sharing bookmarks and publications and relies on folksonomy as a data structure.

7.2 Synthetic datasets

Non-overlapping and noised tricontexts In order to test algorithms’ noise-tolerance 26 triadic contexts have been generated. The initial context contains 30 objects, 30 attributes, 30 conditions, and 3 non-overlapping absolutely dense (with $\rho =1$ ) $10\times 10\times 10$ cuboids on the main diagonal in its three-dimensional matrix representation. Then this context has been noised by the inversions with the probability of a triple inversion varying from $0.1$ to $0.5$ with step $0.1$ (the latter context can be called equiprobable uniform context, because probability of $(g,m,b)\in I$ is equal for every triple). There have been 5 such series of contexts. Table 4 contains the average number of triples and total density for these sets of contexts.

Table 4 Noised contexts

Random uniform triple generation Let $\mathbb {K}=(G,M,B,I)$ be an initial tricontext where $I=\emptyset$. Assume that all triples in $I$ are uniformly generated with probability 0.1, i.e. we produce a uniform context of size $30 \times 30 \times 30$ such that $\forall (g,m,b)\,P((g,m,b)\in I) = 0{.}1$.

Gaussian triple generation Let $\mathbb {K}=(G,M,B,I)$ be an initial tricontext where $I=\emptyset$. For Gaussian triple generation (i.e. nonuniform context), probabilities of triple $(g_i,m_j,b_k)$ being in $I$ defined as follows:

$$\begin{aligned} P((g_i,m_j,b_k) \in I)= \alpha \max _{t=1,\ldots ,T}e^{-\frac{(E_{t_x}-i)^2}{D_{t_x}^2 }} e^{-\frac{(E_{t_y}-j)^2}{D_{t_y}^2 }} e^{-\frac{(E_{t_z}-k)^2}{D_{t_z}^2}} , \end{aligned}$$

(32)

where $T$ is the number of Gaussians’ centres, $E_t$ are the coordinates of Gaussian $t$ center, and $D_t$ are standard deviations from the centers. The coefficient $\alpha \in [0,1]$ allows tuning probabilities inside a particular Gaussian. We generate a context of size $30 \times 30 \times 30$ with $\alpha =1$ containing two Gaussians with $(7,7,7)$ and $(22,22,22)$, and $D=(5,5,5)$.

8 Experimental comparison of the methods

The report of experimental results with graphs and tables is given in Sect. 8.1. The method-by-method and overall discussion of the results with the examples of found triclusters is provided in Sect. 8.2.

8.1 Experimental results

All the methods have been implemented by the authors and incorporated into a single triclustering toolbox. The toolbox has been implemented in C# using MS Visual Studio 2010/2012. All the experiments have been performed on Windows 7 SP1 x64 system equipped with an Intel Core i7-2600 @ 3.40GHz processor and 8 GB of RAM. AlgLib² library was used for performing eigenvalue decomposition.

The following size measure for spectral triclustering has been chosen:

$$\begin{aligned} Size(X,Y,Z)=(|X|+|Y|+|Z|)/(|G|+|M|+|B|). \end{aligned}$$

Parallel versions of OAC-triclustering algorithms and TriBox have also been implemented via parallelization of their outer loops and the computation times for them have been compared.

The results of the experiments on noise tolerance are presented in Fig. 3.

Fig. 3

Similarity for the noise-tolerance experiments

It is clear that every method has managed to successfully find initial cuboids, but the results quickly deteriorate for most of methods with the growth of inversion probability. TriBox has shown the best results as it tries to optimize the density-volume trade-off (which most probably is the best for the areas of the former cuboids with small error probability). Though prime OAC-triclustering has been also rather noise-tolerant, it generated significantly more triclusters (most likely the high number of triclusters is the reason for these results). All the other methods have been unable to provide significant results for noisy contexts. Moreover, as it was expected, no adequate triclusters were generated by any of the methods for the inversion probability $0{.}5$ contexts.

Table 5 contains the results for the experiments with other criteria. The lowest (highest) values of criteria are typed in bold. Note that the lowest value is not necessary the best one, e.g., even though a low value of cardinality is desirable, an output collection of 2 triclusters is rather bad result for its further usage.

Table 5 Results of the experiments on the computation time ($t$, ms), triclusters count ($n$), density ($\rho$, %), coverage ($Cov$, %), and diversity ($Div$, %)

The following values for parameters were selected:

• 1. OAC-triclustering: $\rho _{min}=0$

• 2. SpecTric: $s_{min}=0$

• 3. TriBox: $\lambda _0=\rho (\mathbb {K})$

• 4. Trias: $\tau _G=\tau _M=\tau _B=0$

To show how the values of quality measures vary with different parameters values, we provide the reader with the results on Mobile operators dataset (Table 6).

Table 6 Results of the experiments on mobile operators dataset

We also selected four criteria to build graphs on quality comparison: the cardinality, average density, coverage and the diversity. It may shed light on how to choose a Pareto-optimal method (collection) for a particular dataset and give some clues in general (see Fig. 4). Colored paths on the graph connect points of the same particular method for a chosen range of method parameters. Note that Trias and Tribox have only one point at each plot.

Fig. 4

Pairwise criterion graphs for mobile operators dataset

Reading the pairwise graphs on the triclustering results for Mobile operators dataset (Fig. 4) one can conclude that there is no winning approach. However, these graphs make it possible to find a suboptimal solution. One can see that points for OAC($\prime$) are at the top right corner of each diagram and this is not the case for any of the rest algorithms, thus Trias looses in the triclusters number. There is another suboptimal approach, TriBox, since its points are close to the top right corner for all graphs. Guided by this pairwise plots and the idea which of the quality measures are most important, an analyst can conclude which method is the most suitable for her dataset.

The graphs for synthetic dataset also show that there is no a winning approach. However, for uniform triple generation scheme one can conclude that Trias is the best one with respect to three criteria, $Diversity$, $Coverage$ and $Density$. Moreover, it is possible to see the trade-off between $Density$ and $Coverage$ for OAC($\prime$). The weakness of Spectric is revealed: it has low density, but the rest measures are of high value. OAC($\square$) has extremely poor diversity. Similarly for Gaussian triple generation scheme, Trias found the best patterns with respect to $Diversity$, $Coverage$ and $Density$. One more trade-off appears for OAC($\prime$) between $Diversity$ and $Coverage$. The drawbacks of OAC($\square$) and Spectric remain the same.

For the IMDB dataset Trias again produces highly diverse, absolutely dense and patterns of 100 % $Coverage$, but the number of patterns is too high for analysis. Two suboptimal solutions are OAC($\prime$) and TriBox. It is beneficially that for OAC($\prime$) there is no trade-off between $Cardinality$ and $Diversity$, and $Density$ and $Coverage$.

The Bibsonomy dataset is the biggest one and experiencing intrinsic noise of tagging procedure, therefore it is not a surprise that Trias and OAC($\prime$) discovered many patterns. For OAC($\prime$) it is possible to reach less number of patterns than Trias produces keeping the best level of $Diversity$ and $Coverage$. An analyst may play with OAC($\square$) density to find the balance between $Density$ and $Coverage$ or $Coverage$ and $Diversity$ if she needs less patterns than for the preceding two suboptimal methods.

8.2 Discussion of the results

Trias is one of the most time consuming algorithms considered in the paper, along with TriBox and SpecTric, for large contexts. Thus on the pairwise criteria graphs, the Trias point lies at the right upper corner of three plots (a), (c), (e) and it is close to the origin at the axis $-Cardinality$ for the other three. Although each of the resulting triclusters (triconcepts) can be easily interpreted, their number and small sizes make it difficult to see the general structure of the dataset. Since all of the triconcepts have been generated so that every triple has been covered, the coverage is equal to $1$. Because the concepts are small, the general diversity is rather high. Still, the set diversity depends on the size of the corresponding set: the smaller the set, the greater chance of intersection and the lower the diversity.

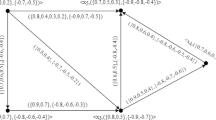
Examples of Trias triconcepts for the IMDB context:

• 1. {The Princess Bride (1987), Pirates of the Caribbean: The Curse of the Black Pearl (2003)}, {Pirate}, {Fantasy, Adventure}

• 2. {V for Vendetta (2005)}, {Fascist, Terrorist, Government, Secret Police , Fight}, {Action, Sci-Fi, Thriller}

SpecTric has displayed rather good computation time only for small contexts. The eigenvalue decomposition of Laplacian matrix takes most computation time. In the future, we intend to test some alternative linear algebra libraries in the toolbox and compare the results as well. The resulting triclusters can be reasonably interpreted, though their average density is low. Their small number makes this method good for dividing the context into several non-overlapping parts. Also the diversity for SpecTric is always equal to $1$ (plots (a) and (e) on the pairwise criteria graphs), because the method generates partitions of the initial context. However, the high diversity leads to rather low coverage because of many discarded edges and there is trade-off between density and diversity (see plot (c)).

Examples of SpecTric triclusters for the IMDB context:

• 1. $\rho =23{.}08\,\%$, {Alien (1979), The Shining (1980), The Thing (1982), The Exorcist (1973)}, {Spaceship, Egg, Parasite, Creature, Caretaker, Colorado, Actress, Blood, Helicopter, Scientist, Priest, Washington D.C., Faith}, {Horror}

• 2. $\rho =2{.}09\,\%$, {The Shawshank Redemption (1994), The Godfather (1972), The Godfather: Part II (1974), ..., Bonnie and Clyde (1967), Arsenic and Old Lace (1944)}, {Prison, Cuba, Business, 1920s, ..., Texas, Cellar}, {Crime, Thriller }

TriBox in this study generates the best triclusters, even though it is often the second best on the pairwise criteria graphs. It totally dominates OAC-box and SpecTric in $Density-Coverage$ axes (plot (c)). The only drawback of this method is high computation time, though the use of the parallel version of TriBox can significantly lower it at multi-core processors. Average density of the resulting triclusters is rather high, they have good interpretability. Coverage and diversity are also high in most cases. The only exception is the set diversity in the situation when some of the sets (objects, attributes or conditions) are small, just as for Trias.

Examples of TriBox triclusters for the IMDB context:

• 1. $100\,\%$, {Million Dollar Baby (2004), Rocky (1976), Raging Bull (1980)}, {Boxer, Boxing}, {Drama, Sport}

• 2. $83{.}33\,\%$, {The Sixth Sense (1999), The Exorcist (1973), The Silence of the Lambs (1991)}, {Psychiatrist}, {Drama, Thriller}

• 3. $33{.}33\,\%$, {Platoon (1986), All Quiet on the Western Front (1930), Glory (1989), Apocalypse Now (1979), Lawrence of Arabia (1962), Saving Private Ryan (1998), Paths of Glory (1957), Full Metal Jacket (1987)}, {Army, General, Jungle, Vietnam, Soldier, Recruit}, {Drama, Action, War}

Box OAC-triclustering has been not that successful. Despite being rather fast (only OAC-triclustering based on prime operators and SpecTric for small contexts are faster) and having good parallel version the resulting triclusters are quite large, have relatively low density and many intersections. It leads to the high coverage ($1$ for $\rho _{min}=0$) and rather low diversities. For example, one can see from pairwise criteria plots that OAC-box may reach optimal values of Density, Diversity and Cardinality (plots (d), (e), and (f)). Also these triclusters are difficult to interpret (unlike SpecTric’s triclusters that also have large size and low density). In many cases extent size is small. Examples are given below:

• 1. $0{.}9\,\%$, {The Shawshank Redemption (1994), The Godfather (1972), Ladri di biciclette (1948), Unforgiven (1992), Batman Begins (2005), Die Hard (1988), ..., The Green Mile (1999), Sin City (2005), The Sting (1973)}, {Prison, Murder, Cuba, FBI, Serial Killer, Agent, Psychiatrist,..., Window, Suspect, Organized Crime , Revenge, Explosion, Assassin, Widow}, {Crime, Drama, Sci-Fi, Fantasy, Thriller, Mystery}

• 2. $1{.}07\,\%$, {The Great Escape (1963), Star Wars: Episode VI - Return of the Jedi (1983), Jaws (1975), Batman Begins (2005), Blade Runner (1982), Die Hard (1988),..., Metropolis (1927), Sin City (2005), Rebecca (1940)}, {Prison, Murder, Cuba, FBI, Serial Killer, Agent, Psychiatrist,..., Shower, Alimony, Phoenix Arizona, Assassin, Widow}, {Drama, Thriller, War}

Prime OAC-triclustering showed rather good results. It is one of the fastest algorithms (though some additional optimization implemented for a non-parallel version made the parallelization inefficient for small datasets). The number of triclusters is high, but they are easily interpreted. Once again for $\rho _{min}=0$ coverage is equal to $1$, but remains high for different $\rho _{min}$. The diversity is usually rather high. According to the pairwise criteria graphs OAC-Prime shows the results even better than Tribox on IMDB and Mobile operators datasets (Fig. 4), but demonstrates rather high number of triclusters on Bibsonomy data as well as Trias. Examples of Prime OAC triclusters for the IMDB context are given below:

• 1. $56.67\,\%$, {The Godfather: Part II (1974), The Usual Suspects (1995)}, {Cuba, New York, Business, 1920s, 1950s}, {Crime, Drama, Thriller}

• 2. $60\,\%$, {Toy Story (1995), Toy Story 2 (1999)}, {Jealousy, Toy, Spaceman, Little Boy, Fight}, {Fantasy, Comedy, Animation, Family, Adventure}

Overall, none of the algorithms is the best over all the five criteria. Yet, based on our experimentation results, one can see that OAC-Prime and OAC-Box are the fastest, whereas TriBox and OAC-Prime are the best over density, coverage, diversity and cardinality. With respect to the noise-tolerance, TriBox is the best, whereas OAC-Prime is the second best. The TriBox and OAC-Prime should be recommended to the users interested in finding interpretable triclusters.

9 Conclusion

In this paper, we presented a general view of triclustering for binary triadic datasets unifying formal triconcepts, density-based heuristics and approximation frameworks. In addition to the conventional computation time criterion, we presented a set of evaluation criteria for the results, oriented at finding interpretable solutions. These criteria—density, coverage, diversity, noise tolerance, and the cardinality—represent different aspects of the interpretability. The cardinality is of an issue because the number of triclusters should correspond to the structure of the dataset under investigation—but this is usually unknown. We cannot help but refer the reader to an analogous issue of “the right number of clusters” in a conventional setting, which found no reasonable solution as yet. We took a number of triclustering algorithms developed by the authors, including a novel algorithm OAC-Prime, and a representative formal triconcept finding algorithm Trias, and presented a number of theoretical results to explore their efficiency and allow making them more efficient in some cases. We designed a comprehensive experimental testing framework including a rich structure and noise generating setup.

The investigation of resource efficiency of the proposed methods proves that OAC-box, OAC-prime, Tribox, and SpecTric have polynomial computational time in the input size, and the number of output patterns is no more than the number of triples in the input data. This contrasts the fact that formal triconcept Trias algorithm has its worst computation time exponential as well as the number of triconcepts. Yet the experimentation on both synthetic and real data shows that there is no one winning method according to the introduced criteria. For example, maximally dense patterns with maximal coverage found with Trias, impose a less than optimal diversity and a very large number of output patterns. The multicriteria choice allows an expert to decide which of the criteria are most important in a specific case and make a choice. Overall, our experiments show that our Tribox and OAC-prime algorithms can be reasonable alternatives to triadic formal concepts and lead to Pareto-effective solutions. Although TriBox is better with respect to noise-tolerance and the number of clusters, OAC-prime is the best on scalability to large real-world datasets.

Further work on triclustering can go in the following directions:

• developing a unified theoretical framework for $n$-clustering,

• finding bridges between probabilistic (Meulders et al. 2002) and algebraic approaches,

• combining several constraint-based approaches to triclustering (e.g., mining dense triclusters first and then frequent tri-sets in them),

• finding better approaches for estimating the tricluster density,

• taking into account features of real-world data in optimization procedures (their sparsity, value distribution, etc.) and online data processing,

• using different bicluster approaches to extend them to triadic data,

• shifting to arbitrary numeric or interval datasets from the binary case [continuing the work (Kaytoue et al. 2014)],

• applying triclustering in recommender systems and social network analysis.

As for the formal triconcept analysis, probably a possible way to go should be in the direction of matrix decomposition developed in Belohlávek and Vychodil (2010); Miettinen (2011). Note that Boolean tensor factorization can be considered as an approach to the reduction of the number of the resulting triconcepts and finding an optimal concept cover is a central problem there (Belohlávek et al. 2013).