Abstract
In this article we prove local well-posedness of the system of equations \(\partial _t h_{i}= \sum _{j=1}^{i}\partial _x^2 h_{j}+ (\partial _x h_{i})^2 + \xi \) on the circle where \(1\le i\le N\) and \(\xi \) is a space-time white noise. We attempt to generalize the renormalization procedure which gives the Hopf-Cole solution for the single layer equation and our \(h_1\) (solution to the first layer) coincides with this solution. However, we observe that cancellation of logarithmic divergences that occurs at the first layer does not hold at higher layers and develop explicit combinatorial formulae for them.
Similar content being viewed by others
Notes
In [10] the processes depend on two spatial parameters x and y, but here we set x to be zero and write x for y for notational simplicity.
A multi-set is like a set where one allows for multiplicity. Using the notation of [1], one sets \(\mathscr {N} {\mathop {=}\limits ^{\text{ def }}}\sqcup _{n \ge 0} [\mathscr {E}]^{n}\) where \([\mathscr {E}]^{n}\) consists of the equivalence classes of elements of \(\mathscr {E}^{n}\) where one identifies tuples in \(\mathscr {E}^{n}\) which are related by a permutation.
However we don’t allow for all products, for instance we do not allow for the cube
 . This type of constraint can be seen in the rule we presented earlier.
. This type of constraint can be seen in the rule we presented earlier.The only difference being the the (j, i) decorations.
In contrast to the situation in [9].
The coefficient in the parenthesis \(\{\cdots \}\) automatically restricts the admissible labels for trees
 . For example, \(n=2\) (2nd layer), if \(\ell =1\) then \(m_1,m_2\) must both be 0, otherwise this coefficient is zero.
. For example, \(n=2\) (2nd layer), if \(\ell =1\) then \(m_1,m_2\) must both be 0, otherwise this coefficient is zero.
References
Bruned, Y., Hairer, M., Zambotti, L.: Algebraic renormalisation of regularity structures (2016). arXiv preprint arXiv:1610.08468
Carlitz, L.: The product of several Hermite or Laguerre polynomials. Monatshefte für Mathematik 66(5), 393–396 (1962)
Chandra, A., Hairer, M.: An analytic BPHZ theorem for regularity structures (2016). arXiv preprint arXiv:1612.08138
Funaki, T., Hoshino, M.: A coupled KPZ equation, its two types of approximations and existence of global solutions. J. Funct. Anal. 273(3), 1165–1204 (2017). https://doi.org/10.1016/j.jfa.2017.05.002
Hairer, M.: Solving the KPZ equation. Ann. Math. (2) 178(2), 559–664 (2013). https://doi.org/10.4007/annals.2013.178.2.4
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014). https://doi.org/10.1007/s00222-014-0505-4
Hairer, M.: The motion of a random string (2016). arXiv preprint arXiv:1605.02192
Hairer, M., Quastel, J.: A class of growth models rescaling to KPZ. Forum Math. Pi 6, e3, 112 (2018). https://doi.org/10.1017/fmp.2018.2
Hairer, M., Shen, H.: A central limit theorem for the KPZ equation. Ann. Probab. 45(6B), 4167–4221 (2017)
O’Connell, N., Warren, J.: A multi-layer extension of the stochastic heat equation. Commun. Math. Phys. 341(1), 1–33 (2016). https://doi.org/10.1007/s00220-015-2541-3
Acknowledgements
A. Chandra gratefully acknowledges financial support from the Leverhulme Trust via an Early Career Fellowship, ECF-2017-226. H. Shen gratefully acknowledges financial support by the NSF Award DMS-1712684 and DMS-1909525. A. Chandra and H. Shen would also like to thank the Isaac Newton Institute for Mathematical Science for support and hospitality during the programme “Scaling limits, rough paths, and quantum field theory”, supported by EPSRC Grant Number EP/R014604/1, where work on this paper was undertaken. D. Erhard gratefully acknowledges financial support from the National Council for Scientific and Technological Development – CNPq via a Universal grant.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alessandro Giuliani.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: A Short Analysis of \(G_i\)
Let \(\zeta \in \mathbb {R}\). We say that a kernel G defined on \(\mathbb {R}^d\setminus \{0\}\) or on a subset thereof is of order \(\zeta \) if for all multiindizes k there exists a constant \(C>0\) such that
Proposition A.1
The kernel \(G_i\) is of order \(-1\) for every \(i\ge 0\).
Proof
The result is well known for the usual heat kernel, see for instance [6, Lemma 7.4]. If \(i=1\), then note that after a partial integration we have the identity
and both kernels on the right hand side are of order \(-2\). The claim therefore follows from [6, Lemma 10.14]. Note that in that result the kernels are supposed to be compactly supported. However, since the heat kernel decays superexponentially fast at infinity it is possible to adapt this result to the present setting. For \(i>1\) we can write \(G_i= G_{i-1}* \partial _x^2 G\) so that we can conclude as in the case \(i=1\). \(\square \)
Appendix B: Useful Identity
The identity
was used in [8, Sect. 6] where the tilde is the reflection, i.e. \(\widetilde{F}(z):=F(-z)\), and the derivative above is with respect to the spatial variable. Iteratively applying this identity we can get useful identities for convolutions of (derivatives of) \(G_m\). For instance we have \(4G_0' * \widetilde{G_1'} = 2 \widetilde{G_1} -G_0 -\widetilde{G}_0\), since
where we used integration by parts to shift a derivative \(2 G * \widetilde{G''} = -2G'*\widetilde{G'} \) in the second step. When the indices are large this calculation can get more involved, for instance, we have \(4G_1' * \widetilde{G_1'} = - G_1 - \widetilde{G_1} + G_0 + \widetilde{G}_0\), because
In order to obtain a general set of identities we define kernels \(D_{i,j}\), for \((i, j) \in \Lambda {\mathop {=}\limits ^{\text{ def }}}\{0,1,2,\dots \}^{2} \) via
For \(i,j > 0\), one has the recursion relation
Indeed, making use of (B.1), we can write
and by shifting a derivative the above recursion relation follows.
When \(i = 0, j > 0\) one has the recursion
Since \(\widetilde{D_{i,j}} = D_{j,i}\) we get, when \(j=0\) and \(i > 0\)
Finally, \(D_{0,0} = \frac{1}{2}[G_{0} + \widetilde{G_{0}}]\).
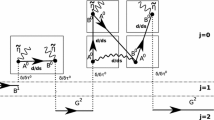
We now use these recursions to find formula for \(D_{i,j}\). A lattice path is a sequence of nearest neighbor edges (steps) of \(\Lambda \) which satisfy the natural adjacency relation.
Let \(B{\mathop {=}\limits ^{\text{ def }}}\{(x,y) \in \Lambda , i=0 \text{ or } j=0\}\) be the boundary of the discrete first quadrant. We denote by W(i, j) the set of all lattice paths \(\gamma \) which
-
Start at (i, j)
-
Only move down or to the left
-
Terminate at a site of B (note, paths are allowed to travel along B for some time, but they always end at a site of B, they can’t go negative.)
For a lattice path \(\gamma \) we denote by \(l(\gamma )\) the number of steps in \(\gamma \). One then has the following formula
where \(\gamma _{\mathrm {end}}\) is the final site visited by \(\gamma \) and F is a map from the sites of B to kernels given as follows: \(F(0,0) = \frac{1}{2}(G + \widetilde{G})\) and
For fixed \((i,j) \in \Lambda \) let B(i, j) be the set of sites of B one can reach via walks in W(i, j). We then get
where \(\left( {\begin{array}{c}i + j - x - y\\ i-x\end{array}}\right) \) counts the number of paths from (i, j) to (x, y). Equivalently,
Rights and permissions
About this article
Cite this article
Chandra, A., Erhard, D. & Shen, H. Local Solution to the Multi-layer KPZ Equation. J Stat Phys 175, 1080–1106 (2019). https://doi.org/10.1007/s10955-019-02278-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02278-4



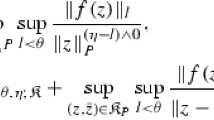
 . This type of constraint can be seen in the rule we presented earlier.
. This type of constraint can be seen in the rule we presented earlier. . For example,
. For example,