Kawasaki Dynamics with Two Types of Particles: Critical Droplets

Abstract

This is the third in a series of three papers in which we study a two-dimensional lattice gas consisting of two types of particles subject to Kawasaki dynamics at low temperature in a large finite box with an open boundary. Each pair of particles occupying neighboring sites has a negative binding energy provided their types are different, while each particle has a positive activation energy that depends on its type. There is no binding energy between particles of the same type. At the boundary of the box particles are created and annihilated in a way that represents the presence of an infinite gas reservoir. We start the dynamics from the empty box and are interested in the transition time to the full box. This transition is triggered by a critical droplet appearing somewhere in the box.

In the first paper we identified the parameter range for which the system is metastable, showed that the first entrance distribution on the set of critical droplets is uniform, computed the expected transition time up to and including a multiplicative factor of order one, and proved that the nucleation time divided by its expectation is exponentially distributed, all in the limit of low temperature. These results were proved under three hypotheses, and involved three model-dependent quantities: the energy, the shape and the number of critical droplets. In the second paper we proved the first and the second hypothesis and identified the energy of critical droplets. In the third paper we prove the third hypothesis and identify the shape and the number of critical droplets, thereby completing our analysis.

Both the second and the third paper deal with understanding the geometric properties of subcritical, critical and supercritical droplets, which are crucial in determining the metastable behavior of the system, as explained in the first paper. The geometry turns out to be considerably more complex than for Kawasaki dynamics with one type of particle, for which an extensive literature exists. The main motivation behind our work is to understand metastability of multi-type particle systems.

Appendices

Appendix A: Computation of N ^⋆

Kurz [16] shows how to construct all polyominoes of minimal perimeter with fixed area, and gives an expression for their number in terms of generating functions. Two basic generating functions

(A.1)

are used to define two composite generating functions

$$ \everymath{\displaystyle }\begin{array}{@{}lll} r(x)=\frac {1}{4} \bigl[a(x)^4+3a\bigl(x^2 \bigr)^2 \bigr], \cr\noalign{\vspace{3pt}} q(x)= \frac {1}{8} \bigl[a(x)^4+3a \bigl(x^2\bigr)^2+2s(x)^2a \bigl(x^2\bigr)+2a\bigl(x^4\bigr) \bigr], \end{array} $$

(A.2)

whose coefficients r _k , q _k of x ^k count the polyominoes as follows. The number of polyominoes of minimal perimeter with area n equals

(A.3)

where $s=\lfloor\sqrt{n}\rfloor$.

We need to count the number of polyominoes of minimal perimeter with area n=ℓ ^⋆(ℓ ^⋆−1)+1 for ℓ ^⋆≥4, i.e., we are only interested in n of the form s ²+s+t with s=ℓ ^⋆−1 and t=1. Kurz [16] counts polyominoes modulo translations, rotations and reflections. We need the number modulo translations only. Therefore we must put in correction factors: 4 for the rotations and 2 for the reflections.

In region RC we retain all c-terms. In region RB we only retain the term with c=1. Indeed, $q_{\ell^{\star}- 1}$ is the number of polyominoes of minimal perimeter when the circumscribing rectangle is a square of side length ℓ ^⋆, and $r_{\ell^{\star}- c^{2} - 1}$ is the number of polyominoes of minimal perimeter when the circumscribing rectangle has side lengths ℓ ^⋆+1,ℓ ^⋆−1. Thus, modulo rotations and reflections, we have

(A.4)

Appendix B: Clarification of Some Statements in [14]

2.1 B.1 Proof of Lemma 1.18 in [14]

The following statement was used in the proof of Lemma 2.2 in [14].

Lemma B.1

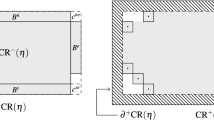
$\mathcal{C}^{\star}_{\mathrm{bd}}$ is a minimal gate.

Proof

Let $\mathcal{A}= \{\eta\in \mathcal{C}^{\star}_{\mathrm{bd}}\colon\, \exists\,\omega\in \varOmega (\eta)\colon\, \omega\cap \mathcal{C}^{\star}_{\mathrm{bd}}=\{\eta\}\}$, and let $\tilde{\mathcal{A}} = \mathcal{C}^{\star}_{\mathrm{bd}}\backslash\mathcal{A}$. In words, for each $\eta\in\mathcal{A}$ there is a path in (□→⊞)_opt entering $\mathcal{G}(\Box,\boxplus)$ via η and reaching ⊞ without hitting $\mathcal{C}^{\star}_{\mathrm{bd}}$ again, while if a path in (□→⊞)_opt enters $\mathcal{C}^{\star}_{\mathrm{bd}}$ via a configuration in $\tilde{\mathcal{A}}$, then it must go back to $\mathcal{C}^{\star}_{\mathrm{bd}}$ before reaching ⊞. We will show that $\tilde{\mathcal{A}}$ is empty. The proof is by contradiction.

Assume that $\eta\in\tilde{\mathcal{A}}$ and let ω∈Ω(η). Let ζ be the last configuration in $\mathcal{C}^{\star}_{\mathrm{bd}}$ visited by ω before reaching ⊞. Then there is an ω′∈(□→⊞)_opt entering $\mathcal{G}(\Box ,\boxplus)$ via ζ. The path ω′′ obtained by joining the part of ω′ from □ to ζ and the part of ω from ζ to ⊞ belongs to (□→⊞)_opt, and η∉ω′′. Therefore η is unessential and, by Theorem 5.1 in [18] (Lemma 1.3 in this paper), it does not belong to $\mathcal{G}(\Box,\boxplus)$. This contradicts the assumption $\eta\subset \mathcal{C}^{\star}_{\mathrm{bd}}\subset \mathcal{G}(\Box, \boxplus)$. □

Lemma 1.18 in [14] (H3a), (H3-c) and Definition 1.5(a) imply that for every $\eta\in\mathcal{C}^{\star}_{\mathrm{att}}$ all paths in (η→□)_opt pass through $\mathcal{C}^{\star}_{\mathrm{bd}}$.

Proof

The proof is by contradiction. Let $\mathcal{C}^{\star}_{\mathrm{att}}\ni\eta= (\hat{\eta}, x)$, and assume that there is a path ω ₁: □→η that does not visit $\mathcal{C}^{\star}_{\mathrm{bd}}$ and such that H(σ)≤Γ ^⋆ for all σ∈ω ₁. By the definition of $\mathcal{C}^{\star}_{\mathrm{att}}$, there exists a configuration $\mathcal{C}^{\star}_{\mathrm{bd}}\ni\zeta= (\hat {\eta}, z)$ such that ζ is obtained from η by moving the particle of type 2 from x to z. Consequently, there exists a path ω ₂ from η to ζ consisting of a sequence of configurations of the type $(\hat{\eta}, y_{i})$ with y _i ∈Λ for all i. Note that, since H(ζ)=Γ ^⋆, the particle of type 2 at site z in ζ has no active bond (it is in ∂ ⁻ Λ) and all configurations in ω ₂ have the same number of particles of both types, we have H(σ)≤Γ ^⋆ for all σ in ω ₂. Since ζ belongs to the minimal gate $\mathcal{C}^{\star}_{\mathrm{bd}}$, there is a path ω ₃: ζ→⊞ such that $\omega_{3} \cap \mathcal{C}^{\star}_{\mathrm{bd}}= \{ \zeta\}$ and such that H(σ)≤Γ ^⋆ for all σ∈ω ₃.

Now consider the following two cases.

• (1) η∈ω ₃. Let ω ₄ be the part of ω ₃ from η to ⊞. Then the path obtained by joining ω ₁ and ω ₄ is a path in (□→⊞)_opt that does not visit $\mathcal{C}^{\star}_{\mathrm{bd}}$. This contradicts the definition of $\mathcal{C}^{\star}_{\mathrm{bd}}$.

• (2) η∉ω ₃. Let ω=ω ₁+ω ₂+ω ₃. Then, by construction, ω∈(□→⊞)_opt. Let $\pi= (\hat{\eta }, w)$ be the configuration in ω visited just before ζ. By definition, $\pi\in \mathcal{P}$. By (the first part of) (H3-a), π consists of a single droplet, and hence w∉∂ ⁻ Λ. Therefore ζ is obtained by “breaking” a droplet of a configuration in $\mathcal{P}$ and not by adding a particle of type 2 in ∂ ⁻ Λ to a configuration in $\mathcal{P}$. This contradicts (the second part of) (H3-a). □

2.2 B.2 Proof of Lemma 2.2 in [14]

In the proof of Lemma 2.2 in [14], the sentence

“Denote by Ω(η) the set of all optimal paths from □ to ⊞ that enter $\mathcal{G}(\Box,\boxplus)$ via η (note that this set is non-empty because $\mathcal{C}^{\star}_{\mathrm{bd}}$ is a minimal gate by Definition 1.4(a)). By Definition 1.4(b), ω _i ∈Ω(η) visits $\hat{\eta}$ before η for all i∈1,…,|Ω(η)|.”

must be replaced by

“Denote by Ω(η) the set of all optimal paths from □ to ⊞ such that $\omega\cap \mathcal{C}^{\star}_{\mathrm{bd}}= \{ \eta\}$ (note that this set is non-empty because $\mathcal{C}^{\star}_{\mathrm{bd}}$ is a minimal gate). By Definition 1.4(b) and by the more precise form of (H3-a), ω _i ∈Ω(η) visits $\hat{\eta}$ before η for all i∈1,…,|Ω(η)|.”

2.3 B.3 Proof of Theorem 1.8 in [14]

In Step 3, the definition of $\rm{CS^{++}}(\hat{\eta})$ should read: $\rm{CS^{++}}(\hat{\eta}) = \partial^{+}CS^{+}(\hat{\eta})\cap \varLambda^{-}$.

In Lemma 2.11, the estimate of Θ ₁ in formula (2.48) should be replaced by

(B.1)

where $\mathcal{P}^{\prime}$ is the set of configurations in $\mathcal{P}$ whose support has lattice distance at least two from ∂ ⁻ Λ. This allow us to always construct a lattice path connecting every two points adjacent to $\operatorname{supp}(\hat{\eta })$ and avoiding ∂ ⁺ Λ, as in the argument used to derive bounds for formula (2.56). The value of Θ ₁ is derived by restricting the sum in (2.50) to $\hat{\eta} \in \mathcal{P}^{\prime}$. This still produces a lower bound for Θ, because $\mathcal{P}^{\prime} \subset \mathcal{P}$. $\mathcal{P}$ should be changed to $\mathcal{P}^{\prime}$ accordingly in formulas (2.53) in Step 3 and (2.61) in Step 4. The bounds Θ ₁ and Θ ₂ will still merge asymptotically, as shown in Step 4, since $| \mathcal{P}| \sim N^{\star} |\varLambda| \sim| \mathcal{P}^{\prime}|$ as Λ→ℤ².

In Step 3, where Θ ₂ is computed, the sentence

“The only transitions in $\mathcal{X}^{\star}$ between $\mathcal{C}^{++}$ and $\mathcal{X}^{\star}\backslash [\mathcal{X}_{\Box}\cup\mathcal{C}^{++}]$ are those where the free particle moves from distance 2 to distance 1 of the protocritical droplet.”

should be replaced by

“The only transitions in $\mathcal{X}^{\star}$ between $\mathcal{C}^{++}$ and $\mathcal{X}^{\star}\backslash [\mathcal{X}_{\Box}\cup\mathcal{C}^{++}]$ are those where the free particle enters $\rm{CS^{++}}(\hat{\eta})$.”