Skip to main content
SpringerLink
Log in

On tackling reverse convex constraints for non-overlapping of unequal circles

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We study the unequal circle-circle non-overlapping constraints, a form of reverse convex constraints that often arise in optimization models for cutting and packing applications. The feasible region induced by the intersection of circle-circle non-overlapping constraints is highly non-convex, and standard approaches to construct convex relaxations for spatial branch-and-bound global optimization of such models typically yield unsatisfactory loose relaxations. Consequently, solving such non-convex models to guaranteed optimality remains extremely challenging even for the state-of-the-art codes. In this paper, we apply a purpose-built branching scheme on non-overlapping constraints and utilize strengthened intersection cuts and various feasibility-based tightening techniques to further tighten the model relaxation. We embed these techniques into a branch-and-bound code and test them on two variants of circle packing problems. Our computational studies on a suite of 75 benchmark instances yielded, for the first time in the open literature, a total of 54 provably optimal solutions, and it was demonstrated to be competitive over the use of the state-of-the-art general-purpose global optimization solvers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. For ease of exposition, we simplify the notation of Eq. (1), as follows: \(x_{i} \leftarrow a_{i^\prime } - a_{j^\prime }\), \(x_{j} \leftarrow b_{i^\prime } - b_{j^\prime }\) and \(\rho _{ij} \leftarrow r_{i^\prime } + r_{j^\prime }\), where \((a_{\ell }, b_{\ell })\) and \(r_{\ell }\) represent the center coordinates and radii, respectively, of two circles \(\ell \in \left\{ i^\prime , j^\prime \right\} \).

  2. For simplicity, we use here a common tolerance \(\varepsilon \) for all constraints in problem (2), but we remark that, in principle, one may use a set of constraint-specific feasibility tolerances that are appropriately scaled for each constraint.

  3. Structural variables x are not necessarily bounded, i.e., \(x^L_i \rightarrow -\infty \) and/or \(x_i^U \rightarrow +\infty \), for any and all \(i \in \{1, 2,\ldots , n\}\).

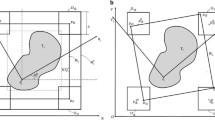
  4. From our computational experience, the number of vertices of \(FR_{ij}\) is usually small (around 10), and thus identifying its concave envelope via enumeration is computationally efficient. Regardless, if the number of vertices of \(FR_{ij}\) is large, one can always properly relax the domain \(FR_{ij}\) and obtain a new bounded polyhedron that contains \(FR_{ij}\) and has a small number of vertices.

References

  1. Specht, E.: http://www.packomania.com/. Accessed 23 Aug 2020

  2. Achterberg, T.: Scip: solving constraint integer programs. Math Program Comput 1(1), 1–41 (2009)

    Article  MathSciNet  Google Scholar 

  3. Achterberg, T., Bixby, R.E., Gu, Z., Rothberg, E., Weninger, D.: Presolve reductions in mixed integer programming. INFORMS J Comput 32(2), 473–506 (2019)

    Article  MathSciNet  Google Scholar 

  4. Alvarez-Valdés, R., Parreño, F., Tamarit, J.M.: Reactive grasp for the strip-packing problem. Computer Op Res 35(4), 1065–1083 (2008)

    Article  Google Scholar 

  5. Anstreicher, K.M.: On convex relaxations for quadratically constrained quadratic programming. Math Program 136(2), 233–251 (2012)

    Article  MathSciNet  Google Scholar 

  6. Balas, E.: Intersection cuts – a new type of cutting planes for integer programming. Op Res 19(1), 19–39 (1971)

    Article  MathSciNet  Google Scholar 

  7. Bao, X., Sahinidis, N.V., Tawarmalani, M.: Multiterm polyhedral relaxations for nonconvex, quadratically constrained quadratic programs. Optim Method Softw 24(4–5), 485–504 (2009)

    Article  MathSciNet  Google Scholar 

  8. Belotti, P., Lee, J., Liberti, L., Margot, F., Wächter, A.: Branching and bounds tighteningtechniques for non-convex minlp. Optim Method Softw 24(4–5), 597–634 (2009)

    Article  Google Scholar 

  9. Berg, M.D., Cheong, O., Kreveld, M.V., Overmars, M.: Computational geometry: algorithms and applications. Springer-Verlag TELOS, Berlin (2008)

    Book  Google Scholar 

  10. Bienstock, D., Chen, C., Munoz, G.: Outer-product-free sets for polynomial optimization and oracle-based cuts. arXiv preprint arXiv:1610.04604 (2016)

  11. Castillo, I., Kampas, F.J., Pintér, J.D.: Solving circle packing problems by global optimization: numerical results and industrial applications. Eur J Op Res 191(3), 786–802 (2008)

    Article  MathSciNet  Google Scholar 

  12. Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math Program 91(2), 201–213 (2002)

    Article  MathSciNet  Google Scholar 

  13. Fischetti, M., Ljubić, I., Monaci, M., Sinnl, M.: On the use of intersection cuts for bilevel optimization. Math Program 172(1–2), 77–103 (2018)

    Article  MathSciNet  Google Scholar 

  14. Hifi, M., M’hallah, R.: A literature review on circle and sphere packing problems: models and methodologies. Adv. Oper. Res. 2009 (2009)

  15. Hillestad, R.J., Jacobsen, S.E.: Reverse convex programming. Appl Math Optim 6(1), 63–78 (1980)

    Article  MathSciNet  Google Scholar 

  16. Horst, R., Tuy, H.: Global optimization: Deterministic approaches. Springer Science and Business Media, NY (2013)

    MATH  Google Scholar 

  17. Jones, D.R.: A fully general, exact algorithm for nesting irregular shapes. J Global Optim 59(2–3), 367–404 (2014)

    Article  MathSciNet  Google Scholar 

  18. Khajavirad, A.: Packing circles in a square: a theoretical comparison of various convexification techniques (2017). Preprint available via Optimization Online at http://www.optimization-online.org/DB_FILE/2017/03/5911.pdf

  19. Locatelli, M., Raber, U.: Packing equal circles in a square: a deterministic global optimization approach. Discret Appl Math 122(1–3), 139–166 (2002)

    Article  MathSciNet  Google Scholar 

  20. López, C.O., Beasley, J.E.: A heuristic for the circle packing problem with a variety of containers. Eur J Op Res 214(3), 512–525 (2011)

    Article  MathSciNet  Google Scholar 

  21. Markót, M.C.: Interval methods for verifying structural optimality of circle packing configurations in the unit square. J Comput Appl Math 199(2), 353–357 (2007)

    Article  MathSciNet  Google Scholar 

  22. Markót, M.C., Csendes, T.: A new verified optimization technique for the “packing circles in a unit square” problems. SIAM J Optim 16(1), 193–219 (2005)

    Article  MathSciNet  Google Scholar 

  23. Markót, M.C., Csendes, T.: A reliable area reduction technique for solving circle packing problems. Computing 77(2), 147–162 (2006)

    Article  MathSciNet  Google Scholar 

  24. Misener, R., Floudas, C.A.: Antigone: algorithms for continuous/integer global optimization of nonlinear equations. J Global Optim 59(2–3), 503–526 (2014)

    Article  MathSciNet  Google Scholar 

  25. Puranik, Y., Sahinidis, N.V.: Domain reduction techniques for global nlp and minlp optimization. Constraints 22(3), 338–376 (2017)

    Article  MathSciNet  Google Scholar 

  26. Rebennack, S.: Computing tight bounds via piecewise linear functions through the example of circle cutting problems. Math Method Op Res 84(1), 3–57 (2016)

    Article  MathSciNet  Google Scholar 

  27. Scheithauer, G.: Introduction to Cutting and Packing Optimization: Problems, Modeling Approaches, Solution Methods, vol. 263. Springer, NY (2017)

    MATH  Google Scholar 

  28. Serrano, F.: Intersection cuts for factorable minlp. In: International Conference on Integer Programming and Combinatorial Optimization, pp. 385–398. Springer (2019)

  29. Stoyan, Y.G., Yas’kov, G.: A mathematical model and a solution method for the problem of placing various-sized circles into a strip. Eur J Op Res 156(3), 590–600 (2004)

    Article  MathSciNet  Google Scholar 

  30. Szabó, P.G., Markót, M.C., Csendes, T.: Global optimization in geometry–circle packing into the square. In: Essays and Surveys in Global Optimization, pp. 233–265. Springer, NY (2005)

    MATH  Google Scholar 

  31. Tardella, F.: On the existence of polyhedral convex envelopes. In: Frontiers in global optimization, pp. 563–573. Springer, NY (2004)

    Book  Google Scholar 

  32. Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math Program 103(2), 225–249 (2005)

    Article  MathSciNet  Google Scholar 

  33. Vigerske, S., Gleixner, A.: Scip: global optimization of mixed-integer nonlinear programs in a branch-and-cut framework. Optim Method Softw 33(3), 563–593 (2018)

    Article  MathSciNet  Google Scholar 

  34. Wang, A., Hanselman, C.L., Gounaris, C.E.: A customized branch-and-bound approach for irregular shape nesting. J Global Optim 71(4), 1–21 (2018)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Akang Wang gratefully acknowledges financial support from the James C. Meade Graduate Fellowship and the H. William and Ruth Hamilton Prengle Graduate Fellowship at Carnegie Mellon University.

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA, 15213, USA

    Akang Wang & Chrysanthos E. Gounaris

  2. Center for Advanced Process Decision-making, Carnegie Mellon University, Pittsburgh, PA, 15213, USA

    Akang Wang & Chrysanthos E. Gounaris

Authors
  1. Akang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chrysanthos E. Gounaris
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chrysanthos E. Gounaris.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, A., Gounaris, C.E. On tackling reverse convex constraints for non-overlapping of unequal circles. J Glob Optim 80, 357–385 (2021). https://doi.org/10.1007/s10898-020-00976-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-020-00976-y

Keywords

Search

Navigation