On vertex-parity edge-colorings

Abstract

A vertex signature $\pi$ of a finite graph G is any mapping $\pi \,{:}\,V(G)\rightarrow \{0,1\}$. An edge-coloring of G is said to be vertex-parity for the pair $(G,\pi )$ if for every vertex v each color used on the edges incident to v appears in parity accordance with $\pi$, i.e. an even or odd number of times depending on whether $\pi (v)$ equals 0 or 1, respectively. The minimum number of colors for which $(G,\pi )$ admits such an edge-coloring is denoted by $\chi '_p(G,\pi )$. We characterize the existence and prove that $\chi '_p(G,\pi )$ is at most 6. Furthermore, we give a structural characterization of the pairs $(G,\pi )$ for which $\chi '_p(G,\pi )=5$ and $\chi '_p(G,\pi )=6$. In the last part of the paper, we consider a weaker version of the coloring, where it suffices that at every vertex, at least one color appears in parity accordance with $\pi$. We show that the corresponding chromatic index is at most 3 and give a complete characterization for it.

1 Introduction

Throughout the article we mainly follow terminology and notation used in West (2001). We consider only finite graphs allowing the presence of loops and multiple edges. Given a graph G, the parameters $n(G)=|V(G)|$ and $m(G)=|E(G)|$, respectively, are its order and size. For $n(G)=1$ the graph G is trivial, and for $m(G)=0, G$ is empty. If $S \subseteq V(G)$ and $V_1,\ldots ,V_k$ are the vertex sets of the components of $G-S$, then every induced subgraph $G[V_i\cup S]$ is an S-lobe in G. A vertex v of degree $d_{G}(v)$ equal to k is called a k-vertex; whenever k equals 0 (resp. 1), we say that v is isolated (resp. pendant). Each v having an even (resp. odd) degree is an even (resp. odd) vertex of G. A graph is even (resp. odd) if all its vertices are even (resp. odd). For a vertex v of G, by $E_G(v)$ we denote the collection of edges of G incident to v.

A $\pi \,{:}\,V(G)\rightarrow \{0,1\}$ is a vertex signature of G, and $(G,\pi )$ is referred to as a pair. A component of G endowed with the respective restriction of $\pi$ is called a component of $(G,\pi )$. If G is connected, then $(G,\pi )$ is a connected pair. Every vertex mapped by $\pi$ to 0 (resp. 1) is a zero-vertex (resp. one-vertex) of $(G,\pi )$.

Consider a pair $(G,\pi )$ and a (not necessarily proper) edge-coloring $\varphi$ of G. For an arbitrary color c, the subgraph induced by its color class is denoted by $G_c$. We say that c appears at a vertex v whenever $v\in V(G_c)$; additionally, c appears at v in parity accordance with $\pi$ if $d_{G_c}(v)\equiv \pi (v) ({\mathrm {mod}}\,2)$. If at every vertex each appearing color is in parity accordance with $\pi$, then $\varphi$ is a vertex-parity edge-coloring of $(G,\pi )$ (when it is clear from the context, we simply say an edge-coloring of $(G,\pi )$). Any such $\varphi$ that uses at most k colors is a k-edge-coloring (more verbosely, a vertex-parity k-edge-coloring), and the considered pair is said to be k-edge-colorable. The vertex-parity chromatic index $\chi _{p}'(G,\pi )$ is the minimum integer k for which $(G,\pi )$ is k-edge-colorable. Clearly, the following are two necessary conditions for the existence of $\chi _{p}'(G,\pi )$:

$(P_1)$ :

Every zero-vertex of $(G,\pi )$ is an even vertex of G.

$(P_2)$ :

Every component of $(G,\pi )$ having a unique one-vertex is empty.

Whenever $(P_1)$ and $(P_2)$ are fulfilled, $\pi$ is a proper vertex signature of G and $(G,\pi )$ is a proper pair.

The introduced coloring notion generalizes a previously known concept. Namely, in the case of $\pi$ identically equal to 1 (i.e. when $\pi$ is the so-called odd signature of G), every vertex-parity edge-coloring of $(G,\pi )$ is already known as an odd edge-coloring of G. Under this confinement, the vertex-parity chromatic index of $(G,\pi )$ is the odd chromatic index of G, denoted by $\chi _{o}'(G)$. Odd edge-colorings were introduced by Pyber in his survey on graph coverings (Pyber 1991) as edge-decompositions of a finite graph into (edge-disjoint) odd subgraphs. He considered only simple graphs and proved that 4 colors suffice for an odd edge-coloring of every simple graph. Motivated by the application of multigraph edge-decomposition into edge-disjoint odd subgraphs (Czap et al. 2012; Lužar and Škrekovski 2013), the present authors considered the same notion for loopless (multi)graphs in Lužar et al. (2015). We proved that 6 colors suffice for an odd edge-coloring of each loopless (multi)graph, and characterized when the odd chromatic index equals 6. As a further improvement of this, in Petruševski (2017) it is characterized when 4 colors suffice for an odd edge-coloring of a loopless graph. For the class of subcubic graphs, a complete characterization in terms of $\chi '_o$ is given in Atanasov et al. (2016).

The most general degree factor, called an ${\mathcal {H}}$-factor, is defined as follows. For a vertex v of a graph G, let ${\mathcal {H}}_v$ denote a non-empty subset of $\{0,1,2,3,\ldots \}$. Then a spanning subgraph K is said to be an ${\mathcal {H}}$-factor of G if $d_K(v)\in {\mathcal {H}}_v$, for each v. The graph G is ${\mathcal {H}}$-factorable if it admits an edge-decomposition consisting entirely of ${\mathcal {H}}$-factors. For general works on ${\mathcal {H}}$-factors and ${\mathcal {H}}$-factorability we refer the reader to Akiyama and Kano (2011), Yu and Liu (2009) and Szabó (2006). A special case of the above-mentioned degree factor is defined as follows. Let g, f be two integer-valued functions on V(G) such that $0\le g\le f$. A spanning subgraph F of G is called a parity (g, f)-factor if $g(v)\le d_F(v)\le f(v)$ and $d_F(v)\equiv f(v) \pmod {2}$, for each v. The existence of parity (g, f)-factors was characterized by Lovász in Lovász (1972). A general characterization of parity (g, f)-factorability is not known.

Instances of such edge-decompositions are strongly related to integer flows in graphs. A parity subgraph H of a graph G is a parity $(0,d_G)$-factor, i.e. a spanning subgraph such that, for every vertex $v, d_{H}(v) \equiv d_{G}(v) \pmod {2}$. In the area of integer flows, a number of important theorems have been proven by using the existence properties of parity subgraphs (see e.g. Jaeger 1979). We refer an interested reader to a recent paper of Shu et al. (2012). Another famous problem in the area of edge-decompositions is the cycle double cover problem (Seymour 1979; Szekeres 1973), which asks whether it is possible to decompose the edges of a graph into even subgraphs such that every edge is contained in exactly two subgraphs. While the former case uses a vertex signature related to the degree of each vertex, in the latter the signature is even.

In this article we consider a general signature and confine to edge-disjoint decompositions (thus colorings), however, an additional study of multiple covering of the edges would also be interesting. Our notion of vertex-parity edge-colorability can be seen as an instance of ${\mathcal {H}}$-factorability (Akiyama and Kano 2011), with ${\mathcal {H}}_v$ equal to either $\{0,1,3,5,7,\ldots \}$ or $\{0,2,4,6,8,\ldots \}$, depending on whether $\pi (v)$ is 1 or 0. Note that this slightly differs from the parity (g, f)-factorability with g identically 0 and $f>d_G$, which in turn can be characterized trivially, since we do not require that every color is used at each one-vertex.

The paper is organized as follows. In Sect. 2, we prove that every proper pair is vertex-parity 6-edge-colorable. Furthermore, we characterize the connected proper pairs that require at least 5 colors. In Sect. 3, we briefly study the related notion of weak vertex-parity edge-colorings.

2 Vertex-parity edge-colorings

2.1 Preliminary results

Given a pair $(G,\pi )$ and a vertex $v\in V(G)$, the degree of v is in accordance with $\pi$ if the congruence $d_{G}(v)\equiv \pi (v)\,({\mathrm {mod}}\,2)$ holds. It is an easy matter to characterize the connected proper pairs that are 1-edge-colorable. Indeed, $\chi _{p}'(G,\pi )=0$ if and only if G is empty, whereas $\chi _{p}'(G,\pi )=1$ if and only if G is non-empty and the degree of each vertex is in accordance with $\pi$. In contrast to this, it remains an open question if deciding whether a given proper pair $(G,\pi )$ is 2-edge-colorable is NP-hard.

This subsection establishes vertex-parity edge-colorability in three cases: 2-edge-colorability is shown whenever the underlying graph is acyclic; next, 3-edge-colorability is proved for every connected proper pair having an even number of one-vertices; finally, 3-edge-colorability is demonstrated for every connected proper pair containing a bridge.

Proposition 1

If $\pi$ is a proper vertex signature of a forest F, then $(F,\pi )$ is vertex-parity 2-edge-colorable.

Proof

Clearly, in every forest the condition $(P_1)$ implies $(P_2)$. We proceed by induction on the number of one-vertices v such that $d_F(v)$ is positive and even. If this number equals zero, then $\chi '_p(F,\pi )\le 1$. Otherwise, select such a one-vertex v and split it into two odd one-vertices $v'$ and $v''$. Since $v'$ and $v''$ belong to different components, by induction, the obtained proper pair admits a vertex-parity 2-edge-coloring. Moreover, after a permutation of colors in the component of $v''$ (if necessary) such that the edges incident to $v'$ are colored differently from the edges incident to $v''$, an identification of $v'$ and $v''$ gives a vertex-parity 2-edge-coloring of $(F,\pi )$. $\square$

Let G be a graph and T be a subset of V(G). Following Bondy and Murty (2008), a spanning subgraph H of G is a T-join if $d_{H}(v)$ is odd for all $v\in T$ and even for all $v\in V(G){\setminus } T$. For example, a parity subgraph is precisely an O(G)-join, where O(G) denotes the set of odd vertices of G. Note that by adding the edges of a cycle to a T-join, we again obtain a T-join. Thus, whenever a T-join of G exists, there also exists such a co-forest C, i.e. a subgraph of G such that $G-E(C)$ is a forest. An obvious necessary condition for the existence of a T-join is that the intersection of T with every component of G is even-sized (possibly empty). The following classical result about T-joins claims this condition also suffices (see e.g. Schrijver 2003).

Lemma 1

If G is a connected graph and T an even-sized subset of V(G), then there exists a T-join of G that is a co-forest.

Using Lemma 1, we prove two results regarding vertex-parity 3-edge-colorability.

Proposition 2

If $(G,\pi )$ is a connected proper pair with an even number of one-vertices, then it admits a vertex-parity 3-edge-coloring. Furthermore, if G is even, then $\chi _{p}'(G,\pi )\le 2$.

Proof

Let T be the set of one-vertices of $(G,\pi )$. By Lemma 1, there is a T-join H of G such that $G-E(H)$ is a forest, which we denote by F. Since the degree of every vertex of H is in accordance with $\pi$, the vertex signature $\pi$ is proper for the spanning subgraphs H and F. Therefore, Proposition 1 implies that

$$\begin{aligned} \chi _{p}'(G,\pi ) \le \chi _{p}'(F,\pi ) + \chi _{p}'(H,\pi ) \le 2+1=3\,. \end{aligned}$$

Additionally, if G is even, then the degree of every vertex of F is also in accordance with $\pi$, which implies that one color is enough for F, and so $\chi _{p}'(G,\pi ) \le 2$. $\square$

Proposition 3

Let $(G,\pi )$ be a connected proper pair such that the graph G contains a bridge. Then $(G,\pi )$ is vertex-parity 3-edge-colorable.

Proof

We first consider the case when the minimum degree of G is 1. By Proposition 2, we may assume that the cardinality of the fiber $\pi ^{-1}(1)$ is odd. Select a pendant vertex u of G, and define $T=\pi ^{-1}(1)\backslash \{u\}$. Since u is a one-vertex, the set T is even-sized, thus we may take a T-join H of G such that $G-E(H)$ is a forest F. Similarly as above, $\pi$ is a proper vertex signature for each of the spanning subgraphs H and F, implying that $\chi _{p}'(G,\pi )\le 3$.

Suppose now that there is no pendant vertex in G. Let vw be a bridge in G, and denote by $G_{v}$ and $G_{w}$, respectively, the components of $G-vw$ containing v and w. For the induced subgraphs $G'=G[V(G_{v})\cup \{w\}]$ and $G''=G[V(G_{w})\cup \{v\}]$ define respective proper vertex signatures $\pi '$ and $\pi ''$ by setting

$$\begin{aligned} \pi '(u)= {\left\{ \begin{array}{ll} \pi (u) &{} \quad \text {if}\, u\in V(G_{v}), \\ 1 &{} \quad \text {if }\, u=w, \end{array}\right. }\quad \hbox {and}\quad \pi ''(u)= {\left\{ \begin{array}{ll} \pi (u) &{} \quad \text {if}\, u\in V(G_{w}), \\ 1 &{} \quad \text {if} \, u=v. \end{array}\right. } \end{aligned}$$

Since both $(G',\pi ')$ and $(G'',\pi '')$ are connected proper pairs with $\delta (G')=\delta (G'')=1$, the first part of the proof implies the existence of respective vertex-parity 3-edge-colorings $\varphi '$ and $\varphi ''$ using the same color set. Moreover, by permuting the colors if necessary, we may assume that $\varphi '(vw)=\varphi ''(vw)$. Then $\varphi ' \cup \varphi ''$ is a vertex-parity 3-edge-coloring of $(G,\pi )$. $\square$

2.2 Tight upper bound for $\chi _{p}'$

As mentioned in the introduction, whenever $\pi$ is the odd signature of $G, \chi '_p(G,\pi )$ equals the odd chromatic index $\chi '_o(G)$. The notion of odd edge-colorability was already studied in Lužar et al. (2015) and Petruševski (2017) for loopless graphs (the confinement to ‘looplessness’ was appropriate for two reasons: first, excepting the trivial non-empty graph, any other connected graph is odd edge-colorable; and second, the addition of loops to a connected non-trivial graph never changes the existence nor the value of its odd chromatic index).

Let us recall some terminology. A bouquet ${\mathcal {B}}_{uv}$ in G is the set $E_G(u)\cap E_G(v)$ for a pair of distinct adjacent vertices u, v. In Lužar et al. (2015), a loopless graph G on three pairwise adjacent vertices was called a Shannon triangle. Here we slightly enlarge the scope of this notion by allowing the presence of arbitrarily many loops at each of the three vertices. Let p, q, r be the parities of the sizes of its three bouquets in a non-increasing order, with 2 (resp. 1) denoting a bouquet of even (resp. odd) size. Then, the considered Shannon triangle G is of type (p, q, r). Observe that the handshake lemma readily implies the equality $\chi _{o}'(G)=p+q+r$. We use a result of Petruševski (2017) (viz. Theorem 5.3).

Theorem 1

(Petruševski 2017) A connected loopless graph G is odd 4-edge-colorable if and only if it is not a Shannon triangle of type (2, 2, 2) or (2, 2, 1).

The vertex-parity edge-colorability of pairs relates to the odd edge-colorability of graphs via the following. Given a graph $G_0$ and a pair $(G,\pi )$, we say that $(G,\pi )$ is a derivative of $G_0$, denoted by $(G,\pi )\preceq G_0$, whenever $\pi ^{-1}(1)=V(G_0)$ and G is obtainable from $G_0$ through a finite (possibly empty) succession of the following two operations:

$(D_1)$ :

subdivide an arbitrary edge (thus creating a new 2-vertex);

$(D_2)$ :

identify any number of newly created 2-vertices.

In particular, if $(D_2)$ is never applied, then $(G,\pi )$ is a subdivision of $G_0$. Note that $(G,\pi )$ is vertex-parity edge-colorable as soon as $G_0$ is odd edge-colorable. Additionally, since any odd k-edge-coloring of $G_0$ naturally induces a vertex-parity k-edge-coloring of $(G,\pi )$, it holds that

$$\begin{aligned} \chi _{p}'(G,\pi )\le \chi _{o}'(G_0). \end{aligned}$$

(1)

For any subdivision $(G,\pi )$ of $G_0$, clearly (1) becomes an equality, but in general it might be strict (cf. Fig. 1).

Fig. 1

The pair $(G,\pi )$ is a derivative of both graphs $G_0'$ and $G_0''$. However, it holds that $\chi _{p}'(G,\pi ) = 4$, whereas $\chi _{o}'(G_0') = 4$ and $\chi _{o}'(G_0'') = 6$

As already stated, a necessary condition for vertex-parity edge-colorability is the properness of the pair. Next we show this also suffices. Moreover, we capture the parameter $\chi '_p$ through $\preceq$ and $\chi '_o$.

Theorem 2

Every connected proper pair $(G,\pi )$ is vertex-parity 6-edge-colorable. Furthermore, there exists a (not necessarily connected) graph $G_0$ such that $(G,\pi )\preceq G_0$ and $\chi _{p}'(G,\pi )= \chi _{o}'(G_0)$.

Proof

We prove the first part of the statement by contradiction. Suppose that $(G,\pi )$ is a counterexample which minimizes m(G). By Proposition 3, G is bridgeless. Furthermore, the minimality assures G is loopless. Thus, Theorem 1 yields that $\pi$ is certainly not the odd vertex signature. Consider an arbitrary zero-vertex w of $(G,\pi )$. We will show that $d_G(w)\ge 4$. Indeed, since $\pi$ is proper, w is necessarily an even vertex of G, hence it only remains to discard the possibility that $d_G(w)=2$. For argument’s sake, suppose this is the case and let $e_{1}$ and $e_{2}$ be the only two edges incident to w, with $v_{1}$ and $v_{2}$, respectively, being their other endpoints (it may happen that $v_{1}=v_{2}$). Suppress w, i.e. remove it and then add an edge $e = v_1v_2$ (an edge is added even if $v_1$ and $v_2$ are already adjacent in G in order to preserve their degrees). The restriction $\pi '=\pi _{|V(G){\setminus }\{w\}}$ is a proper vertex signature of the obtained connected graph $G'$. Therefore, the smaller pair $(G',\pi ')$ admits a 6-edge-coloring $\varphi '$. This $\varphi '$ gives a 6-edge-coloring of $(G,\pi )$ by reintroducing w and coloring the edges $e_{1}, e_{2}$ with the color $\varphi '(e)$. The deduced contradiction confirms $d_G(w)\ge 4$.

Now, select two edges $e,f\in E_G(w)$, which in the case when w is a cut-vertex of G belong to different $\{w\}$-lobes. Split w into two zero-vertices $w_1$ and $w_2$ such that $w_2$ is a 2-vertex whose only incident edges are e and f. The 2-edge-connectedness of G assures the obtained pair is connected. Since it is clearly proper and of the same size as G, but with a zero-vertex of degree 2, it admits a 6-edge-coloring. However, this readily furnishes a 6-edge-coloring of $(G,\pi )$ simply by identifying the zero-vertices $w_1$ and $w_2$. The last contradiction establishes the first part of the theorem.

As for the second part, set $k=\chi '_{p}(G,\pi )$ and let $\varphi$ be a vertex-parity k-edge-coloring of $(G,\pi )$. Keeping this particular coloring on the edges, as long as there is a zero-vertex of degree greater than 2, split it into two zero-vertices such that at least one of them is a 2-vertex with all incident edges colored the same under $\varphi$. By doing so, $\varphi$ remains a vertex-parity edge-coloring of the new pair. Continue applying such splittings until the degree of every zero-vertex reduces to 2. Following this, remove the vertices of each cycle that consists entirely of zero-vertices. Finally, suppress all the zero-vertices of the resulting pair, and denote the underlying graph by $G_0$. A moment’s thought reveals that $(G,\pi )$ is a derivative of $G_0$. Moreover, since the described process clearly transforms $\varphi$ into an odd k-edge-coloring of $G_0$, the equality $\chi _{p}'(G,\pi )= \chi _{o}'(G_0)$ is implied by (1). $\square$

Note that the last result cannot be improved by claiming connectedness for $G_0$ (cf. Fig. 2).

Fig. 2

The connected proper pair $(G,\pi )$ is a derivative only of the disconnected graph obtained as the union of two copies of $K_2$

Corollary 1

For every connected proper pair $(G,\pi )$ that is not a derivative of a Shannon triangle of type (2, 2, 2) or (2, 2, 1), it holds that $\chi _{p}'(G,\pi ) \le 4$.

This in particular means that if there are at least four one-vertices in a connected proper pair, it admits a vertex-parity edge coloring with at most 4 colors. Further, Fig. 1 demonstrates that not every derivative of a Shannon triangle of type (2, 2, 2) requires six colors for a vertex-parity edge-coloring (a similar example can be given for a Shannon triangle of type (2, 2, 1)). In the next subsection we characterize which of these derivatives ask for at least five colors.

The following proposition shows that the bound of 4 colors in Corollary 1 is best possible as there is an infinite family of graphs achieving the upper bound.

Proposition 4

For an integer $k\ge 2$, let $(G_1,\pi _1),\ldots ,(G_k,\pi _k)$ be disjoint connected proper pairs none of which is vertex-parity 3-edge-colorable. For each $i=1,\ldots ,k$, let $v_i$ be an even one-vertex of the i-th pair. Identify $v_1,\ldots ,v_k$ into a new one-vertex v. The obtained pair $(G,\pi )$ is connected and $\chi _{p}'(G,\pi )=4$.

Proof

The pair $(G,\pi )$ is not a derivative of a Shannon triangle of type (2, 2, 2) or (2, 2, 1), as no derivative of a Shannon triangle contains a one-vertex which is a cut-vertex. Therefore, by Corollary 1, it suffices to show that the constructed pair is not vertex parity 3-edge-colorable. Suppose, to the contrary, $\varphi$ is a vertex-parity 3-edge-coloring of $(G,\pi )$. Since $d_G(v)$ is even, precisely two colors, say 1 and 2, appear at v under $\varphi$. On the other hand, since all the identified vertices were even, there must be an index i such that both 1 and 2 are odd at v under $\varphi _i=\varphi _{|E(G_i)}$. But this implies that $\varphi _i$ is a vertex-parity 3-edge-coloring of $(G_i,\pi _i)$, a contradiction. $\square$

As Proposition 4 demonstrates, a succinct characterization of pairs with vertex-parity chromatic index equal to 4 is not straightforward if possible at all.

The particular splitting of zero-vertices used in the latter part of the proof of Theorem 2 is said to be in accordance with the considered edge-coloring $\varphi$. Two principal features of any such splitting are:

$(S_1)$ :

the ‘properness’ of the pair is preserved, i.e. $(P_1)$ and $(P_2)$ continue to hold;

$(S_2)$ :

any zero-vertex of the resulting (terminal) pair has degree 2.

Let us agree that any future reference to splitting of zero-vertices takes into account only those that preserve $(P_1)$. Additionally, if $(P_2)$ is also fulfilled, then we say the splitting is proper. On the other hand, whenever $(S_2)$ holds, we speak of a complete splitting of the zero-vertices of $(G,\pi )$.

Notice that given a connected proper pair with $|\pi ^{-1}(1)|=3$, a splitting of its zero-vertices is proper if and only if it does not separate the set $\pi ^{-1}(1)$, i.e. keeps the three one-vertices in a component, named the $\pi ^{-1}(1)$-component of the considered pair. We end this subsection with an initial characterization of the inequality $\chi _{p}'(G,\pi )\ge 5$, and postpone a structural one for the upcoming.

Proposition 5

Given a connected proper pair $(G,\pi )$ with $|\pi ^{-1}(1)|=3$, the following two statements are equivalent:

(i):

$\chi _{p}'(G,\pi )\ge 5$.

$({ ii})$ :

After any proper complete splitting of the zero-vertices of $(G,\pi )$, the $\pi ^{-1}(1)$-component of the resulting pair is a subdivision of a Shannon triangle of type (2, 2, 2) or (2, 2, 1).

Proof

Suppose there is a proper complete splitting of the zero-vertices of $(G,\pi )$ that results in a pair whose $\pi ^{-1}(1)$-component is not a subdivision of a Shannon triangle of type (2, 2, 2) or (2, 2, 1). By Theorem 1 and the inequality (1), the new pair is vertex-parity 4-edge-colorable (apart from its $\pi ^{-1}(1)$-component, the rest of it is obviously vertex parity 1-edge-colorable). But this naturally induces a vertex-parity 4-edge-coloring of $(G,\pi )$, which confirms that (i) implies $({ ii})$.

Other way around, suppose $k=\chi _{p}'(G,\pi )<5$ and take a k-edge-coloring $\varphi$ of $(G,\pi )$. Implement to its zero-vertices a proper complete splitting that is in accordance with $\varphi$. The $\pi ^{-1}(1)$-component of the resulting pair is clearly k-edge-colorable. Hence, it cannot be a subdivision of a Shannon triangle of type (2, 2, 2) or (2, 2, 1), proving that $({ ii})$ implies (i). $\square$

2.3 Structural characterizations of $\chi _{p}'=5$ and $\chi _{p}'=6$

Given a pair $(G,\pi )$ and a vertex w, a $(w,\pi ^{-1})$-path is a path from w to some one-vertex, for which all its interior vertices are zero-vertices. For any zero-vertex w, consider all $(w, \pi ^{-1})$-paths, and let $S_w$ be the set of one-vertices which are end-vertices of such paths. For every $S\subseteq \pi ^{-1}(1)$ define $Z_S = \{w : S_w = S\}$. Observe that $\pi ^{-1}(0)$ is a disjoint union of all the $Z_S$’s and that $w\in Z_S$ if and only if $S\subseteq \pi ^{-1}(1)$ is minimal such that w belongs to an ‘all zeros’ component of $(G,\pi )-S$. For example, $Z_{\emptyset }$ collects the zero-vertices belonging to the ‘all zeros’ components of $(G,\pi )$ (i.e. the components on which the corresponding restriction of $\pi$ is identically equal to zero); similarly, under the assumptions that $(G,\pi )$ is connected and $\pi (x) = 1, Z_{\{x\}}=\bigcup _{i:\,\,V(H_i)\subseteq \pi ^{-1}(0)}V(H_i)$, where $H_1,\ldots ,H_k$ are the components of $G-x$. The next proposition shows that the set $Z(G)=\bigcup _{x\in \pi ^{-1}(1)}Z_{\{x\}}$ can be safely ignored in regard to $\chi _{p}'(G,\pi )$.

Proposition 6

Given a connected proper pair $(G,\pi )$, let $G'=G-Z(G)$ and $\pi '=\pi _{|V(G')}$. Then $\chi '_p(G',\pi ')=\chi '_p(G,\pi )$.

Proof

We may assume that $|\pi ^{-1}(1)|\ge 2$, as for $|\pi ^{-1}(1)|\le 1$ holds $Z(G)=\emptyset$. For every $x\in \pi ^{-1}(1)$, consider the even graph $G_x=G[\{x\}\cup Z_{\{x\}}]$. Let $\varphi$ be a vertex-parity k-edge-coloring of $(G,\pi )$, and H the subgraph induced by a color class of $\varphi$. For every one-vertex x such that $E(G_x)\cap E(H)\ne \emptyset$, the graph $G_x \cap H$ is even. Therefore, $\varphi _{|E(G')}$ is a k-edge-coloring of $(G',\pi ')$, implying that $\chi _{p}'(G,\pi )\ge \chi _{p}'(G',\pi ')$.

For the reversed inequality, it suffices to observe that any k-edge-coloring $\varphi '$ of $(G',\pi ')$ extends to a k-edge-coloring of $(G,\pi )$ as follows: for each one-vertex x, choose a color appearing at x under $\varphi '$ and then use it on every non-colored edge of $E(G_x)$ (i.e. on every edge which is not a loop at x). $\square$

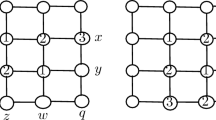
Since the objective of this subsection is to characterize the inequality $\chi _{p}'(G,\pi )\ge 5$ for all connected proper pairs, by Corollary 1, we may from now on restrict to such pairs having $|\pi ^{-1}(1)|=3$, say $\pi ^{-1}(1)=\{a,b,c\}$. Under the last constraint, $\pi ^{-1}(0)\backslash Z(G)$ can be seen as the disjoint union of four (possibly empty) subsets: namely, $Z_{\{a,b\}}, Z_{\{b,c\}}, Z_{\{a,c\}}$, and $Z_{\{a,b,c\}}$. For any two distinct one-vertices x and y of G, we shall consider the induced subgraph $G_{xy}=G[\{x,y\}\cup Z_{\{x,y\}}\cup Z_{\{a,b,c\}}]$ (cf. Fig. 3). Note that $G_{xy}$ can be efficiently determined: for if z denotes the third one-vertex, then $G_{xy}$ is precisely what remains of $G-G_z$ after removing $Z(G-G_z)$.

Fig. 3

An example of a graph with three one-vertices a, b, and c depicted with full circles, and the zero-vertices depicted with empty circles. Note that in the example, the sets $Z_{a,b}$ and $Z_{b,c}$ are empty

It is readily seen that whenever $(G,\pi )$ is a derivative of a Shannon triangle, each of the subgraphs $G_{ab},G_{bc},G_{ac}$ is connected. We proceed by showing that for $\chi _{p}'(G,\pi )\ge 5$ it is necessary that no two of these three subgraphs share a zero-vertex, i.e. $Z_{\{a,b,c\}}=\emptyset$.

Lemma 2

If $(G,\pi )$ is a connected proper pair such that $\pi ^{-1}(1)=\{a,b,c\}$ and $Z_{\{a,b,c\}}\ne \emptyset$, then $\chi _{p}'(G,\pi )\le 4$.

Proof

Let us first establish that for some $v\in Z_{\{a,b,c\}}$ there are three v-$\{a,b,c\}$ paths forming a tree $T\subseteq G$ whose only leaves are a, b, c. Indeed, consider the non-empty family ${\mathcal {W}}$ of pairs $(W_{ab},W_{ac})$, where $W_{ab}$ is an a-b walk from $G_{ab}$, and $W_{ac}$ is an a-c walk from $G_{ac}$ sharing a zero-vertex with $W_{ab}$. Select a member of ${\mathcal {W}}$ that minimizes $|E(W_{ab})\cup E(W_{ac})|$. By the minimality choice, the two walks forming this pair must be paths (seen as subgraphs of G), and $W_{ab}\cap W_{ac}$ must be an initial subpath of both (a subpath starting at a). Say this subpath ends at v. Then $W_{ab}\cup W_{ac}$ is the promised tree T.

Employ the following proper splitting of zero-vertices which ’preserves’ T: as long as there is a zero-vertex w of degree greater than 2 that can be split without violating $(P_1)$ nor altering the adjacency relation of E(T), split w likewise; continue so until no such zero-vertex exists in the obtained proper pair $(G',\pi ')$. Let $v'$ be the label of its only zero-vertex incident to three edges from E(T). Clearly, $v'$ is the only zero-vertex of $(G'-E(T),\pi ')$ having an odd degree. Therefore, there exists a $v'$-$\{a,b,c\}$ path P in $G'-E(T)$, and say it ends at a (by assuming this, $d_{G'-E(T)}(a)$ is not necessarily odd). Define $H=T\cup P$, with the four edges of H incident to $v'$ labeled as in Fig. 4a.

Fig. 4

The graph H and two possible splits of the vertex $v'$

The described splitting of zero-vertices is proper but not complete: namely, $v'$ is the only zero-vertex of $(G',\pi ')$ having degree greater than 2 ($d_{G'}(v')=4$). In order to finish the proof, it suffices to show that $v'$ can be further split producing a proper pair $(G'',\pi '')$ in which at least two of the subgraphs $G''_{ab},G''_{bc},G''_{ac}$ are non-even. Indeed, this would imply that the $\pi ^{-1}(1)$-component of $(G'',\pi '')$ is not a subdivision of a Shannon triangle of type (2, 2, 2) or (2, 2, 1), and subsequently the inequality $\chi _{p}'(G,\pi )\le 4$ would follow from Proposition 5. We consider two cases regarding the parity of $d_G(a)$.

Case 1: The degree $d_G(a)$ is even. Then $d_{G'}(a)$ is also even, and thus $d_{G'_{ab}}(a)$ and $d_{G'_{ac}}(a)$ are of the same parity. We split $v'$ into zero-vertices $v'_1$ and $v'_2$ in accordance with the following:

• If $d_{G'_{ab}}(a)$ and $d_{G'_{ac}}(a)$ are both even, then let $v'_1$ be incident with $e_1$ and f, whereas $v'_2$ is incident with $e_2$ and g (see Fig. 4b);

• If $d_{G'_{ab}}(a)$ and $d_{G'_{ac}}(a)$ are both odd, then let $v'_1$ be incident with $e_1$ and $e_2$, whereas $v'_2$ is incident with f and g (see Fig. 4c).

Since the described final split achieves that $d_{G''_{ab}}(a)$ and $d_{G''_{ac}}(a)$ are odd, the subgraphs $G''_{ab}$ and $G''_{ac}$ are certainly non-even.

Case 2: The degree $d_G(a)$ is odd. Then $(G,\pi )$ has precisely two odd one-vertices, and we may assume the other one is b. Since $d_{G'}(a)$ and $d_{G'}(b)$ are odd, it is enough to make sure that after the final split $G''_{ab}$ is even (this would imply that both $G''_{ac}$ and $G''_{bc}$ are non-even). The following splitting of $v'$ into zero-vertices $v'_1$ and $v'_2$ complies:

• If $d_{G'_{ab}}(a)$ is odd, then let $v'_1$ be incident with $e_1$ and f, whereas $v'_2$ is incident with $e_2$ and g (see Fig. 4b);

• If $d_{G'_{ab}}(a)$ is even, then let $v'_1$ be incident with $e_1$ and $e_2$, whereas $v'_2$ is incident with f and g (see Fig. 4c).

Indeed, after the described final split, $d_{G''_{ab}}(a)$ is even, hence so is the subgraph $G''_{ab}$.

$\square$

Note that the requirement $Z_{\{a,b,c\}}=\emptyset$ is the same as asking that the pairwise intersections of $G_{ab},G_{bc},G_{ac}$ are trivial.

Corollary 2

Given a connected proper pair $(G,\pi )$ with $\pi ^{-1}(1)=\{a,b,c\}$, the following implications hold:

• (i) If $\chi _{p}'(G,\pi )= 5$, then $G_{ab},G_{bc},G_{ac}$ are connected, precisely two of them are even, and their pairwise intersections are trivial.

• (ii) If $\chi _{p}'(G,\pi )= 6$, then $G_{ab},G_{bc},G_{ac}$ are connected, all three are even, and their pairwise intersections are trivial.

In what follows, for simplicity, we occasionally abuse notation by denoting any restriction of $\pi$ with the same label.

Proposition 7

Let $(G,\pi )$ be a connected proper pair with $\pi ^{-1}(1)=\{a,b,c\}$ such that $G_{ab},G_{bc}, G_{ac}$ are connected, at least two of them are even, and their pairwise intersections are trivial. The following statements are equivalent:

• (i) $\chi _{p}'(G,\pi )\ge 5$.

• (ii) In any even subgraph $G_{xy}\in \{G_{ab},G_{bc},G_{ac}\}$, no splitting of the zero-vertices of $(G_{xy},\pi )$ disconnects x from y.

Proof

$(i)\Rightarrow ({ ii})$: Suppose $({ ii})$ fails for say $G_{ab}$, i.e. there exists a splitting of the zero-vertices of $(G_{ab},\pi )$ that disconnects a from b. We show how this can be extended to a proper complete splitting of the zero-vertices of $(G,\pi )$. Fix an a-c path $P_{ac}$ in $G_{ac}$ and a b-c path $P_{bc}$ in $G_{bc}$. First, as long as there is a zero-vertex $w\in (P_{ac} \cup P_{bc}) \,-\, \{a,b,c\}$ of degree $d_G(w)>2$, split it into zero-vertices $w'$ and $w''$, such that $w''$ is of degree 2 and incident only to the edges from $E_G(w)\cap (E(P_{ac})\cup E(P_{bc}))$. This assures that both $P_{ac}$ and $P_{bc}$ ‘survive’ the splitting, thus preserving $(P_2)$. Next, continue with the splitting of zero-vertices until each remaining is of degree 2. The described procedure constitutes a proper complete splitting of the zero-vertices of $(G,\pi )$. Moreover, it results in a pair whose $\{a,b,c\}$-component is not a subdivision of a Shannon triangle. By Proposition 5, the statement (i) is not fulfilled.

$({ ii})\Rightarrow (i)$: Assume that $({ ii})$ holds. Then every proper complete splitting of the zero-vertices of $(G,\pi )$ results in a pair whose $\{a,b,c\}$-component is a subdivision of a Shannon triangle of type (2, 2, 2) or (2, 2, 1). Using Proposition 5 again, the statement (i) is fulfilled. $\square$

Taking into account Corollary 2 and Proposition 7, the intended structural characterizations require just one more auxiliary result. The next lemma provides it.

Lemma 3

For a connected even graph H, let $\pi$ be a vertex signature with $\pi ^{-1}(1)=\{x,y\}$. The following two statements are equivalent:

• (i) At least one splitting of the zero-vertices of $(H,\pi )$ disconnects x from y.

• (ii) The vertices x and y are non-adjacent, and every $\{x,y\}$-lobe is an even subgraph of H.

Proof

$(i)\Rightarrow ({ ii})$: Suppose $({ ii})$ is not fulfilled. If x and y are adjacent, then clearly (i) fails as well. Therefore, by assuming further that x and y are non-adjacent, let L be a non-even $\{x,y\}$-lobe in H. Since x and y are the only odd vertices of L, the handshake lemma assures that no splitting of the zero-vertices of $(L,\pi )$ disconnects x from y. Thus, the statement (i) is not fulfilled.

$({ ii})\Rightarrow (i)$: Assume now that $({ ii})$ holds, and consider an arbitrary $\{x,y\}$-lobe L. Since $d_L(x)$ is even, for an even number, say $2s\ge 0$, of neighbors $u_1,u_2,\ldots ,u_{2s}\in N_L(x)$, the bouquet ${\mathcal {B}}_{u_ix}$ is odd-sized. Select $e_i\in {\mathcal {B}}_{u_ix}$, for $i=1,2,\ldots ,2s$. By setting $T=\{u_1,u_2,\ldots ,u_{2s}\}$, let K be an arbitrary T-join of the connected graph $L-\{x,y\}$. Consider the edge set $S=E(K)\cup \{e_1,e_2,\ldots ,e_{2s}\}$, and denote by [S] the even subgraph of $L-y$ induced by S. Fix a cycle decomposition ${\mathcal {C}}=\{C_1,\ldots ,C_r\}$ of [S]. We use ${\mathcal {C}}$ to construct a splitting of the zero-vertices of $(L,\pi )$ that disconnects x from y:

• First, split each zero-vertex w from [S] as follows. For each $C_i\in {\mathcal {C}}$ containing w, create (from w) a zero-vertex $w''_{C_i}$ of degree 2 incident only to $E(C_i)\cap E_{L}(w)$. Let $L'$ be the graph obtained from L after such splits are successively employed at every zero-vertex belonging to [S].

• Second, note that for each neighbor u of x in $L'-\{e_1,e_2,\ldots ,e_{2s}\}$, the bouquet ${\mathcal {B}}_{ux}$ is even-sized, say it consists of the 2t edges $f_1,f_2,\ldots ,f_{2t}$. Split u repeatedly by creating zero-vertices $u^{(1)},\ldots ,u^{(t)}$, each of degree 2, such that for $i=1,\ldots ,t$ the vertex $u^{(i)}$ is incident only to the edges $f_{2i-1}$ and $f_{2i}$. Denote by $L''$ the graph obtained from $L'$ after the described repeated splitting of each neighbor that x has in $L'-\{e_1,e_2,\ldots ,e_{2s}\}$.

Since the vertex x is clearly disconnected from y in $L''$, the statement (i) holds. $\square$

From Lemmas 2 and 3, Corollary 2, and Proposition 7, one easily deduces the promised characterizations of $\chi _{p}'=5$ and $\chi _{p}'=6$.

Theorem 3

Let $(G,\pi )$ be a connected proper pair. Then $\chi _{p}'(G,\pi )= 5$ if and only if the following conditions hold:

• (1) $|\pi ^{-1}(1)|=3$.

• (2) For $\pi ^{-1}(1)=\{a,b,c\}$, the subgraphs $G_{ab},G_{bc}, G_{ac}$ are connected, precisely two of them are even, and their pairwise intersections are trivial.

• (3) In any even $G_{xy}\in \{G_{ab},G_{bc},G_{ac}\}$, the vertices x and y are adjacent or at least two of the $\{x,y\}$-lobes are non-even.

Theorem 4

Let $(G,\pi )$ be a connected proper pair. Then $\chi _{p}'(G,\pi )= 6$ if and only if the following conditions hold:

• (1) $|\pi ^{-1}(1)|=3$.

• (2) For $\pi ^{-1}(1)=\{a,b,c\}$, the subgraphs $G_{ab},G_{bc}, G_{ac}$ are connected, all three are even, and their pairwise intersections are trivial.

• (3) In any $G_{xy}\in \{G_{ab},G_{bc},G_{ac}\}$, the vertices x and y are adjacent or at least two of the $\{x,y\}$-lobes are non-even.

3 Weak vertex-parity edge-colorings

In the current section, by relaxing the requirement ‘colorwise’, we introduce and study a coloring notion similar to the one considered in the previous section. Once again, let a pair $(G,\pi )$ and an edge-coloring $\varphi$ of G be given. If at every non-isolated vertex of G at least one color appears in parity accordance with $\pi$, then $\varphi$ is a weak vertex-parity edge-coloring of $(G,\pi )$. Any such coloring that uses at most k colors is a weak vertex-parity k -edge-coloring, and the considered pair is weak vertex-parity k -edge-colorable. The weak vertex-parity chromatic index $\chi _{{\mathrm {wp}}}'(G,\pi )$ is the minimum integer k for which $(G,\pi )$ is weak vertex-parity k-edge-colorable.

Obviously, the following two conditions are necessary for the existence of $\chi _{{\mathrm {wp}}}'(G,\pi )$:

$(W_1)$ :

Any pendant vertex of G is a one-vertex of $(G,\pi )$.

$(W_2)$ :

Any non-empty component of $(G,\pi )$ having a unique one-vertex contains a zero-vertex of degree greater than 2.

When $(W_1)$ and $(W_2)$ are fulfilled, we refer to $\pi$ as a weak-proper signature of G, or equivalently say that $(G,\pi )$ is a weak-proper pair (see Fig. 5 for an example of a graph which is not weak vertex-parity edge-colorable). In the special case of the odd signature $\pi$, the above coloring notion was already studied in Petruševski (2015) under the term weak odd edge-coloring of G. In what follows we provide an analogous study for the general case.

Theorem 5

Every connected weak-proper pair $(G,\pi )$ is weak vertex-parity 3-edge-colorable. Furthermore, $\chi '_{{\mathrm {wp}}}(G,\pi )=3$ if and only if the following two conditions hold:

• (i) G is an even graph;

• (ii) the number of one-vertices is odd.

Proof

For simplicity, denote by ${\mathcal {C}}$ the collection of those connected weak-proper pairs satisfying (i) and $({ ii})$, and by ${\mathcal {C}}^c$ the set-theoretic complement of ${\mathcal {C}}$ (within the set of connected weak-proper pairs). First we show that $(G,\pi )\in {\mathcal {C}}^c$ always implies $\chi '_{{\mathrm {wp}}}(G,\pi )\le 2$.

Arguing by contradiction, suppose that $(G,\pi )$ is a counterexample that minimizes m(G). Then G must be loopless and $n(G)\ge 3$.

Fig. 5

A pair which is not weak vertex-parity edge-colorable

Claim 1

${\delta }(G)\ge 2$.

Otherwise, let v be a pendant vertex of G and denote by w its only neighbor. Notice that $(G-v,\pi )\in {\mathcal {C}}$. Indeed, by minimality, the corresponding restriction of $\pi$ must be a weak-proper vertex signature of the graph $G-v$, and if $(G-v,\pi )\in {\mathcal {C}}^c$, this pair would admit a weak vertex-parity edge-coloring $\varphi$ with the color set $\{1,2\}$ such that 1 is in parity accordance with $\pi$ at w. But then, by coloring vw with $2, \varphi$ would extend to a weak vertex-parity 2-edge-coloring of $(G,\pi )$. Now that $(G-v,\pi )\in {\mathcal {C}}$ is established, alter $\pi (w)$ to $1-\pi (w)$, and denote by $\pi '$ the newly obtained vertex signature of $G-v$. Then $(G-v,\pi ')\in {\mathcal {C}}^c$, hence it admits a weak vertex-parity edge-coloring $\varphi '$ with the color set $\{1,2\}$ under which 1 is in parity accordance with $\pi '$ at w. Extend $\varphi '$ by coloring vw with 1. This gives a weak vertex-parity 2-edge-coloring of $(G,\pi )$, a contradiction.

Claim 2

G is bridgeless.

Suppose the contrary and consider a bridge vw of G. We argue similarly to the proof of Proposition 3. Denote by $G_{v}$ and $G_{w}$, respectively, the components of $G-vw$ containing v and w. To the induced subgraphs $G'=G[V(G_{v})\cup \{w\}]$ and $G''=G[V(G_{w})\cup \{v\}]$ assign the weak-proper vertex signatures $\pi '$ and $\pi ''$ ’arising’ from the corresponding restrictions of $\pi$ (as in the proof of Proposition 3). Since none of the connected pairs $(G',\pi ')$ and $(G'',\pi '')$ is even, they both belong to ${\mathcal {C}}^c$. Additionally, by the previous claim, each of the graphs $G'$ and $G''$ is of smaller size than G. Therefore, there exist respective weak vertex-parity edge-colorings $\varphi '$ and $\varphi ''$ of $(G',\pi ')$ and $(G'',\pi '')$, both with the color set $\{1,2\}$. Moreover, by permuting colors if necessary, we may assume $\varphi '(vw)=\varphi ''(vw)$. But then $\varphi ' \cup \varphi ''$ is a weak vertex-parity 2-edge-coloring of $(G,\pi )$, a contradiction.

Claim 3

Every one-vertex v has $d_G(v)=2$.

Suppose v refutes the claim, i.e. $d_G(v)\ge 3$. Without destroying the connectedness, we can split v into one-vertices $v'$ and $v''$ such that $v''$ is of degree 2. Indeed, simply select two edges $e,f\in E_G(v)$, which in the case v is a cut vertex belong to different $\{v\}$-lobes of G, and set $v''$ be incident precisely to e and f. By Claim 2, the connectedness is preserved. Let $(G',\pi ')$ be the pair obtained by suppressing $v''$. Since $(G',\pi ')\in {\mathcal {C}}^c$ and $m(G')<m(G)$, this pair admits a weak vertex-parity 2-edge-coloring $\varphi '$. Notice that $\varphi '$ naturally induces a weak vertex-parity 2-edge-coloring of $(G,\pi )$, a contradiction.

Claim 4

Every zero-vertex w has $d_G(w)=3$.

The choice of $(G,\pi )$ implies that each of its zero-vertices has degree at least 3 (a suppressing argument analogous to the one used in the proof of Theorem 2 discards the possibility of a zero-vertex with degree 2). On the other hand, supposing that a vertex $w\in \pi ^{-1}(0)$ has $d_G(w)\ge 4$, the same line of reasoning as in the proof of the previous claim leads to a contradiction. We leave out the details.

The latter two claims establish that $2\le \delta (G)\le \varDelta (G)\le 3$. Moreover, in the case when G is 2-regular, its order must be even, hence G is not an odd cycle. However, a classical result about 2-edge-colorings (see Bondy and Murty 1976, Lemma 6.1.1) states the following: Every connected graph that is not an odd cycle admits a 2-edge-coloring in which both colors appear at each vertex of degree at least two. Consider such an edge-coloring $\varphi$ of G. This $\varphi$ is clearly a weak vertex-parity 2-edge-coloring of $(G,\pi )$. This contradiction establishes that, indeed, $\chi '_{{\mathrm {wp}}}(G,\pi )\le 2$ holds for every $(G,\pi )\in {\mathcal {C}}^c$.

We are left to prove that $(G,\pi )\in {\mathcal {C}}$ always implies $\chi _{{\mathrm {wp}}}'(G,\pi )=3$. Consider such a pair and let $\varphi$ be an arbitrary edge-coloring of G with the color set $\{1,2\}$. Assume that at every one-vertex at least one (hence both) of the colors is in parity accordance with $\pi$. Since $\pi ^{-1}(1)$ is odd-sized, there is a zero-vertex w such that $d_{G_1}(w)$ is odd. But then $d_{G_2}(w)$ is also odd, implying that no color is in parity accordance with $\pi$ at w. This yields the conclusion that $\varphi$ is not a weak vertex-parity edge-coloring of $(G,\pi )$. Thus, no member of ${\mathcal {C}}$ is weak vertex-parity 2-edge-colorable.

Finally, suppose that there are members of ${\mathcal {C}}$ which are not weak vertex-parity 3-edge-colorable, and among those let $(G,\pi )$ minimize m(G). Then G is loopless and every $w\in \pi ^{-1}(0)$ has $d_G(w)\ge 4$ (otherwise we suppress such a vertex and use induction). Select an arbitrary edge $e\in E(G)$. The graph $G-e$ is connected and non-even. Moreover, $\pi$ is a weak-proper vertex signature of $G-e$. By the first part of our proof, $(G-e,\pi )$ admits a weak vertex-parity 2-edge-coloring $\varphi$. Extend $\varphi$ to E(G) by coloring e with a third color. This clearly furnishes a weak vertex-parity 3-edge-coloring of $(G,\pi )$, a contradiction. $\square$

We can summarize our findings about weak vertex-parity edge-colorability as follows.

Corollary 3

Given a connected pair $(G,\pi )$, the index $\chi _{{\mathrm {wp}}}'(G,\pi )$ exists if and only if the signature $\pi$ is weak-proper. Moreover, it holds that

$$\begin{aligned} \chi _{{\mathrm {wp}}}'(G,\pi )= {\left\{ \begin{array}{ll} 0 &{} \quad \text {if}\, G \text { is empty}\,,\\ 1 &{} \quad \text {if }\, G \text { is non-empty and}\, d_G \equiv \pi ({\mathrm {mod}}\, 2)\,,\\ 3 &{} \quad \text {if }\, G \text { is even and the number of one-vertices is odd}\,, \\ 2 &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$