Skip to main content
SpringerLink
Log in

Diploid versus haploid models of neutral speciation

  • Original Paper
  • Published:
Journal of Biological Physics Aims and scope Submit manuscript

Abstract

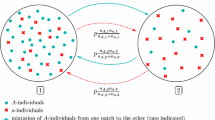
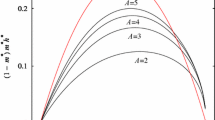
Neutral models of speciation based on isolation by distance and assortative mating, termed topopatric, have shown to be successful in describing abundance distributions and species–area relationships. Previous works have considered this type of process in the context of haploid genomes. Here we discuss the implementation of two schemes of dominance to analyze the effects of diploidy: a complete dominance model in which one allele dominates over the other and a perfect codominant model in which heterozygous genotypes give rise to a third phenotype. In the case of complete dominance, we observe that speciation requires stronger spatial inbreeding in comparison to the haploid model. For perfect codominance, instead, speciation demands stronger genetic assortativeness. Nevertheless, once speciation is established, the three models predict the same abundance distributions even at the quantitative level, revealing the robustness of the original mechanism to describe biodiversity features.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Coyne J. A., Orr H. A.: Speciation. 1st ed. Sinauer Associates, Inc (2004)

  2. Nosil, P.: Ecological Speciation. Oxford University Press, Oxford (2012)

    Book  Google Scholar 

  3. Gavrilets, S.: Models of speciation: Where are we now? J. Hered. 105(Special Issue), 743–755 (2014)

  4. Hubbell, S.: The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press, Princeton (2001)

    Google Scholar 

  5. Kopp, M.: Speciation and the neutral theory of biodiversity. BioEssays 32, 564–570 (2010)

  6. Etienne, R.S., Haegeman, B.: The neutral theory of biodiversity with random fission speciation. Theor. Ecol. 4, 87–109 (2011)

    Article  Google Scholar 

  7. Rosindell, J., Phillimore, A.B.: A unified model of island biogeography sheds light on the zone of radiation. Ecol. Lett. 14, 552–560 (2011)

    Article  Google Scholar 

  8. Mayr, E.: Animal Species and Evolution. Belknap Press, Cambridge (1963)

    Book  Google Scholar 

  9. Rozenzweig, M.L.: Tempo and mode of speciation. Science 277, 1622–1623 (1997)

    Article  Google Scholar 

  10. Dieckmann, U., Doebeli, M.: On the origin of species by sympatric speciation. Nature 400, 354–357 (1999)

    Article  ADS  Google Scholar 

  11. Leimar, O., Doebeli, M., Dieckmann, U.: Evolution of phenotypic clusters through competition and local adaptation along an environmental gradient. Evolution 62(4), 807–822 (2008)

    Article  Google Scholar 

  12. Baptestini, E.M., de Aguiar, M.A.M., Araujo, M.S., Bolnick, D.: The shape of the competition and carrying capacity kernels affects the likelihood of disruptive selection. J. Theor. Biol. 259, 5–11 (2009)

    Article  MathSciNet  Google Scholar 

  13. Pinho, C., Hey, J.: Divergence with gene flow: models and data. Annu. Rev. Ecol. Evol. Syst. 41, 215–230 (2010)

    Article  Google Scholar 

  14. de Aguiar, M.A.M., Baranger, M., Baptestini, E.M., Kaufman, L., Bar-Yam, Y.: Global patterns of speciation and diversity. Nature 460, 384–387 (2009)

    Article  ADS  Google Scholar 

  15. Hoelzer, G.A., Drewes, R., Meier, J., Doursat, R.: Isolation-by-distance and outbreeding depression are sufficient to drive parapatric speciation in the absence of environmental influences. PLoS Comput. Biol. 4, e1000126 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  16. Melian, C.J., Alonso, D., Vázquez, D.P., Regetz, J., Allesina, S.: Frequency-dependent selection predicts patterns of radiations and biodiversity. PLoS Comp. Biol. 6, e100089 (2010)

    Article  Google Scholar 

  17. Fuentes, M.A., Kuperman, M.N., Kenkre, V.M.: Nonlocal interaction effects on pattern formation in population dynamics. Phys. Rev. Lett. 91(15), 158104 (2003)

    Article  ADS  Google Scholar 

  18. Meyer, M., Havlin, S., Bunde, A.: Clustering of independently diffusing individuals by birth and death processes. Phys. Rev. E 54, 5567–5570 (1996)

    Article  ADS  Google Scholar 

  19. Young, W.R., Roberts, A.J., Stuhne, G.: Reproductive pair correlations and the clustering of organisms. Nature 412, 328–331 (2001)

    Article  ADS  Google Scholar 

  20. Houchmandzadeh, B.: Clustering of diffusing organisms. Phys. Rev. E 66, 052902 (2002)

    Article  ADS  Google Scholar 

  21. Lawson, D.J., Jensen, H.J.: Understanding clustering in type space using field theoretic techniques. Bull. Math. Biol. 70, 1065–1081 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Irwin, D.E., Bensch, S., Price, T.D.: Speciation in a ring. Nature 409, 333–337 (2001)

    Article  ADS  Google Scholar 

  23. Irwin, D.E., Bensch, S., Irwin, J.H., Price, T.D.: Speciation by distance in a ring species. Science 307, 414–416 (2005)

    Article  ADS  Google Scholar 

  24. Ashlock, D., Clare, E.L., von Königslöw, T.E., Ashlock, W.: Evolution and instability in ring species complexes: an in silico approach to the study of speciation. J. Theor. Biol. 264, 1202–1213 (2010)

    Article  Google Scholar 

  25. Martins, A.B., de Aguiar, M.A.M., Bar-Yam, Y.: Evolution and stability of ring species. Proc. Natl. Acad. Sci. U.S.A. 110, 5080–5084 (2013)

    Article  ADS  Google Scholar 

  26. Scott, A.D., King, D.M., Marić, N., Bahar, S.: Clustering and phase transitions on a neutral landscape. Europhys. Lett. 102(6), 68003 (2013)

    Article  ADS  Google Scholar 

  27. Baptestini, E.M., de Aguiar, M.A.M., Bar-Yam, Y.: The role of sex separation in neutral speciation. J. Theor. Ecol. 6, 213–223 (2013)

    Article  Google Scholar 

  28. Wright, S.: Breeding structure of populations in relation to speciation. Am. Nat. 74, 232–248 (1940)

    Article  Google Scholar 

  29. Wright, S.: Isolation by distance. Genetics 28, 114–138 (1943)

    Google Scholar 

  30. Kimura, M., Weiss, G.H.: The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 49, 561–576 (1964)

    Google Scholar 

  31. Higgs, P., Derrida, B.: Genetic distance and species formation in evolving populations. J. Mol. Evol. 35, 454–465 (1992)

    Article  Google Scholar 

  32. Dieckmann, U., Doebeli, M.: Evolutionary branching and sympatric speciation caused by different types of ecological interactions. Am. Nat. 156, S77–S101 (2000)

    Article  Google Scholar 

  33. Doebeli, M., Dieckmann, U.: Speciation along environmental gradients. Nature 421, 259–264 (2003)

    Article  ADS  Google Scholar 

  34. Bolnick, D.I., Kirkpatrick, M.: The relationship between intraspecific assortative mating and reproductive isolation between divergent populations. Curr. Zool. 58(3), 484–492 (2012)

    Article  Google Scholar 

  35. Parker, G.A., Partridge, L.: Sexual conflict and speciation. Phil. Trans. R. Soc. B 353, 261–274 (1998)

    Article  Google Scholar 

  36. Schneider, D.M., do Carmo, E., Martins, A.B., de Aguiar, M.A.M.: Toward a theory of topopatric speciation: the role of genetic assortative mating. Physica A 409, 35–47 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  37. Schneider, D.M., do Carmo, E., de Aguiar, M.A.M.: A dynamical analysis of allele frequencies in populations evolving under assortative mating and mutations. Physica A 421, 54–68 (2015)

    Article  Google Scholar 

  38. de Aguiar, M.A.M., Schneider, D.M., do Carmo, E., Campos, P.R.A., Martins, A.B.: Error catastrophe in populations under similarity-essential recombination. J. Theor. Biol. 374, 48–53 (2015)

    Article  MathSciNet  Google Scholar 

  39. Eigen, M., Schuster, P.: The Hypercycle. A principle of natural self-organization. Naturwissenschaften 64, 541–565 (1977)

    Article  ADS  Google Scholar 

  40. Schneider, D. M., Martins A. B., de Aguiar M. A. M. The mutation-drift balance in spatially structured populations. In preparation

  41. Higgs, P.G., Derrida, B.: Stochastic models for species formation in evolving populations. J. Phys. A 24, L985–L991 (1991)

    Article  ADS  MATH  Google Scholar 

  42. Gavrilets, S.: Fitness Landscapes and the Origin of Species. Princeton University Press, Princeton (2004)

  43. Mayr E.: In: Arai R., Kato M., Doi Y. (eds) Biodiversity and Evolution. National Science Museum Foundation, Tokyo (1955)

  44. de Aguiar, M.A.M., Bar-Yam, Y.: The Moran model as a dynamical process on networks and its implications for neutral speciation. Phys. Rev. E 84, 031901 (2011)

Download references

Acknowledgments

This work was partially supported by CNPq and FAPESP.

Author information

Authors and Affiliations

  1. Instituto de Física ‘Gleb Wataghin’, Universidade Estadual de Campinas, Unicamp, 13083-859, Campinas, SP, Brazil

    David M. Schneider, Elizabeth M. Baptestini & Marcus A. M. de Aguiar

Authors
  1. David M. Schneider
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elizabeth M. Baptestini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marcus A. M. de Aguiar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to David M. Schneider.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schneider, D.M., Baptestini, E.M. & de Aguiar, M.A.M. Diploid versus haploid models of neutral speciation. J Biol Phys 42, 235–245 (2016). https://doi.org/10.1007/s10867-015-9404-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10867-015-9404-1

Keywords

Search

Navigation