Skip to main content
SpringerLink
Log in

Design and Kinematic Analysis of the Novel Almost Spherical Parallel Mechanism Active Ankle

  • Published:
Journal of Intelligent & Robotic Systems Aims and scope Submit manuscript

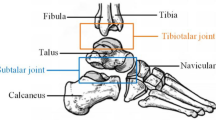
Abstract

The novel mechanism Active Ankle features three degrees of freedom that operate in an almost spherical manner. In comparison to spherical devices, its design offers advantages such as high stiffness, a simple and robust construction, and a good stress distribution. In the present paper, a comprehensive study of the design, analysis, and control of the Active Ankle in its almost-spherical work modality is provided. In particular, the kinematic analysis of the mechanism is conducted, solving the full inverse, the rotative inverse, and the forward kinematic problems. In addition, the manipulator’s workspace is characterized and the kinematic control, that has been implemented on a prototype of Active Ankle, is presented together with experimental results that demonstrate the employability as an ankle joint in a full body exoskeleton.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Al-Widyan, K., Ma, X.Q., Angeles, J.: The robust design of parallel spherical robots. Mech. Mach. Theory 46(3), 335–343 (2011)

    Article  MATH  Google Scholar 

  2. Bargsten, V., de Gea Fernandez, J.: Compi: development of a 6-DOF compliant robot arm for human-robot cooperation. In: Proceedings of the 8th International Workshop on Human-Friendly Robotics. TU München (2015)

  3. Baron, L.: A joint-limits avoidance strategy for arc-welding robots. In: Integrated Design and Manufacturing in Mechanical Engineering (2000)

  4. Bohigas, O., Manubens, M., Ros, L.: Singularities of non-redundant manipulators: a short account and a method for their computation in the planar case. Mech. Mach. Theory 68, 1–17 (2013)

    Article  Google Scholar 

  5. Bongardt, B.: Geometric characterization of the workspace of non- orthogonal rotation axes. J. Geom. Mech. 6(2), 141–166 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bongardt, B.: Inverse kinematics of anthropomorphic arms yielding eight coincidingcircles. In: International Workshop on Computational Kinematics (2017)

  7. Brinker, J., Corves, B.: A survey on parallel robots with delta-like architecture. In: IFToMM World Congress (2015)

  8. Briot, S., Pashkevich, A., Chablat, D.: On the optimal design of parallel robots taking into account their deformations and natural frequencies. In: 33rd Mechanisms and Robotics Conference, Parts A and B, vol. 7, pp 367–376 (2009). https://doi.org/10.1115/DETC2009-86230

  9. Clavel, R.: Conception d’un robot parallèle rapide à 4 degrés de liberté, p 146. EPFL, Lausanne (1991)

  10. Davidson, J.K., Hunt, K.H.: Robots and Screw Theory: Applications of Kinematics and Statics to Robotics. Oxford University Press. ISBN: 9780198562450 (2004)

  11. Featherstone, R: Rigid Body Dynamics Algorithms. Springer-Verlag New York, Inc., Secaucus, USA. ISBN: 0387743146 (2007)

  12. Frindt, M.: Modulbasierte Synthese von Parallelstrukturen für Maschinen in der Produktionstechnik. PhD thesis, Technical University of Braunschweig (2001)

  13. Gallardo-Alvarado, J: Kinematic Analysis of Parallel Manipulators by Algebraic Screw Theory, 1 edn. Springer International Publishing, Cham. ISBN: 978-3-319-31124-1 (2016). https://doi.org/10.1007/978-3-319-31126-5

  14. Gopura, R.A.R.C., Kiguchi, K., Bandara, D.S.V.: A brief review on upper extremity robotic exoskeleton systems. In: 2011 6th International Conference on Industrial and Information Systems, pp 346–351 (2011). https://doi.org/10.1109/ICIINFS.2011.6038092

  15. Gosselin, C., St-Pierre, E., Gagne, M.: On the development of the Agile Eye. IEEE Robot. Autom. Mag. 3(4), 29–37 (1996). https://doi.org/10.1109/100.556480

    Article  Google Scholar 

  16. Herr, H.: Exoskeletons and orthoses: classification, design challenges and future directions. J. NeuroEng. Rehabil. 6(1), 21 (2009)

    Article  Google Scholar 

  17. Huang, J., Tu, X., He, J.: Design and evaluation of the rupert wearable upper extremity exoskeleton robot for clinical and in-home therapies. IEEE Trans. Syst. Man Cybern. Syst. 46(7), 926–935 (2016). https://doi.org/10.1109/TSMC.2015.2497205

    Article  Google Scholar 

  18. Joyeux, S., Albiez, J.: Robot development: from components to systems. In: 6th National Conference on Control Architectures of Robots. Grenoble, France (2011)

  19. Kempe, A.B.: How to Draw a Straight Line (1877)

  20. Khalil, W., Dombre, E.: Modeling, Identification and Control of Robots. Taylor and Francis, New York (2002)

    MATH  Google Scholar 

  21. Khalil, W., Dombre, E.: In: Khalil, W., Dombre, E. (eds.) Modeling, Identification and Control of Robots, 3rd edn., pp. 57–84. Butterworth-Heinemann, Oxford. ISBN: 978-1-903996-66-9 (2002). https://doi.org/10.1016/B978-190399666-9/50004-X, https://www.sciencedirect.com/science/article/pii/B978190399666950004X

  22. Kirchner, E.A., Will, N., Simnofske, M., Vaca Benitez, L.M., Bongardt, B., Krell, M.M., Kumar, S., Mallwitz, M., Seeland, A., Tabie, M., Woehrle, H., Yueksel, M., Hess, A., Buschfort, R., Kirchner, F.: Recupera-reha: Exoskeleton technology with integrated biosignal analysis for sensorimotor rehabilitation. In: Transdisziplinaere Konferenz SmartASSIST, pp 504–517 (2016)

  23. Kong, X., Gosselin, C.M.: Type Synthesis of Parallel Mechanisms. Springer, Berlin. ISBN: 978-3-540-71989-2 (2007). https://doi.org/10.1007/978-3-540-71990-8

  24. Kumar, S., Nayak, A., Bongardt, B., Mueller, A., Kirchner, F.: Kinematic analysis of active ankle using computational algebraic geometry. In: Zeghloul, S., Romdhane, L., Laribi, M. A. (eds.) Computational Kinematics, pp 117–125. Springer International Publishing, Cham (2018)

  25. Kumar, S., Simnofske, M., Bongardt, B., Müller, A., Kirchner, F.: Integrating mimic joints into dynamics algorithms: exemplified by the hybrid recupera exoskeleton. In: Proceedings of the Advances in Robotics, AIR ’17, pp 27:1–27:6. ACM, New York, NY, USA. ISBN: 978-1-4503-5294-9 (2017). https://doi.org/10.1145/3132446.3134891

  26. Li, W., Gao, F., Zhang, J.: A three-DOF translational manipulator with decoupled geometry. Robotica 23(6), 805–808 (2005). https://doi.org/10.1017/S0263574705001700

    Article  Google Scholar 

  27. Luzi, L., Sancisi, N., Parenti Castelli, V.: A new direct position analysis solution for an over-constrained gough-stewart platform. In: Zeghloul, S., Romdhane, L., Laribi, M.A. (eds.) Computational Kinematics, pp. 585–592. Springer International Publishing, Cham. ISBN: 978-3-319-60867-9 (2017)

  28. Merlet, J.-P.: Parallel manipulators: state of the art and perspectives. In: Takamori, T., Tsuchiya, K. (eds.) Robotics, Mechatronics and Manufacturing Systems, pp. 21–26. Elsevier, Amsterdam. ISBN: 978-0-444-89700-8 (1993). https://doi.org/10.1016/B978-0-444-89700-8.50007-5, https://www.sciencedirect.com/science/article/pii/B9780444897008500075.

  29. Merlet, J.-P.: Determination of the orientation workspace of parallel manipulators. J. Intell. Robot. Syst. 13 (2), 143–160 (1995)

    Article  Google Scholar 

  30. Nef, T., Guidali, M., Klamroth-Marganska, V., Riener, R.: ARMin - exoskeleton robot for stroke rehabilitation. In: World Congress on Medical Physics and Biomedical Engineering, September 7-12, 2009, Munich, Germany, pp. 127–130. Springer, Berlin. ISBN: 978-3-642-03889-1 (2009)

  31. Niyetkaliyev, A., Shintemirov, A.: An approach for obtaining unique kinematic solutions of a spherical parallel manipulator. In: IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), pp 1355–1360 (2014)

  32. Sawicki, G.S., Ferris, D.P.: A pneumatically powered knee-ankle-foot orthosis (kafo) with myoelectric activation and inhibition. J. NeuroEng. Rehabil. 6(1), 23 (2009)

    Article  Google Scholar 

  33. Selig, J.M., Li, H.: A geometric newton-raphson method for gough-stewart platforms. In: Kecskeméthy, A., Müller, A. (eds.) Computational Kinematics, pp. 183–190. Springer, Berlin. ISBN: 978-3-642-01947-0 (2009)

  34. Simnofske, M.: Ausrichtungsvorrichtung zum Ausrichten einer Plattform in drei rotatorischen Freiheiten (2015)

  35. Simnofske, M., Kumar, S., Bongardt, B., Kirchner, F.: Active ankle—an almost-spherical parallel mechanism. In: 47th International Symposium on Robotics (ISR) (2016)

  36. Stauffer, R.N., Chao, E.Y.S., Brewster, R.C.: Force and motion analysis of the normal, diseased, and prosthetic ankle joint. Clin. Orthop. Relat. Res. 127(127), 189–196 (1977)

    Google Scholar 

  37. Temple, R.K.G.: The cardan suspension. In: The UNESCO Courier (1988)

  38. Thomas, F., Ros, L.: Revisiting trilateration for robot localization. IEEE Trans. Robot. 21(1), 93–101 (2005)

    Article  Google Scholar 

  39. Valasek, M., Zicha, J., Karasek, M., Hudec, R.: Hexasphere – redundantly actuated parallel spherical mechanism as a new concept of agile telescope. Advances in Astronomy (2010). https://doi.org/10.1155/2010/348286

  40. Villgrattner, T., Schneider, E., Andersch, P., Ulbrich, H.: Compact high dynamic 3 DOF camera orientation system: development and control. J. Syst. Des. Dyn. 5(5), 819–828 (2011)

    Google Scholar 

  41. Vischer, P., Clavel, R.: Argos: a novel 3-DOF parallel wrist mechanism. Int. J. Robot. Res. 19(1), 5–11 (2000). https://doi.org/10.1177/02783640022066707

    Article  Google Scholar 

  42. Wildberger, N.J.: A rational approach to trigonometry. Math Horizons 15(2), 16–20 (2007). http://www.jstor.org/stable/25678720

    Article  Google Scholar 

  43. Wu, G.: Kinematic analysis and optimal design of a wall-mounted four-limb parallel schoenflies-motion robot for pick-and-place operations. J. Intell. Robot. Syst. 85(3), 663–677 (2016). https://doi.org/10.1007/s10846-016-0377-5

    Google Scholar 

  44. Wu, G., Caro, S., Wang, J.: Design and transmission analysis of an asymmetrical spherical parallel manipulator. Mech. Mach. Theory 94, 119–131 (2015)

    Article  Google Scholar 

  45. Yamamoto, S., Hagiwara, A., Mizobe, T., Yokoyama, O., Yasui, T.: Development of an ankle–foot orthosis with an oil damper. Prosthet. Orthot. Int. 29(3), 209–219 (2005)

    Article  Google Scholar 

  46. Zoss, A.B., Kazerooni, H., Chu, A.: Biomechanical design of the berkeley lower extremity exoskeleton (BLEEX). IEEE/ASME Trans. Mechatron. 11(2), 128–138 (2006). https://doi.org/10.1109/TMECH.2006.871087

    Article  Google Scholar 

Download references

Acknowledgements

The work presented in this paper was performed within the project Recupera-Reha, funded by the German Aero-space Center (DLR) with federal funds from the Federal Ministry of Education and Research (BMBF) (Grant 01-IM-14006A).

Author information

Authors and Affiliations

  1. Robotics Innovation Center (RIC), German Research Center for Artificial Intelligence (DFKI), 28359, Bremen, Germany

    Shivesh Kumar, Marc Simnofske & Frank Kirchner

  2. Institute of Robotics and Process Control (IRP), Technical University of Braunschweig, 38106, Braunschweig, Germany

    Bertold Bongardt

  3. Fachbereich Mathematik und Informatik, Arbeitsgruppe Robotik, University of Bremen, Bremen, 28359, Germany

    Frank Kirchner

Authors
  1. Shivesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bertold Bongardt
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marc Simnofske
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Frank Kirchner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shivesh Kumar.

Appendices

Appendix A: Reference Configurations

A set of reference configurations of the mechanism Active Ankle is displayed in Table 10.

Table 10 Reference configurations with joint angles, end-effector poses, and point coordinates
Full size table

Appendix B: Sphere Intersection Problem

The method SphInt in Alg. 9, called from Alg. 5, computes the intersection of three spheres using distance geometry. It is based on the quadrance [42] between two vectors a and b,

$$Q({\boldsymbol{a}, \boldsymbol{b}}) = (\boldsymbol{b} - \boldsymbol{a})\ast (\boldsymbol{b} - \boldsymbol{a}), $$

the squared distance between a and b, and its generalization to vector sets, the Cayley–Menger bideterminants [38].

Appendix C: Representation Conversion Methods

The conversion methods mat2vec and vec2mat, called from Alg. 7 and Alg. 8, are stated in Alg. 12 and Alg. 13.

figure f
figure g
figure h
figure i

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, S., Bongardt, B., Simnofske, M. et al. Design and Kinematic Analysis of the Novel Almost Spherical Parallel Mechanism Active Ankle. J Intell Robot Syst 94, 303–325 (2019). https://doi.org/10.1007/s10846-018-0792-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10846-018-0792-x

Keywords

Search

Navigation