Skip to main content
SpringerLink
Log in

A stochastic model of input effectiveness during irregular gamma rhythms

  • Published:
Journal of Computational Neuroscience Aims and scope Submit manuscript

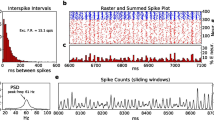
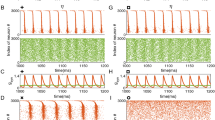
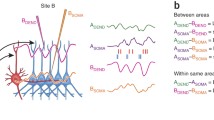
Abstract

Gamma-band synchronization has been linked to attention and communication between brain regions, yet the underlying dynamical mechanisms are still unclear. How does the timing and amplitude of inputs to cells that generate an endogenously noisy gamma rhythm affect the network activity and rhythm? How does such ”communication through coherence” (CTC) survive in the face of rhythm and input variability? We present a stochastic modelling approach to this question that yields a very fast computation of the effectiveness of inputs to cells involved in gamma rhythms. Our work is partly motivated by recent optogenetic experiments (Cardin et al. Nature, 459(7247), 663–667 2009) that tested the gamma phase-dependence of network responses by first stabilizing the rhythm with periodic light pulses to the interneurons (I). Our computationally efficient model E-I network of stochastic two-state neurons exhibits finite-size fluctuations. Using the Hilbert transform and Kuramoto index, we study how the stochastic phase of its gamma rhythm is entrained by external pulses. We then compute how this rhythmic inhibition controls the effectiveness of external input onto pyramidal (E) cells, and how variability shapes the window of firing opportunity. For transferring the time variations of an external input to the E cells, we find a tradeoff between the phase selectivity and depth of rate modulation. We also show that the CTC is sensitive to the jitter in the arrival times of spikes to the E cells, and to the degree of I-cell entrainment. We further find that CTC can occur even if the underlying deterministic system does not oscillate; quasicycle-type rhythms induced by the finite-size noise retain the basic CTC properties. Finally a resonance analysis confirms the relative importance of the I cell pacing for rhythm generation. Analysis of whole network behaviour, including computations of synchrony, phase and shifts in excitatory-inhibitory balance, can be further sped up by orders of magnitude using two coupled stochastic differential equations, one for each population. Our work thus yields a fast tool to numerically and analytically investigate CTC in a noisy context. It shows that CTC can be quite vulnerable to rhythm and input variability, which both decrease phase preference.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Akam, T., & Kullmann, D.M. (2014). Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nature Reviews Neuroscience, 14, 111–122.

    Article  Google Scholar 

  • Bartos, M., Vida, I., & Jonas, P. (2007). Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nature Reviews Neuroscience, 8, 45–56.

    Article  CAS  PubMed  Google Scholar 

  • Benayoun, M., Cowan, J.D., van Drongelen, W., & Wallace, E. (2010). Avalanches in a stochastic model of spiking neurons. Plos Computational Biology, 6(6), e1000,846.

    Article  Google Scholar 

  • Boashash, B. (1992). Estimating and interpreting the instantaneous frequency of a signal. ii. algorithms and applications. Proceedings of the IEEE, 80(4), 540–568.

    Article  Google Scholar 

  • Börgers, C., & Kopell, N. (2008). Gamma oscillations and stimulus selection. Neural Computation, 20(2), 383–414.

    Article  PubMed  Google Scholar 

  • Bressloff, P.C. (2009). Stochastic neural field theory and the system-size expansion. SIAM Journal of Appllied Mathematics, 70(5), 1488–1521.

    Article  Google Scholar 

  • Bressloff, P.C. (2010). Metastable states and quasicycles in a stochastic wilson-cowan model of neural population dynamics. Physical Review E, 82(5), 051,903.

    Article  Google Scholar 

  • Bressloff, P.C., & Newby, J.M. (2013). Metastability in a stochastic neural network modeled as a velocity jump markov process. Preprint (submitted).

  • Brosch, M., Budinger, E., & Scheich, H. (2002). Stimulus-related gamma oscillations in primate auditory cortex. Journal Neurophysiology, 87(6), 2715–25.

    PubMed  Google Scholar 

  • Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. Journal of Computational Neuroscience, 8, 183–208.

    Article  CAS  PubMed  Google Scholar 

  • Brunel, N., & Hakim, V. (1999). Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Computation, 11(7), 1621–1671.

    Article  CAS  PubMed  Google Scholar 

  • Buehlmann, A., & Deco, G. (2010). Optimal information transfer in the cortex through synchronization. Plos Computational Biology, 6(9), e1000,934.

    Article  Google Scholar 

  • Buice, M.A., & Chow, C.C. (2013). Dynamic finite size effects in spiking neural networks. Plos Computational Biology, 9(1), e1002,872.

    Article  CAS  Google Scholar 

  • Buice, M.A., & Cowan, J.D. (2007). Field-theoretic approach to fluctuation effects in neural networks. Physical Review E, 75(5), 051,919.

    Article  Google Scholar 

  • Buzsàki, G. (2006). Rhythms of the Brain: Oxford University Press.

  • Buzsáki, G., & Wang, X.J. (2012). Mechanisms of gamma oscillations. Annual Review of Neuroscience, 35(10), 203–225.

    Article  PubMed Central  PubMed  Google Scholar 

  • Cannon, J., McCarthy, M., Lee, S.J., Börgers, C., Whittington, M., & Kopell, N. (2014). Neurosystems: brain rhythms and cognitive processing. European Journal of Neuroscience, 39(5), 705–719.

    Article  PubMed  Google Scholar 

  • Cardin, J., Carlén, M., Meletis, K., Knoblich, U., Zhang, F., Deisseroth, K., Tsai, L., & Moore, C. (2009). Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature, 459(7247), 663–7.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Csicsvari, J., Jamieson, B., Wise, K., & Buzsáki, G. (2003). Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron, 37(2), 311–22.

    Article  CAS  PubMed  Google Scholar 

  • Dumont, G., Northoff, G., & Longtin, A. (2014). Linear noise approximation for oscillations in a stochastic inhibitory network with delay. Physical Review E, 90(1).

  • Rolls, E.T., Webb, T.J., & Deco, G. (2012). Communication before coherence. European Journal of Neuroscience, 36, 2689–2709.

    Article  PubMed  Google Scholar 

  • Engel, A.K., Kreiter, A.K., König, P., & Singer, W. (1991). Synchronization of oscillatory neuronal responses between striate and extrastriate visual cortical areas of the cat. Proceedings of the National Academy of Sciences of the United States of America, 88(14), 6048–6052.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Ermentrout, B., & Terman, D. (2010). Mathematical foundations of neuroscience: Springer.

  • Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cognitive Science, 9(10), 474–80.

    Article  Google Scholar 

  • Fries, P., Nikolić, D., & Singer, W. (2007). The gamma cycle. Trends Neuroscience, 30(7), 309–16.

    Article  CAS  Google Scholar 

  • Fries, P., Reynolds, J., Rorie, A., & Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science, 291(5508), 1560–3.

    Article  CAS  PubMed  Google Scholar 

  • Gillespie, D.T. (2001). Approximate accelerated stochastic simulation of chemically reacting systems. Journal of Chemical Physics, 115(4), 1716–36.

    Article  CAS  Google Scholar 

  • Gillespie, D.T. (2007). Stochastic simulation of chemical kinetics. Annual Review of Physical Chemistry, 58, 35–55.

    Article  CAS  PubMed  Google Scholar 

  • Ginzburg, I., & Sompolinsky, H. (1994). Theory of correlations in stochastic neural networks. Physical Review E, 50(4), 3171–3191.

    Article  CAS  Google Scholar 

  • Greenwood, P.E., McDonnell, M.D., & Ward, L.M. (2015). Dynamics of gamma bursts in local field potentials. Neural Computation, 27(1), 74–103.

    Article  PubMed  Google Scholar 

  • Grytskyy, D., Diesmann, T.T.M., & Helias, M. (2013). A unified view on weakly correlated recurrent networks. Frontiers Computational Neuroscience, 7, 131.

    Article  Google Scholar 

  • Helias, M., Tetzlaff, T., & Diesmann, M. (2014). The correlation structure of local neuronal networks intrinsically results from recurrent dynamics. Plos Computational Biology, 10(1), e1003,428.

    Article  Google Scholar 

  • Knoblich, U., Siegle, J.H., Pritchett, D.L., & Moore, C.I. (2010). What do we gain from gamma? local dynamic gain modulation drives enhanced efficacy and efficiency of signal transmission. Front Hum Neurosci, 21(4).

  • Kukjin Kang, M.S., Henrie, J.A., & Shapley, R. (2010). Lfp spectral peaks in v1 cortex: network resonance and cortico-cortical feedback. Journal of Computational Neuroscience, 29(3), 495–507.

    Article  PubMed Central  PubMed  Google Scholar 

  • Lachaux, J., Rodriguez, E., Martinerie, J., & Varela, F. (1999). Measuring phase synchrony in brain signals. Human Brain Mapping, 8(4), 194–208.

    Article  CAS  PubMed  Google Scholar 

  • Lindner, B., Doiron, B., & Longtin, A. (2005). Theory of oscillatory firing induced by spatially correlated noise and delayed inhibitory feedback. Physical Review E, 72(2), 061,919–061,933.

    Article  Google Scholar 

  • Mazzoni, A., Panzeri, S., Logothetis, N., & Brunel, N. (2008). Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. Plos Computational Biology, 4, e1000,239.

    Article  Google Scholar 

  • Northoff, G. (2014). Unlocking the Brain, Volume 1: Coding: Oxford University Press.

  • Renart, A, de la Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., & Harris, K.D. (2010). The asynchronous state in cortical circuits. Science, 327(5955), 587–590.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Salinas, E., & Sejnowski, T. (2001). Correlated neuronal activity and the flow of neural information. Nature Reviews Neuroscience, 2(8), 539–50.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Schoffelen, J., Oostenveld, R., & Fries, P. (2005). Neuronal coherence as a mechanism of effective corticospinal interaction. Science, 308(5718), 111–3.

    Article  CAS  PubMed  Google Scholar 

  • Sejnowski, T., & Paulsen, O. (2006). Network oscillations: emerging computational principles. Journal of Neuroscience, 26(6), 1673–6.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Stopfer, M., Bhagavan, S., Smith, B., & Laurent, G. (1997). Impaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature, 390(6655), 70–4.

    Article  CAS  PubMed  Google Scholar 

  • Tiesinga, P. (2012). Motifs in health and disease: the promise of circuit interrogation by optogenetics. European Journal of Neuroscience, 36(2), 2260–72.

    Article  PubMed  Google Scholar 

  • Tiesinga, P., & Sejnowski, T. (2009). Cortical enlightenment: are attentional gamma oscillations driven by ing or ping? Neuron, 63, 727–732.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Tiesinga, P.H., & Sejnowski, T.J. (2010). Mechanisms for phase shifting in cortical networks and their role in communication through coherence. Front Hum Neurosci, 4(196).

  • Tiesinga, P.H.E. (2012). Motifs in health and disease: the promise of circuit interrogation by optogenetics. European Journal of Neuroscience, 36(2).

  • Wallace, E. (2010). A simplified derivation of the linear noise approximation. arXiv:1004.4280.

  • Wallace, E., Benayoun, M., van Drongelen, W., & Cowan, J.D. (2011). Emergent oscillations in networks of stochastic spiking neurons. Plos one, 6(5), e14,804.

    Article  CAS  Google Scholar 

  • Wallace, E., Gillespie, D.T., Sanft, K.R., & Petzold, L.R. (2013). A new perspective on the linear noise approximation. Preprint (submitted).

  • Wang, X., & Buzsáki, G. (1996). Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. Journal of Neuroscience, 16(20), 6402–13.

    CAS  PubMed  Google Scholar 

  • Wilson, H.R., & Cowan, J.D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical Journal, 12(1), 1–24.

    Article  PubMed Central  CAS  PubMed  Google Scholar 

  • Womelsdorf, T., Schoffelen, J., Oostenveld, R., Singer, W., Desimone, R., Engel, A., & Fries, P. (2007). Modulation of neuronal interactions through neuronal synchronization. Science, 316(5831), 1609–12.

    Article  CAS  PubMed  Google Scholar 

Download references

Acknowledgments

This work was supported by the Natural Sciences and Engineering Research Council of Canada (AL) and the University of Ottawa Research Chair in Neurophysics (AL). G.N. thanks CIHR (Canadian Institute of Health Research), the Michael Smith Foundations EJLB-Michael Smith Chair program, and the Hope for Depression Research Foundation (HDRF) for support.

Author information

Authors and Affiliations

  1. Physics Department, 150 Louis Pasteur Ottawa, Ottawa, Ontario, K1N 6N5, Canada

    Grégory Dumont & André Longtin

  2. Mind, Brain Imaging and Neuroethics, Royal Ottawa Healthcare, Institute of Mental Health Research, Ottawa, Canada

    Grégory Dumont & Georg Northoff

  3. Center for Neural Dynamics, University of Ottawa, Ottawa, Canada

    Grégory Dumont, Georg Northoff & André Longtin

Authors
  1. Grégory Dumont
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Georg Northoff
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. André Longtin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Grégory Dumont.

Ethics declarations

Conflict of interests

The authors declare that they have no conflict of interest.

Additional information

Action Editor: Frances K. Skinner

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dumont, G., Northoff, G. & Longtin, A. A stochastic model of input effectiveness during irregular gamma rhythms. J Comput Neurosci 40, 85–101 (2016). https://doi.org/10.1007/s10827-015-0583-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10827-015-0583-3

Keywords

Search

Navigation