Abstract
From first principles, we predict several yet-unknown, low-energy, dynamically stable phases of \(\hbox {HfO}_{2}\). One of the predicted metastable phases has a finite ferroelectric polarization and could be potentially responsible for the ferroelectric and/or antiferroelectric behavior recently reported in thin \(\hbox {(Hf,Zr)O}_{2}\)-based films. Other phases predicted here may potentially form as competing non-ferroelectric phases in thin films, and the possibility of their formation should be taken into account during analysis of experimental thin-film characterization data. These predictions are made possible by an explicit enumeration approach, designed for the case at hand. Our approach outperforms existing theoretical structure prediction methods, including evolutionary algorithms, which have been previously applied to the same problem yet have not identified most of the possible metastable phases found in this study. This suggests that structure enumeration techniques may be indispensable for practical structure prediction problems that seek to identify all low-energy metastable phases rather the single stable (lowest energy) phase.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The interest in metastable hafnia \(\hbox {(HfO}_{2})\) and zirconia \(\hbox {(ZrO}_{2})\) phases has been intensified with the recent reports of ferroelectric and antiferroelectric responses in “doped” (alloyed) and some pure \(\hbox {(Zr,Hf)O}_{2}\) films [1, 2]. This discovery is of great interest to the semiconductor industry and has led to intensive experimental [3,4,5,6,7,8,9,10,11,12,13,14] and theoretical [9, 15,16,17,18,19,20,21,22] research, because these materials are believed to avoid the problems typical for the traditional ferroelectric materials (such as lead zirconate titanate) during integration into microelectronic devices. However, precise identification of the phase(s) in these films is problematic due to experimental limitations such as the broadness of the thin-film diffraction spectra, unknown film texture and strain fields, and possible presence of multiple phases within a single film. Even the most conclusive phase determination to date [3], combining multiple characterization techniques, has had to rely on a pre-postulated set of possible structural candidates, which in turn has relied on a prior theoretical structure prediction study identifying possible metastable phases [15]. While the detailed investigation in Ref. [3] presents quite convincing evidence of a particular (\({ Pca2}_{1}\), or “o-FE”) phase forming at least in the case of ferroelectric Gd-doped \(\hbox {HfO}_{2}\) films, the experimental GIXRD signal has both missing and additional features compared to the predicted pattern of any single candidate phase. The “additional” peaks can be loosely matched to another known phase and thus are usually interpreted as evidence of coexistence of multiple phases within the same thin film. However, it is possible that a yet-unknown structural candidate could turn out to be a better match to all of the experimental data. (Also, note that Ref. [3] also assumes that the phase is orthorhombic merely based on earlier reports, rather than as the conclusion of their structural analysis.) The origin of the antiferroelectric behavior is even less clear. One model has suggested a field-induced first-order transformation between the nonpolar tetragonal (\(P4 2{ /nmc}\)) and polar (ferroelectric-like) \({ Pca2}_{1}\) structures [17]; however, such a model does not explain the key feature of antiferroelectricity, i.e., the disappearance of polarization upon removal (rather than reversal) of the applied field. It is quite possible that additional, yet-unaccounted-for phase(s) may be responsible for the antiferroelectric behavior, but the structural origin of such a possible phase(s) remains unknown.
Even before the discovery of the (anti)ferroelectricity in \(\hbox {(Hf,Zr)O}_{2}\)-based films, there has been a substantial interest in metastable phases of these materials. Indeed, one can argue that today’s importance of zirconia and hafnia across a broad range of applications is due to not only their remarkable inherent properties, but also due to the modification of these properties with changes to the crystalline geometry, together with our ability to intentionally stabilize one of the several possible geometries (metastable phases). For instance, at ambient conditions, addition of yttria can change the bulk phase from monoclinic to cubic, producing materials with applications ranging from dentistry to thermal coatings to nuclear reactor design components to jewelry. In the semiconductor industry, the tetragonal phase is sought after for its high dielectric constant. The tetragonal and cubic phases can be stabilized by simply heating up the pure bulk material, but other phases that may have useful properties remain metastable in pure bulk at all temperatures; stabilizing them for practical use may require a combination of doping, size, strain, and processing techniques. Due to the extreme similarity in both chemistry and size of Zr and Hf atoms, \(\hbox {HfO}_{2}\) and \(\hbox {ZrO}_{2}\) are believed to share the same set of phases, yet this may not be universally true for all metastable phases, as it is not true for the methods to stabilize them: for example, the tetragonal phase is fortuitously stabilized in zirconia thin films by finite-size effects, yet methods to stabilize tetragonal hafnia are sought for as a valuable know-how. In this work, we focus on \(\hbox {HfO}_{2}\) phases in order to avoid dealing with additional compositional degrees of freedom.
Total energies, relative to that of the monoclinic structure \(\hbox {(m-HfO}_{2})\), of the experimentally known (black bars), previously predicted (light brown and dark red bars), and predicted in this work (wide green bars: dynamically stable, narrow light-blue bars: dynamically unstable at \(T=0\) K) \(\hbox {HfO}_{2}\) structures with no more than four formula units (12 atoms) per cell, as calculated for bulk structures at \(T=0\) K. Gray shading indicates the energy range of structures deemed potentially accessible in thin-film experiments (Color figure online)
a, b Substantial displacement of half of the oxygen ions (red) from the cites of the cubic fluorite structure (a) to the partially occupied (light red) sites leads to Pbcm lattice (b). The Hf atoms (blue) and the other half of the oxygen ions undergo minor displacements (not visible) to relieve strain. c, d In these simplified schematics of the relationships between different \(\hbox {HfO}_{2}\) phases, oxygen ions in consecutive planes are shown as balls of different color, and Hf atoms are omitted. Panel c illustrates this notation for the same cubic and Pbcm lattices as in (a, b). Panel d illustrates the general relationship, connecting most of the observed \(\hbox {HfO}_{2}\) phases to oxygen ordering on the partially occupied sites of the Pbcm lattice (Color figure online)
Theoretical structure prediction methods based on density functional theory calculations [23, 24] have seen over a decade of intensive development for their promise to identify yet-unknown metastable phases possessing desirable properties. Just as importantly, theoretical structure prediction can greatly simplify experimental phase identification by offering a short list of possible low-energy metastable structure candidates. Both of these reasons have motivated previous studies in \(\hbox {(Zr,Hf)O}_{2}\). In Ref. [25] Zeng et al. have used the USPEX code [26, 27] to theoretically predict new phases of \(\hbox {HfO}_{2}\) and \(\hbox {Hf}_{\mathrm{n}}\hbox {Si}_{\mathrm{m}}\hbox {O}_{\mathrm{2n+2m}}\) that may exhibit high values of the dielectric constant. USPEX is an evolutionary algorithm for global optimization developed to have a low failure rate [26]. Applied to \(\hbox {HfO}_{2}\), it has identified two new nonpolar structural candidates (space groups P−1, \(\hbox {P2}_{1}\hbox {/m)}\), and confirmed that the polar \(({ Pca2}_{1}\), hereforth referred to as o-FE) structure previously observed [28] in doped \(\hbox {ZrO}_{2}\) could also appear in \(\hbox {HfO}_{2}\). More recently, Huan et al. have used [15] a minima hopping method to identify low-energy metastable phases in \(\hbox {HfO}_{2}\), specifically focusing on the possible identity of the ferroelectric phase(s). Minima hopping is a widely used structure prediction method [29, 30] comprising a series of short molecular dynamics and structural relaxation runs. Ref. [15] has predicted both polar (potential ferroelectric) and nonpolar metastable \(\hbox {HfO}_{2}\) structures, and some of these predictions have later been used during the experimental analysis of Ref. [3].
Despite the value of these earlier \(\hbox {HfO}_{2}\) structure prediction studies [15, 25], two problems are clear. The first problem is the relevance of the predicted structures from the viewpoint of structural energetics. This is illustrated in Fig. 1, where we graphically present the \(T=\hbox {0}\) K, \(P=\hbox {0}\) energies of various \(\hbox {HfO}_{2}\) phases, as calculated in this work, relative to the bulk ground state. In order for a metastable phase to form in experiment, its free energy needs to become lower than those of all other phases. The range of possible changes in the relative free energies of \(\hbox {HfO}_{2}\) phases is estimated below to be less than \(\sim \) 250 meV/f.u. at the experimentally relevant conditions. Indeed, the experimentally observed phases (black bars in Fig. 1) fall within this range, with the exception of the o-II phase, which is stabilized only at high pressures and is not seen in thin-film experiments. However, half of the structures predicted in Ref.15 (dark red bars in Fig. 1) have energies well outside of this range, and thus these predictions are not relevant for the analysis of the experimental data. (This problem does not relate to the predictions of Ref. [25], shown as light brown bars in Fig. 1.) The second problem is that both the evolutionary and the minima hopping methods rely on chance, and it is likely that other low-energy metastable structures remain undiscovered. Indeed, the study of Ref. [25] missed structures in the relevant energy range, while the later study of Ref. [15] found only four new structures over a very broad energy range, clearly not commensurate with the actual density of structures in the energy space. There is no a priori way to determine whether some of the structures that remain unknown may actually be forming in thin films under certain conditions.
In this work, we seek an approach that could identify metastable \(\hbox {HfO}_{2}\) structures within the experimentally relevant energy range in a systematic yet computationally tractable way. It is well known that in some chemical systems, low-energy metastable structures can be explicitly enumerated. For example, in certain metal alloys, all the low-energy structures correspond to different arrangements of atoms on the sites of a specific (e.g., fcc) underlying lattice (with additional small relaxations away from the ideal lattice sites).Footnote 1 Enumerating potential metastable low-energy phases in such systems is reduced to listing all inequivalent ordered “decorations” of sites of the ideal lattice with different atomic species, an approach frequently invoked in alloy theory studies [31, 32]. Of course, \(\hbox {HfO}_{2}\) phases are not alloys and are not usually described as “decorations” of sites of the same underlying lattice. Nevertheless, the low-energy \(\hbox {HfO}_{2}\) phases do share many common geometric features: For example, they can all be considered distortions of the cubic phase, which has a fluorite structure. The only exception is the ultra-high-pressure o-II phase, which is not further discussed below as it is not observed in thin-film experiments (because it has energy outside of the relevant range, cf. Fig. 1). Exploring this commonality between the geometries of \(\hbox {HfO}_{2}\) phases underlies our approach here.
We have recently pointed out that despite the apparent dissimilarity, a number of \(\hbox {HfO}_{2}\) phases can, in fact, be considered “decorations” of the same underlying Pbcm lattice. This lattice is generated from the perfect fluorite structure (shown in Fig. 2a) by displacing oxygen ions in every second (001) plane in ± x ± y direction. There are two possible displaced positions for each oxygen ion (Fig. 2b–c), so that half of the “displaced” lattice sites remain unoccupied. In a true Pbcm phase (reportedly corresponding to a high-pressure, high-temperature phase of \(\hbox {HfO}_{2}\) [33, 34], though the identity of this phase is disputed [35]), the arrangement of oxygen ions and vacancies has no long range order. Our observation in Ref. [18] has been that by “decorating” the Pbcm sites with oxygen ions and vacancies in an ordered fashion, one can generate many observed \(\hbox {HfO}_{2}\) phases, including both the ground state monoclinic \(\hbox {(m-HfO}_{2}\), space group \(P2_{1}/c)\) as well as the orthorhombic o-I and o-FE phases (space groups \({ Pca2}_{1}\) and Pbca). Additional relaxations in atomic positions and cell shape follow in order to relieve strain, to the extent allowed by the symmetry of the ordered oxygen ion/vacancy arrangement, yet those additional relaxations are much smaller than the initial oxygen ion displacements to the sites of the Pbcm lattice.Footnote 2 The resulting hierarchy of structures is illustrated in Fig. 2d.
As indicated in Fig. 2d, Pbcm serves as the underlying lattice for many yet not all the low-energy phases. One of the two known exceptions is the undistorted cubic phase itself, the other is the tetragonal phase \(\hbox {(t-HfO}_{2}\), s.g. \(P4_{2}{ /nmc})\), in which oxygen ions are displaced from the fluorite sites along x rather than \(x\pm y\) direction.Footnote 3 If there are other low-energy metastable structures, it is possible that they might combine oxygen ion displacements along different directions, and some may have components along all the three cubic axes (e.g., \(x+y+z\)). Displacements in different directions need be accounted for during structural search, because they lead to different local symmetries that control which components of the long-range Coulomb forces cancel out. On the other hand, it appears unlikely that very similar displacements lead to multiple equilibrium positions, e.g., there may not be multiple energy minima for an oxygen ion displaced by a different amount in a particular direction.Footnote 4 For our systematic search for metastable phases, we therefore make the following assumptions: (i) All the low-energy structures are represented by (relatively small) distortions of the fluorite structure; (ii) all these structures can be obtained by relaxing atomic positions from an appropriate initial position, such that all the initial positions can be enumerated; (iii) specifically, the initial positions can be generated from the perfect fluorite positions by independently displacing each of the oxygen ions in each of the Cartesian directions by either zero or a fixed amount (such as ± 0.5Å). Note that because similar displacements are not expected to lead to multiple equilibrium positions, different but closely related initial positions are likely to result in the same structure after the geometry relaxation—in this sense, our enumeration of the initial positions is quite different from the structure enumeration used in alloy theory, in which each lattice “decoration” leads to a different relaxed structure. In particular, our approach cannot be used to account for the configurational entropy as is common in alloy studies [31].
Schematics of possible X1 (s.g.13) and X3 (s.g.18) “decorations” of the Pbcm lattice that, unlike those in Fig. 2d, do not relax to low-energy structures due to a substantial decrease in the neighbor oxygen-oxygen distance (“clashing” of the oxygen ions)
A direct application of the enumeration scheme as formulated above would generate a computationally prohibitive number of \(\sim 2.8 \times 10 ^{11}\) “initial” configurations from a single cubic fluorite cell. We therefore introduce an additional criterion to eliminate the initial configurations that are not likely to relax to low-energy structures. Specifically, we exclude configurations in which neighboring oxygen ions move toward each other, leading to a substantial increase in the Coulomb repulsion (“clashing” of oxygen ions). To illustrate this criterion, we turn again to the ordered “decorations” of the Pbcm lattice. While the “decorations” illustrated in the bottom row of Fig. 2d relax to low-energy structures, configurations with “clashing” oxygen ions, such as those illustrated in Fig. 3, lead to much higher energies of the relaxed structures [18] (279 and 269 meV/f.u. above the monoclinic ground state for X1 and X3 structures in Fig. 3). Different specific definitions of a “non-clashing” criterion are possible; here, we adopt the following formulation, serving as our assumption (iv): In any “initial” configuration generated by displacing oxygen ions of the fluorite structure by discrete amounts (as formulated above), if the oxygen ion at position R is displaced to \({{\varvec{R}}}+{\varvec{\delta }}_{R}\) such that \({\varvec{\delta }}_{R}\) has a positive (negative) component along the crystalline axis \(\hat{\alpha } (\hat{\alpha } = \hat{x}, \hat{y}, \hat{z})\), then the oxygen ion at \({{\varvec{R}}}+a/2 \hat{\alpha }\) (respectively at \({{\varvec{R}}} - a/2 \hat{\alpha })\) has to also have a positive (respectively negative) component along the \(\hat{\alpha }\) axis. (Here, a is the fluorite lattice constant, such that a / 2 is the distance between the nearest neighbor oxygen ions). Note that the displacement of the oxygen ion at R does not impose restrictions on the other two components (\(\hat{\beta }\ne \hat{\alpha })\) of the displacement of the oxygen ion at \({{\varvec{R}}}+a/2\hat{\alpha }\). On the other hand, if \({\varvec{\delta }}_{R}\) has nonzero components along two (or three) crystalline axes, then two (or three) neighbor oxygen ions would be required to have specific nonzero components of their initial displacements. It is easy to see that this formulation of the “non-clashing” criterion actually implies that an entire “row” of atoms with given \({\beta }, {\gamma }\) components (\({\beta }, {\gamma } \ne {\alpha })\) has to have the same \(\hat{\alpha }\) component of the displacement; thus, rather than enumerating the displacements of individual oxygen ions, only the displacements of \(\hat{x}, \hat{y}\), and \(\hat{z}\) rows of oxygen ions need be enumerated.Footnote 5 This reduces the number of the “non-clashing” “initial” configurations to the manageable \(\sim 5.3 \times 10^{5}\), starting from a cubic fluorite cell.
We implemented our enumeration procedure as an atkpython script within Virtual NanoLab (VNL) [36]. The “initial” atomic configurations are generated from a single cubic (12-atom) fluorite cell by independently displacing each of the \(\hat{x} , \hat{y}\) and \(\hat{z}\) rows of oxygen ions by − 0.5Å, 0Å, or \(+\) 0.5Å. Coulomb (Madelung) energies of the generated “initial” configurations are calculated within VNL, and structures with equal (in practice differing by less than 0.25 meV/f.u.) Coulomb energies are assumed to be symmetrically equivalent. The atomic positions and cell shapes of the 3289 resulting non-inequivalent configurations are relaxed within generalized gradient approximation (GGA-PBE) [37] using Viena Ab initio Simulations Package (VASP) [38,39,40]. We used the PAW pseudopotentials [41, 42] treating as valence Hf 6s and 5d and O 2s and 2p states. The initial relaxation rounds are performed using the \(2\times 2\times 2\) k-mesh and “soft” oxygen pseudopotentials (“O_s” as supplied with VASP). The structures with energies differing by less than 4 meV/f.u. are deemed as having relaxed to the same final configuration. The geometries of the structures with different energies are further refined using \(4\times 4\times 4\) k-mesh and “regular” oxygen pseudopotentials. The final structure candidates are checked for dynamic stability by calculating the phonon frequencies at the zone center (for a 12-atom unit cell) using density functional perturbation theory as implemented in VASP. The Born charges and the dielectric constant values were also calculated for the dynamically stable structures.
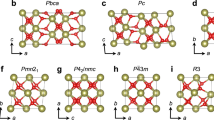
Dynamically stable low-energy \(\hbox {HfO}_{2}\) structures predicted in this study (cf. Table 1). The labels indicate the name assigned by the enumeration schema as well as the space group. Structures (a–c) have centrosymmetric space groups, structure (d) is polar (ferroelectric)
The results of our systematic search are summarized in Table 1. The search identified thirteen inequivalent structures, of which six structures represent the experimentally confirmed phases of \(\hbox {HfO}_{2}\) (monoclinic, tetragonal, cubic, o-FE, and o-II) and the \({ Pmn2}_{1}\) phase previously predicted by Huan et al. [15]. The other seven structures do not appear to have been previously discussed. In Table 1, we reference these new structures by the ID assigned in our enumeration scheme to the corresponding “initial” structure. Of these new structures, four structures (wide green bars in Fig. 1) represent previously unknown, low-energy, dynamically stable phases that may potentially be observed under appropriate experimental conditions. These structures are visualized in Fig. 4, and the relaxed atomic positions are listed in Supplementary Material. Three new structures are found to be dynamically unstable at \(T=0\) K (narrow light-blue bars in Fig. 1). Nevertheless, in two of these structures (xyax-4-19 and xyz-2-2-2), the additional relaxation triggered by the unstable phonon mode is relatively small (< 30 meV/f.u.), and it is possible that anharmonic effects may stabilize these structures at finite temperatures (as happens in many elemental metals, e.g., in bcc Ti [43, 44]). The atomic positions of these structures are also listed in Supplementary Material.
The remaining dynamically unstable structure (xyz-14-14-8) is not deemed experimentally relevant, not only because the unstable phonon mode triggers a substantial energy lowering (255 meV/f.u.), but also because the \(T=0\) K energy for this candidate is well outside the \(\sim \) 250 meV/f.u. range of “reasonable” energies. We now clarify our reason for focusing on this energy range. The free energy change that may lead to formation of a metastable structure can be due to a combination of finite-temperature (primarily vibrational entropy) effects, finite-size (surface) effects, strain, and “doping” (alloying). These aspects have recently been discussed from a theoretical perspective [19,20,21,22, 45]; in particular, changes in the relative free energy of several \(\hbox {HfO}_{2}\), \(\hbox {ZrO}_{2}\), and \(\hbox {HfZrO}_{4}\) phases have been estimated by Materlik et al. [19], who reported that within a wide range of experimentally reasonable conditions and for film thicknesses in 9nm...30 nm range the vibrational entropy, surface, and strain contributions are well within \(<\sim \)180 meV/f.u. The changes due to intentional “doping” (alloying) need be evaluated on a case-by-case basis but can be expected to be \(< < \sim \) 50 meV/f.u. for <10% of isovalent oxide content. (Indeed, 50 meV/f.u. would correspond to 0.5 eV per “dopant” atom, which is much larger than the typical difference between two hypothetical oxide phases at the same composition.) For non-isovalent (e.g., trivalent) “dopants,” an additional small fraction of \(k_{B}T\) per atom can be expected from the entropy of induced vacancies. Assuming that the film processing temperatures stay within \(T_\mathrm{max}\sim 700^{\circ }\hbox {C}\), we estimate that the phases within \(\sim \) 250 meV/f.u. \(\sim k_{B}T_\mathrm{max}\) may have a potential to be stabilized under appropriate conditions.
Analysis of conditions under which the new predicted phases could be stabilized experimentally is beyond the scope of the present study. It is quite likely that some of these structures would not be stabilized under any experimentally relevant conditions. However, on the basis of the available data, all the structures listed in Table 1 (with the exception of the highest energy xyz-14-14-8 structure) should be considered as potential candidates whenever there is indication that an unconventional (different from that observed in bulk at given T) phase is stabilized by thin film, “doping,” and/or processing effects. In Supplemental Materials, we provide the structural data and the predicted XRD patterns for the possible \(\hbox {HfO}_{2}\) phases identified here. Phase characterization in thin \(\hbox {HfO}_{2}\)-based films is notoriously difficult due to a substantial similarity between the competing phases. In particular, the observed peak intensities are frequently hard to explain even assuming a mixture of (previously known) phases [14]. We hope that our predictions may eventually lead to a more accurate future analysis and interpretation of experimental data.
In Table 1, we also list some of the properties of the identified phases, including the \(T=0\) K energy (relative to the monoclinic ground state), band gap, the dielectric constant (along the principal axes of the dielectric tensor), and whether or not the structure is polar (i.e., whether it can be responsible for the ferroelectricity). The energies of several predicted structures are quite low, below those of both the tetragonal and o-FE phases at \(T=0\) K, indicating that these structures can indeed be reasonably expected to be encountered experimentally. One can observe that the band gaps of the predicted phases are larger than or comparable to those of the known phases. In particular, the structures with the lowest energy above the ground state, i.e., xyax-24-5 and xyz-15-17-73, have larger band gaps than all the experimentally confirmed phases. Large band gap values imply decreased leakage at the same thickness if these materials are used as dielectrics. The dielectric constant, on the other hand, is quite low for all of the new dynamically stable phases, particularly for xyz-15-17-73. Two of the predicted new structures have non-centrosymmetric space groups, however, only one of them, xyz-1-9-27, is polar and could give rise to a ferroelectric (or the polarized state of an antiferroelectric) phase; the other non-centrosymmetric structure, xyz-2-2-2, is nonpolar due to the presence of multiple mirror planes.
Note that the band gap values calculated in GGA-PBE are known to be underestimated (by \(\sim \)1.5 eV in \(\hbox {HfO}_{2})\) and are listed here for a relative comparison only. Regarding the accuracy of the dielectric constant evaluation, the relatively small electronic contribution to the dielectric tensor and is slightly overestimated due to the underestimation of the band gap, whereas the ionic contribution may be substantially overestimated due to additional softening of the soft phonon modes. In fact, we find that an attempt to perform a more accurate phonon calculations, interpolating the dynamical matrix obtained using a 2 \(\times \) 2 \(\times \) 2 supercell and accounting for the LO-TO splitting, leads to a prediction of a weak dynamical instability in \(\hbox {t}-\hbox {HfO}_{2}\), which we speculate could be an artifact due to the increased volume in GGA-PBE. The resulting errors in the dielectric constant k increase with increasing the k value (corresponding to approaching the ferroelectric instability), and for the values listed in Table 1 are expected to be substantial only for \(\hbox {t}-\hbox {HfO}_{2}\). However, for dynamically unstable structures, the phonon frequencies may be inaccurate even for the stable modes; we thus did not evaluate k for dynamically unstable structures. Finally, we did not evaluate the actual polarization of the predicted polar structure xyz-1-9-27, because such an evaluation is only meaningful with respect to a specific switching pathway [18, 46], which we did not attempt to identify here.
A few remarks regarding the scope of our search and the comparison of our results to those of Refs. [15, 25] are proper here. As Table 1 indicates, or procedure successfully finds all the experimentally confirmed phases with up to 12 atoms per cell, including the high-energy, non-fluorite-based o-II (Pnma) phase, even though the procedure has been designed to target the low-energy fluorite-based structures. This provides evidence of some generality and breadth of coverage of the relevant phase space. On the other hand, while our enumeration procedure [assumptions (i)–(iv)] may be quite general, in this study we have limited its application to structures generated from the 12-atom cubic fluorite cell. The cubic cell has been chosen, in part, because in the case of atwo-dimensional lattice application of the assumptions (i)–(iv) necessarily requires use of a rectangular cell. However, in three dimensions cells of other shapes are allowed. Moreover, crystal structures can have more than 12 atoms in a primitive cell: in fact, the experimentally observed o-I (Pbca) phase has 24 atoms per cell. A truly exhaustive study combining the oxygen sublattice distortion enumeration (as formulated here) with the cell shape and cell size enumeration can be a subject of a future study.
Compared to the earlier studies of Refs. [15, 25], our procedure has resulted in the largest number of predictions within the experimentally relevant energy range, identifying 4 dynamically stable structures missed by those studies. (Admittedly, Ref. [25] may have identified but not have reported some additional metastable phases with low “fitness” defined as \(\sim { kE}_{g}^{2}\), where k is the dielectric constant and \(E_{g}\) is the GGA-PBE band gap [25]. However, comparison of the k and \(E_{g}\) values for our predictions listed in Table 1 with those reported in Ref. [25] does not support this explanation.) Our procedure has reproduced all the predictions (within the relevant energy range) of Ref. [15]; however, it missed both structures identified in Ref. [25], presumably indicating the importance of considering different undistorted cell shapes. It is worth noting that our structure xyz-15-17-73 turns out to have the same \(P2_{1}/m\) space group as one of the structures identified in Ref. [25]; however, despite the same symmetry, they represent different structures (in particular, they differ by 62 meV/f.u. in energy, with xyz-15-17-73 being more stable)! This illustrates the ambiguity of referring to the structures solely by their space group, which is the primary reason we reference our predictions by the codes assigned by our enumeration procedure. Note that we observed a substantial relaxation for some of the geometries reported in Refs. [15] and [25], despite using the same density functional and VASP code. We tentatively ascribe this to using a different (presumably more accurate) version of Hf pseudopotentials as available with the latest VASP distribution as of the time of this writing.
In conclusion, we have proposed an approach for a systematic (rather than probabilistic) search for metastable phases in \(\hbox {HfO}_{2}\). The approach is based on enumerating “initial” configurations subject to “non-clashing” displacements condition that avoids configurations with high Coulomb energy. Our approach is directly applicable to a metastable phase search in any other fluorite-based ferroelectric and may be further generalizable to other families of crystal structure. Applied to \(\hbox {HfO}_{2}\), our search (limited to structures generated from a 12-atom cubic cell) identifies all experimentally confirmed and one of the three previously predicted metastable \(\hbox {HfO}_{2}\) structures, and in addition predicts four dynamically stable and two potentially temperature-stabilized structures in the experimentally relevant energy range. One of the identified metastable structures exhibits ferroelectric polarization. We suggest that future analysis of thin film experiments in \(\hbox {HfO}_{2}\) should account for the possibility of formation of structures identified here.
Notes
However, predominance of low-energy structures of a particular lattice type is not universal in metal alloys: For example, even alloying two fcc metasl such as Ni and Al may result in a formation of a bcc-based, rather than fcc-based, intermetallic compound (B2 NiAl).
For example, in monoclinic \(\text {HfO}_{2}\), the “initial” oxygen ion displacements are nearly 1Å, whereas the additional cell internal relaxations are \(\sim \)0.3Å for Hf atoms and \(\sim \)0.1Å for the remaining oxygen ions.
Specifically, the oxygen ions are displaced along the tetragonal axis, traditionally denoted z; we denote it x for consistency with the rest of the structures in Fig. 2.
Indeed, the oxygen ion displacements indicated in Fig. 2d are \(\sim \) 0.7...1Å except in tetragonal phase; much larger displacements would inevitably lead to a substantial core overlap and require major structure relaxation to relieve the strain. In tetragonal phase, oxygen ions are displaced by only \(\sim \) 0.3 Å from fluorite positions yet still \(\sim \) 0.6Å relative to other oxygen ions, and an explicit calculation confirms the existence of a single well-defined minimum with respect to the magnitude of oxygen ion displacement.
Our simple formulation of the “non-clashing” criterion may appear excessively stringent: For example, the decoration of the Pbcm lattice shown in Fig. 2d as leading to the monoclinic lattice has some displacement components not satisfying our simple formulation of the “non-clashing” criterion. Nevertheless, we find that the enumeration search performed according to our criterion does successfully find the monoclinic structure, providing a posteriori validation of our procedure.
References
Böscke, T.S., Müller, J., Bräuhaus, D., Schröder, U., Böttger, U.: Ferroelectricity in hafnium oxide thin films. Appl. Phys. Lett. 99, 102903 (2011)
Polakowski, P., Müller, J.: Ferroelectricity in undoped hafnium oxide. Appl. Phys. Lett. 106, 232905 (2015)
Park, M.H., Lee, Y.H., Kim, H.J., Kim, Y.J., Moon, T., Kim, K.D., Müller, J., Kersch, A., Schroeder, U., Mikolajick, T., Hwang, C.S.: Ferroelectricity and antiferroelectricity of doped thin \(\text{ HfO }_{2}\)-based films. Adv. Mater. 27, 1811–1831 (2015). and references therein
Muller, J., Polakowski, P., Mueller, S., Mikolajick, T.: Ferroelectric hafnium oxide based materials and devices: assessment of current status and future prospects. J. Sol. State Sci. Technol. 4, N30–N35 (2015). and references therein
Sang, X., Grimley, E.D., Schenk, T., Schroeder, U., LeBeau, J.M.: On the structural origins of ferroelectricity in \(\text{ HfO }_{2}\) thin films. Appl. Phys. Lett. 106, 162905 (2015)
Hoffmann, M., Schroeder, U., Schenk, T., Shimizu, T., Funakubo, H., Sakata, O., Pohl, D., Drescher, M., Adelmann, C., Materlik, R., Kersch, A., Mikolajick, T.: Stabilizing the ferroelectric phase in doped hafnium oxide. J. Appl. Phys. 118, 072006 (2015)
Schenk, T., Yurchuk, E., Mueller, S., Schroeder, U., Starschich, S., Böttger, U., Mikolajick, T.: About the deformation of ferroelectric hystereses. Appl. Phys. Rev. 1, 041103 (2014)
Lomenzo, P.D., Takmeel, Q., Zhou, C., Fancher, C.M., Lambers, E., Rudawski, N.G., Jones, J.L., Moghaddam, S., Nishida, T.: TaN interface properties and electric field cycling effects on ferroelectric Si-doped \(\text{ HfO }_{2}\) thin films. J. App. Phys. 117, 134105 (2015)
Pešić, M., Fengler, F.P.G., Larcher, L., Padovani, A., Schenk, T., Grimley, E.D., Sang, X., LeBeau, J.M., Slesazeck, S., Schroeder, U., Mikolajick, T.: Physical mechanisms behind the field-cycling behavior of HfO2-based ferroelectric capacitors. Adv. Funct. Mater. 26, 4601–4612 (2016)
Starschich, S., Menzel, S., Böttger, U.: Evidence for oxygen vacancies movement during wake-up in ferroelectric hafnium oxide. Appl. Phys. Lett. 108, 032903 (2016)
Shimizu, T., Yokouchi, T., Oikawa, T., Shiraishi, T., Kiguchi, T., Akama, A., Konno, T.J., Gruverman, A., Funakubo, H.: Contribution of oxygen vacancies to the ferroelectric behavior of \(\text{ Hf }_{0.5}\text{ Zr }_{0.5}\text{ O }_{2}\) thin films. Appl. Phys. Lett. 106, 112904 (2015)
Grimley, E.D., Schenk, T., Sang, X., Pešić, M., Schroeder, U., Mikolajick, T., LeBeau, J.M.: Structural changes underlying field-cycling phenomena in ferroelectric \(\text{ HfO }_{2}\) thin films. Adv. Electron. Mater. 2, 1600173 (2016)
Pal, A., Narasimhan, V.K., Weeks, S., Littau, K., Pramanik, D., Chiang, T.: Enhancing ferroelectricity in dopant-free hafnium oxide. Appl. Phys. Lett. 110, 022903 (2017)
Weeks, S., Pal, A., Narasimhan, V.K., Littau, K., Chiang, T.: Engineering of ferroelectric \(\text{ HfO }_{2}-\text{ ZrO }_{2}\) nanolaminates. ACS Appl. Mater. Interfaces 9, 13440–13447 (2017). doi:10.1021/acsami.7b00776
Clima, S., Wouters, D.J., Adelmann, C., Schenk, T., Schroeder, U., Jurczak, M., Pourtois, G.: Identification of the ferroelectric switching process and dopant-dependent switching properties in orthorhombic \(\text{ HfO }_{2}\): a first principles insight. Appl. Phys. Lett. 104, 092906 (2014)
Huan, T.D., Sharma, V., Rossetti Jr., G.A., Ramprasad, R.: Pathways towards ferroelectricity in hafnia. Phys. Rev. B 90, 064111 (2014)
Reyes-Lillo, S.E., Garrity, K.F., Rabe, K.M.: Antiferroelectricity in thin-film \(\text{ ZrO }_{2}\) from first principles. Phys. Rev. B 90, 140103(R) (2014)
Barabash, S.V., Pramanik, D., Zhai, Y., Magyari-Kope, B., Nishi, Y.: Ferroelectric switching pathways and energetics in \(\text{(Hf, } \text{ Zr)O }_{2}\). ECS Trans. 75, 107–121 (2017). doi:10.1149/07532.0107ecst
Materlik, R., Künneth, C., Kersch, A.: The origin of ferroelectricity in Hf1\(-\)xZrxO2: a computational investigation and a surface energy model. J. App. Phys. 117, 134109 (2015)
Künneth, C., Materlik, R., Kersch, A.: Modeling ferroelectric film properties and size effects from tetragonal interlayer in \(\text{ Hf }_{{1-{\rm x}}}\text{ Zr }_{{\rm x}}\text{ O }_{2}\) grains. J. Appl. Phys. 121, 205304 (2017)
Batra, R., Tran, H.D., Ramprasad, R.: Stabilization of metastable phases in hafnia owing to surface energy effects. Appl. Phys. Lett. 108, 172902 (2016)
Batra, R., Huan, T.D., Jones, J.L., Rossetti, G., Ramprasad, R.: Factors favoring ferroelectricity in Hafnia: a first-principles computational study. J. Phys. Chem. C 121, 4139 (2017)
Woodley, S.M., Catlow, R.: Crystal structure prediction from first principles. Nat. Mater. 7, 937–946 (2008). doi:10.1038/nmat2321
Oganov, A.R. (ed.): Modern Methods of Crystal Structure Prediction. Wiley-VCH, Weinheim (2011)
Zeng, Q., Oganov, A.R., Lyakhov, A.O., Xie, C., Zhang, X., Zhang, J., Zhu, Q., Wei, B., Grigorenko, I., Zhang, L., Cheng, L.: Evolutionary search for new high-k dielectric materials: methodology and applications to hafnia-based oxides. Acta Cryst. C70, 76–84 (2014)
Oganov, A.R., Glass, C.W.: Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys. 124, 244704 (2006)
Lyakhov, A.O., Oganov, A.R., Stokes, H., Zhu, Q.: New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172–1182 (2013)
Kisi, E.H., Howard, C.J.: Crystal structure of orthorhombic zirconia in partially stabilized zirconia. J. Am. Ceram. Soc. 72, 1757–1760 (1989)
Goedecker, S.: Minima hopping: an efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys. 120, 9911–9917 (2004)
Amsler, M., Goedecker, S.: Crystal structure prediction using the minima hopping method. J. Chem. Phys. 133, 224104 (2010)
Ruban, A.V., Abrikosov, I.A.: Configurational thermodynamics of alloys from first principles: effective cluster interactions. Rep. Prog. Phys. 71, 046501 (2008)
Van de Walle, A., Asta, M.: Self-driven lattice-model Monte Carlo simulations of alloy thermodynamic properties and phase diagrams. Model. Simul. Mater. Sci. Eng. 10, 521–538 (2002)
Suyama, R., Horiuchi, H., Kume, S.: Structural refinements of ZrO2 and HfO2 treated at 600 \(^{\circ }\text{ C }\) 6 GPa. Yogyo-Kyokai-Shi 95, 567–568 (1987)
Adams, D.M., Leonard, S., Russell, D.R.: X-ray diffraction study of hafnia under high pressure using synchrotron radiation. J. Phys. Chem. Sol. 52, 1181–1186 (1991)
Ohtaka, O., Yamanaka, T., Kume, S., Hara, N., Asano, H., Izumi, F.: Structural analysis of orthorhombic Hafnia by neutron powder diffraction. J. Am. Ceram. Soc. 78, 233–237 (1995)
Virtual NanoLab version 2016.3, QuantumWise A/S (www.quantumwise.com)
Perdew, J.P., Burke, K., Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
Kresse, G., Hafner, J.: Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993)
Kresse, G., Furthmüller, J.: Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996)
Kresse, G., Furthmüller, J.: Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996)
Blöchl, P.E.: Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994)
Kresse, G., Joubert, D.: From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999)
Grimvall, G., Magyari-Köpe, B., Ozoliņš, V., Persson, K.A.: Lattice instabilities in metallic elements. Rev. Mod. Phys. 84, 945–986 (2012)
Kadkhodaei, S., Hong, Q.-J., van de Walle, A.: Free energy calculation of mechanically unstable but dynamically stabilized bcc titanium. Phys. Rev. B 95, 064101 (2017)
Fischer, D., Kersch, A.: Stabilization of the high-k tetragonal phase in \(\text{ HfO }_{2}\): the influence of dopants and temperature from ab initio simulations. J. Appl. Phys. 104, 084104 (2008)
King-Smith, R.D., Vanderbilt, D.: Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654(R) (1993)
Acknowledgements
The author thanks Dr. Tony Chiang, Dr. Dipu Pramanik, Dr. Blanka Magyary-Kope, Dr. Kevin Ding, Dr. Stephen Weeks, Dr. Vijay Narasimhan, Dr. Ashish Pal, and Dr. Anders Blom for valuable discussions.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Barabash, S.V. Prediction of new metastable \(\hbox {HfO}_{2}\) phases: toward understanding ferro- and antiferroelectric films. J Comput Electron 16, 1227–1235 (2017). https://doi.org/10.1007/s10825-017-1077-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10825-017-1077-5