Abstract
The Verified Software Toolchain builds foundational machine-checked proofs of the functional correctness of C programs. Its program logic, Verifiable C, is a shallowly embedded higher-order separation Hoare logic which is proved sound in Coq with respect to the operational semantics of CompCert Clight. This paper introduces VST-Floyd, a verification assistant which offers a set of semiautomatic tactics helping users build functional correctness proofs for C programs using Verifiable C.





















Similar content being viewed by others
Notes
The “heap” in Verifiable C is actually a step indexed model of CompCert’s memories, following Hobor et al. [17].
Readers can understand the type of P as \(\text {stack} \rightarrow \text {heap} \rightarrow \text {Prop}\). But actually, this predicate must be monotonic w.r.t. the step indexing, i.e. we define it Coq as a dependent pair of a predicate and a proof of monotonicity [3, Part V].
This specification of
 is not strong enough, because it does not say whether the values of \(\llbracket \texttt {x} \rrbracket \) and \(\llbracket \texttt {y} \rrbracket \) change or not after running the function. In actual verification, we will use:$$\begin{aligned} \texttt {swapint(x, y)}: \{\llbracket \texttt {x} \rrbracket = p \wedge \llbracket \texttt {y} \rrbracket = q \wedge p \mapsto a * q \mapsto b\} \{p \mapsto b * q \mapsto a\} \end{aligned}$$
is not strong enough, because it does not say whether the values of \(\llbracket \texttt {x} \rrbracket \) and \(\llbracket \texttt {y} \rrbracket \) change or not after running the function. In actual verification, we will use:$$\begin{aligned} \texttt {swapint(x, y)}: \{\llbracket \texttt {x} \rrbracket = p \wedge \llbracket \texttt {y} \rrbracket = q \wedge p \mapsto a * q \mapsto b\} \{p \mapsto b * q \mapsto a\} \end{aligned}$$In actual Coq code, Clight uses identifiers to represent C variable names and C function names. So, when we write
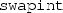 , the real Coq code is “\(\mathsf {\_swapint}\)” which is an identifier, i.e. a positive number, in Coq. Similarly, the real Coq code for
, the real Coq code is “\(\mathsf {\_swapint}\)” which is an identifier, i.e. a positive number, in Coq. Similarly, the real Coq code for
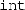 is “\(\mathsf {tint}\)” whose type is \(\mathsf {Clight.type}\), a Coq inductive type representing the syntax tree of C types.
is “\(\mathsf {tint}\)” whose type is \(\mathsf {Clight.type}\), a Coq inductive type representing the syntax tree of C types.Our \(\mapsto \) and \(\mathsf {data\_at}\) predicates take another argument that we omit in this article: a permission-share indicating read-only, read-write, or various other levels of access to the data.
In CompCert 2.4 and earlier versions, the Clight type definition is a Coq inductive type. However, from CompCert 2.5,
 and
and
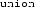 types are represented by name instead of by structure. Specifically, every Clight program is associated with a \(\mathsf {composite\_env}\). A \(\mathsf {composite\_env}\) is a dictionary mapping every
types are represented by name instead of by structure. Specifically, every Clight program is associated with a \(\mathsf {composite\_env}\). A \(\mathsf {composite\_env}\) is a dictionary mapping every
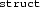 /
/
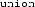 name to a list of all its fields. The meaning of a
name to a list of all its fields. The meaning of a
 or a
or a
 needs to be interpreted by looking it up in the dictionary. From then on, \(\mathsf {reptype}\) and \(\mathsf {data\_at\_rec}\) are no longer Coq functions recursive on Coq inductive structure. The CompCert developers accepted our suggestion that every type should be tagged with a rank, which is a natural number. The ranking system ensures that the rank of a struct type is the max rank of its fields plus one; the rank of a union type is the max rank of its fields plus one; the rank of an array type is the rank of its element type plus one. The rank of elementary types (including pointers) is zero. Our current definition of \(\mathsf {reptype}\) and \(\mathsf {data\_at\_rec}\) are recursive functions on this rank.
needs to be interpreted by looking it up in the dictionary. From then on, \(\mathsf {reptype}\) and \(\mathsf {data\_at\_rec}\) are no longer Coq functions recursive on Coq inductive structure. The CompCert developers accepted our suggestion that every type should be tagged with a rank, which is a natural number. The ranking system ensures that the rank of a struct type is the max rank of its fields plus one; the rank of a union type is the max rank of its fields plus one; the rank of an array type is the rank of its element type plus one. The rank of elementary types (including pointers) is zero. Our current definition of \(\mathsf {reptype}\) and \(\mathsf {data\_at\_rec}\) are recursive functions on this rank.In the Coq development, we use the name
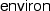 for what we call “stack” in the paper.
for what we call “stack” in the paper.In our Coq development, we actually turn the symbolic
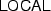 clauses into binary trees first. Then we look up in these trees during symbolic evaluation. We omit the technical details here.
clauses into binary trees first. Then we look up in these trees during symbolic evaluation. We omit the technical details here.All the load and store rules of this section also need typechecking side conditions, i.e., \(\mathsf {tc\_expr}(\varDelta ,e)\) for each involved C expression e. We omit them for brevity.
One might wonder why the expression evaluation function does not directly return a field address. For
 and
and
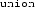 fields, this could work, but for array indices, it wouldn’t, because the field-address operator is only well-defined if the array index is within the array bounds, but adding an integer to a pointer is always defined in CompCert Clight, even if dereferencing it might be undefined. So the evaluation function could only use the field-address operator if the array index is within bounds, but it cannot know whether this is the case, because it does not have access to the array size.
fields, this could work, but for array indices, it wouldn’t, because the field-address operator is only well-defined if the array index is within the array bounds, but adding an integer to a pointer is always defined in CompCert Clight, even if dereferencing it might be undefined. So the evaluation function could only use the field-address operator if the array index is within bounds, but it cannot know whether this is the case, because it does not have access to the array size.The kind of hints we are talking about here are not related to Coq’s hint databases.
References
Affeldt, R., Marti, N.: Towards formal verification of TLS network packet processing written in C. In: Might, M., Van Horn, D., Abel, A., Sheard, T. (eds.) Proceedings of the 7th Workshop on Programming Languages Meets Program Verification, pp. 35–46. ACM (2013)
Appel, A.W.: Verification of a cryptographic primitive: SHA-256. ACM Trans. Program. Lang. Syst. 37(2), 7:1–7:31 (2015)
Appel, A.W., Dockins, R., Hobor, A., Beringer, L., Dodds, J., Stewart, G., Blazy, S., Leroy, X.: Program Logics for Certified Compilers. Cambridge University Press, Cambridge (2014)
Appel, A.W., McAllester, D.: An indexed model of recursive types for foundational proof-carrying code. ACM Trans. Program. Lang. Syst. 23(5), 657–683 (2001)
Bengtson, J., Jensen, J.B., Birkedal, L.: Charge! a framework for higher-order separation logic in Coq. In: ITP, pp. 315–331 (2012)
Berdine, J., Calcagno, C., O’Hearn, P.W.: Symbolic execution with separation logic. In: Yi, K. (ed.) Programming Languages and Systems, Third Asian Symposium, APLAS 2005, Tsukuba, Japan, November 2–5, 2005, Proceedings, Volume 3780 of Lecture Notes in Computer Science, pp. 52–68. Springer (2005)
Beringer, L., Petcher, A., Ye, K.Q., Appel, A.W.: Verified correctness and security of OpenSSL HMAC. In: 24th USENIX Security Symposium, pp. 207–221. USENIX Assocation (2015)
Bernstein, D.J., van Gastel, B., Janssen, W., Lange, T., Schwabe, P., Smetsers, S.: Tweetnacl: a crypto library in 100 tweets. In: Aranha, D.F., Menezes, A. (eds.) Progress in Cryptology—LATINCRYPT 2014—Third International Conference on Cryptology and Information Security in Latin America, Florianópolis, Brazil, September 17–19, 2014, Revised Selected Papers, Volume 8895 of Lecture Notes in Computer Science, pp. 64–83. Springer (2014)
Calcagno, C., Distefano, D., O’Hearn, P., Yang, H.: Compositional shape analysis by means of bi-abduction. SIGPLAN Not. 44, 289–300 (2009)
Chin, W.-N., David, C., Nguyen, H.H., Qin, S.: Automated verification of shape, size and bag properties via user-defined predicates in separation logic. Sci. Comput. Program. 77(9), 1006–1036 (2012)
Chlipala, A.: The Bedrock structured programming system: combining generative metaprogramming and Hoare logic in an extensible program verifier. In: ICFP’13: Proceedings of the 18th ACM SIGPLAN International Conference on Functional Programming (2013)
Clarke, E.M., Kroening, D., Lerda, F.: A tool for checking ANSI-C programs. In Jensen, K., Podelski, A. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, 10th International Conference, TACAS 2004, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2004, Barcelona, Spain, March 29–April 2, 2004, Proceedings, Volume 2988 of Lecture Notes in Computer Science, pp. 168–176. Springer (2004)
Floyd, R.W.: Assigning meanings to programs. In: Proceedings of Symposium in Applied Mathematics, pp. 19–32. Providence, Rhode Island (1967)
Gruetter, S.: Improving the Coq proof automation tactics of the Verified Software Toolchain, based on a case study on verifying a C implementation of the AES encryption algorithm. Master thesis. Ecole Polytechnique Fédérale de Lausanne (2017)
Guéneau, A., Myreen, M.O., Kumar, R., Norrish, M.: Verified characteristic formulae for CakeML. In: Programming Languages and Systems: 26th European Symposium on Programming, ESOP 2017, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017, Uppsala, Sweden, April 22–29, 2017, Proceedings, pp. 584–610. Springer, Berlin (2017)
Hoare, C.A.R.: An axiomatic basis for computer programming. Commun. ACM 12(10), 578–580 (1969)
Hobor, A., Dockins, R., Appel, A.W.: A theory of indirection via approximation. In: Proceedings of the 37th Annual ACM Symposium on Principles of Programming Languages (POPL’10), pp. 171–185 (2010)
Hobor, A., Villard, J.: The ramifications of sharing in data structures. In: Giacobazzi, R., Cousot, R. (eds.) The 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL ’13, Rome, Italy, January 23–25, 2013, pp. 523–536. ACM (2013)
Jung, R., Swasey, D., Sieczkowski, F., Svendsen, K., Turon, A., Birkedal, L., Dreyer, D.: Iris: monoids and invariants as an orthogonal basis for concurrent reasoning. In: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (2015)
Kleymann, T.: Hoare logic and VDM: machine-checked soundness and completeness proofs. PhD thesis, University of Edinburgh, UK (1998)
Krebbers, R.: The C standard formalized in Coq. PhD thesis, Radboud University (2015)
Krebbers, R., Jung, R., Bizjak, A., Jourdan, J.-H., Dreyer, D., Birkedal, L.: The essence of higher-order concurrent separation logic. In: European Symposium on Programming, pp. 696–723. Springer (2017)
Krebbers, R., Timany, A., Birkedal, L.: Interactive proofs in higher-order concurrent separation logic. In: Castagna, G., Gordon, A.D. (eds.) Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, Paris, France, January 18–20, 2017, pp. 205–217. ACM (2017)
Leino, K.R.M.: Dafny: An automatic program verifier for functional correctness. In: Clarke, E.M., Voronkov, A. (eds.) Logic for Programming, Artificial Intelligence, and Reasoning—16th International Conference, LPAR-16, Dakar, Senegal, April 25–May 1, 2010, Revised Selected Papers, Volume 6355 of Lecture Notes in Computer Science, pp. 348–370. Springer (2010)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009)
Mansky, W., Appel, A.W., Nogin, A.: A verified messaging system. In: Proceedings of the 2017 ACM International Conference on Object Oriented Programming Systems Languages & Applications, OOPSLA ’17. ACM (2017)
Matthews, J., Moore, J.S., Ray, S., Vroon, D.: Verification condition generation via theorem proving. In: Hermann, M., Voronkov, A. (eds.) Logic for Programming, Artificial Intelligence, and Reasoning, 13th International Conference, LPAR 2006, Phnom Penh, Cambodia, November 13–17, 2006, Proceedings, Volume 4246 of Lecture Notes in Computer Science, pp. 362–376. Springer (2006)
Nipkow, T.: Hoare logics for recursive procedures and unbounded nondeterminism. In: Bradfield, J.C. (ed.) Computer Science Logic, 16th International Workshop, CSL 2002, 11th Annual Conference of the EACSL, Edinburgh, Scotland, UK, September 22–25, 2002, Proceedings, Volume 2471 of Lecture Notes in Computer Science, pp. 103–119. Springer (2002)
Reynolds, J.: Separation logic: a logic for shared mutable data structures. In: LICS 2002: IEEE Symposium on Logic in Computer Science, pp. 55–74 (2002)
Signoles, J.: Foncteurs impératifs et composés: la notion de projets dans Frama-C. In: Schmitt, A. (ed.) JFLA 2009, Vingtièmes Journées Francophones des Langages Applicatifs, Saint Quentin sur Isère, France, January 31–February 3, 2009. Proceedings, Volume 7.2 of Studia Informatica Universalis, pp. 245–280 (2009)
Wildmoser, M.: Verified proof carrying code. PhD thesis, Technical University Munich (2005)
Acknowledgements
This work was supported in part by NSF grant CCF-1521602 and by DARPA grant FA8750-12-2-0293.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cao, Q., Beringer, L., Gruetter, S. et al. VST-Floyd: A Separation Logic Tool to Verify Correctness of C Programs. J Autom Reasoning 61, 367–422 (2018). https://doi.org/10.1007/s10817-018-9457-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-018-9457-5





 is not strong enough, because it does not say whether the values of
is not strong enough, because it does not say whether the values of 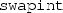 , the real Coq code is “
, the real Coq code is “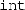 is “
is “ and
and
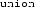 types are represented by name instead of by structure. Specifically, every Clight program is associated with a
types are represented by name instead of by structure. Specifically, every Clight program is associated with a 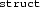 /
/
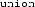 name to a list of all its fields. The meaning of a
name to a list of all its fields. The meaning of a
 or a
or a
 needs to be interpreted by looking it up in the dictionary. From then on,
needs to be interpreted by looking it up in the dictionary. From then on, 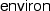 for what we call “stack” in the paper.
for what we call “stack” in the paper.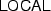 clauses into binary trees first. Then we look up in these trees during symbolic evaluation. We omit the technical details here.
clauses into binary trees first. Then we look up in these trees during symbolic evaluation. We omit the technical details here. and
and
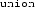 fields, this could work, but for array indices, it wouldn’t, because the field-address operator is only well-defined if the array index is within the array bounds, but adding an integer to a pointer is always defined in CompCert Clight, even if dereferencing it might be undefined. So the evaluation function could only use the field-address operator if the array index is within bounds, but it cannot know whether this is the case, because it does not have access to the array size.
fields, this could work, but for array indices, it wouldn’t, because the field-address operator is only well-defined if the array index is within the array bounds, but adding an integer to a pointer is always defined in CompCert Clight, even if dereferencing it might be undefined. So the evaluation function could only use the field-address operator if the array index is within bounds, but it cannot know whether this is the case, because it does not have access to the array size.