Abstract
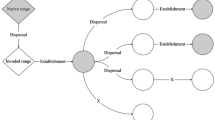
Local effects on the rates of spread of mangrove and associated epifauna were modeled for the Indian River Lagoon, Florida, USA. The model divided the 200-km-long lagoon into 157,330 cells. Data from a hydrodynamic model were used to generate current vectors for each cell at 10-min intervals. Each cell was assigned a habitat type, and releases or recruitment of mangrove propagules or epifauna larvae were based on the suitability of these habitats. Multiple species were included in the model, each with its own life-history parameters. All individuals were followed over 8 years or until mortality occurred. Adults could reproduce and release new larvae or propagules. The mean rates of spread predicted by the model were <1 km year−1 for all species, which were less than the 2 km year−1 predicted for mangroves along this coast. Spread rates were also found to differ among the five inlet source sites used in the model. Epifaunal invertebrate populations spread at similar rates, but spread more rapidly from mangrove habitats than from dock habitats. These results demonstrate that local differences in hydrodynamics and habitat distributions influence the broader regional rates of spread likely to occur with climate change.



Similar content being viewed by others
References
Allen, J. A. & K. W. Krauss, 2006. Influence of propagule flotation longevity and light availability on establishment of introduced mangrove species in Hawai‘i. Pacific Science 60: 367–376.
Ambrose, R. F. & B. V. Nelson, 1982. Inhibition of giant kelp recruitment by an introduced brown alga. Botanica Marina 25: 265–267.
Anil, A. C., L. Khandeparker, D. V. Desai, L. V. Baragi & C. A. Gaonkar, 2010. Larval development, sensory mechanisms and physiological adaptations in acorn barnacles with special reference to Balanus amphitrite. Journal of Experimental Marine Biology and Ecology 392: 89–98.
Aquino-Thomas, J. & C. E. Proffitt, 2014. Oysters Crassostrea virginica on red mangrove Rhizophora mangle prop roots: facilitation of one foundation species by another. Marine Ecology Progress Series 503: 177–194.
Armitage, A. R., W. E. Highfield, S. D. Brody & P. Louchouarn, 2015. The contribution of mangrove expansion to salt marsh loss on the Texas Gulf Coast. PLoS ONE 10: e0125404.
Arnold, S. N., R. S. Steneck & P. J. Mumby, 2010. Running the gauntlet: inhibitory effects of algal turfs on the processes of coral recruitment. Marine Ecology Progress Series 414: 91–105.
Balch, T., B. G. Hatcher & R. E. Scheibling, 1999. A major settlement event associated with minor meteorologic and oceanographic fluctuations. Canadian Journal of Zoology 77: 1657–1662.
Bryan, S. E., A. G. Cook, J. P. Evans, K. Hebden, L. Hurrey, P. Colls, J. S. Jell, D. Weatherley & J. Firn, 2012. Rapid, long-distance dispersal by pumice rafting. PLoS ONE 7: e40583.
Bullard, S. G., N. L. Lindquist & M. E. Hay, 1999. Susceptibility of invertebrate larvae to predators: how common are post-capture larval defenses? Marine Ecology – Progress Series 191: 153–161.
Burrows, M. T., D. S. Schoeman, L. B. Buckley, P. Moore, E. S. Poloczanska, K. M. Brander, C. Brown, J. F. Bruno, C. M. Duarte, B. S. Halpern, J. Holding, C. V. Kappel, W. Kiessling, M. I. O’Connor, J. M. Pandolfi, C. Parmesan, F. B. Schwing, W. J. Sydeman & A. J. Richardson, 2011. The pace of shifting climate in marine and terrestrial ecosystems. Science 334: 652–655.
Caley, M. J., M. H. Carr, M. A. Hixon, T. P. Hughes, G. P. Jones & B. A. Menge, 1996. Recruitment and the local dynamics of open marine populations. Annual Review of Ecology and Systematics 27: 477–500.
Cavanaugh, K. C., J. R. Kellner, A. J. Forde, D. S. Gruner, J. D. Parker, W. Rodriguez & I. C. Feller, 2014. Poleward expansion of mangroves is a threshold response to decreased frequency of extreme cold events. Proceedings of the National Academy of Sciences of United States of America 111: 723–727.
Cavanaugh, K. C., J. D. Parker, S. C. Cook-Patton, I. C. Feller, A. P. Williams & J. R. Kellner, 2015. Integrating physiological threshold experiments with climate modeling to project mangrove species’ range expansion. Global Change Biology 21: 1928–1938.
Chen, I. C., J. K. Hill, R. Ohlemüller, D. B. Roy & C. D. Thomas, 2011. Rapid range shifts of species associated with high levels of climate warming. Science 333: 1024–1026.
Clarke, P. J., 1993. Dispersal of grey mangrove (Avicennia marina) propagules in southeastern Australia. Aquatic Botany 45: 195–204.
Dangremond, E. M. & I. C. Feller, 2016. Precocious reproduction increases at the leading edge of a mangrove range expansion. Ecology and Evolution 6: 5087–5092.
Davis, J. R., 2001. High performance modeling of circulation and transport in the Indian River Lagoon, Florida. Ph.D. Dissertation, University of Florida, Gainsville, FL.
Davis, A. R. & A. J. Butler, 1989. Direct observations of larval dispersal in the colonial ascidian Podoclavella moluccensis Sluiter: evidence for closed populations. Journal of Experimental Marine Biology and Ecology 127: 189–203.
Davis, J. R. & Y. P. Sheng, 2000. High performance estuarine and coastal environmental modeling: The CH3D example. In Estuarine and Coastal Modeling. American Society of Civil Engineers, New York: 470–484.
de Lange, W. P. & P. J. de Lange, 1994. An appraisal of factors controlling the latitudinal distribution of mangrove (Avicennia marina var. resinifera) in New Zealand. Journal of Coastal Research 10: 539–548.
De Ryck, D. J. R., E. M. R. Robert, N. Schmitz, T. Van der Stocken, D. Di Nitto, F. Dahdouh-Guebas & N. Koedam, 2012. Size does matter, but not only size: two alternative dispersal strategies for viviparous mangrove propagules. Aquatic Botany 103: 66–73.
Delgado, P., P. F. Hensel, J. A. Jimenez & J. W. Day, 2001. The importance of propagule establishment and physical factors in mangrove distributional patterns in a Costa Rican estuary. Aquatic Botany 71: 157–178.
Donnelly, M. & L. Walters, 2014. Trapping of rhizophora mangle propagules by coexisting early successional species. Estuaries and Coasts 37(6): 1562–1571. doi:10.1007/s12237-014-9789-2.
Doughty, C. L., J. A. Langley, W. S. Walker, I. C. Feller, R. Schaub & S. K. Chapman, 2016. Mangrove range expansion rapidly increases coastal wetland carbon storage. Estuaries and Coasts 39: 385–396.
Drexler, J. Z., 2001. Maximum longevities of Rhizophora apiculata and R. mucronata propagules. Pacific Science 55: 17–22.
Engle, V. D. & J. K. Summers, 1999. Latitudinal gradients in benthic community composition in Western Atlantic estuaries. Journal of Biogeography 26: 1007–1023.
Everitt, J. H., F. W. Judd, D. E. Escobar & M. R. Davis, 1996. Integration of remote sensing and spatial information technologies for mapping black mangrove on the Texas gulf coast. Journal of Coastal Research 12: 64–69.
Evermann, B. W. & B. A. Bean, 1897. Indian River and its fisheries. Report of Commissioner of Fish and Fisheries, Appendix 5: 223–262.
Farnsworth, E. J. & A. M. Ellison, 1996. Scale-dependent spatial and temporal variability in biogeography of mangrove root epibiont communities. Ecological Monographs 66: 45–66.
Grosberg, R. K., 1981. Competitive ability influences habitat choice in marine invertebrates. Nature 290: 700–702.
Guerra-Castro, E. J. & J. J. Cruz-Motta, 2014. Ecology of fouling assemblages associated with mangrove’s roots: an artificial substrate for manipulative experiments. Journal of Experimental Marine Biology and Ecology 457: 31–40.
Hamilton, J. F., 2005. A coupled hydrodynamic transport model for assessing source-sink recruitment dynamics in estuarine habitats. Ph.D. dissertation, University of Connecticut, Storrs, CT.
Havenhand, J. N. & I. Svane, 1989. Larval behaviour, recruitment, and the role of adult attraction in Ascidia mentula O.F. Muller. In Reproduction, Genetics and Distributions of Marine Organisms. 23rd European Marine Biology Symposium. Olsen & Olsen, Fredensborg, Denmark: 127–132.
Helmuth, B., C. D. G. Harley, P. M. Halpin, M. O’Donnell, G. E. Hofmann & C. A. Blanchette, 2002. Climate change and latitudinal patterns of intertidal thermal stress. Science 298: 1015–1017.
Holloway, M. G. & M. J. Keough, 2002. An introduced polychaete affects recruitment and larval abundance of sessile invertebrates. Ecological Applications 12: 1803–1823.
Hunt, H. L. & R. E. Scheibling, 1997. Role of early post-settlement mortality in recruitment of benthic marine invertebrates. Marine Ecology – Progress Series 155: 269–301.
Jiang, J., D. L. DeAngelis, G. H. Anderson & T. J. Hall III, 2014. Analysis and simulation of propagule dispersal and salinity intrusion from storm surge on the movement of a marsh–mangrove ecotone in South Florida.”. Estuaries and Coasts 37: 24–35.
Kinlan, B. P. & S. D. Gaines, 2003. Propagule dispersal in marine and terrestrial environments: a community perspective. Ecology 84: 2007–2020.
Krauss, K. W., A. S. From, T. W. Doyle, T. J. Doyle & M. J. Barry, 2011. Sea-level rise and landscape change influence mangrove encroachment onto marsh in the Ten Thousand Islands region of Florida, USA. Journal of Coastal Conservation 15: 629–638.
Liu, J. T., 1992. The influence of episodic weather events on tidal residual currents: a case study at Sebastian Inlet, Florida. Estuaries 15: 109–121.
Lonard, R. I. & F. W. Judd, 1991. Comparison of the effects of severe freezes of 1983 and 1989 on native woody plants in the Lower Rio Grande Valley, Texas. Southern Naturalist 36: 213–217.
Marshall, D. J. & M. J. Keough, 2008. The evolutionary ecology of offspring size in marine invertebrates. Advances in Marine Biology 53: 1–60.
McKee, K. L., 1995a. Seedling recruitment patterns in a Belizean mangrove forest: effects of establishment ability and physico-chemical factors. Oecologia 101: 448–460.
McKee, K. L., 1995b. Seedling recruitment patterns in a Belizean mangrove forest: effects of establishment ability and physico-chemical factors. Oecologia 101: 448–460.
McKee, K. L., D. R. Cahoon & I. C. Feller, 2007. Caribbean mangroves adjust to rising sea level through biotic controls on change in soil elevation. Global Ecology and Biogeography 16: 545–556.
Mook, D., 1980. Seasonal variation in species composition of recently settled fouling communities along an environmental gradient in the Indian River Lagoon, Florida. Estuarine and Coastal Marine Science 11: 573–581.
Nettel, A. & R. S. Dodd, 2007. Drifting propagules and receding swamps: genetic footprints of mangrove recolonization and dispersal along tropical coasts. Evolution 61: 958–971.
Occhipinti-Ambrogi, A., 2007. Global change and marine communities: alien species and climate change. Marine Pollution Bulletin 55: 342–352.
Olson, R. R., 1985. The consequences of short-distance larval dispersal in a sessile marine invertebrate. Ecology 66: 30–39.
Osland, M. J., N. Enwright, R. H. Day & T. W. Doyle, 2013. Winter climate change and coastal wetland foundation species: salt marshes vs. mangrove forests in the southeastern United States. Global Change Biology 19: 1482–1494.
Osman, R. W., 1977. The establishment and development of a marine epifaunal community. Ecological Monographs 47: 37–63.
Osman, R. W., 2015. Regional variation in the colonization of experimental substrates by sessile marine invertebrates: local vs. regional control of diversity. Journal of Experimental Marine Biology and Ecology 473: 227–286.
Osman, R. W. & R. B. Whitlatch, 1998. Local control of recruitment in an epifaunal community and the consequences to colonization processes. Hydrobiologia 375(376): 113–123.
Osman, R. W. & R. B. Whitlatch, 2004. The control of the development of a marine benthic community by predation on recruits. Journal of Experimental Marine Biology and Ecology 311: 117–145.
Osman, R. W., R. B. Whitlatch & R. J. Malatesta, 1992. Potential role of micro-predators in determining recruitment into a marine community. Marine Ecology Progress Series 83: 35–43.
Parkinson, R. W., M. Perez-Bedmar & J. A. Santangelo, 1999. Red mangrove (Rhizophora mangle L.) litter fall response to selective pruning (Indian River Lagoon, Florida, U.S.A.). Hydrobiologia 413: 63–76.
Peterson, J. M. & S. S. Bell, 2015. Saltmarsh boundary modulates dispersal of mangrove propagules: implications for mangrove migration with sea-level rise. PLoS One 10: e0119128.
Pickens, C. N. & M. W. Hester, 2011. Temperature tolerance of early life history stages of black mangrove Avicennia germinans: implications for range expansion. Estuaries and Coasts 34: 824–830.
Pitts, P. A., 1989. Upwind return flow in a coastal lagoon: seasonal-scale barotropic transport. Estuaries 12: 92–97.
Proffitt, C. E., E. C. Milbrandt & S. E. Travis, 2006. Red mangrove (Rhizophora mangle) reproduction after Hurricane Charley: comparisons of Charlotte Harbor and Tampa Bay. Estuaries and Coasts 29: 972–978.
Rabinowitz, D., 1978a. Mortality and initial propagule size in mangrove seedlings in Panama. Journal of Ecology 66: 45–51.
Rabinowitz, D., 1978b. Dispersal properties of mangrove propagules. Biotropica 10: 47–57.
Scheltema, R. S., 1974. Biological interactions determining larval settlement of marine invertebrates. Thallasia Jugoslavica 10: 263–296.
Scheltema, R. S., 1986a. Long-distance dispersal by planktonic larvae of shoal-water benthic invertebrates among central Pacific islands. Bulletin of Marine Science 39: 241–256.
Scheltema, R. S., 1986b. On dispersal and planktonic larvae of benthic invertebrates: an eclectic overview and summary of problems. Bulletin of Marine Science 39: 290–322.
Shanks, A. L., B. A. Grantham & M. H. Carr, 2003. Propagule dispersal distance and the size and spacing of marine reserves. Ecological Applications 13: 159–169.
Sheng, Y. P., 1990a. Evolution of a three-dimensional curvilinear-grid hydrodynamic model for estuaries, lakes, and coastal waters: CH3D. In Estuarine and Coastal Modeling. American Society of Civil Engineers, New York: 40–49.
Sheng, Y. P., 1990b. Validation and recent enhancement of a three-dimensional curvilinear-grid finite-difference model for estuarine, coastal and lake circulation: CH3D. In Estuarine and Coastal Modeling. American Society of Civil Engineers, New York: 1097–1103.
Sheng, Y. P., J. R. Davis, D. Sun, C. Qiu, D. Christian, K. Park, T. Kim & Y. Zhang, 2002. Application of an integrated modeling system for estuarine and coastal ecosystems to Indian River Lagoon, Florida. Estuarine and Coastal Modeling 2001: 329–343.
Smith, N. P., 1990. Longitudinal transport in a coastal lagoon. Estuarine, Coastal and Shelf Science 31: 835–849.
Sousa, W. P. & B. J. Mitchell, 1999. The effect of seed predators on plant distributions: is there a general pattern in mangroves? Oikos 86: 55–66.
Stevens, P. W., S. L. Fox & C. L. Montague, 2006. The interplay between mangroves and saltmarshes at the transition between temperate and subtropical climate in Florida. Wetlands Ecology and Management 14: 435–444.
Steward, J. S., R. W. Virnstein, L. J. Morris & E. F. Lowe, 2005. Setting depth, coverage, and light targets for the Indian River Lagoon system, Florida. Estuaries 28: 923–935.
Stieglitz, T. & P. V. Ridd, 2001. Trapping of mangrove propagules due to density-driven secondary circulation in the Normanby River estuary, NE Australia. Marine Ecology Progress Series 211: 131–2001.
Sutherland, J. P., 1980. Dynamics of the epibenthic community on roots of the mangrove Rhizophora mangle, at Bahia de Buche, Venezuela. Marine Biology 58: 75–84.
Thiel, M. & P. A. Haye, 2006. The ecology of rafting in the marine environment. III. Biogeographical and evolutionary consequences. Oceanography and Marine Biology: An Annual Review 44: 323–429.
Todd, C., 1998. Larval supply and recruitment of benthic invertebrates: do larvae always disperse as much as we believe? Hydrobiologia 375–376: 1–21.
Weiss, C. M., 1948. The seasonal occurence of sedentary marine organisms in Biscayne Bay, Florida. Ecology 29: 153–172.
White, J. W., S. G. Morgan & J. L. Fisher, 2014. Planktonic larval mortality rates are lower than widely expected. Ecology 95: 3344–3353.
Woodroffe, C. D., 1990. The impact of sea-level rise on mangrove shorelines. Progress in Physical Geography 14: 483–520.
Worcester, S. E., 1994. Adult rafting versus larval swimming: dispersal and recruitment of a botryllid ascidian on eelgrass. Marine Biology 121: 309–317.
Xu, Y., C. W. Holmes & R. Jaffe, 2007. Paleoenvironmental assessment of recent environmental changes in Florida Bay, USA: a biomarker based study. Estuarine Coastal and Shelf Science 73: 201–210.
Young, C. M., 1988. Ascidian cannibalism correlates with larval behavior and adult distribution. Journal of Experimental Marine Biology and Ecology 117: 9–26.
Young, C. M. & J. L. Cameron, 1989. Differential predation by barnacles upon larvae of two bryozoans: spatial effects at small scales. Journal of Experimental Marine Biology and Ecology 128: 283–294.
Acknowledgements
We gratefully acknowledge the support of this research by grants from the NSF MacroSystems Biology program (EF1065821) and the NASA Climate and Biological Response program (NNX11AO94G). This is Smithsonian Marine Station at Fort Pierce Contribution No. 1063 and TMON Contribution No. 15. We are also grateful to David Christian, Peter Suscy, and Troy Rice of the St. John’s River Water Management District of Florida for providing output of hydrodynamic model data that were used in our model.
Author information
Authors and Affiliations
Corresponding author
Additional information
Guest editors: K. W. Krauss, I. C. Feller, D. A. Friess, R. R. Lewis III / Causes and Consequences of Mangrove Ecosystem Responses to an Ever-Changing Climate
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Hamilton, J.F., Osman, R.W. & Feller, I.C. Modeling local effects on propagule movement and the potential expansion of mangroves and associated fauna: testing in a sub-tropical lagoon. Hydrobiologia 803, 173–187 (2017). https://doi.org/10.1007/s10750-017-3231-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10750-017-3231-2