The central conception of all modern physics is the “Hamiltonian”
Erwin Schrodinger
Abstract
Energy is a crucial concept within classical and quantum physics. An essential tool to quantify energy is the Hamiltonian. Here, we consider how to define a Hamiltonian in general probabilistic theories—a framework in which quantum theory is a special case. We list desiderata which the definition should meet. For 3-dimensional systems, we provide a fully-defined recipe which satisfies these desiderata. We discuss the higher dimensional case where some freedom of choice is left remaining. We apply the definition to example toy theories, and discuss how the quantum notion of time evolution as a phase between energy eigenstates generalises to other theories.




Similar content being viewed by others
Notes
By n-dimensional theories, we mean those where normalized states are determined by n real degrees of freedom.
Geometrically, the set of normalized states correspond to a hyperplane intersection with the cone of all states.
Without time-independence, this map is not necessarily homomorphic. E.g. composition of evolutions for 3 seconds and for 5 seconds is equivalent to evolving the system for 8 seconds only if “5 seconds of evolution” corresponds to the same group element whether the evolution begins at time \(t=0\) or at time \(t=3\;{\mathrm{seconds}}\).
For time-dependent A, one integrates Eq. (19) into a time-ordered exponential: \(M(\tau ) = \mathcal {T}\left\{ \exp \left[ \int _0^\tau A(t)\, \mathrm{d}t \right] \right\} \), where \(\mathcal {T}(\cdot )\) denotes that every term in the expansion of the exponent only appears in increasing time order. This explicit ordering is necessary since in general A(t) and \(A(t')\) might not commute at different times.
[13] use an inverse statement of GEN, and consider the “observability of energy” as a postulate for quantum theory. Namely, they specify that the generator of dynamics should be able to uniquely determine an observable. On top of a set of axioms that restricts theories to Jordan algebras, this uniquely singles out quantum theory.
Allowed means that the transformation maps all states to states and satisfies any other constraints that are part of the theory.
As a pathological example, consider a three level system where \(E_1 = 0\), and \(E_3 = 2 E_2\); a transformation from a state \(\vec {\rho }\) with well-defined energy in \(E_2\) (
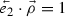 ) to \(\rho '\) where
) to \(\rho '\) where 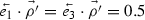 would satisfy INV but not INV*.
would satisfy INV but not INV*.This does not mean that there are no phase dynamics—take for instance the Aharonov-Bohm effect in quantum theory, whereby some global operation induces phases between branches. However, in quantum theory, a transformation with statistically identical action on the states can also be induced by putting pieces of glass on each individual branch; in box-world, a global transformation akin to the Aharonov–Bohm effect is permissible, whereas the analogous local construction that induces the same phase transformation is not possible.
References
Hankins, T.L.: Sir William Rowan Hamilton, p. 64. Johns Hopkins University Press, Baltimore (1980)
Coopersmith, J.: Energy, the Subtle Concept: The Discovery of Feynman’s Blocks from Leibniz to Einstein. Oxford University Press, Oxford (2010)
Arnold, V.I.: Mathematical Methods of Classical Mechanics. Graduate Texts in Mathematics, vol. 60. Springer, New York (1989)
Cohen-Tannoudji, C., Diu, B., Laloe, F.: Quantum Mechanics. Wiley, New York (1977)
Hardy, L.: Quantum theory from five reasonable axioms (2001). arXiv:quant-ph/0101012
Barrett, J.: Information processing in generalized probabilistic theories. Phys. Rev. A 75(3), 032304 (2007). https://doi.org/10.1103/PhysRevA.75.032304
Masanes, L., Müller, M.P.: A derivation of quantum theory from physical requirements. New J. Phys. 13(6), 063001 (2011). https://doi.org/10.1088/1367-2630/13/6/063001
Janotta, P., Hinrichsen, H.: Generalized probability theories: what determines the structure of quantum theory? J. Phys. A 47(32), 323001 (2014). https://doi.org/10.1088/1751-8113/47/32/323001
Popescu, S., Rohrlich, D.: Quantum nonlocality as an axiom. Found. Phys. 24(3), 379–385 (1994). https://doi.org/10.1007/BF02058098
Hardy, L.: Reformulating and reconstructing quantum theory (2011). arXiv:1104.2066 [gr-qc, physics:hep-th, physics:quant-ph]
Dakić, B., Brukner, Č.: Quantum theory and beyond: is entanglement special? In: Hans, H. (ed.) Deep Beauty: Understanding the Quantum World Through Mathematical, pp. 365–392. Cambridge University Press, Cambridge (2011)
Chiribella, G.: DAriano, G.M., Perinotti, P.: Informational derivation of quantum theory. Phys. Rev. A 84(1), 012311 (2011). https://doi.org/10.1103/PhysRevA.84.012311
Barnum, H., Müller, M.P., Ududec, C.: Higher-order interference and single-system postulates characterizing quantum theory. N. J. Phys. 16(12), 123029 (2014). https://doi.org/10.1088/1367-2630/16/12/123029
Barnum, H., Barrett, J., Leifer, M., Wilce, A.: Cloning and broadcasting in generic probabilistic theories (2006). arXiv:quant-ph/0611295
Chiribella, G., Scandolo, C.M.: Entanglement as an axiomatic foundation for statistical mechanics (2016). arXiv:1608.04459 [quant-ph]
Barrett, J., Hardy, L., Kent, A.: No signaling and quantum key distribution. Phys. Rev. Lett. 95(1), 010503 (2005). https://doi.org/10.1103/PhysRevLett.95.010503
Acín, A., Gisin, N., Masanes, L.: From Bell’s theorem to secure quantum key distribution. Phys. Rev. Lett. 97(12), 120405 (2006). https://doi.org/10.1103/PhysRevLett.97.120405
Acín, A., Brunner, N., Gisin, N., Massar, S., Pironio, S., Scarani, V.: Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98(23), 230501 (2007). https://doi.org/10.1103/PhysRevLett.98.230501
Short, A.J., Wehner, S.: Entropy in general physical theories. N. J. Phys. 12(3), 033023 (2010). https://doi.org/10.1088/1367-2630/12/3/033023
Barnum, H., Barrett, J., Clark, L.O., Leifer, M., Spekkens, R., Stepanik, N., Wilce, A., Wilke, R.: Entropy and information causality in general probabilistic theories. N. J. Phys. 12(3), 033024 (2010). https://doi.org/10.1088/1367-2630/12/3/033024
Kimura, G., Nuida, K., Imai, H.: Distinguishability measures and entropies for general probabilistic theories. Rep. Math. Phys. 66(2), 175–206 (2010). https://doi.org/10.1016/S0034-4877(10)00025-X
Müller, M.P., Dahlsten, O.C.O., Vedral, V.: Unifying typical entanglement and coin tossing: on randomization in probabilistic theories. Commun. Math. Phys. 316(2), 441–487 (2012). https://doi.org/10.1007/s00220-012-1605-x
Chiribella, G., Scandolo, C.M.: Entanglement and thermodynamics in general probabilistic theories. N. J. Phys. 17(10), 103027 (2015). https://doi.org/10.1088/1367-2630/17/10/103027
Barnum, H., Barrett, J., Krumm, M., Müller, M.P.: Entropy, majorization and thermodynamics in general probabilistic theories. Electron. Proc. Theor. Comput. Sci. 195, 43–58 (2015). https://doi.org/10.4204/EPTCS.195.4
Chiribella, G., Scandolo, C.M.: Operational axioms for diagonalizing states. Electron. Proc. Theor. Comput. Sci. 195, 96–115 (2015). https://doi.org/10.4204/EPTCS.195.8
Kimura, G., Ishiguro, J., Fukui, M.: Entropies in general probabilistic theories and their application to the Holevo bound. Phys. Rev. A 94(4), 042113 (2016). https://doi.org/10.1103/PhysRevA.94.042113
Krumm, M., Barnum, H., Barrett, J., Müller, M.P.: Thermodynamics and the structure of quantum theory. N. J. Phys. 19(4), 043025 (2017). https://doi.org/10.1088/1367-2630/aa68ef
Chiribella, G., Scandolo, C.M.: Microcanonical thermodynamics in general physical theories. N. J. Phys. 19(12), 123043 (2017). https://doi.org/10.1088/1367-2630/aa91c7
Dahlsten, O.C.O., Garner, A.J.P., Thompson, J., Gu, M., Vedral, V.: Particle exchange in post-quantum theories (2013). arXiv:1307.2529 [quant-ph]
Sorkin, R.D.: Quantum mechanics as quantum measure theory. Mod. Phys. Lett. A 09(33), 3119–3127 (1994). https://doi.org/10.1142/S021773239400294X
Ududec, C., Barnum, H., Emerson, J.: Three slit experiments and the structure of quantum theory. Found. Phys. 41(3), 396–405 (2011). https://doi.org/10.1007/s10701-010-9429-z
Garner, A.J.P., Dahlsten, O.C.O., Nakata, Y., Murao, M., Vedral, V.: A framework for phase and interference in generalized probabilistic theories. N. J. Phys. 15(9), 093044 (2013). https://doi.org/10.1088/1367-2630/15/9/093044
Dahlsten, O.C.O., Garner, A.J.P., Vedral, V.: The uncertainty principle enables non-classical dynamics in an interferometer. Nat. Commun. 5, 4592 (2014). https://doi.org/10.1038/ncomms5592
Garner, A.J.P., Müller, M.P., Dahlsten, O.C.O.: The complex and quaternionic quantum bit from relativity of simultaneity on an interferometer. Proc. R. Soc. A 473, 20170596 (2017). https://doi.org/10.1098/rspa.2017.0596
Lee, C.M., Selby, J.H.: Higher-order interference in extensions of quantum theory. Found. Phys. 47(1), 89–112 (2017). https://doi.org/10.1007/s10701-016-0045-4
Barnum, H., Lee, C.M., Scandolo, C.M., Selby, J.H.: Ruling out higher-order interference from purity principles. Entropy 19(6), 253 (2017). https://doi.org/10.3390/e19060253
Lin, Y.L., Dahlsten, O.C.O.: Tunnelling necessitates negative Wigner function. arXiv:1607.01764 [quant-ph] (2016)
Lee, C.M., Barrett, J.: Computation in generalised probabilisitic theories. N. J. Phys. 17(8), 083001 (2015). https://doi.org/10.1088/1367-2630/17/8/083001
Lee, C.M., Selby, J.H.: Generalised phase kick-back: the structure of computational algorithms from physical principles. N. J. Phys. 18(3), 033023 (2016). https://doi.org/10.1088/1367-2630/18/3/033023
Lee, C.M., Hoban, M.J.: Bounds on the power of proofs and advice in general physical theories. Proc. R. Soc. A 472(2190), 20160076 (2016). https://doi.org/10.1098/rspa.2016.0076
Lee, C.M., Selby, J.H.: Deriving Grover’s lower bound from simple physical principles. N. J. Phys. 18(9), 093047 (2016). https://doi.org/10.1088/1367-2630/18/9/093047
Barrett, J., de Beaudrap, N., Hoban, M.J., Lee, C.M.: The computational landscape of general physical theories (2017). arXiv:1702.08483 [quant-ph]
Lee, C.M., Selby, J.H., Barnum, H..: Oracles and query lower bounds in generalised probabilistic theories (2017). arXiv:1704.05043 [quant-ph]
Garner, A.J.P.: Interferometric computation beyond quantum theory. Found. Phys. (2018). https://doi.org/10.1007/s10701-018-0142-7
Robertson, H.P.: The uncertainty principle. Phys. Rev. 34(1), 163–164 (1929). https://doi.org/10.1103/PhysRev.34.163
Schrödinger, E.: Zum Heisenbergschen Unschrfeprinzip. Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 14, 296–303 (1930)
Hioe, F.T., Eberly, J.H.: $N$-level coherence vector and higher conservation laws in quantum optics and quantum mechanics. Phys. Rev. Lett. 47(12), 838–841 (1981). https://doi.org/10.1103/PhysRevLett.47.838
Kimura, G.: The bloch vector for N-level systems. J. Phys. Soc. Jpn. 72(Suppl.C):185–188 (2003). https://doi.org/10.1143/JPSJS.72SC.185
Bengtsson, I., Życzkowski, K.: Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press, Cambridge (2006)
Bertlmann, R.A., Krammer, P.: Bloch vectors for qudits. J. Phys. A 41(23), 235303 (2008). https://doi.org/10.1088/1751-8113/41/23/235303
Jakóbczyk, L., Siennicki, M.: Geometry of Bloch vectors in two-qubit system. Phys. Lett. A 286(6), 383–390 (2001). https://doi.org/10.1016/S0375-9601(01)00455-8
Chiribella, G., D’Ariano, G.M., Perinotti, P.: Probabilistic theories with purification. Phys. Rev. A 81(6), 062348 (2010). https://doi.org/10.1103/PhysRevA.81.062348
Janotta, P., Lal, R.: Generalized probabilistic theories without the no-restriction hypothesis. Phys. Rev. A 87(5), 052131 (2013). https://doi.org/10.1103/PhysRevA.87.052131
Garner, A.J.P.: Phase and interference phenomena in generalised probabilistic theories. DPhil thesis, University of Oxford (2015)
Spekkens, R.W.: Evidence for the epistemic view of quantum states: a toy theory. Phys. Rev. A 75(3), 032110 (2007). https://doi.org/10.1103/PhysRevA.75.032110
Wilce, A.: A royal road to quantum theory (or thereabouts) (2016). http://arxiv.org/abs/1606.09306
Simon, B.: Representations of Finite and Compact Groups. American Mathematical Society, Providence (1996)
Gottesman, D.: Class of quantum error-correcting codes saturating the quantum Hamming bound. Phys. Rev. A 54(3), 1862–1868 (1996). https://doi.org/10.1103/PhysRevA.54.1862
van Enk, S.J.: A toy model for quantum mechanics. Found. Phys. 37(10), 1447–1460 (2007). https://doi.org/10.1007/s10701-007-9171-3
Pusey, M.F.: Stabilizer notation for Spekkens’s Toy theory. Found. Phys. 42(5), 688–708 (2012). https://doi.org/10.1007/s10701-012-9639-7
Tuckerman, M.: Operators and numerical propagation methods (2002). URL http://www.nyu.edu/classes/tuckerman/mol.dyn/lectures/lecture_9/node1.html
Graydon, M.A.: Quaternions and quantum theory. PhD thesis, University of Waterloo (2011). URL http://hdl.handle.net/10012/6168
Goold, J., Huber, M., Riera, A., del Rio, L., Skrzypczyk, P.: The role of quantum information in thermodynamicsa topical review. J. Phys. A 49(14), 143001 (2016). https://doi.org/10.1088/1751-8113/49/14/143001
Skrzypczyk, P., Short, A.J., Popescu, S.: Work extraction and thermodynamics for individual quantum systems. Nat. Commun. 5, 4185 (2014). https://doi.org/10.1038/ncomms5185
Horodecki, M., Oppenheim, J.: Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 4, 2059 (2013). https://doi.org/10.1038/ncomms3059
Acknowledgements
We thank George Knee and Benjamin Yadin for useful comments. We are grateful for financial support from the UK Engineering and Physical Sciences Research Council, the John Templeton Foundation, the Foundational Questions Institute, EU Collaborative Project TherMiQ (Grant Agreement 618074), the London Institute for Mathematical Sciences and Wolfson College, University of Oxford.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Branford, D., Dahlsten, O.C.O. & Garner, A.J.P. On Defining the Hamiltonian Beyond Quantum Theory. Found Phys 48, 982–1006 (2018). https://doi.org/10.1007/s10701-018-0205-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-018-0205-9





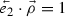 ) to
) to 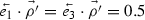 would satisfy INV but not INV*.
would satisfy INV but not INV*.