Quantum Bayesian Decision-Making

Abstract

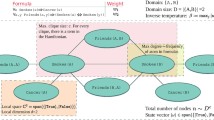
As a compact representation of joint probability distributions over a dependence graph of random variables, and a tool for modelling and reasoning in the presence of uncertainty, Bayesian networks are of great importance for artificial intelligence to combine domain knowledge, capture causal relationships, or learn from incomplete datasets. Known as a NP-hard problem in a classical setting, Bayesian inference pops up as a class of algorithms worth to explore in a quantum framework. This paper explores such a research direction and improves on previous proposals by a judicious use of the utility function in an entangled configuration. It proposes a completely quantum mechanical decision-making process with a proven computational advantage. A prototype implementation in Qiskit (a Python-based program development kit for the IBM Q machine) is discussed as a proof-of-concept.

Appendix

1.1 A Complexity Comparison

The decision-making processes we aim at comparing require inequality (50) to be satisfied. It assures that the decision maker chooses with certainty the best action.

$$\begin{aligned} \forall _{n{\setminus } \{max\}} EU(action_{max}) - EU(action_n) > \delta _{action_{max}} + \delta _{action_{n}} \end{aligned}$$

(50)

Thus, to compare Process A and Process B it is necessary to consider all terms that are different. Therefore, the error term $\delta _a$ for Process A is related to directly sampling values for the expected utilities, while in Process B the expected utility is determined indirectly. For this reason, in Process B it is necessary to apply error propagation rules:

$$\begin{aligned} EU(a|e)+\delta _{EU(a|e)}= \sum _{R} (P(Result=r|a,e)+\delta _b)*U(r) \end{aligned}$$

(51)

Before applying error propagation to this equation, we need to normalize it so that EU(a|e)/k is equal to P(a).

$$\begin{aligned} P(a)+\delta _a= \sum _{R} (P(Result=r|a,e)+\delta _b)*F(r) \end{aligned}$$

(52)

where the normalization function (F(r)) is expressed as,

$$\begin{aligned} F(r)=\frac{U(r)}{\sum _a\sum _r U(r)*P(r|a,e)} \end{aligned}$$

(53)

Here, again, the mean value of U(r) is used:

$$\begin{aligned} F(r)=\frac{U(r)}{\sum _a\sum _r P(r|a,e)*U(r)}=\frac{U(r)}{\sum _a \frac{1}{N_r}} =\frac{U(r)}{\frac{N_a}{N_r}}= \frac{N_r*U(r)}{N_a} \end{aligned}$$

(54)

$$\begin{aligned} F(r)= \frac{1}{N_a} \end{aligned}$$

(55)

Expressing the equation that determines the error term $\delta _a$ as a function of the error term $\delta _b$ yields

$$\begin{aligned} \delta _a=\sqrt{ \sum _{R} \delta _b^2*F(r)^2} \end{aligned}$$

(56)

Using Eq. (55) we obtain:

$$\begin{aligned} \delta _a=\sqrt{ \sum _{R} \delta _b^2*{(\frac{1}{N_a})}^2} \end{aligned}$$

(57)

Then, assuming that $\delta _b$ is similar, which is in favor of Process B because it minimizes the $\delta _a$ term:

$$\begin{aligned} \delta _a=\sqrt{ N_r*\delta _b^2*{(\frac{1}{N_a})}^2} \end{aligned}$$

(58)

yielding,

$$\begin{aligned} \delta _a={(\frac{\sqrt{ N_r}}{N_a})}*\delta _b \end{aligned}$$

(59)

With the relation between the error terms determined, it is possible to compare the difference of the computational effort involved in both processes, assuming again the mean terms for the probabilities:

$$\begin{aligned} \sqrt{\frac{N_a}{N_r}}*\frac{A_{r,\alpha }*\frac{1}{N_r}*(1-\frac{1}{N_r})*\delta _a^2*N_a}{A_{a,\alpha }* \frac{1}{N_a}*(1-\frac{1}{N_a})*\delta _b^2} + \dfrac{2*N_a*N_r}{n*2^m*\sqrt{\dfrac{N_r}{P(e)}}*\dfrac{A_{a,\alpha }*\frac{1}{N_a}*(1-\frac{1}{N_a})}{\delta _a^2}} \end{aligned}$$

(60)

Let us call the term on the right,

$$\begin{aligned} t_1= \dfrac{2*N_a*N_r}{n*2^m*\sqrt{\dfrac{N_r}{P(e)}}*\dfrac{A_{a,\alpha }*\frac{1}{N_a}*(1-\frac{1}{N_a})}{\delta _a^2}} \end{aligned}$$

(61)

Using 59,

$$\begin{aligned} \sqrt{\frac{N_a}{N_r}}*\frac{N_r}{N_a}*\frac{A_{r,\alpha }*\frac{1}{N_r}*(1-\frac{1}{N_r})}{A_{a,\alpha }*\frac{1}{N_a}*(1-\frac{1}{N_a})} + t_1 \end{aligned}$$

(62)

also,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}}*\frac{A_{r,\alpha }*\frac{1}{N_r}*(1-\frac{1}{N_r})}{A_{a,\alpha }*\frac{1}{N_a}*(1-\frac{1}{N_a})}+ t_1 \end{aligned}$$

(63)

and,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}}*\frac{A_{r,\alpha }*(\frac{1}{N_r}-\frac{1}{N_r^2})}{A_{a,\alpha }*(\frac{1}{N_a}-\frac{1}{N_a^2})} + t_1 \end{aligned}$$

(64)

From Inglot (2010) we obtain a lower bound for $A_{\alpha ,k}$. Although these terms are different for distinct values of $\alpha$, we consider the one where $\alpha$ is not leaning to zero too fast. Thus,

$$\begin{aligned} A_{\alpha ,k} \ge k + 2*\log {\frac{1}{\alpha }} - \frac{5}{2} \end{aligned}$$

(65)

With this equation it is possible to define a better value for the difference between the computational efforts,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}}*\frac{(N_r + 2*\log {\frac{1}{\alpha }} - \frac{7}{2})*(\frac{1}{N_r}-\frac{1}{N_r^2})}{(N_a + 2*\log {\frac{1}{\alpha }}-\frac{7}{2})*(\frac{1}{N_a}-\frac{1}{N_a^2})} + t_1 \end{aligned}$$

(66)

As

$$\begin{aligned} \lim _{N_r\rightarrow \infty } (N_r + 2*\log {\frac{1}{\alpha }} - \frac{7}{2})*(\frac{1}{N_r}-\frac{1}{N_r^2})=1 \end{aligned}$$

(67)

and,

$$\begin{aligned} \lim _{N_a\rightarrow \infty } (N_a + 2*\log {\frac{1}{\alpha }}-\frac{7}{2})*(\frac{1}{N_a}-\frac{1}{N_a^2})=1 \end{aligned}$$

(68)

it is possible to approximate the expression to

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}}*\frac{(N_r + 2*\log {\frac{1}{\alpha }} - \frac{7}{2})*(\frac{1}{N_r}-\frac{1}{N_r^2})}{(N_a + 2*\log {\frac{1}{\alpha }}-\frac{7}{2})*(\frac{1}{N_a}-\frac{1}{N_a^2})} + t_1 \approx \sqrt{\frac{N_r}{N_a}} +\dfrac{2*N_a*\sqrt{N_r*P(e)}*\delta _a^2}{n*2^m} \end{aligned}$$

(69)

Writing the term of $\delta _a$ as a function of its dimension and a factor that adjusts the precision,

$$\begin{aligned} \delta _a = \dfrac{1}{c*N_a} \end{aligned}$$

(70)

we obtain,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}} +\dfrac{2*\sqrt{N_r*P(e)}}{N_a*c^2*n*2^m} \end{aligned}$$

(71)

Rewriting this the expression as,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}} * (1+\dfrac{2*\sqrt{P(e)}}{\sqrt{N_a}*c^2*n*2^m}) \end{aligned}$$

(72)

Because,

$$\begin{aligned} \dfrac{2*\sqrt{P(e)}}{\sqrt{N_a}*c^2*n*2^m} \ge 0 \end{aligned}$$

(73)

for any value of the composing variables, then,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}} * (1+\dfrac{2*\sqrt{P(e)}}{\sqrt{N_a}*c^2*n*2^m}) \ge \sqrt{\frac{N_r}{N_a}}. \end{aligned}$$

(74)

we prove that the relation between Process A and B is under bounded by,

$$\begin{aligned} \sqrt{\frac{N_r}{N_a}} \end{aligned}$$

(75)