Abstract
We study the effect of group size on cooperation in voluntary contribution mechanism games. As in previous experiments, we study four- and eight-person groups in high and low marginal per capita return (MPCR) conditions. We find a positive effect of group size in the low MPCR condition, as in previous experiments. However, in the high MPCR condition we observe a negative group size effect. We extend the design to investigate two- and three-person groups in the high MPCR condition, and find that cooperation is highest of all in two-person groups. The findings in the high MPCR condition are consistent with those from n-person prisoner’s dilemma and oligopoly experiments that suggest it is more difficult to sustain cooperation in larger groups. The findings from the low MPCR condition suggest that this effect can be overridden. In particular, when cooperation is low other factors, such as considerations of the social benefits of contributing (which increase with group size), may dominate any negative group size effect.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The voluntary contributions mechanism (VCM) has become a widely used experimental framework for studying cooperation. In typical experiments participants are assigned to n-player groups. Each group member is endowed with tokens and chooses how many to place in a private account, from which that person earns α money units per token, and how many to place in a group account, from which every person in the group earns β money units per token. Parameters are chosen so that private and collective interests are in conflict: the group maximizes earnings by contributing all tokens to the group account (nβ>α), but each group member has a private incentive to place her tokens in her private account (α>β). This task is then repeated over a number of periods.Footnote 1
One factor that might be expected to affect contributions to the group account is the size of the group. Previous VCM studies have found that, if there is an effect of group size, it is in the direction of higher contributions in larger groups (see Sect. 2 for a review). An explanation for this finding can be based on the private and social costs and benefits of a contribution. For each token contributed to the group account a contributor incurs a cost of α and a benefit of β money units regardless of group size, whereas the social benefits of the contribution, n times β money units, increase with group size. If individuals care about more than just own earnings, and instead internalize some of the social benefits of contributing, they may be willing to contribute more in larger groups where the social benefits are larger.
Interestingly, findings from other experimental settings where there is a tension between private and collective interests, such as n-person prisoner’s dilemma or oligopoly experiments, suggest that increasing the size of the group may have a negative impact on cooperation, as subjects find it more difficult to attain collectively optimal outcomes in larger groups. For example, Marwell and Schmitt (1972) and Bonacich et al. (1976) study n-person iterated prisoner’s dilemmas where they vary n while keeping constant the private and social costs and benefits of cooperating.Footnote 2 They find that cooperation rates are lower in larger groups. Numerous subsequent studies report further evidence that cooperation is inversely related to group size, usually using groups of size between two and seven, although, as Kollock (1998) notes in a review of this literature, in some studies the decrease in cooperation as group size increases tapers off quickly.Footnote 3
Similarly, a large literature on experimental oligopolies finds that cooperation (i.e. collusion) is more difficult in larger groups (i.e. when there are more competitors). For example Fouraker and Siegel (1963) examine the textbook Bertrand model under duopoly and triopoly treatments. Although equilibrium predictions are the same for both treatments, prices are higher among duopolies. Similarly, Dolbear et al. (1968) study a model of price competition with differentiated goods where equilibrium predictions are independent of the number of competitors, and they too find prices to be higher in smaller markets. Relatedly, Isaac and Reynolds (2002) design two- and four-firm posted-offer markets with capacity constraints so that benchmark predictions (competitive, collusive, Cournot-Nash) are comparable, and find that prices are higher in two-firm markets. Other studies examine models where equilibrium predicts a numbers effect. Even here, there is evidence of a negative effect of group size on collusion beyond that predicted. Huck et al. (2004), for instance, study the textbook homogeneous goods Cournot model with two, three, four or five firms per market, where the equilibrium prediction is that quantities are higher in larger markets. In the experimental two-firm markets there is evidence of collusion and firms produce less than the Nash level. As the number of firms increases markets become more competitive and firms tend to produce even more than the Nash level. Orzen (2008) studies a price-competition setting where standard theory predicts that expected prices increase with the number of firms in the market. In the experiment he finds the opposite effect: outcomes are more collusive in two- than four-firm markets.
There are several possible explanations for these negative effects of group size on cooperation. One is based on the idea that a number of factors conducive to cooperation, such as social pressure and social incentives, may be more effective in small than larger groups (Olson 1965). Other authors (Marwell and Schmitt 1972) have suggested the ‘bad apple’ hypothesis. Many individuals are willing to cooperate, but only as long as others do so as well. Thus, if a group contains one non-cooperator (a ‘bad apple’) cooperation will unravel. In a population containing a fixed proportion of non-cooperators larger groups are more likely to unravel. Another possibility is that, as discussed by Kim and Walker (1984), individuals in small groups have a greater perception that their free-riding may have an impact on others’ willingness to cooperate in the future.
These considerations suggest that the observed group size effects in VCM experiments reflect a combination of factors that may operate in opposite directions. A positive effect of group size stems from the increased social benefits from a contribution, while a negative effect stems from the difficulty of sustaining cooperative outcomes in larger groups. This led us to conjecture that the moderately positive effects observed in previous VCM experiments may reflect the focus of the literature on groups of four or more players, which in the standard VCM setup is already sufficiently large to make it difficult to sustain cooperation, and where the positive effects may dominate. We conjectured that the negative effect of group size may be more evident in smaller groups, while the positive effect is more evident in larger groups.
To test these conjectures we compare cooperation rates in VCM experiments varying the number of players matched into a group. As in the previous VCM literature on group size effects, we also vary the marginal per capita return from contributions to the group account (MPCR=β/α): either low (0.3) or high (0.75). For both low and high MPCR we compare four- and eight-person groups, as in previous studies. For the high MPCR setting we extend the analysis to smaller groups of two and three players.Footnote 4
As in previous studies, in our low-MPCR treatments we observe a significantly positive effect of group size on contributions. This positive effect is already evident in the first period of the experiment where contributions are 12 % higher in eight- than four-person groups. In both treatments contributions steadily decline across periods, but we do not observe a faster unraveling of cooperation in larger groups. The picture is different in the high-MPCR treatments. Here initial contributions are around 75 % of endowments in all treatments. However, treatments differ in how cooperation unravels across periods, with contributions declining faster in larger groups. The overall effect of group size on cooperation is negative: average contributions are highest in two-person groups and lowest in eight-person groups, with contributions in three- and four-person groups taking intermediate values.
Thus, in our VCM experiments we observe both a positive and negative effect of group size on cooperation. However, contrary to our initial conjecture, whether the positive or negative effects dominate does not seem to depend on the size of the group: in our high-MPCR treatments we do observe a negative effect of group size on cooperation also for groups of four or more players. Rather, our findings suggest that which effect dominates depends on how conducive the VCM environment is to cooperation. In settings that are particularly conducive to cooperation (like our high-MPCR treatments) contributions are already high, and there is limited scope for improving on such high levels of cooperation. Here the negative effects of group size are more evident as the initially high cooperation levels deteriorate faster in larger groups. In contrast, in settings that are unfavorable to cooperation (like our low-MPCR treatments) there is more scope for group size to have a positive effect on initial cooperation, and less scope for it to affect the decline of contributions over time.
The remainder of the paper is organized as follows. In the next section we review previous evidence on group-size effects in VCM experiments. In Sect. 3 we describe our experimental design and procedures. In Sect. 4 we present the results, and Sect. 5 concludes.
2 Group size effects in previous VCM experiments
We are aware of six previous studies that have systematically examined the effects of group size in VCM games holding other game parameters constant. These studies are listed in Table 1, along with the MPCR and group sizes used in each treatment. We also report the average contributions as a percentage of endowments and levels of statistical significance.Footnote 5
With the exception of Goeree et al. (2002) who use one-shot games, all studies use repeated VCM games. In most studies group composition does not change across periods (partners matching protocol). In Carpenter (2007) groups are randomly reformed at the beginning of each new period (strangers matching protocol). Group size effects are studied by varying the number of players matched in a group. In all studies group sizes are varied in a between-subject design, except in Goeree et al. (2002) who use a within-subject design. Most studies have investigated group size effects using groups of 4 or more players. An exception is Goeree et al. (2002) who compare groups with 2 and 4 players.Footnote 6
Most studies report a positive effect of group size on cooperation. The effect seems stronger in settings where the MPCR is low. The reported effect is not always statistically significant, although in some cases this may reflect our conservative testing procedure. In the studies where subjects interact repeatedly we treat groups in which subjects interact as a single observation, resulting in a small effective sample size. For example, the averages reported for Carpenter (2007) are based on 2100 choices (210 subjects × 10 periods), but only 13 independent groups. It is therefore not surprising that the large observed effect is insignificant.Footnote 7 In some cases, increasing group size is found to reduce average contributions (e.g., in Goeree et al. 2002, or when comparing 40- and 100-person groups in Isaac et al. 1994), although these negative effects are always statistically insignificant.
Overall, the picture that emerges from previous studies is that group size has a moderate, positive effect on cooperation in VCM games. This conclusion is reinforced by the meta-analysis results reported by Zelmer (2003). She uses data from 27 VCM experiments conducted using different parameterizations and procedures, and finds a positive and significant (at the 10 % level) effect of group size on contributions. In the next section we describe a new experiment comparing four- and eight-person VCMs across low and high MPCR conditions, as in several previous studies, and extend the design to study group size effects in smaller two- and three-person groups.
3 Experimental design and procedures
The experiment was conducted at the University of Nottingham using the software z-Tree (Fischbacher 2007) and 364 student subjects from a wide range of disciplines, recruited through the online recruiting system ORSEE (Greiner 2004). Multiple sessions were conducted and no participant took part in more than one session.
At the beginning of each session participants were randomly matched into groups that remained the same for the whole experiment. Participants did not know the identities of the other subjects in the room with whom they were grouped. They were given instructions for the experiment (reproduced in the Electronic Supplementary Material) and these were read aloud by the experimenter. Any questions were answered by the experimenter in private, and no communication between participants was allowed. No information passed across groups during the entire session.
All groups played a ten-period VCM game. In each period, players received an endowment of 20 tokens and had to choose how many to allocate to a public account and how many to keep in a private account. A player earned α points for each token she kept in her private account, and β points from each token allocated to the public account (regardless of which group member had contributed it). At the end of the period players were informed of the decisions and earnings of each group member.
Across sessions we varied the MPCR from contributions to the group account and the number of players matched into a group. In our LOW_4 and LOW_8 treatments we used a low MPCR (β/α=3/10) and subjects played the VCM game in four- and eight-person groups, respectively. In four other treatments we used a high MPCR (β/α=3/4) and subject played the VCM game either in two-person groups (HIGH_2 treatment), three-person groups (HIGH_3), four-person groups (HIGH_4), or eight-person groups (HIGH_8). Table 2 summarizes the experiment design and provides details on the number of sessions, subjects and independent observations for each treatment.
At the end of a session the accumulated point earnings from all periods were converted into cash at a rate of £0.003 (£0.0075) per point in the low (high) MPCR treatments.Footnote 8 Participants’ earnings ranged from £4.60 to £30.25, averaging £12.09, for sessions lasting between 30 and 60 minutes.
4 Results
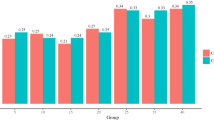
Figure 1 shows average contributions (as percentage of endowment) in the six treatments across the ten periods of the experiment. Consistent with previous studies, in our low-MPCR treatments we observe a positive effect of group size on cooperation: averaging across all periods, contributions are 23 % of endowment in LOW_8 and 11 % in LOW_4. The difference is significant at the 1 % level (p=0.003).Footnote 9
This positive and significant effect of group size is already evident in the first period where contributions are higher in LOW_8 than LOW_4 (52 % vs. 40 %, p=0.042). This suggests that the positive effect of group size operates through a shift in cooperative intentions. On the other hand, group size does not seem to have a negative effect on the ability of groups to sustain cooperative outcomes: contributions steadily decline across periods in both treatments and are equally low in the last period of the experiment (2.7 % in LOW_8 and 0.3 % LOW_4, p=0.182).
We examine these effects of group size on contributions using a Tobit regression of contributions on the variable Group Size, the variable Period, an interaction between the two variables, a dummy variable taking value 1 for contributions made in the last period of the experiment, and a constant. The regression (reported in column 1 of Table 3) shows that, while group size has a significantly positive effect on first-period contributions, it does not have a significant effect on the decay of contributions over time since the coefficient on “Group Size ∗ Period” is negative but insignificantly different from zero.
A different picture emerges in our high-MPCR treatments. Figure 1 suggests that there group size affects cooperation mainly through its impact on the stability of contributions, and has only a modest effect on initial contributions. In fact, Fig. 1 shows that contributions are similar across treatments in the first period (HIGH_2: 77 %; HIGH_3: 71 %; HIGH_4: 74 %; HIGH_8: 77 %).Footnote 10 Between periods 2 and 9 contributions remain fairly stable in HIGH_2, whereas they steadily decline in HIGH_3, HIGH_4 and HIGH_8, with a more pronounced downward trend in HIGH_8. In all treatments there is a noticeable drop in contributions in the last period of the experiment, where contributions are again similar across treatments (HIGH_2: 27 %; HIGH_3: 25 %; HIGH_4: 31 %; HIGH_8: 19 %).Footnote 11 Column 2 of Table 3 confirms that the decline in contributions is more pronounced in larger groups. Moreover, the regression shows that group size has an insignificant effect on first-period contributions.
A consequence of this is that average contributions tend to decrease in group size in the high-MPCR treatments. Averaging across all periods, contributions are highest in HIGH_2 (72 %) and lowest in HIGH_8 (49 %), with contributions in HIGH_3 and HIGH_4 taking intermediate values (55 % and 65 %, respectively). The difference in contributions between HIGH_2 and HIGH_8 is significant at the 1 % level (p=0.004). We also detect significant differences between HIGH_2 and HIGH_3 (p=0.039), and HIGH_4 and HIGH_8 (p=0.071). We do not find significant differences in contributions between HIGH_3 and HIGH_4 (p=0.239), HIGH_2 and HIGH_4 (p=0.388), or HIGH_3 and HIGH_8 (p=0.511). These findings suggest that group size has a predominantly negative effect on cooperation when the MPCR is high and particularly when group size is small. In larger groups of size four or more the negative effect of group size is less evident, but it still tends to dominate any positive effect stemming from the increased social benefits of a contribution.
5 Conclusions
Findings from previous experiments show a variety of group size effects that influence cooperation. The existing literature on group size effects in voluntary contribution mechanism (VCM) has typically uncovered a moderate, positive relation between the number of contributors and average contributions. This positive effect of group size on cooperation may result from the increased social benefits of cooperating in larger groups. On the other hand, several previous studies on n-person prisoner’s dilemma or oligopoly experiments find that larger groups face more difficulties in sustaining cooperative outcomes.
Our study shows that the negative relationship between group size and cooperation observed in other social dilemma and oligopoly experiments can also be observed in VCM experiments. In our high marginal per capita return (MPCR) treatments, we find that cooperation is highest in two-person groups and lowest in eight-person groups. However, our experiment also shows that, as in previous studies, the positive effect of group size on cooperation may dominate the negative effect: in our low MPRC treatments, we find that eight-person groups are significantly more cooperative than four-person groups.
We interpret these results as suggesting that similar group size effects operate in prisoner’s dilemmas, oligopoly and VCM settings. In particular, an increase in group size can have both positive and negative effects. Whether the positive or negative effect is observed in VCMs depends on how conducive the VCM environment is to cooperation. In environments that are favorable to cooperation, there may be limited scope for a positive effect of group size on the already high levels of cooperation, and the negative effects of group size may be more evident. The positive effect of group size may be instead more evident in environments that induce low levels of cooperation.
Notes
Marwell and Schmitt (1972) compare two- and three-person prisoner’s dilemma games, while Bonacich et al. (1976) study three-, six- and nine-person games. In both studies payoff matrices are chosen so that cooperating rather than defecting decreases own payoff, and increases total payoff, by the same amount across games.
Not all studies, however, have investigated the effect of group size on cooperation while keeping constant the private and social incentives to cooperate (e.g., Komorita and Lapworth 1982; Grujić et al. 2012). In some studies, as in Bonacich et al. (1976)’s ‘Rule A’ experiments, the social benefits of the contribution increase with group size, akin to the VCM setting, and group size is found to have a positive effect on contributions.
Note that it is not possible to study two- or three-player VCMs in our low-MPCR condition as in such groups cooperation would be in the interest of neither the group nor the individual group members (i.e. α>nβ>β).
For all studies the original data were either included as an appendix or supplied by the authors. Average contributions are computed holding constant other features of the experiment such as MPCR, subjects’ experience with the VCM (for the Isaac et al. 1984 study), and subject pool (for the Goeree et al. 2002 study). To assess group size effects we apply the same methods as we use below in our own data—two-sided Fisher’s randomization tests treating average contributions in each group across all periods as the unit of observation (see Moir 1998 for a discussion of the randomization test). Exceptions are Goeree et al. (2002) one-shot within-subject experiment, where we treat individual average contributions as the unit of observation, and Carpenter (2007) strangers matching protocol experiment, where we use average contributions in a session as the unit of observation. Isaac et al. (1984) have insufficient number of independent groups to conduct meaningful tests.
Goeree et al. (2002) study experiments where each token contributed to the group account generates an ‘internal’ return to the individual contributing it and an ‘external’ return to the other group members. In Table 1 we use data from their treatments 2 and 6, where ‘internal’ and ‘external’ returns are the same as in a standard VCM experiment.
Carpenter uses regression methods to analyze his data and finds a significant group size effect when contributions are regressed on a group size dummy along with other explanatory variables. However he does not report separate regressions for separate MPCRs. Applying his regression model to the different MPCR treatments separately we found the group size dummy to be significant at the 1 % level for both MPCR values.
The different exchange rates across our low- and high-MPCR treatments ensure that subjects can earn the same amount of British Pounds by keeping all their tokens in the private account.
Here, and throughout the rest of the paper, p-values are based on two-sided Fisher’s randomization test applied to group-level data unless otherwise noted.
In any bilateral comparison the difference in contributions is not statistically significant (p>0.309).
Again, the differences are not statistically significant in any bilateral comparison (p>0.192).
References
Bonacich, P., Shure, G. H., Kahan, J. P., & Meeker, R. J. (1976). Cooperation and group size in the n-person prisoners’ dilemma. The Journal of Conflict Resolution, 20(4), 687–706.
Carpenter, J. (2007). Punishing free-riders: how group size affects mutual monitoring and the provision of public goods. Games and Economic Behavior, 60(1), 31–51.
Chaudhuri, A. (2011). Sustaining cooperation in laboratory public goods experiments: a selective survey of the literature. Experimental Economics, 14(1), 47–83.
Dolbear, F. T., Lave, L. B., Bowman, G., Lieberman, A., Prescott, E., Rueter, F., & Sherman, R. (1968). Collusion in oligopoly: an experiment on the effect of numbers and information. The Quarterly Journal of Economics, 82(2), 240–259.
Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Fouraker, L., & Siegel, S. (1963). Bargaining behavior. New York: McGraw-Hill.
Goeree, J. K., Holt, C. A., & Laury, S. K. (2002). Private costs and public benefits: unraveling the effects of altruism and noisy behavior. Journal of Public Economics, 83(2), 255–276.
Greiner, B. (2004). An online recruitment system for economic experiments. In K. Kremer & V. Macho (Eds.), GWDG Bericht: Vol. 63. Forschung und wissenschaftliches Rechnen (pp. 79–93). Göttingen: Ges. für Wiss. Datenverarbeitung.
Grujić, J., Eke, B., Cabrales, A., Cuesta, J. A., & Sánchez, A. (2012). Three is a crowd in iterated prisoner’s dilemmas: experimental evidence on reciprocal behavior. Scientific Reports, 2.
Huck, S., Normann, H.-T., & Oechssler, J. (2004). Two are few and four are many: number effects in experimental oligopoly. Journal of Economic Behavior & Organization, 53, 435–446.
Isaac, R. M., & Reynolds, S. S. (2002). Two or four firms: does it matter? Research in Experimental Economics, 9, 95–119.
Isaac, R. M., & Walker, J. M. (1988). Group size effects in public goods provision: the voluntary contributions mechanism. The Quarterly Journal of Economics, 103, 179–199.
Isaac, R. M., Walker, J. M., & Thomas, S. H. (1984). Divergent evidence on free riding—an experimental examination of possible explanations. Public Choice, 43(2), 113–149.
Isaac, R. M., Walker, J. M., & Williams, A. W. (1994). Group-size and the voluntary provision of public goods—experimental evidence utilizing large groups. Journal of Public Economics, 54, 1–36.
Kim, O., & Walker, J. M. (1984). The free rider problem—experimental-evidence. Public Choice, 43(1), 3–24.
Kollock, P. (1998). Social dilemmas: the anatomy of cooperation. Annual Review of Sociology, 24, 183–214.
Komorita, S. S., & Lapworth, W. C. (1982). Cooperative choice among individuals versus groups in an n-person dilemma situation. Journal of Personality and Social Psychology, 42(3), 487–496.
Ledyard, J. O. (1995). Public goods: a survey of experimental research. In A. E. Roth & J. H. Kagel (Eds.), The handbook of experimental economics (pp. 111–181). Princeton: Princeton University Press.
Marwell, G., & Ames, R. (1979). Experiments on the provision of public goods I: resources, interest, group size, and the free-rider problem. American Journal of Sociology, 84(6), 1335–1360.
Marwell, G., & Schmitt, D. R. (1972). Cooperation in a three-person Prisoner’s Dilemma. Journal of Personality and Social Psychology, 21(3), 376–383.
Moir, R. (1998). A Monte Carlo analysis of the fisher randomization technique: reviving randomization for experimental economists. Experimental Economics, 1(1), 87–100.
Olson, M. (1965). The logic of collective action. Cambridge: Harvard University Press.
Orzen, H. (2008). Counterintuitive number effects in experimental oligopolies. Experimental Economics, 11(4), 390–401.
Weimann, J., Brosig-Koch, J., Hennig-Schmidt, H., Keser, C., & Stahr, C. (2012). Public-good experiments with large groups (Working Paper n. 120009). Otto-von-Guericke University Magdeburg FEMM.
Zelmer, J. (2003). Linear public goods experiments: a meta-analysis. Experimental Economics, 6, 299–310.
Acknowledgements
We thank David Cooper, two anonymous referees, Jeffrey Carpenter, Jimmy Walker, Joachim Weimann, and participants at the 2013 ESA Meeting in Zurich for useful comments. Sefton thanks the ESRC (grant ES/K002201/1) and Nosenzo the Leverhulme Trust (ECF/2010/0636) for financial support.
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Nosenzo, D., Quercia, S. & Sefton, M. Cooperation in small groups: the effect of group size. Exp Econ 18, 4–14 (2015). https://doi.org/10.1007/s10683-013-9382-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-013-9382-8