Abstract
We employ a \(\varDelta CoVaR\) model in order to measure the potential impact of temperature fluctuations on systemic risk, considering all companies from the STOXX Europe 600 Index, which covers a wide range of industries for the period from 1/1/1990 to 29/12/2017. Furthermore, in this study, we decompose temperature into 3 factors; namely (1) trend, (2) seasonality and (3) anomaly. Findings suggest that, temperature has indeed a significant impact on systemic risk. In fact, we provide significant evidence of either positive or nonlinear temperature effects on financial markets, while the nonlinear relationship between temperature and systemic risk follows an inverted U-shaped curve. In addition, hot temperature shocks strongly increase systemic risk, while we do witness the opposite for cold shocks. Additional analysis shows that deviations of temperature by \(1\,^{\circ }\hbox {C}\) can increase the daily Value at Risk by up to 0.24 basis points. Overall, higher temperatures are highly detrimental for the financial system. Results remain robust under the different proxies that were employed to capture systemic risk or temperature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding the empirical relationship between climate change and financial markets is gaining much prominence within the recent climate - finance literature. Literature has shown that temperature is a risk factor that can erratically affect economic activity (Dell et al. 2014; IPCC 2014). At the same time, the persistent trend of rising temperature has been spreading uncertainty to the whole financial system and thus it significantly contributes to systemic risk (e.g., Battiston et al. 2017). The systemic risk element of temperature has a twofold justification. First, variations of temperature can trigger a direct revaluation of climate sensitive assets. Particularly, equity losses can occur due to direct exposures to climate shocks such as natural catastrophes, changes in climate policy and increased energy costs (ESRB Advisory Scientific Committee 2016). Second, firms that possess climate sensitive assets could affect the financial system given their high interconnection with other businesses, thereby increasing systemic risk indirectly (Battiston et al. 2017). For instance, on one hand, temperature could affect agricultural output (i.e., direct impact of temperature) (Schlenker and Roberts 2009), while on the other, agricultural firms that experience abnormal losses due to weather conditions might subsequently transmit uncertainty to their counterparts or to other industries with which they trade (i.e., indirect impact of temperature) (Miranda and Glauber 1997). Amid climate change, radical uncertaintyFootnote 1 impedes the capacity of financial markets to operate efficiently. The reason is that investors’ expectations about future environmental regulations and climate change events are highly disparate and therefore climate sensitive assets are impossible to be reevaluated instantaneously (Aglietta and Espagne 2016; Karydas and Xepapadeas 2019). Instead, what can be observed, historically, is investors’ reaction on temperature changes. With these in mind, our overriding priority is to investigate whether systemic risk is conditioned on temperature changes. At the same time, we also address other noteworthy questions such as: Is climate uncertainty priced in financial markets? How much is the cost for the financial system? Do we have only losers or also gainers?
As far as the motivation of our study is concerned, it should be noted that in this paper, we combine knowledge from (1) the effects of temperature on stock markets and (2) the broader systemic risk literature. The first strand of the literature concentrates mainly on how temperature innovations influence stock market returns (e.g., Cao and Wei 2005; Bansal and Ochoa 2011; Novy-Marx 2014; Donadelli et al. 2017b; Balvers et al. 2017). This strand has mainly identified that temperature has macroeconomic risk characteristics that affect stock market returns. A possible explanation has been given by labour productivity scholars. In particular, Hsiang (2010), Donadelli et al. (2017b), Letta and Tol (2018) underscore that temperature and productivity are negatively related and this could potentially lead to financial turmoil, considering that their interaction might change the components of aggregate supply and demand (ESRB Advisory Scientific Committee 2016; Dafermos et al. 2017). In close relation to this, Weagley (2018) supports that extreme temperatures would increase the energy demand and consequently increase operational cost for firms. By contrast, Cao and Wei (2005) offers an alternative justification by claiming that temperature variations can affect financial behaviour as temperature has been found to cause psychological disturbances.
The second strand of the literature highlights the importance of systemic risk on financial stability; especially during financial crises (e.g., crisis 2007–2009), when financial stability seems quite vulnerable to rises in systemic risk. Systemic risk does not only affect financial markets but it can also have severe consequences to the real economy (Galati and Moessner 2013). For this reason, policymakers and researchers have developed analytic tools in order to measure and predict rises in systemic risk (e.g., Engle and Manganelli 2004; White et al. 2015; Adrian and Brunnermeier 2016). Accordingly, the main objective of these tools is to stress the equilibria generated by exogenous shocks. Empirical examples are abundant, for instance, Reboredo and Ugolini (2015) who study systemic risk dependency across European sovereign debt markets, Mensi et al. (2017a) who find that oil price volatility generates systemic risk to currencies and vice versa. Along a similar vein, de Mendonça and da Silva (2018) show that liquidity, profitability, leverage and interest rates have important role in triggering systemic risk fluctuations in the financial sector.
In this regard, to empirically examine whether temperature shocks affect systemic risk, we follow the Conditional Value at Risk (CoVaR) literature (Adrian and Brunnermeier 2016). CoVaR is a systemic risk measure that is robust to spillover effects and distribution assumptions and is defined as the spread between the Value at Risk of the financial system and that of an institution under distress. The attractiveness of CoVaR lies in its ability to pinpoint the root of economic crises, while computationally can be easily facilitated through a quantile regression framework. The motivation of using CoVaR stems from the fact that some firms might be affected by climate change while others not. This method offers a unique potential to identify both an asset that has the highest risk exposure and the interconnectedness of this asset with other assets across the financial system. Given that temperature can directly trigger macroeconomic alterations (Dell et al. 2014), climate-sensitive firms inevitably absorb the initial shock emerging from these alterations and transmit it even further, generating spillovers to the whole economy. Hence, with the use of CoVaR, we can examine the Value at Risk dependency on temperature fluctuations.
Our study provides the following main contributions. First, while previous literature investigates whether temperature affects stock market returns (Cao and Wei 2005; Bansal et al. 2016; Apergis and Gupta 2017; Balvers et al. 2017), this is the first study, to the best of our knowledge, to empirically investigate if temperature has an impact on systemic risk. Our study is motivated by prior literature underlining the systemic element of climate change (Aglietta and Espagne 2016; ESRB Advisory Scientific Committee 2016; Battiston et al. 2017). Second, the study provides strong evidence from the European Union; an area highly committed to climate change mitigation. Contrary to existing literature that uses lower frequency data, we use 28 years of daily data that might directly account for both short-term and long-term temperature effects. That is, either quarterly or annual data cannot fully detect temperature variations because crucial information about temperature is cancelled out. Thus, CoVaR can measure the maximum daily losses attributed to changes in temperature. Finally, we decompose temperature as suggested by the climate change literature (Vecchio and Carbone 2010; Ji et al. 2014) and thus we provide a more meaningful and articulate picture of temperature effects. Particularly, the decomposition employed in this study implies that we provide evidence about the unexpected temperature variations on the systemic risk of firms.
The main findings of the study indicate that, in a panel data sample of 600 firms for 7305 trading days in 17 different EU countries from 1/1/1990 to 29/12/2017, temperature has a prominent role in affecting the 99% daily and monthly CoVaR. In particular, we document that temperature has a nonlinear effect on systemic risk. Moreover, we observe that temperature shocks contain a systemic risk factor that strongly increases the losses of firms. What is more, cold shocks have a negative contribution to systemic risk, while the effect of hot shocks appears to be positive. Alternative model specifications, such as different systemic risk and temperature shock proxies as well as lower frequency examination, establish the robustness of the results with some small variations across different industries. Particularly, in line with Balvers et al. (2017), we demonstrate that manufacturing firms seem to be the ones mostly affected by temperature variations.
The findings of the study are very important to promote the climate-finance research. Scholars can monitor climate-sensitive firms that have spillover effects to the whole financial system. IPCC (2014) forecasts higher frequency and magnitude of extreme weather events and rising temperatures. For this reason, our study pinpoints a possible way of measuring firms' climate systemic impact and thus helps the financial system to be equipped with adequate tools and knowledge in view of further climate change deterioration.
The remainder of the paper is structured as follows: Sect. 2 outlines the previous climate change - financial literature and states the hypotheses. Section 3 presents the data, the CoVaR methodology, the temperature components and the testable regressions. In Sect. 4, results are reported. Section 5 summarises and concludes.
2 Literature Review and Hypotheses
2.1 Systemic Risk
We commence this section by presenting a brief review of the literature on systemic risk. Systemic risk can be defined as the increase in losses due to the spreading of financial distress across firms (Engle and Manganelli 2004; Adrian and Brunnermeier 2016). There is a large body of literature that proposes different methods in order to model systemic risk. Assessing systemic risk has been highlighted especially during financial crises (Galati and Moessner 2013).
Value at Risk (VaR) is the most widespread measure of losses due to its simplicity. The VaR for any firm given can be written as:
where \(X_{}^{i}\) is the stock return losses of a firm i for which \(VaR{q}^{i}\) is defined and \(q\%\) is the quantile of the probability distribution, where the upper tail of the distribution denotes the highest financial losses. However, VaR is not sufficiently focused on systemic risk and this is because VaR is a sample of returns of a firm i at isolation. Thus, VaR neglects the spillover effects, which are responsible for spreading the risk. Another problematic setting in VaR calculation is that financial time-series are highly skewed, indicating that VaR underestimates or overestimates the actual risk. As described by Angelidis et al. (2007), in order to forecast the risk accurately, VaR modelling needs to accommodate non-symmetrical fat tails.
Dealing with the skewness of returns, Giot and Laurent (2003) propose univariate and multivariate ARCH models based on skewed student distribution. Furthermore, Engle and Manganelli (2004) use a combination of quantile regressions with GARCH models in order to allow for relaxation of any distribution assumptions, but at the same time this method assumes that systemic risk has a short autoregressive memory. Similarly, White et al. (2015) propose a method that utilizes vector autoregressive models simultaneously with the associated quantile of stock returns. This method is robust to outliers and tailors different variables in order to deal with the spillover effects.
The most recent contributions to VaR modelling emphasise the importance of spillover effects (e.g., Girardi and Tolga Ergün 2013; Reboredo et al. 2016; Mensi et al. 2017b; Karimalis and Nomikos 2018). In the influential study of Adrian and Brunnermeier (2016), the VaR of the whole financial sector is conditional on one particular firm under distress; this is known in the risk literature as CoVaR. CoVaR can be easily measured by quantile regressions. \(\varDelta CoVaR\), which is the main risk measure of this analysis, is the difference between the CoVaR of a firm under distress and the CoVaR of the median state of this firm. Adrian and Brunnermeier (2016) show that \(\varDelta CoVaR\) is a robust method, which captures the tail dependency of stock returns, and the sensitivity of \(\varDelta CoVaR\) can be tested by accommodating different micro and macro risk variables.
2.2 Temperature and Economy
We now move on to discuss why temperature is a macroeconomic risk factor. Rising global temperature can have an impact on the economy and activate macroeconomic alterations. Fankhauser and Tol (2005), Stern (2007), Du et al. (2017), Colacito et al. (2018) argue that climate change will have a direct effect on countries' GDP due to the fact that they have to bear the consequences of extreme weather events, such as rainstorms, extreme temperatures and floods. Having quantified this effect, Horowitz (2009) documents that 1 \(^{\circ }\)C increase in average temperature would decrease the world GDP by 3.8%. Heal and Kriström (2002), Dell et al. (2014), Donadelli et al. (2017a), Arbex and Batu (2018) underline that temperature shocks are inevitably connected with agricultural outcome, health, tourism, productivity, energy consumption, research & development and to some extent the economic performance of firms. Schlenker and Roberts (2009) identify that temperature changes can have an impact on agricultural products; their findings indicate that different temperature change scenarios can lead to decrease in the average crop yield from 30 to 82% by the end of the century. Moreover, Deschenes (2014) underscores that the direct recipient of climate change is humans, and the main threat is whether humans will be able to adapt to the new environment or not. According to World Health Organization,Footnote 2 (2016) the direct cost to health will be 2–4 billion USD annually by 2030 due to the increasing number of deaths caused by climate change. Letta and Tol (2018) find a strongly negative relationship between total factor productivity and temperature. Donadelli et al. (2017b) support that temperature shifts have a long run negative effect on labour productivity. Hsiang (2010) finds that increasing temperature by 1 \(^{\circ }\)C can have negative effect of 2.4% on labour productivity. Similar finding is supported by Graff Zivin and Neidell (2014) who identify that a temperature rise reduces the hours worked in industries.
Besides, literature supports that temperature is a risk factor that affects the economy. Global warming can bring financial instability because it directly affects components of aggregated demand for energy (Dafermos et al. 2017; Weagley 2018). Therefore, to some extent macroeconomic consequences are attributed to climate change, however the main challenge is to test if temperature risk is transmitted to financial markets.
2.3 Temperature and Financial Markets
Before turning to the empirical climate-finance literature, it is sequential to understand the link between stock price movements and temperature. This link can be summarised in four main points: (1) evidence from psychological literature shows that temperature affects investors’ mood (Kamstra et al. 2003; Cao and Wei 2005); (2) temperature acts as a reminder and increases investors’ concerns about imminent de-carbonised policies (Karydas and Xepapadeas 2019); (3) extreme temperatures would increase energy consumption, and thus firms have to bear higher cost to maintain standard working conditions (Weagley 2018); and (4) temperature shocks act as a systematic negative productivity shock, which in turn affect the stock valuations (Balvers et al. 2017; Donadelli et al. 2019).
A summary of the empirical literature is given by Table 1. In the seminal contributions of Kamstra et al. (2003), Cao and Wei (2005), a stock market anomaly was observed; high temperature causes apathy towards financial markets while cold temperature is followed by higher risk-taking. Temperature-stock anomaly is also supported by Novy-Marx (2014) who states that global warming can be used as a proxy because it has a significant role in predicting financial anomalies.
Additionally, Bansal and Ochoa (2011) present that temperature is a source of aggregated risk and they identify a temperature beta in the stock market, which is the risk exposure of stocks to the temperature. They perform cross sectional regressions for different portfolios sorted by country and their results indicate that countries closer to Equator hold a strong and negative temperature risk premium but moving away from Equator the effect becomes positive. Negative beta is followed by higher stock returns, implying that there is a higher compensation for assets that are exposed to higher temperatures. Bansal et al. (2016) add long-run temperature shifts in their analysis in order to separate the long from the short run effect of the temperature. They, overall, find that temperature risk has a negative effect on equity valuations. Similarly, Balvers et al. (2017) examine the effect of temperature shocks on the cost of equity. By taking different portfolios and incorporating temperature shocks in asset pricing models, the authors identify that temperature is a risk factor that has significant and negative effect on firms’ stock returns that operate in climate sensitive industries. Their findings suggest that 0.22% of the total cost of equity is attributed to temperature risk. Therefore, it can be argued that temperature is an aggregated risk factor that influences the stock returns depending on the geographical latitude (Bansal and Ochoa 2011) and the industry (Balvers et al. 2017). Temperature negatively affects productivity and therefore the results are not surprising since productivity shocks play a crucial role in equity valuations (Garlappi and Song 2016). In align with the theory of finance, temperature risk can be categorised as a risk factor that has a negative effect on equity evaluations (Chen and Wang 2012).
2.4 Temperature Information
Before proceeding to state our hypotheses, it is important to investigate the different temperature proxies used in relevant analyses and the information content of temperature data.
There is a plethora of proxies about the temperature effects. While, Kamstra et al. (2003) employ daily raw temperature data as predictive variable of stock returns, most of the studies use temperature anomaly. Temperature anomaly is defined either as the difference between the daily temperature and the average historic temperature, or as the innovations of temperature, when lower frequency data are examined (Cao and Wei 2005; Novy-Marx 2014; Bansal et al. 2016; Apergis and Gupta 2017; Donadelli et al. 2017b, 2019). This method eliminates the seasonality of the raw temperature data but at the same time, it contains information about both the trend and temperature shocks. Temperature trend and shocks are two different components, which need to be distinguished. According to IPCC (2014), temperature trend follows a linear gradual increase and can be observed for the last 150 years, while temperature shocks are more extreme since about 1950. Dealing with the different temperature components, Balvers et al. (2017) decompose the monthly temperature series and obtain temperature shocks. Even though, their paper estimates shocks through detrended analysis, they neglect to distinguish between cold and hot shocks as it was previously suggested by Cao and Wei (2005), Novy-Marx (2014). Temperature shocks can be either cold or hot and can have significantly different economic consequences (Dell et al. 2012).
Notwithstanding the use of lower frequency temperature data in the climate-economy literature (Hsiang 2010; Dell et al. 2012; Du et al. 2017; Colacito et al. 2018), while climate-finance studies tend to use higher frequency data (Kamstra et al. 2003; Cao and Wei 2005; Apergis and Gupta 2017). This can be explained by the unavailability of higher frequency macroeconomic and, sometimes, temperature data (particularly in developing countries) as well as, there are conceptually different research objectives between economists and finance scholars.
To provide more insights about temperature information, we now turn our attention to climate change literature. Daily temperature records are characterized by nonlinearities. By using monthly or annual aggregated data, critical information could be missed and temporal resolution will be reduced (Vecchio and Carbone 2010). For this reason, an empirical decomposition on daily data can provide us with meaningful information. As Vecchio and Carbone (2010) explain temperature contains three equally important components; (1) trend, (2) seasonality and (3) anomaly. Trend is usually referred to as the gradual increase in the average temperature which is a linear function that can vary over time (Ji et al. 2014). Seasonality is an oscillatory factor with constant frequency (\(\approx\) 365 days) and it is probably the least important component in terms of the information contained. In contrast, the anomaly component corresponds to the temperature variation, which is the unexpected temperature deviations from the detrended and deseasonalized mean temperatures.
2.5 Hypotheses of the Study
According to Dell et al. (2014), temperature can be seen as a macroeconomic risk variable, which can potentially affect not only different economies but also individual firms. We extend this concept and, particularly, the unedited research question we posit is whether and, if so, how systemic risk responds to temperature changes. For instance, assume that a highly leveraged firm experiences losses from unanticipated temperature changes. This may impair the firm’s ability to meet its financial obligations, and pose a threat to the financial system as a whole (ESRB Advisory Scientific Committee 2016). To put it differently, we ask whether a firm’s losses that result from temperature changes can be causal of losses to other firms within the industry or the economy.
Synchronously, Horowitz (2009), Schlenker and Roberts (2009), Dell et al. (2012), Dell et al. (2014), Aglietta and Espagne (2016), Du et al. (2017) underline the importance of nonlinear temperature effects on different economic activities. Aggregate economic losses accelerate with increasing temperature; according to different scenarios an average temperature increase beyond 2 \(^{\circ }\)C would amplify economic losses, while temperature increase below this threshold does not seem to cause a sizeable reaction to the economy (IPCC 2014). For a similar reason, if temperature has nonlinear effects on the economy, then higher temperatures should amplify investors’ concerns about climate change. Therefore, in the remainder of this research, we explore a nonlinear relation between temperature changes and systemic risk.
Hypothesis 1:
Temperature has asymmetric effects on systemic risk.
It should be recognized that the multifaceted information content of temperature change might hinder a direct identification of its effects on the economy and financial markets. Moreover, if information about temperature is regarded as a significant pricing factor of stocks, then stock prices, returns and losses should respond to unanticipated changes in temperature, rather than to trend or seasonality. Therefore, to ascertain whether the asymmetric temperature effects are driven by unanticipated changes to temperature, and to delve deeper into the temperature-systemic risk nexus, we decompose the temperature variable into trend, seasonality component and anomaly, as suggested by Vecchio and Carbone (2010), Balvers et al. (2017). Temperature anomaly should lead to gradual devaluation of climate-sensitive assets (Bansal et al. 2016) and thus we expect the entire financial system to be affected. As Jacobsen and Marquering (2009) claim, raw temperature might be correlated with different seasonal patterns and thus results might be driven by seasonal unobserved characteristics. For this reason, similarly with Hypothesis 1, temperature anomaly should be an appropriate measure to account for the potential asymmetries.
Hypothesis 2:
Temperature anomaly has asymmetric effects on systemic risk.
There is adequate literature to support that temperature shocks have an effect on the productivity of firms (see e.g., Hsiang 2010; Graff Zivin and Neidell 2014; Dafermos et al. 2017; Donadelli et al. 2017b). Productivity is depleted by temperature shocks; in turn, productivity shocks can explain a large variation in the cross section of stock returns (Garlappi and Song 2016). To be more explicit, temperature shocks should generate concerns to investors about global warming and thus a positive impact of temperature shocks on systemic risk is expected.
It is worth noting that for its most part, the climate-finance literature does not distinguish between hot and cold temperature shocks. Yet, in practice, temperature shocks can either be positive (e.g. a heat wave) or negative (e.g., extremely low temperatures). Pilcher et al. (2002) puts forward the argument that, on one hand, exposure to cold weather can negatively affect reasoning and memory tasks, while on the other, hot exposure reduces attentional and perceptual tasks. Therefore, considering these distinct effects on performance, it would be interesting to investigate whether temperature effects hold given that the present study proceeds with a disaggregation of temperature shocks into hot and cold.
Based on the above, there are two main competing views on how hot or cold shocks should influence systemic risk. The first view relates to energy consumption. Authors such as Weagley (2018) maintain that extreme temperature deviations are associated with higher risk taking in financial markets. Weagley (2018) argues that this connection is justified by the additional energy needed in order to cool or heat a particular place in the aftermath of a temperature shock, which can be regarded as an adverse shock to the demand for energy, and can be generally perceived as “bad” news by investors and traders. Therefore, continuous and extreme temperature shocks can increase the energy demand and, in turn, firms will have to factor, in their profit functions, higher long-term operational cost to maintain standard working conditions.
Hypothesis 3a: Hot and Cold temperature shocks should increase systemic risk.
The second view relates to the psychological literature. More particularly, Heal and Kriström (2002), Cao and Wei (2005) identify that extreme temperatures are connected not only with different levels of productivity but also with psychological effects. Particularly, Cao and Wei (2005) find that cold temperature causes aggression and high risk-taking, while hot temperature can affect the mood of investors by causing either aggression or apathy and thus, either high or no risk-taking. In general, aggressive investors will tend to engage in more risky investments. As a result, investors will submit more demand orders for risky stocks, which will lead to an increase (decrease) in stock prices and returns (losses). In turn, lower losses are associated with lower levels of systemic risk. Therefore, according with the psychological literature, hot and cold shocks should decrease systemic risk.
Hypothesis 3b: Hot and cold temperature shocks should decrease systemic risk.
3 Research Design
3.1 Sample
The sample consists of 600 European firms that are included in STOXX 600 Index from the period 1/1/1990 to 29/12/2017. Firms are coming from 10 different industries from 17 different countries (see, Table 2). All the data are in daily frequency, making a strongly balanced panel of 4383,000 firm-day observations. The mean temperature and the precipitation for all 17 different locations have been retrieved from the European Climate Assessment & Dataset (ECA&D).Footnote 3 We match the firms’ main market location with the closest weather station in order to extract the weather data (see, panel C in Table 2). The stock market returns are available at Datastream, while the macroeconomic data are collected from Federal Reserve Bank of St. Louis. We choose this period of examination for the subsequent two reasons. First, financial and weather daily data are scarce before this period. Second, the Intergovernmental Panel on Climate Change (IPCC) and the United Nations Framework Convention on Climate Change (UNFCCC), that are the two most prominent actions against climate change, were established relatively to this period (1988 and 1992, respectively).
A critical issue is the frequency of the data. In the climate-economy literature, temperature is commonly approximated with low frequency data (monthly, quarterly, annually) (Colacito et al. 2018); this is because climate change is a long term phenomenon which systematically affects macroeconomic conditions (e.g. Dell et al. 2014). However, in the case of financial markets, the situation is different. Due to the technology advances, high frequency traders react instantly to relevant news (O’Hara 2015). Another example that further stresses the debate between low and high frequency data, is that if one day of the month is very hot and another day is very cold, then the monthly aggregated result would be downward biased (Vecchio and Carbone 2010). Therefore, the higher the frequency of data, the more precise results we obtain. Although, daily data are used is the main analysis, we also consider monthly data in order to test whether long-run temperature shifts can shape the perception of investors in the financial markets.
3.2 \(\varDelta CoVaR\)
In this sub-section, we define systemic risk as the contribution of Value at Risk (VaR) of one firm to the Value at Risk of the industry, in which this firm operates. For example, how HSBC Bank PLC under distress can transmit instabilities to the whole financial sector in the EU. In this study, a firm under distress is reflected on the 99% of the losses distribution. This part of the distribution represents the highest daily expected losses, which can easily be computed through the traditional VaR method. An alternative procedure to control for VaR, which is robust to outliers, spillover effects and is directly associated with systemic risk, is proposed by Adrian and Brunnermeier (2016):
where \(X^{j}\) is industry return losses conditional on the losses of a particular firm i (\(X_{}^{i}\)) at any part of the distribution (i.e. \(q=99\%\)). \(CoVaR^{j|C(X_{}^{i})}\) is the Value at Risk of the industry j conditional on some event \(C(X_{}^{i})\) of institution i. CoVaR can be implicitly estimated by running the following quantile regression:
where the predictive values of \(X_{q}^{j}\) are the Value at Risk of financial system conditional on \(X_{}^{i}\). Therefore \(CoVaR_{q}^{i}={\widehat{X}}_{q}^{j}\) and \(CoVaR_{q}^{i}\) is the VaR of j conditional on VaR of i at any q given. Additionally, to more effectively approximate systemic risk we use the \(\varDelta CoVaR\) measure, which is the change in CoVaR of institution i at \(q=99\%\) to its median state (\(q=50\%\)). The median state of any institution can be estimated by running the Eq. (2) at \(q=50\%\) and then saving its fitted values (\(CoVaR_{q}^{j|VaR_{50}^{i}}\)). In other words, we run Eq. (2) twice at \(\hbox {q}=99\%\) and at \(\hbox {q}=50\%\), and save the fitted values. Then, \(\varDelta CoVaR\) can be measured as shown in Eq. (3):
3.3 Temperature Decomposition
We focus on the short-term temperature variations related to the 28-year time-span of our sample. In order to extract the short behaviour of temperature, we consider time-series decomposition. In the traditional time-series decomposition, the data can be a product of three components as shown by Zarnowitz and Ozyildirim (2006):
where t denotes the time, Temp is the time series of the raw temperature data, Trend is the trend-cycle component, Season is the seasonality and Anom is the anomaly component. The frequency of the seasonality can be easily defined as a 365 day cycle by including all weekend temperatures and excluding the 29th of February when the year is leap. We repeat this procedure for the 17 different market locations over the 28 years of our sample period.
The trend-cycle component contains the long-term temperature characteristics and it corresponds to A persistent temperature increase. We are now able to remove the seasonality from the raw temperature data. Finally, anomaly is defined as the unexpected temperature variations for any given day of our sample. It is important to underline that superscript t is retained only if t corresponds to market calendar day.
3.4 Empirical Model
Having defined \(\varDelta CoVaR_{q}^{i}\) (hereafter, \(\varDelta CoVaR_{i,t}\)), we are now in a position to examine if higher temperature can incite extreme losses of firms. Hence, we add a nonlinear setting in the following regression:
where, i and t denotes the firm and day respectively with \(i=1,\ldots , \ 600\) and \(t= 01/01/1990,\ldots , \ 29/12/2017\) (7305 trading days), k corresponds to the geographical market location with \(k=1,\ldots ,\ 17\), p is the industry with \(p=1,\ldots ,\ 10\) (see, Table 2 Panel A and B) and \(\phi\) is the year with \(\phi =1990,\ldots ,\ 2017\). We add an autoregressive term of systemic risk (\(\varDelta CoVaR_{i,t-1}\)) to account for the short memory of systemic risk. Following Apergis and Gupta (2017), Donadelli et al. (2017b), we add precipitation (Preci) as an alternative weather proxy, which is measured as millimetres of water fallen at a particular site for any given day. We also use Monday dummy (Mon) and January dummy (Jan) in order to capture some seasonal effects (Zhang and Jacobsen 2013; Apergis and Gupta 2017). We then follow the finance literature and add some important determinants of systemic risk (White et al. 2015; Adrian and Brunnermeier 2016). TED, which is defined as the difference between the 3 month LIBOR rate and Treasury bill rate, can capture the short term liquidity risk. Credit is the spread between Moody’s Baa corporate bond and the 10-year treasury bond. TED and Credit are known to capture variations of stock returns. Market return (Mar.R) as the daily return of STOXX 600 Index. Equity volatility (Vol) is defined as the 22-day rolling standard deviation of the daily stock market return. Yield presents the 10-year government bond yields for the European Union, which is available in monthly frequency. Finally, we include Size which is defined as the logarithm of the last daily market value of each firm. Our model also includes year, country and industry dummies in order to absorb the remaining heterogeneity of systemic risk.
Equation (5) is tested with pooled OLS and it can provide an answer to Hypothesis 1. The standard errors are robust correcting for heteroskedasticity. Our model is free of multicollinearity according to the variance inflation factor (VIF) test and we also perform augmented Dickey-Fuller unit root test for all variables in order to observe the auto-correlation of our data.Footnote 4
To answer Hypothesis 2, Temp and \(Temp_{}^{2}\) are substituted with (1) the Trend to identify the deterministic process of the temperature data and (2) the anomaly (Anom) and the squared value of anomaly (\(Anom^2\)) as stochastic temperature components.
where Z is a vector that contains all of the remaining explanatory variables appearing in Eq. (5).
Finally, answering Hypothesis 3 demands to incorporate hot and cold temperature shocks. We calculate positive and negative temperature shocks, in line with Weagley (2018). A simplified way to calculate these shocks is through the energy needed to cool or heat a place, which can be approximated similar to a standard temperature derivative contract. Such a contract would consider that for temperature more than 18 \(^{\circ }\)C, any workplace needs to be cooled, while the place needs to be heated if the temperature is less than 18 \(^{\circ }\)C. Based on this logic, the Chicago Mercantile Exchange trades weather derivative contracts around this threshold (65 Fahrenheit degrees) (Perez-Gonzalez and Yun 2013; Elias et al. 2014).
where CDD is the cooling degree day and HDD is the heating degree day. In other words, if \(\hbox {CDD}=0\) then it indicates that this is a cold day, while if \(\hbox {CDD}>0\) this day is hot. Therefore, in Eq. (5), Temp and \(Temp^2\) are substituted with either CDD or HDD:
3.5 Descriptive Statistics
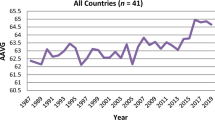
Table 3 reports the descriptive statistics for the variables of the study. 99% \(\varDelta CoVaR\) takes values from 0.43 to 7% with higher values indicating higher systemic risk. Temp represents the raw temperature data. The 600 firms of our sample experience an average temperature of 10.6 \(^{\circ }\)C. A more articulated picture of the variables of interest is shown in Figs. 1 and 2, while a more detailed picture of the temperature components is shown in Fig. 3. Interestingly, for the 28 years of our examination the temperature has increased by 0.6 \(^{\circ }\)C (see, Trend in Fig. 3). Also, Anom reports minimum value of − 22.25 and maximum of 13.2, displaying the most extreme unexpected cold and hot temperatures respectively. In terms of the distribution, apart from the temperature variables that are very close to satisfy the normality conditions, the rest of the variables are not normally distributed. Furthermore, comparing the mean, 1st percentile (Q1) and 99th percentile (Q99), we can conclude that our analysis does not seem to have extreme outliers except from the market capitalization (Size), which is also a sign of the heterogeneity of our sample.
Temperature, \(\varDelta CoVaR\) and interconnectedness. Temperature corresponds to the average raw temperature data as recorded by the 17 weather stations. 99% \(\varDelta CoVaR\) is the average \(\varDelta CoVaR\) of the 600 firms of our sample and \(h^{j,i}\) is the average dynamic conditional covariance of our sample, and is calculated as shown in “Appendix 2”
Temperature series decomposition. The decomposition is based on Eq. (4). The data used are the weighted temperature records as retrieved by the 17 weather stations. The moving average of temperature anomaly has been calculated as the 260-day rolling average of the absolute values of temperature anomaly; the right vertical axis scales the grey line
At a first glance, in line with our expectations, temperature seems to have a quadratic effect on systemic risk (Fig. 4). In order to provide a clearer picture of the relationship, we proceed to examine each one of our Hypotheses.
4 Empirical Results
4.1 Regression Analysis
Table 4 reports the OLS regression results based on Eqs. 5 and 6, with the dependent variable 99% \(\varDelta CoVaR\). The total number of observations reaches approximately 2.75 million, while the R-squared is more than 20%. The economic interpretation of \(\varDelta CoVaR\) is similar to the interpretation of the correlation coefficients (Adrian and Brunnermeier 2016). Most of the control variables appear significant, with the January dummy, market return and market capitalization being the ones decreasing systemic risk, while precipitation, Monday dummy, TED, credit risk, volatility and yield are associated with higher \(\varDelta CoVaR\). However, the lagged \(\varDelta CoVaR\), precipitation and volatility do not affect systemic risk. Column 1 indicates that higher temperature (Temp) is associated with higher systemic risk. Columns 2 provides direct support of Hypothesis 1, that temperature has a nonlinear effect on systemic risk. The coefficients of both linear and squared terms of temperature are statistically significant, with the former being positive while the latter is negative, indicating that temperature-risk relationship follows an inverted U-shaped curve. This finding confirms our expectations; thus, we can conclude that temperature has positive and asymmetric effects on the daily losses of firms (Hypothesis 1).
In columns 3–6 (Table 4), we add the decomposed temperature time series to test Hypothesis 2 (temperature anomaly). We consider three different specifications of temperature anomaly, (1) the temperature anomaly (Anom) from the decomposed temperature series, (2) the first difference of Anom (\(D.Anom= Anom_{k,t}-Anom_{k,t-1}\)), and (3) a relative measure of temperature, which is the difference between the Anom and the average European anomaly (\(EU.Anom= Anom-\varSigma _{k=1}^{K=17}Anom/K\)) . In column 3, temperature anomaly seems to increase \(\varDelta CoVaR\) at 5% level of significance. Moving to column 4, we witness that temperature anomaly and systemic risk follow an inverted U-shaped curve. When testing for the innovations in temperature anomaly (D.Anom and \(D.Anom^2\) in column 5) and the average EU anomaly temperature (EU.Anom and \(EU.Anom^2\) in column 6), both seem to monotonically increase systemic risk of firms. This finding indicates that the temperature-risk relationship is both positive and nonlinear. Thus, there is a strong evidence to support that temperature variations can influence the perception of financial markets about climate change. Thus far, Hypothesis 2, that temperature anomaly has an asymmetric effect on systemic risk, can be partially supported.
Spillover effects from a firm to the financial markets might need some time to be observed. Similarly, temperature effects are commonly categorised as long-term phenomena. To ascertain whether the frequency of data can potentially moderate the results, we aggregate daily data to a monthly frequency by taking the median values of every month. Table 5 reports the monthly estimations. Results are more positive compared to the daily data estimations (Table 4). Particularly, higher temperatures significantly increase systemic risk (columns 1 and 2). The slope of this relationship appears to be steeper, and hence Hypothesis 1 is partially supported. Regarding Hypothesis 2, both Anom and EU.Anom strongly increase systemic risk, as both the level and quadratic terms are positive, while temperature innovations (D.Anom) seem to exhibit an inverted U-shaped curve with the \(\varDelta CoVaR\). Surprisingly, when daily data were examined, the relationship appeared both positive and asymmetric, while at the monthly frequency, the positive sign dominates. A possible explanation is that temperature changes have adverse long-term effects, while in the short-term, this effect is weaker.
Furthermore, Table 6 presents the results on Hypothesis 3, which distinguishes between hot and cold temperature shocks. Columns 1 and 3 report the hot shock (CDD) and the cold shock (HDD) estimations, respectively. Columns 2 and 4 test for nonlinear effects of CDD and HDD. Our results suggest that hot shocks have a linear and positive association with systemic risk, while the effect of cold shocks is negative and significant. Particularly, higher CDD and lower HDD tend to be associated with higher systemic risk. Taken together, the results indicate that high temperatures are detrimental for the financial system, but low temperatures are not. At the same time, there is not enough evidence to support nonlinear temperature shock effects. Additionally, there is some ambiguity regarding which is the most appropriate way to justify the temperature shock-systemic risk relationship; either energy consumption or psychological effects. Our findings indicate that the former is related to hot shocks, while the latter to the cold shocks. Particularly, hot shocks increase systemic risk, as stated in Hypothesis 3a, while cold shocks decrease systemic risk, in line with Hypothesis 3b.
In order to provide evidence about the aggregated temperature shock effects, we transform our daily data into a monthly frequency. Table 7 reports estimations based on monthly data. It seems that the level coefficients for CDD and HDD remain positive and negative, respectively, in line with the daily examination. Surprisingly, the quadratic coefficients follow a different pattern than the one in the daily analysis. Hot shocks and systemic risk exhibit an inverted U-shaped curve, while cold shocks and systemic risk exhibit a U-shaped curve. Daily analysis clearly shows that temperature shocks have a linear effect, while monthly analysis demonstrates that this effect is asymmetric. It can be suggested that hot (cold) shocks are not adequately approximated; for instance if one day of the month is very hot while the other is very cold then the median effect is negligible (Vecchio and Carbone 2010). Therefore, the results might be downward biased when lower frequency temperature shocks are examined.
Even though, extreme temperatures might be associated with higher energy consumption and thus one would expect a higher systemic risk, this is only true for hot shocks. These findings can have a threefold explanation, in line with Cao and Wei (2005), Bansal et al. (2016), Apergis et al. (2016).
First, consistently with the energy-consumption-based view, hot weather is expected to increase demand and prices of electricity (Hypothesis 3a). In turn, high energy prices may increase operational costs of firms, and eventually these firms may incur losses. The results imply that an imminent increase in electricity prices can be considered by stock market investors and traders as “bad” news. Subsequently, investors and traders tend to sell off stocks, which leads to a propagation of losses within and across the industries, which in turn destabilises the financial system. Thus, the results are supportive of Hypothesis 3a, but not Hypothesis 3b, which postulates a negative relation between hot shocks and systemic risk. However, if hot weather causes apathy among stock market traders and investors, they are likely not to engage in riskier investments. Even if hot temperature causes aggression, Griffitt and Veitch (1971) assert that such aggression can be causal of an increased antisocial behaviour, which is not necessarily consistent with individual risk-taking. On the contrary, it can even lead to increased pessimism about future stock prices and returns, which can further translate into heightened risk aversion (Lucey and Dowling 2005). Risk-averting investors tend to sell off riskier stocks, which trigger a collapse (rise) in stock prices and returns (losses). The ensuing losses can propagate within and across the industries, and give rise to higher levels of systemic risk.
Second, if the energy-consumption based view holds, cold shocks are expected to increase systemic risk. However, the results do not accord with Hypothesis 3a. Instead, they agree with the second view, which builds on investor psychology to predict a negative relation between cold temperature shocks and systemic risk (Hypothesis 3b). According to Cao and Wei (2005), lower temperatures are associated with increased risk-taking as investors become more aggressive. As a result, investors tend to buy risky assets. These purchases, in turn, drive up (down) stock prices and returns (losses), and are associated with a bull market stance. Therefore, the net effect on investors' risk preferences depends upon the balance between concerns about increasing energy demand and/or other psychological factors. Arguably, the latter dominates the former, which manifests in a negative effect of HDD. This leads to lower losses from securities trading, which are transmitted within the industry, in which the firm operates, and across other industries of the economy.
Yet a third explanation, which caters to both hot and cold shocks, underscores the geographical location. In this regard, Bansal et al. (2016) advocate that countries with hotter climate also perform poorly in terms of financial development and are not well equipped to deal with adverse shocks. Therefore, hot shocks might negatively affect countries such as Italy, Spain and Portugal as their financial markets are quite vulnerable to exogenous shocks (Engle et al. 2014). By contrast, cold shocks, occurring mainly in the northern Europe coincide with markets that have higher financial stability.
4.2 Portfolio Analysis
Climate change is a risk factor that should have more detrimental effect on industries such as Agriculture, Health Care and Manufacturing and less detrimental effect on Services (Schlenker and Roberts 2009; Deschenes 2014; Balvers et al. 2017). In order to test the sensitivity of the previous results, we construct industry portfolios. Ten portfolios are constructed in respect to Table 2 Panel A. Then, we run regressions separately for every portfolio to observe the temperature effects within each industry. According to Dell et al. (2014), Balvers et al. (2017), we expected to identify some variations of the results depending on how vulnerable the industry is to weather patterns. Table 8 presents the results for Hypotheses 1, 2 and 3. First, in column 1, temperature (Temp) coefficient is positive for 9 portfolios and in 6 of them is statistically significant, the squared term (\(Temp_{}^{2}\)) is negative in 8/10 portfolios while it is only significant in 3 portfolios. The results illustrate that temperature asymmetrically affects the losses of Financials, Health Care and Oil & Gas portfolios, while 4 portfolios (Technology, Consumer Services, Telecommunications and Utilities) are unaffected and 3 portfolios (Consumer Goods, Industrials, Basic Materials) are linearly affected. Second, in order to test Hypothesis 2, we now pay attention to the coefficient of temperature anomaly (Anom in column 2). As it is shown, on average, Consumer Goods, Oil & Gas and Basic Materials are significantly affected by the temperature anomaly; findings are in line with Balvers et al. (2017) who underline the direct detrimental temperature effects on the manufacturing sector. Even though, we can partially support Hypothesis 1 about the nonlinear effect of temperature, we are unable to support the same for the temperature anomaly when examined at a sector level. Overall, results indicate that higher temperatures increase systemic risk.
The importance of analysing very cold and hot temperatures has been also underlined by Luterbacher et al. (2004), whose results show that extreme temperatures can affect the economy. In columns 3 and 4 in Table 8, regression results are reported based on Eq. (8) for different industries, using 99% \(\varDelta CoVaR\) as the dependent variable. This table provides further evidence regarding Hypothesis 3. In line with our previous estimations, hot shocks (CDD) have significantly positive effects on different industries (4 out of 10 industries) while cold shocks (HDD) decrease systemic risk (5 out of 10 industries). On average, there is a robust evidence that Consumer Goods, Industrials, Basic Materials and Utilities are industries that are most vulnerable to hot shocks; in line with Dell et al. (2014), Balvers et al. (2017). While, Consumer goods, Oil & Gas, Industrials, Consumer Services and Basic Materials can benefit from lower temperatures. Results also show that temperature effects do not negatively affect industries such as Technology, Consumer Services and Telecommunications. This finding implies that temperature shocks can influence the investment climate, particularly when climate sensitive firms are considered. Therefore, institutional investors and traders make investment decisions based on two principles; (i) how sensitive to climate change industries are and (ii) cold weather is “good” news, while hot weather is ‘bad” news for the financial markets.
4.3 Robustness Checks
The degree of interconnection in stock returns can be seen as a proxy for return-spillover effects between a firm and the financial system (Billio et al. 2012). To corroborate our results, we use two additional dependent variables as measures of interconnectedness. First, we focus on the endogenous risk between firm and industry losses by taking the first principal component (PC1) (see more in “Appendix 1”). Second, we compute the dynamic conditional covariance (\(h^{j,i}\)) in an endogenous system, constituted by losses of firm i and industry j (see more in “Appendix 2”). Because \(h^{j,i}\) already accounts for the dynamics in the model, the autoregressive variable is omitted. In addition, both variables account for a degree of volatility in the market and therefore volatility (Vol) variable is excluded in order to avoid any simultaneity problem.
The results are reported in Table 9, columns 1–4 and columns 5–8 show the estimations for PC1 and \(h^{j,i}\), respectively. In line with the previous estimations, PC1 appears to confirm Hypothesis 1 and reject Hypotheses 2; temperature and PC1 exhibit an inverted U-shaped curve (Temp and \(Temp^2\) coefficients are positive and negative respectively, in column 1); the effect of temperature anomaly on PC1 does not follow a nonlinear pattern, but this linearly increases (column 2). Regarding Hypothesis 3, hot shocks (CDD) increase the interconnection of the financial markets (column 3), but cold temperatures (HDD) seem to decrease this interconnection (column 4). In terms of \(h^{j,i}\), the results appear qualitatively similar with the previous specifications. The conditional covariances between a firm and its industry are equally affected by temperature effects. Importantly, the only difference with PC1 estimations, is that both raw temperature and temperature anomaly monotonically increase the firm-industry interconnection (see \(h^{j,i}\) in columns 5 and 6).
4.4 Additional Results
In order to provide more plausible results, we consider the \(\varDelta ^{\EUR {}}CoVaR\) methodology. In Eqs. (5), (6) and (8), we remove Size variable since it is used to compute the \(\varDelta ^{\EUR {}}CoVaR\), which in turn is our new alternative dependent variable. Therefore, \(\varDelta ^{\EUR {}}CoVaR_{i,t} = Size_{i,t} \times \varDelta CoVaR_{i,t}\). The \(\EUR\) sign denotes the change of the size of the firm in Euro amounts conditional on any variable. Size is the market capitalization of any firm i at any day t and \(\varDelta CoVaR\) is defined as previously. We also consider both the 99% and 95% \(\varDelta ^{\EUR {}}CoVaR\) in order to measure a reasonable confidence interval of the losses. To attain stationarity, in line with Adrian and Brunnermeier (2016), we normalise the \(\varDelta ^{\EUR {}}CoVaR\) by the cross-sectional average market capitalization and our new measure is now expressed in basis points. In contrast with the \(\varDelta CoVaR\), the \(\varDelta ^{\EUR {}}CoVaR\) takes into account the size of every institution which is closely related to the “Too big to fail” suggestion, indicating that poor performance of large firms would have amplified negative consequences to the financial system.
The results are reported in Table 10, where columns 1–4 use 99% \(\varDelta ^{\EUR {}}CoVaR\) and columns 5–8 use 95% \(\varDelta ^{\EUR {}}CoVaR\) as dependent variable. As shown, \(\varDelta ^{\EUR {}}CoVaR\) is substantially different from \(\varDelta CoVaR\). In column 1, Temp is positive and significant at 1% but \(Temp^{2}\) is insignificant. The Temp coefficient of 0.147 implies that an increase in temperature by 1 \(^{\circ }\)C would increase \(\varDelta ^{\EUR {}}CoVaR\) by 0.147 basis points of daily market equity losses at the 99% quantile. In column 2, Anom is positive and its squared term is negative, representing an inverted U-shaped curve, confirming Hypothesis 2. Regarding CDD and HDD, results illustrate that hot shocks increase and cold shocks decrease systemic risk (Hypothesis 3). Particularly, the impact of temperature shocks is estimated to cause daily losses ranging between -0.303 and 0.239 basis points. This findings show that temperature is priced in financial markets. Despite the relatively “small” effect, we can claim that information about climate change is appreciated by investors. Specifically, it can be implied that low temperatures are perceived as “good” news, while high temperatures as “bad” news for the financial market. Overall, results can be explained by the climate change uncertainty, expectations about increasing energy demand and by psychological factors. Hence, investors are highly uncertain about the probability distribution of future payoffs, since their future expectations are based on current weather events.
5 Discussion and Conclusions
The purpose of this paper is to examine if systemic risk is driven by temperature changes. Systemic risk is measured by making use of the \(\varDelta CoVaR\) methodology (Adrian and Brunnermeier 2016), while temperature data is retrieved from the closest weather stations to the firms’ main market locations. Using a sample of 600 European firms listed in STOXX 600 Index for 7305 trading days in 17 different financial markets, we find that temperature has a versatile effect on the losses of firms. To be more explicit, in line with the existing climate change literature, we decompose the temperature series to (1) trend, (2) seasonality and (3), anomaly components. In turn, we make the following assumptions: (1) temperature has asymmetric effects on systemic risk, (2) similarly, temperature anomaly has nonlinear effects on systemic risk and (3) hot and cold shocks are detrimental (beneficial) for the financial system. On general principles, all of our hypotheses can be partially supported to some extent, under all different specifications; however, we do record certain deviations among industries.
Our results provide support to the argument that temperature affects systemic risk. Specifically, raw temperature data and temperature anomaly seem to either increase or exert nonlinear effect on systemic risk. We argue that these asymmetries can be explained on the basis of decomposed temperature factors. For instance, on the one hand we show, in line with the psychological literature, that cold temperature shocks significantly decrease the \(\varDelta CoVaR\), while, on the other, we have adequate evidence to support, in line with the energy consumption view, that hot shocks positively influence systemic risk. More importantly, the portfolio analysis demonstrates that the manufacturing sector is strongly influenced by temperature changes (Balvers et al. 2017), while Technology, Telecommunications and Consumer Services firms seem to be unaffected by temperature. Finally, a numerical example based on the alternative measure of systemic risk, \(\varDelta ^{\EUR {}}CoVaR\), suggests that 1 \(^{\circ }\)C temperature change can increase systemic risk by up to 0.24 basis points.
Our study is important for many different stakeholders, as it provides informed insights in connection with the impact of climate change. While proposing hedging strategies and adaptation mechanisms are rather challenging, this paper underscores that the examination of the climate-finance relationship should receive priority and be further promoted. In addition, given the sample market of our study, our findings are quite useful to European firms that operate in relatively developed and well-informed markets and have the capacity to protect themselves against climate change (e.g., by purchasing weather derivatives). An interesting avenue for future research, would be to investigate how financial markets react to temperature changes in developing countries (Dell et al. 2012).
In turn, our findings can have important research implications. Scholars can gauge the effect of climate change on the financial system. The intuition for using \(\varDelta CoVaR\) rests in its unique capability to identify, among others, systemic climate sensitive firms that could potentially affect the entire financial system. Therefore, future studies should also investigate particular characteristics of these firms. Our findings also suggest that temperature variations are priced in financial markets. This finding could be important for the asset pricing literature (Apergis and Gupta 2017). It can be suggested that market participants fear the regulatory pressure arising from changes in climate patterns (Balvers et al. 2017); this can be an alternative channel that helps to rationalise our results.
On a final note, the main limitation of this study is the assumption that temperature recorded on a firm’s primary market location affects the activity and the performance of investors and employees, respectively; thus contributing to higher levels of risk. However, it is also true that firms are able to mitigate this impact by diversifying activities to different countries or even continents that are subject to very different weather patterns. In this regard, gathering temperature data from multiple business locations might help resolve this issue. In line with arguments mentioned above, our results do not apply to all the financial markets. EU is an area adherent to environmental regulations (e.g. emissions trading scheme), and thus investors might be highly driven by climate change effects. As Bansal and Ochoa (2011) assert, heterogeneous temperature effects depend on geographic location. For this reason, similar studies should be conducted about different areas of the world, such as the United States, in order to determine (and compare) the accuracy of our findings.
Notes
Radical uncertainty hypothesis has been described by Aglietta and Espagne (2016) and defined as collective prudential actions that minimise the probability of occurrence of unforeseen events due to high uncertainty. For instance, investors might be driven away from climate sensitive firms (selling climate sensitive stocks) because they anticipate unexpected climate events.
Retrieved from http://www.who.int/mediacentre/factsheets/fs266/en/.
Non-stationary data are transformed into stationary by taking their first difference (D.).
References
Adrian T, Brunnermeier MK (2016) CoVaR. Am Econ Rev 106(7):1705–1741. https://doi.org/10.1257/aer.20120555
Aglietta M, Espagne E (2016) Climate and finance systemic risks: more than an analogy? The climate fragility hypothesis. Working paper https://doi.org/10.13140/RG.2.1.2378.6489
Angelidis T, Benos A, Degiannakis S (2007) A robust VaR model under different time periods and weighting schemes. Rev Quant Finance Account 28(2):187–201. https://doi.org/10.1007/s11156-006-0010-y
Apergis N, Gupta R (2017) Can (unusual) weather conditions in New York predict South African stock returns? Res Int Bus Finance 41:377–386. https://doi.org/10.1016/j.ribaf.2017.04.052
Apergis N, Gabrielsen A, Smales LA (2016) (unusual) weather and stock returns–i am not in the mood for mood: further evidence from international markets. Finance Mark Portf Manag 30(1):63–94. https://doi.org/10.1007/s11408-016-0262-z
Arbex M, Batu M (2018) Weather, climate and the economy: welfare implications of temperature shocks. University of Windsor, Department of Economics Working Paper Series n 17-07
Balvers R, Du D, Zhao X (2017) Temperature shocks and the cost of equity capital: implications for climate change perceptions. J Bank Finance 77:18–34. https://doi.org/10.1016/j.jbankfin.2016.12.013
Bansal R, Ochoa M (2011) Temperature, aggregate risk and expected returns (No. w17575). National Bureau of Economic Research
Bansal R, Kiku D, Ochoa M (2016) Price of long-run temperature shifts in capital markets (No. w22529). National Bureau of Economic Research
Battiston S, Mandel A, Monasterolo I, Schütze F, Visentin G (2017) A climate stress-test of the financial system. Nat Clim Change 7(4):283–288. https://doi.org/10.1038/nclimate3255
Billio M, Getmansky M, Lo AW, Pelizzon L (2012) Econometric measures of connectedness and systemic risk in the finance and insurance sectors. J Financ Econ 104(3):535–559. https://doi.org/10.1016/j.jfineco.2011.12.010
Cao M, Wei J (2005) Stock market returns: a note on temperature anomaly. J Bank Finance 29(6):1559–1573. https://doi.org/10.1016/j.jbankfin.2004.06.028
Chen N, Wang WT (2012) Kyoto Protocol and capital structure: a comparative study of developed and developing countries. Appl Financ Econ 22(21):1771–1786. https://doi.org/10.1080/09603107.2012.676732
Colacito R, Hoffmann B, Phan T (2018) Temperature and growth: a panel analysis of the United States. J Money Credit Bank 51(2) https://doi.org/10.1111/jmcb.12574
Dafermos Y, Nikolaidi M, Galanis G (2017) A stock- flow-fund ecological macroeconomic model. Ecol Econ 131:191–207. https://doi.org/10.1016/j.ecolecon.2016.08.013
Dell M, Jones BF, Olken BA (2012) Climate shocks and economic growth: evidence from the last half century. Am Econ J Macroecon 4(3):66–95. https://doi.org/10.1109/LPT.2009.2020494
Dell M, Jones BF, Olken BA (2014) What do we learn from the weather? The new climate-economy literature. J Econ Lit 52(3):740–798. https://doi.org/10.3386/w19578
Deschenes O (2014) Temperature, human health, and adaptation: a review of the empirical literature. Energy Econ 46:606–619. https://doi.org/10.1016/j.eneco.2013.10.013
Donadelli M, Gruning P, Juppner M, Kizys R (2017a) Global temperature risk, R&D expenditure, and Growth. SAFE WP No 188 Bank of Lithuania WP No 09/2018
Donadelli M, Jüppner M, Riedel M, Schlag C (2017b) Temperature shocks and welfare costs. J Econ Dyn Control 82:331–355. https://doi.org/10.1016/j.jedc.2017.07.003
Donadelli M, Jüppner M, Paradiso A, Schlag C (2019) Temperature volatility risk. Working Paper n 05/2019, Department of Economics, Ca’Foscari University
de Mendonça HF, da Silva RB (2018) Effect of banking and macroeconomic variables on systemic risk: an application of \(\Delta\)COVAR for an emerging economy. North Am J Econ Finance 43:141–157. https://doi.org/10.1016/j.najef.2017.10.011
Du D, Zhao X, Huang R (2017) The impact of climate change on developed economies. Econ Lett 153:43–46. https://doi.org/10.1016/j.econlet.2017.01.017
Elias R, Wahab M, Fang L (2014) A comparison of regime-switching temperature modeling approaches for applications in weather derivatives. Eur J Oper Res 232(3):549–560. https://doi.org/10.1016/j.ejor.2013.07.015
Engle R (2002) Dynamic conditional correlation: a simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J Bus Econ Stat 20(3):339–350. https://doi.org/10.1198/073500102288618487
Engle R, Manganelli S (2004) CAViaR: Conditional autoregressive value at risk by regression quantiles. J Bus Econ Stat 22(4):367–381. https://doi.org/10.1198/073500104000000370
Engle R, Jondeau E, Rockinger M (2014) Systemic risk in Europe. Rev Finance 19(1):145–190. https://doi.org/10.1093/rof/rfu012
ESRB Advisory Scientific Committee (2016) Too late, too sudden: Transition to a low-carbon economy and systemic risk. Reports of the Advisory Scientific Committee https://www.esrb.europa.eu/pub/pdf/asc/Reports_ASC_6_1602.pdf
Fankhauser S, Tol RS (2005) On climate change and economic growth. Resourc Energy Econ 27(1):1–17. https://doi.org/10.1016/j.reseneeco.2004.03.003
Galati G, Moessner R (2013) Macroprudential policy—a literature review. J Econ Surv 27(5):846–878. https://doi.org/10.1111/j.1467-6419.2012.00729.x
Garlappi L, Song Z (2016) Can investment shocks explain the cross section of equity returns? Manag Sci 63(11):3829–3848. https://doi.org/10.1287/mnsc.2016.2542
Giot P, Laurent S (2003) Value-at-risk for long and short trading positions. J Appl Econom 18(6):641–664. https://doi.org/10.1002/jae.710
Girardi G, Tolga Ergün A (2013) Systemic risk measurement: multivariate GARCH estimation of CoVaR. J Bank Finance 37(8):3169–3180. https://doi.org/10.1016/j.jbankfin.2013.02.027
Graff Zivin J, Neidell M (2014) Temperature and the allocation of time: implications for climate change. J Labor Econ 32(1):1–26. https://doi.org/10.1086/671766
Griffit W, Veitch R (1971) Hot and crowded: influence of population density and temperature on interpersonal affective behavior. J Personal Soc Psychol 17(1):92–98. https://doi.org/10.1037/h0030458
Heal G, Kriström B (2002) Uncertainty and climate change. Environ Resour Econ 22(1–2):3–39. https://doi.org/10.1023/A:1015556632097
Horowitz JK (2009) The income-temperature relationship in a cross-section of countries and its implications for predicting the effects of global warming. Environ Resour Econ 44(4):475–493. https://doi.org/10.1007/s10640-009-9296-2
Hsiang SM (2010) Temperatures and cyclones strongly associated with economic production in the Caribbean and Central America. Proc Natl Acad Sci 107(35):15367–72. https://doi.org/10.1073/pnas.1009510107
IPCC (2014) The intergovernmental panel on climate change fifth assessment report. http://www.ipcc.ch/pdf/assessment-report/ar5/syr/SYR_AR5_FINAL_full.pdf
Jacobsen B, Marquering W (2009) Is it the weather? Response. J Bank Finance 33(3):583–587. https://doi.org/10.1016/j.jbankfin.2008.09.011
Ji F, Wu Z, Huang J, Chassignet EP (2014) Evolution of land surface air temperature trend. Nat Clim Change 4(6):462–466. https://doi.org/10.1038/nclimate2223
Kamstra MJ, Kramer LA, Levi MD (2003) Winter blues: a sad stock market cycle. Am Econ Rev 93(1):324–343. https://www.aeaweb.org/articles?id=10.1257/000282803321455322
Karimalis EN, Nomikos NK (2018) Measuring systemic risk in the European banking sector: a copula CoVaR approach. Eur J Finance 24(11):944–975. https://doi.org/10.1080/1351847X.2017.1366350
Karydas C, Xepapadeas A (2019) Pricing climate change risks: CAPM with rare disasters and stochastic probabilities. CER-ETH—Center of Economic Research at ETH Zurich, Economics Working Paper Series, 19/311, 2019 https://doi.org/10.3929/ethz-b-000320545
Letta M, Tol RSJ (2018) Weather, climate and total factor productivity. Environ Resour Econ 73:283–305. https://doi.org/10.1007/s10640-018-0262-8
Lucey BM, Dowling M (2005) The role of feelings in investor decision-making. J Econ Surv 19(2):211–237. https://doi.org/10.1111/j.0950-0804.2005.00245.x
Luterbacher J, Dietrich D, Xoplaki E, Grosjean M, Wanner H (2004) European seasonal and annual temperature variability, trends, and extremes since 1500. Science 303(5663):1499–1503. https://doi.org/10.1126/science.1093877
Mensi W, Hammoudeh S, Shahzad SJH, Al-Yahyaee KH, Shahbaz M (2017a) Oil and foreign exchange market tail dependence and risk spillovers for MENA, emerging and developed countries: VMD decomposition based copulas. Energy Econ 67:476–495. https://doi.org/10.1016/j.eneco.2017.08.036
Mensi W, Hammoudeh S, Shahzad SJH, Shahbaz M (2017b) Modeling systemic risk and dependence structure between oil and stock markets using a variational mode decomposition-based copula method. J Bank Finance 75:258–279. https://doi.org/10.1016/j.jbankfin.2016.11.017
Miranda MJ, Glauber JW (1997) Systemic risk, reinsurance, and the failure of crop insurance markets. Am J Agric Econ 79(1):206–215. https://doi.org/10.2307/1243954
Novy-Marx R (2014) Predicting anomaly performance with politics, the weather, global warming, sunspots, and the stars. J Financ Econ 112(2):137–146. https://doi.org/10.1016/j.jfineco.2014.02.002
OECD (2008) Handbook on constructing composite indicators: methodology and user guide. OECD Publishing https://doi.org/10.1787/9789264043466-en
O’Hara M (2015) High frequency market microstructure. J Financ Econ 116(2):257–270. https://doi.org/10.1016/j.jfineco.2015.01.003
Perez-Gonzalez F, Yun H (2013) Risk management and firm value: evidence from weather derivatives. J Finance 68(5):2143–2176. https://doi.org/10.1111/jofi.12061
Pilcher JJ, Nadler E, Busch C (2002) Effects of hot and cold temperature exposure on performance: a meta-analytic review. Ergonomics 45(10):682–698. https://doi.org/10.1080/00140130210158419
Reboredo JC, Ugolini A (2015) Systemic risk in European sovereign debt markets: a CoVaR-copula approach. J Int Money Finance 51:214–244. https://doi.org/10.1016/j.jimonfin.2014.12.002
Reboredo JC, Rivera-Castro MA, Ugolini A (2016) Downside and upside risk spillovers between exchange rates and stock prices. J Bank Finance 62:76–96. https://doi.org/10.1016/j.jbankfin.2015.10.011
Schlenker W, Roberts MJ (2009) Nonlinear temperature effects indicate severe damages to US crop yields under climate change. Proc Natl Acad Sci 106(37):15594–15598. https://doi.org/10.1073/pnas.0906865106
Stern NH (2007) The economics of climate change: the Stern review. Cambridge University Press, Cambridge
Vecchio A, Carbone V (2010) Amplitude–frequency fluctuations of the seasonal cycle, temperature anomalies, and long-range persistence of climate records. Phys Rev E 82(6):066101. https://doi.org/10.1103/PhysRevE.82.066101
Weagley D (2018) Financial sector stress and risk sharing: evidence from the weather derivatives market. Rev Financ Stud 32(6):2456–2497. https://doi.org/10.1093/rfs/hhy098
White H, Kim TH, Manganelli S (2015) VAR for VaR: measuring tail dependence using multivariate regression quantiles. J Econom 187(1):169–188. https://doi.org/10.1016/j.jeconom.2015.02.004
Zarnowitz V, Ozyildirim A (2006) Time series decomposition and measurement of business cycles, trends and growth cycles. J Monet Econ 53(7):1717–1739. https://doi.org/10.1016/j.jmoneco.2005.03.015
Zhang CY, Jacobsen B (2013) Are monthly seasonals real? A three century perspective. Rev Finance 17(5):1743–1785. https://doi.org/10.1093/rof/rfs035
Acknowledgements
We are grateful to two anonymous referees for their constructive comments and suggestions that helped us to improve the scope and clarity of this research. We also thank Professor Badi Baltagi, Tobias Adrian, Simone Manganelli and Cristina Belles-Obrero, as well as seminar participants at University of Portsmouth and University of Sussex for their valuable suggestions and rewarding discussions. We would like to gratefully acknowledge the support of the University of Portsmouth, where this research was developed.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: PCA
The appendix bellow proposes the construction of a measure of connectedness with principal component analysis (PCA), methodologically similar to the study of Billio et al. (2012).
Instead of running PCA among all institutions simultaneously, we focus on the causal spillovers (endogenous risk) between a firm and its industry; we repeat this procedure for all the firms in the sample (600). Particularly, the two variables of interest are the firm (\(X^i\)) and industry (\(X^j\)) losses. In the PCA, the number of variables, that join the system, should be equal to the number of extracted components, also variables should be correlated; in fact, the correlation between (\(X^i\)) and (\(X^j\)) is, on average, 48%. As shown below, the principal components are new variables that combine the returns of firm i with the returns of industry j:
where the weights a are chosen so that: (1) the components are uncorrelated and (2) the first component accounts for the maximum possible variance of the set (OECD 2008). The first component (PC1) is used as a measure of connectedness and it is our alternative dependent variable. PC1 satisfies the Kaiser criterion that components with more than 1 eigenvalue, make sense to be included in the analysis. In this instance, PC1 explains 74% of the variability between the returns of firms and their industries, with eigenvalue 1.48, while PC2 explains the remaining 26 % with eigenvalue 0.52.
Appendix 2: DCC
Adrian and Brunnermeier (2016) build on a bivariate diagnonal VECH-GARCH to estimate the conditional covariance between the firm and industry’s losses, an alternative dynamic systemic risk measure. Similarly, we employ a parsimonious DCC-GARCH(1,1) model to identify the dynamic conditional correlation and the conditional covariance between the firm and industry’s returns; as proposed by Engle (2002):
\({\mathbf{X}}_{t} \equiv ({X}_{t}^{j}, {X}_{t}^{i})'\) is a vector of daily return losses of j industry and i firm, \(\epsilon _t\) is a vector of random disturbance terms, \({\mathbf{v_t}}\) is a vector of normal, independent and identically distributed innovations, and \({\mathbf{H}_{t}}\) is the conditional variance and covariance matrix, defined as:
where \({h}_{t}^{j,i}\), the conditional covariance, is another measure of interconnection between firm and industry. It is conceptually similar to the alternative dynamic approaches of Billio et al. (2012), Adrian and Brunnermeier (2016). \({\mathbf{D_t}}\) is a diagonal matrix of conditional variances [\({\mathbf{D}}_{t}=diag(\sigma {^{j}}_{t}^{2}) , \ \sigma {^{i}}_{t}^{2})\)] from the univariate GARCH(1,1), and \({\mathbf{R_t}}\) is the time-varying quasicorrelation matrix, which is calculated as:
and \({{\mathbf{R}}_{t}}\) has the following form:
where \(\mathbf{u_t}={\mathbf{D}}_{t}^{-1/2}\epsilon _{t}\) and \(\mathbf{u_t}\) is used to estimate the parameters of the conditional correlation, \({\mathbf{Q}}_{t}\) is the time-varying covariance matrix of \(\mathbf{u_t}\), \(\bar{\mathbf{Q}}\) (\(\bar{\mathbf{Q}}=E[\mathbf{u_t}{} \mathbf{u_t}^{'}]\)) is the unconditional variance and covariance matrix of \(\mathbf{u_t}\) and parameters a and b should be non-negative and less than unity in aggregate. The coefficients of conditional mean and conditional variance models are estimated by maximizing the log-likelihood function for any t observation as shown below:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tzouvanas, P., Kizys, R., Chatziantoniou, I. et al. Can Variations in Temperature Explain the Systemic Risk of European Firms?. Environ Resource Econ 74, 1723–1759 (2019). https://doi.org/10.1007/s10640-019-00385-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-019-00385-0