Mint: MDL-based approach for Mining INTeresting Numerical Pattern Sets

Abstract

Pattern mining is well established in data mining research, especially for mining binary datasets. Surprisingly, there is much less work about numerical pattern mining and this research area remains under-explored. In this paper we propose Mint, an efficient MDL-based algorithm for mining numerical datasets. The MDL principle is a robust and reliable framework widely used in pattern mining, and as well in subgroup discovery. In Mint we reuse MDL for discovering useful patterns and returning a set of non-redundant overlapping patterns with well-defined boundaries and covering meaningful groups of objects. Mint is not alone in the category of numerical pattern miners based on MDL. In the experiments presented in the paper we show that Mint outperforms competitors among which IPD, RealKrimp, and Slim.

1 Introduction

The objective of pattern mining is to discover a small set of interesting patterns that describe together a large portion of a dataset and can be easily interpreted and reused. Actually pattern mining encompasses a large variety of algorithms in knowledge discovery and data mining aimed at analyzing datasets (Vreeken and Tatti 2014). Present approaches in pattern mining are aimed at discovering an interesting pattern set rather than a set of individually interesting patterns, where the quality of patterns is evaluated w.r.t. both the dataset and other patterns. One common theoretical basis for pattern set mining relies on the Minimum Description Length principle (MDL) (Grünwald 2007), which is applied to many types of patterns, e.g. itemsets (Vreeken et al. 2011), patterns of arbitrary shapes in 2-dimensional data (Faas and van Leeuwen 2020), sequences (Tatti and Vreeken 2012a), graphs (Bariatti et al. 2020), etc.

Contrasting the recent advances in pattern mining, algorithms for mining numerical data appear to be insufficiently explored. To date, one of the most common ways to mine numerical pattern sets relies on the application of itemset mining to binarized datasets. This is discussed below in more detail but before we would like to mention an alternative to numeric pattern mining which is “clustering”.

In the last few decades, clustering algorithms have been extensively developed, and many different and efficient approaches have been proposed (Jain 2010; van Craenendonck et al. 2017; Jeantet et al. 2020). However, there is an important conceptual difference between pattern mining and clustering. In pattern mining the description comes first, while in clustering the primacy is given to the object similarity. In other words, numerical pattern mining is more interested in the description of a group of objects in terms of a set of attributes related to these objects, while clustering focuses more on the detection of these groups of objects based on their commonalities as measured by a similarity or a distance. The former entails some requirements for the ease of interpretation, i.e., the resulting patterns should describe a region in the “attribute space” that is easy to interpret. By contrast, in clustering, the focus is put on groups of objects or instances. The clusters can be constrained to have certain shapes, e.g., spheres in K-means or DBSCAN, but still the similarity of objects remains the most important characteristic of clusters. For example, clustering techniques such as agglomerative single-linkage clustering in a multidimensional space may return clusters of very complex shapes. Usually no attention is paid to these shapes while this is one of the most important preoccupations in numerical pattern mining.

Accordingly, in this paper, we propose an MDL-based approach to numerical pattern set mining called Mint for “Mining INTeresting Numerical Pattern Sets”. Mint computes numerical patterns as m-dimensional hyper-rectangles which are products of m intervals, where the intervals are related to the attributes and their values. Mint does not require any frequency threshold. For each pattern the frequency threshold is adapted according to the MDL principle and depends on the size of the pattern, pattern neighbors, and the size of the pattern set. The main benefits of the present approach are that (i) Mint does not need to explore the pattern space in advance as candidates for optimal patterns are computed on the fly, (ii) the total number of explored patterns is at most cubic (and it is at most quadratic at each iteration) in the number of objects with distinct descriptions considered as vectors of attribute values, (iii) Mint is based on MDL and outputs a small set of non-redundant informative patterns, (iv) a series of experiments shows that Mint is efficient and outputs sets of patterns of very high quality. The discovered patterns are diverse, non-redundant, cover almost entirely the whole dataset by a reasonable (i.e., relatively small) number of patterns. Furthermore they describe meaningful groups of objects with quite precise boundaries.

Actually, there are two versions of Mint, the first one is based on a covering strategy while the second one, called GMint for Greedy Mint, is based on a greedy approach when computing the candidate patterns. The results returned by both versions of Mint algorithm are quite close but the GMint version is much faster. Moreover, Mint algorithm is able to mine numerical patterns both for small and on large datasets, and it is most of the time more efficient, outputting more concise and better fitting patterns, as compared to its competitors IPD (an MDL-based method for discretization), RealKrimp, and Slim. In particular, the encoding scheme on which relies Mint is based on prequential plug-in codes, which have better theoretical properties than the codes used in IPD, RealKrimp, and Slim.

The paper has the following structure. In Sect. 2 we discuss the state-of-the-art algorithms in pattern mining for numerical data. Section 3 introduces the main notions used in the paper while in Sect. 4 we describe the basis of the proposed method. Next Sect. 5 relates the experiments carried out for illustrating the good behavior and the strengths of Mint. Finally, Sect. 7 concludes the paper with a discussion about the potential of Mint and some directions for future work.

2 Related work

The problem of pattern mining has been extensively studied for binary data –itemset mining– but remains much less explored for numerical data. Hence a common way to mine patterns in numerical data relies on a binarization of data and then application of itemset mining algorithms. Meanwhile, a number of approaches was designed for mining numerical datasets possibly involving binarization and taking into account the type of the data at hand. In this section we firstly discuss different numerical data preprocessing approaches allowing the use of itemset mining and then we discuss state-of-the art approaches in numerical pattern mining.

2.1 Numerical data preprocessing

Data preprocessing is the cornerstone for discovering patterns of good quality and relies on discretization or binarization tasks.

Discretization. Discretization relies on partitioning the range of attribute values into intervals and then mapping the intervals into integers for preserving the order of the intervals. The existing discretization techniques can be categorized into univariate and multivariate techniques.

Univariate discretization includes all the methods where attributes are considered independently. An attribute range may be split into intervals of equal width or equal height w.r.t. frequency. Another way to split an attribute range is by using K-means algorithm (Dash et al. 2011), where some criteria are used for assessing the quality of clustering and choosing an optimal K. A more flexible approach consists in splitting based on the MDL principle (Kontkanen and Myllymäki 2007; Rissanen et al. 1992) which is discussed below.

However, considering each attribute range independently does not preserve the interaction between attributes and, as a consequence, may make some patterns not recognizable. Multivariate discretization techniques were proposed to tackle this issue. In (Mehta et al. 2005; Kang et al. 2006), multivariate discretization is based on principal component analysis and independent component analysis, respectively. However, both techniques do not guarantee taking into account possible complex interactions between attributes and require some assumptions on either distribution or correlation (Nguyen et al. 2014). Accordingly, Nguyen et al. (2014) address these problems proposing an MDL-based algorithm, called IPD, for multivariate discretization. The algorithm works in unsupervised settings contrasting a related approach in (Fayyad and Irani 1993; Boullé 2006; Bondu et al. 2010). Indeed, MDL is used in a large number of approaches and is detailed below in § 2.2.

Binarization. Discretization is not the only step to accomplish before applying an itemset mining algorithm. Another important operation is binarization, i.e., the transformation of discrete values into binary attributes. Binarization should be carefully taken into account as it may affect the results of itemset mining and induce loss of information. Moreover, binarization is associated with the risk of introducing artifacts and then obtaining meaningless results.

A simple and popular binarization is based on “one-hot encoding”, where each discrete value is associated with one binary attribute. The number of attributes may become very large which can lead to an excessive computational load. Moreover, one-hot encoding does not necessarily preserve the order of discrete values.

By contrast, interordinal scaling preserves the order of values by introducing for each discrete value v two binary attributes “$x \ge v$” and “$x\le v$”. However, in (Kaytoue et al. 2011) it was shown that, with a low-frequency threshold, mining itemsets in interordinally scaled data becomes much more expensive than mining hyper-rectangles in numerical data. Hyper-rectangles here are studied in the framework of interval pattern structures.

An alternative approach to interordinal scaling (Srikant and Agrawal 1996) consists in computing more general itemsets based on considered discrete values. The authors introduce the notion of partial completeness w.r.t. a given frequency threshold. This notion allows one to formalize the information loss caused by partitioning as well as to choose an appropriate number of intervals w.r.t. chosen parameters. As interordinal scaling, this approach suffers from pattern explosion. In addition, this method requires to set some parameters, e.g., frequency threshold and completeness level, whose optimal value is unknown.

Despite its limitations, one-hot encoding remains a good option provided that suitable constraints can be defined for avoiding attribute explosion and allowing tractable computation.

Numerical attribute set assessment based on ranks. One of the main drawbacks of the approaches mentioned above, which consider discretization and binarization as mandatory preprocessing steps, is that the quality of the output depends on the quality of the discretization. In mining numerical patterns, when the boundaries (given in red) of patterns are not well aligned with vertical axes, as shown in the figure on the right, uniform boundaries will produce imprecise descriptions, while using exact boundaries may greatly complicate pattern mining.

An alternative approach that “simulates” multi-threshold discretization is proposed in a seminal paper (Calders et al. 2006). It consists in (i) considering the ranks of attribute values instead of actual real values, and (ii) evaluating the sets of numerical attributes using rank-based measures. The authors propose several support measures based on ranks. In such a way, the problem of dealing with concrete attribute values is circumvented by considering the coherence of the ranked attribute values. Moreover, in (Tatti 2013), two scores based on ranked attribute values have been proposed to evaluate a set of numerical attributes. The scores are used to find the best combinations of attributes w.r.t. rank-based supports.

In all the methods mentioned in this subsection, patterns are understood as combinations of the attribute ranges as a whole. These methods do not provide descriptions related to some particular parts of the range if needed, while this is the main focus of this paper as explained later.

2.2 MDL-based approaches to pattern mining

The MDL approach to pattern set mining is based on the slogan: “the best set of patterns is the set that compresses the database best” (Grünwald 2007). There is a significant amount of papers about the use of the MDL principle in pattern mining as this is very well presented in the report of Galbrun (Galbrun 2020). MDL has been used in many different contexts but hereafter we focus on pattern mining. One of the most famous MDL-based itemset miners is Krimp, introduced in (Siebes et al. 2006) (not under this name), and the last version was presented in (Vreeken et al. 2011). Krimp relies on two steps that consist in (i) generating a set of frequent patterns, and (ii) selecting those minimizing the total description length. While Krimp is an efficient and well-designed itemset miner, it requires that all frequent itemsets should be generated. Moreover, increasing the frequency threshold may lead to a worse compression, so Slim (Smets and Vreeken 2012) was proposed to tackle this issue. In contrast to Krimp, Slim does not require that all itemsets should be generated in advance, since the candidates for optimal itemsets are gradually discovered. Nevertheless, the encoding scheme used in Krimp and Slim shows a range of limitations that are discussed in more detail in Sect. 3.2. In continuation, the DiffNorm algorithm (Budhathoki and Vreeken 2015) is an extension of Slim that is based on a better encoding scheme and can be applied to a collection of datasets for finding the difference in datasets in terms of itemsets. Another MDL algorithm related to the Krimp family was proposed in (Akoglu et al. 2012) for fixing scalability issues. This algorithm deals with categorical data and is less sensitive to combinatorial explosion.

All the aforementioned MDL-based algorithms represent a “model”, i.e. a set of patterns, as a two-column table, where the left-hand column contains the pattern descriptions and the right-hand column contains the associated code words. Another way to store patterns is proposed in the Pack algorithm (Tatti and Vreeken 2008), where the model is encoded as a decision tree, so that a node corresponds to an attribute. A non-leaf node has two siblings reflecting the presence or absence of this attribute in an itemset. The itemset, in turn, is a path from the root to a leaf node. One main difference between the Pack approach and the algorithms of the Krimp family is that 0’s and 1’s are symmetrically considered in Pack.

The Stijl algorithm (Tatti and Vreeken 2012b) is a tree-based MDL approach taking into account both 0’s and 1’s and storing itemsets in a tree. However, contrasting Pack, Stijl relies on “tiles”, i.e., rectangles in a dataset. The tree in Stijl is a hierarchy of nested tiles, where parent-child relations are inclusion relations between tiles. A child tile is created whenever its density –the relative number of 1’s– differs a lot from the parent one. An extension of tile discovery is proposed in (Faas and van Leeuwen 2020) where “geometric pattern mining” with the Vouw algorithm is introduced. This algorithm may consider arbitrarily shaped patterns in raster-based data, i.e., data tables with a fixed order of rows and columns, and it is able to identify descriptive pattern sets even in noisy data. Finally, the discovery of tiles is also closely related to Boolean Matrix Factorization (BMF). In a nutshell, the objective of BMF is to find an approximation of a binary matrix C by a Boolean product of two low-rank matrices A and B. The columns of A and the rows of B describe the factors, which correspond to tiles. The MDL principle can also be applied to the BMF problem (Miettinen and Vreeken 2014; Makhalova and Trnecka 2021).

All the MDL-based algorithms which are surveyed above are applicable to binary or categorical data. Now we focus on a few algorithms which are dealing with pattern mining in numerical data. First of all the RealKrimp algorithm (Witteveen et al. 2014) is an extension of Krimp to real-valued data, where patterns are axis-aligned hyper-rectangles. Even if the algorithm does not require any preprocessing, it actually needs a discretization of the data. Moreover, there is also a “feature selection” step where unimportant hyper-rectangle dimensions are removed. RealKrimp is tailored to mine high-density patterns, and to minimize the combinatorial explosion, it constructs each hyper-rectangle using a pair of neighboring rows sampled from the original dataset. Then, without prior knowledge about the data, the choice of the size of sampling is difficult as a too small sample size may output very general patterns, while a too large sample size may increase the execution time. The problem of an inappropriate sample size may be partially solved by setting a large “perseverance”, i.e., how many close rows should be checked to improve compression when enlarging the hyper-rectangle, and “thoroughness”, i.e., how many consecutive compressible patterns are tolerated. As it can be understood, finding optimal parameters in RealKrimp constitutes an important problem in the pattern mining process. Moreover, the hyper-rectangles in RealKrimp are evaluated independently, meaning that the algorithm searches for a set of optimal patterns instead of an optimal pattern set. The subsequent pattern redundancy may be mitigated by sampling data and computing the hyper-rectangles in different parts of the attribute space. Thereby, RealKrimp relies on many heuristics and has no means to jointly evaluate the set of generated hyper-rectangles. In addition, heuristics imply some prior knowledge about the data which is not always available in practice. All these aspects should be taken into account.

Another approach to mine informative hyper-rectangles in numerical data was proposed in (Makhalova et al. 2019). The approach can be summarized in 3 steps: (i) greedily computing dense hyper-rectangles by merging the closest neighbors and ranking them by prioritizing dense regions, (ii) greedily optimizing an MDL-like objective to select the intervals –sides of hyper-intervals– for each attribute independently, (iii) constructing the patterns using the selected intervals and maximizing the number of instances described by the intervals by applying a closure operator (a closed set is maximal for given support). This approach tends to optimize entropy, which is proportional to the length of data encoded by the intervals and does not take into account the complexity of the global model, i.e., the set of patterns. This simplification is based on the observation that each newly added interval replaces at least one existing interval, and thus, the complexity of the model does not increase. Moreover, the compression process is lossy as the data values can be reconstructed only up to some selected intervals. Finally, the approach allows for feature selection but does not address explicitly the problem of overlapping patterns.

Based on this first experience, below we propose the Mint algorithm, which is based on MDL and aimed at mining patterns in numerical data. We restrict the patterns to be hyper-rectangles as they are the most interpretable types of multidimensional patterns.

As RealKrimp and IPD, Mint deals with discretized data. Both RealKrimp and Mint allow for mining overlapping patterns, however the problem of feature selection is not addressed in Mint. Mint is less dependent on heuristics than RealKrimp and discovers an approximation of an MDL-optimal pattern set rather than an approximation of single optimal patterns.

IPD works in a setting similar to Mint, however, the methods differ in several aspects: (i) IPD searches for globally optimal boundaries (in experiments we show that these boundaries are not quite precise to describe “ground-truth” hyper-rectangles), (ii) IPD returns a grid where adjacent hyper-rectangles may belong to one “ground-truth” hyper-rectangle. Overall, despite the fact that both algorithms deal with numerical data and are aimed at finding meaningful subspaces using the MDL principle, Mint and IPD solve very distinct tasks. At each step IPD decides whether a particular boundary is useless or not, while Mint decides whether a particular hyper-rectangle is different enough from its neighbors and other hyper-rectangles to be considered as a separate pattern. As a consequence, both the total description length and the principles of its minimization are very different in both approaches.

In Mint we introduce the total description length for a set of hyper-rectangles. The proposed encoding adapts some of the best practices of the aforementioned approaches: (i) prequential plug-in codes for patterns  (Budhathoki and Vreeken 2015; Proença and van Leeuwen 2020), (ii) grid-based encoding of the boundaries and reconstruction cost to refine the positions of data points within the hyper-rectangles (Nguyen et al. 2014). In contrast to (Tatti and Vreeken 2008), the patterns are not arranged into a hierarchy and their boundaries are encoded independently from the other patterns in the set. However, patterns still may overlap and even be included in other patterns. As Slim, Mint discovers gradually the candidates for optimal patterns and estimates the length gain to pick the best candidate.

3 Basics

3.1 Formalization of data and patterns

Let $D^*$ be a numerical dataset that consists of a set of objects $G = \{g_1, \ldots , g_n\}$ and a set of attributes $M = \{m_1, \ldots , m_k\}$. The number of objects and attributes is equal to n and k, respectively. Each attribute $m_i \in M$ is numerical and its range of values is denoted by $range(m_i)$. Each object $g\in G$ is described by a tuple of attribute values $\delta (g) = \left\langle v_{i} \right\rangle _{i \in \{1, \ldots , k\}}$.

As patterns we use axis-aligned hyper-rectangles, or “boxes”. In multidimensional data, an axis-aligned hyper-rectangle has one of the simplest descriptions –a tuple of intervals– and thus can be easily analyzed by humans. The hyper-rectangle describing a set of objects B is given by

$$\begin{aligned} h = \left\langle [\min \{v_i \mid v_i \in \delta (g), g\in B \}, \max \{v_i \mid v_i \in \delta (g), g\in B \}]\right\rangle _{i \in \{1, \ldots , k\}}. \end{aligned}$$

We call the i-th interval of a hyper-rectangle the i-th side of the hyper-rectangle. The support of a hyper-rectangle h is the number of objects whose descriptions comply with h, i.e., $sup(h) = |\{ g \in G \mid \delta (g) \in h\}|$.

Often, instead of continuous numerical data, one deals with discretized data, where the continuous range of values $range(m_i)$ is replaced by a set of integers, which are the indices of the intervals. Formally speaking, a range $range(m_i)$ is associated with a partition based on a set of intervals ${\mathcal {B}}_i = \{B_i^j = [c_{j-1}, c_{j}) \mid j = 1, \ldots , l \}$, where $c_0$ and $c_l$ are the minimum and maximum values, respectively, of $range(m_i)$. Thus, each $v \in [c_{j-1}, c_{j})$ is replaced by j.

The endpoints of the intervals can be chosen according to one of the methods considered above, e.g., equal-width, equal-height intervals or using the MDL principle, and the number of the intervals may vary from one attribute range to another attribute range. The endpoints make a discretization grid. The number of the grid dimensions is equal to the number of attributes.

A chosen discretization splits the space $\prod _{i = 1}^{|M|}range(m_i)$ into a finite number of elementary hyper-rectangles $h_e \in \{\prod _{i = 1}^{|M|} B_{i}^{j} \mid B_{i}^{j} \in {\mathcal {B}}_i\}$, i.e., each side of an elementary hyper-rectangle is composed of one discretization interval $B_i^j$. Non-elementary hyper-rectangles are composed of consecutive elementary hyper-rectangles.

For a hyper-rectangle $h = \left\langle [c^{(l)}_i, c^{(u)}_i)\right\rangle _{i \in \{1, \ldots , |M|\}}$, where $c^{(l)}_i$ and $c^{(u)}_i$ are endpoints of intervals from ${\mathcal {B}}_i$, in the discretized attribute space we define the size of the ith side as the number of elementary hyper-rectangles included into this side, i.e., $size(h,i) = |\{B_i^j \mid B_i^j \subseteq [c^{(l)}_i, c^{(u)}_i)\}|$. Further, we use h to denote a hyper-rectangle (pattern), ${\mathcal {H}}$ to denote a set of hyper-rectangles (patterns), and D to denote the dataset $D^*$ discretized w.r.t. the chosen discretization grid.

Example 1

Let us consider a dataset given in Fig. 1 (left). It consists of 13 objects described by attributes $m_1$ and $m_2$. All the descriptions are distinct (unique). Each attribute range is split into 8 intervals of width 1. The discretized dataset is given in Fig. 1 (right). It has 7 unique rows. The non-empty elementary hyper-rectangles correspond to non-empty rectangles induced by the $7 \times 8$ discretization grid. The number of hyper-rectangles is equal to the number of distinct rows in the discretized dataset (given in the middle).

Fig. 1

Dataset over attributes $\{m_1, m_2\}$ and its discretized version (left), representation of the dataset in the plane and its partition into $7 \times 8$ equal-width intervals (right). The discretization grid is given by dotted lines, the corresponding non-empty elementary hyper-rectangles are given by dashed lines. The axis labels show the indices of elementary hyper-rectangles

3.2 Information theory and MDL

MDL (Grünwald 2007) is a general principle that is widely used for model selection and works under the slogan “the best model compresses data the best”. This principle relies on the following: given a sequence that should be sent from a transmitter to a receiver, the transmitter, instead of encoding each symbol uniformly, replaces repetitive sub-sequences with code words. Thus, instead of a symbol-wise encoded sequence, the transmitter sends a sequence of code words and a dictionary. The dictionary contains all used code words and the sub-sequences encoded by them. Using the dictionary, the receiver is able to reconstruct the original sequence. The MDL principle is applied to decide which sub-sequences should be replaced by the code words and which code words should be chosen for these sub-sequences. The code words are associated in such a way that the most frequent sub-sequences have the shortest code words. In our case, the sequence that should be transmitted correspond to a numerical dataset discretized into small equal-width intervals, and as sub-sequences we chose patterns (hyper-rectangles).

Formally speaking, given a dataset D the goal is to select a subset of patterns ${\mathcal {H}}$ that minimizes the description length $L(D, {\mathcal {H}})$. In the crude version of MDL (Grünwald 2007) the description length is given by $L(D, {\mathcal {H}}) = L({\mathcal {H}}) + L({D} | {\mathcal {H}})$, where $L({\mathcal {H}})$ is the description length of the model (set of patterns) ${\mathcal {H}}$, in bits, and $L({D} | {\mathcal {H}})$ is the description length of the dataset D encoded with this set of patterns, in bits.

The length $L({\mathcal {H}})$ characterizes the complexity of the set of patterns and penalizes high-cardinality pattern sets, while the length of data $L(D|{\mathcal {H}})$ characterizes the conformity of patterns w.r.t. the data. $L(D | {\mathcal {H}})$ increases when the patterns are too general and do not conform well with the data. Thus, taking into account both $L({\mathcal {H}})$ and $L(D | {\mathcal {H}})$ allows to achieve an optimal balance between the pattern set complexity and its conformity with the data.

Roughly speaking, the minimization of the total length consists in (i) choosing patterns that are specific for a given dataset, and (ii) assigning to these patterns the code words allowing for a shorter total length $L(D, {\mathcal {H}})$.

In MDL, our concern is the length of the code words rather than the codes themselves. That is why we use a real-valued length instead of an integer-valued length.

Intuitively, the length of code words is optimal when shorter code words are assigned to more frequently used patterns. From the information theory, given a probability distribution over ${\mathcal {H}}$, the length of the Shannon prefix code for $h \in {\mathcal {H}}$ is given by $l(h) = -\log P(h)$ and is optimal. Then we obtain the following probability model: given the usage usg(h) of $h \in {\mathcal {H}}$ in the encoding. The probability distribution ensuring an optimal pattern code length for the chosen encoding scheme is $P(h) = \frac{usg(h)}{\sum _{h_i \in {\mathcal {H}}} usg(h_i)},$ where usage usg(h) of a pattern h is the number of times a pattern h is used to cover objects G in a dataset D. However, this model is based on the assumption that the total number of encoded instances (the length of the transmitting sequence) is known. Moreover, in order to encode/decode the message, the transmitter should know the usages usg(h) of all patterns $h \in {\mathcal {H}}$ and the receiver should know the corresponding probability distribution, which is not usually the case.

Prequential plug-in codes (Grünwald 2007) do not have this kind of limitation. These codes refer to “online” codes since they can be used to encode sequences of arbitrary lengths and they do not require to know in advance the usage of each code word. The codes are based on only previously encoded instances. Moreover, they are asymptotically optimal even without any prior knowledge on the probabilities. The prequential plug-in codes are widely used in recent MDL-based models (Faas and van Leeuwen 2020; Proença and van Leeuwen 2020; Budhathoki and Vreeken 2015).

More formally, the idea of the prequential codes is to assess the probability of observing the n-th element $h^n$ of the sequence based on the previous elements $h^1, \ldots , h^{n-1}$. Thus prequential codes allow for a predictive-sequential interpretation for sequences of arbitrary lengthsi.

Let $H^n$ be the sequence $h^1, \ldots , h^{n-1}, h^{n}$. The probability of the n-th pattern $h^n \in {\mathcal {H}}$ in the pattern sequence $H^n$ is given by

$$\begin{aligned} P_{plug\text{- }in}(h^n) = \frac{\prod _{h \in {\mathcal {H}}} [ \varGamma (usg(h) + \varepsilon ) / \varGamma (\varepsilon )]}{\varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|)/\varGamma (\varepsilon |{\mathcal {H}}|)}, \end{aligned}$$

(1)

where usg(h) is the number of occurrences of pattern h in the sequence $H^n$, and $usg({\mathcal {H}}) = \sum _{h \in {\mathcal {H}}} usg(h)$ is the length of the sequence, i.e., the total number of occurrences of patterns from ${\mathcal {H}}$. $\varepsilon$ is a pseudocount, i.e., the initial usage of patterns, and $\varGamma (x) = \int _{0}^{1}(-\log (t))^{x-1} \,dt$ is the gamma function.

Then the length of the code word associated with $h^n$ is given as follows:

$$\begin{aligned} l(h^n)&= -\log P_{plug\text{- }in}(h^n) =\nonumber \\&=\log \varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|) \nonumber \\&\quad - \log \varGamma (\varepsilon |{\mathcal {H}}|) - \sum _{h \in {\mathcal {H}}}\left[ \log \varGamma (usg(h) + \varepsilon ) - \log \varGamma (\varepsilon )\right] . \end{aligned}$$

(2)

As was mentioned above, we are interested in the length of the code words rather than in the code words themselves. That is why we use real-valued length instead of integer-valued length for the number of bits needed to store the real code words. We give the technical details of the derivation of Equation 1 in Appendix A.

To encode integers, when it is needed, we use the standard universal code for the integers (Rissanen 1983) given by $L_\mathbb {N}(n) = \log n + \log \log n + \log \log \log n + \ldots + \log c_0,$ where the summation stops at the first negative term, and $c_0 \approx 2.87$ (Grünwald 2007). In this paper we write $\log$ for $\log _2$ and put $0 \log 0 = 0$.

4 Mint

We propose an approach to pattern mining in multidimensional numerical discretized data. The main assumption on which we rely is that all the attributes are equally important, i.e., patterns are computed in the whole attribute space. To apply this method we consider a discretized attribute space, i.e., each attribute range is split into equal-width intervals, as it was done in (Witteveen et al. 2014; Nguyen et al. 2014). The choice of equal-width intervals is due to the fact that the cost, in bits, of the reconstruction of a real value here is constant for all intervals. Each object therefore is included into an |M|-dimensional elementary hyper-rectangle. Starting from the elementary hyper-rectangles (each side is composed of one interval), we greedily generalize the currently best patterns and select those that provide the maximal reduction of the total description length. At each step we reuse some of the previously discovered candidates as well as other candidates computed on the fly using the last added pattern.

4.1 The model encoding

Firstly, we define the total description length of the set of hyper-rectangles and the data encoded by them. The total description length is given by $L(D, {\mathcal {H}}) = L({\mathcal {H}}) + L(D | {\mathcal {H}})$, where $L({\mathcal {H}})$ is the description length, in bits, of the set of hyper-rectangles ${\mathcal {H}}$, and $L(D | {\mathcal {H}})$ is the description length, in bits, of the discretized dataset encoded by this set of hyper-rectangles. The initial set of the hyper-rectangles is composed exclusively of elementary hyper-rectangles.

To encode the set of hyper-rectangles ${\mathcal {H}}$, we need to encode the discretization grid and the positions of the hyper-rectangles in this grid. Thus, the total length of the pattern set is given by

$$\begin{aligned} L({\mathcal {H}}) =&\underbrace{ L_\mathbb {N}(|M|) + \sum _{i = 1}^{|M|} L_\mathbb {N}(|{\mathcal {B}}_i|)}_{length\; of\; the\; grid} +&\underbrace{L_\mathbb {N}(|{\mathcal {H}}|) + |{\mathcal {H}}| \left( \sum _{i = 1}^{|M|} \log \left( |{\mathcal {B}}_i| (|{\mathcal {B}}_i| + 1)/2\right) \right) }_{length\; of\; the\; pattern \; set}. \end{aligned}$$

To encode the grid we need to encode the number of dimensions (attributes) |M| and the number of intervals $|{\mathcal {B}}_i|$ within each dimension i. This grid is fixed and is not changed throughout the pattern mining process. To encode the pattern set ${\mathcal {H}}$, given the grid, we need to encode the number of patterns $|{\mathcal {H}}|$ and the positions of their boundaries within each dimension. Since there exist $\left( {\begin{array}{c}|{\mathcal {B}}_i|\\ 2\end{array}}\right) + |{\mathcal {B}}_i|$ possible positions of the boundaries within the i-th dimension, namely $\left( {\begin{array}{c}|{\mathcal {B}}_i|\\ 2\end{array}}\right)$ combinations where the boundaries are different, and $|{\mathcal {B}}_i|$ cases where the lower and upper boundaries belong to the same interval, meaning only one interval from the grid is involved. These positions are encoded uniformly.

The size of the intervals is taken into account in the reconstruction cost $L(D \ominus D({\mathcal {H}}) | {\mathcal {H}})$ (see below). The latter gives the cost of $\log (|{\mathcal {B}}_i|(|{\mathcal {B}}_i| + 1))$ bits for encoding the i-th side of a pattern within the chosen grid.

The code length of a dataset encoded with the set of patterns is given by

$$\begin{aligned} L(D | {\mathcal {H}}) = \underbrace{L_\mathbb {N}(|G|)}_{\begin{array}{c} cost\;of\;encoding\;the\\ \;number\;of\;instances \end{array}} + \underbrace{L(D({\mathcal {H}}) | {\mathcal {H}})}_{\begin{array}{c} cost\;of\;encoding\\ D\;with\;{\mathcal {H}} \end{array} } + \underbrace{L(D \ominus D({\mathcal {H}})| {\mathcal {H}})}_{\begin{array}{c} reconstruction\;cost \end{array}} \end{aligned}$$

where the first component encodes the number of objects, the second one corresponds to the length of data encoded with hyper-rectangles, and the third one corresponds to the cost of the reconstruction of the object description $\delta (g) = \left\langle v_{i} \right\rangle _{i \in \{1, \ldots , |M|\}}$ up to elementary intervals. Let us consider the last two components in more detail.

The cost of the reconstruction of the true real values is constant for all values due to the equal-width discretization and it is not changed during pattern mining, thus is not taken into account in $L(D,{\mathcal {H}})$. The dataset is encoded by exploring all objects in a given order and assigning to each object a code word of the pattern covering this object. According to the MDL principle, each data fragment should be covered (encoded) only once, otherwise, the encoding is redundant. However, some patterns may overlap, i.e., include the same object. A cover strategy then defines which data fragment is an occurrence of which pattern. We discuss the cover strategy in detail in the next section. Here, the usage is defined as follows: $usg(h)= |cover(h, G)|$.

From Equation 2, the length of data encoded with the plug-in codes is

$$\begin{aligned} L(D({\mathcal {H}}) | {\mathcal {H}}) =&\log \frac{\varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|)/\varGamma (\varepsilon |{\mathcal {H}}|)}{\prod _{h \in {\mathcal {H}}} \varGamma (usg(h) + \varepsilon ) / \varGamma (\varepsilon )} = \\ =&\log \varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|) - \log \varGamma (\varepsilon |{\mathcal {H}}|) - \sum _{h \in {\mathcal {H}}} \left[ \log \varGamma (usg(h) + \varepsilon )\right. \\&\left. - \log \varGamma (\varepsilon )\right] , \end{aligned}$$

where $usg({\mathcal {H}}) = \sum _{h \in {\mathcal {H}}} usg(h)$.

Once each object has been associated with a particular pattern, its original description within the pattern up to elementary intervals is encoded in $L(D \ominus D({\mathcal {H}})| {\mathcal {H}})$. We use $D \ominus D({\mathcal {H}})$ to denote the difference (“distortion”) between the initially discretized dataset D and the same dataset encoded with ${\mathcal {H}}$.

To reconstruct the dataset up to the elementary equal-width intervals we encode the positions of each object within the corresponding pattern, this cost is

$$\begin{aligned} L(D \ominus D({\mathcal {H}}) | {\mathcal {H}}) = \sum _{\begin{array}{c} h\in {\mathcal {H}} \end{array}}usg(h)\log ({size(h)}) = \sum _{\begin{array}{c} h\in {\mathcal {H}} \end{array}}usg(h)\Bigg (\sum _{i = 1}^{|M|}\log ({size(h,i)})\Bigg ), \end{aligned}$$

where size(h, i) is the number of elementary intervals that compose the side i of the pattern h.

Example 2

Let us consider an encoding of the data by patterns according to the model introduced above for the case of the running example. We take the set of two hyper-rectangles ${\mathcal {H}} = \{h_{11}, h_{12}\}$, which are given in Fig. 1. Let the cover of $h_{11}$ be $cover(h_{11}, G) = \{g_1, g_2, g_3, g_{4}\}$ and cover of $h_{12}$ be $cover(h_{12}, G) = \{g_5,\ldots , g_{13}\}$. Then, the encoding of the pattern set is given by $L({\mathcal {H}}) = L_\mathbb {N}(2) + (L_\mathbb {N}(7) + L_\mathbb {N}(8) ) + L_\mathbb {N}(2) + 2 \cdot (\log 28 \cdot \log 36)$. Here, we need $\log 28 \cdot \log 36$ bits to encode each pattern, i.e., $\log n$ bits to encode uniformly n possible positions of the boundaries for each side of the hyper-rectangle.

The length of data encoded by ${\mathcal {H}}$ is given by $L(D({\mathcal {H}})) = L_{\mathbb {N}}(13) + \log \varGamma (13 + \varepsilon \cdot 2) - \log \varGamma (\varepsilon \cdot 2) - [\log \varGamma (8 + \varepsilon ) - \log \varGamma (\varepsilon ) + \log \varGamma (4 + \varepsilon ) - \log \varGamma (\varepsilon )]$. The reconstruction error is equal to $L(D \ominus D({\mathcal {H}})) = 9 \cdot (\log (3) + \log (4)) + 4 \cdot (\log (5) + \log (5))$, i.e., we need to encode the positions of the data points within the corresponding hyper-rectangles up to the elementary hyper-rectangles.

As we can see from the example above, the patterns can overlap. In such a case, one relies on a cover strategy to decide which pattern to use to encode each object. In the next section we introduce the algorithm that defines this strategy and allows for computing patterns minimizing the total description length.

4.2 The Mint algorithms

The objective of the Mint algorithm is to compute in a numerical dataset a pattern set which is the best w.r.t. the MDL principle.

4.2.1 Computing minimal pattern set

Let M be a set of continuous attributes, G be a set of objects having a description based on attributes M, ${\mathcal {P}}$ be a set of all possible |M|-dimensional hyper-rectangles defined in the space $\prod _{m \in M}range(m)$, and $cover$ be a cover strategy. One main problem is to find the smallest set of hyper-rectangles ${\mathcal {H}} \subseteq {\mathcal {P}}$ such that the total compressed length $L(D, {\mathcal {H}})$ is minimal.

The pattern search space in numerical data, where patterns are hyper-rectangles, is infinite. Even considering a restricted space, where all possible boundaries of the hyper-rectangles are limited to the coordinates of the objects from G, the search space is still exponentially large. The introduced total length $L(D, {\mathcal {H}})$ does not exhibit (anti)monotonicity property over the pattern set and thus does not allow us to exploit some efficient approaches to its minimization. Hence, to minimize $L(D, {\mathcal {H}})$, we resort to heuristics.

4.2.2 Cover strategy

As mentioned above, some hyper-rectangles (patterns) may overlap. To ensure the minimality of encoding, i.e., that each object (data point) is exclusively covered by one pattern, we introduce a cover strategy. We call log-volume of pattern h the number of elementary hyper-rectangles in logarithmic scale that h contains, namely $lvol(h) = \sum _{i = 1}^{|M|}\log size(h,i)$. The support of h is the number of objects from G that h contains, i.e., $sup(h,G) = \{g \in G \mid g \in h\}$. For the sake of simplicity, we write sup(h) instead of sup(h, G) when the support is computed on the whole set of objects. We say that a point $(v_1, \ldots v_{|M|})$ is lexicographically smaller than a point $(w_1, \ldots w_{|M|})$ if for the first position i where $v_i \ne w_i$ the following inequality holds: $v_i < w_i$ (for all the preceding elements $v_j = w_j$, $j = 1, \ldots , i - 1$). Then $h_1$ is lexicographically smaller than $h_2$ if the lexicographically smallest point of $h_1$ is lexicographically smaller than the lexicographically smallest point of $h_2$.

The standard cover order of hyper-rectangles is given as follows:

$$\begin{aligned} lvol \uparrow , \quad sup \downarrow , \quad \text {lexicographically} \uparrow , \end{aligned}$$

where $\uparrow$ / $\downarrow$ denote ascending / descending orders, respectively. Thus, the patterns are ordered w.r.t. their volume in ascending direction ($pvol \uparrow$). The patterns having the same volume are ordered w.r.t. their support in descending direction ($sub \downarrow$), and the patterns having the same volume and support are ordered lexicographically in ascending direction ($lex \uparrow$). The pseudocode of the cover algorithm is given in Algorithm 1. Given a set of patterns ${\mathcal {H}}$ the Cover algorithm arranges them in the standard cover order (line 2), and starts to cover gradually all yet uncovered objects ${\mathcal {U}}$. At each iteration of the loop (lines 4-9), Cover extracts the top pattern h from the list of patterns ${\mathcal {H}}^*$ arranged in the standard cover order. Then all uncovered objects included in h are declared as covered. These objects make a set $cover(h, G, {\mathcal {H}})$ and are removed from the set of uncovered objects.

Table 1 Patterns $h_2$, $h_8$, $h_9$, and $h_{10}$ in the standard cover order

Example 3

Let us consider the running example given in Fig. 1 and pattern set ${\mathcal {H}}^*= \{h_2, h_9, h_8, h_{10}\}$. Pattern $h_2$ is on top since it has the smallest volume, patterns $h_9$ and $h_8$ are located just after $h_2$ because they have the smallest volume among the remaining ones, $h_9$ is located before $h_8$ because it has larger support. The last pattern is $h_{10}$, since it has the largest volume. In this particular case we did not use the lexicographical order since all patterns differ by their volume or support. When there are two patterns with the same volume and support, they are lexicographically ordered. For example, if the considered patterns had the same volume and support, they would be ordered in the lexicographical order as follows: $h_{10}$, $h_{2}$, $h_{9}$, and $h_8$. Since $(0, {0}) {<} ({0},{4}) {<} ({4},{4}) {<} (4,{7})$.

4.2.3 Main algorithm

Mint starts from elementary hyper-rectangles sequentially discover patterns that minimize the description length $L(D, {\mathcal {H}})$ by merging a pair of currently optimal patterns from ${\mathcal {H}}$. To compute a candidate pattern based on a pair of patterns, we introduce the join operator $\oplus$ which computes the join of two hyper-rectangles $h_j$ and $h_k$. Then, given $h_j = \langle [ v_i^{(l)}, v_i^{(u)}) \rangle _{i \in \{1, \ldots , |M|\}}$ and $h_k = \langle [ w_i^{(l)}, w_i^{(u)})\rangle _{i \in \{1, \ldots , |M|\}}$, the join $h_j \oplus h_k$ is given by the smallest hyper-rectangle containing $h_j$ and $h_k$, i.e., $h_j \oplus h_k = \langle [\min (v_i^{(l)}, w_i^{(l)}), \max (v_i^{(u)}, w_i^{(u)})) \rangle _{i \in \{1, \ldots , |M|\}}$.

The minimization of $L( D, {\mathcal {H}})$ consists in computing iteratively candidates using pairs of currently optimal patterns and selecting one that provides the largest gain in the total description length. For candidate $h_j \oplus h_k$, the length gain is given by:

$$\begin{aligned} \begin{aligned}&\varDelta L({\mathcal {H}}, D, h_j, h_k) \\&\quad = L(D, {\mathcal {H}}) - L(D, {\mathcal {H}} \cup \{h_j \oplus h_k\} \setminus \{h_j, h_k\}) \\&\quad = \underbrace{L_\mathbb {N} (|{\mathcal {H}}|) - L_\mathbb {N}(|{\mathcal {H}}| - 1) + \left( \sum _{i = 1}^{|M|} \log \left( |{\mathcal {B}}_i| (|{\mathcal {B}}_i| + 1)/2\right) \right) }_{\varDelta L({\mathcal {H}})} \\&\quad \quad + \underbrace{\log \frac{\varGamma (|G|+ \varepsilon |{\mathcal {H}}|)}{\varGamma (|G|+ \varepsilon (|{\mathcal {H}}|-1))} + \log \frac{\varGamma ( \varepsilon (|{\mathcal {H}}| - 1))}{\varGamma ( \varepsilon |{\mathcal {H}}|)} - \log \frac{\varGamma (usg(h_j) + \varepsilon )\varGamma (usg(h_k) + \varepsilon )}{\varGamma (usg(h_j \oplus h_k) + \varepsilon )\varGamma (\varepsilon )}}_{\varDelta L(D ({\mathcal {H}}))} \\&\quad \quad + \underbrace{usg(h_j) size(h_j) + usg(h_k)size(h_k) - usg(h_j \oplus h_k) size(h_j \oplus h_k)}_{\varDelta L(D \ominus D({\mathcal {H}}))}. \end{aligned} \end{aligned}$$

(3)

The term “gain” stands for the difference between the total description lengths obtained using the current pattern set ${\mathcal {H}}$ and the pattern set where patterns $h_j$ and $h_k$ are replaced by its join $h_j \oplus h_k$.

Since computing the gain in the total description length for each candidate $h_j \oplus h_k$ is computationally expensive (i.e., it requires recomputing the cover using Algorithm 1 for each candidates), we use an approximate cover to estimate $\varDelta L$. Then the approximate cover of a candidate $h_j \oplus h_k$ is defined as the union of the covers of $h_j$ and $h_k$, i.e. $cover(h_j \oplus h_k, G) = cover(h_j, G) \cup cover(h_k, G)$. The cover of the remaining patterns from ${\mathcal {H}}$ does not change. As above, the usage of $h_j \oplus h_k$ is simply the cardinality of its cover, i.e., $usg(h_j \oplus h_k) = |cover(h_j \oplus h_k, G)|$. Since initially each object is covered by one pattern, in the new cover each object will be covered by one pattern as well. Finally the cover of the candidate with the highest gain is recomputed using Algorithm 1.

The pseudocode of Mint is given in Algorithm 2. At the beginning, the optimal patterns ${\mathcal {H}}$ are the elementary hyper-rectangles (line 2) induced by an equal-width discretization into a chosen number of intervals $|{\mathcal {B}}_i|$, $i = 1, \ldots , |M|$. We also set an additional parameter k to limit the number of candidates corresponding to k nearest neighbors. For large datasets and large number of intervals $|{\mathcal {B}}_i|$, setting a low value $k \ll |G|$ reduces the computational effort. In the discretized space, the elementary hyper-rectangles are points, thus the distance between them is the Euclidean distance. Then, given a hyper-rectangle $h_j \oplus h_k$, the neighbors are the neighbors of $h_j$ and $h_k$. The main loop in lines 5-21 consists in selecting the best candidates from the current set of candidates ${\mathcal {C}}$, updating the set of optimal patterns ${\mathcal {H}}$, and collecting new candidates in ${\mathcal {C}}_{new}$. Once all candidates from ${\mathcal {C}}$ have been considered in the inner loop (lines 8-19), the new candidates from ${\mathcal {C}}_{new}$ become current ones (line 20). In the inner loop, lines 8-19, the candidates that minimize the total description length are selected one by one. They are considered by decreasing gain $\varDelta L$. At each iteration of the inner loop, the candidate $h_j \oplus h_k$ providing the largest gain $\varDelta L$ is taken. New pattern set ${\mathcal {H}}^*$ includes $h_j \oplus h_k$ and does not contain $h_j$ and $h_k$. We compute new cover by ${\mathcal {H}}^*$ using Algorithm 1 and then the total length $L(D, {\mathcal {H}}^*)$ (line 11). If $h_j \oplus h_k$ allows for a shorter total description length, patterns $h_j$ and $h_k$ are replaced with $h_j \oplus h_k$ in ${\mathcal {H}}$, and the candidates based on the newly added pattern are added to ${\mathcal {C}}_{new}$ (line 14) and are no more considered at the current iteration. In ${\mathcal {C}}_{new}$ we store pairs of indices making new candidates, and only in line 20 we compute candidates by calculating the gains $\varDelta L$ that they provide. These gains, however, are computed only for patterns $h_j \oplus h_k$ where both $h_j, h_k$ are still present in the set ${\mathcal {H}}$. Postponing the computation of candidates to line 20 allows us to reduce the number of candidates and to speed up pattern mining. The outer loop stops when there are no more candidates in ${\mathcal {C}}$.

Complexity of Mint. In the beginning, the number of candidates, i.e., pairs of elementary hyper-rectangles (line 4) is $O(min(|{\mathcal {H}}|^2, k \cdot |{\mathcal {H}}|))$, where $|{\mathcal {H}}|$ is the number of non-empty elementary hyper-rectangles. The number of elementary hyper-rectangles does not exceed the number of objects |G|. Thus, setting $k \ll |{\mathcal {H}}|$ we have the number of candidates $O(k \cdot |{\mathcal {H}}|) \sim (k \cdot |{G}|)$ which is linear w.r.t. the number of objects. Further, the number of hyper-rectangles can only decrease. Computing a candidate $h_j \oplus h_k$ takes O(|M|). The number of candidates added to ${\mathcal {C}}_{new}$ at each iteration of the inner loop is equal to $|{\mathcal {H}}| - 2$, $|{\mathcal {H}}| - 3$, etc. Thus, the total number of candidates is $O(|{\mathcal {H}}|^2)$. The total complexity of computing candidates is $O(|M|\cdot |{\mathcal {H}}|^2)$. Searching for the maximal gain among the candidates takes $O(|{\mathcal {H}}|^2)$ time. Since there can be at most ${\mathcal {H}}$ iterations, computing the maximal gain takes $O(|{\mathcal {H}}|^3)$. When adding a candidate to ${\mathcal {H}}$ we need to maintain the standard cover order of hyper-rectangles, that takes $O(\log |{\mathcal {H}}|)$. Moreover, recomputing the cover takes in the worse case $O(|{\mathcal {H}}||G|)$. Since the maximal number of candidates is $|{\mathcal {H}}|^2$, the cover recomputing increases the complexity of Mint by $O\big (|{\mathcal {H}}|^2 (\log |{\mathcal {H}}| + |{\mathcal {H}}||G|)\big )$.

In the worst case, where $|{\mathcal {H}}|=|G|$, the complexity is $O(|G|^2 (|M| + |{G}| + log|G| + |G| ^2)) \sim O(|G|^2|M| + |G|^4)$, however it is possible either to set a small number of initial intervals $|{\mathcal {B}}_i|$ ensuring $|{\mathcal {H}}|\ll |G|$ or to restrict the number of candidates.

Example 4

Let us consider how the algorithm works on the running example from Fig. 1.

Initially, the set of hyper-rectangles consists of elementary ones, i.e., $h_1, \ldots , h_7$ (Fig. 2). We restrict the set of candidates by considering only 2 nearest neighbor for each pattern (they are given in Fig. 2, left). Thus, the set of candidates is given by ${\mathcal {C}} = \{h_1 \oplus h_2, h_1 \oplus h_3, h_2 \oplus h_4, h_3 \oplus h_4, h_4 \oplus h_5, h_4 \oplus h_6, h_5 \oplus h_7, h_6 \oplus h_7\}$. In the cases, when the number of equidistant nearest neighbor is greater than k, we select k of them with the smallest indices.

The patterns are added in the following order: $h_8 = h_5 \oplus h_7$, $h_9 = h_4 \oplus h_6$, $h_{10} = h_1 \oplus h_3$, which corresponds to decreasing gain.

After that, set ${\mathcal {C}}$ does not contain candidates that can improve the total length. Thus, Mint proceeds by considering the candidates from ${\mathcal {C}}_{new} = \{h_j \oplus h_k \mid j, k = 2, 8, 9, 10, j \ne k\}$, which are the candidates composed of pairs of recently added patterns and the unused old ones. The newly added patterns are $h_{11} = h_{8} \oplus h_{9}$ and $h_{12} = h_{2} \oplus h_{10}$. The new candidate set is ${\mathcal {C}}_{new} = \{h_{11} \oplus h_{12}\}$. The algorithm terminates, the set of hyper-rectangles corresponding to the smallest total description length is ${\mathcal {H}} = \{h_{11}, h_{12}\}$.

Fig. 2

The sequential changes in the set of currently optimal patterns. The initial set of hyper-patterns is composed of elementary ones, i.e., $h_1, \ldots , h_7$

4.2.4 Greedy Mint (GMint)

The Mint algorithm can be not efficient in some situations because it requires recomputing the cover each time a new pattern enters the set ${\mathcal {H}}$. For reducing the computational time and reaching a better efficiency, the cover strategy proposed in § 4.2.2 and implemented in Algorithm 1 is approximated by using the same cover as in the estimate of $\varDelta L$, i.e., the cover of $h_j \oplus h_k$ is given by $cover(h_j \oplus h_k, G) = cover(h_j, G) \cup cover(h_k, G)$, and it remains unchanged for the other patterns in ${\mathcal {H}}$. The latter means that line 11 of Algorithm 2 is replaced with ${\mathcal {L}}_{new} = {\mathcal {L}}_{total} - \varDelta L$. This modification gives rise to the Greedy Mint (GMint) version of Mint and is the only difference between the both versions. Indeed, GMint does not recompute the covering but adjusts the cover only locally for the newly added patterns.

In terms of complexity, based on this optimized strategy, we get rid in the GMint version of the heaviest component of the complexity term in Mint, which is $O(|G|^2 (log|G| + |G| ^2))$. Then the total time complexity is $O(|G|^2 (|M| + |{G}|))$.

Comparison of complexity of GMint with other miners. The theoretical complexity of the algorithms related to (G)Mint algorithms is estimated based on different features. In RealKrimp, the size of the sampling s mainly affects the time complexity, the cost of computing the first hyper-rectangle is $O(|M|s^2\log s + |M||G|s)$, additional ones are mined in $O(|M|s^2 + |M||G|s)$. In the worst case, where the sample size is proportional to the number of objects, the time complexity is $O(|M||G|\log |G|)$ and $O(|M||G|^2)$ for the first and additional hyper-rectangles, respectively. In Mint the main component is the number of hyper-rectangles which is at most |G|, thus, the total time complexity is $O(|M||G|^2 + |G|^3)$. Thus, both RealKrimp and Slim have polynomial complexity w.r.t. the dataset size. Slim has the largest worst-case complexity $O(|{\mathcal {C}}|^3 |G||I|)$, where $|C|=O(2 ^{\min (|G|, |I|)})$ is the number of the candidates, which can be exponential in the size of the dataset. Moreover, the size of the dataset used in Slim is larger than the size of the dataset used by Mint and RealKrimp, since the number of attributes |I| in a binarized dataset is larger than the number of attributes |M| in the discretized one. Thus, RealKrimp and (G)Mint have polynomial complexity in the input size. However, in practice, GMint works much faster as shown in the experiments.

Fig. 3

Step-wise computing of the cover by Mint and GMint. The objects $\varvec{g_i}$ for which the cover is recomputed and added patterns $\varvec{h_i}$ are highlighted in bold

Example 5

Let us consider the difference in the cover strategy of Mint and GMint. According to the cover strategy used in Mint (§ 4.2.2), a newly added pattern is inserted in the list of patterns ordered w.r.t. the standard cover order. After insertion, the cover of data is recomputed starting from the first altered position in the pattern list. Depending on the position of insertion, there will be more recomputing if the pattern list is altered at the top and less recomputing if the list is altered at the bottom. It appears that recomputing is much more important for Mint than for GMint. In Fig. 3, we show the order of pattern insertion used by both algorithms to cover data. In bold we indicate the objects for which the cover is recomputed at each step and patterns which are added. As we can see, in both cases the hyper-rectangles cover the same objects, however Mint requires much more computational efforts. For example, at Step 1 in Mint, when $h_8$ is added, we need to recompute the cover for all patterns except for $h_4$ (which is at the top of the list), because the list is changed from the 2nd position. Meanwhile in GMint the cover is recomputed only for objects covered by $h_5$ and $h_7$, since they constitute a new pattern. In Appendix C we show in experiments that both strategies return almost the same pattern sets with almost the same compression quality, but Mint requires much more time.

5 Experiments

In this section, we compare Mint with Slim and RealKrimp –the most similar MDL-based approaches to numerical pattern mining.

Slim and RealKrimp are not fully comparable with our approach since they have their own parameters that actually affect both the performance and the quality of the results. Slim works with binarized data, while Mint and RealKrimp work with discretized data. However, Slim and Mint allow for choosing the number of discretization intervals. Slim is better adapted to mine patterns in datasets with a coarse discretization. A coarse discretization results in a moderate increase in the number of attributes, while a fine discretization usually results in a drastic increase and can make the task intractable. By contrast, Mint is able to mine patterns efficiently even in datasets with fine discretization. A last difference is that Slim and Mint evaluate a pattern set as a whole, while RealKrimp evaluates each pattern in a set independently.

In the experiments we report the results for GMint, as Mint provides the same results as GMint but requires more time. Moreover, Mint and GMint are qualitatively and quantitatively compared in Appendix C.

5.1 Datasets

We selected datasets from the UCI repository (Dua and Graff 2017) that are generally used in itemset mining, and discretized with the LUCS-KDD DN software (Coenen 2003). Since Mint implicitly discretizes datasets into equal-width intervals, we were compelled to use the same data discretization for other algorithms. The choice of the optimal number of intervals depends both on the chosen algorithm and the dataset. In experiments we do not tune the parameters specifically for each dataset and each algorithm. We considered the parameters that work generally well for the considered algorithms, namely splitting into 5 intervals (as in LUCS-KDD repository, where the number of intervals is limited to 5 for each attribute) and into $\sqrt{|G|}$.

Since the proposed discretization into 5 intervals may be non-optimal, we also use IPD discretization, which is expected to provide only necessary discretization intervals, thus should be the most suitable for Slim. Moreover, as Slim deals with binary data, we additionally transform each discretization interval into a binary attribute. The parameters of the real-world datasets are given in Table 2.

5.2 Parameters of the algorithms

The discretization described above (into 5, $\sqrt{|G|}$ itervals) is performed in Mint implicitly, thus is set as a parameter. We set the number of neighbors, considered for computing candidates, to be equal to the number of intervals. The performance of Mint with other parameters is reported in Appendix E.

RealKrimp relies on a set of parameters, the most important among them are sample size, perseverance, and thoroughness. Sample size defines the size of the dataset sample that will be used to compute patterns. We consider samples of size $\sqrt{|G|}$, 0.25|G| and 0.5|G|. The sample size affects the running time: the smaller samples allow for faster pattern mining operations, while too small samples may prevent to discover interesting patterns. Perseverance regulates the behavior of RealKrimp to reach a global minimum of the description length. Large values of perseverance help to reach a global minimum. Perseverance is then set to 1/5 of the sample size. Thoroughness is the maximal number of consecutive non-compressible hyper-intervals that should be considered. We set thoroughness equal to 100.

Table 2 Description of datasets and the parameters of the discretization (applicable to Mint and Slim) and the compression ratio of Mint. All attributes are numerical

5.3 Compression ratio

Firstly, we consider the main quality measure of the MDL-based methods, namely compression ratio. Since Mint is not comparable to other pattern mining approaches, namely Slim and RealKrimp, we report only the compression ratio of Mint in Table 2 (the lower values, the better). Mint provides the best compression for the data discretized into $\sqrt{|G|}$ intervals. High compression ratio (worse compression) for data discretized into 5 intervals is quite expected, since this coarse discretization provides large elementary hyper-rectangles that cannot be compressed efficiently. For IPD discretized data, high compression ratios may indicate that the IPD-discretization grid splits the space into hyper-rectangles that Mint considers as separate patterns and does not compress further, while low compression ratios indicate the cases where IPD returns hyper-rectangles that can be further efficiently compressed by Mint.

We report the compression ratios for other methods and discuss the issues related to their incomparability in Appendix D.

5.4 Running time

The running time is reported in Table 3. The cases where pattern sets are not computed are indicated in the table with “$\ldots$”. The performance of Slim and Mint is affected by the number of discretization intervals, while the performance of RealKrimp depends heavily on the sample size.

The running time show that for small datasets ($<1k$) all methods work fast and often complete the work in less than a second. For average-sized ($<50k$) and large ($>50k$) datasets the running time depends on the chosen parameters. Slim mines fast patterns in datasets with a coarse discretization (into 5 intervals). However, for fine discretizations (into $\sqrt{|G|}$ or IPD) the running time increases drastically. For example, for “shuttle” dataset, Slim terminates in 1 second, when the number of intervals is 5, while when the attribute ranges are split into $\sqrt{|G|}$ intervals and by IPD, Slim requires 17394 and 650 seconds, respectively. Again for Slim, the scalability issues are especially pronounced for datasets with a large number of attributes, e.g., for “gas sensor” dataset, Slim terminates in 8206, ...,¹ and 72488 seconds, while Mint requires only 5, 956, and 54 seconds for the same discretization parameters.

RealKrimp also suffers from poor scalability: for average- or large-sized datasets, setting a small sample size, e.g., $\sqrt{|G|}$, does not allow to find a sufficient amount of interesting patterns, while setting a reasonable sample size (0.25|G| or 0.5|G|) results in a drastic increase of the running time and memory requirement.

Our experiments show that Mint, dealing with the same discretization as Slim, requires less time to mine patterns, especially for large datasets. However, it is not enough to assess the performance of the patterns by considering their running time. It is also important to study how many patterns they return and which kind of patterns.

Table 3 Running time, in seconds, of Slim and Mint and RealKrimp

5.5 Number of MDL-selected patterns

Intuitively, the number of patterns should be small but enough sufficient to describe all interesting relations between attributes. The number of MDL-selected patterns for the studied methods is reported in Table 4. The table shows that, given the same discretization, Slim returns usually a larger number of patterns than Mint. As with the running time, Slim is sensitive to a large number of attributes and in this case usually returns a much larger number of patterns than Mint. For example, for “gas sensor” dataset Slim returns 1608, ...,² and 9554 patterns, while Mint, with the same discretization settings, returns only 306, 571 and 897 patterns, respectively.

RealKrimp, on the contrary, returns a much smaller number of patterns than Mint and Slim. For example, for “gas sensor” dataset it returns only 4, 30, and 49 patterns for samples of size $\sqrt{|G|}$, 0.25|G|, and 0.5|G|, respectively. Taking into account the running time, we can conclude that with the chosen parameters, the average running time per pattern is much larger for RealKrimp than for Slim and Mint. Thus, RealKrimp has the highest “cost” in seconds of generating a pattern.

Table 4 The number of MDL-selected patterns by Slim and Mint for discretization into 5, $\sqrt{|G|}$ intervals and the IPD discretization

Now, let us examine the quality of the generated patterns.

5.6 Pattern similarity (redundancy)

Pattern similarity is particularly important for RealKrimp, where patterns are mined w.r.t. other patterns, but evaluated independently, and there are no guarantee of avoiding the selection of very similar patterns. To study pattern similarity, we consider the average pairwise Jaccard similarity computed w.r.t. the sets of objects that the patterns describe. We take into account all occurrences of patterns in data rather than their usage in the data cover (which is, by definition, non-redundant).

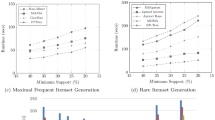
However, the average pairwise Jaccard similarity applied to a large pattern set may not be able to spot “local” redundancy, i.e., when there is a small subsets of almost the same patterns. To tackle this issue, we consider instead for each pattern we select at most 10 patterns among the most similar patterns w.r.t. Jaccard similarity and report the average value (removing the repetitive pairs if they appear). The average values of similarity are presented in Fig. 4a.

Fig. 4

The average values of quality measures

The results of the experiments show that on average the pairwise Jaccard similarity is the smallest for Mint, and only slightly higher for Slim. In Slim higher values are caused by the fact that each object can be covered by different non-overlapping itemsets, thus these increased values of the Jaccard similarity are partially caused by the specificity of the model. RealKrimp has the largest values of the Jaccard similarity, close to 1 (see Fig. 4a). This result is quite expected since the patterns are evaluated independently, thus the method does not minimize redundancy in the pattern set.

5.7 Purity of patterns

To evaluate the significance of the resulting patterns, we measure their purity by considering the classes of objects they describe. The class labels are not used during pattern mining and are considered only for assessing the pattern quality. We assign to a pattern a label of the majority class of objects described by it. In Fig. 4b we show the accuracy patterns computed based on objects the pattern describes. The results show that Slim and Mint, being based on the same discretizations, have quite similar average accuracy. RealKrimp return patterns with high accuracy for small datasets, however, loses in accuracy on large datasets.

5.8 Accuracy of pattern descriptions

As it was mentioned in the introduction, in pattern mining it is important not only to describe meaningful groups of objects but also to provide quite precise boundaries of these groups. Unfortunately, we cannot evaluate how precise are the pattern boundaries for the real-world datasets since we do not have any ground truth patterns.

To evaluate the precision of pattern boundaries of patterns we use synthetic datasets. We generate 6 types of 2-dimensional datasets with different numbers of patterns and different positions of patterns w.r.t. other patterns, shown in Fig. 5. The detailed parameters of the synthetic datasets are given in the extended version of the paper. The ground truth patterns are highlighted in different colors. Further, we use ${\mathcal {T}}$ to denote a set of ground truth hyper-rectangles. For all these types of data, we generate datasets where each pattern contains 100, 200, 500, 700, 1000 objects.

In Fig. 5, the “simple” datasets consist of separable patterns. The “variations” datasets contain adjacent patterns and thus allow for variations in pattern boundaries. The “inverted” datasets include the most complicated patterns for Mint and Slim since they treat asymmetrically dense and sparse regions. It means that these algorithms are not able to identify the hole in the middle. Instead of this hole, we may expect a complicated description of the dense region around this hole. “Simple overlaps” contains overlapping patterns, while “simple inclusion” and “complex inclusion” can also contain patterns that are subsets of other patterns.

Fig. 5

Six types of generated synthetic dataset

For synthetic datasets we use the same settings as for real-world datasets, i.e., discretization into 5, $\sqrt{|G|}$ intervals, and IPD discretization (for Mint and Slim) and the default settings from (Witteveen 2012) for RealKrimp.

We evaluate the quality of patterns using the Jaccard similarity applied to hyper-rectangles. For two hyper-rectangles $h_1$ and $h_2$ the Jaccard similarity is given by $Jaccard(h_1, h_2) = {area(h_1 \cap h_2)}/{area(h_1 \oplus h_2)}$, where $h_1 \cap h_2$ and $h_1 \oplus h_2$ is the intersection and join of $h_1$ and $h_2$, respectively.

Fig. 6

Average Jaccard similarity of hyper-rectangles

We begin with the average pairwise Jaccard similarity of the computed patterns:

$$\begin{aligned} Jcd({\mathcal {H}}) = \frac{\sum _{h_i, h_j \in {\mathcal {H}}, i \ne j}Jaccard(h_1, h_2)}{0.5|{\mathcal {H}}|(|{\mathcal {H}}| - 1)}. \end{aligned}$$

The values reported in Fig. 6 show that Slim returns non-redundant patterns since they are non-overlapping, while RealKrimp returns very similar patterns. These patterns are redundant since even for the “simple” datasets, where all ground truth patterns are separable and non-overlapping, the patterns returned by RealKrimp are very similar. The similarity of Mint-selected patterns is very low, but it increases for the datasets with overlapping patterns, e.g., “simple overlaps” or “simple inclusion”, and is almost 0 for the datasets with non-overlapping patterns, e.g., “simple” or “variations”.

The next question is how well the boundaries of the computed patterns from ${\mathcal {H}}$ are aligned with the boundaries of the ground truth patterns from ${\mathcal {T}}$, i.e., the patterns that we generated.

To compute Jaccard similarity between two different pattern sets ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$ we take into account for each $h_1 \in {\mathcal {H}}_1$ only the most Jaccard-similar pattern $h_2 \in {\mathcal {H}}_2$:

$$\begin{aligned} Jcd({\mathcal {H}}_1, {\mathcal {H}}_2) = \frac{\sum _{h_1 \in {\mathcal {H}}_1} \max _{h_2 \in {\mathcal {H}}_2}Jaccard(h_1, h_2)}{|{\mathcal {H}}_1|}. \end{aligned}$$

(4)

The idea behind this measure is to assess how similar the “matched” pairs from ${\mathcal {H}}_1$ and ${\mathcal {H}}_2$. This measure asymmetric.

In Fig. 6 we show the average values of $Jcd({\mathcal {H}}, {\mathcal {T}})$ and $Jcd({\mathcal {T}}, {\mathcal {H}})$. The values of $Jcd({\mathcal {H}}, {\mathcal {T}})$ close to 1 indicate that all computed patterns are very similar to patterns given in ground truth. The worst results corresponds to Slim: even with a “smart” IPD discretization, the boundaries computed by Slim are not very precise. The low values for fine discretized data are explained by the inability of Slim to merge elementary hyper-rectangles.

Mint with IPD-discretization returns also quite poor results. However, in the best settings (discretization into $\sqrt{|G|}$ intervals), Mint and RealKrimp have quite high values of $Jcd({\mathcal {H}}, {\mathcal {T}})$. The latter means that all patterns from ${\mathcal {H}}$ are quite similar to the patterns given by ground truth.

The values $Jcd({\mathcal {T}}, {\mathcal {H}})$ close to 1 correspond to the case where each ground truth pattern has at least one pattern in ${\mathcal {H}}$ that is very similar to ground truth patterns. The results show that the quality of Mint-generated patterns for the default discretization into $\sqrt{|G|}$ intervals is the best. For some datasets RealKrimp works equally well, e.g., “simple overlaps” or “simple inclusion”, but for others, it may provide quite bad results, e.g., for the simplest set of patterns contained in the “simple” datasets.

Comparing the values of $Jcd({\mathcal {H}}, {\mathcal {T}})$ and $Jcd( {\mathcal {T}}, {\mathcal {H}})$ we may conclude that RealKrimp returns a lot of similar patterns, but these patterns do not match the ground truth patterns as well as the patterns generated by Mint. Thus, the experiments show that Mint (with a fine discretization) returns patterns with quite precise boundaries and outperforms the state-of-the-art MDL-based pattern miners.

6 Visualization of some hyper-rectangles for synthetic data

Despite the fact that Jaccard similarity describes well the quality of patterns ${\mathcal {H}}$ and their alignments with ${\mathcal {T}}$, it does not allow to examine patterns entirely. In Fig. 7 we show the patterns computed by Slim, RealKrimp, and Mint, when applied to the “simple inclusion” dataset with 3 ground truth patterns having support equal to 200. The patterns for other datasets, due to limited space, are reported in the extended version of the paper.³

As it can be seen, Slim returns patterns that are completely determined by the chosen discretization. This is a typical limitation of itemset mining algorithms when applied to numerical data.

Mint returns 5 patterns. Among them two patterns that correspond exactly to the ground truth patterns and the remaining three patterns describe the smallest ground truth pattern. Nevertheless, their join gives a quite correct pattern. RealKrimp distinguishes only 2 patterns correctly and at the same time it returns a lot of similar patterns. Indeed the number of patterns discovered by RealKrimp is 18 while the number of the ground truth patterns is only 3. Then it is quite hard for RealKrimp to find a good combination of patterns allowing the reconstruction of the third pattern. It can be concluded that redundant patterns are raising a more important problem for RealKrimp than for Mint.

Fig. 7

The results of pattern mining for “Simple inclusion” dataset, support of the ground truth patterns is 200

For all other datasets we observe quite the same behavior. Slim returns very imprecise patterns, whose quality depends on the quality of the discretization grid. RealKrimp returns well-aligned patterns within a large number of very similar patterns. By contrast, Mint returns a reasonable number of patterns, which are less redundant than those returned by RealKrimp, and usually quite well aligned with the ground truth patterns.

7 Discussion and conclusion

In this paper we propose a formalization of numerical pattern set mining problem based on MDL principle and we focus on the following characteristics: (i) interpretability of patterns, (ii) precise pattern descriptions, (iii) non-redundancy of pattern sets, and (iv) scalability. In the paper we study and materialize these characteristics, and we also propose a working implementation within a system called Mint.

By “interpretability” we mean not only the ability to explain why a particular pattern is selected, but also the ease of analyzing a set of discovered numerical patterns for a human agent. With this regard, patterns of arbitrary shapes or even polygons may be not an appropriate choice when considering multidimensional numerical data. This is why we decided to work with one of the most common shapes, namely “hyper-rectangles”, which are currently used in numerical pattern mining and related tasks.

Another important requirement is that the boundaries of patterns should be “well-defined” and “quite precise”. By contrast, a common approach to numerical pattern mining consists in data discretization and binarization followed by reduction to itemset mining. Such an approach suffers from various drawbacks among which (i) the boundaries of patterns are not well-defined and this heavily affects the output, (ii) the scalability is not good because of the potential exponential number of attributes due to scaling, (iii) the information loss related to the loss of the interval order within a range may be very important.

In our experiments we compare the behavior of Mint with the MDL-based itemset set miner Slim (associated with a scaling of numerical data). The experiments demonstrate that Slim generally provides quite poor patterns. Actually, when the discretization is too fine, Slim is not able to merge patterns into larger patterns, while when the discretization is too coarse the algorithm returns very imprecise boundaries. In addition, we also consider another MDL-based algorithm, namely RealKrimp, which is, to the best of our knowledge, the only MDL-based approach dealing with numerical pattern mining without any prior data transformation. However, one main limitation of RealKrimp is that it mines patterns individually and then the resulting patterns are very redundant.

Furthermore, in the experiments, both RealKrimp and Slim show a poor scalability. Mint may also have a high running time for some large datasets, but in staying still at a reasonable level. Mint may be correlated with IPD –for “Interaction-Preserving Discretization”– but both systems perform different tasks. Mint could work in combination with IPD since the latter does not return exactly patterns but mainly MDL-selected boundaries. The elementary hyper-intervals induced from IPD results are only fragments of ground truth patterns. Then Mint could be applied to merge these elementary hyper-rectangles into larger hyper-rectangles.

Indeed, our experiments show that the data compressed by IPD can be even more compressed in applying Mint, i.e., the patterns as computed by IPD should still be completed for being comparable to those discovered by Mint. However, as the experiments show, directly applying Mint to fine discretized data allows to obtain better results than applying IPD as a preprocessing step. This can be explained by the fact that IPD returns uniform or global boundaries, which are less precise than the boundaries specifically “tuned” by Mint for each pattern.

For summarizing, the Mint algorithm shows various very good capabilities w.r.t. its competitors, among which a good behavior on fine discretized datasets, a good scalability, and an output of a moderate including non-redundant patterns with precise boundaries. However, there is still room for improving Mint, for example in avoiding redundant patterns and in the capability of mining sparse regions in the same manner as dense ones.

Future work may be followed in several directions. Here, Mint works with an encoding based on prequential plug-in codes. It could be interesting to reuse another encoding and to check how the performance of the system evolve, trying to measure what is the influence of the encoding choice. Moreover, we should consider more datasets and especially large and complex datasets, and try to measure the limit of the applicability of Mint, for in turn improving the algorithm in the details. In general, more experiments should still be considered for improving the quality of Mint. Another interesting future direction is to use Mint in conjunction with a clustering algorithm. This could be a good way of associating descriptions or patterns with classes of individuals discovered by a clustering process. In this way a description in terms of attribute and ranges of values could be attached to the discovered clusters and complete the definition of the set of individuals which are covered. This could be reused in ontology engineering for example, and as well in numerous tasks where clustering is heavily used at the moment.

Appendices

Appendix A Derivation of the plug-in codes

Let $H^n$ be the sequence $h^1, \ldots , h^{n-1}, h^{n}$. The idea of the prequential codes is to assess the probability of observing the n-th element $h^n$ of the sequence $H^n$ based on the previous elements $h^1, \ldots , h^{n-1}$: $P_{plug\text{- }in}(h^n) = \prod _{i=1}^{n}P(h^i | h ^{i-1}).$

Initially, a uniform distribution over ${\mathcal {H}}$ is defined with a pseudo-count $\varepsilon$ over the set of patterns ${\mathcal {H}}$, i.e., the probability of $h^0$ is given by $P(h^0) = \frac{\varepsilon }{\varepsilon \cdot |{\mathcal {H}}|}$. Then, during the process of transmitting/receiving messages, the pattern probabilities and lengths are updated w.r.t. the patterns observed so far.

At each single step, the distribution P over ${\mathcal {H}}$ is multinomial with parameters $(\theta _{1}, \ldots , \theta _{|{\mathcal {H}}|})$, where $\theta _{i}$ corresponds to a pattern $h_i \in {\mathcal {H}}$. With the subscript indices we arbitrarily enumerate patterns in ${\mathcal {H}}$. The superscript indices denote the sequence number of patterns in the transmitting sequence. Further, we will see that the order of patterns in the sequence $h^1, \ldots , h^n$ does not affect the length of the encoded sequence. This length depends only on the number of times each pattern appears in the sequence.

Taking into account the initial probabilities, the maximum-likelihood estimates of the parameters of the multinomial distribution, given the sequence $H^n = h^1\ldots h^n$, are the following:

$$\begin{aligned} {\hat{\theta }}_{h^n}(h) = \frac{usg(h |h^1 \ldots h^n) + \varepsilon }{\sum _{h^*\in {\mathcal {H}}}usg(h^*| h^1 \ldots h^n) + \varepsilon |{\mathcal {H}}|}, \end{aligned}$$

(5)

where $usg(h | h^1 \ldots h^n)$ is the number of occurrences of pattern h in the sequences observed so far (up to the n-th pattern included). The maximum likelihood (ML) estimates from Equation 5 are equivalent to the probability estimates of a pattern h based on its frequency in $H^h$ with Laplace smoothing having parameter $\varepsilon$ (Manning et al. 2008).

Thus, taking as the probability model the multinomial distribution with the parameters estimated according to the ML principle, the plug-in probability of the n-th pattern in the sequence $H^n$ is given by

$$\begin{aligned} P_{plug\text{- }in}(h^n) = \prod _{i = 1}^{n}P(h^i |h ^{i-1}) = \prod _{i = 1}^{n}P_{{\hat{\theta }}_{h^{i-1}}}(h^i). \end{aligned}$$

(6)

Combining together Equations 5 and 6 we obtain the following probability of the n-th pattern $h^n \in {\mathcal {H}}$ in the pattern sequence $H^n$:

$$\begin{aligned} P_{plug\text{- }in}(h^n) = \frac{\prod _{h \in {\mathcal {H}}} \prod _{j = 0}^{usg(h) - 1}(j + \varepsilon )}{\prod _{j = 0}^{usg({\mathcal {H}}) - 1}(j + \varepsilon |{\mathcal {H}}|)} = \frac{\prod _{h \in {\mathcal {H}}} \varGamma (usg(h) + \varepsilon ) / \varGamma (\varepsilon )}{\varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|)/\varGamma (\varepsilon |{\mathcal {H}}|)}, \end{aligned}$$

(7)

where usg(h) is the number of patterns in $H^n$, and $usg({\mathcal {H}}) = \sum _{h \in {\mathcal {H}}} usg(h)$ is the length of the sequence, i.e., the total number of occurrences of patterns from ${\mathcal {H}}$, and $\varGamma$ is the gamma function. Then, the code length of $h^n$ is

$$\begin{aligned} l(h^n)&= -\log P_{plug\text{- }in}(h^n) = \sum _{i = 1}^{n} - log P_{{\hat{\theta }}_{H^{i-1}}}(h^i) \\&=\log \varGamma (usg({\mathcal {H}}) + \varepsilon |{\mathcal {H}}|) - \log \varGamma (\varepsilon |{\mathcal {H}}|) \\&\quad - \sum _{h \in {\mathcal {H}}}\left[ \log \varGamma (usg(h) + \varepsilon ) - \log \varGamma (\varepsilon )\right] . \end{aligned}$$

The length $l(h^n)$ can be interpreted as the sum of the log loss of the prediction errors made by sequentially predicting $h^{i}$ based on the predictor in the family of multinomial distributions over ${\mathcal {H}}$ that would have been the best for sequentially predicting the previous patterns $h^1, \ldots , h^{i-1}$.

Appendix B The ML estimates of the parameters of the multinomial distribution

Let ${\mathcal {H}}$ be a set of n patterns, i.e., $n = |{\mathcal {H}}|$ and $x_i$ be the number of times $h_i \in {\mathcal {H}}$ appears in the sequence of patterns of length N. Then, the probability of the multinomial distribution for the given sequence has the following form:

$$\begin{aligned} p(x_1, \ldots , x_n \mid p_1, \ldots , p_n) = \frac{N!}{x_1! \ldots x_n!} \prod _{i = 1}^{n}p_i ^{x_i}. \end{aligned}$$

The log-likelihood function then is the following:

$$\begin{aligned} \ell (p_1, \ldots , p_n) = \log (N!) - \sum _{i = 1}^{n}\log (x_i!) + \sum _{i = 1}^{n} x_i \log (p_i). \end{aligned}$$

To find the ML estimates we need to maximize this function w.r.t. $p_1, \ldots , p_n$ given the constraint on the probabilities $\sum _{i = 1}^{n}i = 1$. Applying the methods of Lagrange multipliers we get the following equation:

$$\begin{aligned} {\mathcal {L}}(p_1, \ldots , p_n, \lambda ) = \ell (p_1\ldots , p_n) + \lambda (1 - \sum _{i = 1}^{n} (p_i)). \end{aligned}$$

Thus

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\mathcal {L}}}{\partial p_i} = \frac{x_i}{p_i} - \lambda = 0, i = 1, \ldots , n\\ \frac{\partial {\mathcal {L}}}{\partial \lambda } = 1 - \sum _{i = 1}^{n}p_i = 0 \end{array}\right. } \end{aligned}$$

Taking into account the pseudo-counts, we get $x_i = usg(h_i) + \varepsilon$, where $usg(h_i)$ is the number of times the pattern $h_i$ appears in the sequence.

Thus,

$$\begin{aligned} {\left\{ \begin{array}{ll} p_i = \frac{usg(h_i) + \varepsilon }{\lambda }, i = 1, \ldots , n\\ \sum _{i = 1}^{n}p_i = 1 \end{array}\right. } \end{aligned}$$

Putting the last equation into the first one we get $p_i = \frac{usg(h_i) + \varepsilon }{\sum _{i = 1}^{n}{usg(h_i}) + \varepsilon |{\mathcal {H}}|}$.

Appendix C Mint vs GMint

We compare the results of Mint and GMint w.r.t. the main characteristics, namely the number of patterns, the running time, and the compression ratio, for datasets discretized into 5, $\sqrt{|G|}$ intervals, and IPD-based discretization. The results are given in Table 5. We report values in the format $x \pm y$, where x is for GMint, and $x \pm y$ is for Mint. For example, for “breast wisconsin”, GMint returns 54 patterns while Mint returns 5 patterns more, thus 59. The running time of GMint is 0 seconds while the running time of Mint is 97 seconds longer. The compression ratio is 31% for both methods.

The results show that for the default settings (the number of intervals and neighbors is equal to $\sqrt{|G|}$), both algorithms return almost the same number of patterns, the compression ratio for GMint is greater than for Mint by less than 1%. However, the execution time for middle-sized datasets is drastically smaller for GMint.

In the other discretization settings, GMint returns a smaller number of patterns with almost the same compression ratio and it takes much shorter time. A smaller number of patterns in GMint can be explained by the following. In GMint the estimate of the length gain $\varDelta L$ (line 8 in Algorithm 2) is equal to the actual length gain, while in Mint we recompute the cover, and thus the actual gain can be different. Thus, when we check the condition $\varDelta L > 0$ in line 8 in GMint, the gain is exactly $\varDelta L$ and then patterns $h_j$ and $h_k$ ensuring this gain are merged, while in Mint the total length computed in line 11 can be longer, i.e., the actual gain is negative, and then patterns $h_j$ and $h_k$ are not merged.

Table 5 The number of selected patterns (# patt.), running time, and compression ratio (in percents). The characteristics are reported as $x \pm y$, where x is for GMint and $x \pm y$ for Mint

Apeendix D Compression ratio of the MDL-based pattern miners

RealKrimp mines each pattern independently from others, thus the compression ratio of a pattern set is not measurable. Slim and Mint have different encoding schemes and compress binary and discretized datasets, respectively. Thus the compression ratios are not fully comparable. However, for the sake of completeness, we report the compression ratios that they provide in Fig. 8. As it is expected, Slim works better in the case of a coarse discretization. For example, for equal-width discretization into 5 intervals, Slim provides a much better compression than Mint for datasets such as “aliva”, “shuttle”, “sensorless dd”, and “mini”. However, Mint works consistently better for fine discretized datasets (Fig. 8 in the middle, where the number of intervals is $\sqrt{|G|}$). This can be explained by the fact that IPD and Mint compress the same dataset, while Slim uses an additional binarization step and compresses a dataset containing less information, i.e., in a binarized dataset the interval order is not preserved. For IPD-discretized data, Slim often ensures a better compression. This can be explained by the fact that IPD compresses the same data as Mint, and Mint may be unable to compress further the same dataset. By contrast Slim compresses a dataset that was additionally binarized. Thus, the better compression of Slim may be partially explained by artifacts caused by this data transformation.

Fig. 8

Compression ratios of Slim and Mint for different discretizations (into 5 intervals, $\sqrt{|G|}$ and by IPD discretizer), the smaller values are better

Fig. 9

The ratio of the total description length of Slim by the total description length Mint. The values close to 1 (horizontal line) corresponds to the cases where the total description lengths provided by both methods are almost the same

Another important characteristic of MDL-based approaches is the total description length resulting from compression. Because of the different forms of data used by Slim and Mint (binary and discrete, respectively), the algorithms may have quite different compressed total description lengths.

Nevertheless, we report them. The ratio of the total length of Slim by the total length of Mint is given in Fig. 9. As in the case of the compression ratio, RealKrimp does not allow computing the total length of data encoded by a pattern set, as it computes only length gains provided by single patterns. Fig. 9 shows that the total length of Slim is usually about 2 times greater than the total length of Mint. The latter can be explained, in particular, by the redundancy caused by data binarization. Then it can be concluded that the encoding of discretized data provided by Mint is more concise than the encoding of the binarized data used in Slim.

Appendix E Optimal Optimal number of intervals and neighbors

In Mint we use two parameters that can affect the results: the number of discretization intervals and the number of neighbors used to compute the candidates. For a dataset with |G| objects and |M| attributes, we consider the following numbers: (i) 5, $0.5 \sqrt{|G|}$, $\sqrt{|G|}$, $2 \sqrt{|G|}$ discretization intervals, and (ii) 5, $0.5 \sqrt{|G|}$, $\sqrt{|G|}$, $2 \sqrt{|G|}$, $0.5 \sqrt{|G||M|}$, $\sqrt{|G||M|}$, $2 \sqrt{|G||M|}$ nearest neighbors.

Fig. 10

Average compression ratio, number of patterns, and running time of real-world (top) and synthetic (bottom) dataset for different combinations of the parameters of Mint

Then we evaluate the performance of Mint regarding compression ratio, number of patterns, and running time. In Fig. 10 we show the average values for 9 real-world datasets (“iris”, “waveform”, “wine”, “breast wisconsin”, “spambase”, “parkinsons”, “haberman”, “ecoli”, “statlog satimage”) and for 30 synthetic datasets (6 types of datasets given in Fig. 5, each type has 5 versions where patterns have support 100, 200, 500, 700, and 1000).

The first figure has one dark horizontal line corresponding to discretization into 5 intervals and different numbers of neighbors. For such a coarse discretization, Mint compresses quite bad as the compression ratio is around 0.45. For finer discretizations, i.e., into $0.5\sqrt{|G|}$, $\sqrt{|G|}$, and $2\sqrt{|G|}$ in the next 3 light-blue horizontal lines, the compression ratio is around 0.40 and does not changes a lot when the number of candidates changes (i.e., the colors on the horizontal line do not change a lot).

For finer discretized datasets the number of neighbors does not affect a lot the results. It appears that with a large number of discretized intervals, the results of Mint are less affected by the chosen heuristics.

Taking into account the considered three characteristics, the best and the most “stable” results in the shortest time are achieved by splitting the attribute range into $\sqrt{|G|}$ intervals and by taking $\sqrt{|G|}$ nearest neighbors to compute pattern candidates.