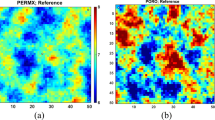
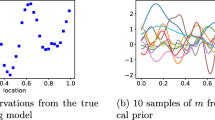
Abstract
In the strong-constraint formulation of the history-matching problem, we assume that all the model errors relate to a selection of uncertain model input parameters. One does not account for additional model errors that could result from, e.g., excluded uncertain parameters, neglected physics in the model formulation, the use of an approximate model forcing, or discretization errors resulting from numerical approximations. If parameters with significant uncertainties are unaccounted for, there is a risk for an unphysical update, of some uncertain parameters, that compensates for errors in the omitted parameters. This paper gives the theoretical foundation for introducing model errors in ensemble methods for history matching. In particular, we explain procedures for practically including model errors in iterative ensemble smoothers like ESMDA and IES, and we demonstrate the impact of adding (or neglecting) model errors in the parameter-estimation problem. Also, we present a new result regarding the consistency of using the sample covariance of the predicted nonlinear measurements in the update schemes.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Bennett, A.F.: Inverse Methods in Physical Oceanography. Cambridge University Press (1992)
Bocquet, M., Sakov, P.: Joint state and parameter estimation with an iterative ensemble Kalman smoother. Nonlinear. Processes. in. Geophysics., European Geosciences Union (EGU) 20(5), 803–818 (2013)
Bocquet, M., Sakov, P.: An iterative ensemble Kalman smoother. Q.. J.. R.. Meteorol.. Soc.. 140, 1521–1535 (2014)
Carrassi, A., Vannitsem, S.: Deterministic treatment of model error in geophysical data assimilation. In: Ancona, F, Cannarsa, P, Jones, C, Portaluri, A (eds.) Mathematical Paradigms of Climate Science, Springer INdAM Series, vol. 15, pp 175–213. Springer, Cham (2016)
Chen, Y., Oliver, D.S.: Ensemble randomized maximum likelihood method as an iterative ensemble smoother. Math. Geosci. 44, 1–26 (2012)
Chen, Y., Oliver, D.S.: Levenberg-Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification. Computat. Geosci. 17, 689–703 (2013)
Eknes, M., Evensen, G.: Parameter estimation solving a weak constraint variational formulation for an Ekman model. J. Geophys. Res. 102(C6), 12.479–12.491 (1997)
Emerick, A.A., Reynolds, A.C.: History matching time-lapse seismic data using the ensemble Kalman filter with multiple data assimilations. Computat. Geosci. 16(3), 639–659 (2012)
Emerick, A.A., Reynolds, A.C.: Ensemble smoother with multiple data assimilation. Comput. Geosci. 55, 3–15 (2013)
Evensen, G.: Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 99(C5), 10.143–10.162 (1994)
Evensen, G.: The ensemble Kalman filter: theoretical formulation and practical implementation. Ocean. Dyn. 53, 343–367 (2003)
Evensen, G: Data Assimilation: The Ensemble Kalman Filter, 2nd edn. Springer (2009)
Evensen, G.: The ensemble Kalman filter for combined state and parameter estimation. IEEE Control. Syst. Mag. 29(3), 83–104 (2009b)
Evensen, G.: Analysis of iterative ensemble smoothers for solving inverse problems. Computat. Geosci. 22(3), 885–908 (2018). https://doi.org/10.1007/s10596-018-9731-y
Evensen, G., Eikrem, K.S.: Strategies for conditioning reservoir models on rate data using ensemble smoothers. Computat. Geosci. 22(5), 1251–1270 (2018). https://doi.org/10.1007/s10596-018-9750-8
Evensen, G., van Leeuwen, P.J.: Assimilation of Geosat altimeter data for the Agulhas current using the ensemble Kalman filter with a quasi-geostrophic model. Mon. Weather. Rev. 124, 85–96 (1996)
Harlim, J.: Model error in data assimilation. In: Franzke, C (ed.) Nonlinear and Stochastic Climate Dynamics. also available as arXiv:abs/1311.3579. Cambridge University Press, Cambridge (2017)
Kitanidis, P.K.: Quasi-linear geostatistical therory for inversing. Water. Resour. Res. 31(10), 2411–2419 (1995)
Neal, R.M.: Sampling from multimodal distributions using tempered transitions. Stat. Comput. 6(4), 353–366 (1996)
Oliver, D.S., He, N., Reynolds, A.C.: Conditioning permeability fields to pressure data. In: ECMOR – 5th European Conference on the Mathematics of Oil Recovery (1996)
Reynolds, A.C., Zafari, M., Li, G: Iterative forms of the Ensemble Klman Filter. In: ECMOR – 10th European Conference on the Mathematics of Oil Recovery (2006)
Sakov, P., Oliver, D.S., Bertino, L.: An iterative EnKF for strongly nonlinear systems. MonWeather. Rev. 140, 1988–2004 (2012)
Sakov, P., Haussaire, J.M., Bocquet, M.: An iterative ensemble Kalman filter in the presence of additive model error. Q. J. R. Meteorol. Soc. https://doi.org/10.1002/qj.3213 (2018)
Stordal, A., Elsheikh, A.H.: Iterative ensemble smoothers in the annealed importance sampling framework. Adv. Water. Resour. 86, 231–239 (2015)
Acknowledgements
The work has benefited from the interaction and collaborations with the Nordforsk Nordic center of excellence in data assimilation, EMBLA. In-depth discussions with Patrick Raanes, regarding the linear-regression derivation, have helped to improve the manuscript, and the author is also grateful for comments by Geir Nævdal and Alberto Carrassi on early versions of the manuscript. Constructive comments by three anonymous reviewers lead to the inclusion of a section on how to practically account for model errors in reservoir history matching and the section on the specification of model errors.
Funding
This work was supported by the Research Council of Norway and the companies AkerBP, DEA, ENI, Petrobras, Equinor, Lundin, and Neptune Energy, through the Petromaks–2 project DIGIRES.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Evensen, G. Accounting for model errors in iterative ensemble smoothers. Comput Geosci 23, 761–775 (2019). https://doi.org/10.1007/s10596-019-9819-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10596-019-9819-z