Abstract
The 2015 Paris Agreement commits countries to pursue efforts to limit the increase in global mean temperature to 1.5 °C above pre-industrial levels. We assess the consequences of achieving this target in 2100 for the impacts that are avoided, using several indicators of impact (exposure to drought, river flooding, heat waves and demands for heating and cooling energy). The proportion of impacts that are avoided is not simply equal to the proportional reduction in temperature. At the global scale, the median proportion of projected impacts avoided by the 1.5 °C target relative to a rise of 4 °C ranges between 62 and 95% across sectors: the greatest reduction is for heat wave impacts. The 1.5 °C target results in impacts that would be between 27 and 62% lower than with the 2 °C target. For each indicator, there are differences in the proportions of impacts avoided between regions depending on exposure and the regional changes in climate (particularly precipitation). Uncertainty in the proportion of impacts that are avoided for a specific sector depends on the range in the shape of the relationship between global temperature change and impact, and this varies between sectors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Paris Agreement reached at the United Nations Framework Convention on Climate Change (UNFCCC) climate conference in December 2015 aims to hold “the increase in global average temperature to well below 2 °C above pre-industrial levels and to pursue efforts to limit the temperature increase to 1.5 °C above pre-industrial levels, recognising that this would significantly reduce the risks and impacts of climate change” (UNFCCC 2015). However, so far, there is limited evidence on the impacts that would be avoided if the 1.5 °C target was achieved by 2100. This is because most impact assessments have used climate scenarios constructed from climate models forced by Representative Concentration Pathways (RCPs). The median increase in temperature under the lowest RCP (RCP2.6) is 1.6 °C above pre-industrial levels, but 56% of climate models simulate an increase above 1.5 °C and 22% above 2 °C (Collins et al. 2013). The one study that has so far explicitly assessed impacts at 1.5 °C (Schleussner et al. 2016) compared them with impacts at 2 °C, but did not compare them with impacts under unmitigated climate change. It compared scenarios constructed from time periods in climate model simulations that had mean global temperature increases of 1.5 or 2 °C, but a non-trivial portion of the difference between the two periods may be due to multi-decadal climatic variability rather than the underlying climate change signal.
This paper presents an assessment of the global and regional scale impacts that would be avoided with an increase in global mean surface temperature in 2100 of 1.5 °C above pre-industrial levels, relative to the impacts that would arise with increases of 2 °C and more. It considers impacts on exposure to water resources stress, river flooding, heat waves and drought and changes in the demands for cooling and heating energy.
2 Methods
2.1 Overview of approach
The assessment uses global and regional damage functions (updated and enhanced from Arnell et al. 2016) which relate indicators of impact to increase in global mean surface temperature. Figure 1 shows global damage functions, and regional damage functions are presented in Supplementary Material.
Global damage functions showing the relationship between change in global mean surface temperature (relative to 1850–1899 as a proxy for pre-industrial) and impact, for seven impact indicators. For population exposed to drought and flooding, and the energy indicators, the damage functions assume the 2100 SSP2 socio-economic scenario. The different lines represent 21 climate model patterns
The damage functions are constructed by calculating impacts using spatially explicit impact models with climate scenarios representing incremental increases in global mean temperature. Climate scenarios are derived from Coupled Model Intercomparison Project, Phase 5 (CMIP5) climate models (Taylor et al. 2012) using pattern scaling, and there is one damage function for each climate model. For socio-economic impact indicators, impacts are dependent on socio-economic scenario and time, so there is a different damage function for each socio-economic scenario and time horizon. The damage functions all show impact relative to a 1961–1990 baseline climatology, which (from HadCRUT4: Morice et al. (2012)) is 0.32 °C above 1850–1899, a proxy for pre-industrial levels.
The impacts that are avoided under one change in global mean temperature above pre-industrial relative to another are determined simply from the damage functions, assuming that all CMIP5 patterns are equally plausible. Impacts at temperature increases of 1 to 3 °C above pre-industrial levels in 2100 are compared with impacts at increases of 2 to 5 °C above pre-industrial. As a context, the median estimate of the increase in global mean temperature in 2100 under the high emission scenario RCP8.5 is 4.6 °C (IPCC 2013), and increases in 2100 with unmitigated emissions under the five Shared Socio-Economic Pathways (SSPs: Riahi et al. 2017) range from 3 to 5.1 °C: the ‘middle-of-the-road’ SSP2 scenario has an estimated increase of 3.8 °C (range 3.8–4.2 °C).
2.2 Climate scenarios
Spatial climate scenarios at a resolution of 0.5 × 0.5° were constructed for incremental changes in global mean surface temperature using the pattern scaling method (Tebaldi and Arblaster 2014). Patterns were diagnosed from 21 CMIP5 climate models (Taylor et al. 2012) using ClimGen (Osborn et al. 2016; Supplementary Material), in each case pooling across all available simulations for each model (across RCP forcing scenarios and, where available, ensemble members). Scenarios describe changes relative to the model 1961–1990 climate in mean monthly temperature, precipitation, vapour pressure and cloud cover, and—in an extension of traditional pattern scaling approaches—changes in the interannual variability of monthly precipitation (Osborn et al. 2016). The scenarios are applied to the 1961–1990 baseline climatology (CRU TS: Harris et al. 2014) using the delta method. The pattern-scaled scenarios represent just the effect of climate change forcing and do not incorporate the effects of unforced multi-decadal climatic variability which would increase the estimated range in future impacts for a given change in global mean temperature.
Pattern scaling involves several assumptions (Collins et al. 2013; James et al. 2017). The key assumption is that the relationship between global mean surface temperature and climate variable at a place is linear (after transformation in the case of precipitation). This is a reasonable assumption (Osborn et al. 2016) where the dimensionless patterns for a particular climate model are constructed by pooling all simulations made by that model (different forcings, different initial conditions), and deviations from this assumption are small relative to the spread between climate models. A more challenging assumption is that the change per degree change in global mean temperature does not vary with the rate of temperature increase. For example, the pattern of change in precipitation corresponding to an increase in global temperature of 1.5 °C is assumed to be the same regardless of whether that increase occurs by 2050 or 2100. A related assumption is that the patterns are the same for as long as global average temperature remains at the same level (for example, once temperatures have been stabilised), even though the slow response of parts of the climate system might lead to continued regional climate changes after global temperature stabilisation (as shown for example by Gillett et al. 2011). However, pattern scaling represents a ‘useful approximation’ (Collins et al. 2013), recognising that the scaling may be less reliable for scenarios where global average temperature stabilises. At low forcing levels, the regional effects on climate of land use change and aerosols may be large relative to the effect of increasing greenhouse gas concentrations, and these are not represented in the pattern-scaled scenarios. The implications of the potential limitations to pattern scaling are discussed in Sect. 5.
The only other potentially plausible method of constructing scenarios corresponding to specific changes in global mean temperature is to sample from climate model runs at the time when the defined changes occur (e.g. Schleussner et al. 2016; James et al. 2017). However, this approach is sensitive to multi-decadal variability, and differences between different time periods (and temperatures) will represent the combined effect of the different amount of forcing and multi-decadal variability. The approach also assumes—like pattern scaling—that the change per degree change in global mean temperature does not vary with the rate of temperature increase.
2.3 Impact indicators
Impacts are characterised by seven indicators, representing impacts on water resources, river flooding, agriculture, heat waves and the demand for energy for heating and cooling. In each case, the period 1961–1990 is used to characterise the reference ‘no climate change’ climate and is defined using the CRU TS3.22 global climatology (Harris et al. 2014).
2.3.1 Water resources
The impacts of climate change on water resources are characterised by the population exposed to drought. Drought is here represented by the standardised runoff index (SRI: Shukla and Wood 2008), calculated from monthly runoff simulated using the MacPDM.09 global hydrological model (Gosling and Arnell 2010). MacPDM.09 operates at a spatial resolution of 0.5 × 0.5° at a daily time step. It calculates daily runoff from daily precipitation and potential evaporation (calculated using the Penman-Monteith formula) and accounts for the storage of precipitation as snow and its subsequent melting. Daily precipitation is derived stochastically from the input monthly precipitation total and number of rain days (Gosling and Arnell 2010). MacPDM.09 has been included in global hydrological model intercomparisons (Haddeland et al. 2011) and shown to perform consistently with other global hydrological models.
The SRI is calculated here with the following steps. First, a time series of runoff accumulated over a given number of months (here 12) is constructed over the baseline 1961–1990 period. This time series is then standardised to calculate SRI by (i) estimating the exceedance probability of each value from its rank and (ii) converting these exceedance probabilities into standard normal deviates (with zero mean and unit variance). An empirical relationship is then constructed between accumulated runoff and SRI. This relationship is used to convert time series of simulated future runoff to SRI. A ‘drought’ is defined to occur when the SRI is less than − 1.5—which occurs 6.8% of the time in the baseline period—and drought frequency for a given time series of monthly runoff is determined by counting the number of months with SRI less than − 1.5. The average annual population exposed to drought is then calculated by multiplying grid cell population by the proportion of time the cell is in drought, and summing across all cells in a region. This indicator characterises exposure to drought rather than direct drought impact, because water management interventions are frequently implemented in order to reduce drought impacts.
At the global scale, the proportion of population exposed to drought increases under all 21 climate model patterns as global temperature increases (Fig. 1). However, there is considerable variability between regions (Supplementary Material). For example, drought frequency decreases in a large proportion of models in East Africa, South Asia and Central Asia, and in a substantial minority of models in West and Central Africa, and East Asia. In a number of cases, regional average drought frequency decreases for small increases in temperature and then increases as temperatures increase further. This regional-scale non-linearity occurs for a combination of two reasons. First, in some individual grid cells, drought frequency decreases as rainfall increases and potential evaporation increases, but increases once the increase in evaporation offsets the increase in precipitation. Second, different parts of a region may respond to increasing temperatures at different rates.
2.3.2 River flooding
Exposure to river flooding is characterised by the average annual number of people living in major floodplains affected by floods greater than the baseline 30-year flood. Flood frequency distributions for baseline and future climates are calculated by fitting a generalised extreme value (GEV) distribution to the daily flows simulated by MacPDM.09 for each 0.5 × 0.5° grid cell (Arnell and Gosling 2016), and the future frequency of the baseline 30-year flood determined from the future distributions. Floodplain boundaries are taken from the UNEP PREVIEW data set (preview.grid.unep.ch), and the proportion of grid cell population living in designated floodplains was calculated by overlaying a high-resolution gridded population data set with the floodplain boundaries. The proportion is assumed not to change over time. The indicator is similar in principle to that used by Hirabayashi et al. (2014), although they used the baseline 100-year flood as a threshold and counted exceedances rather than use fitted frequency curves. This indicator characterises exposure to flooding rather than direct flood impact, because it does not incorporate adaptations to the flood risk.
At the global scale, the population exposed to river flooding increases with increase in global mean temperature (Fig. 1). However, as with exposure to drought, there is considerable variability between regions (Supplementary Material). In some regions, one climate model produces responses very different to the others (but the anomalous model varies between regions), and in some regions—particularly central Europe, eastern Europe and Russia, and the USA—the relationship between impact and global temperature increase is complicated. This typically occurs in regions where flood peaks are currently usually generated by snowmelt, and as temperature increases, the relative contribution of snowmelt and rain-generated floods changes.
2.3.3 Cropland exposed to drought
The impacts of climate change on croplands is characterised by the average annual proportion of cropland that is exposed to drought. Here, drought is characterised by the standardised precipitation evaporation index (SPEI: Vicente-Serrano et al. 2010), calculated from monthly precipitation and potential evaporation (calculated using the Penman-Monteith formula). The SPEI is calculated from the monthly difference between precipitation and potential evaporation in exactly the same way as the SRI using a threshold of − 1.5, but using accumulations over 6 months. It is assumed that the area of cropland (Ramankutty et al. 2008) remains constant over time. Sensitivity analyses showed that varying the cropland area had little effect on the proportion exposed to drought.
At the global scale, the frequency of droughts affecting croplands increases with increasing global temperature (Fig. 1). Frequencies increase in all regions under virtually all climate model patterns (Supplementary Material). The damage functions for cropland drought exposure are different to those for water resources drought for three reasons. They are based on precipitation minus potential evaporation rather than on runoff (which is effectively precipitation minus actual evaporation), they are based on 6-month rather than 12-month accumulations, and they are spatially integrated across cropland rather than population.
SPEI is used as a proxy for climate impacts on agricultural production, which will of course also be affected by changes in crop growth (dependent on changes hot and cold spells, carbon fertilisation and nutrient availability) and agricultural practices.
2.3.4 Heat waves
The effect of climate change on hot extremes is characterised by the average annual number of ‘heat wave days’. A hot day is defined to occur if the daily maximum temperature is more than two standard deviations above the reference climate (1961–1990) warm season average maximum temperature, where the warm season is defined by the 3-month period in the reference climate with the highest average temperature. The standard deviation is calculated from the days in the reference climate warm season. A heat wave is defined to be a period of at least five consecutive hot days, and the number of heat wave days is the number of days in a heat wave. This definition means that neither periods with fewer than five consecutive hot days nor the first 4 days of a heat wave are counted. The regional average number of heat wave days is constructed by weighting each 0.5 × 0.5° grid square by its 2010 population.
Hot days and heat waves are calculated from daily maximum temperatures, which are constructed from the monthly climate scenarios by interpolating to produce a smooth annual cycle and adding historical daily temperature anomalies calculated from the WATCH climate data set (Weedon et al. 2011). These daily anomalies preserve the historical variability in temperature anomalies from day to day, and it is assumed that this variability continues into the future. This may change as climate changes. However, preliminary analyses using the ISIMIP projections (Warszawski et al. 2014) suggest little consistency between models in changes in variability, and a sensitivity analysis assuming that the anomaly standard deviation increases with temperature found that this had no effect on the difference in impacts between different changes in global temperature.
The frequency of heat wave days increases dramatically as global mean temperature increases (Fig. 1), and although it increases in each region (Supplementary Material), the amount of increase varies. It is greatest in tropical and sub-tropical regions where the standard deviation of warm season daily maximum temperature is least, and therefore, a smaller increase in temperature leads to a larger increase in heat wave frequency.
2.3.5 Energy demands for heating and cooling
The impacts of climate change on demands for energy are characterised by the estimated residential demands for energy for cooling and heating. These are simulated using a variation on Isaac and van Vuuren’s (2009) residential energy demand model, which essentially estimates heating and cooling requirements from accumulated degree days below (for heating) or above (for cooling) specific thresholds, along with projected future population, wealth, household size and assumptions about the changing efficiency of cooling and heating technologies. Whilst heating energy demands are a simple function of heating degree days, cooling energy demands are a more complicated function of temperature because the penetration of air conditioning is assumed to increase with temperature as well as GDP. A threshold of 18 °C is used to define both heating and cooling degree days.
As expected, global residential heating demands decrease and cooling demands increase (Fig. 1). However, the total heating and cooling demand shows a much more complicated pattern, globally and regionally (Supplementary Material). This is because the relative contribution of heating and cooling demands to total demands, and the sensitivity of demands to temperature change, varies between regions. At the global scale, total demand changes little with increases up to 2 °C above 1961–1990, for example, and in Australia, total demand falls at first and then increases as the rise in cooling demands offsets the fall in heating demands. The implications for the energy supply system of changes in cooling and heating demands are different, because these demands occur in different seasons.
2.4 Socio-economic scenarios
The water resources and river flooding indicators require projections of future population, and the energy indicators require both population and GDP projections. The analysis here focuses on the SSP2 middle-of-the-road scenario (Fricko et al. 2017) which has a population of nine billion in 2100. Sensitivity analyses (Supplementary Material) use other socio-economic scenarios.
2.5 An overview of the indicators and the characterisation of differences in impacts at different warming levels
The analysis here uses a small set of indicators of impact, which do not incorporate the effects of adaptation to changing risks: they characterise exposure to impact rather than projected actual impacts. For most of the sectors, there are a number of alternative indicators, and these could give different indications of the effect of achieving climate policy targets on the impacts that are avoided.
The damage functions exhibit a range of shapes, and—particularly at the regional level—can describe relationships between temperature and impact that change direction beyond a particular increase in temperature. As outlined above, this occurs for three reasons. In some cases, the relationship between temperature and impact changes direction in a specific location, for example where increasing temperatures alter the balance between snow and rain-generated floods. In other cases, changes occur at different rates in different parts of a region, so (e.g.) the regional aggregate change peaks before declining at higher temperatures. This occurs with the drought indicators. In a third set of cases, the sum of two competing impacts can show a complex response to increasing temperature: this occurs with the total residential heating plus cooling demand indicator.
For each of the indicators, climate change can in principle have either adverse or beneficial impacts. At the global scale, impacts on exposure of both people and cropland to drought and exposure to river flooding are adverse for any increase in temperature, but this is not necessarily the case at the regional scale (see regional damage functions in Supplementary Material). Exposure to heat waves and increases in demand for cooling energy increase everywhere, and demand for heating energy decreases everywhere (a benefit). The sum of heating and cooling demands increases in some regions and decreases in others, depending on the relative importance of the two. The effects of achieving a policy target on the impacts of climate change are therefore complicated, and there are a number of potential outcomes. These are classified in Fig. 2. In essence, a climate policy may not only result in lower adverse impacts but also lower beneficial impacts, and can also result in adverse impacts becoming worse and adverse impacts becoming beneficial or beneficial impacts increasing.
3 Global-scale impacts avoided with a 1.5 °C target
Figure 3 shows the proportion of impacts that are avoided in 2100 for different target temperature increases, relative to increases of 2, 3, 4 and 5 °C. In each case, the shaded area shows the range across all 21 CMIP5 models. The median avoided impact from the 21 models is shown by the thin solid line, and the median reduction in benefits (for the heating energy indicator) is shown by the thin dotted line. A percentage avoided greater than 100% means that adverse impacts become beneficial impacts. Note that the effect of meeting a climate policy target on heating energy demands is to reduce the beneficial impacts of climate change.
The proportion of global-scale impacts that are avoided in 2100, relative to 2, 3, 4 and 5 °C above pre-industrial (represented by colours blue, green, orange and red respectively). The shaded area shows the range across all 21 models, and the thin solid lines show the median proportion of impacts avoided (proportion of benefits avoided for the heating energy indicator). The dashed lines show the proportional reduction in global mean temperature at each target temperature. An avoided proportion greater than 100% indicates that adverse impacts become beneficial impacts at the lower temperature
If the proportion of impacts avoided were simply equal to the proportional reduction in increase in temperature, then the 1.5 °C target would avoid 68% of the impacts which would have been experienced at 4 °C and 30% of the impacts at 2 °C (note that impacts are calculated relative to the 1961–1990 climate, which is 0.32 °C warmer than pre-industrial). These proportions are shown by the thick dashed lines in Fig. 3. In practice, the proportion of impacts avoided with the 1.5 °C target varies between sectors (Table 1), and in most cases, the proportion avoided is greater than the proportional reduction in temperature. This is because the damage functions are typically curved (Fig. 1), and in most cases, the functions suggest an increasing change in impact with higher increases in temperature. The cropland drought and heating energy functions are the least curved, so the proportion of impacts avoided for these indicators are closest to the proportional reduction in temperature. The difference between the curves for a given indicator depends on the range in shape of the damage functions between the 21 climate model patterns. This uncertainty range is particularly small for the heating and cooling energy indicators, but very high for the combined heating and cooling demands.
The magnitude of the impacts that are avoided varies with socio-economic scenario, but the proportion of impacts that are avoided is generally consistent across socio-economic scenarios (Supplementary Material). A significant exception, however, is for the combined heating and cooling demand indicator. This is because the balance between cooling and heating demands varies between different socio-economic scenarios—because the penetration of air conditioning is strongly influenced by GDP—and so, the increases in cooling demands relative to the decreases in heating demands vary with SSP. In SSP2, total demand increases with climate change (Fig. 1). In SSP1 and SSP5, total demand increases under most climate model patterns but decreases under others, whilst in SSP3 and SSP4, total demand decreases under all climate scenarios. The effects of climate mitigation policy on total heating and cooling demand are therefore very dependent on assumed socio-economic changes.
4 Regional avoided impacts
At the global scale, impacts for all but the heating energy indicator become increasingly adverse with increasing levels of warming (with some exceptions at low warming levels): heating energy demands reduce with greater warming. At the regional scale, however, the picture is much more complicated. In some regions, impacts may be either adverse or beneficial depending on climate model pattern, and in some cases, impacts (adverse or beneficial) are lower at higher levels of warming than lower levels (see the regional damage functions in Supplementary Material). Plots such as Fig. 3 are therefore misleading at the regional scale (and also could be misleading at the global scale with other indicators that show less consistent changes in impact with level of warming).
Figure 4 illustrates the complexity in the relationship between impacts at 4 and 1.5 °C, for three regions for the drought and flooding indicators. In each case, some climate model patterns suggest that adverse impacts would be less at lower levels of warming, whilst others imply that beneficial impacts would be less. In central Europe and Russia, one model implies that the reduction in flood risk would be greater at lower levels of warming (‘benefits improve’), and under one model, an increase in risk at 4 °C would become a reduction in risk at 1.5 °C. Figure 4 also plots the median impact at 4 and 1.5 °C and shows that the median can give a misleading indication of both impacts and the proportion of impacts that are avoided (see the population exposed to drought in South Asia, for example, where the median apparent effect of a lower level of warming is to reduce further drought frequency). Similar plots for each region and indicator are presented in Supplementary Material.
The relationship between impacts at 4 and 1.5 °C above pre-industrial levels, for three regions and for two impact indicators. The black dots show the individual climate model patterns, and the red dots show the ensemble median. Impacts are scaled so that the largest impact at 4 °C is equal to 1. Similar plots for all regions and indicators are shown in Supplementary Material
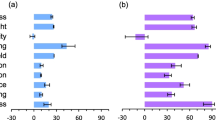
The regional diversity in the effect of lowering warming is summarised in Fig. 5, which shows the proportion of the 21 climate models which produce the different types of effect on impacts categorised in Fig. 2. It compares impacts at 1.5 °C with those at 4 °C: a comparison of 1.5 °C with 2 °C is shown in Supplementary Material.
Regional variation in the estimated proportions of adverse and beneficial impacts that are avoided by a temperature increase of 1.5 °C relative to an increase of 4 °C. The type of effect is colour-coded according to Fig. 2, and the chart shows the proportion of climate model patterns with a given type of effect
Exposure to heat waves is reduced by more than 75% in all models in each region, and the increase in cooling energy demands is reduced by more than 50% everywhere (with a larger proportion reduction in Europe, Russia and Canada). The exposure of cropland to drought reduces everywhere, but the proportional reduction varies between models. In a couple of regions, one model simulates a reduction in drought frequency at 4 °C, and this reduction becomes even greater at 1.5 °C (blue in Fig. 5). The reduction in heating energy demands is less at 1.5 °C than 4 °C in all regions, but there is a variation in the proportion of this beneficial impact that is lost by limiting warming to 1.5 °C. In Europe and North America, for example, it is between 50 and 75% under all climate model patterns, but in West Africa, it is less than 25% for more than half of the 21 climate models suggest that the reduction will be less than 25%.
The regional variations for the other indicators are rather more complicated. Across most regions, the proportion of regional population exposed to drought decreases if warming is limited to 1.5 °C under all climate model patterns, to varying extents. In parts of Asia and Africa, the population exposed to drought decreases at 4 °C under a minority of climate models (just over half of the 21 models in South Asia). In these regions, limiting the increase in temperature to 1.5 °C leads either to a smaller reduction (‘benefits less’) or a greater reduction (benefits improve). A large proportion of climate models suggest a reduction in flood exposure at 4 °C in some regions (particularly Europe, Russia, the USA, the Middle East and North Africa). Limiting the increase to 1.5 °C again lessens the reduction in exposure or, in a small number of cases leads to an even greater reduction in exposure. Regional variation in the effects of limiting the temperature increase is particularly stark for the sum of heating and cooling demands. Limiting the temperature rise to 1.5 °C reduces the increase in total demands in Africa, South and South-East Asia and Latin America, but leads to a smaller reduction in demands (benefits less) in the rest of the world. In Australasia and South America, limiting the increase in temperature results in a greater reduction in total demands in a large minority of models.
5 Caveats
A number of caveats apply to this analysis and the interpretation of the results. It is assumed that pattern scaling can be used to estimate changes in regional climate consistent with relatively small increases in temperature (arising, for example, from emissions that have been stabilised). It is assumed that all 21 CMIP5 models used here are equally plausible. The analysis uses 1961–1990 to characterise ‘current’ climate. Later reference periods would be warmer and the apparent temperature-related impacts smaller, and different reference periods would have different spatial patterns of precipitation upon which changes are superimposed. The estimated precipitation-driven impacts could therefore be different to those estimated here, but would not be any more plausible because there is no clear climate change signal on the variability in precipitation from decade to decade. The analysis does not include the effects of multi-decadal internal climatic variability on future impacts (particularly important for the precipitation-driven indicators), but this would change only the range in estimated impacts and not the central estimates or the proportional difference between different temperature increases. The approach used is appropriate for snapshots of impacts at a particular time period, but does not characterise the accumulation of impacts over time: these may be more different between temperature targets than the snapshot of impacts in 2100. The approach is not appropriate for impacts that are dependent on the rate of change in climate over time, such as impacts dependent on sea-level rise or evolving ecosystems. Finally, the estimated proportions of impacts avoided are dependent on the indicators of impact that are have been used: for each of the sectors, different indicators are available, and we have not considered impacts on all human or any natural systems (e.g. Warren et al. 2013). The indicators characterise exposure and do not incorporate adaptation, which will affect absolute impacts and possibly also relative impacts at different temperature levels. We have also used only one indicator for each sector, but in practice, many dimensions of climate change may be relevant. For example, impacts on agricultural production are likely to be affected not only by drought but also by the frequency of hot and cold spells, flooding, carbon fertilisation and agricultural practices.
6 Conclusions
This study has quantified the potential benefits of limiting the increase in temperature in 2100 to 1.5 °C above pre-industrial levels, relative to a 2 °C target and other higher temperature levels, for seven impact indicators. Climate change can have beneficial as well as adverse consequences (for example a reduction in drought frequency in some regions), and the effects of reducing temperatures on impacts are therefore complicated. Not only may adverse impacts be reduced, but beneficial impacts may be reduced too. Adverse impacts may become beneficial at lower temperatures, and beneficial impacts may be increased or become adverse. At the global scale, the impacts of unmitigated climate change under all the indicators considered here are adverse, but at the regional scale, there is a mixture of adverse and beneficial impacts. It is therefore difficult to represent in a simplified way the effects of climate policy on the regional impacts of climate change: what is clear, however, is that the median effect is not necessarily very representative at the regional scale.
The proportion of impacts that are avoided by a specific policy target is not simply equal to the proportional reduction in temperature, due to differences between indicators and regions in the shape of the relationship between global temperature change and impact. At the global scale, the median estimates of the proportion of impacts across sectors avoided by the 1.5 °C target relative to 4 °C range between 62 and 95%, and impacts at 1.5 °C are between 27 and 62% lower than impacts at 2 °C. These proportions are greater than the proportional reduction in temperature and depend on the shape of the relationship between temperature increase and impact.
However, there is much more diversity in the effects of achieving a particular climate policy target at the regional level. This is partly because of the regional variability in exposure and partly because of the regional uncertainty in the effect of climate change—particularly change in precipitation. The uncertainty in the avoided impacts is also greater at the regional level than at the global level, due to greater variability in the shape of the relationship between temperature and impact across climate models. The effects of achieving a climate policy target—such as 1.5 °C—therefore vary between regions.
References
Arnell NW, Gosling SN (2016) The impacts of climate change on river flood risk at the global scale. Clim Chang 134:387–401
Arnell NW et al (2016) Global-scale climate impact functions: the relationship between climate forcing and impact. Clim Chang 134:475–487
Collins M et al (2013) Long-term climate change: projections, commitments and irreversibility. In: Stocker T et al (eds) Climate change 2013: the physical science basis. Report of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Fricko O et al (2017) The marker quantification of the Shared Socioeconomic Pathway 2: a middle-of-the-road scenario for the 21st century. Glob Environ Chang. 42:251–267.https://doi.org/10.1016/j.gloenvcha.2016.06.004
Gillett NP et al (2011) Ongoing climate change following complete cessation of carbon dioxide emissions. Nat Geosci 4:83–87
Gosling SN, Arnell NW (2010) Simulating current global river runoff with a global hydrological model: model revisions, validation and sensitivity analysis. Hydrol Process 25(7):1129–1145
Haddeland I et al (2011) Multimodel estimate of the global terrestrial water balance: setup and first results. J Hydrometeorol 12:869–884
Harris I et al (2014) Updated high-resolution grids of monthly climatic observations—the CRU TS3.10 dataset. Int J Climatol 34:623–642
Hirabayashi Y et al (2014) Global flood risk under climate change. Nat Clim Chang 3:816–821
IPCC (2013) Summary for policymakers. In climate change 2013: the physical science basis. In: Stocker TF et al (eds) Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Isaac M, van Vuuren DP (2009) Modeling global residential sector energy demand for heating and air conditioning in the context of climate change. Energy Policy 37:507–521
James R et al (2017) Characterizing half-a-degree difference: a review of methods for identifying regional climate responses to global warming. WIREs Clim Change 8:e457. https://doi.org/10.1002/wcc.457
Morice CP et al (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J Geophys Res 117:D08101. https://doi.org/10.1029/2011JD017187
Osborn TJ et al (2016) Pattern-scaling using ClimGen: monthly-resolution future climate scenarios including changes in the variability of precipitation. Clim Chang 134:353–369
Ramankutty N et al (2008) Farming the planet: 1. Geographic distribution of global agricultural lands in the year 2000. Glob Biogeochem Cycles 22:Gb1003. https://doi.org/10.1029/2007gb002952
Riahi K et al (2017) The Shared Socioeconomic Pathways and their energy, land use and greenhouse gas emission implications: an overview. Glob Environ Chang. 42:153–168. https://doi.org/10.1016/j.gloenvcha.2016.05.009
Schleussner C-F et al (2016) Differential climate impacts for policy-relevant limits to global warming: the case of 1.5°C and 2°C. Earth Syst Dyn 7:325–351
Shukla S, AW Wood (2008) Use of a standardized runoff index for characterizing hydrologic drought. Geophys Res Lett 35. https://doi.org/10.1029/2007GL032487
Taylor KE et al (2012) An overview of CMIP5 and the experimental design. Bull Am Meteorol Soc 93:485–498
Tebaldi C, Arblaster JM (2014) Pattern scaling: its strengths and limitations, and an update on the latest model simulations. Clim Chang 122:459–471
UNFCCC (2015) Adoption of the Paris Agreement FCCC/CP/2015/L.9/Rev.1. United Nations
Vicente-Serrano SM, Bergueria S, Lopez-Moreno JI (2010) A multi-scalar drought index sensitive to global warming: the standardised precipitation evapotranspiration index – SPEI. J Clim 23:1696–1711
Warren R et al (2013) Quantifying the benefit of early climate change mitigation in avoiding biodiversity loss. Nat Clim Chang 3:678–682
Warszawski L et al (2014) The Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP): project framework. Proc Natl Acad Sci 111:3228–3232
Weedon GP et al (2011) Creation of the WATCH forcing data and its use to assess global and regional reference crop evaporation over land during the twentieth century. J Hydrometeorol 12:823–848
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 3114 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Arnell, N.W., Lowe, J.A., Lloyd-Hughes, B. et al. The impacts avoided with a 1.5 °C climate target: a global and regional assessment. Climatic Change 147, 61–76 (2018). https://doi.org/10.1007/s10584-017-2115-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-017-2115-9