Abstract
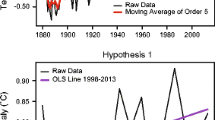
To characterize observed global and hemispheric temperatures, previous studies have proposed two types of data-generating processes, namely, random walk and trend-stationary, offering contrasting views regarding how the climate system works. Here we present an analysis of the time series properties of global and hemispheric temperatures using modern econometric techniques. Results show that: The temperature series can be better described as trend-stationary processes with a one-time permanent shock which cannot be interpreted as part of the natural variability; climate change has affected the mean of the processes but not their variability; it has manifested in two stages in global and Northern Hemisphere temperatures during the last century, while a second stage is yet possible in the Southern Hemisphere; in terms of Article 2 of the Framework Convention on Climate Change it can be argued that significant (dangerous) anthropogenic interference with the climate system has already occurred.
Similar content being viewed by others
References
Andreou A, Spanos A (2003) Statistical adequacy and the testing of trend versus difference stationary. Econom Rev 22:217–237
Banerjee A, Lumsdaine RL, Stock JH (1992) Recursive and sequential tests of the unit root and trend break hypotheses: theory and international evidence. JBES 10(3):271–287
Bloomfield P (1992) Trend in global temperature. Clim Change 21:1–16
Bruckner T, Schellnhuber HJ (1999) Climate change protection: the tolerable windows approach. (IPTS Report 34)
Crowley TJ (2000) Causes of climate change over the past 1000 years. Science 289:270–277
Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74:427–431
Elliott G, Rothenberg TJ, Stock JH (1996) Efficient tests for an autoregressive unit root. Econometrica 64:813–836
Enders W (2003) Applied econometric time series. Wiley, New York
Folland CK et al (1992) Observed climate variability and change. In: Houghton JT, Callander BA, Varney SK (eds) Climate change 1992: the supplementary report to the IPCC scientific assessment. Cambridge University Press, Cambridge
Folland CK et al (2001a) Global temperature change and its uncertainties since 1861. Geophys Res Lett 28:2621–2624
Folland CK et al (2001b) Observed climate variability and change. In: Houghton JT et al (eds) Climate change 2001: the scientific basis. Cambridge Univ Press, Cambridge, pp 99–181
Galbraith J, Green C (1992) Inference about trends in global temperature data. Clim Change 22:209–221
Gay C, Estrada F, Conde C (2007) Some implications of time series analysis for describing climatologic conditions and for forecasting. An illustrative case: Veracruz, Mexico. Atmosfera 20(2):147–170
Hansen J, Lebedeff S (1987) Global trends of measured surface air temperature. J Geophys Res 92:13345–13372
Harvey DI, Mills TC (2000) Detecting climate change using smooth transitions. (Economic Research Paper 00/21, Department of Economics, Loughborough University); (available at http://www.lboro.ac.uk/departments/ec/Research/Discussion%20Papers%202000/Research%20Papers%202000/erp00–21.pdf)
Harvey DI, Mills TC (2002) Unit roots and double smooth transitions. J Appl Stat 29(5):675–683
Hatanaka M (1996) Time-series-based econometrics. Unit roots and cointegration. Oxford University Press, Oxford
Hodrick RJ, Prescott EC (1997) Postwar U.S. business cycles: an empirical investigation. J Money Credit Bank 29:1–16
IPCC (2001) Climate change 2001: synthesis report 2001. In: Watson RT, the Core Writing Team (eds) Contribution of working group I, II, and III to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, 397 pp
IPCC (2007) Climate change 2007: the physical science basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, 996 pp
Joachim H, Schnellnhuber HJ et al (ed) (2006) Avoiding dangerous climate change. Cambridge University Press, Cambridge
Jones PD, Mann ME (2004) Climate over past millennia. Rev Geophys 42:RG2002. doi:10.1029/2003RG000143
Jones PD, Moberg A (2003) Hemispheric and large-scale surface air temperature variations: an extensive revision and an update to 2001. J Clim 16:206–223
Jones PD et al (2001) Adjusting for sampling density in grid-box land and ocean surface temperature time series. J Geophys Res 106:3371–3380
Kärner O (1996) Global temperature deviations as a random walk. J Climate 9:656–658
Kaufmann RK, Stern DI (1997) Evidence for human influence on climate from hemispheric temperature relations. Nature 388:39–44
Kaufmann RK, Kauppi H, Stock JH (2006a) Emissions, concentrations, & temperature: a time series analysis. Clim Change 77:249–278. doi:10.1007/s10584-006-9062-1
Kaufmann RK, Kauppi H, Stock JH (2006b) The relationship between radiative forcing and temperature: what do statistical analyses of the instrumental temperature record measure? Clim Change 77:279–289. doi:10.1007/s10584-006-9063-0
Kim D, Perron P (2007) Unit root tests allowing for a break in the trend function under both the null and the alternative hypotheses. Unpublished manuscript. Department of Economics, Boston University
Kwiatkowski D, Phillips PCB, Schmidt P, Shin Y (1992) Testing the null hypothesis of stationarity against the alternative of a unit root. J Econom 54:159–178
Lumsdaine R, Papell DH (1997) Multiple trend breaks and the unit-root hypothesis. REStat 79(2):212–218
MacKinnon JG (1996) Numerical distribution functions for unit root and cointegration tests. J Appl Econ 11:601–618
Maddala GS, Kim IM (1998) Unit roots, cointegration and structural change. Themes in Modern Econometrics, Cambridge Univ Press
Mann ME, Jones PD (2003) Global surface temperature over the past two millennia. Geophys Res Lett 30(15):1820. doi:10.1029/2003GL017814
Mann ME, Bradley RS, Hughes MK (1998) Global scale temperature patterns and climate forcing over the past six centuries. Nature 392:779–787
Mann ME, Bradley RS, Hughes MK (1999) Northern Hemisphere temperatures during the past millennium: inferences, uncertainties and limitations. Geophys Res Lett 26:759–762
Nelson CR, Plosser CI (1982) Trends and random walks in macroeconomic time series: some evidence and implications. J Monet Econ 10:139–162
Ng S, Perron P (2001) Lag length selection and the construction of unit root tests with good size and power. Econometrica 69(6):1519–1554
Ng S, Perron P (2005) A note on the selection of time series models. OBES, Department of Economics, University of Oxford, vol 67, no 1, pp 115–134, 02
Perron P (1989) The great crash, the oil price shock, and the unit root hypothesis. Econometrica 99:1361–1401
Perron P, Vogelsang T (1993) Erratum: the great cash, the oil price shock and the unit root hypothesis. Econometrica 61:248–249
Perron P (1997) Further evidence on breaking trend functions in macroeconomic variables. J Econom 80(2):355–385
Perron P, Qu Z (2007) A simple modification to improve the finite sample properties of Ng and Perron’s unit root tests. Econ Lett 94:12–19
Perron P, Yabu T (2007) Testing for shifts in trend with an integrated or stationary noise component. Forthcoming in JBES. Available at http://people.bu.edu/perron/papers/breakpaper.pdf
Perron P, Zhu X (2005) Structural breaks with deterministic and stochastic trends. J Econom 129:65–119
Said E, Dickey DA (1984) Testing for unit roots in autoregressive moving average models of unknown order. Biometrika 71:599–607
Schneider SH (2002) Can we estimate the likelihood of climatic changes at 2100? Clim Change 52(4):441–451
Spanos A, Mcguirk A (2002) Where do statistical models come from? The problem of specification uncertainty in empirical modeling. (Virginia Tech working paper) (available at http://www.econ.ucy.ac.cy/seminars/Spanos.pdf)
Stern DI, Kaufmann RK (1997) Time series properties of global climate variables: detection and attribution of climate change. (Working Papers in Ecological Economics. The Australian National University, Center for Resource and Environmental Studies Ecological Economics Programme) (available at http://eprints.anu.edu.au/archive/00000665/00/eep9702.pdf)
Stern DI, Kaufmann RK (1999) Is there a global warming signal in hemispheric temperature series? (Working Papers in Ecological Economics. The Australian National University, Center for Resource and Environmental Studies Ecological Economics Programme) (available at http://www.bu.edu/cees/research/workingp/pdfs/9903.pdf)
Stock JH (1994) Unit roots, structural breaks, and trends. In: Engle R, McFadden D (eds) Handbook of econometrics, vol IV, pp 2739–2841. North-Holland, New York
Vogelsang TJ, Perron P (1998) Additional tests for a unit root allowing the possibility of breaks in the trend function. Int Econ Rev 39:1073–1100
Woodward WA, Gray HL (1993) Global warming and the problem of testing for trend in time series data. J Clim 6:953–962
Woodward WA, Gray HL (1995) Selecting a model for detecting the presence of a trend. J Clim 8:1929–1937
Zheng X, Basher RE (1999) Structural time series models and trend detection in global and regional temperature series. J Clim 12:2347–2358
Zivot E, Andrews D (1992) Further evidence on the Great Crash, the oil price shock, and the unit root hypothesis. JBES 10(3):251–270
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gay-Garcia, C., Estrada, F. & Sánchez, A. Global and hemispheric temperatures revisited. Climatic Change 94, 333–349 (2009). https://doi.org/10.1007/s10584-008-9524-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-008-9524-8