Seasonal volatility in agricultural markets: modelling and empirical investigations

Abstract

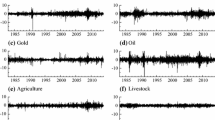
This paper deals with the issue of modelling the volatility of futures prices in agricultural markets. We develop a multi-factor model in which the stochastic volatility dynamics incorporate a seasonal component. In addition, we employ a maturity-dependent damping term to account for the Samuelson effect. We give the conditions under which the volatility dynamics are well defined and obtain the joint characteristic function of a pair of futures prices. We then derive the state-space representation of our model in order to use the Kalman filter algorithm for estimation and prediction. The empirical analysis is carried out using daily futures data from 2007 to 2019 for corn, cotton, soybeans, sugar and wheat. In-sample, the seasonal models clearly outperform the nested non-seasonal models in all five markets. Out-of-sample, we predict volatility peaks with high accuracy for four of these five commodities.

Appendices

Proofs

In this Appendix, we give the proofs of several propositions found in the paper.

Proof of Proposition 1

The proof is an extension of the proof of Proposition 2.1 of Schneider and Tavin (2018) to the case where the variance mean-reversion level $\theta$ is time-dependent. Going from $\theta$ to $\theta (t)$ leads to changes in two places. The first is in Lemma A.1 of Schneider and Tavin (2018), which needs to be modified as follows.

Lemma 1

Let $\theta : \mathbb {R}_0^+ \rightarrow \mathbb {R}^+$ be the seasonal mean-reversion level function, let

$$\begin{aligned} \hat{\theta }_T(\lambda ) := \int _0^T e^{\lambda t} \theta (t) dt \end{aligned}$$

be its transform, and let the function $f_1$ be given by $f_1(t) := \sum _{k=1}^2 u_k e^{- \lambda _j(T_k - t)}$. Then:

$$\begin{aligned} \sigma \int _0^T f_1(t) \sqrt{v(t)} d\tilde{B}(t) = \left[ f_1(t) v(t) \right] _0^T - f_1(0) \kappa \hat{\theta }_T(\lambda ) + (\kappa - \lambda ) \int _0^T f_1(t) v(t) dt. \end{aligned}$$

(33)

Proof

Multiplying equation Eq. (10) by $f_1(t)$ and then integrating from 0 to T gives:

$$\begin{aligned} \int _0^T f_1(t) dv(t) = \int _0^T f_1(t) \kappa (\theta (t) - v(t)) dt + \sigma \int _0^T f_1(t) \sqrt{v(t)} d\tilde{B}(t). \end{aligned}$$

(34)

Using Itô-integration by parts (see Øksendal (2003)), we also have:

$$\begin{aligned} \int _0^T f_1(t) dv(t)&= \left[ f_1(t) v(t) \right] _0^T - \int _0^T v(t) df_1(t) \nonumber \\&= \left[ f_1(t) v(t) \right] _0^T - \lambda \int _0^T f_1(t) v(t) dt. \end{aligned}$$

(35)

Equating the right hand sides of Eqs. (34) and (35) gives:

$$\begin{aligned} \sigma \int _0^T f_1(t) \sqrt{v(t)} d\tilde{B}(t)&= \left[ f_1(t) v(t) \right] _0^T - \lambda \int _0^T f_1(t) v(t) dt - \int _0^T f_1(t) \kappa (\theta (t) - v(t)) dt \\&= \left[ f_1(t) v(t) \right] _0^T - \kappa \int _0^T f_1(t) \theta (t) dt + (\kappa - \lambda ) \int _0^T f_1(t) v(t) dt \\&= \left[ f_1(t) v(t) \right] _0^T - f_1(0) \kappa \int _0^T e^{\lambda t} \theta (t) dt + (\kappa - \lambda ) \int _0^T f_1(t) v(t) dt \\&= \left[ f_1(t) v(t) \right] _0^T - f_1(0) \kappa \hat{\theta }_T(\lambda ) + (\kappa - \lambda ) \int _0^T f_1(t) v(t) dt, \end{aligned}$$

which proves the lemma.

The second change in the proof is due to the appearance of $\theta$ in the generator of the process v. As in Schneider and Tavin (2018), let the function h be given by:

$$\begin{aligned} h(t,v) = {{\mathbb {E}}} \left[ \exp \left( i \frac{\rho }{\sigma } f_1(T) v(T) + \int _t^T q(s) v(s) ds \right) \right] . \end{aligned}$$

Now h satisfies the partial differential equation (PDE):

$$\begin{aligned} \frac{\partial h}{\partial t} (t,v) + \kappa (\theta (t) - v(t)) \frac{\partial h}{\partial v} (t,v) + \frac{1}{2} \sigma ^2 v(t) \frac{\partial ^2 h}{\partial v^2} (t,v) + q(t) v(t) h(t,v) = 0, \end{aligned}$$

(36)

with terminal condition:

$$\begin{aligned} h(T,v) = \exp \left( i \frac{\rho }{\sigma } f_1(T) v(T) \right) . \end{aligned}$$

Again, we know from Duffie et al. (2000) that h has affine form:

$$\begin{aligned} h(t,v) = \exp \left( A(t,T) v(t) + B(t,T) \right) , \end{aligned}$$

(37)

with $A(T,T) = i \frac{\rho }{\sigma } f_1(T), B(T,T) = 0.$ Putting (37) in (36) gives:

$$\begin{aligned} B_t + A_t v + \kappa (\theta (t) - v) A + \frac{1}{2} \sigma ^2 v A^2 + q v = 0, \end{aligned}$$

and collecting the terms with and without v leads to the two ordinary differential equations (ODE):

$$\begin{aligned} A_t - \kappa A + \frac{1}{2} \sigma ^2 A^2 + q&= 0, \end{aligned}$$

(38)

$$\begin{aligned} B_t + \kappa \theta (t) A&= 0. \end{aligned}$$

(39)

This completes the proof of the proposition. $\square$

Note that $\theta$ only appears in the second ODE (39), and that the closed-form expression previously given for A in Schneider and Tavin (2018) can still be used. Only the function B changes due to the time-dependence of $\theta$.

Proof of Proposition 2

It is well known that the stochastic differential equation (SDE) given in Eq. (7) has a unique strong solution.

• (i) The drift function $b(t, v_t) := \kappa (\theta (t) - v(t))$ in the SDE given in Eq. (6) is Lipschitz continuous w.r.t the second argument, i.e.

  $$\begin{aligned} | b(t, x) - b(t, y) | \le K | x - y |, \end{aligned}$$

  where we can choose $K = \kappa$, since $| b(t, x) - b(t, y) | = \kappa | x - y |$. Proposition 5.2.13 (Yamada and Watanabe) of Karatzas and Shreve (1988) thus guarantees the existence of a unique strong solution to (6) with continuous sample paths.

• (ii) The comparison result given in Proposition 5.2.18 of Karatzas and Shreve (1988) establishes $v_t \ge \tilde{v}_t$ a.s. for all $t \ge 0$ under the hypothesis that the drift function $b(t, v_t)$ is continuous. Now, if $\theta$ has a discontinuity at time $t_1$, we know from applying this argument to the interval $[0, t_1[$ that $\tilde{v}_{t} \le v_{t} \forall t \in [0, t_1[$ (a.s.). It then follows from the continuity of the sample paths that $\tilde{v}_{t_1} \le v_{t_1}$ (a.s.), and we can apply the argument again to the interval $]t_1, t_2[$ to obtain $\tilde{v}_{t} \le v_{t} \forall t \in ]t_1, t_2[$ (a.s.). Since by assumption the set $\mathcal {T}$ of times where $\theta$ has discontinuities has no limit points, we can proceed in this manner to cover all of $\mathbb {R}_0^+$.

• (iii) The Feller condition $\sigma ^2 < 2 \kappa \theta _{{\textit{min}}}$ for $\theta _{{\textit{min}}}$ implies the strict positivity a.s. of $\tilde{v}$. The strict positivity of v itself therefore follows immediately from (ii).

$\square$

Transforms of the seasonality functions

In this appendix we show how the integral transforms $\hat{\theta }_T(\lambda )$ can be calculated for the sinusoidal, sawtooth and triangle patterns. To the best of our knowledge, there are no closed-form expressions for the transforms of the exponential-sinusoidal and spiked patterns; we have also tried to solve these two integrals with the computer algebra software Maple, but without success.

The transform of the sinusoidal pattern is given by:

$$\begin{aligned} \hat{\theta }_T(\lambda )&= \frac{b e^{\lambda T}}{\lambda ^2+4\pi ^2}\left( 2 \pi \sin {\left( 2 \pi (T-t_0)\right) } + \lambda \cos {\left( 2 \pi (T-t_0)\right) } \right) \nonumber \\&\quad + \frac{b}{\lambda ^2+4\pi ^2}\left( 2 \pi \sin {\left( 2\pi t_0 \right) - \lambda \cos {\left( 2\pi t_0 \right) }} \right) + \frac{a}{\lambda }\left( e^{\lambda T}-1\right) . \end{aligned}$$

(40)

The transform of the sawtooth pattern is given by:

$$\begin{aligned} \hat{\theta }_T(\lambda )&= \frac{1}{\lambda }\left( a+b\left( \frac{1}{\lambda }-t_0 \right) \right) -\frac{e^{-\lambda T}}{\lambda }\left( a+b\left( T+\frac{1}{\lambda }-t_0 \right) \right) \nonumber \\&\quad -\frac{be^{\lambda t_0}}{\lambda } \left( \left\lfloor T-t_0 \right\rfloor e^{\lambda (T-t_0)} - \left( \sum ^{\left\lfloor T-t_0 \right\rfloor }_{k=1}{e^{\lambda k}}\right) \mathbb {1}_{\left\{ T \ge t_0\right\} } + \mathbb {1}_{\left\{ T<t_0\right\} }+e^{-\lambda t_0}-1 \right) , \end{aligned}$$

(41)

where $\left\lfloor . \right\rfloor$ denotes the floor function, $\mathbb {1}$ is the indicator function and, by convention, $\sum ^{p}_{k=1}{e^{\lambda k}}=0$ if $p<1$.

The transform of the triangle pattern is given by

$$\begin{aligned}&\hat{\theta }_T(\lambda ) = \frac{a}{\lambda }\left( e^{\lambda T}-1 \right) + \frac{b e^{\lambda t_0}}{\lambda }\left[ \left( z_2 + \left( \frac{2}{\lambda }e^{-\frac{\lambda }{2}}+e^{-\lambda t_0}(z_2-t_0) \right) \mathbb {1}_{\left\{ t_0> \frac{1}{2} \right\} } - e^{-\lambda t_0}(z_2-t_0)\mathbb {1}_{\left\{ t_0 \le \frac{1}{2} \right\} } \right) \right. \nonumber \\&\quad + \left( \left( \frac{2}{\lambda } e^{\frac{\lambda }{2}} + z_2 e^{\lambda }-z_1 \right) \sum ^{n-1}_{k=0}{e^{\lambda k}}+ e^{\lambda n}\left( \left( \frac{2}{\lambda }e^{\frac{\lambda }{2}}-z_3 e^{\lambda \alpha } \right) \mathbb {1}_{\left\{ \alpha > \frac{1}{2} \right\} } + z_3 e^{\lambda \alpha }\mathbb {1}_{\left\{ \alpha \le \frac{1}{2} \right\} } -z_1 \right) \right) \mathbb {1}_{\left\{ T \ge t_0\right\} } \nonumber \\&\quad + \left( e^{\lambda (T-t_0)}\left( z_2+T-t_0 \right) -z_2 \right) \mathbb {1}_{\left\{ T-t_0 \in [-\frac{1}{2},0[ \right\} } \nonumber \\&\quad - \left. \left( \frac{2}{\lambda }e^{-\frac{\lambda }{2}} + e^{\lambda (T-t_0)}\left( z_2+T-t_0 \right) + z_2 \right) \mathbb {1}_{\left\{ T-t_0 \in [-1,-\frac{1}{2}[ \right\} } \right] , \end{aligned}$$

(42)

with $n = \left\lfloor T-t_0 \right\rfloor$, $\alpha = T- t_0 - \left\lfloor T-t_0 \right\rfloor$, $z_1 = \frac{1}{2} + \frac{1}{\lambda }$, $z_2 = \frac{1}{2} - \frac{1}{\lambda }$ and $z_3 = z_1 - \alpha$, and with the convention $\sum ^{p}_{k=0}{e^{\lambda k}}=0$ if $p<0$.

The proof of (40) is straightforward. The proofs of (41) and (42) are lengthy and omitted here for brevity, but available from the authors upon request.

Expected integrated variance

We provide the proofs of the two results given in Sect. 3.2 of the main manuscript. These results correspond to the expected integrated variance of a futures with maturity $T_m$. For more details on these developments we refer to Bollerslev and Zhou (2002) and Kaeck and Alexander (2012).

The Cox–Ingersoll–Ross square-root process is described by the following SDE:

$$\begin{aligned} dv_t = \kappa (\theta - v_t) dt + \sigma \sqrt{v_t} dB_t, \quad v_0 > 0. \end{aligned}$$

We know that for $T > t$:

$$\begin{aligned} E_t[v_T] = e^{-\kappa (T - t)} v_t + \theta \left( 1 - e^{-\kappa (T - t)} \right) . \end{aligned}$$

(43)

It follows, by exchanging the integrals, that:

$$\begin{aligned} E_t \left[ \int _t^T v_s ds \right]&= \int _t^T E_t[v_s] ds \\&= \int _t^T e^{-\kappa (s - t)} v_t + \theta \left( 1 - e^{-\kappa (s - t)} \right) ds \\&= \frac{1 - e^{-\kappa (T - t)}}{\kappa } v_t + \theta (T - t) - \theta \frac{1 - e^{-\kappa (T - t)}}{\kappa }. \end{aligned}$$

When the mean-reversion level is time-dependent, the dynamics and the expected variance at time $T>t$ become:

$$\begin{aligned}&dv_t = \kappa (\theta (t) - v_t) dt + \sigma \sqrt{v_t} dB_t, \quad v_0 > 0.\nonumber \\&E_t[v_T] = e^{-\kappa (T - t)} v_t + \kappa e^{-\kappa T} \int _t^T e^{\kappa u} \theta (u) du. \end{aligned}$$

(44)

It follows, by exchanging the integrals twice, that:

$$\begin{aligned} E_t \left[ \int _t^T v_s ds \right]&= \int _t^T E_t[v_s] ds \\&= \int _t^T \left[ e^{-\kappa (s - t)} v_t + \kappa e^{-\kappa s} \int _t^s e^{\kappa u} \theta (u) du \right] ds \\&= \frac{1 - e^{-\kappa (T - t)}}{\kappa } v_t + \kappa \int _t^T \int _t^s e^{-\kappa s} e^{\kappa u} \theta (u) du \; ds \\&= \frac{1 - e^{-\kappa (T - t)}}{\kappa } v_t + \kappa \int _t^T e^{\kappa u} \theta (u) \int _u^T e^{-\kappa s} ds \; du \\&= \frac{1 - e^{-\kappa (T - t)}}{\kappa } v_t + \int _t^T \left( 1 - e^{-\kappa (T - u)} \right) \theta (u) du. \end{aligned}$$

It can be easily verified that this expression is equal to the expression obtained above when the function $\theta$ is constant.

Let $T_m$ be the maturity of a futures contract, with $T_m> T > t$. We now calculate the expression (43) with an exponential damping factor:

$$\begin{aligned} E_t[e^{-\lambda (T_m - T)} v_T]&= e^{-\lambda (T_m - T)} E_t[v_T] \\&= e^{-\lambda (T_m - T)} \left[ e^{-\kappa (T - t)} v_t + \theta \left( 1 - e^{-\kappa (T - t)} \right) \right] . \end{aligned}$$

It follows, by exchanging the integrals, that:

$$\begin{aligned} E_t \left[ \int _t^T e^{-\lambda (T_m - s)} v_s ds \right]&= \int _t^T E_t[e^{-\lambda (T_m - s)} v_s] ds \\&= \int _t^T e^{-\lambda (T_m - s)} \left[ e^{-\kappa (s - t)} v_t + \theta \left( 1 - e^{-\kappa (s - t)} \right) \right] ds \\&= v_t \int _t^T e^{(\lambda - \kappa ) s - \lambda T_m + \kappa t} ds + \theta \int _t^T \left( e^{-\lambda (T_m - s)} - e^{(\lambda - \kappa ) s - \lambda T_m + \kappa t} \right) ds \\&= v_t \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) \\&\quad + \theta \frac{1}{\lambda } \left( e^{-\lambda (T_m - T)} - e^{-\lambda (T_m - t)} \right) \\&\quad - \theta \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) . \end{aligned}$$

We now calculate the expression (44) with an exponential damping factor:

$$\begin{aligned} E_t[e^{-\lambda (T_m - T)} v_T]&= e^{-\lambda (T_m - T)} E_t[v_T] \\&= e^{-\lambda (T_m - T)} \left[ e^{-\kappa (T - t)} v_t + \kappa e^{-\kappa T} \int _t^T e^{\kappa u} \theta (u) du \right] . \end{aligned}$$

It follows, by exchanging the integrals twice, that:

$$\begin{aligned} E_t \left[ \int _t^T e^{-\lambda (T_m - s)} v_s ds \right]&= \int _t^T E_t[e^{-\lambda (T_m - s)} v_s] ds \\&= \int _t^T e^{-\lambda (T_m - s)} \left[ e^{-\kappa (s - t)} v_t + \kappa e^{-\kappa s} \int _t^s e^{\kappa u} \theta (u) du \right] ds \\&= v_t \int _t^T e^{(\lambda - \kappa ) s - \lambda T_m + \kappa t} ds \\&\quad + \int _t^T \int _t^s \kappa e^{-\lambda T_m + \lambda s - \kappa s + \kappa u} \theta (u) du \; ds \\&= v_t \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) \\&\quad + \int _t^T \int _u^T \kappa e^{(\lambda - \kappa ) s -\lambda T_m + \kappa u} \theta (u) ds \; du \\&= v_t \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) \\&\quad + \int _t^T \frac{\kappa }{\lambda - \kappa } \theta (u) \left( e^{(\lambda - \kappa ) T -\lambda T_m + \kappa u} - e^{(\lambda - \kappa ) u -\lambda T_m + \kappa u} \right) du \\&= v_t \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) \\&\quad + \int _t^T \frac{\kappa }{\lambda - \kappa } \theta (u) \left( e^{-\lambda (T_m - T) - \kappa (T - u)} - e^{-\lambda (T_m - u)} \right) du \\&= v_t \frac{1}{\lambda - \kappa } \left( e^{-\lambda (T_m - T) - \kappa (T - t)} - e^{-\lambda (T_m - t)} \right) \\&\quad + \frac{\kappa }{\lambda - \kappa } e^{-\lambda (T_m - T)} \int _t^T e^{-\kappa (T - u)} \theta (u) du \\&\quad - \frac{\kappa }{\lambda - \kappa } \int _t^T e^{-\lambda (T_m - u)} \theta (u) du. \end{aligned}$$

Note that $\frac{-\kappa }{\lambda - \kappa } = 1 - \frac{\lambda }{\lambda - \kappa }$. When setting $\lambda = 0$ and/or $\theta (u) = \theta = {\textit{const}}$, we find the previous results obtained above.

Average volatilities

This appendix provides the average volatilities computed from our datasets, with a breakdown per contract and per calendar month.

In Table 8, we report, for each commodity, the average volatility of each futures series in our sample. In Table 9, we report, for each commodity, the average volatility per calendar month of the first futures contract. In addition, we identify the two calendar months with the highest volatilities.

Table 8 Average volatilities for each futures contract in our dataset

Table 9 Average volatilities, per calendar month, for the first futures series (c1) in our dataset

Estimated parameters

In this appendix we report, for the six seasonality patterns examined, the results of the maximum likelihood estimation procedure for Corn (Table 10), Cotton (Table 11), Soybeans (Table 12), Sugar (Table 13) and Wheat (Table 14).

Table 10 Estimated parameters for Corn

Table 11 Estimated parameters for Cotton

Table 12 Estimated parameters for Soybeans

Table 13 Estimated parameters for Sugar

Table 14 Estimated parameters for Wheat

Additional plots

See Fig. 5.

Results with alternative datasets

The results obtained with the alternative datasets are found in this appendix.

Fig. 5

Results of the likelihood-ratio tests for each commodity: seasonal models versus the non-seasonal model. The bars represent the values taken by the D statistic of the test. The horizontal lines correspond to the significance thresholds where the (null) hypothesis of a non-seasonal model is rejected at 99% (green), 99.9% (red) and 99.99% (black) confidence levels. Tested seasonal models are numbered as: 1. sinusoidal, 2. exp-sinusoidal, 3. triangle, 4. sawtooth and 5. spiked. Upper left Corn. Upper right Cotton. Centre left Soybeans. Centre right Sugar. Bottom Wheat. (Color figure online)

Table 15 Summary of the results obtained with the considered models estimated with the alternative datasets: log-likelihood, AIC, BIC, Statistics D1 and D2 of the likelihood-ratio tests and their p-values, AIC differences $\varDelta _{{\textit{aic}}}$ and Akaike weights $\omega _i$

Table 16 Model rankings for each commodity

Table 17 Summary of the results obtained with the alternative datasets for the volatility peaks prediction: the selected seasonal models, the majority vote of these models and the non-seasonal model

The estimation results obtained with the alternative datasets, described in Sect. 4.7 of the main text, are presented in Table 15. This table shows, for each commodity and model, the log-likelihood obtained, the AIC, the BIC, the value taken by the statistic D1 of the first likelihood ratio test, its p-value and the AIC difference and Akaike weight. In addition, it provides the log-likelihood obtained after estimating the nested versions of the models considered, obtained when setting $\lambda =0$, and the value taken by the statistic D2 of the second likelihood ratio test and its p-value. We provide the model rankings for each commodity in Table 16. These rankings are based on the AIC differences described and discussed in Sect. 5 of the main text. In this table, we also provide the ranking of models obtained across commodities by computing the sum of their ranks. Table 17 presents the results of this volatility peak prediction in the alternative datasets. For each commodity, we provide the results obtained using the three seasonal models selected and the non-seasonal model. We also provide the results for a meta-predictor that combines the three seasonal predictors via a majority vote. For each model we provide: accuracy rate, RMSE ratio against a random walk and the Diebold-Mariano statistic, $S_{{\textit{DM}}}$, for the model against the non-seasonal model.

• Table 15: the likelihood scores are higher than those obtained with the initial datasets, except for cotton. Likelihood-ratio tests confirm the importance of modelling the seasonality and the Samuelson effect. For seasonality, the obtained p-values are slightly higher for corn, sugar and wheat, compared to the results with the initial datasets. However, for all commodities, the majority of confidence levels associated with the seasonality test remain above 99.99%, and all of them are above this value for the Samuelson effect.

• Table 16: the ranking of models is now different, but the three best-ranked models remain the same for each commodity and in the overall ranking. The non-seasonal model is always ranked sixth, i.e. last. The best-performing model in the overall ranking now changes: while the sinusoidal pattern performed best with the initial datasets, the spiked pattern now performs best with the alternative datasets. This remark points toward model uncertainty with respect to the best seasonality pattern, and supports the selection of the top three models for the out-of-sample analysis. The in-sample performance spread between best and worst models, as measured by $\varDelta _{{\textit{aic}}}$ of the sixth model, is tighter for corn and cotton. This indicates a slightly weaker evidence of seasonality for these commodities in the alternative datasets, in line with the above comments.

• Table 17: when predicting volatility peaks during the 2017–2019 period, results are similar to those obtained with the initial datasets. The seasonal models always perform better than the non-seasonal benchmark. Accuracy rates near or above 80% are reached with seasonal models for corn, soybeans and wheat. For cotton, accuracy rates obtained with seasonal models are near 70%. The p-values of the Diebold-Mariano tests are lower with the alternative datasets, indicating a stronger evidence in favor of the model against a random walk predictor. In line with the initial dataset, sugar is the only commodity where the futures-based model developed in the paper fails to perform better than a random predictor.

Conclusion: in this robustness check, we clearly confirm the results already obtained with the initial datasets.