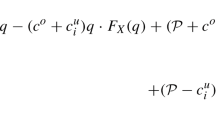Abstract
In this paper, we are concerned with the optimal order quantities for a risk-averse newsvendor with backlogging, where it is assumed that all or part of the unsatisfied demands can be fullfilled by backordering. The optimal order quantities are derived under the famous conditional value-at-risk (CVaR) criterion and mean-CVaR criterion on controlling the profit loss due to the uncertainty of market demands. With the optimal order quantities to the proposed models, several important monotone properties are obtained and their relationships with the existing results are discussed. Moreover, it is shown in this paper that low risk means low expected profit while high expected profit comes with high risk. Finally, we present some managerial insights for the risk-averse newsvendor model under backlogging.





Similar content being viewed by others
References
Agrawal, V., & Seshadri, S. (2000). Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem. Manufacturing and Service Operations Management, 2, 410–423.
Anastasios, X., Dimitrios, V., & Eleftherios, I. (2012). Optimal newsvendor policies for dual-sourcing supply chains: A disruption risk management framework. Computers & Operations Research, 39(2), 350–357.
Bai, C., Govindan, K., Satir, A., & Yan, H. (2019). A novel fuzzy reference-neighborhood rough set approach for green supplier development practices. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03456-z.
Biswajit, S., & Iikyeong, M. (2014). Improved quality, setup cost reduction, and variable backorder costs in an imperfect production process. International Journal of Production Economics, 155, 204–213.
Bolton, G. E., & Katok, E. (2008). Learning-by-doing in the newsvendor problem: A laboratory investigation of the role of experience and feedback. Manufacturing & Service Operations Management, 10(3), 519–538.
Chen, S., Wang, H., Xie, Y., & Qi, C. (2014). Mean-risk analysis of radio frequency identification technology in supply chain with inventory misplacement: Risk-sharing and coordination. Omega, 46, 86–103.
Chen, Y., Xu, M., & Zhang, Z. G. (2009). A risk-averse newsvendor model under the CVaR criterion. Operations Research, 57, 1040–1044.
Choi, S., & Ruszczyński, A. (2011). A multiproduct risk-averse newsvendor with exponential utility function. European Journal of Operational Research, 214, 78–84.
Choi, T. M., Li, D., & Yan, H. (2008). Mean-variance analysis for the newsvendor problem. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 38, 1169–1180.
Eeckhoudt, L., Gollier, C., & Schlesinger, H. (1995). The risk averse (and prudent) newsboy. Management Science, 41, 786–794.
Emilio, C., Alba, V. O. N., & Pepa, R. C. (2016). Robust newsvendor problem with autoregressive demand. Computers & Operations Research, 68, 123–133.
Eric, T. A., Gavan, J. F., & Duancan, S. (2006). Measuring and mitigating the costs of stockouts. Management Science, 52, 1751–1763.
Gan, X., Sethi, S. P., & Yan, H. (2004). Coordination of supply chains with risk-averse agents. Production and Operations Management, 13, 135–149.
Gan, X., Sethi, S. P., & Yan, H. (2005). Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer. Production and Operations Management, 14, 80–89.
Ghiami, Y., & Beullens, P. (2016). Planning for shortages? Net present value analysis for a deteriorating item with partial backlogging. International Journal of Production Economics, 178, 1–11.
Gruen, T., & Corsten, D. (2002). Rising to the challenge of out-of-stocks. ECR Journal, 2, 45–58.
Gurnani, H., & Tang, C. S. (1999). Note: Optimal ordering decisions with uncertain cost and demand forecast updating. Management Science, 45, 1456–1462.
Jaksic, M., & Fransoo, J. C. (2015). Optimal inventory management with supply backordering. International Journal of Production Economics, 159, 254–264.
Johansen, S. G., & Thorstenson, A. (2014). Emergency orders in the periodic-review inventory system with fixed ordering costs and compound Poisson demand. International Journal of Production Economics, 157, 147–157.
Li, B., Hou, P., Chen, P., & Li, Q. (2016). Pricing strategy and coordination in a dual channel supply chain with a risk-averse retailer. International Journal of Production Economics, 178, 154–168.
Lodree, E. J, Jr. (2007). Advanced supply chain planning with mixtures of backorders, lost sales, and lost contract. European Journal of Operational Research, 181, 168–183.
Mehmet, S., Jacqueline, M. B. R., Rene, H., & Jack, G. (2018). Modeling a green inventory routing problem for perishable products with horizontal collaboration. Computers & Operations Research, 89, 168–182.
Montgomery, D. C., Bazaraa, M. S., & Keswani, A. K. (1973). Inventory models with a mixture of backorders and lostsales. Naval Research Logistics Quarterly, 20, 255–263.
Pando, V., San José, L. A., García-Laguna, J., & Sicilia, J. (2013). A newsboy problem with anemergency order under a general backorder rate function. Omega, 41, 1020–1028.
Pentico, D. W., Toews, C., & Drake, M. J. (2015). Approximating the EOQ with partial backordering at an exponential or rational rate by a constant or linearly changing rate. International Journal of Production Economics, 162, 151–159.
Rockafellar, R. T., & Uryasev, S. (2000). Optimization of conditional value-at-risk. The Journal of Risk, 2, 21–41.
Rockafellar, R. T., & Uryasev, S. (2002). Conditional value-at-risk for general loss distributions. Journal of Banking & Finance, 26, 1443–1471.
San josé, L. A., Sicilia, J., & Garciá-Laguna, J. (2006). Analysis of an inventory sys-tem with exponential partial backordering. International Journal of Production Economics, 100, 76–86.
Schweitzer, M. E., & Cachon, G. P. (2000). Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence. Management Science, 46, 404–420.
Sphicas, G. P. (2014). Generalized EOQ formula using a new parameter: Coefficient of backorder attractiveness. International Journal of Production Economics, 155, 143–147.
Taleizadeh, A. A., Khanbaglo, M. P. S., & Cárdenas-Barrón, L. E. (2016). An EOQ inventory model with partial backordering and reparation of imperfect products. International Journal of Production Economics, 182, 418–434.
Turgut, M., Serhan, D., & Ismail, S. B. (2013). Tactical inventory and backorder decisions for systems with predictable production yield. International Journal of Production Economics, 143, 294–303.
Wang, Y. J., Sun, X. F., & Meng, F. X. (2016). On the conditional and partial trade credit policy with capital constraints: A Stackelberg model. Applied Mathematical Modelling, 40(1), 1–18.
Weng, Z. K. (2004). Coordinating order quantities between the manufacturer and the buyer: A generalized newsvendor model. European Journal of Operational Research, 156, 148–161.
Wouter, L., El-Houssaine, A., Khaled, Ha, & Bernard, P. (2018). Analysis of an improved branch-and-cut formulation for the inventory-routing problem with transshipment. Computers & Operations Research, 98, 137–148.
Wu, J., Li, J., Wang, S., & Cheng, T. C. E. (2009). Mean-variance analysis of the newsvendor model with stockout cost. Omega, 37, 724–730.
Wu, M., Zhu, S. X., & Teunter, R. H. (2014). A risk-averse competitive newsvendor problem under the CVaR criterion. International Journal of Production Economics, 156, 13–23.
Xu, J., Zhou, X. H., Zhang, J. H., & Long, D. Z. Y. (2019). The optimal channel structure with retail costs in a dual-channel supply chain. International Journal of Production Research. https://doi.org/10.1080/00207543.2019.1694185.
Xu, M., & Li, J. (2010). Optimal decisions when balancing expected profit and conditional value-at-risk in newsvendor models. Journal of Systems Science and Complexity, 23, 1054–1070.
Xu, X., Chan, C. K., & Langevin, A. (2018). Coping with risk management and fill rate in the loss-averse newsvendor model. International Journal of Production Economics, 195, 296–310.
Xu, X., & Chan, F. T. S. (2019). Optimal option purchasing decisions for the risk-averse retailer with shortage cost. Asia-Pacific Journal of Operational Research, 36(2), 1–25.
Xu, X., Chan, F. T. S., & Chan, C. K. (2019). Optimal option purchase decision of a loss-averse retailer under emergent replenishment. International Journal of Production Research, 57(4), 4594–4620.
Xu, X., Meng, Z., Ji, P., Dang, C., & Wang, H. (2016). On the newsvendor model with conditional value-at-Risk of opportunity loss. International Journal of Production Research, 54(8), 2449–2458.
Xu, X., Meng, Z., Shen, R., Jiang, M., & Ji, P. (2015). Optimal decisions for the loss-averse newsvendor problem under CVaR. International Journal of Production Economics, 164, 146–159.
Xu, X., Wang, H., Dang, C., & Ji, P. (2017). The loss-averse newsvendor model with backordering. International Journal of Production Economics, 188, 1–10.
Xue, W., Ma, L., & Shen, H. (2015). Optimal inventory and hedging decisions with CVaR consideration. International Journal of Production Economics, 162, 70–82.
Zhang, J., Liu, H., Yu, G., Ruan, J., & Chan, F. T. S. (2019). A three-stage and multi-objective stochastic programming model to improve the sustainable rescue ability by considering secondary disasters in emergency logistics. Computers & Industrial Engineering, 135, 1145–1154.
Zhang, J., Liu, Y., Zhao, Y., & Deng, T. (2018). Emergency evacuation problem for a multi-source and multi-destination transportation network: Mathematical model and case study. Annals of Operations Research. https://doi.org/10.1007/s10479-018-3102-x.
Zhang, Y., & Yang, X. (2016). Online ordering policies for a two-product, multi-period stationary newsvendor problem. Computers & Operations Research, 74, 143–151.
Zheng, M., Wu, K., & Shu, Y. (2016). Newsvendor problems with demand forecast updating and supply constraints. Computers & Operations Research, 67, 193–206.
Zhou, Y. J., Chen, X. H., & Wang, Z. R. (2008). Optimal ordering quantities for multi-products with stochastic demand: Return-CVaR model. International Journal of Production Economics, 112, 782–795.
Zhou, Y. W., & Wang, S. D. (2009). Manufacturer-buyer coordination for newsvendor-type-products with two ordering opportunities and partial backorders. European Journal of Operational Research, 198, 958–974.
Acknowledgements
This work was supported by the National Natural Science Foundation of China with Grant 71871026, the Shandong Social Science Planning Foundation with Grant 20CJJJ06 and the Innovation Method Fund of China with Grant 2018IM020200. The authors would also like to thank the Qilu Young Scholars and Tang Scholars of Shandong University for financial and technical support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 4.1
Define
By the definition of the profit function \(P(q, \xi )\) in (1), it can be easily checked that
It follows from Rockafellar and Uryasev (2002) that h(q, v) is jointly concave in (q, v).
We note that the CVaR model (4) is equivalent to
To solve this problem, we distinguish between two cases: \( b\le \frac{ w(p_1)(p_1-c_s) }{1-w(p_1)}\) and \(b\ge \frac{ w(p_1)(p_1-c_s) }{1-w(p_1)} \) respectively.
(i) \( b\le \frac{ w(p_1)(p_1-c_s) }{1-w(p_1)}\). The proof below aims to find the optimal solution of the inner problem of (9) when a particular q is given. We consider the following three cases.
Case 1 \(v<(r-c)q\). For this case, it follows from (8) that
and hence
It follows from the concavity of \(h(q, \cdot )\) that the maximum of \(h(q, \cdot )\) cannot be attained for this case.
Case 2 \((r-c)q \le v < (p-c)q\). For this case, it follows from (8) that
and
Obviously, it satisfies \(\frac{\partial h(q,v)}{\partial v}|_{v=(r-c)q}=1>0\). If \(q\ge F^{-1}(1-\alpha )\), we must have
By the continuous differentiability of \(h(q, \cdot )\), there exists \(v^* \in [(r-c)q, (p-c)q)\) such that
which implies
It follows from the concavity of \(h(q, \cdot )\) that the maximum of \(h(q, \cdot )\) is attained at \(v^*\) when \(q\ge F^{-1}(1-\alpha )\).
Case 3. \(v \ge (p-c)q \). For this case, it follows from (8) that
and
Note that \(\alpha >0\), we have
If \(q\le F^{-1}(1-\alpha )\), we have
Due to the continuous differentiability of \(h(q, \cdot )\), there must exist \(v^*\) such that
which implies
It follows from the concavity of \(h(q, \cdot )\) that the maximum of \(h(q, \cdot )\) is attained at \(v^*\) when \(q\le F^{-1}(1-\alpha )\).
Putting together the three cases, we have proved that the optimal solution \(v^*\) to the inner problem of (9) is given by
Therefore, the problem (9) is reduced to
Since \(v^*\) is a linear function of q, \(h(q, v^*)\) is concave in q due to the fact that h(q, v) is jointly concave in (q, v). The rest of the proof is to show that the maximum of \(h(q, v^*)\) is attained.
We consider two situations. One is \(q\ge F^{-1}(1-\alpha )\). It follows from (8) and (10) that
and
By the concavity of \(h(q, v^*)\) in q, the maximum of \(h(q, v^*)\) cannot be achieved for this situation.
The remaining situation is \( q\le F^{-1}(1-\alpha ) \). It follows from (8) and (10) that
and
Since it satisfies
There must exist \(q_1^*\in (0, F^{-1}(1-\alpha ))\) such that
which gives
It follows from the concavity of \(h(q, v^*)\) that \(q^*_1\) is the optimal solution of (11), and hence is also the optimal solution of (9) for the case of i).
(ii) \(b\ge \frac{w(p_1)(p_1-c_s) }{1-w(p_1)}\). The proof is similar to the case of i), which is omitted herein. This completes the proof. \(\square \)
Proof of Corollory. 4.2
Since \(F(\cdot )\) is monotonically increasing, it follows from the formula of \(q_1^*\) that \(q_1^*\), as a function of c, \(p_1\), b, r and \(c_s\), has the corresponding increasing or decreasing properties as stated in the corollary. This completes the proof. \(\square \)
Proof of Corollory. 4.3
The proof is similar to that of Corollary. 4.2, which is omitted herein. \(\square \)
Proof of Corollory 4.4
It follows from (1) that
We calculate
If \(b \le \frac{w(p_1)(p_1-c_s) }{1-w(p_1)} \), it follows with Theorem 4.1 that \(q^*_1=F^{-1} \Big ( \frac{(1-\alpha )(p-c+b-w(p_1)(p_1-c_s+b))}{p-r+b-w(p_1)(p_1-c_s+b)}\Big )\) and \(\frac{\partial q^*_1 }{\partial \alpha }\le 0\). We recall that
which gives
We also recall \(q_1^* \le q_0^*\). The monotonicity of \(F(\cdot )\) implies
It follows with (12) and \(\frac{\partial q^*_1 }{\partial \alpha }\le 0\) that
which proves that \(\texttt {E\;}[P(q^*_1, \xi )]\) is decreasing in the confidence level \(\alpha \) when \(b \le \frac{w(p_1)(p_1-c_s) }{1-w(p_1)} \). The proof for the case of \(b\ge \frac{w(p_1)(p_1-c_s) }{1-w(p_1)}\) is similar to that for the case of \(b \le \frac{w(p_1)(p_1-c_s) }{1-w(p_1)} \), which is omitted herein. This completes the proof. \(\square \)
Proof of Theorem 4.5
The proof is similar to that for Theorem 4.1, which is omitted herein. \(\square \)
Rights and permissions
About this article
Cite this article
Zhang, J., Chan, F.T.S. & Xu, X. The optimal order decisions of a risk-averse newsvendor under backlogging. Ann Oper Res 329, 225–247 (2023). https://doi.org/10.1007/s10479-020-03636-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-020-03636-2