Abstract
Very short manufacture cycle times are required if continuous carbon fibre and epoxy composite components are to be economically viable solutions for high volume composite production for the automotive industry. Here, a manufacturing process variant of resin transfer moulding (RTM), targets a reduction of in-mould manufacture time by reducing the time to inject and cure components. The process involves two stages; resin injection followed by compression. A flow simulation methodology using an RTM solver for the process has been developed. This paper compares the simulation prediction to experiments performed using industrial equipment. The issues encountered during the manufacturing are included in the simulation and their sensitivity to the process is explored.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The higher specific modulus of carbon composites materials offers light weighting opportunities over aluminium and steel for the automotive industry. In this sector, composite design proves cost effective when the part count of structures is significantly reduced, leading to large components with complex geometry. To manufacture these components at the volumes and cycle times required by the automotive sector, fast curing resins and high pressure, high volume flow rates are needed in liquid moulding processes.
The volume flow rate necessary will be in the realms of 35-85 g/s dependent on component size and the resin cure time at the tool temperature, the trade-off is illustrated in Fig. 1. Impingement mixing equipment similar to that used in the reaction injection moulding (RIM) and structural reaction injection moulding (SRIM) processes allows the resin to be injected at a high volume flow rate. However, the resultant injection pressure to achieve the desired flow rate through the porous medium can be in excess of 200 bar, exceeding the capability of the equipment.
This is certainly true in the RTM process, as the fabric is in its compressed form to its designed thickness and hence the permeability of the fabric is quite low. Thus a very high injection pressure is required to maintain high flow rates needed, as the resin has to flow from one end of the mould to the other end in the in-plane direction, as shown in Fig. 2a. One way to overcome this is to create a gap between the mould wall and the preform surface and inject the resin to flood this gap, and in a second stage the tool compression pushes the resin through the thickness, as shown in Fig. 2b. This would require the resin to just flow through the thickness of the fabric. However, the compression phase can reduce the permeability of the fabric in the thickness direction quite dramatically by two to three orders of magnitude, which may again require very large pressures to flow even this short distance. The process does not lend itself to geometries with any amount of draw, since compression is not applied on surfaces that deviate from perpendicular to the force applied. The more maligned the surface, the less compression, and resin will not wet out the preform.
a) Standard RTM process in which the resin is injected into a compressed preform in the in-plane direction b) Injection Compression RTM in which the resin is introduced in the gap between the preform and the mould wall and compressed after it floods the preform surface c) Mould wall in contact with the uncompressed preform introducing the in-plane flow with a low fibre volume fraction followed by compaction
Another way to address this is shown in Fig. 2c in which the preform is in its uncompressed form but is in contact with the tool surface. Resin is injected and flows in the in-plane direction. The compression is applied after the resin injection is complete to obtain the desired thickness, in order to obtain the fibre volume fraction required without bleeding resin from within the sealed cavity, a metered volume of resin is injected corresponding to the desired fibre volume fraction at the nominal thickness. The closing tool redistributes the resin in the partially filled material in order to complete wet-out and achieve a higher volume fraction.
The press closes the mould at an assigned speed and will close the mould using the assigned force limit. The press force is needed to overcome the elastic force from preform compression, the fluid pressure and to compact the mould seals. If the mould reaction forces exceed the assigned press force, then the mould will not completely close. We will call this process Advanced Liquid Composite Moulding (ALCM). Fundamental to the ALCM process is that the preform is not over compacted such that when the gap is maintained during resin injection, a space is not left between the preform and the mould surface. The flow front thus remains in-plane in the preform.
In order for the process to work the preform must be sufficiently stable to resist being washed by the resin. Means to stabilise the preform include clamping inside the mould that serve to grip the preform mechanically, using a sufficient amount of binder to maintain a compacted preform at the mould temperature and selection of a fabric with close weave or stitch that is able to resist wash. This work is focussed on the feasibility of using a Darcy flow solver to simulate the ALCM process and validate it on an industrial size component.
2 Previous Work on Modelling Injection Compression Process
An RTM tool suitable for the high pressure process will need to be strong and robust and will therefore have high cost and long lead time. Development tools that are not intended for a long production will need to be strong to withstand the press forces and can also cost a significant amount. Flow simulation of the process can be used for the specification and procurement of complex and expensive tools, and to create an industrialised and robust design and process.
In terms of the process model a mould filling simulation can provide resin arrival time and resin velocity and pressure. If coupled with heat transfer analysis and cure kinetics model can provide the cure progression and therefore material state history to give better predictions on the material distortion. Currently there are many flow simulations that describe the resin flow in a RTM or VARTM process using Darcy’s law [1] as shown below.
Equation 1 describes volumetric flow in terms of the pressure gradient (∇p) across a porous media; the flow is a function of the viscosity μ of the fluid and permeability K of the media through which it is permeating. The permeability of the fabric is determined separately as a function of fibre volume fraction (FVF) and reduces dramatically as the fibre volume increases.
Many studies to model injection-compression moulding process have been conducted in the past. In a very early attempt, Han et al. [2] incorporate flow in gaps in the model by lumped permeability approach, i.e. the permeability is homogenised between the preform and the gap, showing fairly accurate prediction of pressure profile and flow front position. The author (Han [2]) concludes that conventional LCM simulation code can be modified to simulate the injection/compression process with the advantage of reducing the moulding pressure significantly and a more regular filling pattern.
Simacek et al. [3] [4] and Bhat et al. [5] have developed injection-compression RTM simulation by three-dimensional analysis. The analysis considers no preform deformation under compaction, in their approach in three distinct phases; initial injection into the narrow gap between the preform and the mould tool, closing the gap, and wetted preform compaction. Merrotte et al. [6] [7] devised an analytical model to predict the force and wet-out of the preform under compaction, representing the case with through thickness deformation of the preform under compaction.
In order to make a simultaneous prediction of preform compression along with the resin flow in the injection followed by compression process (with through thickness deformation of the preform under compaction), Pillai et al. [8] use a mechanical mesh to simulate preform compaction, and a flow mesh to simulate the motion of the resin in the preform and gap. Discretised into layers of material in the preform, the layer material properties are used to compute compaction and changes to permeability, and the flow mesh is adapted to the calculated layer changes. Pillai et al. [9] assign a layer in the 3D mesh for gap resin and apply non-linear material properties on 3D geometry. The method is a novel approach to the injection-compression simulation, however the work has not demonstrated any correlation to experiment.
Researchers applying an in-plane flow to the injection followed by compression process include Bickerton and Abdullah [10], who present an analytical solution. The analytical solution follows Darcy’s law and calculates resin force across filled nodes with fibre force based on compression tests. Using experimental apparatus to inject fluid inside a compression test machine, experiments of injection followed by compression are made and both constant speed and constant force compression. Good correlation was found between the experiments and numerical predictions, concluding that shorter fill times have a trade-off with higher clamping force to compact.
Kelly et al. [11] made an in-plane simplification for simulation of the injection-compression process using FEM/CV method using SimLCM ‘a purpose built finite element code under development at the University of Auckland’. The authors couple Darcy flow to a change in thickness of the mould. The simulation is used to calculate clamping force and output shear and normal stresses. Different compaction models are applied to wet and dry fabric. Friction between the tool and fabric is measured and applied at all angled surfaces. The experimental clamping force is compared to the simulation result showing a good correlation for the flat disc and hemisphere studied.
This work uses flow simulation software LIMS (Liquid Injection Moulding Simulation) from the University of Delaware to model the ALCM process. The flow simulation uses finite element and control volume method. The solver uses Darcy law to describe the physics of the flow and to solve nodal pressures. Flow is progressed by Darcy’s law and control volume filling. The software supports 1D, 2D and 3D elements. It is possible to modify model parameters at each timestep in the simulation, this is achieved using script control of the simulation. In the next section, we will describe the ALCM experiments and results and then show how we can use LIMS solver to model this process.
3 ALCM Experiment
3.1 Equipment, Materials and Method
The industrial equipment used for the experiments to manufacture the component comprises of a 36000kN press from Schuler and high pressure injection equipment from Krauss-Maffei (KraussMaffei RimStar Compact). The equipment is located at the National Composites Centre in the UK.
The flat plaque manufactured in the experiments has dimensions 1240 × 790 mm with an additional side tab from which the panel is injected measuring 318 × 147 mm. The nominal cavity thickness is 2.5 mm. Figure 3 shows the panel geometry and the preform in the open tool prior to resin injection.
The preform consists of four plies of 600gsm biaxial non-crimp fabric. Two plies each of [0,90] and [+,-45] oriented fibre fabric is arranged into quasi-isotropic lay-up. The fabric is made with a double tricot polyester stitch and has been coated with a heat activated cross-linking binder. The preform is prepared by consolidating oversized plies and heating under vacuum. The consolidated stack once cooled is trimmed to the component dimensions by CNC ply cutter, before being placed in the mould.
The fast cure resin from Solvay has a cure time of 7 min at 110 °C. At 110 °C, once mixed the resin has a period of 90 s before the viscosity rises sharply as the cure progresses rapidly and resin gelation begins.
The manufacturing process in the experiment injects the resin at a fixed volume flowrate of 75 g/s into the steel tool, which is maintained at 110 °C by an oil heating system. In-mould pressure is recorded by three Kistler pressure sensors at locations indicated in Fig. 3.
The mould is evacuated for 60 s prior to resin injection, at which point the vacuum valve is closed. Trials off-line demonstrated that the preform is heated fully to 110 °C within this time. In the injection stage the mould tool gap is set to 0.5 mm. The press is allowed a maximum 8500kN force to close the mould.
3.2 Partial Fill to Obtain Flow Fronts
Prior to manufacturing a full panel, interrupted filling is performed where the injection is stopped after 4.2, 11 and 14 s. As this is a fast curing resin, the resin front will solidify within a minute or less providing information about the movement of the flow front that can then be compared with the simulation result. The overlaid images of the short shots are shown in Fig. 4.
It can be seen from the partially filled panels that the presence of large areas of dry fabric validate the low fibre volume filling. There is no resin flooding on the preform surface, supporting the two-dimensional simulation approach.
3.2.1 Race Tracking Channels
The experimental flow front pattern shown in Fig. 4 reveal that the flow front is influenced by the presence of a gap around the mould perimeter. As the resistance to resin flow is very low in this gap, resin races in these channels affecting the flow front pattern. Investigation revealed that the race tracking channel is present due to the fibre clamping edge feature in the tool which creates the gap, as shown in Fig. 5. This feature was designed to shorten the cavity height to prevent the preform from moving during injection by gripping the preform at the edges through compression.
3.3 Pressure inside the Mould during Panel Manufacturing
A panel, designated panel 74, is injected with 1350 g of resin, equating to 18 s of injection time. By calculation this gives a final fibre volume fraction of 55% at nominal thickness, however the calculation does not account for any resin lost into the tool. The tool is fully sealed so there is no resin bleed and any resin leaving the component remains between the component and the tool.
The injection duration of 18 s ensures that the injection is complete prior to the rapid increase in viscosity of the resin at 110 °C temperature.
Shown on the graph in Fig. 6, the prescribed gap of 0.5 mm is recorded by the press as 0.45 mm by four corner LVDT on the press. The press records the force from the oil pressure of the 6 hydraulic cylinders of the upstroke press. The initial force on closing the press is recorded as 6000kN, this is the force to compress the seals and preform. During the injection the force to maintain the fixed gap increases. Once injection is complete after 18 s, the press closes at 0.1 mm/s until the maximum force limit of 8500kN is reached and the press can close no further.
4 Process Model
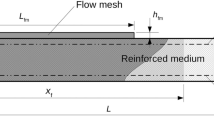
The process model for the ALCM process uses 2D elements to represent the preform. The z-direction gap allocated in the first stage of resin injection is incorporated by increasing the preform thickness. The fibre volume fraction is modified with the altered thickness and the corresponding permeability is included through reference to a constitutive model.
Inspection of the flow front on partially filled panels shown in Fig. 7 revealed that the flow front is lagging from top to bottom. The flow lag through the thickness is seen to be dependent on the sequence of plies. The lag has been measured at maximum 10 mm on a 2.5 mm thickness in planar sections as shown in Fig. 7, therefore an in-plane flow assumption is still justified.
4.1 Simulation Procedure
A two-dimensional mesh is created for the mould tool geometry, based on either the upper or lower mould surface. Equivalent to the manufacturing process, the simulation is set up in two stages. The first stage for resin injection and the second stage for mould closure and compaction.
The procedure to model injection followed by compression for the ALCM process is similar to the work by Simacek and Advani [3] using LIMS to simulate the injection compression moulding in the presence of preform surface flooding. The differences are that the ALCM simulation is employed in 2D for in-plane flow only, whereas Simacek has employed a 3D method for impregnation through the thickness.
4.1.1 First Stage: Resin Injection
In the first stage the press z-direction set gap is assigned for resin injection. The gap value is added to the mould cavity nominal thickness, giving the preform thickness, and from this the preform fibre volume fraction is calculated. The initial material properties of the preform are defined based on the fibre volume fraction and are assigned to elements in the mesh. The properties of the 2D elements are thickness, fibre volume fraction and permeability. 1D elements properties are cross section area, fibre volume fraction and permeability. Element properties remain fixed throughout the resin injection stage.
The resin inlet is defined at the appropriate node or nodes and the constant injection flow rate is assigned. The solution follows standard Darcy flow methodology in LIMS. A fill time or pressure limit is prescribed to stop the solution, ending with a partially filled component.
4.1.2 Second Stage: Mould Closure
In the second stage of manufacture, the tool closes due to the applied press force. The simulation initiates tool closing with application of a press closing velocity. At each timestep, the subsequent change in cavity height is applied to element thickness. As the thickness changes, the associated control volume changes. The preform volume doesn’t change as the thickness changes, therefore the porous volume changes. The change to resin volume utilises mass conservation to pass resin into unfilled element volumes.
The simulation achieves filling progression by calculating a volume flow rate at every node that corresponds to the porous volume lost by the change in thickness. The calculation is applied at filled nodes, designating the filled node as an injection gate with the calculated flow rate assigned for the next timestep.
Before the solution proceeds to the next timestep, the fibre volume fraction is calculated according to the new thickness of the tool cavity. The permeability corresponding to the fibre volume fraction is deduced by the constitutive model described in section 4.3 and the new material properties are applied to elements in the model.
The assumption has been made that press force closing results in thickness change only. The change to porosity is assumed to be even through the thickness and thus can be represented in two-dimensions.
The model assumes that the change in the preform volume is evenly distributed in the thickness direction and that the preform is fixed during the injection stage and any preform movement due to fibre wash is not incorporated in the model.
4.1.3 Force or Speed Closing
In the simulation, the press closure can be controlled by a prescribed closure speed or by a force limit (where the speed is adjusted at each timestep so as not to exceed the force limit). If a closure speed is assigned, no force limit is set.
Assigning a force limit requires an additional step in the calculation. The closure force necessary to close the mould will be composed of the force due to the resin pressure, the elastic force due to fabric compaction and the elastic force to compress mould seals. The limiting resin force is calculated from the constituents.
In the calculation of the force limit closure, an initial closure distance is calculated from an initial press closure speed. Force is calculated (comprising nodal pressure, fabric and seals compaction) and if the force exceeds the set force limit, then the closure distance is decreased by adjusting the closure speed, and the force is recalculated. The solution cannot proceed to the next timestep until the closure distance is reduced such that the force limit is not exceeded. The press speed therefore varies between timesteps.
Elastic force from fabric compression is calculated for the adjusted fibre volume fraction at each time step following the constitutive relation derived for the laminate. This elastic force is included in the force calculation for the closing force limit. The force to compress the mould seals is included as a constant (based on experiments) for simplicity.
Total force due to resin pressure is determined by summing the resin force calculated at each node i, \( {F}_{resin}=\sum \limits_i^n\left({P}_i\times {A}_i\right) \). Force due to preform compaction is calculated from the compaction stress determined by constitutive model for preform compaction described in section 4.3 and preform area (Felastic = σcAtotal) The press force is the sum of the resin force, elastic force and force due to seals compaction as shown below in Eq. 2.
Once calculated, the new material properties are assigned to every element in the model. Note that for surfaces that are not perpendicular to the press force direction, the thickness change in terms of local element orientation is calculated.
The solution ends when the final thickness is reached or every CV is filled.
4.2 Simulation Procedure
The procedure is explained by the flow chart in Fig. 8 where the press is closed by input press speed.
Stages of filling in LIMS are shown in Fig. 9. The first stage of resin injection is shown by Fig. 9a, the filled elements are coloured by fill time and the unfilled elements remain red. At the beginning of the second stage depicted by Fig. 9b, the filled nodes are injection gates. At the end of the second stage in Fig. 9c, all the nodes are filled. The elements are coloured by fill time and the nodes are all injection gates with the exception of the final two nodes in the right side corners.
4.3 Constitutive Models
The form of the constitutive models used in the simulation for the fabric compaction and permeability are taken from the literature. The constants needed for our fabric are characterized from laboratory experiments and are described below.
4.3.1 Preform Compression
Samples of the consolidated layup prepared in the same way as the experiment are compressed in between parallel plate fixtures in a 250kN Instron. To follow the manufacturing process the samples are tested at 110 °C, with the platens contained within a convection oven for the test. Once the samples are in the fixture and the temperature is stable, the platens close at 0.0833 mm/s (5 mm/min) and the Instron force is recorded. The platens are held at a distance of 2.5 mm for 1 min, since this is the final thickness of the cavity in the mould tool. The experiment was repeated 8 times and the data is plotted in Fig. 10.
Measured preform compaction data and derived model with comparable compaction stress presented by Grieser et al [12]
The compression stress and fibre volume fraction are calculated from the force output and sample geometry and mass. A power law model as shown in Eq. 3 is fit to the experimental data, where A = 55,000,000 and n = 10.9. The results from the experiment and the model fitting is shown in Fig. 10.
The results are comparable to the compaction stresses for carbon fibre NCF presented by Grieser et al. [12] and are shown on the data in Fig. 10 as well. Note that the compaction behaviour of the wet fibres will be different, and that stress relaxation is observed in the samples held at constant thickness for a minute which is not addressed in the model.
4.3.2 Permeability
Permeability of each material in the preform is measured experimentally using permeability rig as used in [13]. For in-plane permeability, when a laminate consists of different plies or plies are oriented in different directions, thickness weighting is applied following rule of mixtures to derive a homogeneous permeability through the thickness [14].
Where K1,2 are the laminate permeabilities in the principal directions and t is the laminate total thickness. For a number of plies n, ki ant ti are the ith ply permeability and thickness.
The Kozeny-Carman constitutive model for permeability is used to describe the change of permeability with fibre volume fraction (vf)
here c is the Kozeny-Carman constant determined by fitting the measured permeability value at a known FVF [15, 16]. The relationship is widely accepted as an approximation for extrapolation of permeability within a range of fibre volume fractions.
Kozeny-Carman constant is calculated from the experimental data at the given fibre volume fraction for both principal directions, and the permeability for a range of fibre volume fractions is extrapolated. The corresponding constant c for the preform K1 and K2 in-plane permeabilities are 6.33 × 10−9 m2 and 1.51 × 10−10 m2 respectively. The fit is shown in Fig. 11.
Preform permeability extrapolated using Kozeny-Carman eq. 5 (solid line = range of experiment fibre volume fraction)
4.4 Viscosity
The tool temperature is maintained at 110C within a tolerance of +/-2 °C. The resin and hardener components are maintained at 80 °C and 40 °C respectively, the temperature of the mixed resin is measured to be 76.6 °C when it enters the tool.
Resin viscosity has been measured on neat samples in an ARES2 shear rheometer. The initial mix viscosity over a temperature range is shown in Fig. 12. The initial mix viscosity at 75 °C is 0.1 Pas, the simulation is run with constant viscosity of 0.1 Pas as the filling is complete within a few seconds we do not expect the viscosity to change significantly with that time period.
4.5 Resin Channel
Without a porous medium for the resin to pass through, the flow in the channels at the component perimeter will not follow Darcy for flow through porous media. In order to incorporate the resin channel flow into the simulation a method is employed to approximate resin channel flow to Darcy flow by an equivalent channel permeability. This method has been used by several researchers studying the effect of resin channels [17].
Flow in the channels is geometry dependant since the velocity profile will be different for different geometry channels the permeability will also differ. The area of the channels are measured from six samples at the edge of the panels. The corresponding channel permeabilities are approximated based on rectangular and equilateral triangle approximation to the channel geometry shown in Eqs. 6 and 7 respectively [17, 18].
A triangular channel approximation is used for the channel at the fibre clamp feature. The permeability is calculated from the channel area, Ac by approximating the measured channel area to an equilateral triangle.
For the purpose of simulating the effect of the resin channel, a single channel is included in the model. The channel encompasses the effect of the fibre clamp channel and the preform edge to tool channel. The region of over-compacted laminate in the fibre clamp, which has different permeability to the bulk material, is omitted. The combined maximum and minimum area and permeabilities for the channels have a range of permeability from 3.9 × 10−7 to 2.1 × 10−8 m2, see Table 1.
The simulation is representing the preform edge in a simplified way as illustrated in Fig. 13 averaging the edge effect to a single channel. The simulation assumes a constant section channel around the whole perimeter whereas in reality the channel is seen to be variable in cross section area. This approach was taken since the section variations are not currently known in advance for each panel and is not expected to change the flow patterns significantly.
The combined maximum and minimum channel area have a range from 7.1 × 10−7 m2 to 1.6 × 10−5 m2 and have a range of channel permeability from 3.9 × 10−7 m2 to 2.1 × 10−8 m2, see Table 1.
The channel at the fibre clamp feature is consistently present in the panels but the edge to tool channel varies. The channels have all been measured at the end of the process and are subject to the change in thickness under compaction force, chemical shrinkage on cure and thermal contraction when cooled after removal from the tool. If measured during the process the areas measured would actually be larger.
In filling the panel the resin flows from the inlet into the preform and reaches first to the fibre clamp racetrack channel, only when the resin flows through the over-compacted material in the fibre clamp will the resin reach the racetrack channel around the edge of the component. If the material between the channels is cut short, or damaged in some way then the resin will flow into the channel around the edge sooner. The resin channel in the simulation is given cross sectional area of 5 × 10−6 m2 from the average combined area calculated in Table 1. The assigned channel permeability ranges between 1 × 10−6 and 1 × 10−9 m2. Utilising a constant area across all models, as shown in Fig. 14, removes the resin volume variable between simulations, the variation in the distribution of channels is encompassed by modifying the permeability.
4.5.1 Treatment of Resin Channels in the Compression Stage
During the second stage of the simulation, a change of thickness is applied as press force is applied to close the tool. The resin channel at the fibre clamp feature around the perimeter should not change since the machined feature geometry is not changing. However the height of the resin channel between the preform and the tool edge will reduce by the same amount as the press closes. The simulation has combined the two channels and the over compacted laminate, which will also reduce permeability as the mould closes, as a single edge effect. Since the unchanging fibre clamp feature is consistently filled, the simulation remains with fixed channel area and permeability during the press closure stage.
5 Simulation and Experiment Comparison
The simulation was run with the input parameters for the material (fabric and resin) and process parameters for the designated panel 74, the results of which for the pressure and filling pattern were compared during the injection and compression stage.
5.1 Injection Stage
Experimental setup to manufacture panel 74 are used for experiment and simulation comparison. The Injection flow rate is 75 g/s, 18 s injection is assigned corresponding to 1350 g resin (Table 2).
The pressure time history from the simulation for the range of racetrack permeabilities at the inlet location is shown in Fig. 15.
The inlet pressure sensor in the simulation records resin arrival earlier than the simulation. The lag is indicative of the delay for the resin to pass through the laminate thickness, since the pressure sensor is embedded in the opposite tool surface to the resin inlet.
Both the simulation and the experiment report a change in pressure gradient just after 2 s when the side tab fills with resin. The simulation with racetrack permeability of 5 × 10−8 m2 closely matches the rising pressure of the experiment in the early stages of injection.
Since the simulation is modelling constant flow injection, the pressure traces at the inlet show an increasing pressure throughout injection, however the experiment pressure plateaus contrary to the simulation. Two possible explanation could be (i) the viscosity of the resin continues to drop due to increase in temperature reducing the resistance to flow and/or (ii) the flow is dual scale, with the fiber tows filling at a later stage. A pressure droop in such cases would be very likely. Although we could model these two effects, we did not address this issue as that would require characterising the dual scale permeability of the fabric and is beyond the scope of this work. However we did explore the effect of changing viscosity during the filling.
5.1.1 Viscosity Effect
The viscosity dependence on temperature and cure may warrant full three-dimensional non-isothermal analysis of the process to fully account for the heat transfer from the tool and heated preform to the in-coming flow of mixed resin. However, the following linear approximation in Fig. 16 is made from the initial mix viscosity at 75 °C and the viscosity development at 110 °C.
Using the measured weight of panel 74 preform, the fibre volume fraction is greater than the nominal value and is applied to the simulation. The inlet pressure is shown in Fig. 17. With introduction of time dependent viscosity in the simulation and measured preform weight taken into account, omitting the first 2 s, the simulation prediction of inlet pressure falls within 12% of the experiment. It is possible that if we introduce dual scale flow, we may be able to account for the remaining difference.
5.2 Compression Stage
After injection is complete, the press is closed utilising the full prescribed press force. Applying a range of limiting forces in the simulation alters the speed of press closure, although this is akin to true press control, the press closure speed is fixed. The final thickness is the only limiting factor in the simulation the press is always permitted to close to nominal thickness which is not the case in reality.
Controlling the simulation by assigning a prescribed closure speed the force required to close the press is calculated from the nodal pressure. In the simulation although the press is permitted to close to nominal thickness with no force limit, it is possible to read the thickness obtained from the known maximum force. By this method the final thickness is 2.75 mm at a press force of 8500kN compared to the 2.71 mm thickness measured in the experiment in Fig. 18.
5.3 Fill Pattern
The model with edge resin channel permeability of 5 × 10–8 m2 is selected to most accurately represent the experiment fill pattern. Resin arrival correlates at the corner within 1 s (5%) indicating that the flow pattern correlates. The model with edge resin channel permeability of 5 × 10–8 m2 is run with resin volume corresponding to the partially filled panels shown in Fig. 4. The partially filled panels fill pattern by comparison to the experiment (see Fig. 19) match the flow front.
Since the flow front is advancing with a partial saturation of fiber tows in the experiments, the volume averaged flow front approximation in the simulation is behind the flow front advancement seen in the experiment. Simacek and Advani [19] present a method whereby the lagging tow wet-out is included by adding one dimension elements at every node to represent saturation of the tow, allowing the partially saturated region to be determined. However, definition of the properties of the tow and the fibre are not easily obtainable.
6 Discussion
In order to implement the ALCM simulation as a predictive tool to aid designers, assumptions for the simulation input would be made prior to a component being manufactured. The initial assumptions applied to the simulation were:
-
Constant viscosity
-
A range of constant resin channel section
-
Fibre volume fraction calculated on nominal preform weight and tool cavity geometry
-
Constitutive models based on measured data
-
power law for compaction
-
Kozeny-Carman for permeability
-
It was found that the dominant factors in determining the fill pattern are the resin channel geometry and secondly the fibre volume fraction of the porous media. Fluid pressure is most influenced by the resin channel geometry, resin viscosity and bulk permeability.
6.1 Resin Channels
It has been shown that the resin channels present in the preform and the tool will determine the component filling pattern. The influence of resin channels has also been shown to reduce the injection pressure. The pressure reduction aspect of the resin channels is appealing in the high pressure process. Without resin channels, the injection pressure predicted by the simulation would exceed the capability of the equipment.
Predictive assumptions regarding resin channels could be made with a range of geometries. The simulation results presented are based on the measured variability of the preforms and the tool geometry. Using a constant section to represent channel geometries averages the effects of any sectional variations along the channel length. The wide range of outputs for the potential range of inputs illustrates the importance of controlling variation of the preform in the process.
6.2 Preform Variation
Preform variation will occur in the guise of dimensional tolerances and fabric areal weight tolerance. Dimensional variation is due to cutting tolerance and lost fibres, or fraying, on the edges. The variation on the areal weight will be dictated by the fabric manufacturers’ tolerance. Therefore it is possible to determine a range of fibre volume fraction bounded by the maximum and minimum tolerances. Since the process operates on fixed cavity height the fibre volume fraction will vary between components depending on these bounds.
6.3 Viscosity
The injection time targeted at under 20 s ensured minimal resin cure at the manufacture temperature of 110 °C. This allowed the initial approximation of constant viscosity prior to cure effects increasing resin viscosity causing gelation. However study of the resin temperature found that the resin temperature profile could not be assumed constant at the tool temperature.
The pressure has a linear dependency to the fluid viscosity in Darcy flow (Eq. 1 describes volumetric flow in terms of the pressure gradient (∇p) across a porous media; the flow is a function of the viscosity μ of the fluid and permeability K of the media through which it is permeating), and channel flow. It therefore follows that the viscosity profiles greatly affect the pressure in the simulation. A viscosity profile was devised based on initial viscosity at the resin mix temperature and the process temperature, using data obtained from laboratory tests. This viscosity profile assigned in the simulation, is found to better correlate to the measured experimental pressure.
Deléglise et al. [20] addressed the change in resin viscosity by the same approach to include a time dependant viscosity relation in the RTM process with on-line mixing, and the present work agrees with Deléglise et al. [20] that inclusion of viscosity will significantly alter the process pressure.
The approximation of viscosity to a best fit curve allowed the implementation on a (simple) 2D model. A more accurate representation of viscosity requires time dependant temperature gradient through thickness.
6.4 Permeability
The material characteristic permeability is central to calculating the correct pressure (Eq. 1 describes volumetric flow in terms of the pressure gradient (∇p) across a porous media; the flow is a function of the viscosity μ of the fluid and permeability K of the media through which it is permeating). Therefore the validity of the constitutive models for permeability and compaction are significant. The permeability constitutive model has been created following Kozeny-Carman based on a single fibre volume fraction data point. Variation to fabric weight will affect the permeability. Endruweit et al [13] report normal distribution around permeability measurement on the same material at the same fibre volume fraction yielding limits greater than + − 50%.
In addition the permeability was derived for the material with binder, however the material did not undergo consolidation at temperature, therefore the binder was not active in the material as it is in the manufacturing process. Binder has been shown to affect permeability, increasing permeability by more than double at 10% concentration [21]. The location of the binder particles whether inside or outside the tow can either increase or decrease resistance to flow [22]. The binder activation therefore is anticipated to affect the permeability.
Added to this variation, measurement of permeability for flow calculations has been proven highly variable. The outcome of a benchmark exercise [23] to define in-plane permeability found that different procedures result in a scatter of data of up to one order of magnitude in measured principal permeability values on the same fabric at any given volume fraction. The scatter of data for permeability measurement is both due to material variation and error in measurement [23].
Researchers presenting permeability of a biaxial NCF fabric [13] show scatter of 22.5% and 26.1% for K1 and K2 between individual experiments which are interpreted with best fitting lines. It is evident that precise data for permeability and porosity for a given set-up is difficult to define. To use this data in a flow prediction needs consideration that the accuracy will deviate from the input data. Permeability input should envelop a range. Endruweit and Long [24] use stochastic modelling to include variations in permeability caused by fibre spacing to output variation to flow front position and fill time. Considering such variations, the predictions of pressure from the simulations are within the realm of what to expect.
7 Conclusion
Manufacturing experiments using an approach to lower fibre volume fraction during injection have been carried out. Experiments have shown that the gap used in the ALCM process does not create a space for resin flooding on the preform surface and the flow front travels in-plane in the process, thus validating the application of 2D elements in the simulation.
Notably the resin channels that are present in the mould are instrumental to lowering the inlet pressure. The resin channels are a feature of the mould design and preform preparation. Variability in the preform will have a direct effect on the cavity pressure. Both the areal weight of the fabric and the dimensional variation due to cutting tolerance, in-plane shrinkage and losing fibres from the edge due to handling damage.
The simulation predicts the press force necessary to compress to the final part thickness, and conversely the thickness obtainable from the given press force correlates within 0.05 mm between the experiment and the simulation. This simulation could be used to determine optimum inlet position and process parameters such as gap size and press force.
The simulation has been made based on some initial data and assumptions around the manufacturing process. It was found that accurate fill pattern can be predicted with selection of appropriate properties for resin channels.
A constitutive model for resin viscosity is implemented in the simulation. Without a temperature profile for the resin throughout the process on which to base the model, a regression fit was used. It was found that the representation of viscosity improved the correlation of pressure. The resin viscosity value along with permeability values are key to determining the accurate inlet pressure.
The correlation between the simulation and experiment can be improved by further including some of the tendencies observed with the flow in dual scale porous media. Greater accuracy might be achieved with more detailed analysis, however working practically within a large design space, the merits of the prediction would be to comparatively assess multiple manufacture set-ups with understanding of the simulation limitations. The simulation can be useful to design the gate locations and resin channels around the mould to reduce the pressure required to fill large structures in a few seconds.
References
H. Darcy, Les fontaines publiques de la ville de Dijon: exposition et application ... Victor Dalmont, (1856)
Han, K., Ni, J., Toth, J., Lee, L.J., Greene, J.P.: Analysis of an injection/compression liquid composite molding process. Polym. Compos. 19(4), 487–496 (1998)
Simacek, P., Advani, S.G.: Simulating three-dimensional flow in compression resin transfer molding process. Revue Européenne des Eléments. 14(6–7), 777–802 (2005)
Simacek, P., Advani, S.G., Iobst, S.A.: Modeling flow in compression resin transfer molding for manufacturing of complex lightweight high-performance automotive parts. J. Compos. Mater. 42(23), 2523–2545 (2008)
Bhat, P., Merotte, J., Simacek, P., Advani, S.G.: Process analysis of compression resin transfer molding. Compos. A: Appl. Sci. Manuf. 40(4), 431–441 (2009)
Merotte, J., Simacek, P., Advani, S.G.: Resin flow analysis with fiber preform deformation in through thickness direction during compression resin transfer molding. Compos. A: Appl. Sci. Manuf. 41(7), 881–887 (2010)
Merotte, J., Simacek, P., Advani, S.G.: Flow analysis during compression of partially impregnated fiber preform under controlled force. Compos. Sci. Technol. 70(5), 725–733 (2010)
Pillai, K.M., Tucker III, C.L., Phelan Jr, F.R.: Numerical simulation of injection/compression liquid composite molding. Part 1. Mesh generation. Compos. A: Appl. Sci. Manuf. 31(1), 87–94 (2000)
Pillai, K.M., Tucker, C.L., Phelan, F.R.: Numerical simulation of injection/compression liquid composite molding. Part 2: preform compression. Compos. A: Appl. Sci. Manuf. 32(2), 207–220 (2001)
Bickerton, S., Abdullah, M.Z.: Modeling and evaluation of the filling stage of injection/compression moulding. Compos. Sci. Technol. 63(10), 1359–1375 (2003)
Kelly, P.A., Bickerton, S.: A comprehensive filling and tooling force analysis for rigid mould LCM processes. Compos. A: Appl. Sci. Manuf. 40(11), 1685–1697 (2009)
Grieser T., Mitschang P.: Investigation of the compaction behavior of carbon fiber NCF for continuous preforming processes, Polym. Compos., p. n/a-n/a, (2015)
Endruweit, A., Mcgregor, P., Long, A., Johnson, M.S.: Influence of the fabric architecture on the variations in experimentally determined in-plane permeability values. Compos. Sci. Technol. 66(11–12), 1778–1792 (2006)
Long, A.C., Blanchard, P.J., Rudd, C.D., Smith, P.: The development of an integrated process model for liquid composite moulding. Compos. A: Appl. Sci. Manuf. 29(7), 847–854 (1998)
Potter, K.: Resin Transfer Moulding. Chapman and Hall, London (1997)
Gebart, B.R.: Permeability of unidirectional reinforcements for RTM. J. Compos. Mater. 26, 1100–1133, 1990
Advani, S.G., Sozer, E.M.: Process Modelling in Composites Manufacturing. CRC Press, Second (2011)
Steenkamer, D., Wilkins, D., Karbhari, V.: The influence of preform joints on the processing of RTM composites. Compos. Manuf. 6(1), 23–34 (1995)
Simacek, P., Advani, S.G.: A numerical model to predict fiber tow saturation during liquid composite molding. Compos. Sci. Technol. 63(12), 1725–1736 (2003)
Deléglise, M., Le Grognec, P., Binetruy, C., Krawczak, P., Claude, B.: Modeling of high speed RTM injection with highly reactive resin with on-line mixing. Compos. A: Appl. Sci. Manuf. 42(10), 1390–1397 (2011)
Shih, C.-H., Lee, L.J.: Tackification of textile Fiber preforms in resin transfer molding. J. Compos. Mater. 35(21), 1954–1981 (2001)
Estrada, G., Vieux-Pernon, C., Advani, S.G.: Experimental characterization of the influence of tackifier material on preform permeability. J. Compos. Mater. 36(19), 2297–2310 (2002)
Arbter, R., et al.: Experimental determination of the permeability of textiles: a benchmark exercise. Compos. A: Appl. Sci. Manuf. 42(9), 1157–1168 (2011)
Endruweit, A., Long, A.C.: Influence of stochastic variations in the fibre spacing on the permeability of bi-directional textile fabrics. Compos. A: Appl. Sci. Manuf. 37(5), 679–694 (2006)
Acknowledgments
This work was supported by the Engineering and Physical Sciences Research Council [grant number EP/K50323X] by provision of the EngD scholarship through support of the Industrial Doctorate Centre in Composites Manufacture. Industrial support to this programme from Jaguar Land Rover JLR is recognised with appreciation. Flow simulation software and support from the University of Delaware and use of equipment and facilities at the National Composite Centre UK are also gratefully accredited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Martin, F.A., Warrior, N.A., Simacek, P. et al. Simulation and Validation of Injection-Compression Filling Stage of Liquid Moulding with Fast Curing Resins. Appl Compos Mater 26, 41–63 (2019). https://doi.org/10.1007/s10443-018-9682-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10443-018-9682-4