Introduction

The ground-based augmentation system (GBAS) provides corrections and integrity information for global navigation satellite system (GNSS) signals to provide navigation guidance for precision approach and landing for civil aviation. GBAS is based on the differential GNSS technique, whereby errors in GNSS range measurements are corrected in the range domain. The corrections delivered in real time are based on measurements by multiple ground reference GNSS receivers usually placed at or near an airport with their locations precisely known. GBAS is now in operation at many airports globally to support Category-I precision approaches. GBAS provides aircraft with differential range corrections for each satellite with an elevation angle higher than 5° as well as integrity information through VHF Data Broadcast stations. GBAS also provides approach path information. The aircraft in flight then presents the lateral and vertical deviations from the desired approach path to the pilot in-command.

Civil aviation transitions to CAT II and III operations and existing ILS (Instrument Landing System) procedures are gradually replaced or supplemented by GBAS Landing System (GLS) procedures. GBAS will increasingly become a safety-critical application of GNSS for civil aviation requiring a high level of accuracy, integrity, continuity, and availability of service. The requirements are defined by the International Civil Aviation Organization (ICAO) (ICAO 2014). Standards for avionics are further refined by relevant standardizing organizations such as RTCA (RTCA 2008a, b)/EUROCAE. EUROCAE also defined minimum operational performance standards for GBAS ground subsystem (EUROCAE 2013). To date, GBAS has been standardized based on the use of single-frequency GNSS (L1, centered at 1.57542 GHz) only.

Impact of the ionosphere on GBAS and mitigation

The propagation delay of GNSS signals due to the ionosphere is one of the most significant sources of ranging error. Ionospheric delay is proportional to the total number of electrons in a unit area (total electron content, or TEC) along the signal propagation path between a satellite and a receiver. Further, the ionospheric delay is inversely proportional to the square of the signal frequency. We express ionospheric delay in units of meters calculated at the GPS L1 frequency (1.57542 GHz). At the L1 frequency, 0.16 meters of delay is equivalent to 1 TEC Unit (TECU, or 1016 electrons/m2). In GBAS, the ionospheric delay is corrected as a part of the total ranging error including tropospheric delay, satellite clock error, and satellite ephemeris error from the range measurements recorded by the reference receivers. These differential corrections are valid as long as the ionospheric delay is homogeneous in space. Since the ionosphere is spatially variable, however, differential correction errors associated with spatial decorrelation of the ionospheric delay, or in other words ionospheric spatial gradients, must be considered and mitigated.

In GBAS, normally occurring gradients in ionospheric delay, commonly termed “nominal ionospheric gradients,” are mitigated by determining a conservative one-sigma parameter (σ vig) (ICAO 2014) to bound the uncertainty in the nominal vertical ionospheric delay gradient. This parameter is of the order of several millimeters per kilometer at the GPS L1 frequency (Lee et al. 2007). This value is broadcast by GBAS ground systems and is an input to aircraft calculation of protection levels, which bound errors in the position-domain (Rife and Pullen 2007). When these protection levels exceed the alert limits, which are the designated safe limits, the GBAS service becomes unavailable.

However, it is known that ionospheric delay may greatly deviate from nominal levels due to various disturbances (Mendillo 2006). For example, enhancements in ionospheric TEC associated with strong geomagnetic storms (Foster et al. 2002) may result in slant ionospheric delay gradients of more than 400 mm/km (Pullen et al. 2009) or approximately 100 times the typical value of σ vig. If differential correction errors associated with such anomalous ionospheric delay gradients were to be bounded by the protection levels, they would almost always exceed the alert limit, and the GBAS service would be unavailable to airspace users. Therefore, anomalous ionospheric delay gradients are usually treated separately from nominal ionospheric delay gradients. To the extent possible, they are detected, and the affected satellites are excluded by integrity monitors deployed in the GBAS ground and airborne subsystems. Anomalous gradients that cannot be detected to the required integrity probability must be mitigated by separately limiting the aircraft satellite geometry to ensure that aircraft potentially exposed to such gradients do not experience unsafe position errors. This latter approach is known as “geometry screening” (Seo et al. 2012).

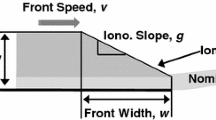
To design the integrity monitors relevant to the ionospheric delay gradient and therefore ensure that an acceptable level of safety is reached, characteristics of ionospheric delay gradients must be defined. In GBAS, an ionospheric delay gradient is usually approximated by an infinitely long front. The range of ionospheric delay gradients possible over a given region is referred to as the “ionospheric threat model.” It should be noted that the ionospheric threat model used for civil aviation has to be sufficiently protective but should not be too conservative because systems used for civil aviation must be safe and at the same time sufficiently available for approach and landing operations.

It is common to define the ionospheric threat model in terms of slant ionospheric delay gradient, i.e., without conversion from a slant to vertical delays. The ionospheric threat model is defined to bound worst-case ionospheric delay gradients. However, it is difficult to estimate the occurrence probability of extremely large ionospheric delay gradients that occur very infrequently. The lack of a large database of observed extreme gradients makes it impractical to derive an upper bound on gradient magnitude by normal statistical methods. Instead, the upper bound of the ionospheric threat model is selected to exceed any ionospheric delay gradients that have ever been observed in an area of interest.

For example, ICAO has defined a reference ionospheric threat model to be used in the validation of new standards and the verification of new GBAS equipment enabling Category-II/III approach and landing (ICAO Navigation Systems Panel, GBAS CAT II/III Development Baseline SARPs.). Since ionospheric conditions vary with magnetic latitude, the USA has defined its own ionospheric threat model applicable over the Conterminous US (CONUS) for Category-I GBAS (Pullen et al. 2009). Similar studies have also been conducted in Australia (Terkildsen 2010), South Korea (Kim et al. 2014), Germany (Mayer et al. 2009), and more widely over Europe (Schlüter et al. 2013). These studies are based on observations in the magnetic mid-latitude region, where strong ionospheric disturbances that may impact GBAS do not frequently occur. The studies conducted for these mid-latitude regions show that all ionospheric delay gradients fall well within the bounds of the GBAS Category-I ionospheric threat model for CONUS. On the other hand, in the low magnetic latitude region where ionospheric disturbances regularly occur, as discussed in the next subsection, only a few studies have been conducted (Saito et al. 2012a; Rungraengwajiake et al. 2015; Lee et al. 2015).

Low-latitude ionospheric disturbances

As noted above, the ionosphere behaves differently at different magnetic latitudes. The low-magnetic latitude ionosphere may be defined as the ionosphere that is affected by the equatorial plasma fountain, which generates the equatorial ionization anomaly (EIA) crests at around ±15° magnetic latitude. It is characterized by various ionospheric disturbances unique to the region (Kelley 2008). Among them, plasma bubbles are known as the most dynamic ionospheric disturbance in the region. Plasma bubbles are regions of low ionospheric plasma density that develop over the magnetic equator and rise vertically as high as 1000 km or more, somewhat like a “bubble” in water (Woodman and LaHoz 1976). The east–west and north–south cross sections of a plasma bubble are illustrated in the left panels of Fig. 1. As a bubble rises higher, it expands in the poleward direction along the earth’s magnetic field lines. The typical longitudinal width is about 100 km, and the typical latitudinal extent can be up to several thousands of km. Since the boundary between the outside and inside of a plasma bubble is very narrow, the ionospheric delay on nearby satellite-receiver paths may vary drastically depending on whether they pass inside or outside the bubble. Therefore, a plasma bubble may be observed as a sharp drop or recovery in ionospheric delay, as shown in Fig. 1 (right), and can generate a large ionospheric delay gradient that may impact GBAS, as illustrated in Fig. 2.

Fig. 1
figure 1

General features of plasma bubbles. Left cross sections of plasma bubble in a zonal-vertical plane over the magnetic equator (top) and in a meridional-vertical plane (bottom) are illustrated. Right an example of plasma bubbles seen on an ionospheric delay map is also shown. Two ovals indicate plasma bubbles

Full size image
Fig. 2
figure 2

Plasma bubble and differential range error in GBAS

Full size image

It is important to note that the characteristics of plasma bubbles are very different from the characteristics of mid-latitude ionospheric disturbances. The physical mechanism of plasma bubbles, the Rayleigh–Taylor plasma instability (Dungey 1956) is very different from those of mid-latitude ionospheric disturbances. Plasma bubbles occur much more frequently than mid-latitude ionospheric disturbances of sufficient magnitude to impact GBAS. The seasonal and local time variation of plasma bubble occurrences is also very different. Plasma bubbles occur almost every day, potentially anytime between dusk and dawn, in certain seasons (Burke et al. 2004). Therefore, the characteristics of plasma bubbles and their impact on GBAS must be assessed separately from those of mid-latitude disturbances.

ICAO APAC ionospheric studies task force (ISTF)

With the increasing demand for GNSS implementation for air navigation, the ICAO Asia-Pacific Air Navigation Planning and Implementation Regional Group (APANPIRG) recognized the need to assess regional ionospheric characteristics and their potential impact on GNSS in 2010. Some States/Administrations in the ICAO APAC region are situated in the low-magnetic latitude region where the ionospheric characteristics are different from those in the mid-latitude region and have not been as thoroughly studied. In the region spanning longitudes 60°E to 120°W that includes most of Asia and the Pacific Ocean, the characteristics of ionospheric disturbances in the low-magnetic latitudes can be regarded as similar (Burke et al. 2004).

Recognizing the need to mitigate the ionospheric threat, the Communication, Navigation, and Surveillance (CNS) subgroup of ICAO APANPIRG decided to assess the ionospheric characteristics in their region in an internationally coordinated manner. Thus, the ionospheric studies task force (ISTF) was established in 2011 by the CNS subgroup to facilitate ionospheric data collection, sharing, and analysis. The ISTF was also tasked to develop regional ionospheric threat models for GBAS and SBAS. The latest terms of reference of the ISTF are published by the ICAO APAC Office [International Civil Aviation Organization Asia Pacific Office, Revised terms of reference of ISTF. Attachment A to the report of the third meeting of ionospheric studies task force (ISTF/3)]. GNSS measurement data were collected and shared by the contributing States/Administrations. Subject matter experts from the member States/Administrations shared and analyzed the data cooperatively. Cooperation among multiple states to analyze ionospheric delay gradient data across the low-latitude Asia-Pacific region and provide a single reference model for GBAS implementation in the region is novel from both a scientific and engineering point of view.

Scope

The objective of this study is to present the results of an ionospheric threat assessment for GBAS in the Asia-Pacific region by the ICAO APAC ISTF based on data contributed by a number of States/Administrations and regional organizations and analyzed by ISTF members. The methods used to analyze the collected data are explained in the next section. A section to introduce the data used in this study follows. Finally, results of the analysis are presented and discussed.

Methodology

Two tools are used to analyze collected GPS data, find examples of anomalous ionospheric behavior, and derive estimates of ionospheric delay gradients. One is the long-term ionosphere anomaly monitoring (LTIAM) software package developed by the US Federal Aviation Administration (FAA) and the Korea Advanced Institute of Science and Technology (KAIST), South Korea (Jung and Lee 2012). LTIAM was developed for the purpose of continually evaluating the validity of the existing CONUS threat model and updating it if gradients not bounded by the model are discovered in future observations. LTIAM software implements a simplified and automated algorithm to estimate precise slant ionospheric delays using dual-frequency (L1 and L2) GNSS measurements at all available pairs of GNSS receivers. The delay difference between a pair of receivers tracking a GNSS satellite is divided by the baseline distance between those receivers to give an estimate of the ionospheric delay gradient. Additionally, LTIAM estimates the ionospheric delay gradient based on the difference between the code and carrier-phase measurements (code-minus-carrier, or CMC) of the L1 signal.

LTIAM automatically selects and outputs measurement pairs that have large estimated ionospheric delay gradients. These candidates are manually verified by visual inspection, including comparisons between dual-frequency and L1 CMC gradient estimates, to confirm that the observed gradients are due to ionospheric behavior as opposed to receiver faults or post-processing errors such as undetected cycle slips in carrier-phase measurements or code-carrier leveling uncertainty. This is necessary because those errors can generate large apparent ionospheric gradients which are not real. Candidates which are not verified manually are discarded, as they are not reliable. LTIAM is a robust tool for processing a large amount of data in a reasonable amount of time.

The other tool is the single-frequency carrier-based and code-aided technique (SF-CBCA) developed by the Electronic Navigation Research Institute, Japan (Fujita et al. 2010; Saito et al. 2012b). SF-CBCA uses single-frequency carrier-phase and code measurements to estimate ionospheric delay differences between a pair of GNSS receivers. The process includes ambiguity resolution of carrier-phase differences. Since it is based on single-frequency measurements, it is free from ionospheric delay difference estimation error caused by inter-frequency bias, which is difficult to calibrate perfectly in dual-frequency measurements. On the other hand, errors associated with ephemeris errors become larger as the distance between a pair of GNSS receivers becomes longer. Therefore, SF-CBCA is suitable for receiver pairs with relatively short baselines of as much as 10 km, though very precise relative positions of the receivers are needed. In addition, by using three GNSS receivers, which give three unique combinations of two GNSS receivers, the validity of the solutions can be checked by taking the cyclic sum of the ionospheric delay differences from the three pairs (Saito et al. 2012b). With the cyclic sum check, the worst-case error of gradient estimation can be limited at most to the ionospheric delay equivalent to a half wavelength of the L1 signal divided by the distance between stations.

These two methods have been shown to produce equivalent results. LTIAM is based on the ionospheric delay values derived from dual-frequency measurements. Thus, the derivation of ionospheric delay gradients by LTIAM is straightforward. The equivalency of the ionospheric delay gradients estimated by SF-CBCA and by the dual-frequency method is demonstrated by Saito and Yoshihara (2017).

In this study, both methods (LTIAM and SF-CBCA) have been used. Which method was used to analyze a particular data set depended on the details of that data set, such as the distances between receivers, the availability of very precise station locations, and the computing environment of the analyzing center. In LTIAM analysis, a satellite elevation mask of 10° was applied, because L1 CMC validation is difficult at lower elevation angles due to multipath noise in code measurements. An elevation mask of 0° was used in SF-CBCA analysis.

Data analyzed

The data used in this study was collected and shared by the member States/Administrations and regional organizations in the ICAO APAC region. Table 1 summarizes the locations of data sources, and corresponding data periods, and the analysis method used for each set of data. Data from Hong Kong, Hyderabad, and Bangalore were collected in periods covering a whole solar cycle. Data from other locations also collected around the last solar maximum period, which occurred in 2011. Figure 3 shows the geographic distribution of the data sources. It can be seen that the data sources are widely distributed over the region of interest, both in longitude from 78°E to 124°E and in latitude from 7°S to 24°N (−17 to +20° in magnetic latitude).

Table 1 Data used for analysis
Full size table
Fig. 3
figure 3

Locations where the ionospheric delay gradients are analyzed. Dashed line shows the magnetic equator

Full size image

Results and discussion

In the following, all the ionospheric delay gradients are discussed with regard to the L1 frequency, with units of millimeters of delay per kilometer of baseline, because current GBAS is defined purely for single-frequency L1 GNSS signals.

Figure 4 shows an example of ionospheric delay gradient analysis results using LTIAM for data recorded in Singapore. This example shows the largest gradient observed in Singapore. It was observed on GPS PRN 32 satellite on March 26, 2012, and it represents the largest gradient derived by LTIAM over the set of data collected and analyzed by ISTF. Geomagnetic activity was quiet during the period of observation (K p ≤ 1+) (World Data Center for Geomagnetism, Kyoto, http://wdc.kugi.kyoto-u.ac.jp). Figure 4 (top, left) shows the ionospheric delay values of the two receivers (SNYP and SLOY, which are separated by about 13.7 km in a roughly west-to-east direction) over several hours in the late afternoon and evening. The local time at 104°E is 6.9 h ahead of UT. A strong plasma bubble of ionospheric delay depletion first affected SNYP at around 13.5 UT and moved eastward to affect SLOY a few minutes later. Figure 4 (top, right) shows the resulting ionospheric delay gradient estimates derived from both dual-frequency and CMC measurements. Figure 4 (bottom, right) shows the close-up of Fig. 4 (top, right) from 13.25 to 14.11 UT. The maximum gradient of about 505.2 mm/km occurred at about 1340 UT, after SNYP had experienced almost all of the depletion while SLOY was just beginning to be affected and thus observed a much higher delay. Figure 4 (top, right) also shows that both dual-frequency and CMC estimates of gradient over time agree closely, which helps validate that erroneous receiver measurements did not create this event. As shown in Fig. 4 (bottom, left), this large gradient was observed at a relatively low-elevation angle of (21.05°).

Fig. 4
figure 4

Largest gradient event observed at Singapore on March 26, 2012. Dual-frequency ionospheric delays observed by the two receivers for the GPS PRN 32 satellite (top-left), gradient (top-right), satellite elevation angle (bottom-left), and close-up of gradients estimated by dual-frequency and CMC measurements (bottom-right) are shown

Full size image

Figure 5 shows another example of LTIAM ionospheric delay gradient analysis results. This example shows the largest gradient observed in Hong Kong, China, which occurred on the GPS PRN 07 satellite on April 11, 2013. It was the second largest gradient derived by LTIAM. The geomagnetic activity was quiet (K p ≤ 2). The distance between the two receivers of HKSS and HKWS that made these observations of PRN 07 is 6.81 km. As shown in the top panels of Fig. 5, there were two disturbances around 14.25 and 16.3 UT (LT = UT + 7.6 h at 114°E). Figure 5 (bottom, right) shows the close-up of Fig. 5 (top, right) from 16.0 to 16.55 UT. From 16.37 UT, the gradient estimated by L1 CMC starts to drop from +21.3 mm/km continuously to −456.4 mm/km. The gradient obtained from dual-frequency measurements followed the gradient estimated from CMC until it jumped back to about −100 mm/km, which was apparently due to cycle slips in carrier-phase measurements. In this case, the real largest gradient is estimated as −477.7 mm/km from the CMC measurements by taking the constant gradient of +21.3 mm/km that occurred before the disturbance as the reference level. As shown in Fig. 5c, this gradient was observed at a very low-elevation angle (11.75°).

Fig. 5
figure 5

Same as Fig. 4, but is plotted for the largest gradient event observed at Hong Kong China on April 11, 2013, for the GPS PRN 07 satellite

Full size image

Figure 6 shows an example of ionospheric delay gradient analysis results by SF-CBCA for data recorded in Ishigaki, Japan, which is south of the Japanese home islands and is about 250 km east of Taiwan. Figure 6 (top) shows ionospheric delay observed at Ishigaki on the GPS PRN 22 satellite on April 3, 2008. The magnetic activity on the day was very quiet (K p ≤ 1). It can be seen that multiple plasma bubbles (i.e., multiple drops in ionospheric delay) passed over Ishigaki. Figure 6 (middle) shows the ionospheric delay gradients for the same period observed by a receiver pair separated by 1.37 km in a roughly east-to-west direction. The largest gradient of 518 mm/km was observed at 12.48 UT (LT = UT + 8.3 h at 124.2°E) corresponding to the sharp drop in ionospheric delay at the same time. At Ishigaki, there are five GNSS receivers (Saito et al. 2012a). The gradient values are validated by checking the consistency with gradients measured by other nearby receiver pairs. As shown in Fig. 6 (bottom), the largest gradient was observed at a relatively low-elevation angle (18.45°).

Fig. 6
figure 6

Largest gradient observed at Ishigaki, Japan on April 3, 2008. Dual-frequency ionospheric delay observed by one of the receivers for the GPS PRN 22 satellite (top), gradient (middle), satellite elevation angle (bottom) are shown

Full size image

In contrast to these events with large gradients observed at low-elevation angles, a relatively large gradient was observed at a high-elevation angle (77°) at Hyderabad, India. Though it was not the largest gradient observed at Hyderabad, it is worthwhile to show this example due to its combination of high gradient and high elevation angle. Figure 7 shows the results of the analysis of this example as derived by LTIAM. It was observed on March 1, 2015, on the GPS PRN 06 satellite. The magnetic activity on this day was moderate (K p ≤ 5+), but it was quiet when these plasma bubbles were observed (K p ≤ 3−). Multiple plasma bubbles, some small and some large, were observed from about 16.0 to 19.0 UT (LT = UT + 5.2 h at 78.5°E). At around 18.3 UT, sharp drops in the ionospheric delay were observed, as shown in Fig. 7 (top, left). Associated with these sharp drops, the estimated gradient continuously increased to +308 mm/km from −51 mm/km for a receiver pair (HYDE and HYDR) separated by 9.28 km, as shown in the right panels of Fig. 7. The continuous behavior of the gradient derived by dual-frequency measurements, and its consistency with that derived by L1 CMC measurements, indicates that the gradient is likely to be real. As shown in Fig. 7 (bottom, left), the elevation angle of the GPS PRN 06 satellite was quite high (77°).

Fig. 7
figure 7

Same as Fig. 5, but is plotted for the large gradient event at a high-elevation angle (77°) at Hyderabad, India on March 1, 2015, for the GPS PRN 06 satellite

Full size image

Figure 8 shows all of the ionospheric delay gradients larger than 100 mm/km obtained from the data listed in Table 1 as a function of satellite elevation angle. From Ishigaki and Bangkok data analyzed by SF-CBCA, no validated gradient data was obtained at elevation angles below 10°. From other data analyzed by LTIAM, no gradient data was obtained at elevation angles below 10°, because dual-frequency data at low elevation angles are very noisy, and satellites below an elevation angle of 10° were not used. Therefore, there are no data points at elevation angles below 10° in the figure. Nevertheless, according to previous studies in other regions (Pullen et al. 2009; Terkildsen 2010; Kim et al. 2014; Lee et al. 2015), there is no evidence that gradients in the elevation range of 5°–10° are significantly larger than gradients at an elevation angle of 10°. Weak elevation angle dependence, i.e., increasing ionospheric gradient with decreasing elevation angle, can be seen in the figure as well as in these previous studies. However, because little data below 10° is present, the extension of the maximum gradient in the threat model below 10° must be regarded as speculative at the current time.

Fig. 8
figure 8

Ionospheric gradients larger than 100 mm/km as a function of the elevation angle. Different signs indicate different locations where the gradients are observed. Dotted lines show the gradients following Eq. (1) with the vertical gradient values in Table 2

Full size image

An example of functions that give physically significant elevation angle dependence is the slant factor function, which gives the relationship between slant and vertical ionospheric delays with an assumption of a thin ionospheric shell at a fixed altitude (thin-shell model).

$$g\left( {\text{El}} \right) = S\left( {\text{El}} \right) \cdot g_{0} \;[{\text{mm}}/{\text{km}}]$$
(1)

where \(g_{0}\) is the vertical ionospheric delay gradient. S(El) is the slant factor as a function of the elevation angle (El) with an assumed ionospheric shell height of 350 km (ICAO 2014) and is given by:

$$S\left( {\text{El}} \right) = \frac{1}{{\sqrt {1 - \left( {\frac{{R_{\text{e}} \cos {\text{El}}}}{{R_{\text{e}} + 350}}} \right)^{2} } }}$$
(2)

where R e is the radius of the earth at the equator (6378.14 km).

The dotted curves in Fig. 8 show the gradient calculated by (1) with different equivalent vertical gradient values summarized in Table 2. Most of the largest gradients obtained in this study (i.e., those above 300 mm/km) follow the shape of these slant factor functions. Curve C1 closely fits the envelope of the gradient distribution except for the single event of 349 mm/km at 77° from Hyderabad, which is not bounded. Unbounded events like this are of concern for the development of an ionospheric threat model for use in civil aviation because of the demanding (1–10−7~−9) integrity requirements and because only a limited number of anomalous gradient observations are available. Curve C2 is chosen so that it passes through the data point of 349 mm/km at 77°. Curve C3 is chosen to bound all the gradients with a certain margin. All these curves, however, appear to be too conservative at low-elevation angles, with values at the lowest elevation angles more than twice the maximum observed gradient, although data at elevation angles below 10° is limited. Too much conservatism should be avoided in civil aviation, because it would degrade the availability of the system, as pointed out earlier. Therefore, the threat model needs to be defined considering the balance between safety margin and availability.

Table 2 Equivalent vertical gradients for curves in Fig. 8
Full size table

In Fig. 9 and Table 3, three options for the ionospheric threat model are presented. The solid line is the first option, in which the upper bound on the ionospheric delay gradient is constant at 600 mm/km for all elevation angles. The 600 mm/km value is chosen so that all the observed gradients are well bounded. This value exceeds the largest gradient values in the data set by about 15%. This 15% margin is considered to be sufficient to bound the measurement and analysis errors. Moreover, the data set includes data for one solar cycle (11 years) at three locations, which are Hong Kong, Hyderabad, and Bangalore, plus data from other locations. Considering that the exposure time of the most critical phase of precision approach as 15 s (ICAO 2014), three times 11 years, which is 1.04 × 109 s, is equivalent to 7 × 107 15-s samples, which approaches the integrity level required for Category-I approach (1–10−7). Therefore, a bound of 600 mm/km value on gradients in the APAC region has significant statistical weight when applied to Category-I approach. For Category-II/III approach and landing that require integrity level of 1–10−9, more data and analysis are likely to be needed. In fact, because of the rarity of extreme ionospheric events, continued monitoring of ionospheric gradients is recommended to support Category-I, II, and III approaches to detect any future events that might exceed the bounds of this threat model.

Fig. 9
figure 9

Same as Fig. 8. The symbols indicate locations where the gradients were observed as shown in Fig. 8. Horizontal solid line is drawn at 600 mm/km (Option 1 in Table 3). Dashed and dash-doted lines show the Options 2 and 3, respectively, in Table 3

Full size image
Table 3 Options of ionospheric threat model
Full size table

As noted above, a constant bound of 600 mm/km is reasonably larger than the largest gradients derived by LTIAM (505.2 mm/km) and SF-CBCA (518 mm/km) plus the maximum potential measurement errors for each event (19.5 and 65.7 mm/km, respectively). The dashed line is the second option, in which the upper bound is constant at 600 mm/km at elevation angles from 5° to 30° and then linearly decreases to 400 mm/km at 90°. The dash-dotted line is the third option, in which the upper bound is constant at 600 mm/km at elevation angles from 5° to 38.16° and then decreases to 400 mm/km at 90° using the definition of S(El) given in (2). The high-elevation part of Option 3 is the same as Curve C3 in Fig. 8. All three options completely bound all observed data points.

The next question is which option should be adopted. Both Options 2 and 3 are less conservative than Option 1 at higher-elevation angles. However, there is no clear physical basis for having a linear decrease, as in Option 2. Option 3 has some physical basis and is the least conservative among the three options at higher-elevation angles.

Because the number of available samples of large gradients at high-elevation angles is limited, it is most reasonable to adopt Option 1, which is a constant upper bound of 600 mm/km for all elevation angles. When more gradient samples are obtained in the future and more confidence gained in the statistics, the conservative margin that Option 1 provides at higher-elevation angles may be reduced.

Note that while Options 1, 2, or 3 in Table 3 are meant to extend down to a minimum elevation angle of 5°, the lack of observations below 10° means that use of this threat model below 10° is speculative and is based on engineering judgment and experience with previous observations of ionospheric anomalies. Further analysis by SF-CBCA, which is more robust against the disturbances that affect low-elevation measurements, may provide observations below 10° from the existing data set and provide more confidence on the gradient bound in the elevation angle range between 5° and 10°.

The upper bound of 600 mm/km on the ionospheric delay gradient in this model is higher than those in similar threat models established for mid-latitude regions (Pullen et al. 2009; Mayer et al. 2009; Terkildsen 2010; Schlüter et al. 2013), which have bounds as large as 425 mm/km. It is also higher than those found in previous studies of the Asia-Pacific region (Kim et al. 2014; Rungraengwajiake et al. 2015). However, it is lower than the largest gradient found in Brazil (850 mm/km) (Lee et al. 2015), which is also in the low-latitude region. This longitudinal difference across the low-latitude region may be real or may be due to the limited observations of large gradients conducted to date. Further study is needed to understand this difference better, if it exists, and its physical basis.

Conclusion

GPS observation data obtained in the Asia-Pacific region was analyzed for anomalous ionospheric delay gradients to develop a regional ionospheric threat model for GBAS. The largest gradient value in the analyzed data was 518 mm/km at Ishigaki, Japan, while gradients almost this large were also observed at Hong Kong and Singapore. Most of the observed gradients above 300 mm/km appear to have an elevation angle dependence that is similar to the slant factor function. However, the slant factor function cannot bound all the gradients without being too conservative.

Therefore, the upper bound of the ionospheric delay gradient was chosen to be constant at 600 mm/km without any elevation angle dependence for the proposed GBAS ionospheric threat model for the ICAO Asia-Pacific region. More data analysis is desirable to demonstrate that this model continues to bound future gradients and to support Category-II/III approach and landing. It is hoped that future data analysis will provide a stronger justification to reduce the gradient bound at higher elevation angles. Furthermore, it would be desirable to obtain low-noise data at elevation angles below 10° to provide additional support for using the threat model down to 5°, as is currently done in GBAS.