Abstract
The analytical solution describing the one-dimensional displacement of the center of mass of a tracer during an injection, drift, and extraction test (push-pull test) was expanded to account for displacement during the injection phase. The solution was expanded to improve the in situ estimation of effective porosity. The truncated equation assumed displacement during the injection phase was negligible, which may theoretically lead to an underestimation of the true value of effective porosity. To experimentally compare the expanded and truncated equations, single-well push-pull tests were conducted across six test wells located in a shallow, unconfined aquifer comprised of unconsolidated and heterogeneous silty and clayey fill materials. The push-pull tests were conducted by injection of bromide tracer, followed by a non-pumping period, and subsequent extraction of groundwater. The values of effective porosity from the expanded equation (0.6–5.0%) were substantially greater than from the truncated equation (0.1–1.3%). The expanded and truncated equations were compared to data from previous push-pull studies in the literature and demonstrated that displacement during the injection phase may or may not be negligible, depending on the aquifer properties and the push-pull test parameters. The results presented here also demonstrated the spatial variability of effective porosity within a relatively small study site can be substantial, and the error-propagated uncertainty of effective porosity can be mitigated to a reasonable level (< ± 0.5%). The tests presented here are also the first that the authors are aware of that estimate, in situ, the effective porosity of fine-grained fill material.
Résumé
La solution analytique décrivant le déplacement unidimensionnel du centre de masse d’un traceur lors d’un test d’injection, de dérive et d’extraction (test « push-pull ») a été développée pour prendre en considération le déplacement au cours de la phase d’injection. La solution a été étendue pour améliorer l’estimation in situ de la porosité efficace. L'équation tronquée supposant un déplacement pendant la phase d'injection était négligeable, ce qui pourrait théoriquement conduire à une sous-estimation de la valeur réelle de la porosité efficace. Pour comparer expérimentalement les équations étendues et tronquées, des essais de « push-pull » dans un puits unique ont été effectués dans six puits d'essai situés dans un aquifère peu profond et libre composé de matériaux de remplissage non consolidés et hétérogènes silteux et argileux. Les essais « push-pull » ont été réalisés en injectant un traceur de bromure, suivi d’une période sans pompage, et d’une période suivante de pompage d’eaux souterraines. Les valeurs de la porosité efficace obtenues à partir de l'équation étendue (0.6 à 5.0%) étaient sensiblement supérieures à celles de l'équation tronquée (0.1 à 1.3%). Les équations étendues et tronquées ont été comparées aux données des études antérieures de « push-pull » de la littérature et ont démontré que le déplacement pendant la phase d'injection peut être négligeable ou pas, en fonction des propriétés de l'aquifère et des paramètres des tests de « push-pull ». Les résultats présentés ici ont également démontré que la variabilité spatiale de la porosité efficace à l’échelle d’un site d’étude relativement petit peut être importante, et l’incertitude de l’erreur propagée de la porosité efficace peut être atténuée à un niveau raisonnable (< ±0.5%). Les tests présentés ici constituent selon les auteurs les premières estimations, in situ, de la porosité efficace d’un matériau de remplissage de granulométrie fine.
Resumen
La solución analítica que describe el desplazamiento unidimensional del centro de masade un trazador durante una prueba de inyección, deriva y extracción (prueba “push-pull”) seamplió para tener en cuenta el desplazamiento durante la fase de inyección. La solución seexpandió para mejorar la estimación de la porosidad efectiva in situ. La ecuación truncadaasumida para el desplazamiento durante la fase de inyección fue insignificante, lo queteóricamente puede conducir a una subestimación del verdadero valor de la porosidad efectiva.Para comparar experimentalmente las ecuaciones expandidas y truncadas, se realizaron ensayos“push pull” en un pozo simple a través de seis pozos de ensayo situados en un acuífero somero yno confinado compuesto de materiales arcillosos y limosos no consolidados y heterogéneos. Losensayos “push-pull” se realizaron mediante la inyección de un trazador de bromuro, seguido deun período de no bombeo, y posterior extracción de agua subterránea. Los valores de porosidadefectiva de la ecuación expandida (0.6 a 5.0%) fueron sustancialmente mayores que a partir de laecuación truncada (0.1 a 1.3%). Las ecuaciones expandidas y truncadas se compararon con losdatos de estudios previos de ensayos “push-pull” de la literatura y demostraron que eldesplazamiento durante la fase de inyección puede o no ser insignificante, dependiendo de laspropiedades del acuífero y de los parámetros del ensayo “push-pull”. Los resultados presentadosaquí también demuestran que la variabilidad espacial de la porosidad efectiva dentro de un sitiode estudio relativamente pequeño puede ser sustancial y la incertidumbre propagada por error dela porosidad efectiva puede ser mitigada a un nivel razonable (<± 0.5%). Los ensayos que sepresentan son también los primeros en que los autores son conscientes de esa estimación, in situ,de la porosidad efectiva de un material de relleno de grano fino.
摘要
对描述注入期间示踪剂中心一维错位、漂移和抽取试验(推拉试验)进行了扩展以解释注入阶段的错位。扩展解决方案改善了有效孔隙度的现场估算水平。缩减的方程式假定注入期间的错位可以忽略不计,这个方程式理论上可导致有效孔隙度真实数值的低估。为了比较扩展的和缩减的方程式,对位于浅层、非承压的、由松散及异质相粉砂质和粘土质填充物质组成的含水层的六个实验井进行了单井推拉实验。推拉试验包括注入溴化物示踪剂,然后经过一个非抽水期,然后再抽取地下水。从扩展方程式得到的有效孔隙度值 (0.6 至 5.0%) 实际上大于从缩减方程式得到的有效孔隙度值 (0.1 至 1.3%)。扩展方程式和缩减方程式与文献中记载的先前推拉试验研究中的数据进行了对比,显示注入期的错位可以或不可以忽略不计,这取决于含水层特性和推拉试验参数。这里展示的结果还说明,在相对小的研究区内有效孔隙度的变化可以很大,有效孔隙度误差传播的不确定性可减缓到一个合理的水平 (< ±0.5%)。这里展示的试验也是首次作者在现场估算细颗粒充填物质的有效孔隙度。
Resumo
A solução analítica que descreve o deslocamento monodimensional do centro de massade um traçador durante a injeção, movimento e extração (teste “push-pull”) foi expandida paralevar em conta o deslocamento durante a fase de injeção. A solução foi expandida para melhorara estimativa da porosidade efetiva. A equação truncada assume que o deslocamento durante afase injeção é insignificante, o que pode teoricamente levar a uma subestimativa do valor real daporosidade efetiva. Para comparar experimentalmente as equações expandida e truncada, testes“push-pull” em poços individuais foram realizados em seis poços alocados num aquífero rasolivre, caracterizado por materiais de aterro siltosos e argilosos inconsolidados e heterogêneos. Ostestes “push-pull” foram realizados injetando brometo como traçador, seguido de um períodosem bombeamento, e posteriormente extração da água subterrânea. Os valores de porosidadeefetiva da equação expandida (0.6 a 5.0%) foram substancialmente maiores do que aquelesprovenientes da equação truncada (0.1 a 1.3%). As equações expandida e truncada foramcomparadas com dados provenientes de estudos “push-pull” anteriores na literatura, edemonstradas que o deslocamento durante a fase de injeção pode ou não ser insignificante,dependendo das propriedades do aquífero e dos parâmetros do teste “push-pull”. Os resultadosaqui apresentados também demonstraram que a variabilidade espacial da porosidade efetivadentro de um estudo relativamente pequeno pode ser substancial e a incerteza propagada comerro da porosidade efetiva pode ser mitigada a certo nível razoável (< ± 0.5%). Os testes aquiapresentados são também os primeiros de conhecimento dos autores a estimar, em condições insitu,a porosidade efetiva de materiais de aterro de granulometria fina.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The effective porosity of saturated porous media is a fundamental hydrogeological parameter for modeling the fate and transport of dissolved-phase contaminants in the subsurface. Reliable modeling is highly dependent on accurate characterization of effective porosity. Field-scale tracer-based methods are particularly attractive to estimate effective porosity because they are based on direct measurements of the in situ transport of a dissolved-phase constituent. The single-well push-pull test method has been developed to estimate effective porosity and has been successfully applied in situ (Istok 2013). However, the current analytical model (Hall et al. 1991) assumes the transport of the tracer during the push phase is negligible, which may or may not be an appropriate assumption in all cases. Theoretically, neglecting to account for the transport of the tracer during the push phase may lead to an underestimation of effective porosity. In this study, the analytical solution to describe the displacement of a tracer during a push-pull test was expanded to account for the push phase and then applied in situ to estimate the effective porosity across six test wells located in a shallow, unconfined aquifer.
Effective porosity can be qualitatively defined as the volume of the void spaces through which water or other fluids can travel (by advection) in a rock or sediment divided by the total volume of the rock or sediment (Fetter 2001). Domenico and Schwartz (1998) explained that effective porosity implies some connectivity through the porous medium and is more closely related to permeability than is total porosity. The definition and conceptualization of effective porosity has led to the use of more descriptive terms such as mobile porosity, kinematic porosity, and dynamic porosity. Determining the appropriate value of effective porosity for groundwater models can be challenging, due in part, to the spatial heterogeneity of porous media. Field-scale tracer-based studies have shown that effective porosity in granular porous media can range from 40% (alluvial sediments; fine sands, and glacial till) to 0.4% (layered medium sand) and in fractured porous media from 60% (fractured dolomite and limestone) to 0.5% (fractured chalk) (Gelhar et al. 1992). There is also increasing evidence that effective porosity is dependent on the scale at which it is assessed, which suggests that field-scale methods may be more appropriate to inform groundwater models (Li 1995; Stephens et al. 1998).
Methods to estimate effective porosity typically rely on calculating proxy parameters such as specific yield (Meinzer 1923a) or correlating grain-size distribution and soil-water characteristic curves to representative values of specific yield (Meinzer 1923b). Estimation-based methods have the disadvantage of being indirect but are relatively simple to conduct. Methods to calculate effective porosity typically rely on conducting tracer-based tests and interpretation of subsequent breakthrough curves (Stephens et al. 1998). Tracer-based methods have the advantage of being direct but can be relatively difficult to conduct, especially at the field scale. Moreover, the interpretation of breakthrough curves requires careful consideration of the properties of the tracer and the porous medium—for example, tracer mass transport mechanisms such as: (1) sorption to the porous medium, (2) diffusion from mobile to immobile pore water, (3) volatilization to the unsaturated zone, and (4) degradation or transformation are not truly representative of the void spaces through which water can travel by advection, i.e., effective porosity (Davis et al. 1980; Turnadge and Smerdon 2014).
Hall et al. (1991) developed a relatively simple tracer-based method to calculate effective porosity based on conducting and interpreting the data from a single-well push-pull test. A single-well push-pull test is conducted by injecting (push phase) a volume of water containing a tracer into a single well, followed by a non-pumping period (drift phase), and subsequent extracting (pull phase) of groundwater from the same well in order to generate a breakthrough curve (Istok 2013). A single-well push-pull test has the threefold advantage of being direct, simple, and field scale. The Hall et al. (1991) method was theoretically developed for a confined, homogeneous, and isotropic aquifer but was experimentally validated at the field scale in an unconfined, heterogeneous, and sandy aquifer. Hall et al. (1991) compared the effective porosity calculated from a single-well push-pull test to a dual-well natural-gradient test and found that both tests yielded similar values. However, the Hall et al. (1991) method assumed that: (1) the transport of the tracer during the push phase was negligible, and (2) the uncertainty in the calculation of effective porosity was negligible. Moreover, the Hall et al. (1991) application was limited to a single well. Although the assumptions and spatially limited application by Hall et al. (1991) may have been valid and appropriate, respectively, for their case study, they may not be appropriate at other sites with variable aquifer properties, other push-pull test parameters, and different study objectives.
The purpose of this study was to utilize the single-well push-pull test method to characterize the magnitude and spatial variability of effective porosity within a shallow, unconfined aquifer. The novelty of this study was threefold: (1) the expansion of the Hall et al. (1991) analytical solution to include the transport of the tracer during the push phase, (2) the performance of an uncertainty analysis for the calculation of effective porosity, and (3) the assessment of the spatial variability of effective porosity within the study site.
Materials and methods
Theory
The volume of water injected into, or extracted from, an aquifer at a constant pumping rate, is given by:
where:
- V :
-
volume of water [L3]
- Q :
-
constant pumping rate [L3/T]
- t :
-
elapsed time during pumping [T]
By convention, the pumping rate (Q) is positive during injection and negative during extraction. If the aquifer is confined, homogeneous, and isotropic, and if the ambient groundwater flow is negligible, the cylindrical volume of water injected into, or extracted from, a fully penetrating well, is given by:
where:
- r :
-
radius of water [L]
- b :
-
saturated aquifer thickness [L]
- n e :
-
effective porosity [dimensionless]
If the saturated aquifer thickness is constant, equating Eqs (1) and (2), and rearranging gives:
Equation (3) describes the leading- or trailing-edge position of a particle of water within an expanding or contracting cylindrical volume of water as it is injected into, or extracted from, an aquifer.
Darcy’s law can be written to include effective porosity as:
where:
- v :
-
average linear groundwater velocity [L/T]
- K :
-
hydraulic conductivity [L/T]
- dh/dr :
-
hydraulic gradient [L/L]
Equation (4) describes the average linear velocity of a particle of water within an aquifer due to ambient groundwater flow.
Velocity, in general terms, is given by:
where:
- Δr :
-
traveled distance [L]
- Δt :
-
elapsed time [T]
Equation (5) can be rearranged to give:
Equation (6) describes the average position of a particle of water within an aquifer due to ambient groundwater flow. The one-dimensional (1D) displacement of the center of mass of a tracer, after completion of the injection, drift, and extraction phases of a push-pull test, is zero (Fig. 1). The displacement of the center of mass of the tracer is given by:
where:
- r 1 :
-
displacement during injection [L]
- r 2 :
-
displacement during drift [L]
- r 3 :
-
displacement during extraction [L]
The displacement of the tracer during: (1) the injection phase, is due to injection pumping (r i) and ambient groundwater flow (r a1), (2) the drift phase, is due to ambient groundwater flow (r a2), and (3) the extraction phase, is due to extraction pumping (−r e) and ambient groundwater flow (r a3) (Fig. 1). The components of the displacement of the center of mass of the tracer during the push-pull test can be substituted in Eq. (7) to give:
where:
- r i :
-
displacement due to injection pumping [L]
- r a1 :
-
displacement due to ambient groundwater flow [L]
- r a2 :
-
displacement due to ambient groundwater flow [L]
- r e :
-
displacement due to extraction pumping [L]
- r a3 :
-
displacement due to ambient groundwater flow [L]
The components in Eq. (8) can be substituted by their corresponding equations given in Eqs. (3) and (6) to give:
The components in Eq. (9), due to injection (first term) and extraction (fourth term), represent the leading- or trailing-edge position of the tracer within an expanding or contracting cylindrical volume of water, whereas the components due to ambient groundwater flow (vΔt a1, vΔt a2, and vΔt a3), represent the average displacement of the tracer. The average displacement of the tracer, due to injection, occurs when one-half of the mass of the tracer has been injected and is given by:
where:
- Q i :
-
injection rate [L3/T]
- τ i :
-
time elapsed from the start of water injection until the center of mass of the tracer is released [T]
In volumetric terms, Eq. (10) can be rewritten to give:
where:
\( {\mathcal{V}}_{\mathrm{i}} \) = volume of water injected until the center of mass of the tracer is released [L3].
The average displacement of the tracer, due to extraction, occurs when one-half of the mass of the tracer has been recovered and is given by integration of the concentration versus volume data, i.e., the breakthrough curve, as:
where:
- M e :
-
one-half of the mass of the recovered tracer [M]
- V 0 :
-
volume of water recovered at the start of extraction pumping [L3]
- V 1 :
-
volume of water recovered at the end of extraction pumping [L3]
- C(V):
-
concentration of the tracer (C) [M/L3] as a function of the volume (V) [L3] of water extracted
The corresponding volume at which one-half of the mass of the tracer has been recovered is given by evaluating the solution to Eq. (12) at M e by:
where:
- M \( \left({\mathcal{V}}_{\mathrm{e}}\right) \) :
-
mass of the tracer (M) [M] as a function of volume (\( {\mathcal{V}}_{\mathrm{e}} \)) [L3] at which one-half of the mass of the tracer has been recovered
It is important to note that the solution to Eq. (12) can be estimated numerically, as opposed to solved analytically, and doing so would allow for estimating \( {\mathcal{V}}_{\mathrm{e}} \). The corresponding times at which \( {\mathcal{V}}_{\mathrm{i}} \) and \( {\mathcal{V}}_{\mathrm{e}} \) occur are given as:
Substituting \( {\mathcal{V}}_{\mathrm{i}} \) in Eq. (11), \( {\mathcal{V}}_{\mathrm{e}} \) in Eq. (13), τ i in Eq. (14), and τ e in Eq. (15) for Q i τ i, Q e τ e, Δt a1, and Δt a3 in Eq. (9), respectively, gives:
where:
t d = Δt a2 (time elapsed from the end of water injection until the start of water extraction) [T]
Equation (16) describes the average position of the center of mass of the tracer during the injection, drift, and extraction phases. Rearranging Eq. (16) to solve for average linear groundwater velocity gives:
Equating Eqs. (17) and (4), and solving for effective porosity (n e) gives:
Equation (18) describes effective porosity (n e1) as a function of the aquifer properties, e.g., saturated thickness (b), hydraulic conductivity (K), and hydraulic gradient (dh/dr), and the transport of the center of mass of the tracer during the injection (\( {\mathcal{V}}_{\mathrm{i}} \), τ i), drift (t d), and extraction (\( {\mathcal{V}}_{\mathrm{e}} \), τ e) phases. Equations (17) and (18) are very similar to the Leap and Kaplan (1988) and Hall et al. (1991) equations, respectively.
From Leap and Kaplan (1988):
From Hall et al. (1991):
However, Eqs. (17) and (18) account for the transport of tracer during the injection phase (\( {\mathcal{V}}_{\mathrm{i}} \), τ i), whereas Eqs. (19) and (20) do not. If the transport of the tracer during the injection phase is truly negligible, then \( {\mathcal{V}}_{\mathrm{i}} \) and τ i are equal to zero, and Eqs. (17) and (18) are equivalent to Eqs. (19) and (20), respectively. If the transport of the tracer during the injection phase is not truly negligible, then \( {\mathcal{V}}_{\mathrm{i}} \) and τ i are greater than zero, and Eq. (17) will yield lower values of average linear groundwater velocity than Eqs. (19), and (18) will yield higher values of effective porosity than Eq. (20).
Study site
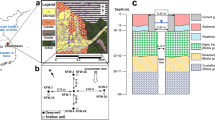
The study site is in Area 2 of the Oak Ridge Integrated Field Research Challenge (OR-IFRC) site at the Department of Energy’s Oak Ridge Reservation (ORR) in Oak Ridge, Tennessee, USA (Fig. 2). A typical geologic profile of Area 2 consists of approximately 6 m of unconsolidated and heterogeneous materials comprised of silty and clayey fill (mostly fine grained soil and clay-rich residuum), related to historical construction activities, underlain by undisturbed and clay-rich weathered bedrock (Moon et al. 2006; Watson et al. 2004; Fig. 3). Slug tests indicated that the hydraulic conductivity of the fill materials was approximately two orders of magnitude greater than the weathered bedrock, e.g., 10−6 versus 10−8 m/s, respectively (Fig. 3). The study site contains 13 monitoring wells (FW218–FW230), six of which were used as test wells (FW220–FW225), and one of which was used as a source well (FW229) for groundwater injectate for the single-well push-pull tests, as discussed in section ‘Effective porosity’ (Fig. 2). The test wells were installed by direct push coupled with continuous electrical resistivity profiling. The test wells are constructed of 1.9-cm inside diameter schedule-80 polyvinyl chloride (PVC) pipe and are screened from 3.7 to 6.1 m below ground surface (mbgs; Fig. 3). The test wells are screened within the fill materials and were vertically terminated at contact with the undisturbed weathered bedrock; the contact with undisturbed weathered bedrock was determined by a substantial increase in difficulty of advancing the direct-push drill string and a concomitant and notable increase in electrical resistivity (Fig. 3). The test wells are fully screened across the unconfined aquifer (Fig. 3). The source well is constructed of 5.1-cm inside diameter schedule-40 PVC pipe and is screened from 3 to 7.5 mbgs. The shallow groundwater aquifer is unconfined and the depth to groundwater is approximately 3.5 mbgs (Fig. 3). The site-wide average magnitude and direction of the hydraulic gradient, as determined graphically, is approximately −0.045 m/m and to the south/southwest, respectively (Fig. 2).
Plan-view maps of the study site: a country map showing study site location in the southeastern United States, b area map showing study site location in Area 2 of the OR-IFRC, and c study site map showing well locations, groundwater-level elevations, and groundwater-level elevation iso-contours (m amsl = meters above mean sea level)
The physical properties of the fill materials, in which the test wells are screened, are poorly characterized compared to those at other study sites located within Area 2. This is due, in part, to environmental safety policies at the site, which is located adjacent to highly contaminated areas. As a result of these policies, it was not feasible to collect core samples for evaluation of material properties during this study. However, previous investigations at nearby sites in Area 2 indicate that fill commonly used in this part of the ORR consisted mainly of locally obtained silty and clayey material derived from decomposition of shale and limestone. Fill material at the study site is expected to be similar in composition. It should be noted that the chemical and biological properties of the groundwater system at the study site are better characterized. A previous study by Paradis et al. (2016) reported that despite the high level of aquifer heterogeneity within Area 2, the biogeochemical processes associated with the reduction and oxidation of uranium within the study site wells (FW218–FW227) were spatially consistent; nevertheless, the spatial variability of the physical properties of the fill materials, e.g., effective porosity, were unknown at the time of this study.
Hydraulic gradient
The hydraulic gradient, within the vicinity of each test well, was estimated using ArcMap (version 10.5) software. The depth to groundwater, relative to the top of the casing (surveyed to 0.3-cm above mean sea level) of each site well, was measured using an electronic water level indicator (Solinst) immediately prior to conducting single-well pumping and push-pull tests. The depth to groundwater measurements were converted to meters above mean sea level (m amsl) and uploaded to ArcMap, along with the coordinates (latitude and longitude) of each site well, to create a point shape file. The groundwater elevation data were interpolated, using the spline tool, to create a digital elevation model (raster file) of the water table (cell size = 0.15 m, weight = 0, all other parameters set at default). The slope of the water table was calculated using the slope tool (z-factor = 1.171 × 10−5, based on the latitude of the study site). The average slope, within a 1-m radius about each test well, was calculated using the zonal statistics tool. The rationale for a 1-m radius, as representative of the hydraulic conditions within the vicinity of each test well, was based on Eq. (3) which describes the leading-edge position of a particle of water within an expanding cylindrical volume of water as it is injected into an aquifer, i.e., the maximum frontal position of bromide tracer during the injection phase of a push-pull test. An effective porosity of 5% was assumed, a priori. For a 20-L injection volume and a saturated aquifer thickness of 2.5 m, the radius in Eq. (3) would be approximately 0.25 m. It is important to note that Eq. (3) ignores heterogeneity and the drift phase of the push-pull tests which would lead to an underestimation of radius; therefore, a 1-m radius was assumed. The slope at each test well was converted from degrees to hydraulic gradient values and inputted into Eqs. (18) and (20) to estimate effective porosity.
Hydraulic conductivity
The hydraulic conductivity, within the vicinity of each test well, was estimated by conducting single-well pumping tests. Single-well pumping tests were conducted according to the methodology of Robbins et al. (2009) and Aragon-Jose and Robbins (2011). In brief, groundwater was pumped from each test well at a constant discharge rate using a peristaltic pump (Geotech Geopump) and stored in a 208-L plastic drum. The discharge rate was measured using a graduated cylinder and a stop watch. The depth to groundwater was measured using an electronic water level indicator (Solinst). The discharge rate and depth to groundwater were measured sequentially until steady-state conditions were achieved; steady-state conditions were defined as a change in drawdown less than 1.2 cm over the course of 15 min during a constant discharge rate.
Single-well pumping test data were analyzed according to the general methodology of Robbins et al. (2009) and Aragon-Jose and Robbins (2011). In brief, the steady-state discharge and drawdown values, along with the construction details of the test wells, e.g., saturated screen length and radius of well, were used to calculate the hydraulic conductivity using the half-ellipsoid flow equation, described analytically by Dachler (1936). Graphs showing single-well pumping test data can be found in the electronic supplementary material (ESM).
Effective porosity
The effective porosity, within the vicinity of each test well, was estimated by conducting single-well push-pull tests. Single-well push-pull tests were conducted according to the general methodology of Istok (2013). In brief, 23 L of groundwater (injectate) were collected from the up-gradient well FW229 (Fig. 2) using a peristaltic pump and stored in a plastic carboy. Three grams of potassium bromide (KBr; Sigma-Aldrich) were then added to 20 L of the injectate and mixed by recirculation using a peristaltic pump for a target concentration of 100 mg/L bromide. During mixing of the injectate, three samples were collected in 20-ml scintillation vials and were analyzed for bromide. The concentration of bromide was determined in the field using a bromide ion selective half-cell electrode (Thermo Scientific Cat. No. 9435BN) coupled with a double junction reference electrode (Thermo Scientific Cat. No. 900200). The minimum detection limit for bromide was 1 mg/L and the reproducibility of bromide measurements was ±2%. Immediately prior to injection, 1 L of groundwater was purged from the test well (approximately two test well volumes) and three samples were collected and analyzed for the background concentration of bromide. The push phase of the test consisted of low-flow (approximately 250–400 ml/min) injection of the 20-L bromide-amended injectate followed immediately by the injection of 3 L of nonamended injectate (herein referred to as the “chase”) using a peristaltic pump. The injection of the chase was conducted to clear the test well volume (approximately 0.5 L) of the bromide-amended injectate. The total push time (tracer plus chase) ranged from approximately 1–1.5 h. The injectate was then left to drift in the groundwater system under nonpumping conditions for up to 2 h. The pull phase of the test consisted of low-flow extraction (approximately 100 to 300 ml/min) of up to 65 L of groundwater and sequential collection of 20-ml samples which were analyzed for bromide.
Single-well push-pull test data were analyzed according to the general methodology of Istok (2013). In brief, the time (τ i) and volume (\( {\mathcal{V}}_{\mathrm{i}} \)) at which the center of mass of bromide was released were calculated by evaluating Eqs. (10) and (11), respectively. The concentration of bromide versus the volume and time elapsed during the pull phase of the tests were generated to calculate the volume (\( {\mathcal{V}}_{\mathrm{e}} \)) and time (τ e) at which the center of mass of bromide was recovered. \( {\mathcal{V}}_{\mathrm{e}} \) and τ e were calculated by numerical integration of the bromide versus time data (Thomas et al. 2008). \( {\mathcal{V}}_{\mathrm{e}} \) and τ e were concomitant with one half of the region between the bromide and volume/time data. Graphs showing single-well push-pull test data can be found in the electronic supplementary material (ESM).
Uncertainly analysis
The uncertainty in the measured parameters, e.g., volume injected/extracted, pumping rate, drawdown, elapsed time, etc. and the propagated error in the calculated parameters, e.g., hydraulic gradient, hydraulic conductivity, and effective porosity, were analyzed according to the “Data Analysis Toolkit # 5: Uncertainty analysis and error propagation”, by Kirchner (2001). More specifically, the simple rules for sums and differences, and for products and ratios, were used.
Results
Hydraulic gradient results
The static water table was relatively stable immediately prior to, and after, conducting the single-well pumping and push-pull tests (data not shown). The site-wide average magnitude and direction of the static hydraulic gradient was similar to pretest conditions, e.g., −0.045 (Fig. 2). The near-well (1-m radius) hydraulic gradient at each test well, immediately prior to conducting the push-pull tests, ranged from a low of −0.020 in test well FW224 to a high of −0.085 in test well FW221 (Table 1). The range of hydraulic gradient values were notably greater than those previously reported at other test sites by Hall et al. (1991) and Istok (2013).
Hydraulic conductivity results
During the single-well pumping tests, steady-state discharge and drawdown conditions were achieved within a few minutes after the tests began and were maintained for approximately 1 h (data not shown). The drawdown was typically less than 10% of the static saturated screen length (data not shown). Static water levels were stable prior to initiating the pumping tests and recharge to near-static water levels generally occurred within 0.5 h after pumping stopped (data not shown). The hydraulic conductivity for each test well was then calculated by inputting the steady-state discharge and drawdown values, along with the saturated well screen length and radius, into the half-ellipsoid flow equation (Dachler 1936). The hydraulic conductivity ranged from a low of 2.1 × 10−6 m/s in test well FW225 to a high of 1.6 × 10−5 m/s in test well FW224 (Table 1). The range of hydraulic conductivity values were within those representative of silts and fine sands (Domenico and Schwartz 1998) and notably less than those previously reported at other test sites by Hall et al. (1991) and Istok (2013) (Table 1).
Effective porosity results
The breakthrough curves of bromide, during the pull phase of the tests, showed sharp and short-lived increases followed by gradual and non-linear decreases (Fig. 4). It is important to note that the concentrations of bromide in the test wells prior to injection were below the minimum detection limit (~1 mg/L) and that the concentration of bromide in the injectate was near the target concentration (~100 mg/L; data not shown). The time (τ e) from the start of the pull phase until the center of mass of bromide was recovered ranged from a low of 0.85 h (3,077 s) in test well FW223 to a high of 1.14 h (4,087 s) in test well FW222 (Fig. 4; Table 2). The corresponding volume (\( {\mathcal{V}}_{\mathrm{e}} \)) at which the center of mass of bromide was recovered ranged from a low of 6 L (0.006 m3) in test well FW225 to a high of 15 L (0.015 m3) in test well FW221 (Fig. 4; Table 2).
The saturated aquifer thickness (~2.4 m) was similar among all test wells (Table 2). The drift times (t d) were similar among five of the six wells (~1.8 h on average), whereas the drift time in test well FW225 was notably short (~0.5 h; Table 2). The percent mass recovery of bromide ranged from a low of 41% in test well FW225 to a high of 71% in test well FW221 (data not shown). In general, the experimental design, aquifer properties (Table 1), and results of the push-pull tests (Table 2) for this study were more similar to those from Istok (2013) than from Hall et al. (1991). However, it should be noted that the drift times (t d) for this study were substantially less than Istok (2013).
The effective porosity (n e) for each test well was calculated by inputting the parameters from Tables 1 and 2 into the expanded and truncated equations, Eqs. (18) and (20), respectively. The effective porosity (n e1), per Eq. (18), ranged from a low of 0.6% in test well FW220 to a high of 5.0% in test well FW221 (Table 3). It should be noted that the negative value of n e1 (−0.1%) in test well FW225 indicated that one or more input parameters for Eq. (18) were not valid; this issue is discussed in section ‘Discussion: effective porosity’. The effective porosity (n e2), per Eq. (20), ranged from a low of 0.1% in test wells FW220 and FW225 to a high of 1.3% in test well FW221 (Table 3). The effective porosity, per Eq. (18), which accounts for the transport of tracer during the injection phase, was substantially larger than that of Eq. (20), which does not account for the transport of tracer during the injection phase (Table 3). The range of effective porosity, per Eq. (18), was representative of the lower end of those calculated from field-scale tracer-based studies conducted in granular porous media, whereas the range per Eq. (20) was representative of those conducted in fractured porous media (Gelhar et al. 1992). The effective porosity from Hall et al. (1991), per Eqs. (18) and (20), were almost identical (6.2 versus 6.1%, respectively), whereas from Istok (2013) they were notably different, i.e., the expanded equation (n e1) yielded substantially higher effective porosity than the truncated equation (n e2; 37 versus 13%; Table 3).
Uncertainty analysis results
The percent standard errors of the hydraulic gradient (dh/dr), hydraulic conductivity (K) and drift time (t d) were typically less than ±2% (Table 4). The percent standard errors of the remaining parameters, e.g., saturated aquifer thickness (b) and the times (τ i, τ e) and volumes (\( {\mathcal{V}}_{\mathrm{i}} \), \( {\mathcal{V}}_{\mathrm{e}} \)) at which the center of mass of bromide was released and recovered, were typically greater than ±2% but less than ±5% (Table 4). The error-propagated uncertainty in effective porosity (n e1) was less than ±0.5% (Fig. 5). It should be noted that an uncertainly analysis of effective porosity for the studies by Hall et al. (1991) and Istok (2013) was not possible due to the lack of available data on the uncertainty of pumping rates, volumes injected/extracted, etc.
Effective porosity (n e1) per Eq. (18) for tests in this study (FW220–FW224). Test well FW225 is omitted due to invalid results (see section ‘Discussion: effective porosity ’). Error bars represent the uncertainty
Discussion
Discussion: hydraulic gradient
The range of the near-well hydraulic gradient (−0.020 to −0.085 m/m) in the test wells was relatively small (within a single order of magnitude) and representative of the site-wide average (−0.045 m/m). The spatial variability of the hydraulic gradient was expected due to the high level of aquifer heterogeneity within Area 2 (Moon et al. 2006; Watson et al. 2004). However, it must be noted that the near-well hydraulic gradient was not measured directly, i.e., graphically, rather it was estimated based on a digital elevation model as discussed in section ‘Hydraulic gradient. Therefore, there is a level of uncertainty in the near-well hydraulic gradient that must be recognized; nevertheless, the model-generated values of the near-well hydraulic gradient are likely much more representative of the near-well conditions than the graphically determined values at the site-wide scale.
Discussion: hydraulic conductivity
The steady-state discharge and drawdown conditions among the test wells were consistent with the methodology of Robbins et al. (2009) and Aragon-Jose and Robbins (2011). It should be noted that the Robbins et al. (2009) study was conducted in a confined aquifer comprised of fine sands, whereas this study was conducted in an unconfined aquifer comprised of silty and clayey fill. However, Aragon-Jose and Robbins (2011) demonstrated the validity of the Robbins et al. (2009) method in an unconfined aquifer comprised of sandy till and within test wells whose screens crossed the water table; these hydrogeologic and test well conditions were very similar to those in this study. Aragon-Jose and Robbins (2011) recommended that a valid application of the Robbins et al. (2009) method in unconfined aquifers required minimal drawdown with respect to the static saturated well screen length. The drawdown in this study was typically less than 10% of the static saturated screen length and was within the general range of the percent drawdown reported by Aragon-Jose and Robbins (2011; ~8–12%).
There is a level of uncertainty in the measured drawdown within the test wells that must be recognized. The total drawdown within a well during pumping may due to a number of components, including: (1) aquifer loss, (2) skin layer loss, (3) gravel pack loss, (4) well screen loss, (5) up-flow loss in well interior, (6) partial penetration of well screen, and (7) seepage face (Houben 2015a, b). As previously discussed in section ‘Study site’, the well screens fully penetrate the unconfined aquifer and were installed without a gravel pack, i.e., the well screens are in direct contact with the fill materials. The wells were also routinely developed by mechanical means, i.e., surge and purge, to limit skin layer loss. The pump intake was set at mid-screen, i.e., 50% of the screen length, to limit up-flow loss in the well interior (Houben and Hauschild 2011); therefore, it is likely that the drawdown during pumping, in order of importance, was attributed to: (1) the aquifer and (2) a seepage face. A seepage face would lead to overestimating drawdown during pumping and underestimating hydraulic conductivity. In turn, underestimating hydraulic conductivity would lead to underestimating effective porosity. Nevertheless, the presence and extent of any seepage face during pumping was not known; however, by limiting the drawdown to approximately less than 10% of the static saturated screen length, the effects of a seepage face were likely mitigated.
The range of hydraulic conductivity (2.1 × 10−6–1.6 × 10−5 m/s) in the test wells was relatively small (within a single order of magnitude) and within the lower and upper method detection limits (~10−8–10−4 m/s; Robbins et al. 2009); the range of hydraulic conductivity was also within that representative of silts and fine sands (Domenico and Schwartz 1998). However, Watson et al. (2013) reported that the hydraulic conductivity of the fill material, in Area 2 test wells immediately east of the study site, was approximately 3.8 × 10−4 m/s. Therefore, the range of hydraulic conductivity reported in this study was notably less (up to two orders of magnitude) than to the value previously reported. It is important to note that Watson et al. (2013), and Phillips et al. (2008), also reported that the fill material was gravelly, whereas no gravel component is known to exist within the area of this study site. Therefore, the lack of a gravel component in the fill material within the study site may explain the lower values of hydraulic conductivity. In summary, the single-well pumping test data and analysis suggested that the variability in the hydraulic conductivity of the fill material was relatively low and within that representative of silts and fine sands.
Discussion: effective porosity
The breakthrough curve for a non-reactive tracer released from an instantaneous point source, as it passes a fixed point of observation, should resemble a bell-shaped curve when its transport is governed by advection and dispersion during steady-state groundwater flow in a homogeneous and an isotropic granular porous medium (Baetsle 1969). The breakthrough curves for bromide, observed during the pull phase of the tests, resembled bell-shaped curves that were truncated at the leading edges (early time) and possibly skewed towards the following edges (late time). The truncation at the leading edge indicated that the full spatial extent of the injectate did not move beyond the test wells during the drift phase. Ideally, the entire injectate should drift beyond the test wells under natural-gradient (non-pumping) conditions and then the entire injectate should be pumped back to the test wells under forced-gradient (extraction pumping) conditions (Leap and Kaplan 1988). However, if the injectate drifts too far from the test wells, it may only partially return during the pull phase and lead to a low mass recovery of the tracer. Although it may be tempting to suggest that the drift times in this study were too short, it must be noted that the average percent mass recovery of the tracer (bromide) was far less than 100% (60 ± 10%, data not shown). Therefore, an increase in the drift time would have likely resulted in a lower mass recovery of bromide, and thus a weaker signal for analysis. In addition to advective mass transport, diffusive mass transport of bromide from mobile to immobile pore water may partially explain the low mass recovery of bromide; mobile to immobile diffusive mass transport is well documented and described at the OR-IFRC site and at the nearby west Beak Creek Valley site (Luo et al. 2005; Mayes et al. 2003; McKay et al. 2000; Reedy et al. 1996). The extent of sorption or degradation of bromide was likely negligible based on previous batch and column studies which demonstrated that mass recoveries of bromide from OR-IFRC soils and sediments are nearly 100% under acidic to neutral pH (4.5–7; Hu and Moran 2005; McCarthy et al. 2000); the pH at the study site ranges from approximately 6.5–8 (Paradis et al. 2016).
With regard to the possible skewness of the breakthrough curves towards the following edge, this suggested that mass transport mechanisms in addition to advection and dispersion and/or anisotropy and heterogeneity of the porous media were present. The likelihood that the fill materials were packed in the vertical direction suggests that permeable media at the site were anisotropic. The variability in the magnitude of the hydraulic conductivity among the test wells (2.1 × 10−6–1.6 × 10−5 m/s) also indicates a certain amount of heterogeneity. Although a thorough investigation of advection, dispersion, and other mass transport mechanisms was not an objective of this study, the skewness of the breakthrough curves towards the following edge may be attributed to numerous small-scale heterogeneities in aquifer hydraulic properties during radially convergent flow to a well (Pedretti et al. 2013). In summary, the breakthrough curves suggested that the injectate drifted some distance beyond the test wells under natural-gradient conditions and that an adequate amount of tracer (bromide) was recovered during the pull phase to accurately calculate effective porosity using Eqs. (18) and (20).
The effective porosity values from the expanded equation (0.6–5.0%) were substantially larger than those from the truncated equation (0.1–1.3%) which indicated that the transport of the tracer during the injection phase was not truly negligible. From Hall et al. (1991), the effective porosity values were almost identical (6.2 versus 6.1%) which indicated that the transport of the tracer during the injection phase was truly negligible. From Istok (2013), the effective porosity values were notably different (37 versus 13%), as in the tests presented here, which indicated that the transport of the tracer during the injection phase was not truly negligible. Therefore, the agreement, or lack thereof, of effective porosity from the expanded versus the truncated equation can clearly identify and quantify the relative importance of accounting for the transport of tracer during the injection phase, as shown in the tests presented here and in those from the literature (Hall et al. 1991; Istok 2013).
The negative value of effective porosity (−0.1%), using the expanded equation for test well FW225, suggested that the volume of water extracted until the center of mass of the tracer was recovered (\( {\mathcal{V}}_{\mathrm{e}} \)) was less than the volume of water injected until the center of mass of the tracer was released (\( {\mathcal{V}}_{\mathrm{i}} \)); this is impossible due to the law of conservation of mass. An inspection of the breakthrough curve of bromide for test well FW225 shows that pumping stopped despite bromide concentrations greater than 20 mg/L, whereas pumping stopped in the remaining five test wells at bromide concentrations less than 10 mg/L. Therefore, it is likely that the total pump-back time in test well FW225 was too short to return an adequate volume of water representative of the true center of mass of bromide. As expected, this error in the application and data analysis of the push-pull test goes unrecognized when using the truncated equation, as shown by a positive value of effective porosity (0.1%) for test well FW225.
This is the first measurement of effective porosity in a fine-grained fill material that the authors are aware of; hence, there is no “expected” range of values for effective porosity in this type of material. The effective porosity values from the expanded equation (0.6–5.0%) were more similar to those previously calculated from field-scale tracer-based studies conducted in unconsolidated, heterogeneous, and fine-grained granular porous media, whereas those from the truncated equation (0.1–1.3%) were more similar to those from fractured porous media (Gelhar et al. 1992; Hall et al. 1991; Stephens et al. 1998). Based on the hydrogeology of the study site, i.e., silty and clayey fill, the effective porosity values from the expanded equation are likely more accurate than those from the truncated equation. Moreover, the push-pull tests by Istok (2013) were conducted in a gravel and sand aquifer, which also suggests that the effective porosity of 37% from the expanded equation is likely more accurate than the 13% from the truncated equation. However, it must be emphasized that values of effective porosity are dependent on the type of tracer and the nature of the porous media—for example, in column experiments by van der Kamp et al. (1996), values of effective porosity were equal to or far less than the total porosity, depending on the type of solute tracer. van der Kamp et al. (1996) attributed these findings to phenomena such as: (1) ion exclusion, (2) enclosed pores, and (3) bound water. At the nearby west Bear Creek Valley site, McKay et al. (2000) conducted a multi-well natural-gradient tracer study and demonstrated that the mean arrival times of colloidal tracers were up to 500 times faster than those reported for solute tracers from previous tests at the site conducted by Lee et al. (1992). McKay et al. (2000) attributed these findings to transport of the colloids through fractures, whereas the solute tracers experienced substantial diffusion into the immobile pore water in the fine-grained matrix between fractures. This demonstrates that different types of tracers can experience different effective porosities in the same material and implies that even the same solute tracer may encounter different pore regions (mobile and immobile pore water) over the duration of a tracer experiment. Therefore, the magnitude of the effective porosities calculated in this study may not be truly representative of the void spaces through which water can flow.
Lastly, and perhaps most importantly, it must be recognized that both the expanded and truncated equations were theoretically developed for confined aquifers as opposed to unconfined aquifers. However, the only in situ study to experimentally test the validity of the truncated equation was by Hall et al. (1991). Hall et al. (1991) arrived at similar values of effective porosity (~6%) from both single-well push-pull and dual-well natural-gradient tests which were conducted in an unconfined, heterogeneous, and sandy aquifer. Therefore, there is clearly a need to: (1) experimentally test the expanded solution for the confined case, and (2) theoretically develop an expanded solution for the unconfined case.
Discussion: uncertainty analysis
The error-propagated uncertainty in the calculated values of effective porosity was relatively small (< ± 0.5%), due in part, to the careful consideration for the precise determination of the aquifer properties, e.g., hydraulic gradient, hydraulic conductivity, and saturated aquifer thickness, and the push-pull test parameters, e.g., the times and volumes at which the center of mass of bromide was released and recovered. However, the uncertainty analysis failed to capture the effects of: (1) the presence and extent of seepage face during extraction pumping, and (2) applying an analytical solution developed for a confined aquifer to an unconfined aquifer. The presence and extent of a seepage face could have been determined using a down-well device with video capability during extraction pumping. However, this was not possible due to the small diameter (1.9 cm) of the wells and the presence of down-well tubing (0.64 cm diameter) which limited the physical space to deploy such a device. The effects of applying an analytical solution developed for a confined aquifer to the unconfined aquifer in this study was not known; however, as previously discussed in section ‘Discussion: effective porosity’, Hall et al. (1991) demonstrated the validity of the truncated analytical solution, developed for a confined aquifer, as applied to an unconfined, heterogeneous, and sandy aquifer.
Conclusions
The conclusions of this study are as follows: (1) the analytical solution to describe the displacement of the center of mass of a tracer during a push-pull test can be expanded to account for displacement during the injection phase, (2) the transport of a tracer during the injection phase of a push-pull test may not be truly negligible, (3) the failure to account for displacement during the injection phase may lead to a substantial underestimation of the magnitude of effective porosity, (4) single-well push-pull tests can be readily applied to multiple wells within a study site to assess the spatial variability of effective porosity, and (5) the error-propagated uncertainty in the value of effective porosity can be mitigated to a reasonable level by careful consideration for the precise determination of the aquifer properties and the push-pull test parameters. Finally, it must be recognized that there is a need to theoretically develop and experimentally test the expanded solution presented here for the case of an unconfined aquifer and for different types of aquifer materials.
Change history
23 October 2018
In the recent article by Paradis et al. (2018), an error was made when developing a conceptual model and an analytical solution to describe the one-dimensional displacement of the center of mass of a non-reactive tracer during a single-well injection, drift, and extraction test (push-pull test).
23 October 2018
In the recent article by Paradis et al. (2018), an error was made when developing a conceptual model and an analytical solution to describe the one-dimensional displacement of the center of mass of a non-reactive tracer during a single-well injection, drift, and extraction test (push-pull test).
References
Aragon-Jose AT, Robbins GA (2011) Low-flow hydraulic conductivity tests at wells that cross the water table. Ground Water 49(3):426–431. https://doi.org/10.1111/j.1745-6584.2010.00742.x
Baetsle LH (1969) Migration of radionuclides in porous media. In: Duhamel AMF (ed) Progress in nuclear energy. Health Physics series, 12th edn. Pergamon, Elmsford, NY, pp 707–730
Dachler R (1936) Grundwasserstromung [Ground-water flow]. Springer, Vienna
Davis SN, Thompson GM, Bentley HW, Stiles G (1980) Ground-water tracers: a short review. Ground Water 18(1):14–23. https://doi.org/10.1111/j.1745-6584.1980.tb03366.x
Domenico PA, Schwartz FW (1998) Physical and chemical hydrogeology, 2nd edn. Wiley, New York
Fetter CW (2001) Applied hydrogeology, 4th edn. Prentice Hall, Upper Saddle River, NJ
Gelhar LW, Welty C, Rehfeldt KR (1992) A critical review of data on field-scale dispersion in aquifers. Water Resour Res 28(7):1955–1974. https://doi.org/10.1029/92wr00607
Hall SH, Luttrell SP, Cronin WE (1991) A method for estimating effective porosity and groundwater velocity. Ground Water 29(2):171–174. https://doi.org/10.1111/j.1745-6584.1991.tb00506.x
Houben GJ (2015a) Review: Hydraulics of water wells—flow laws and influence of geometry. Hydrogeol J 23(8):1633–1657. https://doi.org/10.1007/s10040-015-1312-8
Houben GJ (2015b) Review: Hydraulics of water wells—head losses of individual components. Hydrogeol J 23(8):1659–1675. https://doi.org/10.1007/s10040-015-1313-7
Houben GJ, Hauschild S (2011) Numerical modeling of the near-field hydraulics of water wells. Ground Water 49(4):570–575. https://doi.org/10.1111/j.1745-6584.2010.00760.x
Hu QH, Moran JE (2005) Simultaneous analyses and applications of multiple fluorobenzoate and halide tracers in hydrologic studies. Hydrol Process 19(14):2671–2687. https://doi.org/10.1002/hyp.5780
Istok JD (2013) Push-pull tests for site characterization. Springer, Heidelberg, Germany
Kirchner J (2001) Analysis of environmental data. University of California Berkeley. http://seismo.berkeley.edu/~kirchner/eps_120/EPSToolkits.htm. Accessed 1 June 2016
Leap DI, Kaplan PG (1988) A single-well tracing method for estimating regional advective velocity in a confined aquifer: theory and preliminary laboratory verification. Water Resour Res 24(7):993–998. https://doi.org/10.1029/WR024i007p00993
Lee RR, Ketelle RH, Bownds JM, Rizk TA (1992) Aquifer analysis and modeling in a fractured, heterogeneous medium. Ground Water 30(4):589–597. https://doi.org/10.1111/j.1745-6584.1992.tb01535.x
Li H (1995) Effective porosity and longitudinal dispersivity of sedimentary rocks determined by laboratory and field tracer tests. Environ Geol 25(2):71–85
Luo J, Cirpka OA, Wu WM, Fienen MN, Jardine PM, Mehlhorn TL, Watson DB, Criddle CS, Kitanidis PK (2005) Mass-transfer limitations for nitrate removal in a uranium-contaminated aquifer. Environ Sci Technol 39(21):8453–8459. https://doi.org/10.1021/es050195g
Mayes MA, Jardine PM, Mehlhorn TL, Bjornstad BN, Ladd T, Zachara JM (2003) Transport of multiple tracers in variably saturated humid region structured soils and semi-arid region laminated sediments. J Hydrol 275(3–4):141–161. https://doi.org/10.1016/s0022-1694(03)00039-8
McCarthy JF, Howard KM, McKay LD (2000) Effect of pH on sorption and transport of fluorobenzoic acid ground water tracers. J Environ Qual 29(6):1806–1813
McKay LD, Sanford WE, Strong JM (2000) Field-scale migration of colloidal tracers in a fractured shale saprolite. Ground Water 38(1):139–147. https://doi.org/10.1111/j.1745-6584.2000.tb00211.x
Meinzer OE (1923a) Outline of ground-water hydrology, with definitions. US Geological Survey Water Suppl Pap 494
Meinzer OE (1923b) The occurrence of ground water in the United States, with a discussion of principles. US Geological Survey Water Suppl Pap 489
Moon JW, Roh Y, Phelps TJ, Phillips DH, Watson DB, Kim YJ, Brooks SC (2006) Physicochemical and mineralogical characterization of soil-saprolite cores from a field research site, Tennessee. J Environ Qual 35(5):1731–1741. https://doi.org/10.2134/jeq2005.0123
Paradis CJ, Jagadamma S, Watson DB, McKay LD, Hazen TC, Park M, Istok JD (2016) In situ mobility of uranium in the presence of nitrate following sulfate-reducing conditions. J Contam Hydrol 187:55–64. https://doi.org/10.1016/j.jconhyd.2016.02.002
Pedretti D, Fernandez-Garcia D, Bolster D, Sanchez-Vila X (2013) On the formation of breakthrough curves tailing during convergent flow tracer tests in three-dimensional heterogeneous aquifers. Water Resour Res 49(7):4157–4173. https://doi.org/10.1002/wrcr.20330
Phillips DH, Watson DB, Kelly SD, Ravel B, Kemner KM (2008) Deposition of uranium precipitates in dolomitic gravel fill. Environ Sci Technol 42(19):7104–7110. https://doi.org/10.1021/es8001579
Reedy OC, Jardine PM, Wilson GV, Selim HM (1996) Quantifying the diffusive mass transfer of nonreactive solutes in columns of fractured saprolite using flow interruption. Soil Sci Soc Am J 60(5):1376–1384
Robbins GA, Aragon-Jose AT, Romero A (2009) Determining hydraulic conductivity using pumping data from low-flow sampling. Ground Water 47(2):271–276. https://doi.org/10.1111/j.1745-6584.2008.00519.x
Stephens DB, Hsu KC, Prieksat MA, Ankeny MD, Blandford N, Roth TL, Kelsey JA, Whitworth JR (1998) A comparison of estimated and calculated effective porosity. Hydrogeol J 6(1):156–165. https://doi.org/10.1007/s100400050141
Thomas GB Jr, Weir MD, Hass J, Giordano FR (2008) Numerical integration Thomas’ calculus, 11th edn. Pearson, London, pp 603–619
Turnadge C, Smerdon BD (2014) A review of methods for modelling environmental tracers in groundwater: advantages of tracer concentration simulation. J Hydrol 519:3674–3689. https://doi.org/10.1016/j.jhydrol.2014.10.056
van der Kamp G, Van Stempvoort DR, Wassenaar LI (1996) The radial diffusion method, 1: using intact cores to determine isotopic composition, chemistry, and effective porosities for groundwater in aquitards. Water Resour Res 32(6):1815–1822. https://doi.org/10.1029/95wr03719
Watson DB, Kostka JE, Fields MW, Jardine PM (2004) The Oak Ridge Field Research Center conceptual model. US Department of Energy, Oak Ridge, TN
Watson DB, Wu WM, Mehlhorn T, Tang GP, Earles J, Lowe K, Gihring TM, Zhang GX, Phillips J, Boyanov MI, Spalding BP, Schadt C, Kemner KM, Criddle CS, Jardine PM, Brooks SC (2013) In situ bioremediation of uranium with emulsified vegetable oil as the electron donor. Environ Sci Technol 47(12):6440–6448. https://doi.org/10.1021/es3033555
Acknowledgements
This material by ENIGMA – Ecosystems and Networks Integrated with Genes and Molecular Assemblies (http://enigma.lbl.gov), a Scientific Focus Area Program at Lawrence Berkeley National Laboratory – is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Biological & Environmental Research, under contract number DE-AC02-05CH11231. The authors would like to thank Tonia Mehlhorn from the Oak Ridge National Laboratory and Julian Fortney from the University of Tennessee Knoxville for their assistance and helpful suggestions during the field-based portion of this study. The authors would also like to thank Eriko Gordon and Emma Dixon from the University of Tennessee Knoxville for their assistance with the final production of the manuscript. Finally, the authors would like to thank the two anonymous reviewers for their insightful comments and helpful suggestions which greatly improved the quality of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 104 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Paradis, C.J., McKay, L.D., Perfect, E. et al. Push-pull tests for estimating effective porosity: expanded analytical solution and in situ application. Hydrogeol J 26, 381–393 (2018). https://doi.org/10.1007/s10040-017-1672-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-017-1672-3