Abstract
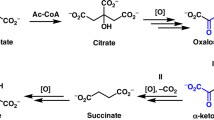
Reaction pathways of side products (formate, glycolate, and tartronate) from dihydroxyfumarate (DHF) were theoretically investigated as DHF is an intermediate in the process of producing tartrates and oxalate from glyoxylate of the citric acid cycle. The proposed pathways for each reaction were mapped by density functional theory (DFT) calculations. The transitions states were confirmed by analyzing the vibrational frequency and the intrinsic reaction coordinate (IRC) theory. The corresponding reaction activation energy, enthalpy change, Gibb’s free energy change, and rate of reactions were calculated to get a clear picture of the whole reaction pathway. In the whole process, the decarboxylation reaction showed the highest energy barrier of 20–23 kcal/mol. Proton transfer and hydroxylation reactions were almost barrierless. As most of these reactions have very low energy barrier, our findings elucidate the high probability of those reactions under experimental conditions.














Similar content being viewed by others
References
Kasting J (1993) Earth’s early atmosphere. Science 259:920–926
Orgel LE (1998) The origin of life – how long did it take? Orig Life Evol Biosph 28:91–96
Oparin AI (1924) ProischogdenieZhizni. MoscovskyRobotschii.
Oparin AI (1965) Origin of life2nd edn. Dover Publication
Miller SL (1953) A production of amino acids under possible primitive earth conditions. Science 117:2
Miller SL (1955) Production of some organic compounds under possible primitive earth conditions. J Am Chem Soc 77:2351–2361
Schwartz W (1967) Sidney W. Fox (Herausgeber), The origin of prebiological systems and of their molecular matrices. XX + 482 S., 110 Abb., 35 Tab, vol 7. Academic Press. $ 8. Z Allg Mikrobiol, New York, London 1965, pp 245–245
Cleaves II HJ, ScottAM HFC, Leszczynski J, Sahai N, Hazen R (2012) Mineral-organic interfacial processes: potential roles in the origins of life. Chem Soc Rev 41:5502–5525
Haldane JBS (1929) The origin of life. Ration Annu 148:8
MillerSS UHC (1959) Organic coumpound synthesis on primitive earth. Science 130:7
Parker ET, Cleaves HJ, Dworkin JP, Glavin DP, Callahan M, Aubrey A, Lazcano A, Bada JL (2011) Primordial synthesis of amines and amino acids in a 1958 Miller H2S-rich spark discharge experiment. Proc Natl Acad Sci U S A 108:5526–5531
Morowitz HJ (1999) A theory of biochemical organization, metabolic pathways, and evolution. Complexity 4:39–53
QuayleJR FT (1978) Evolutionary aspects of autotrophy. Microbiol Rev 42:251–273
Eschenmoser A (2007) The search for the chemistry of life’s origin. Tetrahedron 63:12821–12844
Wächtershäuser G (1990) Evolution of the first metabolic cycles. Proc Natl Acad Sci U S A 87:200–204
Hartman H (1975) Speculations on the origin and evolution of metabolism. J Mol Evol 4:359–370
McFadden BA (1973) Autotrophic CO2 assimilation and the evolution of ribulose diphosphate carboxylase. Bacteriol Rev 37:289–319
Morowitz HJ, Kostelnik JD, Yang J, Cody GD (2000) The origin of intermediary metabolism. Proc Natl Acad Sci U S A 97:7704–7708
Sagi VN, Punna V, Hu F, Meher G, Krishnamurthy R (2012) Exploratory experiments on the chemistry of the “Glyoxylate Scenario”: formation of ketosugars from dihydroxyfumarate. J Am Chem Soc 134:3577–3589
Butch C, Cope ED, Pollet P, Gelbaum L, Krishnamurthy R, Liotta CL (2013) Production of tartrates by cyanide-mediated dimerization of glyoxylate: a potential abiotic pathway to the citric acid cycle. J Am Chem Soc 135:13440–13445
Butch CJ, Wang J, Gu J, Vindas R, Crowe J, Pollet P, Gelbaum L, Leszczynski J, Krishnamurthy R, Liotta CL (2016) pH-controlled reaction divergence of decarboxylation versus fragmentation in reactions of dihydroxyfumarate with glyoxylate and formaldehyde: parallels to biological pathways. J Phys Org Chem 29:352–360
Eschenmoser A (2007) On a hypothetical generational relationship between HCN and constituents of the reductive citric acid cycle. Chem Biodivers 4:554–573
Zhao Y, Truhlar DG (2008) The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor Chem Accounts 120:215–241
Ayala PY, Schlegel HB (1997) A combined method for determining reaction paths, minima, and TS geometries. J Chem Phys 107:375–384
Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2018) Gaussian 09, Revision E.01, Inc., Wallingford CT.
MarvinView, ChemAxon. 2014, (6.3.0).
Walker M, Harvey AJA, Sen A, Dessent CEH (2013) Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions. J Phys Chem A 117:12590–12600
Hohenstein EG, Chill ST, Sherrill CD (2008) Assessment of the performance of the M05 − 2X and M06 − 2X exchange-correlation functionals for noncovalent interactions in biomolecules. J Chem Theory Comput 4:1996–2000
Mennucci B (2012) Polarizable continuum model. Wiley Interdiscip Rev Comput Mol Sci 2:386–404
Fukui K (1981) The path of chemical reactions - the IRC approach. Acc Chem Res 14:363–368
Funding
This work was jointly supported by NSF and the NASA Astrobiology Program under the NSF Center for Chemical Evolution, CHE1004570. The computation time was provided by the Extreme Science and Engineering Discovery Environment (XSEDE) by National Science Foundation grant number OCI-1053575 and XSEDE award allocation number DMR110088 and by the Mississippi Center for Supercomputer Research.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is dedicated to Professor Zdzislaw Latajka, on occasion of his 70th Birthday in recognition of his numerous vital research contributions.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper belongs to the Topical Collection Zdzislaw Latajka 70th Birthday Festschrift.
Electronic supplementary material
ESM 1
(DOCX 184 kb)
Rights and permissions
About this article
Cite this article
Khan, M., Kar, S., Wang, J. et al. Theoretical study of formate, tartrate, tartronate, and glycolate production from 6-carbon trioxylate intermediate in the citric acid cycle. J Mol Model 25, 347 (2019). https://doi.org/10.1007/s00894-019-4240-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00894-019-4240-z