Mathematical modeling of planar physically nonlinear inhomogeneous plates with rectangular cuts in the three-dimensional formulation

Abstract

Mathematical models of planar physically nonlinear inhomogeneous plates with rectangular cuts are constructed based on the three-dimensional (3D) theory of elasticity, the Mises plasticity criterion, and Birger’s method of variable parameters. The theory is developed for arbitrary deformation diagrams, boundary conditions, transverse loads, and material inhomogeneities. Additionally, inhomogeneities in the form of holes of any size and shape are considered. The finite element method is employed to solve the problem, and the convergence of this method is examined. Finally, based on numerical experiments, the influence of various inhomogeneities in the plates on their stress–strain states under the action of static mechanical loads is presented and discussed. Results show that these imbalances existing with the plate’s structure lead to increased plastic deformation.

1 Introduction

Much attention in modern science is paid to the study of the stability of plates and shells that have holes in their structures. Interest in this problem is caused by wide application in many areas of industry (mechanical engineering, instrument production, aviation industry, etc.) which requires the employment of structural elements of perforated plates and shells. Inhomogeneities in plates/shells cause stress concentrations and affect their stress–strain states and mechanical characteristics; therefore, when designing and fabricating structures, it is necessary to take into account the increase in stresses near the areas of their inhomogeneities. Global and local studies of the stress distribution in the vicinity of a discontinuity in a structure like cutouts and cracks play a crucial role in designing plates and shells. The effects of crack/hole sizes, location, and orientation significantly influence both the plates' and shells' static and dynamic responses. The finite element method belongs to one of the frequently used approaches for solving problems for shells under the influence of external pressure. This method can significantly reduce the cost of the experimental part of the study of the behavior of systems containing elements of various shapes, which are weakened by holes.

When calculating physically nonlinear systems, it is necessary to choose a solution algorithm depending on the type and parameters of nonlinearity. A modification of the method of elastic solutions is the method of variable parameters of elasticity proposed by Birger [1]. It is used to solve physically nonlinear problems in the theory of plasticity and creep. The method of solution developed by Ilyushin [2] converges to the result at a linear rate, already validated by the proof presented by Vorovich and Krasovskii in [3]. Vandednbric and Kamat [4] studied the stability of 2D isotropic multilayer composite square plates with round holes and conical shells with internal cuts using the finite element method. Kapnia et al. [5] developed simple and accurate global/local methods for calculating the static response of stepped, simply supported, isotropic and composite plates suffering from circular and elliptical cutouts. Since the Ritz solution did not accurately satisfy the natural boundary conditions at the cutout boundary, the small areas in the hole vicinity were discretized using a finite element mesh. The worked-out methodology was adopted for investigating the composite plates, and the accurate prediction of stresses was reported with considerable savings in CPU time and data storage. Awrejcewicz and Krysko [6] described theoretical and experimental approaches to the analysis of plates and shells. Particular attention was given to the methods used for the analysis of multicomponent inhomogeneities. Their research is related to the study of inhomogeneities, including holes and changes in the thickness of shells of different geometry (round and rectangular) and different boundary conditions. The frequency characteristics of the shells, depending on the inhomogeneous components, were investigated. In particular, experimental studies of small-diameter plates and shells used in electronic engineering were presented, for which the eigenfrequencies and corresponding modes were found. Ghergu et al. [7] derived a limiting model of thin piezoelectric perforated nano-shells based on the extended Koiter model in which three curvilinear coordinates of the elastic displacement field and electric potential are coupled. The existence of a limiting homogeneous constitutive law was established for a piezoelectric composite made of periodically perforated microstructures, the reference configuration of which was a thin shell with fixed thickness. A limiting model was developed based on the periodic unfolding method in combination with Korn's inequality in perforated regions under the assumption that the size of the microstructure tends to zero. The thermal bending of composite shells with selected boundary conditions under a uniform and linearly distributed thermal load was investigated in [8]. The influence of important structural parameters, including the number of notches at the top, fiber angles, and temperature distributions, was estimated based on the semi-analytical finite element method. Awrejcewicz et al. [9] investigated the bending behavior of the shallow laminated shells under static loading using the combination of the R-function theory and the method of spline approximation. Influence of curvature, packing of layers, geometric parameters, and boundary conditions on a stress–strain state was analyzed for shallow shells with cutouts. Dharmin et al. [10] reviewed the works devoted to the analysis of stresses in an infinite plate with various types of notches. Breslavsky [11] analyzed the regularities of the stress intensity distribution in a plate by the method of small parameters on the example of vibrating plates, taking into account geometric and physical nonlinearity, where both the stress intensity values and the nature of their distribution depended on their vibration amplitude. Vanam et al. [12] carried out a static analysis of an isotropic rectangular plate with various boundary conditions and various loading types with the help of an originally developed finite element analysis tool and the finite element analysis software ANSYS. The authors presented correlations between both approaches, as they achieved the optimal thickness of the plate subjected to different loading and boundary conditions. Kalita and Halder [13] studied the static behavior of transversely loaded isotropic and orthotropic plates with central cutout. The deflection and induced stresses exhibited by isotropic/orthotropic plates with central circular and square cutout subjected to transverse loading were calculated using the finite element method (FEM). The dependence of the deflection and stress concentration factor on cutout geometry and size was obtained, and four different boundary conditions were considered. To solve the static problems of stability and supercritical behavior of thin elastic inhomogeneous shells based on geometrically nonlinear relations of the 3D theory of thermoelasticity, a moment scheme of finite elements was used in [14]. A computational technique was developed that considers the geometric features of the elements of an inhomogeneous shell and the multilayer nature of the material based on a universal spatial finite element with additional variable parameters. The influence of various inhomogeneities on nonlinear deformation and buckling was studied using flat isotropic panels under uniform pressure. Supar [15] investigated various configurations of plates with several holes, with different pitches and distances for different modes of destruction. Yang and Kang [16] carried out the stress analysis of an infinite rectangular plate perforated by two unequal circular holes subjected to biaxial uniform stresses. Exact solutions were obtained, and the stress concentration factors for several types of loading conditions were reported.

Dzhabrailov et al. [17] derived the governing equations for the relationship between stress and strain increments under planar loading in the elastoplastic stage. It was based on the theory of small elastic–plastic deformations, but the considered case studies showed the effectiveness of the developed algorithms for shells with plane load outside the elastic limit. Lal et al. [18] investigated a carbon/epoxy composite plate with various cutout shapes under in-plane tensile loading. Variation of in-plane displacement and stress concentration factors with diverse cutout geometries were determined. In addition, the effect of the hole's geometry on the stress distribution around the hole was reported. Numerical analyses of the stress state of a plate with holes located diagonally under the action of a biaxial plane load were carried out in [19,20,21]. Behzad et al. [19] studied buckling of plates with holes taking into account changes in the size of the hole and the thickness of the plate. Wang et al. [20] developed a numerical procedure for the analysis of multiple scattering of flexural waves on a thin plate with round holes, based on the theory of plates according to the Kirchhoff model. Investigations into the problems of the theory of small elastic–plastic deformations for plates and shells using the FEM were carried out in numerous works, including [22, 23]. When developing structures with inhomogeneities or damages, it is necessary to solve a physically nonlinear problem of the theory of elasticity. Outside of linear elasticity, the solution to the problem might be complicated by complex mathematical calculations and the absence of some principles of linear elasticity theory, such as the absence of the potential of internal forces. Salo et al. [24] proposed a variational numerical-analytical method (RVR method) for calculating the strength and stiffness of statically loaded thick orthotropic shell structures based on the Rvachev method [25]. Holes of arbitrary shapes and sizes weaken such plates. Experimental and numerical research studies for perforated steel panels were carried out by Monsef et al. [26]. The influence of different hole patterns and crack locations, obtained as a result of the experiment under cyclic loading, was presented from the experimental samples modeled by the finite element method in ABAQUS. Abuzaid et al. [27] studied the concentration and distribution of stresses in notched areas in piezoelectric actuators for an aluminum plate with opposite semicircular notches using the finite element method for external static loading.

The papers [28, 29] were devoted to constructing a mathematical model of the statics and dynamics of inhomogeneous shells. In the first part of the article [28], a mathematical model of the statics and dynamics of rectangular shells was developed. In contrast, the second part of the article [29] reported the nonlinear dynamics and stability of inhomogeneous axisymmetric shells of variable thickness. The mathematical model was based on the Kirchhoff–Love kinematic hypothesis. In addition, the geometric nonlinearity on the basis of the geometric model of von Kármán and the physical nonlinearity (theory of plastic deformation based on the method of variable parameters of elasticity) were considered.

Krysko et al. [30] presented mathematical models of physically nonlinear beams and plates in 3D and 1D formulation on the basis of the kinematic models of Euler–Bernoulli and Timoshenko. In addition, mathematical models for 3D physically nonlinear beams and plates fabricated from different modular materials were constructed [31]. It is well known and documented that various cutouts in plates reduce their mechanical strength and carrying load ability. In many cases, it leads to their failure, in particular in the dynamic working regimes. The parametric vibrations of orthotropic plates with complex forms and different types of boundary conditions were investigated by Awrejcewicz et al. [32]. Awrejcewicz et al. [33] studied large amplitude free vibration of orthotropic shallow shells of complex shapes with variable thickness considering nonlinear strain–stress relations. The problem was solved based on the R-function theory and variational methods. Awrejcewicz et al. [34] investigated geometrically nonlinear vibrations of shallow laminated shells with complex forms and different boundary conditions. They used the R-function theory, variational Ritz method, the Bubnov–Galerkin method and the fourth-order Runge–Kutta method. The developed approach was validated and employed to new vibration problems for shallow shells with complex planforms and variable thickness of layers.

Kalita and Haldar [35] conducted free vibration analysis of rectangular thin/thick plates with central cutout for various aspect ratios and boundary conditions. It was concluded that rotary inertia had a significant effect on thick plates, while it can be omitted for thin plates. Shufrin and Eisenberger [36] developed a novel semi-analytical method for modeling rectangular plates with variable thickness and cutouts. A multi-term formulation of the extended Kantorovich method was adopted since this approach avoids singularities at the cutout areas. Both the accuracy and the convergence of the solution were examined. Awrejcewicz et al. [37] analyzed dynamical instability and nonlinear parametric vibrations of symmetrically laminated plates with complex shapes and cutouts. A plane stress study was carried out based on the contribution of the Ritz method and R-function theory. Instability zones and response curves for the layer cross- and angle-ply plates with external cutouts were reported. Venkateshappa et al. [38] studied free vibrations of plates with central cutouts employing both laboratory experiments and FEM. It was found that the experimental values of the first, second and third natural frequencies were in good agreement with those of the finite element solution. It was also demonstrated in the case of laminated composite plates that the nondimensional frequency coefficient increased monotonically with an increase in the aspect ratio irrespective of hole size and shapes for the three modes of vibration. Awrejcewicz et al. [39] analyzed linear and geometrically nonlinear vibrations of the three-layered functionally graded shallow shells with complex plan forms and different boundary conditions. Effects of varying material distributions, lamination schemes, curvatures, boundary conditions, and geometrical parameters on natural frequencies and backbone curves were reported. Awrejcewicz et al. [40] employed the R-function theory in free vibration analysis of the FGM plates and shallow shells with temperature dependent properties. The temperature field was modeled as a 1D heat transfer equation, and its solution was obtained through a polynomial power series expansion.

The above analysis of the scientific literature devoted to the study of planar plates with rectangular cuts with inhomogeneities allows us to conclude that research in this direction is insufficiently developed. There is no general theory for studying the stress–strain state and elastic–plastic deformations of plates/shells in the presence of inhomogeneities in the form of holes. Very few works have been carried out on modeling plastic deformations of inhomogeneous plates in a 3D formulation in the literature discussed above. Since the majority of the studies were mainly in a 2D formulation for the Kirchhoff model or the Timoshenko-type model, we strive to fill the gap indicated above by developing mathematical models and a numerical method for studying the elastic–plastic deformation of problems in the theory of plates in a 3D formulation, in this article. Namely, mathematical models of physically nonlinear inhomogeneous planar plates with rectangular cuts are built on the basis of the 3D theory of elasticity. It is based on the deformation theory of plasticity, the Mises plasticity criterion and the method of variable parameters of Birger elasticity, and the convergence theorem devoted to this method for a physically nonlinear body in a 3D formulation. The theory holds for arbitrary deformation diagrams, boundary conditions, transverse loads, material inhomogeneities, and inhomogeneities in the form of holes. The method of finite elements in the form of tetrahedrons and prisms was adopted as a method of investigation, the convergence of this method was investigated, it is noted that for curvilinear cuts of a planar plate, preference should be given to finite elements in the form of tetrahedrons. On the basis of numerical experiments, the influence of various inhomogeneities in the plates on their stress–strain state under the action of static mechanical loads is demonstrated.

The paper is structured as follows. The 3D mathematical model of the problem is introduced in Sect. 2. Section 3 describes the method of variable parameters. Section 4 presents a validation proof of the employed approach to elastic solutions. The case studies of plates with complex geometric shapes and cutouts are given in Sect. 5. Finally, Sect. 6 outlines the concluding remarks of the research carried out.

2 Mathematical 3D model of physically nonlinear plates of arbitrary shape

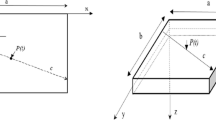
Consider the three-dimensional (3D) body shown in Fig. 1. Principal stresses $\sigma_{x} ,\sigma_{y} ,\sigma_{z}$ and shear stresses $\tau_{xy} = \tau_{yx} ,\tau_{yz} = \tau_{zy} ,\tau_{xz} = \tau_{zx}$ arise under the action of internal forces at every point of a 3D body. These values are shown in Fig. 1 for an elementary parallelepiped cut out around a point on the body.

Fig. 1

Spatial body and stress distribution on the walls of an elementary parallelepiped

Fig. 2

Scheme of convergence of the method of variable parameters of elasticity

The problem is solved with respect to the displacements (и, v, w). The Cauchy equilibrium equations take the following form [41]:

$$ \left\{ \begin{gathered} \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \,\frac{{\partial \tau_{xz} }}{\partial z} + q_{X} = 0, \hfill \\ \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \sigma_{y} }}{\partial y} + \,\frac{{\partial \tau_{yz} }}{\partial z} + q_{Y} = 0, \hfill \\ \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial y} + \,\frac{{\partial \sigma_{z} }}{\partial z} + q_{Z} = 0, \hfill \\ \end{gathered} \right. $$

(1)

where $q_{X} ,q_{Y} ,q_{Z}$ stand for the surface loads on x, y, z.

The relationship between deformations and displacements is as follows:

$$ \varepsilon_{x} = \frac{\partial u}{{\partial x}},\,\,\gamma_{xy} = \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}},\,\,\varepsilon_{y} = \frac{\partial v}{{\partial y}},\,\,\gamma_{yz} = \frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}},\,\,\varepsilon_{z} = \frac{\partial w}{{\partial z}},\,\,\gamma_{zx} = \frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}, $$

(2)

where $\varepsilon_{x} ,\varepsilon_{y} ,\varepsilon_{z}$ are the major deformations, and $\gamma_{xy} ,\gamma_{yz} ,\gamma_{zx}$ are the tangential deformations. The relationship between deformations and stresses reads

$$ \left\{ \begin{gathered} \sigma_{x} = \lambda \theta + 2\mu \varepsilon_{x} ,\,\,\sigma_{xy} = \mu \gamma_{xy} , \hfill \\ \sigma_{y} = \lambda \theta + 2\mu \varepsilon_{y} ,\,\,\sigma_{yz} = \mu \gamma_{yz} , \hfill \\ \sigma_{z} = \lambda \theta + 2\mu \varepsilon_{z} ,\,\,\sigma_{zx} = \mu \gamma_{zx} , \hfill \\ \end{gathered} \right. $$

(3)

where $\theta = \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}}$, $\lambda = \frac{E\,\vartheta }{{(1 + \vartheta )(1 - 2\vartheta )}}$, and $\mu = \frac{E}{2(1 + \vartheta )}$ are elastic Lamé constants. Observe that the Poisson's ratio $\vartheta ({e}_{i},x,y,z)$ and Young's modulus $E(e_{i} ,x,y,z)$ depend on coordinates $x,y,z$, and the intensity of deformations $e_{i}$ is estimated by the method of variable parameters of elasticity developed by Birger [1]. Therefore, the elastic Lamé constants $\lambda$ and $\mu$ also depend on the coordinates and intensity of deformations.

After transformations, the equilibrium equations take the following form:

$$ \left\{ \begin{gathered} (\lambda + \mu )\,\theta_{x} + \mu \,\Delta u + \frac{\partial \lambda }{{\partial x}}\theta + 2\frac{\partial \mu }{{\partial x}}\frac{\partial u}{{\partial x}} + \frac{\partial \mu }{{\partial y}}\left(\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}\right) + \frac{\partial \mu }{{\partial z}}\left(\frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}\right) + q_{X} = 0,\, \hfill \\ \left(\lambda + \mu \right)\theta_{y} + \mu \,\Delta v + \frac{\partial \lambda }{{\partial y}}\theta + \frac{\partial \mu }{{\partial x}}\left(\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}\right) + 2\frac{\partial \mu }{{\partial y}}\frac{\partial v}{{\partial y}} + \,\frac{\partial \mu }{{\partial z}}\left(\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}\right) + q_{Y} = 0, \hfill \\ (\lambda + \mu )\theta_{z} + \mu \,\Delta w + \,\frac{\partial \lambda }{{\partial z}}\theta + \frac{\partial \mu }{{\partial x}}\left(\frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}}\right) + \frac{\partial \mu }{{\partial y}}\left(\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}\right) + 2\frac{\partial \mu }{{\partial z}}\frac{\partial w}{{\partial z}} + q_{Z} = 0, \hfill \\ \end{gathered} \right. $$

(4)

where $\Delta$is the Laplace operator, $\theta_{x}$,$\theta_{y},\, \theta_{z}$ are partial derivatives $\theta$ with regard to the coordinates $x,y,z$, respectively. Displacements (и, v, w) must satisfy the boundary conditions on the surface. Thus, owing to the generalized Hooke's law and the Cauchy conditions, one gets [41]

$$ \left\{ \begin{gathered} X_{v} = \lambda \theta l + G(\frac{\partial u}{{\partial x}}l + \frac{\partial u}{{\partial y}}m + \frac{\partial u}{{\partial z}}n) + G(\frac{\partial u}{{\partial x}}l + \frac{\partial v}{{\partial x}}m + \frac{\partial w}{{\partial x}}n), \hfill \\ Y_{v} = \lambda \theta m + G(\frac{\partial v}{{\partial x}}l + \frac{\partial v}{{\partial y}}m + \frac{\partial v}{{\partial z}}n) + G(\frac{\partial u}{{\partial y}}l + \frac{\partial v}{{\partial y}}m + \frac{\partial w}{{\partial y}}n), \hfill \\ Z_{v} = \lambda \theta n + G(\frac{\partial w}{{\partial x}}l + \frac{\partial w}{{\partial y}}m + \frac{\partial w}{{\partial z}}n) + G(\frac{\partial u}{{\partial z}}l + \frac{\partial v}{{\partial z}}m + \frac{\partial w}{{\partial z}}n), \hfill \\ \end{gathered} \right. $$

(5)

where $l,m,n$ are outer normal direction cosines and $X_{v} ,Y_{v} ,Z_{v}$ stand for the distributed surface load components.

3 Method of variable parameters of elasticity (3D problems)

It is assumed when deriving the governing equations that the elastic modulus E and Poisson's ratio $\vartheta$ are set values. To refine these values, we use Hencky's theory of small elastic–plastic deformations [42], which coincides with the theory of an elastic physically nonlinear body, provided that unloading does not occur at any point of the body. We will mark on the graphs; the points of transition from one loading step to another with decreasing ${\mathcal{E}}_{i}$, that is, in case of unloading. Unloading is subject to the same laws as the loading process, taking into account that materials have nonlinear elastic properties.

When constructing the theory, it is assumed that it can be applied for loading paths close to straight lines. This limitation arises due to the use of the theory of small elastic–plastic deformations in deriving the equations, based on the assumption that the loading path is straight at each point of the body. Nevertheless, Hencky's deformation theory does not contradict the postulates of plasticity [43,44,45]; that is, it is physically consistent even when the trajectory of motion deviates from straight lines. (It was proved in the works of Budiansky [46] and Rabotov [47] under the assumption of a singularity of surface loading.)

It was shown in [48] that when using the von Mises plasticity condition, Budiansky's criterion for the applicability of the deformation theory holds without hardening, especially in the case of an ideal elastoplastic diagram with ${\sigma }_{i}$ and ${\mathcal{E}}_{i}$. The theoretical substantiation of the application of the deformation theory has expanded significantly, thanks to these works. However, a complete verification can only be obtained by comparing the results of calculations with the data of real experiments.

According to the theory, the quantities of E and $\vartheta$ in small elastic–plastic deformations depend not only on the coordinates but also on the stress–strain state at a given point. Birger [1] proposed a method of variable parameters of the theory of elasticity to overcome this problem, consisting of the following statements.

Observe that dependences of deformations and stresses at ${\sigma }_{i}>{\sigma }_{T}$ are nonlinear. Within elastic deformations (${\sigma }_{i}<{\sigma }_{T}$), an increase in stresses by a factor of k causes the same increase in deformations. However, with the occurrence of plastic deformations, this proportionality is violated. Thus, the so far described nonlinearity of the physical equations of the theory of plasticity when solving practical problems causes significant difficulties in solving the practical tasks appropriately. On the other hand, Birger’s method of variable parameters of elasticity allows one to reduce the system to a sequence of linear elasticity problems, which significantly simplifies the solution.

At each point of the body, the intensities of deformations depend on the current stress–strain state relationships and are estimated by the following relation:

$${\varepsilon }_{i}=\frac{\sqrt{2}}{3}\cdot \sqrt{{\left({\varepsilon }_{x}-{\varepsilon }_{y}\right)}^{2}+{\left({\varepsilon }_{y}-{\varepsilon }_{z}\right)}^{2}+{\left({\varepsilon }_{z}-{\varepsilon }_{x}\right)}^{2}+\frac{3}{2\left({\gamma }_{xy}^{2}+{\gamma }_{yz}^{2}+{\gamma }_{zx}^{2}\right)}}.$$

(6)

Although, in general, the dependence of the stress intensity on the strain intensity is usually determined experimentally, there are also available analytical expressions [31].

Consider the Hencky plasticity equation of the following form:

$${\mathcal{E}}_{x}-\mathcal{E}=\psi \frac{1+ }{E}\left({\sigma }_{x}-\sigma \right),\,\, {\mathcal{E}}_{y}-\mathcal{E}=\psi \frac{1+ }{E}\left({\sigma }_{y}-\sigma \right), \,\,{\mathcal{E}}_{z}-\mathcal{E}=\psi \frac{1+ }{E}\left({\sigma }_{z}-\sigma \right),$$

$$\frac{1}{2}{\gamma }_{xy}=\psi \frac{1+\vartheta}{E}{\tau }_{xy},\,\, \frac{1}{2}{\gamma }_{yz}=\psi \frac{1+\vartheta}{E}{\tau }_{yz},\,\, \frac{1}{2}{\gamma }_{zx}=\psi \frac{1+\vartheta}{E}{\tau }_{zx},$$

(7)

where $\psi = \frac{3E}{{2\left( {1 + \vartheta } \right)}}\frac{{\varepsilon_{i} }}{{\sigma_{i} }}$. The first ratio ${\mathcal{E}}_{x}-\mathcal{E}=\psi \frac{1+\vartheta }{E}({\sigma }_{x}-\sigma )$ subject to the dependence $\mathcal{E}= \psi \frac{1-2}{E}\sigma$ will take the following form:

$${\mathcal{E}}_{x}= \psi \frac{1+\vartheta }{E}\left({\sigma }_{x}-\sigma \right)+\mathcal{E}=\psi \frac{1+\vartheta }{E}\left({\sigma }_{x}-\sigma \right)+ \psi \frac{1-2}{E}\sigma .$$

(8)

Continuing the transformations, we represent the plasticity equations in the form

$${\mathcal{E}}_{x}= \frac{1}{{E}^{*}}\left[{\sigma }_{x}-{E}^{*}\left({\sigma }_{y}+{\sigma }_{z}\right)\right], \dots , {\gamma }_{xy}\frac{2\left(1+\vartheta^{*}\right)}{{E}^{*}}{\tau }_{xy}, \dots \left(\stackrel{-}{x,y,z}\right).$$

(9)

The variable parameters of elasticity are as follows:

$${E}^{*}=E \frac{3}{2\left(1+\vartheta\right)\psi +1-2\vartheta},\,\, {\vartheta}^{*}= \frac{\psi \left(1+\vartheta\right)-(1-2\vartheta)}{2\psi \left(1+\vartheta\right)+(1-2\vartheta)},$$

(10)

where E is the elastic modulus, $\vartheta$ the Poisson ratio (in the elastic region), and ψ the plasticity parameter.

The parameters ${E}^{*}$ and ${\vartheta}^{*}$ are called variable parameters of elasticity since they depend on the stress state at a point (plasticity parameter ψ). In the elastic area, we have ψ = 1 and ${E}^{*}=E,$ ${\vartheta}^{*}=\vartheta.$

For an incompressible body (Poisson's ratio $\vartheta$ = 0.5), the following estimation holds:

$${E}^{*}= \frac{E}{\psi }=\frac{{\sigma }_{i}}{{\mathcal{E}}_{i}}=\frac{{\sigma }_{0}}{{\mathcal{E}}_{i}}={E}_{c},$$

(11)

where ${E}_{c}= {\sigma }_{0}/{\mathcal{E}}_{0}$ stands for the secant module. Taking the tensile strain curve as the generalized deformation curve, the following expression for the plasticity parameter $\vartheta$ is obtained:

$$\psi = \frac{3E}{2(1+\vartheta)}\frac{{\mathcal{E}}_{i}}{{\sigma }_{i}}=\frac{3}{2\left(1+\vartheta\right)}\left(\frac{E}{{E}_{c}}-\frac{1-2\vartheta}{3}\right).$$

(12)

Now, the relations (10) and (12) yield the basic formulas of the method of variable parameters of elasticity:

$${E}^{*}= \frac{E}{\psi }=\frac{{\sigma }_{i}}{{\mathcal{E}}_{i}}=\frac{{\sigma }_{0}}{{\mathcal{E}}_{i}}={E}_{c},$$

(13)

$${\vartheta}^{*}=\frac{1}{2}- \frac{1-2\vartheta}{2}\frac{{E}_{c}}{E}.$$

(14)

Suppose the secant modulus replaces the modulus of elasticity in the deformation theory of plasticity equations. In that case, linear equations of the theory of elasticity can be used. Figure 3 shows the geometric interpretation of the convergence of Birger’s method of variable parameters of elasticity for tension. (For compression, it is presented in a similar way.) Correction of the value of Poisson's ratio according to formula (14) plays a less significant role.

Fig. 3

The studied plate with holes

4 Proof of the method of elastic solutions of 3D problems of the theory of plasticity

Vorovich and Krasovsky [3] proposed the application of the method of elastic solutions for the main problems of the theory of small elastic–plastic deformations without any assumptions about the smallness of the parameters. At the same time, the existence of generalized solutions is established, and the convergence of the method is determined.

On the other hand, the study of small elastic–plastic deformations leads to some boundary value problems for nonlinear partial differential equations [45], which many authors studied. For example, in [50], the conditions for the existence of classical solutions of the first boundary value problem in the "small" were clarified.

As it is known in [45], the problem of small elastic–plastic deformations leads to the solution of the following system of differential equations:

$$ \left( {\frac{m}{m - 2} - \frac{\omega }{3}} \right)\theta_{{x_{k} }} + \left( {1 - \omega } \right)\nabla^{2} u_{k} - \frac{2}{3}e_{i} \frac{d\omega }{{de_{i} }}\sum\limits_{s,t = 1}^{3} {\overline{\mathrel\backepsilon}_{ks} } \sum\limits_{l = 1}^{3} {\overline{\mathrel\backepsilon}_{lt} u_{{x_{s} x_{t} }} } + \frac{{\rho X_{k} }}{G} = 0, $$

(15)

where $m$ is the Poisson number; $G$ the shear modulus; $X_{k}$ the mass forces and $\overline{ \mathrel\backepsilon}_{ks}$ are defined by the following relations:

$$ \overline{ \mathrel\backepsilon}_{ks} = \left\{ \begin{gathered} (u_{{kx_{s} }} - \frac{\theta }{3})\frac{\sqrt 2 }{{e_{i} }},\,\,\quad {\text{if}}\,\quad k = s, \hfill \\ (u_{{kx_{s} }} + u_{{sx_{k} }} )\frac{1}{{\sqrt 2 e_{i} }},\,\,\quad {\text{if}}\quad \,k \ne s, \hfill \\ \end{gathered} \right. $$

$$ \theta = e_{xx} + e_{yy} + e_{zz} , $$

$$ e_{i} = \frac{\sqrt 2 }{3}\left[ {(e_{xx} - e_{yy} )^{2} + (e_{xx} - e_{zz} )^{2} + (e_{yy} - e_{zz} )^{2} + \frac{3}{2}(e_{xy}^{2} + e_{zx}^{2} + e_{yz}^{2} )} \right]^{1/2} . $$

Here the function $\omega = \omega (e_{i} )$, describes the plastic properties of the material and satisfies the conditions for actual materials with hardening, i.e., the following estimation holds:

$$ 0 \le \omega (e_{i} ) \le \omega (e_{i} ) + \frac{{{\text{d}}\omega }}{{{\text{d}}e_{i} }}e_{i} \le \lambda < 1. $$

(16)

Let $\Omega$ be a limited area occupied by a deformable body, and $\Gamma$ is its border. In what follows, we consider the following problems.

I. Finding a solution to Eq. (15), if $u_{\left. k \right|\Gamma } = 0.$

II. Finding a solution to the equation (15), if

$$ K\theta \cos (\nu x_{k} ) + \sqrt 2 Ge_{i} \sum\limits_{m = 1}^{3} {\overline{\mathrel\backepsilon}_{km} } \cos (vx_{k} ) = X_{{\nu_{k} }} + GR_{\nu k} , $$

(17)

$$ R_{\nu k} = \sqrt 2 \omega e_{i} \sum\limits_{m = 1}^{3} {\overline{\mathrel\backepsilon}_{km} \cos (vx_{m} )} , $$

(18)

where $K$ is the comprehensive compression modulus, $\cos (vx_{k} )$the cosine of the angle between the normal to $\Gamma$ and the axis $x_{k}$, $X_{{\nu_{k} }}$ the surface forces.

To solve problems I and II, the following functional spaces will be used.

• 1. Let $C_{1}$ be a set of vector functions $v(\varphi_{1} ,\varphi_{2} ,\varphi_{3} ),$ twice continuously differentiable in $\Omega$ and equal to zero in some border strip. We define on $C_{1}$ the following scalar product:

  $$ \begin{aligned} (ab)_{{H_{1\Omega } }} = & \int\limits_{\Omega } {\left\{ {\frac{G}{3}\left[ {\left( {e_{xx}^{(a)} - e_{yy}^{(a)} } \right)\left( {e_{xx}^{(b)} - e_{yy}^{(b)} } \right) + \left( {e_{xx}^{(a)} - e_{zz}^{(a)} } \right)\left( {e_{xx}^{(b)} - e_{zz}^{(b)} } \right)} \right.} \right.} \\ & \left. {\left. { + \left( {e_{yy}^{(a)} - e_{zz}^{(a)} } \right)\left( {e_{yy}^{(b)} - e_{zz}^{(b)} } \right) + \frac{3}{2}\left( {e_{xy}^{(a)} e_{xy}^{(b)} + e_{xz}^{(a)} e_{xz}^{(b)} + e_{yz}^{(a)} e_{yz}^{(b)} } \right)} \right] + \frac{K}{2}\theta^{(a)} \theta^{(b)} } \right\}{\text{d}}\Omega , \\ \end{aligned} $$

  (19)

  and we introduce the notation

  $$ \begin{aligned} (ab) = & \left[ {\left( {e_{xx}^{(a)} - e_{yy}^{(a)} } \right)\left( {e_{xx}^{(b)} - e_{yy}^{(b)} } \right) + \left( {e_{xx}^{(a)} - e_{zz}^{(a)} } \right)\left( {e_{xx}^{(b)} - e_{zz}^{(b)} } \right)} \right. \\ & + \left. {\left( {e_{yy}^{(a)} - e_{zz}^{(a)} } \right)\left( {e_{yy}^{(b)} - e_{zz}^{(b)} } \right) + \frac{3}{2}\left( {e_{xy}^{(a)} e_{xy}^{(b)} + e_{xz}^{(a)} e_{xz}^{(b)} + e_{yz}^{(a)} e_{yz}^{(b)} } \right)} \right]. \\ \end{aligned} $$

  The closure $C_{1}$ in norm (19) we will call $H_{1\Omega }$.

• 2. Similarly, let $C_{2}$ be a set of vector functions $v(\varphi_{1} ,\varphi_{2} ,\varphi_{3} ),$ twice continuously differentiable in $\Omega$ and satisfying the conditions

  $$ \int\limits_{\Omega } {\text{v}} {\text{d}}\Omega = 0,\,\,\int\limits_{\Omega } {{\text{R}} \times {\text{v}}} {\text{d}}\Omega = 0, $$

where $R$ is the radius vector of the point in $\Omega$. On $\Gamma$ the functions $v$ are not subject to any conditions. Dot product with regard to $C_{2}$ is set as before by the expression (19). Closing $C_{2}$ in the introduced norm yields the Hilbert space $H_{2\Omega }$, and

$$ \left\| {\text{v}} \right\|_{{H_{2\Omega } }} = \int\limits_{\Omega } {\left( {\frac{3}{2}Ge_{i}^{2} + \frac{{K\theta^{2} }}{2}} \right)} {\text{d}}\Omega . $$

Definition 1

By a generalized solution of problem I, we mean the vector function $a(u_{1} ,u_{2} ,u_{3} ) \in H_{1\Omega }$ satisfying the integral identity

$$ (a{\text{v}})_{{H_{1\Omega } }} - \frac{G}{3}\int\limits_{\Omega } {\omega \left( {e_{i}^{(a)} } \right)(a{\text{v}}){\text{d}}\Omega } - \frac{1}{2}\int\limits_{\Omega } {\left( {X_{1} \varphi_{1} + X_{2} \varphi_{2} + X_{3} \varphi_{3} } \right)} {\text{d}}\Omega = 0 $$

(20)

for any vector function $v(\varphi_{1} ,\varphi_{2} ,\varphi_{3} )$.

Definition 2

A solution to Problem II is a vector function $b(u_{1} ,u_{2} ,u_{3} ) \in H_{2\Omega }$, satisfying the integral identity

$$ ({\text{bv}})_{{H_{2\Omega } }} - \frac{G}{3}\int\limits_{\Omega } {\omega \left( {e_{i}^{{({\text{b}})}} } \right)({\text{bv}}){\text{d}}\Omega } - \frac{1}{2}\int\limits_{\Omega } {\left( {X_{1} \varphi_{1} + X_{2} \varphi_{2} + X_{3} \varphi_{3} } \right)} {\text{d}}\Omega = \int\limits {\left( {X_{\nu {_{1} }} \varphi_{1} + X_{{{\nu }_{2} }} \varphi_{2} + X_{\nu {_{3} }} \varphi_{3} } \right)} {\text{d}} $$

for any vector function ${\text{v}}(\varphi_{1} ,\varphi_{2} ,\varphi_{3} ) \in H_{2\Omega }$.

Note that if some vector function is a generalized solution of the problem I or II in the sense of the definition adopted here, then all the conditions of equilibrium of the body are satisfied, assuming that they are formulated using Lagrange’s principle of possible displacements. In addition, the generalized solution will always be classical if it is twice differentiable.

Let us introduce the operators $A$ and $B$ in the following way:

$$(Aa{\text{v}})_{{H_{1\Omega } }} - \frac{G}{3}\int\limits_{\Omega } {\omega \left( {e_{i}^{(a)} } \right)(a{\text{v}}){\text{d}}\Omega } + \frac{1}{2}\int\limits_{\Omega } {\left( {X_{1} \varphi_{1} + X_{2} \varphi_{2} + X_{3} \varphi_{3} } \right)} {\text{d}}\Omega\, for anyone\, {\text{v}}(\varphi_{1} ,\varphi_{2} ,\varphi_{3} ) \in H_{1\Omega }$$

and

$$ (B{\text{bv}})_{{H_{2\Omega } }} = \frac{G}{3}\int\limits_{\Omega } {\omega \left( {e_{i}^{{({\text{b}})}} } \right)({\text{bv}}){\text{d}}\Omega } + \frac{1}{2}\int\limits_{\Omega } {\left( {X_{1} \varphi_{1} + X_{2} \varphi_{2} + X_{3} \varphi_{3} } \right)} {\text{d}}\Omega + \int\limits {\left( {X_{\nu {_{1} }} \varphi_{1} + X_{{{\nu }_{2} }} \varphi_{2} + X_{\nu {_{3} }} \varphi_{3} } \right)} {\text{d}} $$

for any ${\text{v}}(\varphi_{1} ,\varphi_{2} ,\varphi_{3} ) \in H_{2\Omega }$. It is easy to show using the Riesz theorem that A and $B$ act in spaces $H_{1\Omega }$ and $H_{2\Omega }$, respectively.

Obviously, finding a generalized solution to the boundary value problem I, is equivalent to solving the operator equation

$$ a = Aa, $$

(21)

and finding a generalized solution to the boundary value problem II, is equivalent to solving the operator equation

$$ b = Bb. $$

(22)

Theorem 1

Let the following conditions be satisfied:

(1) $X_{1} ,X_{2} ,X_{3} \in L_{p} ,\,p \ge {\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 5}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$5$}};$ (2) $\omega \left( {e_{i} } \right)$ satisfies the conditions (16).

Then, the operator $A(a)$ is a contraction operator in the whole space $H_{1\Omega }$ , and the relation

$$\left\| {A(a_{1} ) - A(a_{2} )} \right\|_{{H_{1\Omega } }} \le \lambda \left\| {a_{1} - a_{2} } \right\|_{{H_{1\Omega } }} \,holds\, for\, any\, a_{1} ,a_{2} \in H_{1\Omega }$$

whence it follows that Problem I is uniquely solvable.

Theorem 2

Let all conditions of the Theorem 1 be satisfied; $X_{\nu {_{1} }} ,X_{{{\nu }_{2} }} ,X_{\nu {_{3} }}$ are summed on the boundary of $\Gamma$ with degree $q \ge {\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ ; $\Gamma$ satisfies the conditions of solvability of the second boundary value problem of the theory of elasticity *

[50].

Then, the operator $B(b)$ stands as a compression operator all over the space $H_{2\Omega }$ , and the following relation holds:

$$\left\| {B(b_{1} ) - B(b_{2} )} \right\|_{{H_{2\Omega } }} \le \lambda \left\| {b_{1} - b_{2} } \right\|_{{H_{2\Omega } }} \,for\, any \,b_{1} ,b_{2} \in H_{2\Omega }$$

whence it follows that Problem II is uniquely solvable.

It follows from Theorems 1 and 2 that the method of elastic solutions for the problems of the theory of plasticity under consideration will converge in the corresponding spaces with the speed of a geometric progression, having the denominator $\lambda$ for any choice of the initial approximation.

Theorem 3

Let $X,Y,Z \in L_{2\Omega } ,\, \in L_{2} (m\lambda )$ , and in the case of problem II $X_{\nu {_{1} }} ,X_{{{\nu }_{2} }} ,X_{\nu {_{3} }} \in W_{2}^{(1)}$ be satisfied on the border(*). In this case, the sequences $a_{n}$ , $b_{n}$ of elastic solutions belonging to $W_{2}^{(2)}$ also converge in $W_{2}^{(2)}$ with the speed of the derivative of a geometric progression with the denominator $\lambda$ .

Theorem 3 implies that the sequences of elastic solutions $a_{n}$, $b_{n}$ converge uniformly in $\overline{\Omega }$ with the speed of the derivative of a geometric progression having the denominator $\lambda$ and they themselves belong to $W_{2}^{(2)}$.

(*) The system of external forces in the case of boundary value problem II is statically equivalent to zero.

Remark 1

It is known from [50] that convergence in $H_{i\Omega } ,\,i = 1,2$, implies convergence of $u,v,w$ in $W_{2}^{(1)} .$

Remark 2

We have made an utterly similar consideration for the equations describing the stress state of plates at small elastoplastic deformations. At the same time, conditions for the solvability of the main boundary value problems are obtained, and the method of elastic solutions is substantiated.

Remark 3

Condition (16) of our theorems cannot be weakened, as the example considered in [51] shows; if we take $\lambda = 1$, then Eqs. (15) will not always be solvable.

Remark 4

Note that equations with the operator of the type (21) and (22) can describe many physical processes since deviations from linear relations between the main parameters of the problem often have the character of a “saturation” dependence, keeping conditions (16). In addition to the problems of the theory of plasticity considered here, problems of determining the magnetic field in iron, where "saturation" takes place at high strengths, and problems of the equilibrium of the membrane at large deflections, etc., are of the same type.

5 Plates of complex geometric shapes with material physical nonlinearity

Consider a 3D hole-shaped plate located in R³ (Fig. 3). The plate has a length a, height $h$, and thickness $b$; and it is under the action of a surface load F. In all the problems considered, the plate is clamped along the side faces ${\Omega }_{1}=\{x=0,y \in \left[0,b\right], z \in \left[-h/2,h/2\right]\};{\Omega }_{2}=\{x=l, y \in \left[0,b\right], z\in \left[-h/2,h/2\right]\};{\Omega }_{3}=\{x \in [0,l],y=b,z \in \left[-h/2,h/2\right]\},{\Omega }_{4}=\{x \in [0,l],y=0,z \in \left[-h/2,h/2\right]\}$, i.e., $\left( {u = v = w = 0\,} \right)$. On the top edge ${\Omega }_{5}=\{x \in \left[0,l\right],y \in \left[0,b\right],z=h/2\}$ a uniformly distributed load of intensity F acts, while on the remaining edges and inside the holes, there are no force effects of moments and forces.

The algorithm of the method of Birger’s variable parameters of elasticity consists of the following steps.

• 1. The initial data are entered: the value of external loads, single curve fit parameters $\sigma_{i} = f(\varepsilon_{i} ),$ the Poisson's ratio $\vartheta$ and modulus of elasticity E.

• 2. At the initial stage, we take: ${E}^{*}=E,$ ${\vartheta}^{*}=\vartheta$, ${E}_{c}=E$.

• 3. The elastic problem of calculating the stress–strain state under load with the parameters ${E}^{*},{\vartheta}^{*}$, and the stresses and strains are determined, i.e., the parameters $\sigma_{x} ,...\tau_{xy} ,...\varepsilon_{x} ,...\gamma_{xy}$ are defined.

• 4. Stress intensities $\sigma_{i}$ and deformations $\varepsilon_{i}$ are determined corresponding to the solution of the elastic problem.

• 5. Values of the stress and strain intensities are estimated through the formula $\varepsilon_{i} = \varepsilon_{i(0)} ,\quad \sigma_{i} = \left\{ \begin{gathered} E\varepsilon_{i(0)} \hfill \\ E_{c(1)} \varepsilon_{i(0)} \hfill \\ \end{gathered} \right.$.

• 6. If the condition for the end of iterations is satisfied $\left| {\frac{{\sigma_{i} - \sigma_{i(1)} }}{{\sigma_{i} }}} \right| < \delta ,$ where $\delta$ stands for the assumed accuracy, we go to point 7. If not, the secant module is calculated as $E_{c} = \frac{{\sigma_{i} }}{{\varepsilon_{i} }}$, the variable parameters of elasticity according to formulas (4), and computations are repeated starting from item 3.

• 7. The last calculated values of the intensity of deformations and stresses are finally accepted.

We investigate the stress–strain state in a 3D formulation for several plate configurations, taking physical nonlinearity into account. In all case studies, pure aluminum is taken. The shear modulus ${G}_{0}=23.3(3)\times {10}^{9}\,\left[\mathrm{Pa}\right]$ and Young's modulus ${E}_{0}=70\times {10}^{9}\,[\mathrm{Pa}]$, volumetric module $K=1.94{G}_{0},$ Poisson's ratio $\Gamma$$\vartheta$ = 0.28. We take the dependence of the stress intensity on the strain intensity in the form of a diagram for pure aluminum [52] (${\sigma }_{s}=1023\, \left[\mathrm{bar}\right]=1.023\times {10}^{8}\,\left[\mathrm{Pa}\right]$ ${e}_{s}=0.98\times {10}^{-3})$. In all the problems considered, the plate is clamped along the side faces $\left( {u = v = w = 0\,} \right).$ A uniformly distributed intensity load acts on the upper edge F. In what follows, we calculate the stress–strain state in a 3D formulation for several plates.

5.1 Plates with holes in the corners

Consider a planar rectangular plate having one (Fig. 4a), two (Fig. 4b), four (Fig. 4c) square holes with a side of 10 in the corners, as well as a homogeneous plate (Fig. 4d) subjected to external tranversal load along the axis 0z. The numbers 1–7 indicate the expected stress concentrators' areas, which deserve special attention.

Fig. 4

Schematic representation of the planar rectangular plates having holes in the corners: a—1; b—2; c—4; d no holes

Table 1 shows the values of the integral characteristic of displacements $w = \iiint\limits_{V} {w(x,y,z){\text{d}}V}$ over the plate volume depending on the number of finite elements and their type, for a plate without a notch for a distributed load q = 15. The exact solution is marked in yellow.

Table 1 Values of the integral characteristic of displacements for various shapes and numbers of finite elements under load

The comparisons of integral characteristics obtained with finite elements in the form of tetrahedrons and prisms given in Table 1 are close to each other. For rectangular cutouts of the plate plan, preference should be given to finite elements in the form of prisms; for curvilinear cutouts of the plate plan, preference should be given to tetrahedrons.

We study the convergence of the solution of the FEM for a given problem with a uniformly distributed load q = 11.25 for a plate with four holes (Fig. 4c). The dependence of the integral value of displacements w over the volume of the plate on the number of finite elements N is shown in Fig. 5. For this problem, the solution converges with sufficient accuracy for the number of finite elements N = 7810. In what follows, all results are obtained for finite elements of the same size.

Fig. 5

Dependence of the integral value of displacements w over the volume of the plate versus the number of finite elements

The convergence of the method of variable parameters of elasticity depends significantly on the volume of plastic zones. Table 2 shows how the number of iterations of Birger’s variable elastic parameters method ${(n}_{it})$ depends on the intensity of the transverse load q using the example of a plate with four holes (Fig. 4c).

Table 2 The integral value of the displacements w over the volume of the plate at various loads q for each iteration of the method of elastic variables

Under the boundary conditions of pinching $\left( {u = v = w = 0\,} \right)$ of the faces ${\Omega }_{1},{\Omega }_{2},{\Omega }_{3},{\Omega }_{4}$ and under the action of a mechanical surface load on ${\Omega }_{5},$ zones of plastic deformation appear first near the restrained boundaries of the plate ${\Omega }_{1},{\Omega }_{2},{\Omega }_{3},{\Omega }_{4}$. Further increase in the load yields a region of plastic deformation in the center of the plate. In the presence of notches in the areas 1, 2, 3, 4, 5, 6, 7, shown in Fig. 4 and located in the vicinity of the notches’ corner, an accumulation of stresses arises, leading to plastic deformations.

The dependence of the integral value of the displacements w over plate’s volume with different numbers of holes and the corresponding distribution of plastic deformations are shown in Fig. 6. Figures 6a, b show the results for a plate with a thickness h = 1 (h = 2).

Fig. 6

Dependence of the integral value of displacements w over the volume of a plate with a different number of holes and the distribution of plastic deformations: a h = 1; b h = 2

The obtained dependencies show the holes in the corners of the plate affect the magnitude of displacements over the volume and the distribution of plastic deformations. It should be emphasized that increased stress concentrations appear at the corners of the holes, leading to plastic deformations in these areas.

5.2 Plates with a hole in the center

Consider plates having a square hole with sides 10, 20 and 30 localized in plates center. The dependences of the integral value of displacements w over the volume of a plate with a hole of various sizes and the distribution of plastic deformations are shown in Fig. 7.

Fig. 7

Dependence of the integral value of displacements w over the volume of a plate with a hole of various sizes and the distribution of plastic deformations: a h = 1; b h = 2

The hole in the center of the plate affects the magnitude of displacement over the plate’s volume and the distribution of plastic deformations. Observe that increased stress concentrators appear in the corners of the hole, as in the previous case, and zones of plastic deformations appear.

5.3 Plates with holes in the corners and slits in the center

Consider plates having, in addition to square holes, a narrow hole (slot) of width 1 and length 10. The studied plates are shown in Fig. 8.

Fig. 8

Plate with two (a) and four (b) square holes and slots

The dependences of the integral value of displacements w over the plate’s volume with a hole of various sizes and the distribution of plastic deformations are shown in Fig. 9. (The dashed lines indicate the dependences obtained earlier for plates of the corresponding shape without a defect in the form of a slit).

Fig. 9

Dependence of the integral value of displacements w over the volume of a plate with a different number of holes and the distribution of plastic deformations: a h = 1; b h = 2

The presence of a slot and its location affects the magnitude of displacements and plastic deformations; the zone around the slot stands as an additional stress concentrator, which changes the distribution of plastic deformation zones more than the holes in the corners of the plate.

6 Concluding remarks

In this work, for the first time, 3D mathematical models of plates with complex geometrical shapes and transverse loads are constructed while considering the material's physical nonlinearity. The mathematical models are reliably validated. No kinematic hypotheses that reduce a 3D problem to a 1D one are introduced; problems in a 3D formulation of the theory of elasticity are solved. Finite elements in the form of tetrahedrons are used, and the convergence of the solution via the FEM is treated with high accuracy as a termination criterion for accepting the final values of stresses and intensity of deformation. This is part of the algorithm for the method of Birger’s variable parameter of elasticity. The accuracy depends on the number of elements of the plate partition with regard to plan and thickness.

Based on numerical experiments, the influence of holes in the corners and in the center of the plate; and the presence of a damage in the form of a slot on the stress–strain state of plates of various thicknesses under the action of static mechanical loads are reported. In all examples considered, the presence of inhomogeneity in the geometry of the plate yields increased plastic deformations and increased the values of displacements w. It is shown that the notches are stress concentrators in the plate, which affects its loading capacity significantly.