Abstract
We measured the methane flux of a forest canopy throughout a year using a relaxed eddy accumulation (REA) method. This sampling system was carefully validated against heat and CO2 fluxes measured by the eddy covariance method. Although the sampling system was robust, there were large uncertainties in the measured methane fluxes because of the limited precision of the methane gas analyzer. Based on the spectral characteristics of signals from the methane analyzer and the diurnal variations in the standard deviation of the vertical wind velocity, we found the daytime and nighttime precision of half-hourly methane flux measurements to be approximately 1.2 and 0.7 μg CH4 m−2 s−1, respectively. Additional uncertainties caused by the dilution effect were estimated to affect the accuracy by as much as 0.21 μg CH4 m−2 s−1 on a half-hourly basis. Diurnal and seasonal variations were observed in the measured fluxes. The biological emission from plant leaves was not observed in our studies, and thus could be negligible at the canopy-scale exchange. The annual methane sink was 835 ± 175 mg CH4 m−2 year−1 (8.35 kg CH4 ha−1 year−1), which was comparable to the flux range of 379–2,478 mg CH4 m−2 year−1 previously measured in other Japanese forest soils. This study indicated that the REA method could be a promising technique to measure canopy scale methane fluxes over forests, but further improvement of precision of the analyzer will be required.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Methane (CH4) is a major greenhouse gas with a global warming potential approximately 21 times higher than that of CO2 (Forster et al. 2007). Methane has a radiative forcing of 0.48 W m−2, and it accounts for approximately 18% of the total radiative forcing by long-lived greenhouse gases (Forster et al. 2007). Since preindustrial times, the atmospheric concentration of methane has increased from approximately 770–1,774 ppb. Although the growth rate of atmospheric methane has decreased in the years prior to 2006 (Wuebbles and Hayhoe 2002), renewed growth in these concentrations has been observed since 2007 (Rigby et al. 2008). Although several conflicting hypotheses that largely involve wetland CH4 emissions, anthropogenic CH4 emissions, wild fires, and hydroxyl radical photochemistry have been proposed for the interannual variation of atmospheric CH4 concentrations (Bousquet et al. 2006 and their references), they have not yet adequately explained the observed atmospheric trends and inter-annual variations in methane concentrations.
Terrestrial soils are thought to consume approximately 30–40 Tg methane from the atmosphere annually, accounting for 5–7% of the global methane sink (Wuebbles and Hayhoe 2002). Methane degradation by microbial oxidation in aerobic soils is the planet’s second largest sink of methane, following reaction with tropospheric hydroxyl radicals. Methane flux measurements have been obtained from many forest soils using chamber techniques (King 1997; Ishizuka et al. 2009; Itoh et al. 2009), and they identified large spatial variations in methane uptake that make the quantification of methane uptake at the stand, watershed, regional, and continental scales difficult. Compared with wetlands, forests consist of complex structures with varying vertical distributions of trees and an understory, which are potential methane sources (Keppler et al. 2006), as well as a large spatial variation of soil conditions ranging from anaerobic to aerobic. This variability could make forests alternate between functioning as methane sinks and sources as the results of subtle environmental changes. Itoh et al. (2009) found that methane fluxes measured within a watershed exhibited considerable spatial variations; large dry areas were found to be methane sinks, whereas small wet areas were strong sources, that overwhelmed the total impact of the methane sinks at the watershed level, with a high degree of temporal variability. Ishizuka et al. (2009) compared methane fluxes at 27 temperate forest sites in Japan and found that the annual sink was substantially different at each site (factor of 6.5). It was also found that the rate of methane uptake in Japanese forest soils was very high in comparison to the soils of other regions. This high rate of uptake can be attributed to the high porosity of Japanese soils resulting from their volcanic ash parent materials.
Keppler et al. (2006) suggested that living terrestrial vegetation emits large amounts of methane under aerobic conditions, making forests major methane sources. The global methane production rates from living plants were estimated to be 62–236 Tg CH4 year−1, which may have a considerable effect on the global methane budget. This study generated a vigorous scientific debate and many subsequent studies were performed (e.g., Kirschbaum et al. 2006; Kitaoka et al. 2007; Beerling et al. 2008; Kirschbaum and Walcroft 2008; Bowling et al. 2009). In subsequent experiments, emission rates were found to be quite distinct in each experiment (e.g., Keppler et al. 2006; Kirschbaum et al. 2006; Kitaoka et al. 2007), and some studies failed to measure any emissions (Beerling et al. 2008; Kirschbaum and Walcroft 2008). Consequently, there are large uncertainties in the methane budgets of forest ecosystems.
The micrometeorological measurement of methane flux is a promising method for capturing values that are both spatially and temporally representative (Baldocchi 2003). Previously, this method was applied in ecosystems that represented well-known methane sources, such as rice paddies (Miyata et al. 2000; Takimoto et al. 2010), natural wetlands (Friborg and Christensen 1997; Simpson et al. 1997; Werner et al. 2003; Rinne et al. 2007), and tundra (Harazono et al. 2006; Wille et al. 2008). However, relatively few studies have been conducted in forest ecosystems (Ueyama et al. 2006; Smeets et al. 2009), probably because the measurements of small methane uptakes is much more difficult than the measurement of fluxes from large sources.
The eddy covariance (EC) method is one of the most reliable approaches for measuring vertical turbulent fluxes of heat, water vapor, and CO2 from the Earth’s surface to the atmosphere (Baldocchi 2003). Application of this method requires a gas analyzer with a fast response and high signal stability, that is able to measure the fluctuations associated from all eddies that transport scalar quantities with sufficient precision. In late 1980s, the EC method was applied to methane flux measurements in subarctic tundra by combining a flame ionization detector (FID) with a Zeeman-split HeNe laser (Fan et al. 1992). With the advance of technologies for methane gas analyzer, such as tunable diode laser spectroscopy (TDLS; Billesbach et al. 1998; Baer et al. 2002), the EC method has been widely used to measure methane emissions from a subarctic mire (Friborg and Christensen 1997), a Siberian wetland (Friborg et al. 2003), a peatland (Shurpali and Verma 1998), a black spruce forest (Pattey et al. 2006), a boreal fen (Rinne et al. 2007), a peat meadow (Hendriks et al. 2008), and an arctic tundra (Zona et al. 2009). Although many of those studies successfully quantified methane emissions from the sources in question, measurement in forest ecosystems is still challenging because the magnitude of the methane uptake by aerobic soils is very small compared with the magnitude of the emissions from wetlands. Eugster and Plüss (2010) quantified the detection limit of a state-of-the-art TDLS at 0.35 ppb with an optimum integration time and a white-noise level of 1.5 ppb Hz−1/2, which might be insufficient to measure low rates of methane uptake by the EC method. The closed-path EC system for methane flux also requires large pumps because of the large cavity volume of TDLS systems, which limits the applicability for remote areas where electric power is limited.
The relaxed eddy accumulation (REA) method is a theoretically simple micrometeorological technique in which fluxes are measured using the vertical wind velocity and a conditional sampling of updraft and downdraft air (Businger and Oncley 1990). Because this method does not required a gas analyzer with a rapid response, unlike the EC method, it has begun to attract considerable attention for use in studies of trace gas fluxes (Simpson et al. 1997; Nemitz et al. 2001). An REA system was previously developed by our group (Hamotani et al. 1996, 2001), and its precision and accuracy have been validated (Ueyama et al. 2009). The REA system could be applicable to the measurement of methane fluxes in forest ecosystems, which could enable researchers to use methane gas analyzers for measurements at optimal integration times without high electric power requirements. Consequently, the REA method could have several advantages compared with the EC method for measuring small methane fluxes in forest ecosystems.
In this study, we continuously measured methane fluxes in a larch forest using the REA system developed by our group. The objectives of this study were (1) to determine the applicability and limitations of the REA method for methane flux measurements over forests and (2) to examine the fluxes at diurnal and seasonal timescales as well as possible contribution of plant leaves for the net methane efflux.
2 Methods
2.1 Relaxed eddy accumulation method
The flux of the target gas is calculated as the product of the concentration difference, the standard deviation of the vertical wind velocity, and an empirical constant. According to Businger and Oncley (1990), temperature and methane concentration fluxes can be calculated using the REA method as follows:
where the prime and overbar denote the fluctuation term and the average of a variable, respectively. w, T, C, b, and σ w represent the vertical wind velocity, air temperature, methane concentration, empirical constant, and the standard deviation of the vertical wind velocity, respectively. T up, T down, C up, and C down are the air temperature and the mean methane concentration in the updraft and downdraft, respectively. Finally, b is empirically determined using heat fluxes obtained through the use of the EC method and the mean air temperature of the updraft and downdraft (Hamotani et al. 2001).
2.2 Sampling system
To measure methane fluxes using the REA method, we developed a sampling system (Fig. 1; Hamotani et al. 2001; Ueyama et al. 2009). The system has two major components. One component consists of the measurement of the standard deviation of the vertical wind velocity (σ w) from a sonic anemometer (DA600, Kaijo, Japan). The second component samples air of updraft and downdraft and measures the gas concentration difference; updraft and downdraft conditions were determined using signals from the sonic anemometer. The fluctuation of the vertical wind velocity was sampled at 10 Hz, and σ w was calculated in real time using a data logger (CR1000, Campbell, USA), whereas C up and C down were measured using the methane gas analyzer. The system was fully controlled by the data logger.
We developed two independent sampling systems for CO2 and methane; air was sampled by each system using the same signal from the sonic anemometer. Updraft and downdraft conditions were determined by the difference between the instantaneous and adjacent 15-min moving averages of the vertical wind velocity. Adjacent 15-min moving averages were used because it was impossible to obtain averages in a true Reynolds sense (Bowling et al. 1999). The pump for sampling updraft air operated only under updraft conditions at a rate of 1.2 l min−1 (LPM), whereas the pump for sampling downdraft only operated under downdraft conditions. The sampled air was stored in reservoirs (Tedlar® Bags) with a volume of 20 l (CCK-20, GL Science, Japan). After each 0.5-h sampling period, the stored air in each reservoir flowed through a FID methane gas analyzer (Model APHA-360, Horiba, Japan) at a rate of 0.8 LPM. The air stored for CO2 flux measurements flowed through a closed path infrared gas analyzer (Li-6262, Li-Cor, USA). Methane and CO2 concentrations were collected at rate of 1 Hz via a data logger (CR1000, Campbell, USA) beginning 120 s after the lines were switched.
A sample line cannot be used simultaneously to analyze methane concentrations and collect air. However, such an analysis was necessary to sequentially determine the flux every 0.5 h, and the analysis was performed by preparing two sets of sampling reservoirs (B up and B down in Fig. 1) for a total of four reservoirs (B up(0–30), B up(30–60), B down(0–30), and B down(30–60) in Fig. 1). Our REA system measured the methane flux every 0.5 h, operating on an hourly cycle; the time table of these measurements is shown in Table 1. Further details of the REA system can be found in Ueyama et al. (2009).
Considering the sampling flow rate, the inner diameter of the tube and the tube length between the air inlet and the bags (approximately 40 m), the dead volume inside the tube was approximately 0.5 l and the retention time was 0.4 min. Because the amount of air in the dead volume (sampled during adjacent run) was sufficiently small compared with the sampled air (approximately 18 l), the error associated with the dead volume was considered negligible.
The system had no dead bands for increasing the concentration differences (Bowling et al. 1999) to avoid system instabilities arising from limited sample air. The methane analyzer was automatically calibrated once per week (at 00:00–1:00). In addition to this calibration, the system was checked for bias in the concentration differences between the updraft and downdraft reservoirs twice per day (at 00:00–1:00 and 12:00–13:00). During these inspection periods, the system pumped the same air to the updraft and downdraft reservoirs and measured the reported concentration difference. The difference was expected to be zero, and when small biases were detected (ranging from 0 to 4 ppb with no differences between daytime and nighttime biases), we corrected for these biases in the methane flux calculations.
In this study, we integrated our REA system with a system for measuring the concentration of methane across a vertical gradient (Fig. 1). The same gas analyzer was used to measure concentrations at multiple heights by switching the flow lines leading to the gas analyzer (Table 1). Measurements of each new vertical concentration began 120 s after the lines were switched. The vertical profile of the methane concentrations was only measured when the gas analyzer was not being used for the REA measurements.
2.3 Measurements
Measurements were taken at the Fuji-hokuroku Flux Research Site, Yamanashi, Japan (35°N26′, 138° 45′). This site is located at the northern foothills of Mt. Fuji with a moderate slope of 3–4° and an elevation of approximately 1,100 m. The predominant tree cover at the site is a 50-year-old stand of Japanese larch (Larix kaempferi Sarg.) that is interspersed with evergreen needleleaved species (Pinus densiflora) and mixed broadleaved species (Swida controversa, Quercus serrata, and Quercus crispula). The canopy height is 20–25 m. Because the forest canopy is open, the forest floor is covered by understory species such as Prunus incisa and Dryopteris crassirhizoma. The leaf area index measured by a plant canopy analyzer (LAI-2000, Li-Cor, USA) was 2.9 m2 m−2. The soil consisted mainly of volcanic ash deposits from Mt. Fuji. Since the larch trees were uniformly planted within the study area across approximately 150 ha, measured fluxes were mainly attributable to the larch forest for all wind directions. In 2009, the average annual air temperature was 8.9°C and the total annual precipitation was 1,800 mm. The average soil temperature at 5 cm was 9.6°C, whereas the soil water content at depths of 0, 5, and 10 cm was 0.162, 0.111, and 0.144 m3 H2O m−3 soil in 2009, respectively.
Methane fluxes were measured continuously beginning in February 2009 using a 31-m scaffold tower. The EC method was used to measure the fluxes of heat, water vapor, and CO2 at a height of 35 m above the ground with a sonic anemometer (DA600, Kaijo, Japan) and a closed path infrared gas analyzer (LI-6262, Li-Cor, USA). Sample air was pumped at a flow rate of approximately 5.6 LPM into the gas analyzer through approximately 12.4-m of polyethylene/aluminum composite wall tubing (Dekoron-1300, Furon, USA) with an inner diameter of 4.3 mm. A fine-wire thermocouple thermometer (70 μm in the diameter; COCO-03, Omega, Japan) was also installed near the sonic anemometer to measure fluctuations in air temperature. Data were recorded at a rate of 10 Hz using a datalogger (DR-M3, Teac Corp., Japan) and averaged over 30-min intervals. The vertical wind velocity and air temperature signals were also used by the REA system.
The two REA systems for CO2 and methane measurements were installed at the base of the tower. Updraft and downdraft air samples were pumped to the system through a polyethylene/aluminum composite wall tubing (DK-tube; 1300-6-BK, Nitta Moore, Japan) with an inner diameter of 4 mm. The sample inlets were set at 35 m, and the horizontal distance between the inlets and the sonic anemometer was approximately 0.3 m. For vertical profile measurements, the air inlets were set at 35, 27, 16, and 0.3 m above the ground, and air was directed to the REA system at a flow rate of 1.2 L min−1 (LPM).
2.4 Data processing
Before processing the eddy covariance data, we removed the noise spikes from the raw data and then calculated the covariance every 30 min. We applied corrections for coordinate rotation and air density effects arising from water vapor concentration fluctuations (Webb et al. 1980) as well as corrections for the loss of high-frequency transport arising from sensor separation and line averaging (Moore 1986). The lag time of the sample from the inlet to the cell of the closed-path analyzer was determined by maximizing the covariance between the vertical wind velocity and the CO2 concentration; the median of the determined lag time was applied for all processing. The high-frequency loss for the closed-path system was corrected using an empirical transfer function (Aubinet et al. 2000). Further details of the flux calculations are shown in Hirata et al. (2007).
For the eddy covariance data, we applied a quality test to remove noise attributed to conditions of rain, snow, or fog. Nonstationary and integral turbulence tests (Foken and Wichura 1996) were applied as routine treatments. After these routine treatments, we manually excluded the remaining outliers.
To reduce the effects of random noise in the methane gas analyzer, we excluded data collected using the REA method when the signal of the methane analyzer was unstable. This instability possibly arose from fluctuations in the detector’s flame ionization efficiency or from decreases in the catalyst temperature for the oxidization of nonmethane hydrocarbons as a result of the influence of water vapor. Instability was indicated by a fluctuation of greater than 5 ppb in methane concentrations during the 4-min period for each reservoir. For the methane flux calculations, we excluded the data when the CO2 fluxes measured by the EC and REA methods were different by more than 50% of the absolute value. Finally, we manually excluded the remaining outliers. After these quality tests, only 27% of the data from the measurement period were found to be suitable for analysis.
Gaps in the methane flux data were filled using standard methods. Linear interpolation was applied for small gaps of less than 1.5 h. For larger gaps, a mean diurnal variation method was applied in which the diurnal pattern was determined each day for a 15-day moving window.
In this study, negative fluxes indicated uptake by the forest, whereas positive fluxes indicated emissions to the atmosphere.
2.5 Error analyses
Half-hourly fluxes could have large uncertainties because of the precision of the methane gas analyzer (shown in later section). We averaged the individual half-hourly results for the monthly diurnal patterns and the seasonal variations of 7-day moving windows rather than addressing the individual values. To evaluate the possible error distributions of random errors, we created monthly mean diurnal patterns by resampling our data 1,000 times using a bootstrapping technique and then filling the data gaps using the resulting patterns. Each bootstrapping dataset was averaged for monthly and annual time periods. The frequency distributions of the average values were used to determine the uncertainty of the measurement because the half-hourly random errors could propagate to the monthly diurnal patterns and annual fluxes despite error reductions obtained by increasing the number of samples for averaging.
3 Results
3.1 Specifications of the methane analyzer
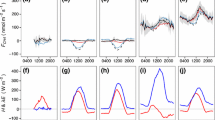
According to the catalog specifications of the FID gas analyzer used in this study, the minimum concentration resolution of the analyzer is 1 ppb, the response time is 60 s, and the precision is ±1% of the absolute value (about ±18 ppb under current atmospheric methane concentrations of 1.8 ppm). According to previous chamber measurements in Japanese forest soils (Ishizuka et al. 2009), the mean methane fluxes were about 3.0 mg CH4 m−2 day−1. Using Eq. 2 with mean monthly diurnal pattern of σ w (Fig. 2), we calculated back the precision required to accurately measure concentration differences by the REA method. The differences ranged from 2 to 10 ppb, where the difference was expected to be small during the daytime with high σ w values. Because the precision seemed insufficient for measuring the methane flux, we checked the precision of the analyzer when in use by the system in this study. A standard gas with a known methane concentration was flowed through the analyzer for approximately 4 h and recorded methane concentrations at a frequency of 1 Hz. The amplitude spectral density of the methane concentrations during the calibration is shown in Fig. 3: each amplitude spectrum was created for a half-hourly period. The amplitude spectral density is a square root of the power spectral density and shows the magnitude of noise on each timescale. The noise was classified with two components: (1) precision of the measurement within each reservoir (dark gray area in Fig. 3) and (2) stability during time for analyzing two reservoirs (light gray area in Fig. 3). First, because our system spent 4 min for measuring the methane concentration of each reservoir (Table 1), the 4-min averaging procedure had random errors of up to 4.5 ppb (dark gray area in Fig. 3); this noise was mostly caused by errors in the low-frequency domain (lower than 0.01 Hz in the dark gray area). Second, the system was affected by lower-frequency noises due to limited stability because there was lag time analyzing the two reservoirs. The lag time was 11 min (Table 1); the start of measurements for C up was scheduled at 2 min, and the end for C down was at 13 min. The evaluated low-frequency noise due to this cycle is up to 4.5 ppb (light gray area in Fig. 3), which was similar to the noise for the precision of the measurement within each reservoir (precision within 4 min). Thus, the precision of the methane gas analyzer was approximately 4.5 ppb.
The evaluated random errors in the fluxes are shown in Fig. 2; the errors were calculated from the diurnal variations of σ w and Eq. 2 using the precision of the methane gas analyzer, 4.5 ppb. Because the σ w was higher in the daytime than in the nighttime, the expected random errors were larger in the daytime. The average daytime and nighttime errors were 1.2 and 0.7 μg CH4 m−2 s−1, respectively. The precision tended to be higher in the summer than in the winter because of the seasonal variations of σ w (Fig. 2).
3.2 Determination of the empirical coefficient
We first determined the empirical constant b by applying Eq. 1 to data collected during the period between February and November 2009. T up and T down were separated from the 10 Hz turbulent fluctuation by referring the updraft and downdraft signals based on the vertical wind velocity (Hamotani et al. 2001; Ueyama et al. 2009), which were consistent with the timing of switching the pumps for C up and C down in the REA sampling system. The relationship between σ w (T up–T down) and the heat flux as measured by the EC method is shown in Fig. 4. The slope of this relationship is the empirical constant b which was determined here to be approximately 0.53. In previous studies, this value was found to be 0.51–0.57 in forests (Hamotani et al. 2001; Ueyama et al. 2009). The high correlation coefficient (0.97) indicates that the REA system’s use of a moving average of vertical wind velocity sufficiently separated the updraft and downdraft conditions. Because there was no systematic change in the b value across seasons, we used the empirical constant of 0.53 throughout the year.
3.3 Validation using the CO2 flux measurements
To validate our REA system, we compared the CO2 fluxes measured by the closed-path EC system and the REA system (Fig. 5). The CO2 fluxes derived from both methods were highly correlated (R 2 = 0.89) and there was no bias (slope of 1.05 and offset of −0.83 μmol m−2 s−1). Although the on–off switching of the pumps used in the system might not be able to respond at a rate of 10 Hz, the turbulent transport by such high-frequency eddies could be negligible over the tall forest canopy, which was confirmed by spectral analyses (Ueyama et al. 2009). These results indicate that the system properly sampled updraft and downdraft air, and they show that our REA system was robust for the measurement of trace gas fluxes relative to the EC system. The data coverage of the EC and REA methods were 26% and 67%, respectively; the low data coverage of the EC method were possibly caused by condensation due to high air humidity and large diurnal temperature ranges.
3.4 Methane flux
The calculated half-hourly methane fluxes are shown in Fig. 6a. The half-hourly fluxes were highly scattered because of a random error in the system of up to 1.2 μg CH4 m−2 s−1. Thus, the scattered nature of the results is due to artificial perturbations rather than actual ecological fluxes. Because our REA system successfully measured the CO2 flux (Fig. 5) as well as the heat flux (Fig. 4), these scattered results can be attributed to a lack of precision in the methane analyzer rather than sampling errors in the system. Despite this scatter, we observed a seasonal shift in methane fluxes, with values indicating methane uptake from mid-May to October.
Half-hourly values (a), monthly mean diurnal pattern (b), and seasonal variations of methane fluxes (c) throughout 2009. The black dots with lines and the gray shadow in b represent the ensemble mean and standard deviation values of each day’s half-hourly measurement in each month, respectively. The white dots, line, and gray shadow in c represent the daily mean, 7-day running mean, and standard deviation values of 7-day methane fluxes, respectively. The detection limits in the half-hourly data were shown in Fig. 2
The random errors observed in the half-hourly calculations could be reduced by increasing the number of samples to be averaged. We examined the diurnal variations for each month by calculating an ensemble mean (Fig. 6b). These variations were only considered when the number of data points for the ensemble mean was greater than 5. Our results show that the diurnal variations in methane flux occurred from May to October, but were not evident in other months. This result suggests that biological activities, such as microbial oxidation in the soil, were responsible for this daytime uptake of methane.
We calculated the daily methane flux by filling data gaps using the diurnal variations. The seasonal variation in flux is shown in Fig. 6c, and a clear seasonal pattern is evident. Because the daily values could be affected by random errors, they were analyzed using 7-day running means. In this forest, significant methane uptake was only apparent during the summer months, when the soil temperature was higher than 10–15°C. During the remainder of the year, measured fluxes were fluctuated between a small methane sink and a methane source, possibly because the fluxes were less than detectable limit of our system. The seasonal maximum and average uptake rates were −21.0 and −2.3 mg CH4 m−2 day−1, respectively. Assuming the January methane flux to be negligible because the ground was covered in snow, the annual methane sink was calculated to be 835 mg CH4 m−2 year−1 (8.35 kg CH4 ha−1 year−1), which was within the range of 379–2478 mg CH4 m−2 year−1 for annual sinks observed using chamber techniques in other Japanese forest soils (Ishizuka et al. 2009).
The monthly and annual error distributions of the methane fluxes were evaluated using the bootstrapping technique (Fig. 7). The largest errors were symmetrically distributed around ±0.4 μg CH4 m−2 s−1 at the monthly timescale (Fig. 7a). The estimated errors were smaller than those expected based on the precision of the gas analyzer (Fig. 2), showing that the averaging procedure effectively canceled out the random errors. The maximum estimated errors were also symmetrically distributed around ±400 mg CH4 m−2 year−1 at the annual timescale (Fig. 7b); the 90% confidence interval of the errors ranged from −171 to 174 mg CH4 m–2 year–1, and thus the annual methane sink was 835 ± 175 mg CH4 m–2 year–1.
According to the profile measurement, methane concentration was most depleted near the soil, whereas the concentration at other heights was not significantly different if we considered the precision of the analyzer. On average, methane concentration at 0.3 m was 10 ppb lower than those at other height (Fig. 8). The concentration difference was similar range throughout the season, and did not show distinct diurnal variations. Even though concentration within the canopy could be highly heterogeneous, the observed concentration profile indicated that observed sink was mainly caused by sink at the forest soil.
4 Discussion
We performed a continuous observation of methane fluxes above a forest canopy using an alternative micrometeorological technique known as the REA method. Our REA method was validated by a comparison against CO2 flux measurements using the EC method. Although previous studies only validated this method based on short-term measurements (Hamotani et al. 2001; Ueyama et al. 2009), we found that the performance of the REA method was suitable for measuring fluxes on the annual time scale. The data coverage of the REA method was also higher than that of the EC method, although the data coverage of the EC method would increase if the sampled air was fully dehydrated. These results indicate that the REA method is a useful tool for measuring fluxes of trace gases such as methane and CO2 at the canopy scale. Because of the lack of adequate methane analyzer for measuring the very small fluxes in the forest canopy via the EC method, the REA method could be an alternative way to measure methane flux over forest canopy. Although we could only validate the performance in CO2 flux measurement, this method could be applicable for methane flux measurements because of scalar transport similarity among scalar quantities (Baker et al. 1992; Bowling et al. 1999).
The REA method has some advantages in trace gas measurements compared with the EC method because it does not require pumps that have high flow rates or a gas analyzer with a fast response time; therefore, the REA method can be operated with low power consumption, which facilitates the application of methane flux measurements in remote areas, where electric power is limited. Current closed-path eddy covariance systems require large pumps with a flow rate of at least 330 LPM (Hendriks et al. 2008), which could limit their applicability to the limited sites that have grid connection. Although an open-path methane analyzer have been available in flux studies (McDermitt et al. 2010), the resolution of these systems is 5 ppb, which is not low enough to measure methane fluxes in the forest canopy via the EC method. Another advantage of the REA method is that it can measure continuous half-hourly fluxes while only using the analyzer for short analysis times (our system only used the analyzer for 14 min per run; Table 1), which enables the same analyzer to be used for simultaneous measurements of vertical concentration profiles (Fig. 1) and multiple chambers. Based on the Allan variance technique (Allan 1966), state-of-the-art methane gas analyzers still have insufficient precision to measure methane fluxes of forests. Previous studies reported this precision to be 1.5 ppb Hz−1/2 (Eugster and Plüss 2010) and 2.9 ppb Hz−1/2 (Kroon et al. 2007). The performance of the analyzers used in these studies was different for each integration time (Eugster and Plüss 2010). The REA method can be designed to use the optimal integration time for the gas analyzer employed, which represents a significant advantage for trace gas flux measurement compared with the EC method.
One possible shortcoming of the REA method is that careful evaluation of \( \overline w \) is necessary to accurately discriminate updraft and downdraft conditions, which could limit the utility of this method under non-stationary conditions. Consequently, the careful validation by means of concurrent evaluation of CO2 flux measurements is necessary in the REA method but not in the EC method. One recent study indicated that the REA method could generate reliable estimates of methane fluxes even though half-hourly fluxes showed relatively large deviations from results of the EC method (Hendriks et al. 2008).
This study increased the precision of measurements made using an FID methane analyzer by increasing the degree of time averaging. Specifically, the precision of measurements made with analyzer improved from 18 to 4.5 ppb (Fig. 3). These results indicate that using the appropriate averaging strategy can increase the precision of a system. Ueyama et al. (2009) also showed that the use of the appropriate averaging time substantially increased the precision of a CO2 gas analyzer. However, despite this precision enhancement, the precision of the FID analyzer was still insufficient for the measurement of half-hourly methane fluxes in our forest ecosystem. Some data were rejected by the quality control criteria because of the random noise of the FID gas analyzer. The random noise also introduced large uncertainties into the half-hourly fluxes. Although we were able to reduce this noise using an averaging procedure, the averaging limited us to treating the data as a monthly diurnal pattern or a moving average of daily values.
Because the effects of humidity were not apparent in previous studies (Ueyama et al. 2009), our system was not dehumidified, which suggests that measured fluxes might have been affected by dilution from the water vapor. Our system could not measure the water vapor flux because water vapor was adsorbed in the REA system. This suggests that the dilution effect was small compared with that in the EC system but might still introduce complex uncertainties. The adsorption of water vapor occurred in the reservoirs, introducing a possible bias in the concentration differences between updraft and downdraft reservoirs in the event of a lag between adsorption and desorption. Although this effect was generally small in the measurements of CO2 fluxes, the effect could be important to the measurement of methane fluxes (Smeets et al. 2009). To correct for this effect, we monitored the bias among the reservoirs twice per day and corrected for this bias in flux calculations (as explained previously). As a result of this monitoring and the bias corrections, we believe that the effect of dilution was relatively small in this study, although it may still have introduced significant uncertainties in the measured fluxes. We theoretically calculated the possible dilution effect of the water vapor flux in the EC measurements using the WPL equation (Webb et al. 1980), and we found that the effect was as large as 0.21 μg CH4 m−2 s−1 in the midsummer season on a half-hourly basis. Part of the diurnal variation observed in the methane fluxes was caused by this effect. However, the diurnal variation seen in Fig. 6b remained even after appropriate corrections for these effects were applied to the methane flux measurements, suggesting that the observed diurnal variations could be caused by ecological fluxes rather than biases or errors in the measurement. In the future, the REA system should be dehumidified for methane flux measurements, as is necessary for the EC method and the gradient method. Considering that it is difficult to fully dehumidify sample air using typical systems, such as the Perma-pure drier, the simultaneous measurements of both CH4 and water vapor in the same cell could be useful for measuring CH4 mixing ratios in flux measurements.
The daily methane uptake was found to be as high as 20 mg CH4 m−2 day−1, which was somewhat higher than the values observed in other Japanese forest soils using chamber measurements. In a comparison of methane fluxes at 27 sites in Japan, Ishizuka et al. (2009) found that the daily maximum uptake ranged from 0.55 to 10.48 mg CH4 m−2 day−1. Considering the large spatial variations in the observed fluxes (factor of 19), the measured peak at this site is reasonable for a Japanese forest. Because the spatial variation of the methane uptake rate is regulated mainly by soil porosity (King 1997; Ishizuka et al. 2009), the high uptake rate we observed could be explained by the high porosity of soil formed by volcanic ash deposits from Mt. Fuji. The low soil water content (annual average of 0.111 m3 H2O m−3 soil at 5 cm depth) also promoted effective gas diffusion within the soil. Because methodological differences between micrometeorological and chamber techniques could cause this difference, a comparison between both methods will be required at the same site in the future.
Although the measured methane flux showed the sink activities only at the summer months (Fig. 6), methane concentration near soil showed lower values throughout the year (Fig. 8). Part of this inconsistency is caused by spatially heterogeneous nature of air within the canopy. Other possibility was caused by limited precision of the flux measurement, where precision during the winter period was lower than those at the summer months (Fig. 2). Consequently, further studies will be required especially for winter period.
Our analysis indicates that the larch forest was a methane sink at the canopy scale, although a recent study proposed that forest ecosystems are potentially a large methane source at the global scale (Keppler et al. 2006). In incubation experiments (Kitaoka et al. 2007), the leaves of the Japanese larch (L. kaempferi) emitted methane at rate of 31.3 ng CH4 g−1 h−1. Based on the measured LAI (2.9 m2 m−2) and the specific leaf area of larch leaves (22.0 m2 kg C−1; White et al. 2000), we calculated canopy scale emissions to be approximately 0.2 ng CH4 m−2 day−1, which was too low a level to be compared with the measured canopy-scale methane uptake and too little to be observed with the current precision of our measurements. Consequently, the methane emission from the leaves of the larch trees could be negligible at the canopy scale, even though it remains uncertain whether leaves emit methane at the low rates reported previously.
The application of micrometeorological techniques provides great advantages in the measurement of methane fluxes in terms of (1) spatial and temporal representativeness, and (2) minimum disturbance to the underlying vegetation and soil. The measured fluxes showed both diurnal and seasonal variations. The results suggest that traditional approaches, such as chamber techniques, yield potentially biased results because the chamber measurements are usually taken at a coarse temporal resolution, typically once or twice per month (e.g., Itoh et al. 2009). Furthermore, chamber measurements often disturb natural conditions by eliminating wind diffusion. Given that methane consumption is strongly related to the methane concentration (King 1997), a decrease in the methane concentration within the chamber headspace might result in an underestimation of methane fluxes. To reduce the uncertainties observed in previous plot scale measurements, future studies should implement micrometeorological measurements with high rates of accuracy and precision.
5 Conclusions
This study is a first report on efforts to measure methane fluxes using the REA method at a temperate forest site throughout an entire season. The system accurately sampled updraft and downdraft air with results that were validated by the CO2 flux measurements obtained by the EC method. The application of micrometeorological measurements provides a great advantage in the continuous measurement of methane fluxes. This study showed that methane fluxes had diurnal and seasonal variations. More traditional approaches to flux measurement usually occur at coarser (e.g., monthly) temporal resolutions, possibly introducing bias into the results. According to the canopy-scale flux measurement, we found that the forest acted as a small methane sink during the summer months. The biological emission from plant leaves was not observed in our study, and thus could be negligible at the canopy-scale exchange.
The fluxes measured using our system had a high level of uncertainty because of the low precision of the FID gas analyzer. For more accurate measurements of methane flux, a more precise gas analyzer will be required. Recently, cavity ringdown laser spectrometers have been made available for flux measurements (Eugster and Plüss 2010), and these are applicable to both the EC and the REA methods (Hendriks et al. 2008; Smeets et al. 2009). Application of these analyzers will allow more accurate flux measurements from the micrometeorological techniques. Because the fluxes observed in this study had a high level of uncertainty, the measured fluxes and their variations should be validated in future studies. To improve our techniques for trace gas flux measurements, the publication of both successful studies and less conclusive results is particularly important because the techniques for methane flux measurement are still developing and numerous issues remain. A greater availability of information and new technologies will improve the availability of advanced techniques for trace gas measurement.
References
Allan DW (1966) Statistics of atomic frequency standards. Proc IEEE 54:221–230
Aubinet M, Grelle A, Ibrom A, Rannik Ü, Moncrieff J, Foken T, Kowalski AS, Martin PH, Berbigier P, Bernhofer Ch, Clement R, Elbers J, Granier A, Grünwald T, Morgenstern K, Pielegaard K, Rebmann C, Snijders W, Valentini R, Vesala T (2000) Estimates of the annual net carbon and water vapor exchange of forests: the EUROFLUX methodology. Adv Ecol Res 30:113–175
Baer DS, Paul JB, Gupta M, O’Keefe A (2002) Sensitive absorption measurements in the near-infrared region using off-axis integrated-cavity-output spectroscopy. Appl Phys B 75:261–265
Baker JM, Norman JM, Bland WL (1992) Field-scale application of flux measurement by conditional sampling. Agric For Meteorol 62:31–52
Baldocchi DD (2003) Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: past, present and future. Glob Chang Biol 9:479–492
Beerling DJ, Gardiner T, Leggett G, McLeod A, Quick WP (2008) Missing methane emissions from leaves of terrestrial plants. Glob Chan Biol 14:1821–1826
Billesbach DP, Kim J, Clement RJ, Verma SB, Ullman FG (1998) An intercomparison of two tunable diode laser spectrometers used for eddy correlation measurements of methane flux in a prairie wetland. J Atmos Ocean Technol 15:197–206
Bousquet P, Ciais P, Miller JB, Dlugokenchy EJ, Hauglustaine DA, Prigent C, Van der Werf GR, Peylin P, Brunke E-G, Carouge C, Langenfelds RL, Lathière J, Papa F, Ramonet M, Schmidt M, Steele LP, Tyler SC, White J (2006) Contribution of anthropogenic and natural sources to atmospheric methane variability. Nature 443:439–443
Bowling DR, Delany AC, Turnipseed AA, Baldocchi DD, Monson RK (1999) Modification of the relaxed eddy accumulation technique to maximize measured scalar mixing ratio differences in updrafts and downdrafts. J Geophys Res 104:9121–9133
Bowling DR, Miller JB, Rhodes ME, Burns SP, Monson RK, Baer D (2009) Soil, plant, and transport influences on methane in a subalpine forest under high ultraviolet irradiance. Biogeosciences 6:1311–1324
Businger JA, Oncley SP (1990) Flux measurement with conditional sampling. J Atmos Ocean Technol 7:349–352
Eugster W, Plüss P (2010) A fault-tolerant eddy covariance system for measuring CH4 fluxes. Agric For Meteorol 150:841–851
Fan SM, Wofsy SC, Bakwin PS, Jacob DJ, Anderson SM, Kebabian PL, McManus JB, Kolb CE (1992) Micrometeorological measurements of CH4 and CO2 exchange between the atmosphere and subarctic tundra. J Geophys Res 97:16627–16643
Foken T, Wichura B (1996) Tools for quality assessment of surface-based flux measurements. Agric For Meteorol 78:83–105
Forster P, Ramaswamy V, Artaxo P, Berntsen T, Betts R, Fahey DW, Haywood J, Lean J, Lowe DC, Myhre G, Nganga J, Prinn R, Raga G, Schulz M, van Dorland R (2007) Changes in atmospheric constituents and in radiative forcing. In Climate Change 2007: The physical science basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change [Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., Miller, H. L. (eds.)]. Cambridge University Press, Cambridge, UK
Friborg T, Christensen TRH (1997) Rapid response of greenhouse gas emission to early spring thaw in a subarctic mire as shown by micrometeorological techniques. Geophys Res Lett 24:3061–3064
Friborg T, Soegaard H, Christensen TR, Lloyd CR, Panikov NS (2003) Siberian wetlands: where a sink is a source. Geophys Res Lett 30:2129. doi:10.1029/2003GL017797
Hamotani K, Uchida Y, Monji N, Miyata A (1996) A system of the relaxed eddy accumulation method to evaluate CO2 flux over plant canopies. J Agric Meteorol 52:135–139
Hamotani K, Monji N, Yamaguchi K (2001) Development of a long-term CO2 flux measurement system using REA method with density correction. J Agric Meteorol 57:93–99
Harazono Y, Mano M, Miyata A, Yoshimoto M, Zulueta RC, Vourlitis GL, Kwon H, Oechel WC (2006) Temporal and spatial differences of methane flux at arctic tundra in Alaska. Mem Natl Inst Polar Res Spec Issue 59:79–95
Hendriks DMD, Dolman AJ, van der Molen MK, van Huissteden J (2008) A compact and stable eddy covariance set-up for methane measurements using off-axis integrated cavity output spectroscopy. Atmos Chem Phys 8:431–443
Hirata R, Hirano T, Saigusa N, Fujinuma Y, Inukai K, Kitamori Y, Takahashi Y, Yamamoto S (2007) Seasonal and interannual variations in carbon dioxide exchange of a temperate larch forest. Agric For Meteorol 147:110–124
Ishizuka S, Sakata T, Sawata S, Ikeda S, Sakai H, Takenaka C, Tamai N, Onodera S, Shimizu T, Kan-na K, Tanaka N, Takahashi M (2009) Methane uptake rates in Japanese forest soils depend on the oxidation ability of topsoil, with a new estimate for global methane uptake in temperate forest. Biogeochemistory 92:281–295
Itoh M, Ohte N, Koba K (2009) Methane flux characteristics in forest soils under East Asian monsoon climate. Soil Biol Beochem 41:388–395
Keppler F, Hamilton JTG, Braβ M, Röchmann T (2006) Methane emissions from terrestrial plants under aerobic conditions. Nature 439:187–191
King GN (1997) Responses of atmospheric methane consumption by soils to global climate change. Glob Chang Biol 3:351–362
Kirschbaum MUF, Walcroft A (2008) No detectable aerobic methane efflux from plant material, nor from adsorption/desorption processes. Biogeosciences 5:1551–1558
Kirschbaum MUF, Bruhn D, Etheridge DM, Evans JR, Farquhar GD, Gifford RM, Paul KI, Winters AJ (2006) A comment on the quantitative significance of aerobic methane release by plants. Funct Plant Biol 33:521–530
Kitaoka S, Sakata T, Koike T, Tobita H, Uemura A, Kitao M, Maruyama Y, Sasa K, Utsugi H (2007) Methane emission from leaves of larch, birch and oak saplings grown at elevated CO2 concentration in northern Japan –preliminary study-. J Agric Meteorol 63:201–206
Kroon PS, Hensen A, Jonker JJ, Zahniser MS, van’t Veen WH, Vermeulen AT (2007) Suitability of quantum cascade laser spectrometry for CH4 and N2O eddy covariance measurements. Biogeosciences 4:715–728
McDermitt D, Burba G, Xu L, Anderson T, Komissarov A, Riensche B, Schedlbauer J, Starr G, Zona D, Oechel W, Oberbauer S, Hastings S (2010) A new low-power, open-path instrument for measuring methane flux by eddy covariance. Appl Phys B. doi:10.1007/s00340-010-4307-0
Miyata A, Leuning R, Denmead OT, Kim J, Harazono Y (2000) Carbon dioxide and methane fluxes from an intermittently flooded paddy field. Agric For Meteorol 102:287–303
Moore CJ (1986) Frequency response corrections for eddy correlation systems. Boundary-Layer Meteorol 37:17–35
Nemitz E, Flynn M, Williams PI, Milford C, Theobald MR, Blatter A, Gallagher MW, Sutton MA (2001) A relaxed eddy accumulation system for the automated measurement of atmospheric ammonia fluxes. Water Air Soil Pollut 1:189–202
Pattey E, Strachan IB, Desjardins RL, Edwards GC, Dow D, MacPherson JI (2006) Application of a tunable diode laser to the measurement of CH4 and N2O fluxes from field to landscape scale using several micrometeorological techniques. Agric For Meteorol 136:222–236
Rigby M, Prinn RG, Fraser PJ, Simmonds PG, Langenfelds RL, Huang J, Cunnold DM, Steele LP, Krummel PB, Weiss RF, O’Doherty S, Salameh PK, Wang HJ, Harth CM, Mühle J, Porter LW (2008) Renewed growth of atmospheric methane. Geophys Res Lett 35. doi:10.1029/2008GL036037
Rinne J, Riutta T, Pihlatie M, Aurela M, Haapanala S, Tuovinen J-P, Tuittila E-S (2007) annual cycle of methane emission from a boreal fen measured by the eddy covariance technique. Tellus 59B:449
Shurpali NJ, Verma SB (1998) Micrometeorological measurements of methane flux in a Minnesota peatland during two growing seasons. Biogeochemistry 40:1–15
Simpson IJ, Edwards GC, Thurtell GW, Hartog G, Neumann HH, Staebler RM (1997) Micrometeorological measurements of methane and nitrous oxide exchange above a boreal aspen forest. J Geophys Res 102:29331–29341
Smeets CJPP, Holzinger R, Vigano I, Goldstein AH, Röckmann T (2009) Eddy covariance methane measurements at a Ponderosa pine plantation in California. Atmos Chem Phys 9:8665–8375
Takimoto T, Iwata T, Yamamoto S, Miura T (2010) Characteristics of CO2 and CH4 flux at barley-rice double cropping field in southern part of Okayama. J Agric Meteorol 66:181–191
Ueyama M, Harazono Y, Okada R, Nojiri A, Ohtaki E, Miyata A (2006) Micrometeorological measurements of methane flux at a boreal forest in central Alaska. Mem Natl Inst Polar Res Spec Issue 59:156–167
Ueyama M, Hamotani K, Nishimura W (2009) A technique for high-accuracy flux measurement using a relaxed eddy accumulation system with an appropriate averaging strategy. J Agric Meteorol 65:315–325
Webb EK, Pearman GI, Leuning R (1980) Correction of flux measurements for density effects due to heat and water vapour transfer. Quart J Roy Meteorol Soc 106:85–100
Werner C, Davis K, Bakwin P, Yi C, Hurst D, Lock L (2003) Regional-scale measurements of CH4 exchange from a tall tower over a mixed temperate/boreal lowland and wetland forest. Glob Chang Biol 9:1251–1261
White MA, Thornton PE, Running SW, Nemani RR (2000) Parameterization and sensitivity analysis of the BIOME-BGC terrestrial ecosystem model: Net primary production controls. Earth Interact 4:1–85
Wille C, Kutzbach L, Sachs T, Wagner D, Pfeiffer E–M (2008) Methane emission from Siberian arctic polygonal tundra: eddy covariance measurements and modeling. Glob Chang Biol 14
Wuebbles DJ, Hayhoe K (2002) Atmospheric methane and global change. Earth Sci Rev 57:177–210
Zona D, Oechel WC, Kochendorfer J, Paw UKT, Salyuk AN, Olivas PC, Oberbauer SF, Lipson DA (2009) Methane fluxes during the initiation of a large-scale water table manipulation experiment in the Alaskan Arctic tundra. Global Biogeochem Cycles. doi:10.1029/2009GB003487
Acknowledgments
We thank all those who contributed to the field observations and data analysis. The measurements were obtained with the help of Mr. Munehisa Okado and Mr. Yuki Morimoto of Osaka Prefecture University. We also thank Dr. Yoshiaki Kitaya and Dr. Toshio Shibuya of Osaka Prefecture University for supporting our CO2 flux measurements. We are grateful to Dr. Hiroki Iwata of the International Arctic Research Center of the University of Alaska, Fairbanks, Dr. Kenshi Takahashi, Dr. Yoshiko Kosugi, and Ms. Ayaka Sakabe of Kyoto University for their constructive discussions of regarding methods of methane flux measurements. We also thank the four anonymous reviewers for constructive comments on earlier versions of the manuscript. This study was partly supported by Grant-in-Aid for Young Scientists (A) (23681004) and the JSPS A3 Foresight Program (CarboEastAsia).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Ueyama, M., Hamotani, K., Nishimura, W. et al. Continuous measurement of methane flux over a larch forest using a relaxed eddy accumulation method. Theor Appl Climatol 109, 461–472 (2012). https://doi.org/10.1007/s00704-012-0587-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-012-0587-0