Abstract
We developed an operationally applicable land-only daily high-resolution (5 km × 5 km) gridding method for station observations of minimum and maximum 2 m temperature (T min/T max) for Europe (WMO region VI). The method involves two major steps: (1) the generation of climatological T min/T max maps for each month of the year using block regression kriging, which considers the spatial variation explained by applied predictors; and (2) interpolation of transformed daily anomalies using block kriging, and combination of the resulting anomaly maps with climatological maps. To account for heterogeneous climatic conditions in the estimation of the statistical parameters, these steps were applied independently in overlapping climatic subregions, followed by an additional spatial merging step. Uncertainties in the gridded maps and the derived error maps were quantified: (a) by cross-validation; and (b) comparison with the T min/T max maps estimated in two regions having very dense temperature observation networks. The main advantages of the method are the high quality of the daily maps of T min/T max, the calculation of daily error maps and computational efficiency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Monitoring temperature extremes is important because they have major impacts on the economy, ecology and human life. Estimating the 2 m minimum and maximum temperature (T min/T max) at high spatial resolution is particularly important. The daily T min/T max is often of more interest than the daily mean temperature (e.g., as an indicator of frost or heat stress in agriculture). However, T min/T max data are usually available from fewer monitoring stations, and the values are less normally distributed than mean temperature values. Therefore, the gridding of T min/T max is more challenging than gridding mean temperature, and so is the focus of this study.
For high-resolution gridding (25 km²) in Europe, at least 40,000 stations would be needed if a density of one station per grid square was required. However, as only a few thousand stations are available, it is essential to generate an appropriate interpolation algorithm that most efficiently uses the available station information and additional predictor information (such as orography or continentality).
A number of studies have investigated the interpolation of daily climate variables to create regional or global data sets. Regression is a well-established interpolation technique that can be used in a variety of ways. Stahl et al. (2006) compared 12 regression variations and kriging methods for interpolating daily maximum and minimum temperatures in British Columbia (Canada). Gaussian filter inverse distance weighting methods (GIDS), which are based on multiple linear regression against predictors, yielded the best results if there was a high-density network of stations available. However, it was noted that methods that determine regression functions locally (such as GIDS) should not be applied in situations where the observed predictor range is too restrictive (e.g., no observations at high elevations). In such cases, the use of ordinary kriging (OK) was recommended.
Numerous studies have shown that a number of very similar techniques are suitable for interpolating temperature and other climate variables (Jarvis and Stewart 2001; Stahl et al. 2006). In universal kriging (UK), the trend of a variable is modeled as a function of the spatial coordinates. If the trend is defined as a linear function of the predictors, it is referred to as kriging with external drift (KeD). Alternatively, the estimation of trends and residuals can be undertaken separately and combined later in a process termed regression kriging (RK), which was proposed by Ahmed and de Marsily (1987) and Odeh et al. (1995). Regression kriging enables the application of nonlinear dependence to predictors. In cases of linear dependence, Hengl et al. (2007) demonstrated the equivalence of KeD and RK. In the present study, RK was preferred because of its greater computational efficiency and robustness.
The quality of the interpolation method is influenced by the explanatory predictors considered, such as elevation (Goovaerts 2000), aspect ratio and distance to the coast (Daly et al. 2002; Hiebl et al. 2009), seasonality and weather conditions (Hewitson and Crane 2005). The unexplained spatial variability of a variable can be considered in an additional step by interpolation of anomalies using other methods (New et al. 2001).
Haylock et al. (2008) described a high-resolution gridded data set of daily precipitation and daily 2 m T min/T max for Europe. They used a three-step interpolation method involving: (a) interpolation of climatological monthly values with three-dimensional thin-plate smoothing splines; (b) kriging interpolation of the daily anomalies with respect to the monthly climatologies; and (c) adding the interpolated anomalies to the climatologies to produce the final result. Splitting of the interpolation process facilitates selection of the most appropriate and efficient method with regard to time and space scales.
We report here an operationally applicable land-only daily high-resolution (5 km × 5 km) gridded algorithm for daily 2 m T min/T max for Europe (WMO region VI). The new algorithm also splits the interpolation process into estimation of monthly climatologies and interpolation of daily anomalies. However, unlike Haylock et al. (2008), we applied RK (Hengl et al. 2007), which allows the application of multiple predictors (including elevation and continentality). We conducted the gridding steps in overlapping subregions (overlap = 250 km wide) to provide more climatologically homogeneous conditions (Fig. 1e). The subregions were determined by merging the Köppen–Geiger climate zones (Sanderson 1999). By merging we increased the number of available stations per region, providing for more robust regression. The new gridding algorithm enables consistent quantification of uncertainties of the daily product.
Section 2 briefly introduces the station data used in the study, Section 3 overviews the predictor data used, and Sect. 4 describes the new algorithm and explains the method for calculating the uncertainty. The final section presents the results and an evaluation of the new method.
2 Station data
This section briefly describes the station data sets used in the interpolation exercise, and the data sets used for evaluation of the new algorithm. To estimate the monthly climatologies, we used data from approximately 3,000 CLIMAT stations (Hoefrichter 2009) providing long-term averages (1961–1990) of monthly mean daily T min and T max observations. The CLIMAT data set has been thoroughly quality controlled and inhomogeneities have been corrected, making this data set a reliable basis for our analysis.
The daily anomalies were based on data from approximately 3,000 synoptic stations (SYNOP). For the period 2005–2008, only about 33% of SYNOP and CLIMAT stations were co-located, as a consequence of the addition of new stations and the removal of other stations since 1990. Data from SYNOP stations are available in near real time, but are not subject to a high level of quality control. Therefore, we introduced a degree of quality control by excluding daily observations that deviated by more than ±5 standard deviations from the averaged regional anomalies.
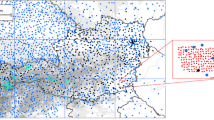
The density of the CLIMAT and SYNOP stations is variable, with the highest density occurring in Central Europe and lowest on the Greenland ice shield (Fig. 1). Approximately, 20 CLIMAT and 20 SYNOP stations are located along the southern coastline of Greenland. No CLIMAT data are available for the entire period 1961–1990 for high-elevation areas including the Greenland ice shield, and currently there is only one SYNOP station on the ice shield (at the Summit, 3,208 m). Despite the sparse station network in Greenland, we included it in the study area because this provided the opportunity to conduct a feasibility study on the use of our method in remote areas.
To evaluate the new algorithm for daily T min and T max we used data from two independent regional observation networks having very high spatial resolution. One, situated in southern Austria, has been in operation since January 2007 and comprises 200 stations covering an area of 29 km × 14 km (Kabas et al. 2008). The other network was situated in the Black Forest, Germany, and was operated in summer 2007. It comprises 96 stations covering an area of 8 km × 12 km (Schneider et al. 2008).
3 Predictors and predictor data sets
In the gridding method, the target variable (mean monthly T min or T max) was linearly regressed against multiple predictors. Useful predictors have to be physically related to temperature, readily available and applicable to the entire interpolation domain of interest, and statistically robust in the regression process. These criteria exclude some apparently good predictors. For example, objective weather classifications (e.g., Bissolli and Dittmann 2001) are only regionally defined, so are not applicable to the entire domain and are therefore not appropriate predictors. Satellite data are potentially useful for detection of such things as cloud and fog, but are potentially subject to the screening of low fog layers (with potential temperature inversion) by thin high clouds. Thus, the use of satellite products is not robust; and these are also affected by a limited period of availability. Hiebl et al. (2009) accounted for urban effects in the generation of a high-resolution climatology in an alpine region, but concluded that there was no general, operationally usable relationship between urban effects and temperature at the daily time scale.
Inversion is the reversal of the temperature lapse rate and leads to strongly modified regional temperature patterns. It predominantly occurs in winter and is often accompanied by fog. Fog prevents marked cooling during the night by limiting the emission of heat, and reduces warming during the day by reflecting solar radiation. Therefore, fog weakens the daily temperature cycle. We tested the inversion index proposed by Daly et al. (2002), but it was not robust and consequently was not used. The selected predictors are described below.
Elevation (Fig. 1a) correlates well with surface temperature, is globally available and is thus a useful predictor. We used high-resolution elevation data obtained from the shuttle radar topography mission (SRTM; see http://dds.cr.usgs.gov/srtm/version2_1/SRTM3/), which provides data within 60° north and south, and represents an improvement on previous high quality and resolution digital elevation model (DEM) products (Jarvis et al. 2004). Pole-wards the data set is complemented by data provided by the United States Geological Survey (USGS; see http://eros.usgs.gov/#/Find_Data/Products_and_Data_Available/gtopo30_info). The original grid spacing of the SRTM data is about 90 m (the gtopo30 grid spacing is approximately 1,000 m) at the equator and increases toward the poles. The two data sets were aggregated to the target resolution (5 km × 5 km) by calculating the average of all grid values within each target grid box. The two DEMs were then merged by linearly weighting across an overlapping area extending 100 km southwards from 60°N.
Climate is strongly affected by the land–sea distribution. We represented this using the continentality index \( K = 1.7\frac{A}{\sin \varphi } - 20.4 \) (Gorczynski 1920) as a predictor. This index was based on the geographical latitude (φ) and the mean annual range of monthly temperatures over the period 1961–1990 (A in °C). The index is defined to usually take values from 0 to 100, with lower values indicating maritime climate and higher values indicating continental climate. We derived this predictor (Fig. 1b) from the Climatic Research Unit (CRU) data (CRU TS 3.00; Mitchell and Jones 2005) for the period 1961–1990.
Geographical latitude is a potential predictor of the pole-ward decrease of mean temperature. However, we used the zonally averaged monthly CRU climate, which typically yields better cross-validation results as a predictor than geographical latitude (not shown).
We quantified the explanatory capacity of the selected predictors using the root-mean square error (RMSE) of the fitted temperatures in comparison with the station observations. To yield a robust estimate, the fitting of the regression function included all available stations within the subregions. Table 1 shows the average of the RMSE values over all subregions and indicates that the best single predictor is the zonal mean temperature (RMSE = 4.0°C). Obviously, adding more predictors reduces the RMSE.
The addition of the inversion index as a predictor resulted in a small reduction of the RMSE. However, inversion is a local phenomenon that cannot be adequately captured when determining the regression coefficients for the climate of an entire subregion (overfitting). Furthermore, artifacts can occur at the inversion height. Thus, only elevation, zonal mean temperature and the continentality index were ultimately selected for inclusion in the study.
4 Gridding method
The gridding method involved a two-step process. Firstly, the climatological monthly T min/T max data were interpolated using block RK, which applied the selected predictors in a multi-linear regression step (Wackernagel 2003). The resulting product is termed a monthly prediction map. Secondly, block simple kriging (SK) was applied to interpolate the normal score transformed daily anomalies. The back-transformed daily anomaly map was added to the monthly prediction map, yielding the final result. These steps are detailed below.
The gridding was performed in a rotated geographical coordinate system with pole at 180°W and 38°N. This placed the center of the study area at the equator of the rotated coordinate system and yielded a quasi-equal area grid across the target region. This enabled application of an isotropic variogram in kriging, minimized the number of grid nodes necessary and maximized the numerical efficiency.
4.1 Block regression kriging of monthly observations
The framework for generating the climatological monthly prediction maps of T min/T max is shown in Fig. 2. We used block RK for the first gridding step, which is a combination of multiple linear regression that considers the spatial variation explained by the used predictors, and block SK for interpolating the regression residuals (the residual mean is zero), i.e., block SK interpolates the variation not explained by the applied predictors (Hengl et al. 2004). We used block kriging (Deutsch and Journel 1998) because the grid node values are valid for areal values and not for point values (as is the case for standard kriging methods) and therefore is spatially more representative.
The regression coefficients necessary for block RK can be estimated from point data (observations and predictors at station locations) if the applied regression function is linear (Heuvelink and Pebesma 1999; Leopold et al. 2006). To account for different climates, we determined the regression coefficients separately for each climate region. The regression coefficients were then applied to block-averaged (25 km2) predictor maps. The predictors, the coverage of the feature space and the covariance of the regression residuals (determined from the variogram, see below) have to be taken into account in determining the regression error (Hengl et al. 2003).
To insure the data were normally distributed, a normal score transformation (Deutsch and Journel 1998) was applied to the regression residuals prior to interpolation. For the kriging process, we used a spherical variogram model, which has a linear behavior near the origin and reaches the sill at the range beyond which autocorrelation becomes zero. For the necessary variogram estimate, we adopted a suboptimal but robust approach (Ahrens and Beck 2008). We estimated a climatological variogram range from normal score transformed monthly regression residuals (separately for T min/T max and each subregion). The range of the variogram of residuals was shorter (approximately 180 and 1,200 km for Central Europe and Greenland, respectively) than the monthly temperature range, which suggests that the trend had been removed. We also estimated a climatological nugget variance, which was 5–20% of the sill variance (dependent on the subregion, and the network density). However, as the nugget variation in the residual variogram reflects the trend estimation error within the regression step (Ali et al. 2005), it was generally not smaller than the nugget variance in the variogram of monthly temperatures.
Following interpolation of the normal score transformed regression residuals using SK, a back-transformation was applied, which yielded a residual map that was added to the regression map. These subregional maps were merged using linear weighting in the 250 km-wide overlap, to yield the monthly prediction maps showing the mean over the period 1961–1990 for T min and T max for the WMO region VI .
Solving the kriging system provided the block SK error variance (Chilès and Delfiner 1999). This was used to produce the quartile map of the interpolated residuals, which were back-transformed. We used half of the inter-quartile range (IQR/2) as an error measure. The quartile map of the interpolated residuals and the regression error map were combined to yield the monthly RK quartile map, following the additive relation described by Hengl et al. (2003).
4.2 Block simple kriging of the daily anomaly
The framework for generating daily prediction maps is shown in Fig. 3. Daily anomalies are the difference between the daily T min/T max observations and the monthly prediction maps. Block SK was used for interpolation of the normal score transformed anomalies and was applied independently in the climatic subregions. This process enabled regional weather phenomena to be accounted for. For the block SK of daily anomalies, we also applied a climatological range and nugget variance with a spherical variogram. This was determined seasonally from normal score transformed daily anomalies. The climatological range of daily variograms was approximately 50 and 500 km for Central Europe and Greenland, respectively, and in both cases the range was shorter than for monthly data. This was because of the considerably larger small-scale variation in daily anomalies compared with the smoothly varying monthly regression residuals. The climatological nugget variance of daily anomalies lay between 5 and 15% of the sill.
The regionally interpolated daily anomaly maps were back-transformed, merged, and added to the monthly prediction map. This yielded the daily prediction maps for T min and T max.
The daily error variance estimated by block SK of the normal score transformed anomalies was used to produce the quartile map of the daily anomalies, which were back-transformed. For interpolation of the monthly residuals, we used IQR/2 as the error measure. The error maps of the monthly predictions and daily anomalies were then combined (Hengl et al. 2003).
Thus, the proposed method applies regression kriging for monthly data and simple kriging for daily anomalies, and is henceforth referred to as regression kriging kriging (RKK).
5 Results and discussion
This section illustrates the application of the block RKK gridding method and provides an evaluation of the temperature and error maps generated. An important part of the evaluation was a comparison with the E-OBS product (Haylock et al. 2008).
5.1 Temperature maps
Figures 4 and 5 illustrate the steps in generating the minimum temperature map for 15 January 2006. The generation of monthly products using block RK is shown in Fig. 4. Panel (a) shows the influence of the predictors on the pattern of the final product. For example, the impacts of elevation and continentality are clearly evident. The residuals of the mean monthly observations to the regressed map were interpolated as shown in panel (b). Most of the large-scale variability was well explained by the regression step, but interpolation of the residuals was an important step at smaller spatial scales. The residual map highlights the regions where the target variable was not well explained by the applied predictors, or where the target variable–predictor relationship could not be adequately estimated because of a lack of data (e.g., in Greenland and alpine regions). The final mean monthly product is shown in panel (c). Figure 4 also shows the uncertainty estimates from block RK (IQR/2). The errors were largest in regions where the temperature pattern was not well explainable by the predictors.
Steps in the generation of the mean monthly T min product (°C), and its uncertainty with respect to January for the period 1961–1990. a The map produced by application of multiple linear regressions; b the gridded regression residuals (0°C is indicated by the dashed line) and c the final monthly product. The d–f indicate the respective errors (°C), calculated as IQR/2
The final steps in generating the daily products are illustrated in Fig. 5. The daily anomalies were interpolated using block SK, as shown in panel (a). Most of the large-scale variability was already adequately explained by the monthly product, but interpolation of the daily anomalies provided important additional information at the regional scale. The cold anomaly over Central Europe and the warm anomaly over Eastern Europe are particularly noteworthy. The daily anomaly map highlighted regions with marked daily temperature anomalies, which were then superimposed on the monthly mean product in the final daily product, shown in panel (b). Figure 5 also shows the uncertainty estimates for the gridded anomalies and the final product. The uncertainty of the final product was dominated by uncertainty in the daily anomaly interpolation (the daily anomalies were greater by one order of magnitude than the monthly regression residuals).
5.2 Cross-validation and comparison with simpler algorithms
We evaluated the performance of the RKK algorithm in three climate regions (Greenland, Central Europe and the Mediterranean) using cross-validation (Wackernagel 2003) and comparison with simpler but commonly used interpolation methods including ordinary kriging (OK) of daily observations and inverse distance weighting (IDW) (Ahrens 2006) of daily observations.
Cross-validation involves sequential removal of each observation from the observational data set, and re-estimation of the observed temperature from the observations in the amended data set using an interpolation method. Thus, the goal was to re-estimate point values at particular station locations. Therefore, these results were based on point interpolation, and not block interpolation. The evaluation criteria were RMSE (perfect score 0°C) and the ratio of the variance of interpolated temperatures and the variance of observed values (VARI, perfect score 1).
The results of the evaluation are summarized in Fig. 6 and Table 2. The RMSE box plots in Fig. 6 illustrate the range of interpolation errors, and the box plots for VARI show the range of relative variance (in both cases for daily T min in January 2007). The RKK clearly outperformed the other methods in terms of both evaluation criteria. The RMSE analysis showed large differences between the climate regions (smallest for Central Europe, largest for Greenland), which demonstrates the value of a dense station network. The RKK also yielded the best score (close to 1) in the VARI analysis, demonstrating its ability to maintain the spatial variability of the temperature field.
Similarly, Table 2 demonstrates the superiority of RKK over OK and IDW (using Central Europe as an example) in terms of both RMSE and VARI. However, RKK overestimated the spatial variability, especially for T min in July. This was a result of the spatial variability imposed by the chosen predictors in the regression step during interpolation.
5.3 Validation of the uncertainty measure
A key issue was to provide a robust uncertainty measure with the RKK, and for this purpose we proposed the IQR. Correct modeling of the local uncertainty implies that 50% of the true values are within the local IQR.
To assess the uncertainty measure, the RKK was tested in two regions that are independent and have dense networks of stations, including a network in southern Austria operated by WegenerNet, and a network in the Black Forrest, Germany. We used block RKK to estimate the daily T min and T max for each test region at a spatial resolution of 5 km × 5 km (observations aggregated to the grid of the block RKK).
Figure 7 shows the percentage of observation within the IQR-provided block RKK. For each network, approximately 50% of the observations fell within the IQR. Also Table 3 shows that with point RKK, an average of approximately 50% of the observations not used in the cross-validation (Sect. 5.2) fell within the IQR for T min and T max in January and July 2007 in Central Europe and the Mediterranean Sea.
However, the widths of the box plots indicate that there were large daily differences. The quality of the predicted temperature and its related uncertainty measure were associated with particular weather conditions, topographical complexity of the region and coverage by network observations. The RKK provided an uncertainty measure that on average (across the climate subregion, and over long time periods) yielded the target precision (50% of the observed values within the IQR), but for single day events at a local scale the uncertainty could be grossly overestimated or underestimated. This is also evidenced in Table 3, which shows that if using non-transformed data the method overestimated the uncertainty (about 80% of the observations fell within the IQR) in the regional observation network areas. Thus, error estimation remains uncertain.
5.4 Comparison with the E-OBS product
We compared maps estimated using the block RKK method with maps based on estimates obtained using a similar product (E-OBS; Haylock et al. 2008). As with the RKK, the E-OBS algorithm involves splitting of the interpolation process into two parts: (1) generation of a monthly map and (2) interpolation and addition of daily anomalies. E-OBS uses elevation and geographical coordinates as predictors by applying three-dimensional smoothing thin-plate splines for interpolation of monthly data, and uses KeD for interpolation of daily anomalies.
Table 4 shows the mean daily ratio of the T min and T max field variances produced by RKK and E-OBS (for Central Europe and the Mediterranean Sea in January and July for the period 2005–2008). The spatial variability of RKK was slightly greater (e.g., the variance in Central Europe was about 25°C).
Figure 8b shows the mean daily T min difference between the E-OBS and the RKK for January in the years 2005–2008. The greatest differences occurred in complex terrain including the alpine region, the Scandinavian mountains and eastern Turkey. One explanation for these differences is that we treated daily anomalies as non-explainable variance (e.g., daily anomalies were not regressed against elevation), while Haylock et al. (2008) used KeD to explain the elevation dependency of the anomalies. Furthermore, we used a different set of predictors to determine the monthly trends. We did not account for an elevation dependency of daily anomalies because of the large uncertainty associated with deriving regression coefficients for daily values, which are highly dependent on weather phenomena at various scales. Moreover, Haylock et al. (2008) determined regression coefficients for the entire target region simultaneously, which could lead to considerable overestimation or underestimation of regional temperature gradients. For instance, the E-OBS algorithm for T min during January produced significantly lower temperatures for Scandinavia, probably because maritime effects were not adequately accounted for (continentality was accounted for in the RKK).
Figure 8a shows the average daily estimation error for each observation station using RKK. The largest estimation errors occurred in areas where there was most difference between the daily maps produced by E-OBS and RKK, including the alpine area, Scandinavia and the Mediterranean Sea. This highlights that large uncertainties mostly arise in areas with low network density and complex terrain.
6 Conclusion
We developed an operationally applicable algorithm (RKK) for generating a high-resolution gridded map of daily minimum and maximum temperatures for the WMO region VI. These maps are unique in their spatial extent, resolution and the number of observation stations used.
The RKK method separates the interpolation process into the estimation of monthly climatologies and the interpolation of daily anomalies. This enables selection of the most appropriate interpolation method for the climatological and daily timescales, respectively. For operational use the target region was separated into seven subregions. This decreased the calculation time by reducing the size of the variance–covariance matrix, which had to be inverted within the kriging process. In addition, the use of climatic subregions enabled local climatic characteristics to be accounted for, which resulted in smaller regression residuals.
An evaluation process indicated the usefulness of the method. For example, the RKK method showed a similar performance to the E-OBS data set (Haylock et al. 2008), and was similarly limited in regions with low station density. Kyselý and Plavcová (2010) recently demonstrated this for the E-OBS data set by comparison with an alternative data set that was generated from a high-density network in the Czech Republic.
A major outcome of the study was in establishing an accurate estimate of the daily interpolation uncertainty (calculated as half the inter-quartile range). The application of a normal score transformation of the monthly regression residuals and daily anomalies prior to interpolation reduced the estimation error and improved the quality of the RKK uncertainty measure (observations within the IQR in approximately 50% of cases with normal score transformation and 80% without transformation).
The use of other predictors should be investigated, such as the incorporation of land cover data, which reflects local energy fluxes and thus has predictive potential for local temperature patterns. The main challenge for the future is that simple static indexes, either topographical or weather based, can capture only a small part of the complex processes involved.
References
Ahmed S, de Marsily G (1987) Comparison of geostatistical methods for estimating transmissivity using data on transmissivity and specific capacity. Water Resour Res 23(9):1717–1737
Ahrens B (2006) Distance in spatial interpolation of daily rain gauge data. Hydrol Earth Sys Sci 10:197–208
Ahrens B, Beck A (2008) On upscaling of rain-gauge data for evaluating numerical weather forecasts. Meteorol Atmos Phys 99(3–4):155–167
Ali A, Thierry L, Abou A (2005) Rainfall estimation in the Sahel. Part I: error function. J Appl Meteor 44:1691–1706
Bissolli P, Dittmann E (2001) The objective weather type classification of the German Weather Service and its possibilities of application to environmental and meteorological investigations. Met Z 10(4):253–270
Chilès JP, Delfiner P (1999) Geostatistics: modeling spatial uncertainty. John Wiley, New York
Daly C, Gibson WP, Taylor GH, Johnson GL, Pasteris P (2002) A knowledge-based approach to the statistical mapping of climate. Clim Res 22:99–113
Deutsch CV, Journel AG (1998) GSLIB: geostatistical software library and user’s guide, 2nd edn. Oxford University Press, New York
Goovaerts P (2000) Geostatistical approaches for incorporation elevation into the spatial interpolation of rainfall. J Hydrol 228:113–129
Gorczynski W (1920) Sur le calcul du degré de continentalisme et son application dans la climatologie. Geogr Annaler 2:324–331
Haylock MR, Hofstra N, Klein Tank AMG, Klok EJ, Jones PD, New M (2008) A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J Geophys Res 113:D20119. doi:10.1029/2008JD010201
Hengl T, Heuvelink GBM, Stein A (2003) Comparison of kriging with external drift and regression-kriging. Technical note, ITC. http://www.itc.nl/library/Papers_2003/misca/hengl_comparison.pdf
Hengl T, Heuvelink GBM, Stein A (2004) A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 120(1-2):75–93
Hengl T, Heuvelink GBM, Rossiter DG (2007) About regression-kriging: from equations to case studies. Comput Geosci 33:1301–1315
Heuvelink GBM, Pebesma EJ (1999) Spatial aggregation and soil process modelling. Geoderma 89(1–2):47–65
Hewitson BC, Crane RG (2005) Gridded area-averaged daily precipitation via conditional interpolation. J Climate 18:41–57
Hiebl J, Auer I, Böhm R, Schöner W, Maugeri M, Lentini G, Spinoni J, Brunetti M, Nanni T, Percec Tadic M, Bihari Z, Dolinar M, Müller-Westermeier G (2009) A high-resolution 1961–1990 monthly temperature climatology for the Greater Alpine Region. Met Z 18(5): doi:10.1127/0941-2948/2009/0403
Hoefrichter K (2009) Erstellung von Klimakarten der mittleren Tagesmaximum-/minimum-temperatur für das Gebiet WMO-VI (Europa und Naher Osten). Deutscher Wetterdienst, Offenbach, KU 23—Regionale Klimaüberwachung
Jarvis CH, Stewart N (2001) A comparison among strategies for interpolating maximum and minimum daily air temperatures. Part II: the interaction between number of guiding variables and the type of the interpolation method. J Appl Meteorol 40:1075–1084
Jarvis A, Rubiano J, Nelson A, Farrow A, Mulligan M (2004) Practical Use of SRTM Data in the Tropics: Comparisons with Digital Elevation Models Generated from Cartographic Data. Working Document 198. International Center for Tropical Agriculture. Cali, Colombia
Kabas T, Binder S, Leuprecht A, Bichler C (2008) Pionierexperiment WegenerNet Klimastationsnetz: Ein neuartiges Messnetz in der Region Feldbach (Steiermark/Österreich) zur Beobachtung von Wetter und Klima mit sehr hoher Auflösung. Wissenschaftlicher Bericht Nr. 23
Kyselý J, Plavcová E (2010) A critical remark on the applicability of the E-OBS European gridded temperature data set for validating control climate simulations. J Geophys Res 115:D23118. doi:10.1029/2010JD014123
Leopold U, Heuvelink GBM, Tiktak A, Finke PA, Schoumans O (2006) Accounting for change of support in spatial accuracy assessment of modelled soil mineral phosphorous concentration. Geoderma 130:368–386
Mitchell TD, Jones PD (2005) An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int J Climatol 25:693–712. doi:10.1002/joc.1181
New M, Todd M, Hulme M, Jones P (2001) Precipitation measurements and trends in the twentieth century. Int J Climatol 21:1899–1922
Odeh IOA, McBratney AB, Chittleborough DJ (1995) Further results on prediction of soil properties from terrain attributes: heterotropic cokriging and regression-kriging. Geoderma 67(3–4):215–226
Sanderson M (1999) The classification of climate from Pythagoras to Koeppen. Bull Am Meteor Soc 80:669–673
Schneider S, Stuhl BB, Steinacker R, Dorninger M (2008) COPS 2007—das Institut für Meteorologie und Geophysik auf Forschungseinsatz im Schwarzwald. ÖGM Bulletin, Wien, Bd 1
Stahl K, Moore RD, Floyer JA, Asplin MG, McKendry IG (2006) Comparison of approaches for spatial interpolation of daily temperature in a large region with complex topography and highly variable station density. Agric For Meteorol 139:224–236. doi:10.1016/j.agrformet.2006.07.004
Wackernagel H (2003) Multivariate geostatistics, 3rd edn. Springer, Berlin, p 387
Acknowledgments
Monthly climate temperatures, based on various station networks, and daily observations were obtained from the Deutscher Wetterdienst (DWD; German Meteorological Service, Offenbach). The authors SK and BA also acknowledge the funding from the DWD and the Hessian initiative for development of scientific and economic excellence (LOEWE) at the Biodiversity and Climate Research Centre (BiK-F), Frankfurt/Main.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: C. Simmer.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Krähenmann, S., Bissolli, P., Rapp, J. et al. Spatial gridding of daily maximum and minimum temperatures in Europe. Meteorol Atmos Phys 114, 151 (2011). https://doi.org/10.1007/s00703-011-0160-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00703-011-0160-x