Chaotic dynamics of a non-autonomous nonlinear system for a smart composite shell subjected to the hygro-thermal environment

Abstract

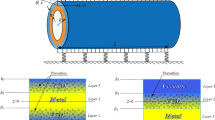
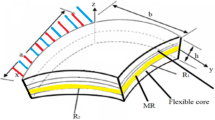
In this research, nonlinear dynamic behaviors of multiscale composites doubly curved shells have been investigated by employing multiple scales Perturbation Method. Three-phase composites shells with polymer/Carbon nanotube/fiber (PCF) according to Halpin–Tsai model have been assumed. The displacement- strain of nonlinear vibration of multiscale laminated doubly curved shells via higher order shear deformation (HSDT) theory and using Green–Lagrange nonlinear shell theory is obtained. The governing equations of composite doubly curved shell have been derived by implementing Hamilton’s principle and shell considered to be simply supported. For investigating correctness and accuracy, this paper is validated by other previous researches. Finally, bifurcation diagram, phase portraits and Poincare maps are investigated. The results indicate different dimensionless force; curvature ratio and kind of distribution pattern have strong influence on nonlinear vibration control of the composite multiscale doubly curved shell.

Appendix

Transformed shell principle coordinate can be expressed by:

$$ \begin{aligned} \bar{Q}_{{11}}^{n} &= Q_{{11}}^{n} cos^{4} \theta + 2\left( {Q_{{12}}^{n} + 2Q_{{66}}^{n} } \right)sin^{2} \theta cos^{2} \theta + Q_{{22}}^{n} sin^{4} \theta \hfill \\ \bar{Q}_{{12}}^{n} &= (Q_{{11}}^{n} + Q_{{22}}^{n} - 4Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{12}}^{n} (sin^{4} \theta + cos^{4} \theta ) \hfill \\ \bar{Q}_{{22}}^{n} &= Q_{{11}}^{n} sin^{4} \theta + 2(Q_{{12}}^{n} + 2Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{22}}^{n} cos^{4} \theta \hfill \\ \bar{Q}_{{66}}^{n} &= (Q_{{11}}^{n} + Q_{{22}}^{n} - 2Q_{{12}}^{n} - 2Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{66}}^{n} (sin^{4} \theta + cos^{4} \theta ) \hfill \\ \bar{Q}_{{44}}^{n} &= Q_{{44}}^{n} cos^{2} \theta + Q_{{55}}^{n} sin^{2} \theta \hfill \\ \end{aligned} $$

(74)

where ${\overline{Q}}_{ij} \left(i,j=\text{1,2},\text{3,4},\text{5,6}\right)$ presented the transformed reduce stiffness modulus.

Motions equations of multiscale composite shell can be expressed in terms of u, v, w, ${\phi }_{x}, {\phi }_{y}$ displacements are obtained by substituting Eqs. (19a–19c) into (33a–33d) yields:

$$ \begin{aligned} & A_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) + A_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + B_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + B_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) - s_{1} E_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad + B_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} E_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{1}{{R_{1} }}\left[ {\hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) + \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right)} \right]\\ & \quad + \frac{{s_{1} }}{{R_{1} }}\left[ {E_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right)} \right. \\ & \quad + E_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + F_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + F_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + F16\left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{11}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) - s_{1} H_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + F_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) + F_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad \left. { - s_{1} H_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right)} \right] \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right) \\ \end{aligned} $$

(75a)

$$ \begin{aligned} & A_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + B_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{12}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + A_{{22}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + B_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }}} \right) - s_{1} E_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{1}{{R_{2} }}\left[ {\hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) + \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right)} \right] \\ & \quad + \frac{{s_{1} }}{{R_{1} }}\left[ {E_{{12}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right)} \right. + E_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + E_{{22}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) \\ & \quad + F_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + F_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{y} }}{{\partial \partial y^{2} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) - s_{1} H_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + F_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + F_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad \left. { - s_{1} H_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right)} \right] \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right) \\ \end{aligned} $$

(75b)

$$ \begin{aligned} & \hat{A}_{{45}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial x}}} \right) + \hat{A}_{{55}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad + \hat{A}_{{44}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) + \hat{A}_{{45}} \left( {\frac{{\partial \phi _{x} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial y}}} \right) \\ & \quad + s_{1} \left[ {E_{{11}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x^{3} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }}} \right)} \right. \\ & \quad + E_{{12}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial x^{3} }} + \frac{{\partial ^{3} u_{0} }}{{\partial x^{2} \partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + F_{{11}} \frac{{\partial ^{3} \phi _{x} }}{{\partial x^{3} }} \\ & \quad + F_{{12}} \frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + F_{{16}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{3} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}}} \right) - s_{1} H_{{11}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{3} }} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{4} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x^{3} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{3} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial x^{3} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + E_{{12}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x\partial y^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + E_{{22}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y^{3} }} + \frac{1}{{R_{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + E_{{26}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} + \frac{{\partial ^{3} u_{0} }}{{\partial y^{3} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + F_{{12}} \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{2} \partial x}} + F_{{22}} \frac{{\partial ^{3} \phi _{y} }}{{\partial y^{3} }} + F_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{3} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x\partial y^{2} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{3} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial y^{3} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + 2E_{{16}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial y\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + 2E_{{66}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }} + \frac{{\partial ^{3} u_{0} }}{{\partial y^{2} \partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + 2F_{{16}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}}} \right) + 2F_{{66}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad - 2s_{1} H_{{16}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{3} \partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial y\partial x^{2} }}} \right) - 2s_{1} H_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{4} w_{0} }}{{\partial x\partial y^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }}} \right) \\ & \quad \left. { - 2s_{1} H_{{66}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y\partial x^{2} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial y^{2} \partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x\partial y^{2} }}} \right)} \right] \\ \end{aligned} $$

$$ \begin{aligned} & \frac{\partial }{{\partial x}}\left( {\frac{{\partial w_{0} }}{{\partial x}}\left\{ {A_{{11}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right)} \right.} \right. + A_{{12}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \left( {\frac{1}{2}\frac{{\partial w_{0} }}{{\partial y}})^{2} } \right)} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{11}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) \\ & \quad + B_{{16}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad \left. { - s_{1} E_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right)} \right\} \\ & \quad + \frac{\partial }{{\partial y}}\left( {\frac{{\partial w_{0} }}{{\partial x}}\left\{ {A_{{16}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}^{2} } \right)} \right) + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right.} \right. \\ & \quad + A_{{66}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) \\ & \quad + B_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right)\left. { - s_{1} E_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right)} \right\} \\ & \frac{\partial }{{\partial x}}\left( {\frac{{\partial w_{0} }}{{\partial y}}\left\{ {A_{{12}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right) + A_{{22}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right.} \right. \\ & \quad + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) - s_{1} E_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right) \\ & \quad - \frac{1}{{R_{2} }}\left\{ {A_{{12}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right) + A_{{22}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right. \\ & \quad + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{{\partial u_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) - s_{1} E_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad \left. { - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right)} \right\} + q^{{hyg}} \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} w_{0} }}{{\partial t^{2} }}} \right) + s_{1}^{2} \bar{I}_{6} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) + s_{1} \left[ {\bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{{\partial v_{0} }}{{\partial y}}} \right)} \right] \\ & \quad - \bar{J}_{4} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ \end{aligned} $$

(75c)

$$ \begin{aligned} & \hat{B}_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{B}_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{D}_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + \hat{D}_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + \hat{B}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \hat{D}_{{16}} \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \hat{D}_{{26}} \frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \hat{D}_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - \hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) - \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right) \\ & \quad = \bar{J}_{1} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} + \bar{K}_{2} \frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }} - s_{1} \bar{J}_{4} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right) \\ \end{aligned} $$

(75d)

$$ \begin{aligned} & \hat{B}_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{D}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + \hat{D}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + \hat{D}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{22}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ \end{aligned} $$

(75e)