Abstract
In the realm of MEMS piezoelectric vibration energy harvesters, cantilever-based designs are by far the most popular. For cantilever-based vibration energy harvesters, the active piezoelectric area near the clamped end is able to accumulate maximum strain-generated-electrical-charge, while the free end is used to house a proof mass to improve the power output without compromising the effective area of the piezoelectric generator since it experiences minimal strain anyway. However, despite while other contending designs do exist, this paper explores five selected micro-cantilever (MC) topologies, namely: a plain MC, a tapered MC, a lined MC, a holed MC and a coupled MC, in order to assess their relative performance as an energy harvester. Although a classical straight and plain MC offers the largest active piezoelectric area, alternative MC designs can potentially offer larger deflection and thus mechanical strain distribution for a given mechanical loading. Numerical simulation and experimental comparison of these 5 MCs (0.5 µm AlN on 10 µm Si) with the same practical dimensions of 500 µm and 2000 µm, suggest a cantilever with a coupled subsidiary cantilever yield the best power performance, closely followed by the classical plain cantilever topology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cantilever-based topologies are the incumbent design of choice within the field of piezoelectric vibration energy harvesting (VEH) (Beeby et al. 2006; Erturk and Inman 2011; Priya and Inman 2009), especially for the MEMS (micro-electromechanical system) iterations of these harvesters (Jeon et al. 2005; Marzencki et al. 2007; Renaud et al. 2008; Andosca et al. 2012). This is primarily because the active piezoelectric area near the clamped end is able to accumulate strain energy, while the free end can house a proof mass without significantly compromising the effective area of the piezoelectric generator since it experiences minimal strain anyway.
While a number of different examples of micro-cantilever (MC) designs for MEMS piezoelectric vibration energy harvesters have been previously explored (Erturk and Inman 2011; Priya and Inman 2009), the most popular design is based on the classical rectangular plain MC topology (Roundy and Wright 2004) with variations in design usually driven by process constraints rather than design objectives. Nonetheless, alternative designs such as tapered cantilevers (Glynne-Jones et al. 2001) have been explored in an attempt to achieve equal distribution of bending strain along the cantilever length.
This paper expands on a previously reported conference paper (Jia and Seshia 2014) and demonstrates that systematic modifications in the specific topology of piezoelectric MEMS cantilever energy harvesters can result in significant differences in the output power response. The work presented here adds to the existing conference paper with the inclusion of further details on design and simulation and experimental results.
While the design objective is to maximise the average strain energy experienced by the harvester for a given mechanical loading, the total available piezoelectric (mechanical-to-electrical) transducer area is likely to be compromised in order to accommodate the additional design complexities. Five different selected cantilever-based topologies are numerically and experimentally compared in an attempt to rank the effectiveness and power performance of each design variation for the purpose of VEH.
2 Design and modelling
2.1 Design
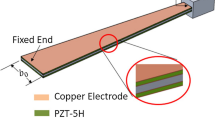
Five different topologies were investigated as shown in Fig. 1. All of the designs had the same overall practical dimensions (2 mm by 0.5 mm). Therefore, this enables relative power performance comparison for a given design area. The designs were fabricated through PiezoMUMPs (MEMSCAP 2013), which used a 0.5 µm aluminium nitride (AlN) on 10 µm doped silicon micro-machining process as shown in the stack of material in Fig. 2. The stack of materials primarily include 10 µm of doped Si device layer that doubles as the bottom electrode, 0.5 µm of AlN layer and 1.02 µm of top metal layer made up of 20 nm Cr and 1000 nm Al.
Apart from the classical plain and the tapered designs, the other topologies included: a primary MC coupled with a subsidiary MC based on (Tang and Li 2013), a MC with etched holes throughout the surface as a means of stiffness reduction inspired by Sevilla et al. (2013), as well as a MC formed by multiple parallel thin beams strongly coupled at the end.
A summary of the 5 topologies, the employed acronyms and optimised dimensions according to COMSOL solid mechanics simulation are listed as the following,
-
MCI: plan micro-cantilever (MC) with 2000 µm length and 500 µm width.
-
MCT: tapered MC with trapezium of 500 µm and 100 µm sides, and 1000 µm length.
-
MCL: lined MC with thirteen 30 µm wide beams separated by 10 µm gap, connected together at the clamped end and the free end.
-
MCH: holed MC with 5 µm square holes separated by 25 µm gap in both length and width.
-
MCC: coupled MC with 1375 µm long and 180 µm wide subsidiary cantilever coupled onto a primary cantilever with 150 µm wide side beams.
The motivation for the tapered MC was to enable roughly equal distribution of strain along the cantilever length; while the rationale behind lined, holed and coupled MC were to reduce the spring stiffness through various design complexities.
The natural frequency \(\omega _{0}\) for a plain cantilever is widely defined by Eq. 1 (Thomson 1998).
where, k is the stiffness constant, m is the effective seismic mass of the resonator, E is the elastic modulus, w is the width of the cantilever, h is the effective thickness of the composite beam, \(m_{b}\) is the mass of the beam, \(m_{l}\) is the end mass if applicable (not used here), and l is the effective length of the cantilever resonator.
As the design variations of MCT, MCL, MCH and MCC are based on etching features from the same design space of MCI, the plain MCI has the largest beam mass. However, significant portions of MCT and MCC constituents as proof mass rather than beam mass. Table 1 presents the estimated beam mass, estimated effective seismic mass of the cantilevers and the thus derived spring constants for the 5 micro-cantilevers.
It can be seen that MCT, MCL and MCC all have notably reduced spring stiffness compared to MCI, while the etched holes design in MCH is not predicted to yield noticeable stiffness reduction over MCI. The main contributing factor to the slight stiffening of MCH compared to MCI is the slight decrease in the effective mass of MCH. The natural frequency (Eq. 1) for the cantilever variants can be fitted by altering the co-efficient for beam mass while computing the effective seismic mass.
2.2 Optimisation
The dimensions employed for the tapered cantilever MCT, cantilever made up of thin beams MCL, cantilever with etched holes MCH and coupled cantilever MCC were chosen according to strain distribution optimisation from COMOSL solid mechanics simulation. Therefore, each of the designs are optimal representations for their respective topologies.
2.2.1 MCT
The rationale of the tapered design was to achieve even distribution of strain along the cantilever length. The angle of the tapered MC to achieve this, illustrated in Fig. 3, was determined through COMSOL simulation of 1000 µm long and 500 µm wide (anchored end) beams with varying degrees of taper. The FEA simulation result is presented in Fig. 4. In this case, the maximum angle of taper possible was 14°, at which case the structure becomes a perfect triangle. At 0°, the structure is a perfect rectangle. While at any angles of taper in between, the cantilever is essentially a trapezium. Percentage of the angle of taper out of the maximum possible angle was also computed for easier comparison.
From Fig. 4e, it can be seen that even strain distribution is achieved when the angle of taper is around 80 % of the total possible angle. Additionally, the length of the active cantilever beam was optimised through COMSOL simulation to maximise the recoverable strain energy. As can be seen from Fig. 5, shorter active beam length gives rise to higher average strain. This is because a larger proportion of the total 2 mm length is diverted to acting as the proof mass. However, shorter active length also results in smaller active transduction area.
The product of average strain and active area from the simulation result suggests that a tapered cantilever with an active length of 1000 µm is optimal. Therefore, coupled with the tapered angle selection, the dimensions of the MCT trapezium shown in Fig. 1b was thus computed.
2.2.2 MCL
The width of the silicon beams, width of the active piezoelectric area and the spacing between each beams for MCL are detailed in Fig. 6. These width dimensions for MCL were partially determined by the restrictions of the design rules of the fabrication process, which required 5 µm minimum spacing between silicon layer and the piezoelectric layer, as well as 4 µm of spacing between the piezoelectric layer and the metal layer. Therefore, for a beam with a width of 30 µm, only 12 µm width at the centre are active piezoelectric transduction region where the AlN layer is fully sandwiched between top electrode and bottom doped silicon. The 9 µm on either ends are used up to accommodate the metal-to-piezo clearance and piezo-to-silicon clearance.
Strain optimisation was carried out for beams with varying width: 20–35 µm, as shown in Fig. 7. Due to the presence of a total 18 µm clearance requirement as mentioned above, the active piezoelectric width was therefore between 2 and 17 µm respectively for the investigated range. The spacing between each beams was fixed at 10 µm for the various width iterations. A summary of selected beam iterations can be seen in Table 2. It can be seen that thinner beams are able to yield higher average strain. However, due to the fast diminishing active piezoelectric area, the total accumulated strain is significantly lower for thinner beams. An optimal value was found to be around individual silicon beam width of 30 µm.
2.2.3 MCH
The same metal-to-piezo and piezo-to-silicon clearance design rule for the fabrication process as mentioned for MCL, also restricted the active piezoelectric area for the holed MC. The ratio of etch holes and gap were determined to ensure relatively significant etch holes while still allowing sufficient spacing in order to accommodate the above mentioned clearance requirements.
Figure 8 illustrates the simulated average strain over active transducer area for equally spaced etch holes varying from 1 to 10 µm. This translates to active piezoelectric transducer region varying from 4 to 34 % of total available area respectively. Although increasing etch hole size helps to increase the attainable average strain per unit loading, the active transducer area decreases at a significantly faster rate due to the presence of the process clearance restrictions.
Figure 9 shows the zoomed in layout of MCH, showing the selected dimensions of the etched holes and the active piezoelectric regions around the holes. As it can be seen, each etch hole is surrounded by 9 µm of clearance on all four directions.
2.2.4 MCC
Through varying the width of the primary beams on either sides, strain distribution and active area were optimised. The range surveyed included primary beams of 100 to 200 µm width as summarised in Table 3. Figure 10 illustrates the optimal width of the primary beams.
As the primary beams are reduced in width, its stiffness decreases and coupled beam increases in size. For the fundamental mode of resonance, the coupled centre subsidiary beam acts as a proof mass. Both the width and mass factors help to improve the average strain experienced by the less wide primary beams. However, the reduction in width also imply a reduction in active transduction area. Therefore, as can be seen from Fig. 10, when primary beams are about 150 µm in width, there is a maximum integrated average strain over the active transducer area.
2.3 Model
Finite element analysis for static loading was used to approximate the strain response of the cantilever beams at a particular amplitude of the equivalent dynamic response, taking into account the mechanical quality factor of the resonator. Figure 11 illustrates the first principal strain response for the MCs when subjected to a loading of 1.5 mN.
COMSOL solid mechanics stationary simulation showing strain distribution for the 5 micro-cantilevers when subjected to a loading of 1.5 mN. Left hand side mass resembles the anchor to the substrate. Either surface or slice (1 slice per µm) 3D plot was chosen for each figure depending on the graphical clarify
It can be seen that tapered MC had approximately similar bending strain gradient across its active piezoelectric transduction area, while all the other MCs exhibited strain concentration near the clamped end. Figure 12a graphically illustrates the strain distribution along the cantilever length for the 5 MCs at this loading condition. MCI has the lowest peak strain near the clamped end, MCT has the roughly flat strain response as intended, MCH has fluctuating strain distribution due to its local features, while MCL and MCT have higher strain peaks.
Figure 12b shows the average strain integrated across the strain distribution for the 5 MCs. The classical MCI fares the lowest, while MCT and MCC take the lead. While mechanical strain maximisation across the cantilever surface for a given input forcing is an important design metric, there is a trade-off involved in sacrificing the active piezoelectric area to accommodate the additional design complexity, as illustrated in Fig. 12c.
The maximum power extractable from the simulated strain response can be calculated by computing the average electric charge generated by Eq. 2 and the power extractable across an ideal impedance given by Eq. 3.
where, q is the charge generated, \(d_{31}\) is the piezoelectric charge constant in the 31 mode, \(\varepsilon _{av}\) is the average strain experienced by the piezoelectric transducer, E is the elastic modulus of the piezoelectric material and \(a_{pz}\) is the active piezoelectric area.
where, P is the peak power, \(\omega\) is the frequency, \(h_{p}\) is the thickness of the piezoelectric layer, \(\varepsilon _{0}\) is the permittivity of free space and \(\varepsilon _{r}\) is the dielectric constant of the piezoelectric material.
Figure 12d illustrates the resulting calculated power based on the simulated strain values. Despite having the highest average strain as seen in Fig. 12b, MCT is only ranked 4th in terms of the predicted power output. MCI fared relatively well due to its large piezoelectric area and is only outperformed by MCC. MCL is consistently ranked 3rd in terms of average strain, piezoelectric area as well as power output. MCH, having the least active area due to the need to provide clearance for top metal layer around each individual hole features, is predicted to yield by far the least extractable power for the same loading.
MCC ranks the second in terms of average strain and retains the same ranking for active piezoelectric transducer area (two side beams, to harness the strain from the first transverse mode response of the primary cantilever) due to minimal design complexity. These factors contributes to the high power prediction for MCC. Therefore, the systematic optimisation of the power performance is primarily a compromise between the average mechanical strain and the active piezoelectric area.
3 Experimental
3.1 Apparatus
Figure 13 shows the micrographs for the fabricated devices. The active piezoelectric area (electrodes sandwiched piezoelectric region) for MCH was further diminished due to over-etch of the top metal layer around the individual hole features as shown in Fig. 13f. However, the stiffness reduction intended was minute by comparing the natural frequency of MCI and MCH. Due to the lack of local fine features for MCI, MCT and MCC, they did not suffer as significantly from the over-etch issue compared to MCH and MCL.
The experimentally measured natural frequency is compared to the FEA simulated eigenfrequencies in Table 4, showing minor deviations expected within fabrication tolerances. MCL and MCH exhibited relatively larger deviations at around 6.5 %, potentially due to the over-etch of the metal, piezoelectric and silicon layers around the fine topological features for these two designs. MCI, MCT and MCC on the other hand, did not have extensive fine local features.
Experimental verification was carried out for both the direct and the inverse piezoelectric response. Through electrically driving the piezoelectric transducers, the mechanical motion can be measured by a laser doppler vibrometer to characterise the electrical-to-mechanical responsiveness for the 5 MCs. On the other hand, by exciting the prototypes on a mechanical shaker and measuring the voltage output across matched resistive loads at their resonant frequencies, the mechanical-to-electrical responsiveness and their relative power performance can be determined.
3.2 Results
Figure 14 presents the measured frequency domain displacement response for the free end tip of the 5 MCs when subjected to an electrical drive signal. The input is a periodic chirp of 250 mV across the bandwidth of 1–100 kHz, except for MCH, which was subjected to 1 V periodic chirp due to its low and noisy responsiveness at lower excitation levels.
Displacement Bode plot of the 5 AlN on Si micro-cantilevers (MC) scanned by laser doppler vibrometer and subjected to a periodic chirp of 250 mV\(_{ac}\) across the displayed frequency span except for MCH, which was subjected to 1 V\(_{ac}\) due to its extremely low responsiveness compared to the noise floor. The plots shown are the differences between a typical signal and a typical noise floor data
The inherent noise floor within the measuring environment, shown in Fig. 14f (measured from an anchored point), was subtracted from the response plots of the 5 MCs in Fig. 14. It should also be noted that the 1st transverse mode of the subsidiary cantilever of MCC is not included as the measurements compared in this figure is taken from the free end tips, which corresponds only to the peak displacement from the primary cantilever.
Also it can be noted, as shown in Table 5, the quality factor for MCC and MCT is notably higher than MCI. Higher quality factor would contribute to higher responsiveness of the devices.
The mechanical response as a function of electrical drive amplitude for the five topologies is compared in Fig. 15. MCC ranks first, closely followed by MCI. MCL and MCT takes the 3rd and 4th spots respectively and MCH performs the worst. This is in agreement with the ranking of the 5 MCs established in Sect. 2.
Comparison of the laser doppler vibrometer measured displacement response of the tip of the 5 MCs free end when driven by varying amplitudes of AC voltage at their respective natural frequencies. For a given electric drive amplitude, coupled MC yielded the most significant mechanical response, followed by plain MC, lined MC, tapered MC and holed MC in descending order
Table 6 and Fig. 16 show the measured power output for the 5MCs when subjected to resonant sinusoidal vibrational input on a mechanical shaker. From Fig. 16, power values for MCH driven at lower acceleration levels were experimentally not measurable. The matched load resistance and natural frequencies for the various prototypes are: 0.3 M\(\Omega\) at 3688 Hz for MCI, 1 M\(\Omega\) at 2938 Hz for MCT, 0.6 M\(\Omega\) at 3375 Hz for MCL, 1.2 M\(\Omega\) at 3531 Hz for MCH and 0.6 M\(\Omega\) at 2891 Hz for MCC.
Comparison of the experimentally measured power resonant power response of the 5 MCs when driven at their respective natural frequencies. The order of mechanical-to-electrical power responsiveness is in agreement with the laser vibrometer measured electrical-to-mechanical responsiveness: coupled MC being the most responsive, followed by plain MC, lined MC, tapered MC and holed MC. Power response below ~20 pW could not be practically measured
The experimentally measured power output at 3 g of input acceleration for the 5 devices are: 1.01 nW for MCI, 0.45 nW for MCT, 0.7 nW for MCL, 0.03 nW for MCH and 1.35 nW for MCC. Thus, the power response ranking from mechanical input is in agreement with the power output ranking established in Sect. 2, as well as the electrical-to-mechanical response measured by vibrometer. This validates the optimised compromise in topology between maximising strain and transducer area. Additionally, factors such as quality factor, difference in capacitance and impedance as well as resonant frequencies also contribute to the variations in performance across the 5 MCs.
MCC, apart from faring the best in terms of the 1st transverse mode response, also further benefits from dual frequency sensitivity (from both its primary and subsidiary cantilevers), whereas the other 4 MCs only possess a single fundamental transverse mode. Though, the power response of the subsidiary cantilever is largely diminished compared to the primary cantilever of MCC, it is still more preferable than higher order resonant modes. This is because at higher order modes, with multiple nodes and anti-nodes, strain cancellation takes place and the power output is severely compromised.
4 Conclusion and future work
Five cantilever-based topologies have been investigated for the purpose of vibration energy harvesting. Coupled micro-cantilevers ranked the highest in terms of power performance and was closely followed by the classical plain cantilever topology. While the tapered, lined and holed cantilevers all experienced higher average mechanical strain than the plain cantilever for a given loading, they performed worse due to the smaller active piezoelectric area. Therefore, a compromise is required while optimising designs between the maximisation of mechanical strain energy accumulation and the total active piezoelectric transducer area.
Future work can investigate the influence of scaling associated with various topologies. This is particularly useful when scaled upwards for topologies such as the lined or holed micro-cantilevers, as the ratio of the active piezoelectric area to the total design area increases. Furthermore, the relative effect of the addition of proof mass to various topologies can also be explored.
References
Andosca R, McDonald TG, Genova V, Rosenberg S, Keating J, Benedixen C, Wu J (2012) Experimental and theoretical studies on mems piezoelectric vibrational energy harvesters with mass loading. Sens Actuators A 178:76–87 [Online]. doi:10.1016/j.sna.2012.02.028
Beeby S, Tudor M, White N (2006) Energy harvesting vibration sources for microsystems applications. Meas Sci Technol 17(12):R175–R195
Erturk A, Inman D (2011) Piezoelectric energy harvesting. Wiley, New Delhi
Glynne-Jones P, Beeby S, White N (2001) Towards a piezoelectric vibration-powered microgenerator. IEE Proc Sci Meas Technol 148(2):68–72 [Online]. doi:10.1049/ip-smt:20010323
Jeon Y, Sood R, Jeong J, Kim S (2005) Mems power generator with transverse mode thin film pzt. Sens Actuators A 122(1):16–22 [Online]. doi:10.1016/j.sna.2004.12.032
Jia Y, Seshia AA (2014) Comparison of five topologies of cantilever-based mems piezoelectric vibration energy harvesters. In: Journal of Physics: Conference Series, vol 557, p 5
Marzencki M, Ammar Y, Basrour S (2007) Design, fabrication and characterization of a piezoelectric microgenerator including a power management circuit. In: Proceedings of Dans Symposium on Design, Test, Integration and Packing of MEMS/MOEMS, Stresa, Italy, 25–27 April 2007, p 4 [Online]. arXiv:0802.3044
MEMSCAP (2013) Piezomumps [Online]. Available: http://www.memscap.com/products/mumps/piezomumps
Priya S, Inman D (2009) Energy Harvsting Technologies. Springer, New York
Renaud M, Karakaya K, Sterken T, Fiorini P, Hoof CV, Puers R (2008) Fabrication, modelling and characterization of mems piezoelectric vibration harvesters. Sens Actuators A 145–146:380–386 [Online]. doi:10.1016/j.sna.2007.11.005
Roundy S, Wright P (2004) A piezoelectric vibration based generator for wireless electronics [Online]. doi:10.1088/0964-1726/13/5/018
Sevilla G, Rojas J, Ahmed S, Hussain A (2013) A wide-band piezoelectric energy-harvester for high-efficiency power generation at low frequencies. In: IEEE Transducers, 16–20 June 2013, pp 2636–2639 [Online]. doi:10.1109/Transducers.2013.6627347
Tang Q, Li X (2013) A wide-band piezoelectric energy-harvester for high-efficiency power generation at low frequencies. In: IEEE Transducers, 16–20 June 2013, pp 697–700 [Online]. doi:10.1109/Transducers.2013.6626862
Thomson W (1998) Theory of vibration with applications, 5th edn. In: Dahleh M (ed) Prentice-Hall Inc, New Jersey
Acknowledgments
This work was supported by EPSRC (Grant EP/L010917/1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jia, Y., Seshia, A.A. Five topologies of cantilever-based MEMS piezoelectric vibration energy harvesters: a numerical and experimental comparison. Microsyst Technol 22, 2841–2852 (2016). https://doi.org/10.1007/s00542-015-2599-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00542-015-2599-z