Abstract
We present 77 new granite whole-rock analyses from the Qattar and Gharib areas, Eastern Desert, Egypt. Both areas include a “normal” granite and either a hypersolvus (Gharib) or an almost plagioclase-free granite (Qattar) enriched in fluorite. According to earlier results, F influences element distribution in granitic melts forming complexes with specific elements as Nb, Ta, Ga, Hf, Th, Zn, Sn, whereas F excludes Ba and Sr. We use principal component analyses to split the granite into chemical groups allowing an unbiased study of the inter-group element distribution. This adds the heavy REEs and Y to the earlier lists of elements with an affinity for F. The light REEs show a decreasing affinity with decreasing atomic mass; fluorine separates Sm from Nd, whereas Zr follows La. Opposite to some, but in accordance with other earlier results, the ratio Nb/Ta is higher in the fluorite-enriched than in the other granite. Weak tetrad effects are present. Zircon in the hypersolvus granite is high in common lead. We suggest F to be instrumental for separating Pb2+ from Pb4+. Two hypotheses may explain the occurrence of the two contrasting granites: they have either different sources, or they are co-magmatic, but the magma was split into two discrete types. We apply the second hypothesis as our working hypothesis. The liquidus has a gentler slope with pressure than the diapir requiring crystallisation to be most important in the lower part of the magma chamber. Our hypothesis suggests that globules of magma, enriched in volatile components, form during crystallisation due to slow diffusion rates in the crystallizing magma. Elements accompanying F are distributed into this magma batch, which has a lowered density and viscosity than the rest of the magma due to its increased contents of volatile components. A mushroom-formed diapir rises, forming the hypersolvus (or almost plagioclase-free) granite. Due to an edge effect, it is concentrated close to the wall of the magma chamber. The size and form of the outcropping granite depend on the intersection of the diapir with the erosion surface. Fluorine only makes it possible to follow the process. The model may be generalised to explain the diversification of non-F enriched granite, since the buoyancy of a magma batch several thousand m3 in size has a much larger impact on the system than the small negative buoyancy of crystals or small crystal aggregates. A-type granite classified merely from its trace element content may form from separated F-enriched magma batches. This may be the reason for their high frequency in the Eastern Desert.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Several aspects of granite evolution are still contradictory and poorly understood. The mineralogical definition of granite limits the variation of its major element composition, whereas the trace elements often show larger variations. A number of various mechanisms are suggested to explain trace- and major-element differences in granite:
-
i.
Crystal differentiation is often advanced to explain compositional variation of magmatic rocks. After having reached a near eutectic composition, thermodynamic laws prevent melts to evolve further, and they restrict any evolution of melts close to a minimum melting composition. Thus, if crystals continue to separate after this stage, major minerals separate in granitic proportions.
-
ii.
For a given source rock, limited major- and trace element variation can be explained by varied degrees of melting.
-
iii.
Protolith heterogeneities explain significant regional-scale compositional differences (for a recent example, see Lindh 2014), but if applied to single intrusions restrictions are imposed both on the size of these heterogeneities and on homogenisation following melting.
-
iv.
Mixing or, due to viscosity and temperature differences, rather mingling of melts is often suggested as explanations.
-
v.
Magmas may split due to volatile enrichment during the crystallisation process followed by separation of the magmas due to their different densities and viscosities (Lindh 2012). This is a non-equilibrium process; there is no need for liquid immiscibility.
In the present paper, we present new petrological, geochemical and chronological data from the post-orogenic fluorite-bearing Qattar and Gharib granites in the Northern Eastern Desert Terrane, Egypt (Fig. 1). The reason for our choice of study areas is the co-occurrence of two granites with well-defined chemical compositions. The present data comprise whole-rock geochemical data, Sm–Nd isotope data and a few U–Pb dating on zircon. Recently, Mahdy et al. (2015) reported whole-rock analyses of granite from the Qattar area, and Mohamed (2012) reported inter alia chemical analyses from the Gharib area. We include these results in our calculations. For the Rare Earth Elements (REE) reported by Mohamed (2012), we merely incorporate data from the more accurate, inductively coupled plasma mass spectrometry (ICP-MS) technique (Table 3).
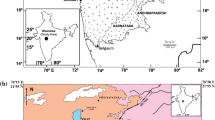
a Qattar map; simplified from El Sayed et al. (2003), the northern part is modified according to El Dabe (2004). The central and parts of the southern parts are based on the map of Mahdy et al. (2015). The Reddah, Saalat and Um-Nafic granites belong to the granite/granodiorite group. This group is considered as a subsolvus granite; same grey shade. b Gharib map; simplified and slightly modified from Abdel-Rahman and Martin (1990). The numbers refer to sample numbers; the leading Q (Qattar, a) and G (Gharib, b) are omitted. Note different scales!
We discuss the processes outlined above. Our results suggest that the mechanism (v) explains much but not all of the observed variation. The magma separation occurs early during the crystallisation. Thus, the amount of crystals in the magma is limited. The residual volatile-enriched melt is extracted and concentrated at one or a few parts in the magmatic body during the final stage of crystallisation (for details see “Discussion: Outline of our model”). For the rocks in our study area, we focus on modifications introduced by increased amounts of F, but in the final part of the discussion, we point out that our model is not limited to F-enriched rocks.
Geological setting
The Eastern Desert terranes belong to the youngest parts of the Arabian-Nubian Shield (Johnson et al. 2011). Typical is silica-rich magmatism, comprising different types of granitoids. These seem to change from older Ca-enriched rocks, including tonalite–trondhjemite–granite suites, to younger Al-enriched granitic rocks (Johnson et al. 2011); the younger group is late- to postorogenic. This magmatism seems to be quasi-continuous in the approximate time-span 660–540 Ma (see compilation by Johnson et al. 2011). Lundmark et al. (2012) recognised six tightly spaced granitic pulses in the Central Eastern Desert: (1) 705–680 Ma; (2) 660 Ma; (3) 635–630 Ma; (4) 610–604 Ma; (5) 599–590 Ma; and (6) 550–540 Ma. They consider the first three pulses as synorogenic, the pulses 4 and 5 to record exhumation of mid-crustal gneisses and pulse 6 to postdate the orogeny. They suggest that their scheme may be extended to the whole Eastern Desert. The ratio of younger granite to older granitoid increases from 1:4 in the Southern Eastern Desert terrane to approximately 1:1 in the Northern terrane (Stern 1979) and 12:1 in Sinai (Bentor 1985).
The younger group mostly forms small, scattered intrusions (≈ 1–10 km2) making up approximately 16% of the basement in the Eastern Desert (Hassan and Hashad 1990). Granite with a composition close to the minimum-melt composition totally dominates this group. The younger granite is calc-alkaline to mildly alkaline with an I-type affinity. Many intrusions are classified as A-type granite (e.g. Abdel-Rahman and Martin 1990; Jahn et al. 1993); the abundance of A-type granite is remarkably high (Stoeser 1986; Johnson et al. 2011).
We base our sampling on existing maps (El Sayed et al. 2003; El Dabe 2004, 2010; Mahdy et al. 2015). However, these maps are not totally consistent with each other, due to inter alia different rock definitions. It is beyond the scope of this presentation to discuss these differences.
Our sampling area occurs close to the escarpments delimiting the Red Sea trough. Between our sampling area and the Red Sea coast, several hundred meters of Miocene sediments cover the basement. Sampling is performed in typical desert areas with high, often inaccessible, well-exposed peaks amid sandy plains and wadies with no exposures (Fig. 1).
Analytical methods
Based on petrographic studies, samples were selected for major and trace elements analysis. A few of these were analysed also for their isotopic composition. The samples were collected well away from sites of known hydrothermal alteration and/or mineralisation and checked for visible alterations.
Major elements were determined with the X-ray fluorescence technique (XRF) at the Mineralogical Department, Hamburg University using a Panalytical Magixpro instrument. The samples were ground and milled and then melted with lithium tetraborate. H2O+ (moisture) was determined as the weight loss after heating to 110 °C for three to 4 h, LOI was determined as the weight loss after heating the dry sample to 1000 °C during 3 h. The analyses were calibrated against recommended values for international rock standards. In addition, analytical precision was estimated from repeated analyses of ‘in-house’ standards. The results are reported in Table 1.
Trace elements were determined with the ICP-MS technique at the AcmeLabs, Vancouver according to their schemes 4B and 1DX. In addition to Acme’s quality control, the precision is calculated from more than fifteen analyses performed on two ‘in-house’ standards from the Geological Department, Lund University, Sweden. Results are reported in Tables 2 and 3. These tables include the estimated precision for each element; for low contents, the precision is less good.
For some elements in the present data set, we have results from both laboratories. The Ba results for the two analytical sets are displayed in Fig. 2. A small laboratory- and/or method-dependent difference is obvious from the equation in Fig. 2. Data from both laboratories also include Ce, Cu, Ga, La, Nb, Nd, Ni, Pb, Rb, Sr, Th, U, Y, Zn and Zr. The corresponding results for these elements are found in Table A, Online Appendix. In the present paper, we use our ICP data for these elements. According to Table A (Online Appendix) the following elements Ba, La, Sr, U, Zn, Ce, Ga, Nb, Ni, Rb, Y and Zr give consistent results for both methods (correlation coefficients > 0.9 comparing the XRF and ICP-MS data; cf Fig. 2). The regressed slope deviates slightly from one and the two data sets display small differences in absolute numbers. These small differences do not influence our conclusions. The X-ray results do not include all rare earth elements (REE). To obtain as consistent REE patterns as possible, we use the ICP-MS data for all the REEs. For the same reason, we use the ICP-MS data for all elements, where the results are similar (see above). We have three additional elements: Cu, Th and Zn for which two data sets exist. We report but do not discuss Cu and Zn, which are not essential for our model. The data set used for these elements is thus of no significance. We prefer the ICP data for Th since AcmeLab reports an accuracy of 0.5 ppm and the Hamburg university analyses are given without decimals.
Comparison of Ba data obtained with XRF (Hamburg University) and ICP-MS (AcmeLab). Note that the hypersolvus granite is totally confined to the lowermost part of the diagram and no other rock has a similarly low content of Ba (see inset). The linear correlation coefficient is 1.00. G16 is the only hypersolvus rock with > 100 ppm Ba. Almost identical diagrams could be displayed for Sr and Y. The inset shows a magnification for Ba < 100 ppm. For clarity, arfvedsonite and biotite hypersolvus granites are not separated in the inset (both marked with open rings). The regression equations for the other elements (incl. linear correlation coefficients), analysed by both laboratories, are displayed in Online Appendix, Table A
Whole-rock Sm–Nd isotope determinations were made at the Swedish Museum for Natural History in Stockholm. The samples were analysed on a Thermo Scientific Triton TIMS using total spiking with a mixed 147Sm/150Nd spike. Concentrations and ratios were reduced assuming exponential fractionation. Sm concentrations were determined in multicollector static mode on Re double filaments. The ratios were normalised to 149Sm/152Sm = 0.516747. Neodymium was also run in static mode on double Re filaments but using rotating gain compensation. The results are reported in Table 4.
Zircon analyses were performed at the Department of Geosciences at the Swedish Museum of Natural History, Stockholm and at GEUS, Copenhagen. In both cases, heavy minerals were separated using a Wilfley table at the Department of Geology, Lund University. The heavy-mineral residue was transferred to disposable Petri dishes and magnetic minerals removed with a hand magnet. Zircon crystals were hand picked directly from the final separate in the Petri dish.
In Stockholm, ID-TIMS (isotope dilution, thermal ionisation mass spectrometer) analyses of zircon were performed. The crystals were spiked with a 205Pb–233−236U tracer and digested in HF:HNO3. Lead and U were extracted by means of standard HCl anion-exchange columns and loaded together onto Re single filaments. The measurements were performed on a Thermo Scientific Triton TIMS. In sample Q6, Pb was measured in the static mode with 204Pb in the axial SEM ion counter and the other masses in the Faraday cups. The analyses of Q16 (except fraction 4) were measured by peak jumping on the ion counter due to smaller signals. Uranium was measured on the ion counter by peak jumping. The calculation of corrected isotope ratios and intercept ages and the drawing of the concordia plots were performed with the ISOPLOT program (Ludwig 2012). The total Pb blank for analyses including column chemistry is generally 1–3 pg and the U blank less than 1 pg. For some of the present analyses, the blanks appear higher. The mass fractionation for Pb is 0.10 ± 0.04% per a.m.u. Uranium mass fractionation was monitored and corrected for by means of the 233−236U ratio of the spike. All analytical errors are given as 2σ. The assigned composition of common Pb is calculated according to the Pb-evolution model of Stacey and Kramers (1975). The results are reported in Table 5.
In Copenhagen, U–Pb determinations of single zircon crystals were performed with the laser ablation-single collector-magnetic sectorfield-ICP-MS (LA-SF-ICP-MS) method. The analyses were performed on a Thermo Finnigan Element2 mass spectrometer coupled to a NewWave UP213 laser ablation system. The data were obtained by single-spot analyses with a spot diameter of 30 μm and a crater depth of approximately 15–20 μm. In a few cases, a spot diameter of 20 μm was used. For quality control, the Plešovice (Sláma et al. 2008) and M127 (Nasdala et al. 2008; Mattey 2010) zircon reference material was analysed. The data could not be reduced due inter alia to a high common lead of unknown age; thus, analytical precision is low, but cannot be specified in numbers. Representative Pb isotope results are reported in Table B, Online Appendix.
Petrographic description
Field and microscopy characteristics
The younger granites in both areas (Fig. 1) consist of chemically distinct groups but with a strictly granitic composition. Pegmatite occurs in rather small amounts mainly as small pods. In the Gharib area, Mohamed (2012) reported frequent pegmatite pods of a size less than 0.5 m in diameter.
The Gharib granite is fine grained at the roof level (Abdel-Rahman and Martin 1990), but its major part is coarse grained. One group of subsolvus and two types of hypersolvus granite occur: the arfvedsonite and the biotite hypersolvus granite (Fig. 1b). Coarse meso-perthite is a major mineral of the Gharib granites.
The two hypersolvus types comprise alkali-feldspar and quartz as major minerals. Biotite and amphibole occur in small amounts. In addition, apatite, allanite, fluorite and zircon are common accessories. In the arfvedsonite hypersolvus granite, fluorite and ilmenite are minor minerals and aenigmatite occurs as an accessory. Fluorite is normally associated with some of the mafic minerals. From its merely incipient cross-hatched twinning, K-feldspar appears incompletely ordered. Inclusions of K-feldspar, zircon and ilmenite occur in quartz crystals. The crystal sizes vary, and irregularly distributed mega-crysts up to 8 mm in diameter are frequent. The major petrographic difference between the two types is the occurrence of arfvedsonite in the one but not in the other. Arfvedsonite is locally altered to astrophyllite, chlorite, titaniferrous biotite and hematite. Abdel-Rahman (1992) reports high Nb contents (up to 5 wt% Nb2O5) in the astrophyllite. Fluorite is closely associated with arfvedsonite and quartz in the arfvedsonite group. Abdel-Rahman and Martin (1990) and Mohamed (2012) give more details.
The subsolvus Gharib granite macroscopically resembles the hypersolvus granite. The main difference is the high amounts of plagioclase and the low amounts of fluorite. Biotite dominates strongly over amphibole.
In all granite types, quartz occurs as macroscopically large rounded grains made up of several single crystals, probably former subgrains rotated into higher-angle contacts. The individual crystals show weak undulatory extinction. More details are given by Mohamed (2012).
In the Qattar area (Fig. 1a), two granite types occur. One of them is similar to the Gharib subsolvus granite. The other granite has a low content of plagioclase but it is not strictly hypersolvus. To retain a similarity in terminology, we denote this granite as essentially hypersolvus, even if this term is not very precise. Dyke rocks are rather frequent. Fluorite and quartz veins are common and in the hypersolvus granite associated with U-mineralisations (El Dabe 2010).
The essentially hypersolvus granite is dominated by rather coarse, often Carlsbader-twinned meso-perthite; cross-hatched twinning occurs but is merely incipient. It contains small amounts of albite-twinned plagioclase, often as inclusions in K-feldspar. Sometimes K-feldspar seems to replace the sparse plagioclase. Quartz of the same character as in the Gharib granite is a major mineral. Biotite and less frequently amphibole occur in small amounts. An important accessory is fluorite both as discrete crystals and as fracture fillings. In the fractures, unidentified minerals forming fibrous crystals occur. They are either opaque or deeply greenish with high birefringence.
The subsolvus Qattar granite is mostly light reddish and medium grained. It is dominated by K-feldspar, quartz and plagioclase. The quartz has the same character as described above. Biotite dominates strongly over amphibole. Incipiently cross-hatched twinned K-feldspar is perthitic, but to a lesser extent than in the hypersolvus variety. Plagioclase is zoned, sub- to anhedral and often sericitised. Fluorite is almost merely observed in small fractures. The difference in fluorite contents between the hyper- and subsolvus granite suggests a difference in the F content, since other potentially F-bearing minerals like biotite, amphibole and apatite only occur in small amounts. More details are given by El Dabe (2004, 2010).
A single thin section of these coarse-grained rocks cannot be representative of the rock. At thin-section scale, the ratio perthite/quartz varies considerably. Thus, all modal estimates are associated with large errors. CIPW estimates of the contents of mafic silicates in the hypersolvus rocks are between 3 and 4 wt%. This gives a relative statistical 2σ error of ± 30% (if determined by point counting, 1000 points) and assuming biotite and amphibole to occur in similar proportions a relative 2σ error approaching ± 50% for each of these minerals. Such determinations are inconclusive.
The granite/granodiorite group (Fig. 1a) is considered slightly older (El Dabe 2004) than the described granites; it is included in the subsolvus granite in Fig. 1a. The group consists of grey to greyish pink, medium-grained rocks, mainly composed of plagioclase, K-feldspar, quartz, biotite and hornblende. Titanite, zircon, allanite and apatite are the main accessories. Relicts of pyroxene are observed in a few thin sections. In descending order of age, El Dabe (2004) distinguished the Um-Salaat, El-Reddah, and Um-Nafic granites in the Qattar area (Fig. 1a). Table C (Online Appendix) displays a sample list.
Description of zircon
The majority of zircon crystals from both areas are strongly altered. The studied crystals from the older granodiorite–tonalite and grey granite group are better preserved than the others. They are prismatic with length/width ratios varying between ≈ 2:1 and > 5:1. In most cases, they are growth zoned, but in more altered crystals, the zonation may be destroyed. The crystals contain inclusions, which are dark in backscatter electron detector (BSE) images (Fig. 3a).
Backscatter electron images of separated zircon crystals. a Well preserved zircon from the sample WUE1 (older granodiorite–tonalite and grey granite, Gharib area), showing growth zonation and a possible core. b Zircon from the sample U3 (granite/granodiorite group, Qattar area) showing growth zonation cut by later growth. This crystal is not typical, but much better preserved than most crystals from this group; it shows the cutting of an inner zonation by an outer one. The typical crystals resemble that shown in c. c Typical zircon from the subsolvus Qattar granite (Q22a) with botryoidal alterations in the centre. d Totally destroyed zircon from the Gharib biotite hypersolvus group (Sample G24). Note BSE-white inclusions. In some crystals, the white inclusions occur as hundreds of small spots
Zircon crystals from the granite/granodiorite group (exemplified by US3; Fig. 3b) have length/width ratios normally between 2:1 and 3:1 but longer crystals occur. They are normally growth zoned, but in a few crystals, this zonation is cut by a younger zonation (Fig. 3b), or the crystal seems to have been eroded and afterwards started to grow again. Inclusions occur, which are dark in BSE images. Some alteration is common; in a few probable zircon crystals, the alteration has proceeded too far to allow a certain identification.
The subsolvus granite (e.g. Q22a, Fig. 3c) has zircons with an originally probably weakly developed growth zonation. Frequently, a diffuse alteration destroys this zonation. Sometimes this destruction is complete. This gives the crystals a mottled pattern in slightly different shades of grey in BSE images. Strong botryoidal alterations are common. The difference between this group and the granite/granodiorite group is minor (see also caption of Fig. 3b; the zircon in Fig. 3b is not typical).
Zircon crystals from the hypersolvus granite are extremely altered (Fig. 3d). In some crystals, it is possible to see reminiscences of a growth zonation, but normally this is obliterated. Almost all crystals are botryoidally altered sometimes along their edges, sometimes in their interiors. The lobes may grow together giving rise to “dome-and-basin” textures resulting in totally altered crystals. Sometimes the botryoidal lobes are destroyed by a more diffuse alteration. BSE images show light and dark inclusions in the crystals. Light inclusions in BSE images may comprise up to 40% of the crystals. Among the inclusions, fluorite containing U, Th, Y and REE in appreciable amounts may be mentioned. According to qualitative EDX (energy dispersive X-ray) analyses, homogenous looking BSE-light areas may have contents of Th reaching 13 wt%. Probably, this is due to unresolvable intergrowths of more than one phase. Uranium, Ca, Fe and Hf sometimes occur in contents above the detection limit of the EDX system. The used EDX system was an Oxford INCA EDS analyser unit with an SI-detector fitted to a Hitachi S3400N SEM. The analyses are merely qualitative to identify elements and to obtain an approximate indication of element ratios; no standards were used.
Results
Geochemical data
Major elements
All hypersolvus granites are strongly evolved; almost all have SiO2 contents above 75 wt% and K2O contents above 4 wt% (Table 1). The sample G2a is an exception; it is rather low in K2O but high in Na2O (Fig. 4a). The subsolvus granites, including the granite/granodiorite group, are less evolved and have a more varying composition than the hypersolvus granites. Even if differences in absolute numbers are small, means of the hyper- and subsolvus granite for all major elements except K are different at a remarkably high significance level (Table 1). The major element compositions reported by Mahdy et al. (2015) and by us are almost identical; we note small but significant differences for Fe and Al. Analyses of the hypersolvus Gharib granite reported by Mohamed (2012) are identical to the ones reported here.
PQ (a) and BQF (b) diagrams according to Debon and Le Fort (1983). P = K – (Na + Ca), Q = Si/3 − (K + Na + 2Ca), B = Fe + Mg + Ti, F = 555 − (Q + B), all expressed in millimoles. M13 and M14 plot outside the central area of field 3 (cf. G2a) in a and outside the area surrounded by the dashed curve in b. All other samples reported by Mahdy et al. (2015) plot in the area 3 in a and within the dash-lined area in b. For clarity, they are omitted from the plot. Numbers in bold refer to the field definitions of Debon and Le Fort (1983). 1 = tonalite/trondhjemite; 2 = granodiorite; 3 = monzogranite (adamellite); 4 = syenogranite (granite); 5 = quartz diorite/gabbro; 6 = quartz monzodiorite; 7 = quartz monzonite; 8 = quartz syenite; 9 = diorite/gabbro; 10 = monzogabbro/monzodiorite; 11 = monzonite: 12 = syenite. The area surrounded by the dashed curve is expanded to the right. The NW–SE ruled field refers to subsolvus granite and the shaded field to hypersolvus granite analysed by Abdel Rahman and Martin (1987, 1990) both from the Gharib area
In a PQ-diagram (Fig. 4a), all hypersolvus rocks, except G2a, plot within a restricted area as monzogranite (adamellite in the terminology of Debon and Le Fort 1983). The samples published by Mahdy et al. (2015) are numbered from M1 to M27 according to the order in their tables. Two samples from Mahdy et al. (2015), M13 and M14, plot slightly outside the main cluster; they are slightly lower in K2O than the other samples. The subsolvus rocks are monzogranitic or syenogranitic to quartz monzonitic. The low contents of Fe and especially Mg define all hypersolvus and most subsolvus granite samples as leuco-granite (Table 1, Debon and Le Fort 1983: B–A diagram, not shown here).
Chemical analyses published by Abdel-Rahman and Martin (1987, 1990) are different from our data (Fig. 4b). Thus, granites in the Gharib area seem to have a larger chemical variation range than reported by us. We have confidence in our data, since for a number of elements, two different laboratories have reproduced the results within close limits (Fig. 2, Table A, Online Appendix), and the data presented by Mohamed (2012) and Mahdy et al. (2015) are almost identical to ours (Fig. 4).
According to the classification by Liégeois and Black (1987), the hypersolvus rocks are alkaline, whereas almost all subsolvus rocks are calc-alkaline (Fig. 5). The analysed rocks are metaluminous to peraluminous, but two samples, G15a and b (arfvedsonite hypersolvus granite), plot slightly below the peralkaline boundary. We note that the majority of the Qattar hypersolvus rocks are peraluminous, whereas the majority of the Gharib hypersolvus rocks are metaluminous (Fig. 5). We consider this as an area-dependent but small difference. The samples reported by Mahdy et al. (2015) are generally slightly higher in Al2O3/(CaO + Na2O + K2O) than ours (Fig. 5; this depends on the slightly higher Al2O3 found by them). A t test confirms that the means are different: significance level 0.05 for the subsolvus and 0.001 for hypersolvus Qattar rocks. No rocks reported by us, but two samples (M13 and M14; cf. the PQ diagram, Fig. 4), reported by Mahdy et al. (2015) have Al2O3/(CaO + Na2O + K2O) > 1.1. This is the boundary ratio for rocks that may be classified as S-type granite (Chappell and White 1992). We have not succeeded to demonstrate any difference between the arfvedsonite and biotite hypersolvus groups in the Gharib area (Fig. 5).
Alumina-saturation diagram. The boundary I-type–S-type granite (Al/(Ca + Na + K) = 1.1 (vertical, dashed line) is according to Chappell and White (1992) and the boundary between calc-alkaline and alkaline granite (thin, dashed, horizontal line) according to Liégois and Black (1987). The samples M13 and M14 plot outside the normal variation range (cf. Fig. 4). R = Reddah granite
Trace elements
The variation ranges of the trace elements are similar in size for the hyper- and subsolvus groups but contents are different; many elements do not overlap (Tables 2, 3 and Figs. 2, 6, 7, 8). Differences in elemental means between the hyper- and subsolvus granite are highly significant for most elements (Tables 2 and 3). The major differences between the hyper- and subsolvus granites are summarised in Table 6.
Classification diagrams according to Wahlen et al. (1987). FG: fractionated felsic granite, OGT: unfractionated I-, M-, and S-type granite. In b, the shaded field refers to analyses of the hypersolvus granite and the ruled field to subsolvus granite (both from the Gharib area) presented by Abdel-Rahman and Martin (1987, 1990)
Primordial mantle-normalised multi-element diagrams (Sun and McDonough 1989). bdl: below detection limit. The Pb data are less reliable and so are P data for the hypersolvus groups (contents close to or below the detection limit). Two samples (Q20a and b) have anomaly high U contents, probably associated with a U-mineralisation. Otherwise they behave as hypersolvus granite. The diagram is constructed by joining each maximum and minimum point in the relevant group. The abnormal sample Q50b is omitted. Due to a different element setup, the data from Mohamed (2012) are not included in the figure
a Chondrite-normalised REE diagram (Sun and McDonough 1989): the Qattar rocks include samples from Mahdy et al. (2015). Two samples Q2b and Q54a are higher than the other Qattar hypersolvus samples. They are included in the diagram thus extending the Qattar hypersolvus field upwards. The diagram is constructed by joining the highest and lowest points, respectively, for each element. bdl: below detection level. b REE diagram for the hypersolvus granites (and corresponding) normalised to the mean of subsolvus granites from the same area. The fields are the ± 1σ deviations from the means. The data for the Sörvik granite come from Lindh (2008). The lines (dashed and solid) give the mean for each group. The two hypersolvus granites from the Gharib area are similar
Whalen et al. (1987) have presented two sets of diagrams to define A-type granite with either Ga/Al or Zr + Nb + Ce + Y as abscissa. They prefer the first series of diagrams as being most decisive. According to their diagrams (Fig. 6), the hyper- and subsolvus groups differ in alkalinity; most hypersolvus granites plot in the A-type granite field but some samples from the Qattar area outside this field but close to its boundaries. It is evident from Fig. 6 that the Gharib samples have a stronger A-type character than the Qattar rocks. The two hypersolvus groups in the Gharib area cannot be separated. The subsolvus groups straddle the boundaries, but the majority of the samples plot outside the A-type granite field. The hypersolvus granite almost always plots in the A-type granite field or close to its boundaries in all the twelve diagrams designed by Whalen et al. (1987, not shown here), whereas the subsolvus granite plots in the non-A-type fields. The inter-group differences are mainly due to the abscissa (Fig. 6); the element Zr is not decisive. In the Gharib area, Zr shows a significant albeit small increase in the hypersolvus granite but in the Qattar area, no difference can be documented between the two granite types (Table 2).
The multi-element patterns are different for the sub- and hypersolvus granite (Fig. 7). The hypersolvus granite has extremely low contents of Ba, Sr, P, Eu and Ti. In many cases, these elements are below those of the primitive mantle (Sun and McDonough 1989) and sometimes even below the detection limit (Tables 2, 3). This is particularly noteworthy for Ba and Eu, which are strongly incompatible in the mantle. With the exception of the samples G15a, b and G16, the hypersolvus granite has a significantly lower Zr/Hf ratio than the subsolvus granite (Table 2); the latter has a ratio close to the primordial mantle value, 31.4 (Wood 1979). In both areas, the U and Th contents are higher in the hypersolvus than in the subsolvus granite, and the Th/U ratio is lower in the hypersolvus granite (Table 2). The Nb-dip between U and K considered typical for continental rocks is absent from the hypersolvus but present in the subsolvus groups (Fig. 7, Table 6).
REE contents are partly area dependent. In the Gharib area, the hypersolvus granite has a higher total sum of REEs than the subsolvus granite (significance 0.001), whereas no significant difference is found for the Qattar area (Table 3). In the Gharib area, the hypersolvus granite has a higher normalised content of the light REEs (LREEs) than the subsolvus granite, but in the Qattar area, we find the opposite relation (Fig. 8b). In both areas, the normalised content of the heavy REEs (HREEs) is higher in the hyper- than in the subsolvus granite (Fig. 8) and the negative Eu anomalies of the hypersolvus granite are much deeper than those of the subsolvus granite (Fig. 8); one subsolvus sample from the Gharib area (G1b) has even a weak positive Eu anomaly (cf also Table 6).
Mahdy et al. (2015) suggest that the granite suites have a continuous chemical variation, but their chemical variation diagrams show a clear grouping similar to ours (cf. Fig. 9); a t test confirms that most element group-averages are different at high significance levels (0.001 or 0.01).
Principal component analyses. a and b based on SiO2, TiO2, Al2O3, Fe2O3, MgO, CaO, Na2O, K2O, P2O5, Ba, Ga, Hf, Nb, Rb, Sr, Ta, Th, U, Zr, Y REEs. c, d Based only on the listed trace elements. The means are not included in the calculations, only plotted on the diagrams. In a and b, the first factor encompasses 50.8% and the second 16.7% of the variation; in c and d, 54.5% and 19.2%, respectively. The extremely low P content in the hypersolvus granite causes large analytical errors. In b and c, HREE stands for the HREEs not specifically marked on the diagram (too close to be well resolved). The Sörvik special granite (Lindh 2008, 2012) is a late Proterozoic fluorite-enriched granite occurring as part in a “normal” granite. The plotted point represents the mean of the two F-enriched special samples. e Gives an eigenvector component plot for all listed elements for the Gharib area and f the corresponding plot for the Qattar area. They also show the better separation of LREEs and HREEs in the Qattar than in the Gharib area. b, c, e and f show the LREEs not to behave according to “established models” but seem less incompatible the lighter they are
The tetrad effects were determined and tested for significance according to Monecke et al. (2002), but their scheme does not allow the sign to be obtained; this was determined according to Irber (1999). We have recalculated the analyses published by Mahdy et al. (2015) to be comparable with ours. In the Gharib area, no significant tetrad effects are found. In the Qattar area, a number of hypersolvus rocks show a positive (convex) significant effect for the first tetrad; one of these (Q51b) may be due to a positive Ce-anomaly. The majority of the samples with a significant effect were published by Mahdy et al. (2015). Conspicuous, strong, negative (concave) effects for all tetrads are recorded for the subsolvus samples first published by El Sayed et al. (2003) and republished by Mahdy et al. (2015). This is extremely rare (cf. Irber 1999; Monecke et al. 2002) and totally unexpected due to shielding by the large number of 4f electrons. We have no opinion, whether the differences are due to analytical artefacts or are real.
Geochemical grouping
A multivariate statistical approach is the most efficient way to demonstrate the coherence of and differences among groups in an unbiased way; we prefer to use a principal component analysis (PCA, Fig. 9), especially designed to show groupings.
A PCA is based on the correlation matrix, from which the eigenvectors are extracted. The size of the eigenvectors is proportional to their part of the total sample variance. The eigenvectors are orthogonal in an n-dimensional space, where n is given, in this case, by the number of elements used in the analysis. In a PCA, the eigenvectors are not rotated and thus remain uncorrelated. This is contrary to a factor analysis, where factors are rotated to maximise the grouping, but rendering their interpretation more difficult; they are no longer uncorrelated. The analysis gives an unbiased description of the sample variance, which is open to a geochemical interpretation.
We have performed four different PCAs (Fig. 9) and used two different types of plots: (i) we perform a co-ordinate transformation with the eigenvectors as co-ordinate axes, and then the analytical result is plotted (Fig. 9a, d), and (ii) the eigenvector components (element or element oxides) are plotted on the unit circle (Fig. 9b, c, e, f). The first type of plot shows the grouping of the analyses but gives no information on the construction of the eigenvectors. The second type shows how the eigenvectors are constructed but nothing about the sample grouping. As an example, in Fig. 9b, La and Ce are extremely important for the second eigenvector but without significance for the first eigenvector. The opposite applies to Y and the HREEs. Of minor importance in both eigenvectors are K2O and Na2O (cf. Table 1). The eigenvectors are normally referred to as factors when describing the variation.
The two first PCAs (Fig. 9a–d) are based on all granite groups. The first PCA includes all elements except those with a poor precision (Fig. 9a, b). The second PCA (Fig. 9c, d) is restricted to the trace elements. The third and fourth PCAs include all elements but are restricted to one area in each plot, Gharib (Fig. 9e) and Qattar (Fig. 9f).
In Fig. 9a and d, we note three groups: a tight group of hypersolvus Qattar granites including the samples reported by Mahdy et al. (2015) with Q50b as an outlier, a less tight group of Gharib hypersolvus granite with G2a, G15b and G16 as outliers and a scattering of subsolvus granite but without overlap with the hypersolvus groups. The PCA does not discriminate between the biotite and arfvedsonite hypersolvus granites. The mean of the two F-enriched samples of the Palaeo-Proterozoic Sörvik granite (Baltic Shield; Lindh 2008) plots together with the Gharib hypersolvus samples.
Even if the majors are important, their exclusion does not change the pattern (Fig. 9c, d). However, if the analysis is rerun with only the major elements (not shown in Fig. 9), the Gharib and Qattar hypersolvus groups are not separated (expected from Fig. 9b), and the separation between hyper- and subsolvus granite is weakened but is still evident. We could only include two of the subsolvus samples reported by Mahdy et al. (2015), since the other analyses were originally taken from El Sayed et al. (2003) with a different element setup. For the same reason, analyses reported by Mohamed (2012) are not included in the multivariate statistical analyses.
We have repeated the PCA for the Qattar and Gharib granites separately (Fig. 9e, f). The HREEs, Y, Nb, Ta, Ga and Si are concentrated at the hypersolvus end, and Ba, Sr, Eu, Ti, Al, Mg, Ca and P are concentrated at the subsolvus end. Uranium, Th and Hf are positioned towards the hypersolvus end, albeit less strongly. The attraction for the hypersolvus end of the LREEs decreases with decreasing atomic mass (Fig. 9b, c, e, f); Zr tends to follow La (Fig. 9b, c, e, f). The element distribution between hyper- and subsolvus granite is better illustrated by Fig. 9e and f than by Fig. 9b and d, since area-specific differences are excluded. The major elements merely mirror normal chemical variations, but we point out the divergent behaviour of K, Na and Fe, which is inconsistent with a major role of crystal fractionation (cf. Figs. 2, 6, 7, 8, 9c–e, Table 1). We may add Zn and Sn (not included in the PCA; inferior precision) to elements allocated to the hypersolvus granite.
The chemical differences between the arfvedsonite and biotite hypersolvus groups are small; the separation in the diagrams is poor with a conspicuous overlap. The biotite hypersolvus granite is suggested to be more strongly separated from the subsolvus granite than the arfvedsonite hypersolvus granite (Fig. 9a), but the overlap is large and does not allow any conclusions. The elements TiO2, P2O5, Cs, Ga, Rb, Sr, Ta, Th and U (significance between 0.05 and 0.01, Tables 1 and 2) are consistent with this suggestion, but Zr and the LREEs are not (Tables 2 and 3; these significance levels for these t tests are not displayed in Tables 1, 2 and 3). The elements which are different in the arfvedsonite and biotite hypersolvus granites are those that discriminate between the Qattar and Gharib hypersolvus granites (Fig. 9b, c, e, Tables 1 , 2 and 3). In a few samples, some elements plot between the clusters. It has, however, not been possible to find any systematic deviations. One deviating element is not correlated to another deviating element; deviations scatter among elements and samples.
Figure 9 includes the compositional variance associated with the two first eigenvectors. We have associated the first vector with the F-enrichment. This vector describes slightly more than half the chemical variation. We cannot exclude that F is involved also in other vectors, but nevertheless a large part of the chemical variation is due to other processes (e.g. source rock differences, both area-dependent and -independent.
Isotope results
Table 5 gives the results from the TIMS U–Pb isotope determinations. A conventional plot of all data points for the sample Q16 (hypersolvus granite, Fig. 10a) gives an upper intercept age of 572 ± 35 Ma (MSWD = 5.4). Most points are strongly discordant, but one point (Q16:1) is reasonably concordant supporting the interpretation of the upper intercept age as a crude approximation of the intrusion age. Using only the three points which give the best fit (crystals 1, 2 and 5) results in the same age but with a smaller error, 569 ± 9 Ma (MSWD = 0.33). This age falls between the 5th and 6th periods of granite intrusions suggested by Lundmark et al. (2012); the interpretation is uncertain, since the age is obtained from merely a three-point discordia including strongly discordant points. Moussa et al. (2008) report a U–Pb zircon age of 605 ± 3 Ma for the Qattar hypersolvus granite, which is the best determination so far obtained for this granite. They used the SIMS method including only concordant points in their calculations.
If the fraction 4 (immense error, Fig. 10b) is excluded from the age calculations of the sample U3, we obtain an upper intercept age of 605 ± 36 Ma (MSWD = 2.3). This age is identical with the age obtained by Moussa et al. (2008) for the Qattar hypersolvus granite and indistinguishable from the age of Q16 (large errors). It falls within the 4th period of granite intrusions suggested by Lundmark et al. (2012). However, the large error and the discordance make interpretations uncertain. The results suggest merely a small age difference between the Qattar hypersolvus and the Um-Salaat granites. Even if our results are consistent with field evidence suggesting the Um-Salaat granite to be older than the Qattar hypersolvus granite (El Dabe 2010), results overlap and are inconclusive.
Errors of three of the determined five fractions from G22 (Gharib hypersolvus granite, Table 5, Fig. 10c) are large. All fractions are discordant and have high contents of common lead. Using all fractions, the upper intercept age is 614 ± 87 Ma. If fractions 4 and 5 are omitted (largest errors), the resulting upper intercept age becomes 583 ± 18 Ma (MSWD = 1.5). If fractions 1 and 4 (the most discordant fractions) are omitted, an upper intercept age of 587 ± 17 Ma (MSWD = 3.6) is obtained. The large errors prevent a good estimate of the intrusion age; the age is probably between 580 and 590 Ma with a 2σ error of at least 20 Ma. The high MSWD suggests that some process have influenced the isotope system. Common lead is extremely high, the 206Pb/204Pb ratio varies between 74 and 498, and the large common-lead corrections introduce errors.
The high content of common Pb in sample Q6 (subsolvus granite), evident from its low 206Pb/204Pb ratios (Table 5), explains the impossibility to obtain a U–Pb isotope age for this sample. This is obvious from the 207Pb–206Pb ages ranging from − 175 to 1145 Ma (Table 5). In addition, some influence from unknown BSE-dark inclusions cannot be excluded. Data from this sample are not displayed in Fig. 10.
Figure 11 gives the gas-corrected results for representative Pb isotope determinations with the LA-SF-ICP-MS technique. Results for these analyses are given in Online Appendix, Table B. In total, 97 zircon crystals were tested. A high amount of common lead with a more or less uniform distribution is typical. All analysed crystals were examined in BSE images before and after the isotope analyses. These images do not display any obvious inclusions or grey shade irregularities, which could explain the different common-lead contents in the various crystals. The radiogenic isotope ratio varies within single crystals. Consequently, it is not possible to constrain any age for these rocks. The results support the high, but strongly variable contents of common lead found by TIMS (Table 5).
Results from the time-resolved Pb isotope determinations, representative samples using the laser ablation-single collector-magnetic sector field-ICP-MS method. The results are gas corrected using Hg isotopes, but no other correction is applied. The abscissa gives the time in seconds after firing of the laser. Results are given in Table B, Online Appendix. a Counting rate for the isotope 204Pb. Note the very high counting rates for most crystals. The rates vary among crystals. The crystals G25b-4 and Q22b-35 show systematic changes but in different directions. 204Pb is almost totally missing at the start of the analysis Q22a-24. b Isotope ratio 206Pb/204Pb displaying the extreme and constant contents of common lead in G16a-13 and Q22b-24. c207Pb/206Pb: Note change of scale! The two crystals G16a-13 and Q22b-24 have extremely high ratios. Note that the radiogenic Pb-ratio is not homogeneous in the crystal G16a-13; it shows an extreme variation
Realistic Sm–Nd depleted mantle model ages (DePaolo 1981) are not obtainable from the hypersolvus samples (Table 4; negative or extremely young), suggesting that some process has separated Sm from Nd. The samples used for Sm–Nd isotope determinations were chosen to include the few samples with intermediate Nd/Sm ratios to obtain an even spread along the 147Sm/144Nd axis. The obtained errorchrons (Fig. 12) are associated with large errors and MSWDs: for the granites at Gharib 538 ± 150 Ma and 127, respectively. For the granites at Qattar, the results depend on whether the sample U3 (granite–granodiorite group) was included or not. Excluding U3 gives an age of 583 ± 34 Ma and an MSWD of 11, including this sample gives 593 ± 32 Ma and an MSWD of 19 (Fig. 12). These data indicate the age of the separation of the elements Sm and Nd from each other but not that of the intrusion. However, the intrusion ages (Moussa et al. 2008 and our TIMS data) and Sm–Nd separation ages are similar. The rocks seem to have a source with an identical Nd isotope composition at approximately 0.6 Ga (Fig. 12).
Errorchron plots, Sm–Nd isotope data. Some process has separated Sm from Nd resulting in errorchrons with overlapping ages and initial ratios. Gharib data: (143Nd/144Nd)0 = 0.51209 ± 0.00014, errorchron age 538 ± 150 Ma, MSWD = 127. Qattar data (excl. U3): (143Nd/144Nd)0 = 0.512154 ± 0.00042, errorchron age 583 ± 34 Ma, MSWD = 11. Qattar data (incl. U3): (143Nd/144Nd)0 = 0.512139 ± 0.00039, errorchron age 593 ± 32 Ma, MSWD = 19
Discussion
General considerations
Granite groups
The granite–granodiorite group at Qattar is chemically similar to the Qattar subsolvus granite. These rocks are similar in age but errors prevent a conclusive statement. In the following text, these rocks are dealt with as one group. The Gharib biotite and arfvedsonite hypersolvus granites are treated as one group, since they are chemically similar, even if not identical (c.f. Fig. 9 and above). However, in some cases, we explicitly point out dissimilarities. The Qattar and Gharib granites are similar but probably not identical in age.
Working hypothesis
Two different possibilities exist, on which to base our interpretation: (i) the hyper- and subsolvus granites have different sources or (ii) they were co-magmatic. In the latter case, they may be interrelated by crystal fractionation (cf. Mahdy et al. 2015), different degrees of melting, mixing or a splitting of the magma into batches (unmixing). Mahdy et al. (2015) considered the subsolvus and hypersolvus granites in the Qattar area to be co-magmatic and related by crystal differentiation, but they presented no real evidence for this. The hypersolvus granite has a peculiar and restricted composition; in the case of different sources, the protolith of the hypersolvus granite should have an odd composition.
The four published maps for the Qattar area (El Sayed et al. 2003; El Dabe 2004, 2010; Mahdy et al. 2015) show some differences in details. Contact lines are drawn differently; this has no bearing on our model. Slightly different varieties are either shown as separate units or lumped together; neither is this of any importance for our discussion. No formal definition of these rock units exists. At least in the Qattar area, the two granite types seem to intrude in an intricate pattern (Fig. 1a), but the major part of the subsolvus granite is found in the south (Mahdy et al. 2015) and the Um-Salaat, El-Reddah, and Um-Nafic granites in the northeast (El Dabe 2004).
According to our unpublished data and to El Gaby (oral communication 2007), a close relation between two granites of similar composition is common in the Eastern Desert. The younger granite is often but not always enriched in fluorite (El Gaby, oral communication 2007). Outcrops in a very restricted area of the much older Sörvik granite (Lindh 2008, 2012) show similar geochemical peculiarities and F-enrichment as the hypersolvus granite (e.g. Fig. 9). In the Sörvik case, it is almost impossible for this small volume to have a source of its own.
According to field evidence, the subsolvus granite is older than the hypersolvus granite (El Dabe 2004, 2010), but the age difference is small and not possible to quantify (see above; Fig. 10). The possibility that the more evolved, hypersolvus granite formed and intruded first is thus ruled out by field evidence. The subsolvus granite cannot have formed first leaving the restitic source as the protolith of the hypersolvus granite. This is ruled out by chemical arguments: the first melting event depletes the source leading to a more depleted magma, a less evolved rock and to a higher required temperature for the second melting event, which in this scenario would have formed the low-temperature hypersolvus granite. Sm–Nd results (Fig. 12, Table 4) in combination with the U–Pb zircon age (Moussa et al. 2008, Fig. 10, Table 5) suggest that Sm and Nd were separated from each other in near connection, but not necessarily simultaneously with the intrusion; the Sm–Nd data are not consistent with normal interpretation models (Table 4).
The occurrence of only a few intermediate samples in the Sm–Nd isotope diagram (Fig. 12) is consistent with our model but cannot be forwarded as positive evidence for it; mixing of two different magmas would give intermediate samples.
The presented arguments make us choose the second of the alternatives as our working hypothesis: the granites are co-magmatic (c.f. Mahdy et al. 2015). However, we cannot exclude the first alternative: the magmas had different sources. Irrespective of whether the granites had different sources or formed from one magma, the process responsible for either the formation of the source rocks or the magma evolution was capable of inter alia splitting Sm and Nd from each other (Fig. 12 and Tables 4, 5). This splitting resulted in a distribution opposite to that expected from CHARAC processes (CHarge-And-RAdius-Controlled; Jahn et al. 2001).
Mixing
Mixing requires samples to occur in the same order irrespective of element, when the elements are ordered in increasing or decreasing amount between their end-member compositions. Among our samples, some elements in a few rocks appear intermediate between the hyper- and subsolvus groups, but unsystematically. Efforts to test for element mixing according to hyperbolic equations (Langmuir et al. 1978; Lindh et al. 2006) are accordingly negative. The bi-modal character of most elements (Tables 1, 2 and 3; Figs. 2, 4, 5, 6, 7, 8 and 9b, c, e, f) makes the fitting of our data to hyperbolas difficult and show the extremely well-constrained chemical difference between the hyper- and subsolvus granites. Thus, mixing or mingling cannot play any significant role in the evolution of the Gharib and Qattar granite suites.
Fractional crystallisation
Crystal settling is a simple mechanism for magmatic differentiation, but the high, non-Newtonian viscosity of granite magma restricts settling. An effort to calculate the degree of differentiation or variation of degree of melting was performed for the major elements in the Qattar granite using only our data. The standard CIPW-norms were recalculated to include biotite instead of orthopyroxene. Excess Al in corundum-normative rocks was recalculated as muscovite. The rock analyses were plotted together with the normative mineral compositions in two- and three-element plots (not shown here) including Si, Al, Fe, Mg, Fe+Mg, Ca, Na and K. Due to scatter and small differences in major-element compositions, linear trends are poor. To explain the differences between the means of hyper- and subsolvus granite, these plots suggest merely between 2 and 3% fractionation or difference in degree of melting. The minerals responsible for the differences would be approximately 80% plagioclase (probably including some K-feldspar) and 20% biotite. Crystal settling is consistent with this small degree of fractionation. If crystal settling would be responsible for the variation beyond this point, the crystalline major phases must settle in granitic proportions. The similar major-element composition of the Gharib and Qattar granites gives an analogous result for the Gharib granites.
As a demonstrative example for the trace elements, we choose Ba in the Gharib granite. In the hypersolvus granite, the lowest Ba content is 4 ppm (Table 2; below that of the primordial mantle; Sun and McDonough 1989). This corresponds to a depletion ratio of 0.007 compared to the mean of the Gharib subsolvus granite with SiO2 > 74 wt% (Table 1) and to an even stronger depletion, if rocks with a lower SiO2 content were included. According to a compilation by Rollinson (1993), Ba-distribution coefficients for a rhyolitic magma and plagioclase range from 0.31 to 1.5 and for K-feldspar from 4.3 to 11.4. Using the values preferred by Condie (written communication), 0.3 and 6.0, respectively, we arrive at a total distribution coefficient of 2.1 (settling minerals: one-third of each K-feldspar, plagioclase and quartz). The limiting case of Rayleigh-law crystal differentiation requires 98% differentiation to obtain the observed depletion of the subsolvus magma. This number is extremely sensitive to the applied and uncertain distribution coefficients, but nevertheless not realistic considering the major-element results.
Sparks et al. (1977) discussed yield stresses (τ) between 70 and 450 Pa for granitic magmas; we restrict our discussion to a very conservative τ ≤ 25 Pa. Assuming Bingham viscosities and spherical crystals, the minimum radius of settling crystals is estimated from a simplified calculation: the gravitation force is equalised to the sum of the opposed forces: the frictional force in Stokes law for zero settling velocity and the force due to τ. Deviations from a sphere are not important.
If a granitoid magma should evolve by crystal settling beyond an early point, quartz and feldspars must be involved. With a density difference of 3 × 102 kgm−3 between magma and crystal (high for granitic magma—feldspar or quartz), the critical radius for a crystal to settle is 2.5 cm (τ = 25 Pa) according to the Bingham model. This number is in excellent agreement with that obtained by Sparks et al. (1977). A decreased density difference or an increased τ increases the required minimum radius. Thus, merely large crystals of feldspar or quartz settle, but minute crystals of apatite (density difference 0.9 × 103 kgm−3 critical radius ≈ 8.5 mm), zircon (density difference 2.4 × 103 kgm−3 critical radius ≈ 3 mm), or monazite (density difference 2.7 × 103 kgm−3 critical radius ≈ 2.8 mm), do not. The required negative buoyancy is larger than obtainable from small single crystals or crystal aggregates.
In a pseudoplastic magma, crystals smaller than those indicated by the Bingham model settle, but extremely slowly; calculations for this model require more data. We use a small τ (c.f. Sparks et al. 1977); using a higher τ, the required radii for settling would be larger in both the Bingham and the pseudoplastic models. At the beginning of crystallisation, the viscosity is probably closer to Newtonian, which could allow some crystal settling. If crystal settling should explain the very tight chemical composition of the hypersolvus granites, some minor-sized accessory phases must have been almost totally eliminated from large portions of the granite (tens of km3s) to cumulate in the hypersolvus granite but others have not. We have difficulties to understand how this is physically possible.
Most of the differences between the two rock types discussed here cannot be explained by crystal differentiation, but requires a non-CHARAC process. This conclusion is at variance with that obtained by Mahdy et al. (2015). Their only support for crystal differentiation to explain the chemical evolution is their suggested smooth distribution of rock compositions. However, according to our tests, their data are grouped in the same way as ours.
Liquid immiscibility
Liquid immiscibility is a non-CHARAC mechanism. However, to the best of our knowledge, no liquid immiscibility has been documented by any method for silicic liquids with low Mg contents. Thus, liquid immiscibility cannot explain the evolution of the presently studied rocks.
Outline of our model
We have argued for a working hypothesis involving a co-magmatic model (cf. Mahdy et al. 2015), even if we have pointed out that the two-source model cannot be discarded beyond doubt. Mixing and liquid immiscibility are not important for the chemical variation of the Gharib and Qattar granites; crystal differentiation and/or different degrees of melting could merely explain a small part of the variation; we disagree with Mahdy et al. (2015) in this respect. Thus, we look for possible additional processes in the magma chamber to develop a model.
A temperature profile defined by conduction is inconsistent with melting at mid-crustal depths. Such a scenario requires an external energy source, e.g. a simultaneous intrusion of mafic magma, but no such indications are at hand. The granite magma must have formed in the lower crust and then ascended into a shallower chamber.
The basic assumption for our model is the simplest possible: in the magma chamber, the initial temperature distribution was close to equilibrium, i.e. essentially adiabatic. Thus, the magma temperature increases with a few tenths of a degree per km, whereas the liquidus temperature increases with approximately 3°/km (values used by Best 2002). This small temperature difference is decisive for the onset of crystallisation of magma compositions close to the temperature of the minimum melting composition; the magma mainly crystallises from the bottom and upwards (Fig. 13). However, initial crystallisation starts at the magma-chamber boundaries especially in the roof region (Fig. 13), which gives rise to a fine-grained rock (Abdel-Rahman and Martin 1990), acting as an isolating layer and thus resulting in a decreased heat diffusion into the surrounding country rocks.
Cartoon showing the proposed evolution model; not to scale. (1) Initial temperature distribution with rapid cooling at the top and the sides (not shown, only vertical section) of the magma chamber with consequent rapid crystallisation (cf. fine-grained top region, Abdel-Rahman and Martin 1990) and more slow crystallisation in the bottom region. Close to the crystals, globules of depleted magma enriched in volatile components (2) form. They coalesce during the continuing crystallisation (3) and assemble into larger pots (4). These pots may coalesce to form a lighter and less viscous layer (5), which rises at the edge (edge effect, Ramberg 1967) and (6) spreads like a mushroom at the top (Davies 1999). The present erosion surface exposes both granites (6)
When crystallising, the residual magma enriches in volatile components. If out-ward diffusion is slower than this enrichment, a volatile-enriched magma-residue forms at the crystallisation sites (Fig. 13). The residual liquid, probably with some suspended crystals, percolates slowly upwards replacing settling crystal. The suspended crystals have a tendency to lag behind and far from all arrives into small pockets, where the residual liquid assembles (Fig. 13). The crystallisation continues with the major element in granitic proportions, enriching the residual liquid in volatile components. With time, these small pockets coalesce into larger batches (Fig. 13). The “evolved” magma batches (cf. Tables 1, 2 and 3, Fig. 9a, e), which due to the crystallisation sites are principally located in the lower regions of the chamber (Fig. 13), may reach several thousands of m3 in size. The magma in the upper regions is unaffected by this fluid-component enrichment as long as its temperature is close to the liquidus. After having reached a sufficient size, the “evolved” magma rises due to buoyancy. Two different factors are of importance for the mechanical separation of the two magma batches: (i) edge effects and (ii) the viscosity and density differences of the two magmas.
Ramberg (1967) has shown that diapirs start to rise at the edge of a buoyant layer. In our case, the buoyant layer comprises the batches of volatile-enriched magma, and the boundary of the magma chamber constitutes the edge; country rock heterogeneities may also add to edge effects; in our examples, the magma intrudes into the Dokhan volcanics, the Hammamat metasediments and older granitoid rocks (Fig. 1). Since both the viscosity and the density of the fluid-enriched magma are lowered compared to its surrounding magma, it forms diapiric “mushrooms” with thin stems and large heads (Davies 1999); heads may coalesce into a large outcrop concentrated at the edge (Fig. 1). This explains the spatial separation of the two granites. Small pockets of “evolved” magma, which did not coalesce into larger layers, explain small outcrops of hypersolvus rock; cf. the Sörvik granite (Lindh 2008). The evolved magma batches have lower liquidus and solidus temperatures than their mother magma and appear as a younger granitic phase in the field, even if the absolute age difference is small. Thus, the suggested rock distribution is consistent with our model. Below we discuss our results and how they support our model.
Trace elements
An important difference between the Gharib and Qattar hypersolvus granites and most other granitic rocks is their increased fluorite content. Additional non-analysed fluid components are Cl, S and H2O. In the present granites, no mineralogical evidence suggests an enrichment of any of these components. Fluorine is a volatile element and is consequently enriched in the residual magma batch. Mohamed (2012) found liquid inclusions with a high salinity in the Gharib hypersolvus rock. He calculated them as NaCl-equivalents; a recalculation into NaF-equivalents gives a significantly lower, but still high salinity.
Jahn et al. (2001) and Gu et al. (2011) emphasise the importance of F for the element distribution in granitic melts. Gu et al. (2011) specifically mentioned Ga, Hf, Nb, Sn, Ta, Th and Zn (cf. Table 6) to follow F. We may add U, Y and the HREEs to this list (Table 6). Ga and Sn form complexes with F (Gu et al. 2011 and authors referenced by them), which explains why these elements follow F. The F-enriched (hypersolvus) granite has a lower Zr/Hf ratio than the subsolvus one (Tables 2, 5, 6); this is expected from the results presented by Jahn et al. (2001) and from the listed elements of Gu et al. (2011). Niobium and Ta form F-complexes, which explain the missing continental signature of an Nb-dip in our hypersolvus granite spidergrams (Fig. 7, Table 6; Jahn et al. 2001; Gu et al. 2011 and authors referenced by them). Other designs of multi-element diagrams (e.g. Wood 1979; not shown here) show also a missing Ta-dip. The hypersolvus granites are impoverished in, e.g. Ba and Sr (Tables 2 and 6).
Jahn et al. (2001) presented data with almost no difference in the ratio Y/Ho as a function of the F content. This is in accordance with our data (Table 7), but at variance with data presented by Gu et al. (2011), who found this ratio to decrease with increasing F content of the magma. Jahn et al. (2001) suggested that the small existing differences in the behaviour of Ho and Y are due to the presence of 4f-electrons in Ho but not in Y. According to our data, Y increases at the same rate as the HREEs in both granite types, and the decreased amount of LREE in the hypersolvus granite results in an increased Y/LREE ratio (Table 7, exemplified with the Y/Pr ratio). The Palaeo- to Midproterozoic Sörvik granite follows the same pattern as the Qattar and Gharib granites (Lindh 2012; Table 7).
The normalised ratios (La/Lu)N (Gd/Lu)N, (La/Sm)N and (ΣLREE/ΣHREE)N are higher in the subsolvus than in the hypersolvus granite in both areas (Tables 3, 6); the same relation exists in the Palaeo- to Midproterozoic Sörvik granite (cf. also Jahn et al. 2001; Gu et al. 2011). For the hypersolvus granite (ΣLREE/ΣHREE)N ratio is lower than the reference value (Table 7). The relative difference in this ratio is consistent with a preferred extraction of HREEs over LREEs triggered by F from a common magma, but not with CHARAC-based processes. The difference is larger in the Gharib than in the Qattar area (5.4 times and 2.7 times, respectively, cf. also Figs. 9e, f and 12). These results suggest that the LREEs have a decreasing affinity for F with decreasing atomic mass (Fig. 9e, f).
Opposite to the results of Gu et al. (2011), the hypersolvus granite has Nb/Ta ratios close to the mean crustal value, but the subsolvus granite has a lower ratio (Table 7). The differences are larger in the Gharib than in the Qattar area (Table 7). Differences in behaviour of Nb and Ta in magmatic processes are difficult to predict, due to their identical valence-electron structures and almost identical atomic, covalent and van der Waal’s radii (WebElements URL: http://www.webelements.com or almost any textbook in general chemistry). More studies on the behaviour of Nb and Ta in F-enriched magmas are wanted.
Figure 9e and f displays the general pattern of element distribution between the hyper- and subsolvus granites. The LREEs behave in a similar way in both areas, but in the Qattar area, they are less strongly distributed towards the hypersolvus end. The arfvedsonite granite is more similar to the Qattar granite than the biotite hypersolvus granite (not shown in Fig. 9e).
A consequence of the present data is that some A-type granites in the sense of Whalen et al. (1987) may form due to the presence of F without representing a special magma type. An example: in Fig. 6, the ratio (Na2O + K2O)/CaO is not typical for A-type granite and also the Ce content is low, in spite of the suggested A-type character of the hypersolvus granite. Fluorine influences the two abscissas used by Whalen et al. (1987), the Ga/Al ratio and Zr + Nb + Ce + Y (Fig. 6). Especially the Ga/Al ratio is strongly influenced by F (cf. Table 7). Whalen et al. (1987) consider this ratio to be more significant than the sum Zr + Nb + Ce + Y for their classification of A-type granite. Johnson et al. (2011) and Lundmark et al. (2012) mention that fluorite is common in the Eastern Desert and Lundmark et al. (2012) also refer to several F-associated mineralisations. A regional enrichment of F in the Eastern Desert Terranes may thus be an explanation for its abundance of A-type granite. Our trace element data are consistent with the F-enrichment and also consistent with our suggested model.
Common lead
The content of common Pb in zircon is high but varies among crystals (Table 5, Fig. 11, Table B, Online Appendix); c.f. also Johnson et al. (2011) and Lundmark et al. (2012). The uniformly distributed Pb in our time-resolved LA-SF-ICP-MS analyses (Fig. 11) suggests it to be structurally bound and not exclusively occurring in micro-inclusions in the crystals. In the absence of significant metamictization, this suggests an originally high Pb content. Zircon does not accept high Pb contents: the Pb2+-ion has a large radius (1.43 Å; WebElements URL: http://www.webelements.com), and the difference in formal charge between Pb2+ and Zr4+ is large.
The ions Pb4+ and Zr4+ have the same formal charge and similar radii, Pb4+: 1.08 Å and Zr4+: 0.98 Å; the Pb4+ radius is similar to those of, e.g. Gd3+, 1.19 Å and Tb4+, 1.02Å (WebElements URL: http://www.webelements.com), with high distribution coefficients between zircon and silicate melt. An introduction of Pb4+ may explain high amounts of common lead, but the mineralogical composition of the hypersolvus granite does not suggest a high degree of oxididation. Thus, to get a high content of Pb4+ into a magma batch, a separation of differently charged Pb ions must be followed by a selected transport of Pb4+ into the separated batch, where it is allocated into crystallizing zircon.
Urabe (1985, 1987) pointed out that at low pressures, Pb and Zn are distributed into fluids released from metaluminous granite, and Pb–Cl complexes were advanced as a transport mechanism of Pb in ore formation processes (Urabe 1985, 1987; Webster 1997). The radius ratio Pb2+/Cl− is 0.73 and the ratio Pb4+/F− is 0.77 (WebElements URL: http://www.webelements.com). These ratios are calculated for sixfold co-ordination but the ratios for eightfold co-ordination should be similar. This makes it geometrically possible for F− to form complex ions with Pb4+, suggesting F-enriched magmas to have a preference for Pb4+ to Pb2+. The use of ionic radii involves a simplification, since the Pauling electronegativity of Pb4+ is high (2.33; WebElements URL: http://www.webelements.com), giving the bond a significant covalent character. This hypothesis is forwarded here and is consistent with our data, but it needs independent testing.
The tetrad effects
The tetrad effect is in most cases insignificant; a few cases of a positive deviation from linearity are noted. Other authors, e.g. Irber (1999), Jahn et al. (2001), Monecke et al. (2002) and Gu et al. (2011) have found correlations between various element ratios and the tetrad effect. We find a negative log–log correlation between the first tetrad and the ratio Zr/Hf; correlation coefficient − 0.79. A weaker correlation exists between the same ratio and the third and total tetrads. No sample with a significant first tetrad has Zr/Hf > 20. For the element ratios K/Ba and Nb/Ta, some significant Pearson’s correlations are found with the first tetrad, but scatter is large and does not allow any conclusions; the low number of samples with a significant effect impairs any conclusions. These correlations suggest a small tetrad effect, even if most individual values are insignificant. Correlation coefficients ≪ 1 hint to the importance of analytical errors and/or unknown factors.
The number of significant positive first tetrad effects is larger in the hypersolvus than in the subsolvus granite. Mahdy et al. (2015) reported the majority of these effects; in our data set, the difference is smaller. However, the insignificant first tetrad effects in our set are numerically higher for the hypersolvus than for the subsolvus granite; this merely shows a tendency. These observations and the small size of the tetrad effect suggest a free volatile phase but that exsolution was late and the exsolved phase small (Irber 1999). This is consistent with the rarity of pegmatite.
Additional reflections
No model explains every feature of the observed chemical variations. Several factors are important. For example, in the Gharib area, we note differences between the chemical compositions reported by us and those reported by Abdel-Rahman and Martin (1987, 1990). Thus, the chemical variation in the Gharib area is probably rather large and this may be the explanation for the separation into two hypersolvus granites. Our model explains the general splitting into one granite type enriched in elements suggested to follow F and one granite type more impoverished in these elements but enriched in elements, which do not follow F (examples Ba, Sr), but not the differences between the biotite and arfvedsonite hypersolvus granites. It must be taken into account that many, partly poorly known, processes go on simultaneously in a granitic magma and the result, the crystallised granite, is the result of these combined processes. Here, we have pointed out and stressed one process.
The rocks discussed here are not unique. We give a few examples: similar rocks are scattered in the Eastern Desert (our unpublished results). Some Chinese granites have similar trace element compositions as the hypersolvus granites discussed here (see, e.g. Jahn et al. 2001; Gu et al. 2011). Christiansen et al. (2007) discussed the similarities between rapakivi granites and some Cenozoic topaz bearing rhyolites from the United States. These rocks show similarities with, but also some differences from the hypersolvus granite studied here. Christiansen et al. (2007) explain the chemical composition with extreme fractionation of melts formed at a low degree of melting. They do not discuss the role of F, but they repeatedly mention the high content of F in those rocks. Breitner (2012) discussed the nearly simultaneous intrusion of S- and A-type granites in central Europe. He suggests a model with two magmas, but he does not exclude the possibility that the magmas had a common source. He shows photos with bastnäsite-group minerals in fluorite (c.f. Lindh 2012) and Hf-enriched zircon crystals similar to the ones found by us. He notes the high F content of the A-granite but does not discuss the chemical influence of F.
Generalisation
The quantity of the volatile-enriched magma is impossible to estimate. Any effort to determine the modal composition of the rocks is associated with immense errors due to irregularly distributed mega-crysts (a thin-section is not representative), low amounts of mafic minerals (statistical counting errors up to 50 rel %), and the unattainable vertical distribution of granite types. Our calculation of the extent of the possible “crystal differentiation” is associated with large errors and, most important, it is impossible to determine the amounts of originally present crystals, the amount of newly formed crystals that has not left the volatile-enriched magma, the amount that rests in the original magma and the amount that settles.
Our model does not suggest that the evolved magma batch must have a hypersolvus composition. This is the case in the Gharib but not entirely in the Qattar region (“essentially” hypersolvus) and not in the Sörvik area (Lindh 2012). Whether the separated batch is hypersolvus or not depends primarily on the Ca content of the mother magma. If Ca in the “evolved” magma is sufficiently low, it is included into a single feldspar phase together with Na and K. Otherwise the evolved magma crystallises two feldspar phases.
The separation into a fluid-enriched and fluid-impoverished batch is independent of the presence of F. Splitting explains internal contacts and small compositional differences in ordinary granitic rocks in a simple way. In the absence of F, the evolved magma is neither enriched in the HFSEs nor strongly impoverished in Ba and Sr, but appears merely as a slightly more evolved part of the granite. This is a simpler way to explain variations in granite composition than suggesting gravitational differentiation, which are impossible for crystal phases appearing late in the crystallisation sequence. The difference between this process and classical crystal fractionation is a question of size. A crystal nucleates and grows as a discrete body; many crystals form and they do not coalesce. The evolved liquid, possibly with some small crystals, may assemble and coalesce into larger bodies which due to buoyance will rise after having reached a sufficient size.
Depending on the position of the intersection between the present-day erosion surface and this mushroom(s), we may find a large outcropping granite body, the head or coalesced heads, or a small body, the stem (cf. Fig. 13). The surrounding magma may even be invisible but present under today’s erosion surface or totally eroded away. We will continue testing our hypothesis with other young granites in Egypt but we welcome tests from other parts of the world on rocks of other ages. As an example, we have included the Swedish, much older Sörvik granite (Lindh 2012). Even if our data are consistent with the proposed model, a model involving two discrete sources cannot be ruled out.
Conclusions
-
1.
In both the Qattar and Gharib areas, a hypersolvus (or essentially hypersolvus according to our definition) and a subsolvus granite occur.
-
2.
Magmas may split into volatile enriched and impoverished batches in a disequilibrium process. Of course, other processes contribute to the chemical variation of the rocks.
-
3.
F is important as a complexing agent for a large number of trace elements. We have added the HREEs and Y to an earlier list. These elements are concentrated into the volatile- and F-enriched batch, which has made it possible to lance our model. F may also have caused a splitting of Pb2+ and Pb4+.
-
4.
The volatile-enriched “evolved” batch separates and rises as a diapir. If generalised this is an important mechanism for granite “differentiation”. This mechanism is consistent with different sizes and forms of granite intrusions depending on the intersection between the erosion surface and the diapir.
-
5.
If A-type granite is classified only from its trace element content, an increased F content gives an A-type character to the granite. If generalised, this means that A-type granite may be the result of a separated F-enriched magma batch.
References
Abdel-Rahman A-FM (1992) Mineral chemistry and paragenesis of astrophyllite from Egypt. Mineral Mag 56:17–26
Abdel-Rahman A-FM, Martin F (1987) Late Pan-African magmatism and crustal development in northeastern Egypt. Geol J 22:281–301
Abdel-Rahman A-FM, Martin F (1990) The Mount Gharib A-type granite, Nubian Shield: petrogenesis and role of metasomatism at the source. Contrib Mineral Petrol 104:173–183
WebElements. http://www.webelements.com/. Accessed 04 Feb 2018
Bentor Y (1985) The crustal evolution of the Arabo-Nubian massif with special reference to the Sinai Peninsula. Precambrian Res 28:1–74
Best MG (2002) Igneous and metamorphic petrology. Blackwell Science Ltd, Oxford
Breitner K (2012) Nearly contemporaneous evolution of the A- and S-type fractionated granites in the Krušné hory/Erzgebirge Mts, Central Europe. Lithos 151:105–121
Chappell BW, White AJR (1992) I-type and S-type granites in the Lachlan fold belt. Trans R Soc Edinburgh: Earth Sci 83:1–26
Christiansen EH, Haapala I, Hart GL (2007) Are Cenozoic topaz rhyolites the erupted equivalents of Proterozoic rapakivi granites? Examples from the western United States and Finland. Lithos 97:219–246
Davies GF (1999) Dynamic Earth: plates, plumes and mantle convection. Cambridge University Press, Cambridge
Debon F, Le Fort P (1983) A chemical-mineralogical classification of common plutonic rocks and associations. Trans R Soc Edinburgh Earth Sci 73:135–149
DePaolo DJ (1981) Neodymium isotopes in the Colorado Front Range and crust—mantle evolution in the Proterozoic. Nature 291:193–196
El Dabe MM (2004) Geology and radioelements distribution in Gabal Salaat, El Bali and Gabal El Reddah Environs, North Eastern Desert, Egypt. Master thesis, Assiut University
El Dabe MM (2010) Geology, geochemistry and radioactivity of some alkali feldspar granite intrusions in the North Eastern Desert, Egypt. PhD thesis, Assiut University
El Sayed MM, Shalaby MH, Hassanen MA (2003) Petrological and geochemical constraints on the tectonomagmatic evolution of the late Neoproterozoic granitoid suites in the Gattar area, North Eastern Desert, Egypt. Neues Jb Miner Abh 178:239–275
Gu L-X, Zhang Z-z, Wu C-z, Gou X-q, JLiao J-j, Yang H (2011) A topaz- and amazonite-bearing leucogranite pluton in eastern Xinjiang, NE China and its zoning. J Asian Earth Sci 42:885–902
Hassan MA, Hashad AH (1990) Precambrian of Egypt. In: Said R (ed) The geology of Egypt. Balkema, Rotterdam, pp 201–245
Irber W (1999) The lanthanide tetrad effect and its correlation with K/Rb, Eu/Eu*, Sr/Eu, Y/Ho, and Zr/Hf of evolving peraluminous granite suites. Geochim Cosmochim Acta 63:489–508
Jahn S, Matheis G, Mohamed EH, Tarnish MO, Shalaby IM (1993) Rare-metal province central Eastern Desert, Egypt, III. In: Thorweihe U, Schandelmeier H (eds) Geoscientific Research in Northeast Africa, proceedings of the international conference on geoscientific research in Northeast Africa, Berlin, 1993. Balkema, Rotterdam, Brookfield, pp 489–494
Jahn B-M, Wu F, Capdevila R, Martineau F, Zhao Z, Wang Y (2001) Highly evolved juvenile granites with tetrad REE patterns: the Woduhe and Baerzhe granites from the Great Xing’an Mountains in NE China. Lithos 59:171–198
Johnson PR et al (2011) Late Cryogenian-Ediacaran history of the Arabian-Nubian Shield: a review of depositional, plutonic, structural, and tectonic events in the closing stages of the northern East African Orogen. J Afr Earth Sci 61:167–232
Langmuir CH, Vocke RD, Hanson GN, Hart SR (1978) A general mixing equation with applications to Icelandic basalts. Earth Planet Sci Lett 37:380–392
Liégeois JP, Black R (1987) Alkaline magmatism subsequent to collision in the Pan-African belt of the Adrar des Iforas. In: Fitton JG, Upton BGJ (eds) Alkaline igneous rocks, vol 30. Special Publications. Geological Society of London, London, pp 381–401
Lindh A (2008) The geochemistry of the Sörvik granite—a TIB-1 granite. GFF 130:139–152
Lindh A (2012) Minute-sized crystals of HFSE minerals in evolved, fluorite-bearing granite, an example from the Sörvik granite, central Sweden. GFF 134:283–294
Lindh A (2014) Chemical composition of Late Svecofennian granite in the Bothnian Basin, Central Sweden. GFF 136:483–502
Lindh A, Kjöllerström A, Solyom Z (2006) Strong, localised country-rock contamination and partial homogenisation of a mafic magma: an example from west central Sweden. Lithos 86:212–228
Ludwig KR (2012) A geochronological toolkit for Microsoft Excel. Special Publication 5: 75 pp, Berkely Geochronological Center, Berkely
Lundmark AM, Andresen A, Hassan MA, Augland LE, Boghdady GY (2012) Repeated magmatic pulses in the East African Orogen in the Eastern Desert, Egypt: an old idea supported by new evidence. Gondwana Res 22:227–237
Mahdy NM, El Kalioubi BA, Wohlgemuth-Ueberwasser CC, Shalaby MH, El-Afandy AH (2015) Petrogenesis of U- and Mo-bearing A2-type granite of the Gattar batholith in the Arabian Nubian Shield, Northeastern Desert, Egypt: evidence for the favorability of host rocks for the origin of associated ore deposits. Ore Geol Rev 71:57–81
Mattey JM (2010) Analysis of the relative decay constants of 235U and 238U by multi-step CA-TIMS measurements of closed-system natural zircon samples. Chem Geol 275:186–198
Mohamed AM (2012) Geochemistry and fluid evolution of the peralkaline rare-metal granite, Gabal Gharib, Eastern Desert of Egypt. Arab J Geosci 5:697–712
Monecke T, Kempe U, Monecke J, Sala M, Wolf D (2002) Tetrad effect in rare earth element distribution patterns: a method of quantification with application to rock and mineral samples from granite-related rare metal deposits. Geochim Cosmochim Acta 66:1185–1196
Moussa EMM, Stern RJ, Manton WI, Ali KA (2008) SHRIMP zircon dating and Sm/Nd isotopic investigations of Neoproterozoic granitoids, Eastern Desert, Egypt. Precambrian Res 160:341–356
Nasdala L et al (2008) Zircon M257—a homogeneous natural reference material for the ion microprobe U-Pb analysis of zircon. Geostand Geoanal Res 32:247–265
Ramberg H (1967) Gravity, deformation and the Earth’s crust as studied by centrifuged models. Academic Press, London
Rollinson H (1993) Using geochemical data: evaluation, presentation, interpretation. Longman Group, Harlow
Sláma J et al (2008) Plešovice zircon—a new natural reference material for U-Pb and Hf isotopic microanalysis. Chem Geol 249:1–35
Sparks RSJ, Pinkerton H, MacDonald R (1977) The transport of xenoliths in magmas. Earth Planet Sci Lett 35:234–238
Stacey JS, Kramers JD (1975) Approximation of terrestrial lead isotope evolution by a two-stage model. Earth Planet Sci Lett 26:207–221
Stern RJ (1979) Late Precambrian crustal environments as reconstructed from relict igneous minerals, Central Eastern Desert of Egypt. Ann Geol Surv Egypt 9:9–31
Stoeser DB (1986) Distribution and tectonic setting of plutonic rocks of the Arabian Shield. J Afr Earth Sci 4:21–46
Sun SS, McDonough WF (1989) Chemical and isotopic systematics of oceanic basalts; implications for mantle composition and processes. In: Saunders AD, Norry MJ (eds) Magmatism in the ocean basins, vol 42. Geological Society Special Publications. Geological Society of London, London, pp 313–345
Urabe T (1985) Aluminous granite as a source magma of hydrothermal ore deposits: an experimental study. Econ Geol 80:148–157
Urabe T (1987) The effect of pressure on the partitioning ratios of lead and zinc between vapour and rhyolite melts. Econ Geol 82:1049–1052
Webster JD (1997) Exsolution of magmatic volatile phases from Cl-enriched mineralizing granitic magmas and implications for ore metal transport. Geochim Cosmochim Acta 61:1017–1029
Whalen JB, Currie KL, Chappell BW (1987) A-type granites: geochemical characteristics, discrimination and petrogenesis. Contrib Mineral Petrol 95:407–419
Wood DA (1979) A variably veined suboceanic upper mantle—genetic significance for mid-ocean ridge basalts from geochemical evidence. Geology 7:499–503
Acknowledgements
Mrs. E. Thun, Hamburg, performed the XRF analyses. We are indebted to the Late Prof. Samir El-Gaby for discussions on the geology of Egypt. The University of Assiut granted logistical and financial support for fieldwork. We acknowledge the use of laboratory facilities at Lund University, the Museum of Natural Science in Stockholm and the Geological Survey of Denmark and Greenland (GEUS).
Funding
Funding was obtained from Vetenskapsrådet (the Swedish Research Council): MENA-Swedish Research Links Program Grant Number 348-2005-5548 to A. Lindh and M. A. Abu El-Rus. We thank Axel Renno and an anonymous reviewer for constructive criticism, and the editor, Prof Wolf-Christian Dullo, and the editorial manager, Monika Dullo, for their help in various ways.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lindh, A., Abu El-Rus, M.A., Mohamed, M.AM. et al. A model for granite evolution based on non-equilibrium magma separation: evidence from the Gharib and Qattar fluorite-bearing granites, Eastern Desert, Egypt. Int J Earth Sci (Geol Rundsch) 108, 1201–1232 (2019). https://doi.org/10.1007/s00531-019-01701-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00531-019-01701-1