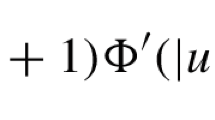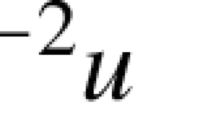Abstract
We prove the existence of infinitely many solutions \(\lambda _1, \lambda _2 \in \mathbb {R}\), \(u,v \in H^1(\mathbb {R}^3)\), for the nonlinear Schrödinger system
where \(a,\mu >0\) and \(\beta \le -\mu \) are prescribed. Our solutions satisfy \(u\ne v\) so they do not come from a scalar equation. The proof is based on a new minimax argument, suited to deal with normalization conditions.
Similar content being viewed by others
Notes
Indeed, in [16] the authors exploit a uniform-in-\(\beta \) Palais–Smale condition to derive the convergence of the whole minimax structure to a limit problem.
In [6] we showed that \({\mathcal {P}}_\beta \) is a \(\mathcal {C}^1\) manifold since this was enough for our purpose, the extra regularity is straightforward.
References
Bahri, A., Lions, P.L.: Morse index of some min-max critical points. I. Application to multiplicity results. Commun. Pure Appl. Math. 41(8), 1027–1037 (1988)
Bartsch, T., Dancer, N., Wang, Z.-Q.: A Liouville theorem, a-priori bounds, and bifurcating branches of positive solutions for a nonlinear elliptic system. Calc. Var. Partial Differ. Equ. 37(3–4), 345–361 (2010)
Bartsch, T., de Valeriola, S.: Normalized solutions of nonlinear Schrödinger equations. Archiv der Math. 100(1), 75–83 (2012)
Bartsch, T., Jeanjean, L.: Normalized solutions for nonlinear Schrödinger systems. Proc. R. Soc. Edinb. (2015). (to appear), arXiv:1507.04649
Bartsch, T., Jeanjean, L., Soave, N.: Normalized solutions for a system of coupled cubic Schrödinger equations on \(\mathbb{R}^3\). J. de Math. Pures et Appl. 106(4), 583–614 (2016)
Bartsch, T., Soave, N.: A natural constraint approach to normalized solutions of nonlinear Schrödinger equations and systems. J. Funct. Anal. 272(12), 4998–5037 (2017)
Cao, D., Chern, I.-L., Wei, J.: On ground state of spinor Bose–Einstein condensates. NoDEA Nonlinear Differ. Equ. Appl. 18, 427–445 (2011)
Dancer, E., Wei, J., Weth, T.: A priori bounds versus multiple existence of positive solutions for a nonlinear Schrödinger system. Ann. de l’Inst. Henri Poincare (C) Non Linear Anal. 27(3), 953–969 (2010)
Fibich, G., Merle, F.: Self-focusing on bounded domains. Phys. D 155(12), 132–158 (2001)
Ghoussoub, N.: Duality and perturbation methods in critical point theory, volume 107 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge (1993). With appendices by David Robinson
Gou, T., Jeanjean, L.: Existence and orbital stability of standing waves for nonlinear Schrödinger systems. Nonlinear Anal. 144, 10–22 (2016)
Jeanjean, L.: Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28(10), 1633–1659 (1997)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. the locally compact case, part 1. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(2), 109–145 (1984)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. the locally compact case, part 2. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(4), 223–283 (1984)
Nguyen, N.V., Wang, Z.-Q.: Existence and stability of a two-parameter family of solitary waves for a 2-coupled nonlinear Schrödinger system. Discrete Contin. Dyn. Syst. 36(2), 1005–1021 (2016)
Noris, B., Tavares, H., Terracini, S., Verzini, G.: Convergence of minimax structures and continuation of critical points for singularly perturbed systems. J. Eur. Math. Soc. 14(4), 1245–1273 (2012)
Noris, B., Tavares, H., Verzini, G.: Existence and orbital stability of the ground states with prescribed mass for the \(L^2\)-critical and supercritical NLS on bounded domains. Anal. PDE 7(8), 1807–1838 (2014)
Noris, B., Tavares, H., Verzini, G.: Stable solitary waves with prescribed \(L^2\)-mass for the cubic Schrödinger system with trapping potentials. Discrete Contin. Dyn. Syst. 35(12), 6085–6112 (2015)
Pierotti, D., Verzini, G.: Normalized bound states for the nonlinear Schrödinger equation in bounded domains. Preprint (2016). arXiv:1607.04520
Solimini, S.: Morse index estimates in min-max theorems. Manuscr. Math. 63(4), 421–453 (1989)
Stuart, C.A.: Bifurcation for Dirichlet problems without eigenvalues. Proc. Lond. Math. Soc. 45(1), 169–192 (1982)
Stuart, C.A.: Bifurcation from the continuous spectrum in \(L^2\)-theory of elliptic equations on \(\mathbb{R}^N\). Recent Methods in Nonlinear Analysis and Applications, Liguori, Napoli (1981)
Acknowledgements
Nicola Soave is partially supported by the project ERC Advanced Grant 2013 No. 339958 “Complex Patterns for Strongly Interacting Dynamical Systems - COMPAT”, by the PRIN-2015KB9WPT_010 Grant: “Variational methods, with applications to problems in mathematical physics and geometry”, and by the GNAMPA group.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bartsch, T., Soave, N. Multiple normalized solutions for a competing system of Schrödinger equations. Calc. Var. 58, 22 (2019). https://doi.org/10.1007/s00526-018-1476-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-018-1476-x