Modeling discharge rating curves with Bayesian B-splines

Abstract

River discharges are traditionally modeled by employing a standard power-law methodology. Recently, the Bayesian approached has successfully been applied to improve the estimates of the standard power-law. In this article, an extension to the standard power-law based on Bayesian B-splines is developed and tested on data sets from 61 different rivers. The extended model is evaluated against the standard power-law using two measures, the Deviance Information Criterion and Bayes factor. The extended model captures deviations in the data from the standard power-law but reduces to the standard power-law when that model is adequate. The standard power-law is inadequate for 26% of the rivers while the extended model provides an adequate fit in all of those cases and for the remaining 74% of the rivers the extended model and the power-law model both give adequate fit with almost identical estimates.

Appendix

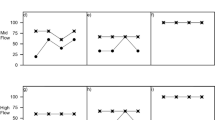
1.1 Trace plots and the Gelman–Rubin convergence measure

Figures 9 and 10 show trace plots of the chains from the posterior simulations and plots of the evolution of the Gelman–Rubin convergence measure for Models 1 and 2, respectively.

Fig. 9

Trace plots of the chains from the posterior simulations (left panel) and plots of the evolution of the Gelman–Rubin convergence measure (right panel) for a, b, ψ and c in Model 1 for the data set from Jokulsa a Dal River

Fig. 10

Trace plots of the chains from the posterior simulations (left panel) and plots of the evolution of the Gelman–Rubin convergence measure (right panel) for a, b, b ₂ and λ₆ in Model 2 for the data set from Jokulsa a Dal River

1.2 Prior distributions

The following prior distributions are proposed for the unknown parameters.

$$ p(\varphi) = \hbox{N}(\varphi | \mu_{\varphi}=0,\sigma^2_{\varphi}=0.82^2) $$

$$ p(b) \propto \hbox{N}(b | \mu_{b}=2.15,\sigma^2_{b}=0.4^2)I(0.5 < b < 5) $$

$$ p(c) \propto \hbox{N}(c | \mu_{c}=75,\sigma^2_{c}=50^2)I(c < w_{0}) $$

$$ p(\eta^2) \propto \hbox{Inv}-\chi^2(\eta^2 | \nu_\eta=10^{-12},S^2_{\eta}=1 ) $$

$$ p(\psi) \propto \hbox{N}(\psi | \mu_{\psi}=0.8,\sigma^2_{\psi}=0.25^2) I(0 < \psi < 1.2) $$

$$ p(b_2) \propto \hbox{N}(b_2 | \mu_{b2}=2.15,\sigma^2_{b2}=0.4^2)I(1 < b_2 < 6) $$

$$ p(c_2) \propto \hbox{N}(c_2 | \mu_{c2}=75,\sigma^2_{c2}=50^2)I(c_2 < w_{0}) $$

$$ p(\tau^2) \propto \hbox{Inv}-\chi^2 (\tau^2 {|} \nu_{\tau}=10^{-12},S^2_{\tau}=1 ) $$

$$ p(\phi) = \hbox{Beta}(\phi|\alpha_{\phi}=20,\beta_{\phi}=0.5) $$

$$ p(\lambda|\tau^2,\phi) \propto \hbox{N}(\lambda | 0,\tau^2 (I-\phi C)^{-1} M ) $$

where I(A) is such that I(A) = 1 if A is true and I(A) = 0 otherwise. In the prior distribution for λ, I is an identity matrix, M is a diagonal matrix and C is a neighbourhood matrix with constants on the first off-diagonals, other elements are equal to zero.

1.3 The Gibbs sampler

A Gibbs sampler with Metropolis–Hastings steps is used to sample from the posterior distribution. The conditional distribution of each parameter or vector of parameters in Model 2 is found and presented below. The Gibbs sampler is applied by sampling iteratively from these conditional distributions. The parameters are $\varphi, b, c, \eta^2, b_2, c_2, \lambda, \tau^2$ and ϕ. As before, let θ be a vector containing these parameters. Terms independent of the variable being viewed are denoted by d ₁, d ₂ and d ₃.

1.3.1 The conditional distribution of $\varphi$

The conditional posterior distribution of $\varphi$ has density proportional to

$$ p(\varphi|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(\varphi) $$

The logarithm of $p(\varphi|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(\varphi|\hbox{rest})\} \\ =& \sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(\varphi)\} + d_1\\ =& -\frac{1}{2\eta^2}\sum_{i=1}^{n}\frac{\{q_i - a(\varphi)(w_i - c)^b - \sum_{l=1}^{L}\lambda_l G_l(w_i)\}^2}{(w_i - c_2)^{2 b_2}}\\ & -0.5\sigma^{-2}_{\varphi}(\varphi - \mu_{\varphi})^2 + d_2. \\ \end{aligned} $$

1.3.2 The conditional distribution of b

The conditional posterior distribution of b has density proportional to

$$ p(b|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(b) $$

The logarithm of $p(b|\hbox{rest})$ p(b|rest) is equal to

$$ \begin{aligned} \log& \{p(b|\hbox{rest})\} \\ =& \sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(b)\} + d_1\\ =& -\frac{1}{2\eta^2}\sum_{i=1}^{n}\frac{\{q_i - a(\varphi)(w_i - c)^b - \sum_{l=1}^{L}\lambda_l G_l(w_i)\}^2}{(w_i - c_2)^{2 b_2}}\\ & -0.5\sigma^{-2}_{b}(b - \mu_{b})^2 + d_2 \\ \end{aligned} $$

for 0.5 < b < 5.

1.3.3 The conditional distribution of c

The conditional posterior distribution of c has density proportional to

$$ p(c|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(c) $$

The logarithm of $p(c|\hbox{rest})$ is equal to

$$ \begin{aligned} \log&\{p(c|\hbox{rest})\} \\ =& \sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(c)\} + d_1\\ =& -\frac{1}{2\eta^2}\sum_{i=1}^{n}\frac{\{q_i - a(\varphi)(w_i - c)^b - \sum_{l=1}^{L}\lambda_l G_l(w_i)\}^2}{(w_i - c_2)^{2 b_2}}\\ & -0.5\sigma^{-2}_{c}(c - \mu_{c})^2 + d_2 \\ \end{aligned} $$

for c < w ₀.

1.3.4 The conditional distribution of η²

The conditional posterior distribution of η² has density proportional to

$$ p(\eta^2|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(\eta^2) $$

Let $\kappa = (a(w_1 - c)^b, \ldots, a(w_n - c)^b)^{{\rm T}}$ and $g_i = (G_1(w_i), \ldots, G_L(w_i)),$ such that g _i λ = ∑ ^L _l=1 λ _l G _l (w _i ). Let H be an n × L matrix with ith row equal to g _i . Then κ + Hλ is the mean of q. Let

$$ Q=\hbox{diag}((w_1 - c_2)^{-2 b_2}, \ldots, (w_n - c_2)^{-2b_2}) $$

The logarithm of $p(\eta^2|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(\eta^2|{\rm rest})\} \\ =&\sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(\eta^2)\} + d_1 \\ =& -\frac{n}{2}\log(\eta^2) -\frac{1}{2\eta^2}(q-\kappa - H\lambda)^{\rm {T}}Q(q-\kappa - H\lambda) \\ & -(\nu_{\eta}/2+1)\log(\eta^2) - \frac{\nu_{\eta}S^2_{\eta}}{2\eta^2} + d_2 \\ \end{aligned} $$

The above density is proportional to an inverse chi-square density, that is,

$$ p(\eta^2|\hbox{rest}) = \hbox{Inv}-\chi^2(\eta^2|\nu_{\eta,{{\rm post}}},S^2_{\eta,{{\rm post}}}) $$

where

$$ \begin{aligned} \nu_{\eta,{{\rm post}}} =& \nu_{\eta}+n \\ S^2_{\eta,{{\rm post}}} =& \nu^{-1}_{\eta,{\rm post}}\left\{s^2_{0} + (q-\kappa - H\lambda)^{\rm {T}}Q(q-\kappa - H\lambda) \right\}, \end{aligned} $$

where s ²₀  = ν_η S ²_η .

1.3.5 The conditional distribution of b ₂

The conditional posterior distribution of b ₂ has density proportional to

$$ p(b_2|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(b_2) $$

The logarithm of $p(b_2|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(b_2|\hbox{rest})\} \\ =&\sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(b_2)\} + d_1\\ =& -b_2 \sum_{i=1}^{n}\log(w_i-c_2) \\ & -\frac{1}{2\eta^2}\sum_{i=1}^{n}\frac{\{q_i - a(\varphi)(w_i - c)^b - \sum_{l=1}^{L}\lambda_l G_l(w_i)\}^2}{(w_i - c_2)^{2 b_2}}\\ & -0.5\sigma^{-2}_{b2}(b_2 - \mu_{b2})^2 + d_2 \\ \end{aligned} $$

for 1 < b ₂ < 6.

1.3.6 The conditional distribution of c ₂

The conditional posterior distribution of c ₂ has density proportional to

$$ p(c_2|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(c_2) $$

The logarithm of $p(c_2|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(c_2|\hbox{rest})\} \\ =&\sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(c_2)\} + d_1\\ =& -b_2 \sum_{i=1}^{n}\log(w_i-c_2) \\ &-\frac{1}{2\eta^2}\sum_{i=1}^{n}\frac{\{q_i - a(\varphi)(w_i - c)^b - \sum_{l=1}^{L}\lambda_l G_l(w_i)\}^2}{(w_i - c_2)^{2 b_2}} \\ & -0.5\sigma^{-2}_{c2}(c_2 - \mu_{c2})^2 + d_2 \\ \end{aligned} $$

for c ₂ < w ₀.

1.3.7 The conditional distribution of λ

The conditional posterior distribution of λ has density proportional to

$$ p(\lambda|\hbox{rest}) \propto \prod_{i=1}^{n}p(q_{i}|\theta,w_i)p(\lambda|\tau^2,\phi) $$

where the support of λ is constrained by

$$ a(\varphi)(w_i - c)^b + \sum_{l=1}^{L}\lambda_l G_l(w_i)>0 $$

for all w _i  > w ₀ and λ _L  = 0. Let Q _λ = τ⁻² M ⁻¹(I − ϕC). The logarithm of $p(\lambda|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(\lambda|\hbox{rest})\} \\ =&\sum_{i=1}^{n}\log\{p(q_{i}|\theta,w_i)\} + \log\{p(\lambda|\tau^2,\phi)\} + d_1 \\ =& -\frac{1}{2}(q-\kappa - H\lambda)^{{\rm T}}\eta^{-2}Q(q-\kappa - H\lambda) \\ & -\frac{1}{2}\lambda^{{\rm T}}Q_{\lambda}\lambda + d_2 \\ =& -\frac{1}{2}\lambda^{{\rm T}}(H^{{\rm T}}\eta^{-2}QH + Q_{\lambda})\lambda +\lambda^{\rm {T}}H^{{\rm T}}\eta^{-2}Q(q-\kappa) + d_3\\ \end{aligned} $$

The above density is proportional to a multivariate normal density, that is,

$$ p(\lambda|\hbox{rest}) = \hbox{N}(\lambda|\mu_{\lambda,{\rm post}},\Upsigma_{\lambda,{\rm post}}) $$

where

$$ \begin{aligned} \Upsigma_{\lambda,{\rm post}} =& (H^{{\rm T}}\eta^{-2}QH + Q_{\lambda})^{-1} \\ \mu_{\lambda,{\rm post}} =& \Upsigma_{\lambda,{\rm post}} H^{{\rm T}}\eta^{-2}Q(q-\kappa). \end{aligned} $$

The above density is sampled under the above constraints.

1.3.8 The conditional distribution of τ²

The conditional posterior distribution of τ² has density proportional to

$$ p(\tau^2|\hbox{rest}) \propto p(\lambda|\tau^2,\phi)p(\tau^2) $$

The logarithm of $p(\tau^2|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(\tau^2|\hbox{rest})\} \\ =&\log\{p(\lambda|\tau^2,\phi)\} + \log\{p(\tau^2)\} + d_1 \\ =&-\frac{L}{2}\log(\tau^2) -\frac{1}{2\tau^2}\lambda^{{\rm T}}M^{-1}(I-\phi C)^{-1}\lambda \\ & -(\nu_{\tau}/2+1)\log(\tau^2) - \frac{\nu_{\tau}S^2_{\tau}}{2\tau^2} + d_2 \\ \end{aligned} $$

The above density is proportional to an inverse chi-square density, that is,

$$ p(\tau^2|\hbox{rest}) = \hbox{Inv}-\chi^2(\tau^2|\nu_{\tau,{\rm post}},S^2_{\tau,{\rm post}}) $$

where

$$ \begin{aligned} \nu_{\tau,{\rm post}} =& \nu_{\tau} + L \\ S^2_{\tau,{\rm post}} =& \nu^{-1}_{\tau,{\rm post}}\{\nu_{\tau} S^2_{\tau} + \lambda^{\rm {T}}M^{-1}(I-\phi C)^{-1}\lambda \}. \end{aligned} $$

1.3.9 The conditional distribution of ϕ

The conditional posterior distribution of ϕ has density proportional to

$$ p(\phi|\hbox{rest}) \propto p(\lambda|\tau^2,\phi)p(\phi) $$

The logarithm of $p(\phi|\hbox{rest})$ is equal to

$$ \begin{aligned} \log& \{p(\phi|\hbox{rest})\} \\ =& \log\{p(\lambda|\tau^2,\phi)\} + \log\{p(\phi)\} + d_1 \\ =&\frac{1}{2}\sum_{l=1}^{L}\log(1-\phi c_l) -\frac{1}{2\tau^2}\lambda^{\rm {T}}M^{-1}(I-\phi C)^{-1}\lambda \\ &+(\alpha_{\phi}-1)\log(\phi) + (\beta_{\phi}-1)\log(1-\phi) + d_2\\ \end{aligned} $$

where $c_1, \ldots, c_L$ are the eigenvalues of C. A Metropolis–Hastings step based on the above is used to draw samples from the conditional distribution of ϕ.