Abstract
We introduce a large class of random Young diagrams which can be regarded as a natural one-parameter deformation of some classical Young diagram ensembles; a deformation which is related to Jack polynomials and Jack characters. We show that each such a random Young diagram converges asymptotically to some limit shape and that the fluctuations around the limit are asymptotically Gaussian.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Random partitions...
An integer partition, called also a Young diagram, is a weakly decreasing finite sequence \(\lambda =(\lambda _1,\ldots ,\lambda _l)\) of positive integers \(\lambda _1\ge \cdots \ge \lambda _l>0\). We also say that \(\lambda \) is a partition of \(|\lambda |:=\lambda _1+\cdots +\lambda _l\).
Random partitions occur in mathematics and physics in a wide variety of contexts, in particular in the Gromov–Witten and Seiberg–Witten theories, see the overview articles of Okounkov [24] and Vershik [30].
1.2 ...And random matrices
Certain random partitions can be regarded as discrete counterparts of some interesting ensembles of random matrices. We shall explore this link on a particular example of random matrices called \(\beta \)-ensembles or \(\beta \)-log gases [8], i.e. the probability distributions on \(\mathbb {R}^n\) with the density of the form
where V is some real-valued function and Z is the normalization constant. In the special cases \(\beta \in \{1,2,4\}\) they describe the joint distribution of the eigenvalues of random matrices with natural symmetries; the investigation of such ensembles for a generic value of \(\beta \) is motivated, among others, by statistical mechanics. In this general case the problem of computing their correlation functions heavily relies on Jack polynomial theory [8, Chapter 13].
1.3 Random Young diagrams related to log-gases
Opposite to the special cases \(\beta \in \{1,2,4\}\), in the generic case of \(\beta \)-ensembles there seems to be no obvious unique way of defining their discrete counterparts and several alternative approaches are available, see the work of Moll [23] as well as the work of Borodin et al. [2]. In the current paper we took another approach based on a deformation of the character theory of the symmetric groups.
The class of random Young diagrams considered in the current paper as well as the classes from [2, 23] are of quite distinct flavors and it is not obvious why they should contain any elements in common, except for the trivial example given by the Jack–Plancherel measure. The problem of understanding the relations between these three classes does not seem to be easy and is out of the scope of the current paper.
1.4 Random Young diagrams and characters
The names integer partitions and Young diagrams are equivalent, but they are used in different contexts; for this reason we will use two symbols \(\mathcal {P}_{n}\) and \(\mathbb {Y}_{n}\) to denote the same object: the set of integer partitions ofn, also known as the set of Young diagrams withnboxes. Any function on the set of partitions (or its some subset) will be referred to as character.
Suppose that for a given integer \(n\ge 0\) we are given some convenient family \((\chi _\lambda )\) of functions \(\chi _\lambda :\mathcal {P}_{n}\rightarrow \mathbb {R}\) which is indexed by \(\lambda \in \mathbb {Y}_{n}\). We assume that \((\chi _\lambda )\) is a linear basis of the space of real functions on \(\mathcal {P}_{n}\) and that for each \(\lambda \in \mathbb {Y}_{n}\)
where \(1^n=(1,1,\ldots ,1)\) is a partition of n which consists of n parts, each equal to 1. We will refer to the functions from the family \((\chi _\lambda )\) as irreducible characters.
Our starting point is some character \(\chi :\mathcal {P}_{n}\rightarrow \mathbb {R}\) which fulfills an analogous normalization
We consider its expansion in the basis of irreducible characters
If the coefficients in this expansion are non-negative numbers, they define a probability measure \(\mathbb {P}_\chi \) on the set \(\mathbb {Y}_{n}\) of Young diagrams with n boxes; this probability measure is in the focus of the current paper.
1.5 Irreducible characters of symmetric groups: Plancherel measure
The most classical choice of the family \((\chi _\lambda )\) in (1.1) stems from the representation theory of the symmetric groups. For a Young diagram \(\lambda \in \mathbb {Y}_{n}\) with n boxes let \(\rho _\lambda :\mathfrak {S}(n) \rightarrow M_k(\mathbb {R})\) denotes the corresponding irreducible representation [25] of the symmetric group \(\mathfrak {S}(n)\). For a permutation \(\pi \in \mathfrak {S}(n)\) we define the value of the irreducible character\(\chi _\lambda \)of the symmetric group as the fraction of the traces
Since one can identify a permutation \(\pi \) with its cycle decomposition, it follows that the irreducible character \(\chi _\lambda (\pi )\) is also well-defined if \(\pi \in \mathcal {P}_{n}\) is a partition of n.
For this classical choice of \((\chi _\lambda )\) several results are available. Firstly, for a specific \(\chi =\chi _{{{\mathrm{reg}}}}\) given by
the corresponding probability measure \(\mathbb {P}_{\chi _{{{\mathrm{reg}}}}}\) is the celebrated Plancherel measure [1, 12, 20, 31] on the set of Young diagrams with n boxes. The probability measures \(\mathbb {P}_\chi \) for more general choices of \(\chi \) have been investigated, among others, in [3, 4, 26].
1.6 Irreducible Jack characters
In the current paper we will use another, more general, family \((\chi ^{(\alpha )}_\lambda )\) of irreducible characters in (1.1). Our starting point is the family of Jack polynomials\(J^{(\alpha )}_\lambda \) [11] which can be regarded as a deformation of the family of Schur polynomials; a deformation that depends on the parameter \(\alpha >0\). We use the normalization of Jack polynomials from [21, Section VI.10].
We expand Jack polynomial in the basis of power-sum symmetric functions:
The above sum runs over partitions \(\pi \) such that \(|\pi |=|\lambda |\). For a given integer \(n\ge 1\), any Young diagram \(\lambda \in \mathbb {Y}_{n}\) and any partition \(\pi \in \mathcal {P}_{n}\) we define the irreducible Jack character\(\chi ^{(\alpha )}_\lambda \) as
Above,
denotes the length of the partition \(\pi =(\pi _1,\ldots ,\pi _l)\), while \(\ell (\pi )=l\) denotes its number of parts. Also, the numerical factor \(z_\lambda \) is defined by
where \(m_i(\lambda ):=\big |\{k: \lambda _k=i\}\big |\) is the multiplicity of i in the partition \(\lambda \).
It is worth pointing out that in the special case \(\alpha =1\) the corresponding Jack character \(\chi ^{(1)}_\lambda (\pi )=\chi _\lambda (\pi )\) coincides with the irreducible character (1.2) of the symmetric group \(\mathfrak {S}(n)\), see [5, 19].
1.7 Probability measures \(\mathbb {P}^{(\alpha )}_\chi \)
With \(\chi _\lambda :=\chi _\lambda ^{(\alpha )}\) given by the irreducible Jack characters, (1.1) takes the following more specific form
If the coefficients \(\mathbb {P}^{(\alpha )}_\chi (\lambda )\ge 0\) are non-negative, we will say that \(\chi \) is a reducible Jack character. The resulting probability measure \(\mathbb {P}^{(\alpha )}_\chi \) on \(\mathbb {Y}_{n}\) is in the focus of the current paper.
In the simplest example of \(\chi :=\chi _{{{\mathrm{reg}}}}\) given by (1.3) the corresponding probability measure \(\mathbb {P}^{(\alpha )}_{\chi _{{{\mathrm{reg}}}}}\) turns out to be the celebrated Jack–Plancherel measure [2, 5, 9, 22, 23, 28] which is a one-parameter deformation of the Plancherel measure.
1.8 Random Young diagrams related to Thoma’s characters
An additional motivation for considering this particular class of random Young diagrams stems from the research related to the problem of finding extremal characters of the infinite symmetric group \(\mathfrak {S}(\infty )\), solved by Thoma [29]. Vershik and Kerov [32] found an alternative, more conceptual proof of Thoma’s result, which was based on the observation that characters of\(\mathfrak {S}(\infty )\)are in a natural bijective correspondence with certain sequences\((\lambda _1\nearrow \lambda _2\nearrow \cdots )\)of growing random Young diagrams.
The original Thoma’s problem can be equivalently formulated as finding all homomorphisms from the ring of symmetric functions to real numbers which are Schur-positive, i.e. which take non-negative values on all Schur polynomials. In this formulation the problem naturally asks for generalizations in which Schur polynomials are replaced by another interesting family of symmetric functions. Kerov et al. [17] considered the particular case of Jack polynomials and they proved that a direct analogue of Thoma’s result holds true also in this case. The main idea behind their proof was that the probabilistic viewpoint from the above-mentioned work of Vershik and Kerov [32] can be adapted to the new setting of Jack polynomials. Thus, a side product of the work of Kerov et al. is an interesting, natural class of random Young diagrams which fits into the framework which we consider in the current paper, see Sect. 1.16 and the forthcoming paper [7] for more details.
1.9 Cumulants
For partitions \(\pi _1,\ldots ,\pi _k\) we define their product\(\pi _1 \cdots \pi _k\) as their concatenation, for example \((4,3) \cdot (5,3,1)=(5,4,3,3,1)\). In this way the set of all partitions \(\mathcal {P}=\bigsqcup _{n\ge 0} \mathcal {P}_{n}\) becomes a unital semigroup with the unit \(1=\emptyset \) corresponding to the empty partition; we denote by \(\mathbb {R}[\mathcal {P}]\) the corresponding semigroup algebra, the elements of which are formal linear combinations of partitions. Any character \(\chi :\mathcal {P}\rightarrow \mathbb {R}\) with \(\chi (\emptyset )=1\) can be canonically extended to a linear map \(\chi :\mathbb {R}[\mathcal {P}]\rightarrow \mathbb {R}\) (such that \(\chi (1)=\chi (\emptyset )=1\)) which will be denoted by the same symbol.
For partitions \(\pi _1,\ldots ,\pi _\ell \) we define their cumulant with respect to the character \(\chi :\mathcal {P}\rightarrow \mathbb {R}\) as a coefficient in the expansion of the logarithm of an analogue of a multidimensional Laplace transform
where the operations on the right-hand side should be understood in the sense of formal power series with coefficients either in \(\mathbb {R}[\mathcal {P}]\) or in \(\mathbb {R}\).
In the special case when each partition \(\pi _i=(l_i)\) consist of just one part we will use a simplified notation and we will write
For example,
1.10 Asymptotics
In the current paper we consider asymptotic problems which correspond to the limit when the number of boxes \(n\rightarrow \infty \) of the random Young diagrams tends to infinity. This corresponds to considering a sequence\((\chi _n)\) of reducible characters \(\chi _n:\mathcal {P}_{n}\rightarrow \mathbb {R}\) and the resulting sequence\((\mathbb {P}^{(\alpha )}_{\chi _n})\) of probability measures on \(\mathbb {Y}_{n}\).
We also allow that the deformation parameter \(\alpha (n)\) depends on n; in order to make the notation light we will make this dependence implicit and write shortly \(\alpha =\alpha (n)\).
1.11 Hypothesis: asymptotics of \(\alpha \)
All results of the current paper will be based on the assumption that \(\alpha =\alpha (n)\) is a sequence of positive numbers such that
holds true for \(n\rightarrow \infty \) for some constants \(g\), \(g'\).
Note that the most important case when \(\alpha \) is constant fits into this framework with \(g=0\). The generic case \(g\ne 0\) will be referred to as double scaling limit.
1.12 Hypothesis: approximate factorization of characters
In the following we will use the following convention. If \(\chi _n:\mathcal {P}_{n}\rightarrow \mathbb {R}\) is a function on the set of partitions of n, we will extend its domain to the set
of partitions of smaller numbers by setting
i.e. we extend the partition \(\pi \) by adding an appropriate number of parts, each equal to 1.
In this way the cumulant \(k^{\chi _n}_\ell (l_1,\ldots ,l_\ell )\) is well defined if \(n\ge l_1+\cdots +l_\ell \) is large enough.
Definition 1.1
Assume that for each integer \(n\ge 1\) we are given a function \(\chi _n:\mathcal {P}_{n}\rightarrow \mathbb {R}\). We say that the sequence \((\chi _n)\) has approximate factorization property [26] if for each integer \(\ell \ge 1\) and all integers \(l_1,\ldots ,l_\ell \ge 2\) the limit
exists and is finite.
We say that the sequence \((\chi _n)\) has enhanced approximate factorization property if, additionally, in the case \(\ell =1\) the rate of convergence in (1.11) takes the following explicit form:
for each \(l\ge 2\) there exist some constants \(a_{l+1},b_{l+1}\in \mathbb {R}\) such that
and
where g is given by (1.9).
Example 1.2
It is easy to check that for \(\chi _{{{\mathrm{reg}}}}\) from (1.3) all higher cumulants vanish:
and the first cumulant takes a particularly simple form
It follows that that the sequence \((\chi _n)\) for which \(\chi _n:=\chi _{{{\mathrm{reg}}}}\) fulfills the enhanced approximate factorization property.
1.13 Drawing Young diagrams
1.13.1 Anisotropic Young diagrams
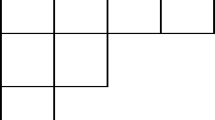
The usual way of drawing Young diagrams is to represent each individual box as a unit square, see Fig. 1 (left). However, when dealing with random Young diagrams related to Jack polynomials it is more convenient to represent each box as a rectangle with width \(w>0\) and height \(h>0\) such that
A Young diagram viewed like this becomes a polygon contained in the uppper-right quaterplane which will be denoted by \(T_{w,h}\lambda \), see Fig. 1 (right). We will refer to such polygons as anisotropic Young diagrams; they have been first considered by Kerov [15].
1.13.2 Russian convention: profile of a Young diagram
We draw (anisotropic) Young diagrams on the plane with the usual Cartesian coordinates (x, y). However, it is also convenient to use the Russian coordinate system (u, v) given by
This new coordinate system gives rise to the Russian convention for drawing (anisotropic) Young diagrams, see Fig. 2.
The boundary of a Young diagram \(\lambda \) drawn in the Russian convention (the solid zigzag line on the right-hand side of Fig. 2) is a graph of a function \(\omega _\lambda \) which will be called the profile of \(\lambda \). If the Young diagram is replaced by an anisotropic Young diagram \(T_{w,h}\lambda \) we define in an analogous way its profile \(\omega _{T_{w,h}\lambda }\).
The anisotropic Young diagram from Fig. 1 shown in the French and Russian conventions. The solid line represents the profile of the Young diagram. The coordinate system (u, v) corresponding to the Russian convention and the coordinate system (x, y) corresponding to the French convention are shown
1.14 The first main result: law of Large Numbers
The following theorem is a generalization of the results of Biane [4] who considered the special case \(\alpha =1\) and the corresponding representations of the symmetric groups.
Theorem 1.3
(Law of large numbers) Assume that \(\alpha =\alpha (n)\) is such that (1.9) holds true. Assume that \(\chi _n:\mathcal {P}_{n}\rightarrow \mathbb {R}\) is a reducible Jack character; we denote by \(\lambda _n\) the corresponding random Young diagram with n boxes distributed according to \(\mathbb {P}^{(\alpha )}_{\chi _n}\). We assume also that the sequence \((\chi _n)\) of characters fulfills the enhanced approximate factorization property.
Then there exists some deterministic function \(\omega _{\Lambda _\infty }:\mathbb {R}\rightarrow \mathbb {R}\) with the property that
where
and the convergence in (1.15) holds true with respect to the supremum norm, in probability. In other words, for each \(\epsilon >0\)
Remark 1.4
The concrete formula for the profile \(\omega _{\Lambda _\infty }\) may be obtained by computing the corresponding R-transform and Cauchy transform, see for example [4, Theorem 3].
The proof is postponed to Sect. 5.
1.15 The second main result: Central Limit Theorem
We keep the notations from Theorem 1.3. The difference
is a random function on the real line which quantifies the (suitably rescaled) discrepancy between the shape of the random (anisotropic) Young diagram \(\Lambda _n\) and the limit shape. We will regard \({\Delta }_n\) as a Schwartz distribution on the real line \(\mathbb {R}\) or, more precisely, as a random vector from this space.
The following result is a generalization of Kerov’s CLT [10, 12] which concerned Plancherel measure in the special case \(\alpha =1\) as well as a generalization of its extension by the first-named author and Féray [5] for the generic fixed value of \(\alpha >0\). Indeed, Example 1.2 shows that the assumptions of the following theorem are fulfilled for \(\chi _n:=\chi _{{{\mathrm{reg}}}}\), thus CLT holds for Jack–Plancherel measure in a wider generality, when\(\alpha =\alpha (n)\)may vary withn.
On the other hand the following result is also a generalization of the results of the second-named author [26] who considered a setup similar to the one below in the special case \(\alpha =1\).
Theorem 1.5
(Central Limit Theorem) We keep the assumptions and the notations from Theorem 1.3.
Then for \(n\rightarrow \infty \) the random vector \({\Delta }_n\) converges in distribution to some (non-centered) Gaussian random vector \(\Delta _\infty \) valued in the space \((\mathbb {R}[x])'\) of distributions, the dual space to polynomials.
The above statement about the convergence of the random vector \({\Delta }_n\) should be understood in a rather specific sense, formulated with help of some suitable test functions. Namely, for each finite collection of polynomials \(f_1,\ldots ,f_k \in \mathbb {C}[x]\) we claim that the joint distribution of the random variables
converges to the Gaussian distribution.
Informally speaking: asymptotically, for \(n\rightarrow \infty \)
where \(\omega _{\Lambda _\infty }\) is a deterministic curve and \(\Delta _\infty \) is a Gaussian process.
Remark 1.6
In order to prove Theorem 1.5 it is enough to show that the joint distribution of any finite family of random variables \((Y_k)_{k\ge 2}\) converges as \(n\rightarrow \infty \) to a (non-centered) Gaussian distribution, where
is (up to a simple scalar factor) the value of the Schwartz distribution \(\Delta _n\) evaluated on a suitable polynomial test function.
The proof is postponed to Sect. 6.
1.16 Example
Let \(\alpha >0\) be a fixed positive integer. For a given integer \(i>0\) consider the rectangular Young diagram
with \(n':=\alpha i^2\) boxes. We will assume that \(n'\) is an even number. The special case \(\alpha =1\) was considered already by Biane [3, Figures 1–3].
Using a random iterative procedure introduced by Kerov [14] which is an inverse of the Plancherel growth process and which will be presented in detail in a forthcoming paper [7] we remove half of the boxes from the rectangular Young diagram \((i^{\alpha i})\); the resulting random Young diagram with \(n:=\frac{1}{2} n'\) boxes will be denoted by \(\lambda _n\). We will use the same transformation
in order to scale both the original rectangular Young diagram \((i^{\alpha i})\) as well as the resulting random Young diagram \(\lambda _n\).
We notice that the anisotropic Young diagram \(T(i^{\alpha i})\) is a square, see Fig. 3; we shall denote it by S. As we shall see in [7], the distribution of the random Young diagram \(\lambda _n\) can be equivalently formulated via (1.7) in terms of the corresponding natural reducible Jack character and Theorem 1.3 as well as Theorem 1.5 are applicable. Thus the sequence of random anisotropic Young diagrams \(\Lambda _n=T\lambda _n\) converges to some deterministic limit \(\Lambda _\infty \). Not very surprisingly, this limit \(\Lambda _\infty \) turns out to be the bottom half of the square S, see Fig. 3.
Diagonal gray lines form a heatmap showing probabilities that a given segment belongs to the profile of the random Young diagram \(\Lambda _n\) (the intensity of color corresponds to the probability). The rectangular grid of anisotropically stretched boxes is clearly visible. The blue dashed line depicts the limit profile \(\omega _{\Lambda _\infty }\). In order to save space, only the neighborhood of \(\Lambda _\infty \) is shown. The red solid line depicts the mean value \(t\mapsto \mathbb {E}\omega _{\Lambda _n}(t)\). In this example \(\alpha =4\), \(i=5\), \(n=50\)
The analogue of Fig. 4 for \(\alpha =4\), \(i=10\), \(n=200\). The increased number of boxes is compensated by a decrease of the size of the individual boxes. With this choice of scaling, the fluctuations of random Young diagrams \(\Lambda _n\) around \(\Lambda _\infty \) tend to zero as \(n\rightarrow \infty \)
Figures 4 and 5 are an illustration of the Law of Large Numbers (Theorem 1.3): as the number of boxes \(n\rightarrow \infty \) tends to infinity, suitably scaled random Young diagrams \(\Lambda _n\) indeed seem to converge to the deterministic limit \(\Lambda _\infty \).
The analogue of Fig. 4 for the profiles \(\sqrt{n}\ \omega _{\Lambda _n}\) for which only the second Russian coordinate v was anisotropically stretched by factor \(\sqrt{n}\). In this example \(\alpha =4\), \(i=5\), \(n=50\)
The analogue of Fig. 6 for \(\alpha =4\), \(i=10\), \(n=200\). In this scaling the fluctuations of \(\sqrt{n}\ \omega _{\Lambda _n}\) (“the shaded area” of the heatmap) around \(\sqrt{n}\ \omega _{\Lambda _\infty }\) do not vanish as \(n\rightarrow \infty \). Also the discrepancy between the mean value of these fluctuations \(\sqrt{n}\ \mathbb {E}\omega _{\Lambda _n}\) (the red solid line) and the ‘first-order approximation’ \(\sqrt{n}\ \omega _{\Lambda _\infty }\) (the dashed blue line) does not vanish as \(n\rightarrow \infty \)
The analogue of Fig. 6 for \(\alpha =4\), \(i=20\), \(n=800\). As \(n\rightarrow \infty \), the amplitude of the oscillations of the discrepancy \(\sqrt{n}\ \left( \mathbb {E}\omega _{\Lambda _n}- \omega _{\Lambda _\infty } \right) \) remain roughly constant, but their frequency tends to infinity and thus the discrepancy converges in the sense of Schwartz distributions
In order to speak about CLT one should consider a more refined scaling: the one in which one stretches the second Russian coordinate v by a factor of \(\sqrt{n}\). This scaling has a bizarre feature: each individual box is drawn as a parallelogram in which the difference \(v_{{\text {max}}}-v_{{\text {min}}} =\sqrt{\alpha }+\frac{1}{\sqrt{\alpha }}\) of the v-coordinates of the top and the bottom vertex does not depend on n so one cannot claim that the size of an individual box converges to zero; nevertheless the area of an individual box does converge to zero. Figures 6, 7 and 8 illustrate this choice of the scaling.
Theorem 1.5 implies in particular that the limit
exists as a Schwartz distribution on the real line; the convergence holds in the weak sense, i.e. the limit
exists and is finite for an arbitrary integer \(k\ge 0\).
The convergence in (1.19) is illustrated in Figs. 6, 7 and 8: the function \(\mathbb {E}\Delta _n\) is the difference between the red solid curve (i.e. the plot of \(\sqrt{n} \ \mathbb {E}\omega _{\Lambda _n}\)) and the blue dashed curve (i.e. the plot of \(\sqrt{n}\ \omega _{\Lambda _\infty }\)). As one can see on these examples, the function \(\mathbb {E}\Delta _n\) has oscillations of period and amplitude related to the grid of the boxes of the Young diagrams. As \(n\rightarrow \infty \), the amplitude of these oscillations does not converge to zero (so that the convergence in the supremum norm does not hold) but their frequency tends to infinity (which is sufficient for convergence in the weak topology).
The central limit theorem in Theorem 1.5 is somewhat reminiscent to CLT for random walks. A significant difference lies in the nature of the limit object: in the case of the random walks it is the Brownian motion which has continuous trajectories while in the case considered in Theorem 1.5 it is a random Schwartz distribution \(\Delta _\infty \) for which computer simulations (such as the one shown in Fig. 9) suggest that it has quite singular ‘trajectories’, reminiscent to that of the white noise. A systematic investigation of such trajectory-wise properties of \(\Delta _\infty \) via short-distance asymptotics of the covariance of the corresponding Gaussian field is out of the scope of the current paper.
1.17 Content of the paper
In Sect. 2 we introduce the main algebraic tool for our considerations, namely Theorem 2.3 which gives several convenient characterizations of the approximate factorization property. In Sect. 3 we prove this result. Section 4 is devoted to some technical results, mostly related to probability measures which are uniquely determined by their moments. In Sect. 5 we give the proof of Law of Large Numbers (Theorem 1.3). Finally, in Sect. 6 we give the proof of Central Limit Theorem (Theorem 1.5).
2 Approximate factorization of characters
The purpose of this section is to give a number of conditions which are equivalent to the approximate factorization property (Definition 1.1). These conditions often turn out to be more convenient in applications, such as the ones from [7].
2.1 Conditional cumulants
Let \(\mathcal {A}\) and \(\mathcal {B}\) be commutative unital algebras and let \(\mathbb {E}:\mathcal {A}\rightarrow \mathcal {B}\) be a unital linear map. We will say that \(\mathbb {E}\) is a conditional expectation value; in the literature one usually imposes some additional constraints on the structure of \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathbb {E}\), but for the purposes of the current paper such additional assumptions will not be necessary.
For any tuple \(x_1,\ldots ,x_\ell \in \mathcal {A}\) we define their conditional cumulant as
where the operations on the right-hand side should be understood in the sense of formal power series in variables \(t_1,\ldots ,t_\ell \).
Note that the cumulants for partitions which we introduced in Sect. 1.9 fit into this general framework: for \(\mathcal {A}:=\mathbb {R}[\mathcal {P}]\) one should take the semigroup algebra of partitions, for \(\mathcal {B}:=\mathbb {R}\) the real numbers and for \(\mathbb {E}:=\chi :\mathbb {R}[\mathcal {P}]\rightarrow \mathbb {R}\) the character.
2.2 Normalized Jack characters
The usual way of viewing the characters of the symmetric groups is to fix the irreducible representation \(\lambda \) and to consider the character as a function of the conjugacy class \(\pi \). However, there is also another very successful viewpoint due to Kerov and Olshanski [16], called dual approach, which suggests to do roughly the opposite. Lassalle [18, 19] adapted this idea to the framework of Jack characters. In order for this dual approach to be successful one has to choose the most convenient normalization constants. In the current paper we will use the normalization introduced by Dołęga and Féray [5] which offers some advantages over the original normalization of Lassalle. Thus, with the right choice of the multiplicative constant, the unnormalized Jack character \(\chi ^{(\alpha )}_\lambda \) from (1.5) becomes the normalized Jack character\({{\mathrm{Ch}}}^{(\alpha )}_\pi (\lambda )\), defined as follows.
Definition 2.1
Let \(\alpha >0\) be given and let \(\pi \) be a partition. For any Young diagram \(\lambda \) the value of the normalized Jack character\({{\mathrm{Ch}}}_\pi ^{(\alpha )}(\lambda )\) is given by:
where
denotes the falling power and \(\chi ^{(\alpha )}_\lambda (\pi )\) is the Jack character (1.5). The choice of an empty partition \(\pi =\emptyset \) is acceptable; in this case \({{\mathrm{Ch}}}_\emptyset ^{(\alpha )}(\lambda )=1\).
Each Jack character depends on the deformation parameter \(\alpha \); in order to keep the notation light we will make this dependence implicit and we will simply write \({{\mathrm{Ch}}}_{\pi }(\lambda )\).
2.3 The deformation parameters
In order to avoid dealing with the square root of the variable \(\alpha \) which is ubiquitous in the subject of Jack deformation, we introduce an indeterminate \(A := \sqrt{\alpha }\). The algebra of Laurent polynomials in the indeterminate A will be denoted by \(\mathbb {Q}\left[ A,A^{-1}\right] \).
A special role will be played by the quantity
which already appeared in the numerator on the left-hand side of (1.9).
2.4 The linear space of \(\alpha \)-polynomial functions
In a paper [27] the second-named author has defined a certain filtered linear space of \(\alpha \)-polynomial functions. This linear space consists of certain functions in the set \(\mathbb {Y}\) of Young diagrams with values in the ring \(\mathbb {Q}\left[ A,A^{-1}\right] \) of Laurent polynomials and, among many equivalent definitions, one can define it using normalized Jack characters.
Definition 2.2
([27, Proposition 5.2]) The linear space of \(\alpha \)-polynomial functions is the linear span (with rational coefficients) of the functions
over the integers \(k\ge 0\) and over partitions \(\pi \in \mathcal {P}\).
The filtration on this vector space is specified as follows: for an integer \(n\ge 0\) the subspace of vectors of degree at most n is the linear span of the elements (2.3) over integers \(k\ge 0\) and over partitions \(\pi \in \mathcal {P}\) such that
2.5 Algebras \(\mathscr {P}\) and \(\mathscr {P}_\bullet \) of \(\alpha \)-polynomial functions
The vector space of \(\alpha \)-polynomial functions can be equipped with a product in two distinct natural ways (which will be reviewed in the following). With each of these two products it becomes a commutative, unital filtered algebra.
Firstly, as a product we may take the pointwise product of functions on\(\mathbb {Y}\). The resulting algebra will be denoted by \(\mathscr {P}\) (the fact that the \(\mathscr {P}\) is closed under such product was proved by Dołęga and Féray [5, Theorem 1.4]).
Secondly, as a product we may take the disjoint product\(\bullet \), see [27, Section 2.3], which is defined on the linear base of Jack characters by concatenation (see Sect. 1.9) of the corresponding partitions
The resulting algebra will be denoted by \(\mathscr {P}_\bullet \).
2.6 Two probabilistic structures on \(\alpha \)-polynomial functions
Assume that \(\chi :\mathcal {P}_{n}\rightarrow \mathbb {R}\) is a reducible Jack character and let \(\mathbb {P}_\chi \) be the corresponding probability measure (1.7) on the set \(\mathbb {Y}_{n}\) of Young diagrams with n boxes. With this setup, functions on \(\mathbb {Y}_{n}\) can be viewed as random variables; we denote by \(\mathbb {E}_\chi \) the corresponding expectation.
Let us fix a partition \(\pi \in \mathcal {P}_{n}\); we denote by \(\chi ^{(\alpha )}_\# (\pi )\) the random variable \(\mathbb {Y}_{n}\ni \lambda \mapsto \chi ^{(\alpha )}_\lambda (\pi )\) given by irreducible Jack character (1.5). From the way the probability measure \(\mathbb {P}_\chi \) was defined in (1.7) it follows immediately that
Any \(\alpha \)-polynomial function F can be restricted to the set \(\mathbb {Y}_{n}\) of Young diagrams with n boxes; thus it makes sense to speak about its expected value \(\mathbb {E}_\chi F\). In the case when \(F={{\mathrm{Ch}}}_\pi \) is a Jack character, this expected value can be explicitly calculated thanks to (2.4):
By considering the multiplicative structure on \(\alpha \)-polynomial functions given by the pointwise product, we get in this way a conditional expectation \(\mathbb {E}_\chi :\mathscr {P}\rightarrow \mathbb {R}\); the corresponding cumulants will be denoted by \(\kappa _{\ell }^{\chi }\).
On the other hand, by considering the disjoint product, we get a conditional expectation \(\mathbb {E}_\chi :\mathscr {P}_\bullet \rightarrow \mathbb {R}\); the corresponding cumulants will be denoted by \(\kappa _{\bullet \ell }^{\chi }\).
2.7 Equivalent characterizations of approximate factorization of characters
The following result, Theorem 2.3, is the key tool for the purposes of the current paper. Its main content is part (a); roughly speaking, it states that each of the four families of numbers (2.6)–(2.9) can be transformed into the others. Each of these four families describes some convenient aspect of the characters \(\chi _n\) in the limit \(n\rightarrow \infty \). To be more specific:
-
The family (2.8) (and its subset, the family (2.7)) has a direct probabilistic meaning. It contains information about the cumulants of some random variables which might be handy while proving probabilistic statements such as Central Limit Theorem or Law of Large Numbers.
-
On the other hand, the cumulants appearing in the families (2.6) and (2.9) are purely algebraic and do not have any direct probabilistic meaning. However, their merit lies in the fact that in many concrete applications (such as the ones from [7]) it is much simpler to verify algebraic conditions (A) and (D) than their probabilistic counterparts (B) and (C).
Theorem 2.3
(The key tool) Assume that \(\alpha =\alpha (n)\) is such as in Sect. 1.11. Assume also that for each integer \(n\ge 1\) we are given a reducible Jack character \(\chi _n:\mathcal {P}_{n}\rightarrow \mathbb {R}\).
-
(a)
Equivalent characterization of approximate factorization property.
Then the following four conditions are equivalent:
-
(A)
for each integer \(\ell \ge 1\) and all integers \(l_1,\ldots ,l_\ell \ge 2\) the limit
$$\begin{aligned} \lim _{n\rightarrow \infty } k^{\chi _n}_\ell (l_1,\ldots , l_\ell ) \ n^{\frac{l_1+\cdots +l_\ell +\ell -2}{2}} \end{aligned}$$(2.6)exists and is finite;
-
(B)
for each integer \(\ell \ge 1\) and all \(x_1,\ldots ,x_\ell \in \{{{\mathrm{Ch}}}_1,{{\mathrm{Ch}}}_2,\ldots \}\) the limit
$$\begin{aligned} \lim _{n\rightarrow \infty } \kappa ^{\chi _n}_{\ell }(x_{1},\ldots ,x_{\ell })\ n^{- \frac{\deg x_1+ \cdots + \deg x_\ell - 2(\ell -1)}{2}} \end{aligned}$$(2.7)exists and is finite;
-
(C)
for each integer \(\ell \ge 1\) and all \(x_1,\ldots ,x_\ell \in \mathscr {P}\) the limit
$$\begin{aligned} \lim _{n\rightarrow \infty } \kappa ^{\chi _n}_{\ell }(x_{1},\ldots ,x_{\ell })\ n^{- \frac{\deg x_1+ \cdots + \deg x_\ell - 2(\ell -1)}{2}} \end{aligned}$$(2.8)exists and is finite;
-
(D)
for each integer \(\ell \ge 1\) and all \(x_1,\ldots ,x_\ell \in \mathscr {P}_\bullet \) the limit
$$\begin{aligned} \lim _{n\rightarrow \infty } \kappa ^{\chi _n}_{\bullet \ell }(x_{1},\ldots ,x_{\ell })\ n^{- \frac{\deg x_1+ \cdots + \deg x_\ell - 2(\ell -1)}{2}} \end{aligned}$$(2.9)exists and is finite.
-
(A)
-
(b)
Assume that the conditions from part (a) hold true. Furthermore, assume that for \(\ell =1\) the rate of the convergence of any of the four expressions under the limit symbol in (2.6)–(2.9) is of the form
$$\begin{aligned} {\text {const}}_1+ \frac{{\text {const}}_2+o(1)}{\sqrt{n}} \end{aligned}$$(2.10)in the limit \(n \rightarrow \infty \) and all choices of \(l_1\) (respectively, for all choices of \(x_1\)); the constants depend on the choice of \(l_1\) (respectively, \(x_1\)).
Then for \(\ell =1\) the rate of convergence of each of the four expressions (2.6)–(2.9) is of the form (2.10).
When \(\alpha =1\), part (a) of the above result corresponds to [26, Theorem and Definition 1]. The proof is postponed to Sect. 3.
3 Proof of Theorem 2.3
In the current section we shall prove the key tool, Theorem 2.3.
Additionally, concerning part (a) of Theorem 2.3 we shall discuss the exact relationship between the limits of the quantities (2.6)–(2.9) in the case \(\ell \in \{1,2\}\). This relationship provides the information about the limit shape of random Young diagrams in Theorem 1.3 as well as about the covariance of the limit Gaussian process describing the fluctuations in Theorem 1.5.
Concerning part (b) of Theorem 2.3 we shall discuss the exact relationship between the constants which describe the fine asymptotics (2.10) of the quantities (2.6)–(2.9) in the case \(\ell =1\). This relationship provides the information about the mean value \(\mathbb {E}\Delta _\infty \) of the limit Gaussian process from Eq. 1.19.
3.1 Approximate factorization property for \(\alpha \)-polynomial functions
Definition 3.1
Let \(\mathcal {A}\) and \(\mathcal {B}\) be filtered, commutative, unital algebras and let \(\mathbb {E}:\mathcal {A}\rightarrow \mathcal {B}\) be a unital map. We say that \(\mathbb {E}\) has approximate factorization property if for all choices of \(x_1,\ldots ,x_\ell \in \mathcal {A}\) we have that
We consider the filtered unital algebras \(\mathscr {P}_\bullet \) and \(\mathscr {P}\) from Sect. 2.5, and as a conditional expectation between them we take the identity map:

We denote by \(\kappa _{\bullet }:=\kappa _{\mathscr {P}_\bullet }^{\mathscr {P}}\) the conditional cumulants related to the conditional expectation (3.2).
We are now ready to state the main auxiliary result, proved very recently by the second-named author, which will be necessary for the proof of the key tool, Theorem 2.3.
Theorem 3.2
([27, Theorem 2.3]) The identity map (3.2) has approximate factorization property.
3.2 Approximate factorization for \(\alpha =1\)
We denote by \(\mathscr {P}^{(1)}\) a version of the filtered algebra of \(\alpha \)-polynomial functions \(\mathscr {P}\) obtained by the specialization \(\alpha :=1\), \(\gamma :=0\); analogously we denote by \(\mathscr {P}^{(1)}_\bullet \) the algebra \(\mathscr {P}^{(1)}\) equipped with the multiplication given by the disjoint product.
The following result has been proved earlier by the second-named author.
Theorem 3.3
([26, Theorem 15]) The identity map

has approximate factorization property.
Theorems 3.2 and 3.3 are of the same flavor. There are two major differences between them: firstly, the arrows in (3.2) and (3.3) point in the opposite directions; secondly, the algebra \(\mathscr {P}\) is more rich than its specialized version \(\mathscr {P}^{(1)}\), in particular the variable \(\gamma \in \mathscr {P}\) is not treated like a scalar since \(\deg \gamma =1 >0\).
3.3 Proof of Theorem 2.3, part (a)
This proof follows closely its counterpart from the work of the second-named author [26, Theorem and Definition 1] with the references to Theorem 3.3 replaced by Theorem 3.2 and, occasionally, the roles of \(\mathscr {P}\) and \(\mathscr {P}_\bullet \) reversed. We present the details below.
3.3.1 Proof of the equivalence (A)\(\iff \)(D)
The quantities (2.6) and (2.9) coincide with their counterparts from the work of the second-named author [26, Eqs. (12) and (13)]. The equivalence of the conditions (A) and (D) was proved in [26, Section 4.7].
3.3.2 Proof of the equivalence (B)\(\iff \)(C)
The implication (C)\(\implies \)(B) is immediate since \({{\mathrm{Ch}}}_1,{{\mathrm{Ch}}}_2,\ldots \in \mathscr {P}\).
The following result was proved by the second-named author [26, Corollary 19] (note that the original paper does not contain the assumption (3.5) without which it is not true). The proof did not use any specific properties of the filtered algebra \(\mathscr {P}\) and thus it remains valid also in our context when the original algebra of polynomial functions is replaced by the algebra of\(\alpha \)-polynomial functions.
Lemma 3.4
Assume that \(X\subseteq \mathscr {P}\) is a set with the property that each \(z\in \mathscr {P}\) can be expressed as a polynomial in the elements of X:
for some \(n\ge 0\) and \(z_{i,j}\in X\) in such a way that such that for each value of \(1\le i\le n\)
in other words the degree of each monomial should be bounded from above by the degree of z.
Under the above assumption, if condition (B) holds true for all \(x_1,\ldots ,x_\ell \in X\) then more general condition (C) holds true for arbitrary \(x_1,\ldots ,x_\ell \in \mathscr {P}\).
We claim that the set \(X=\{\gamma ,{{\mathrm{Ch}}}_1,{{\mathrm{Ch}}}_2,{{\mathrm{Ch}}}_3,\ldots \}\) generates the filtered algebra \(\mathscr {P}\) in the way specified in Lemma 3.4. Indeed, by the way the filtration on \(\mathscr {P}\) was defined (cf. Definition 2.2) it is enough to check the assumption of Lemma 3.4 for \(z=\gamma ^k {{\mathrm{Ch}}}_{\pi }\) for integer \(k\ge 0\) and a partition \(\pi =(\pi _1,\ldots ,\pi _\ell )\); we will do it by induction over \(\deg z=k+|\pi |+\ell \). We write
The first summand on the right-hand side is of the form which is fits the framework given by the right-hand side of (3.4). By [5, Corollary 2.5, Corollary 3.8], the second summand on the right-hand side is of smaller degree, thus the inductive hypothesis can be applied. This concludes the proof.
We claim that (2.7) holds true for all \(x_1,\ldots ,x_\ell \in X\). Indeed, in the case when \(x_1,\ldots ,x_\ell \in \{{{\mathrm{Ch}}}_1,{{\mathrm{Ch}}}_2,\ldots \}\) this is just the assumption (C). Consider now the remaining case when \(x_j=\gamma \) for some index j. For \(\ell =1\) the corresponding expression from (2.8) is equal to
which by (1.9) converges to a finite limit, as required. For \(\ell \ge 2\), the corresponding cumulant
vanishes because it involves a deterministc random variable \(\gamma \). It follows immediately that the limit (2.8) exists.
In this way we verified that the assumptions of Lemma 3.4 are fulfilled. Condition (C) follows immediately.
3.3.3 Proof of the equivalence (C)\(\iff \)(D)
The proof will follow closely the ideas from [26, Section 4.7] with the roles of the cumulants \(\kappa ^{\chi _n}\) and \(\kappa ^{\chi _n}_{\bullet }\) interchanged. The original proof was based on the observation that the conditional cumulants (denoted in the original work [26] by the symbol \(k^{{\text {id}}}=\kappa _{\mathscr {P}^{(1)}}^{\mathscr {P}_\bullet ^{(1)}}\)) related to the map (3.3) fulfill the degree bounds (3.1) given by the approximate factorization property. By changing the meaning of the symbol \(k^{{\text {id}}}\) and setting \(k^{{\text {id}}} :=\kappa ^{\mathscr {P}}_{\mathscr {P}_\bullet } =\kappa _{\bullet }\) to be the conditional cumulants related to the map (3.2) and by applying Theorem 3.2 we still have in our more general context that the cumulants \(k^{{\text {id}}}\) fulfill the degree bounds (3.1). The reasoning from [26, Section 4.7] is still valid in our context.
3.4 Functionals \(\mathcal {S}_k\)
For a Young diagram \(\lambda \), a real number \(\alpha >0\) and an integer \(k\ge 2\) we define
where the integral on the right-hand side is taken over a polygon on the plane defined by the Young diagram \(\lambda \) (drawn in the French convention). In order to keep the notation light we shall make the dependence on \(\alpha \) implicit and we shall simply write \(\mathcal {S}_k(\lambda ):=\mathcal {S}_k^{(\alpha )}(\lambda )\).
In [27, Proposition 4.6] the second-named author proved that \(\mathcal {S}_k\in \mathscr {P}\) is an \(\alpha \)-polynomial function of degree k.
3.5 Free cumulants \(\mathcal {R}_k\)
In many calculations related to the asymptotic representation theory it is convenient to parametrize the shape of the Young diagram \(\lambda \) by free cumulants\(\mathcal {R}_k(\lambda )\) (which depend on the parameter \(\alpha \) in our settings). In the context of the representation theory of the symmetric groups these quantities have been introduced by Biane [3].
For the purposes of the current paper it is enough to know that for a fixed Young diagram \(\lambda \) its sequence of functionals of shape and its sequence of free cumulants are related to each other by the following simple systems of equations [6, Eqs. (14) and (15)]:
where we use a shorthand notation \(\mathcal {S}_k=\mathcal {S}_k(\lambda )\), \(\mathcal {R}_k=\mathcal {R}_k(\lambda )\). In fact, the above-cited papers [3, 6] concerned only the special isotropic case \(\alpha =1\), however the passage to the anisotropic case \(\alpha \ne 1\) does not create any difficulties, see the work of Lassalle [19] (who used a different normalization constants) as well as of the first-named author and Féray [5] (whose normalization we use).
3.6 The case \(\alpha =1\)
The main advantage of free cumulants lies in the combination of the following two facts.
-
Each free cumulant \(\mathcal {R}_k\) of a given Young diagram \(\lambda \) can be efficiently calculated [3] and its dependence on the shape of \(\lambda \) takes a particularly simple form (more specifically, “\(\mathcal {R}_k\) is a homogeneous function”).
-
The family \((\gamma ,\mathcal {R}_2,\mathcal {R}_3,\ldots )\) forms a convenient algebraic basis of the algebra \(\mathscr {P}\) with \(\deg \gamma =1\) and \(\deg \mathcal {R}_k=k\). In the special case \(\alpha =1\) (which corresponds to \(\gamma =0\)) the expansion of \({{\mathrm{Ch}}}_l\) in this basis takes the following, particularly simple form:
$$\begin{aligned} {{\mathrm{Ch}}}_l= \mathcal {R}_{l+1} + (\text {terms of degree at most }l-1). \end{aligned}$$(3.8)
One of the consequences of (3.8) is that in the special case \(\alpha =1\) the relationship announced in Theorem 2.3(b) between the refined asymptotics of the four quantities (2.6)–(2.9) for \(\ell =1\) takes the following, particularly simple form. Assume that there exists some sequence \((a_l)\) with the property that
note that it is a stronger version of (2.10) with \({\text {const}}_2\equiv 0\); then
where
and
see (3.6) for the last equality and [26] for more details.
3.7 Details of Theorem 2.3 part (a) in the generic case \(\alpha \ne 1\)
The original proof of [26, Theorem and Definition 1] was based on the idea of expressing various elements F of the algebra of \(\alpha \)-polynomial functions \(\mathscr {P}^{(1)}\) (such as the characters \({{\mathrm{Ch}}}_\pi \) or the conditional cumulants \(\kappa _{\bullet }\) of such characters) as polynomials in the basis \(\mathcal {R}_2,\mathcal {R}_3,\ldots \) of free cumulants and studying the top-degree of such polynomials, as we did in Sect. 3.6. In our more general context of \(\alpha \ne 1\) (or, in other words, \(\gamma \ne 0\)) the corresponding polynomial for F might have some extra terms which depend additionally on the variable \(\gamma \). These extra terms might influence the asymptotic behavior of random Young diagrams. We shall discuss this issue in more detail in the remaining of this section as well as in Sect. 3.9.
3.7.1 The first-order asymptotics when \(\alpha \) is constant
The first-named author and Féray [5, Proposition 3.7] proved that the degree of
with respect to the filtration from Sect. 3.6 remains equal to \(l+1\) even when we pass from \(\mathscr {P}^{(1)}\) to \(\mathscr {P}\) or, in other words, that the degree of the extra terms is bounded from above by \(l+1\). In the asymptotics when \(\alpha \) is a constant and does not depend on n (or, more generally, when the constant g from (1.9) fulfills \(g=0\)), it follows that \(\gamma =O(1) \ll O\left( n^{\frac{{{\mathrm{deg}}}\gamma }{2}}\right) \). Since each extra term is divisible by the monomial \(\gamma \), it follows that the contribution of the extra terms is negligible when compared to the unique original top-degree term \(\mathcal {R}_{l+1}\). It follows that in this asymptotics the relationships between the quantities \((a_l)\), \((a'_l)\) and \((a''_l)\) which provide the first-order asymptotics of, respectively, the characters, the mean value of free cumulant, and the mean value of the functionals of shape, remain the same as in Sect. 3.6 for the case \(\alpha =1\).
From Theorem 3.2 it follows that an analogous result holds true for the conditional cumulant (covariance)
and the degree of F remains equal to \(l_1+l_2\) when we pass from \(\mathscr {P}^{(1)}\) to \(\mathscr {P}\). A reasoning similar to the one above implies that not only the proof of [26, Theorem and Definition 1] remains valid in our context for \(\ell =2\), but also the relationships between the quantities (2.6)–(2.9) which provide the first-order asymptotics of cumulants remain the same as in [26, Theorem 3].
Anticipating the proof of Theorem 1.5, the above considerations imply the following explicit description of the covariance of the limiting Gaussian process \(\Delta _\infty \).
Corollary 3.5
The covariance of the Gaussian process \(\Delta _\infty \) describing the limit fluctuations of random Young diagrams from Theorem 1.5 coincides with its counterpart for \(\alpha =1\) from [26, Theorem 3].
3.7.2 The first-order asymptotics in the double scaling limit
In the asymptotics when \(\alpha =\alpha (n)\) depends on n in a way described in Sect. 1.11 with \(g\ne 0\), the extra terms in both examples (3.15), (3.16) considered above are of the same order as the original terms. It follows that the relationship between the quantities \((a_l)\), \((a'_l)\) and \((a''_l)\) is altered and depends on the constant \(g\) from (1.9), see Sect. 3.9.2 below. Also the covariance of the Gaussian process describing the fluctuations of random Young diagrams is altered; finding an explicit form for this covariance is currently beyond our reach because no closed formula for the top-degree part of the conditional cumulant \(\kappa _{\bullet }({{\mathrm{Ch}}}_{l_1},{{\mathrm{Ch}}}_{l_2})\) (an analogue of the results of [27, Section 1] for \({{\mathrm{Ch}}}_n\)) is available.
3.8 Refined asymptotics of characters
In order to find more subtle relationships between the asymptotics of various quantities appearing in Theorem 2.3 we need an analogue of Equation (3.8) between the character \({{\mathrm{Ch}}}_l\) and the free cumulants in the generic case \(\alpha \ne 1\). We present below two such formulas: the one from Sect. 3.8.1 is conceptually simpler and will be sufficient for the scaling when \(\alpha \) is fixed; in the case of the double scaling limit we will need a more involved formula from Sect. 3.8.2.
3.8.1 The rough estimate
We start with the formula expressing the top-degree part of the normalized Jack character \({{\mathrm{Ch}}}_l\) modulo terms divisible by \(\gamma ^2\) which follows follows from [19, Section 11] combined with the degree bounds of the first-named author and Féray [5, Proposition 3.7] as well as from [27, Theorem A.3]:
3.8.2 Closed formula for top-degree part of Jack characters
Let us fix an integer \(l\ge 1\). We will view the symmetric group \(\mathfrak {S}(l)\) as the set of permutations of the set \([l]:=\{1,\ldots ,l\}\) and its subgroup
as the set of permutations of the same set [l] which have l as a fixpoint. Consider the set
The group \(\mathfrak {S}(l-1)\) acts on \(\mathcal {X}_l\) by coordinate-wise conjugation:
The orbits of this action define an equivalence relation \(\sim \) on \(\mathcal {X}_l\); the corresponding equivalence classes have a natural combinatorial interpretation as non-labeled, rooted, bicolored, oriented maps withledges which is out of scope of the current paper (see [27, Section 1.4.3] for details).
For a permutation \(\pi \) we denote by \(C(\pi )\) the set of its cycles.
We say that a triple \((\sigma _1,\sigma _2,q)\) is an ‘expander’ [27, Appendix A.1], see also [6], if \(\sigma _1,\sigma _2\in \mathfrak {S}(l)\) are permutations and \(q:C(\sigma _2)\rightarrow \{2,3,\ldots \}\) is a function on the set of cycles of \(\sigma _2\) with the following two properties:
and for every set \(A\subset C(\sigma _2)\) such that \(A\ne \emptyset \) and \(A\ne C(\sigma _2)\) we have that
The following is a refined version of the formula (3.17).
Lemma 3.6
([27, Theorem A.3 and Theorem 1.6]) For each integer \(l\ge 1\) the expansion of the character \({{\mathrm{Ch}}}_l\) as a polynomial in the variables \(\gamma ,\mathcal {R}_2,\mathcal {R}_3,\ldots \) is given by
where the first sum runs over the representatives of the equivalence clases.
3.9 Proof of part (b) of Theorem 2.3
3.9.1 The scaling when \(\alpha \) is constant
Part (b) of Theorem 2.3 concerns the trivial case \(\ell =1\) which one can easily prove from scratch, based on (3.17). We shall present a detailed proof only for a specific case which will be useful in applications (more specifically, for the proof of Theorem 1.5 from Sect. 6) and we shall assume that the refined asymptotics of characters specified in part (b) of Theorem 2.3 holds true for the quantity (2.6). The other implications are analogous.
For a specific choice of the constants
for some sequences \((a_l)\) and \((b_l)\), it is a simple exercise to use (2.1) and (3.17) in order to show that
where \((a'_l)\) is given again by (3.13) and \((b'_l)\) is the unique sequence which fulfills
In particular, (3.20) shows that the refined asymptotics of characters specified in part (b) of Theorem 2.3 holds true for the quantity (2.7).
Consider now the quantity under the limit symbol in (2.8) for \(\ell =1\) and for the specific choice of \(x_1=\mathcal {S}_l\). Equation (3.6) implies that the refined asymptotics of characters specified in part (b) of Theorem 2.3 holds true for the quantity (2.8):
with the constants given by (3.14) and
We conclude the proof by pointing out that for \(\ell =1\) the expression under the limit symbol in (2.8) coincides with its counterpart from (2.9). \(\square \)
Remark 3.7
One can see that generically for \(\alpha \ne 1\) and \(\gamma \ne 0\) (even if the initial characters \(\chi _n(l)\) have small subleading terms which corresponds to \(b_l\equiv 0\)) the subleading terms in (3.23) are much bigger than their counterparts for \(\alpha =1\) from (3.12), namely they are of order \(\frac{1}{\sqrt{n}}\) times the leading asymptotic term. As we shall see in Sect. 6, this leads to non-centeredness of the limiting Gaussian process \(\Delta _\infty \).
3.9.2 The double scaling limit
In the double scaling limit \(g\ne 0\) considered in Sect. 1.11 the reasoning presented in Sect. 3.9.1 above remains valid if one replaces all the references to (3.17) by Lemma 3.6. Note, however, that the relationship (3.13) in this new context takes the form
while (3.22) takes the form
4 Technical results
This section is devoted to some technical results necessary for the proof of Theorem 1.3.
4.1 Slowly growing sequence of moments determines the measure
Lemma 4.1
Assume that \(\mu \) is a probability measure which is supported on the interval \([x_0,\infty )\) (respectively, on the interval \((-\infty ,x_0]\)) for some \(x_0\in \mathbb {R}\) and such that
holds true for some constant C and all integers \(l\ge 1\), where
is the l-th moment of \(\mu \).
Then the measure \(\mu \) is uniquely determined by its moments.
Similarly, if the measure \(\mu \) is supported on the real line \(\mathbb {R}\) and such that
holds true for some constant C and all integers \(l\ge 1\), then the measure \(\mu \) is uniquely determined by its moments.
Proof
In the case when \(\mu \) is supported on the interval \([0,\infty )\) this is exactly Stieltjes moment problem, while in the case when \(\mu \) is supported on the real line \(\mathbb {R}\) this is exactly the Hamburger moment problem. It is easy to check that the assumptions (4.1), and (4.2) imply that the Carleman’s conditions in both Stieltjes and Hamburger, respectively, problems are satisified and it follows that the measure \(\mu \) is uniquely determined by its moments.
Now, assume that \(\mu \) is a probability measure which is supported on the interval \([x_0,\infty )\). We define a probability measure \(\mu _{x_0}\) supported on the interval \([0,\infty )\), as a translation of \(\mu \) that is, for any measurable set \(A \subset \mathbb {R}\) we have
Let us compute the moments of \(\mu _{x_0}\):
This leads to the following inequalities:
By Carleman’s criterion it means that the measure \(\mu _{x_0}\) is uniquely determined by its moments, which is equivalent by the construction that the measure \(\mu \) is uniquely determined by its moments, too.
The case, when \(\mu \) is supported on the interval \((-\infty ,x_0]\) is analogous, and we leave it as a simple exercise. \(\square \)
4.2 Slow growth of \((\mathcal {R}_n)\) implies slow growth of \((\mathcal {S}_n)\)
Lemma 4.2
Let \((\mathcal {S}_l)_{l\ge 2}\) be a sequence of real numbers and let \((\mathcal {R}_l)_{l\ge 2}\) given by (3.7) be the corresponding sequence of free cumulants. Assume that the sequence of free cumulants fulfills the estimate
for some constants \(m,C\ge 0\) and all \(l\ge 2\).
Then the sequence \((\mathcal {S}_l)\) fulfills an analogous estimate
possibly for another value of the constant C.
Proof
The expansion (3.6) for \(\mathcal {S}_l\) in terms of the free cumulants gives immediately:
Since
we can bound the sum on the right-hand side of (4.5) as follows:
which plugged into (4.5) yields
which finishes the proof. \(\square \)
4.3 Estimates on some classes of permutations
Recall that for a permutation \(\pi \) we denote by \(C(\pi )\) the set of its cycles. The length
of a permutation \(\pi \in \mathfrak {S}(l)\) is defined as the minimal number of factors necessary to write \(\pi \) as a product of transpositions.
Lemma 4.3
For all integers \(r\ge 0\) and \(l\ge 1\)
Proof
We claim that for each permutation \(\pi \in \mathfrak {S}(l)\) such that \(\Vert \pi \Vert =r\) there exist at least r transpositions \(\tau \) with the property that the permutation \(\pi ':= \pi \tau \) fulfills \(\Vert \pi '\Vert =\Vert \pi \Vert -1\). Indeed, each such a transposition is of the form \(\tau =(a,b)\) with \(a\ne b\) being elements of the same cycle of \(\pi \); it follows that the number of such transpositions is equal to
By repeating inductively the same argument for the collection of permutations \((\pi ')\) obtained above, it follows that the permutation \(\pi \) can be written in at least r! different ways as a product of r transpositions. Since there are \(\left( {\begin{array}{c}l\\ 2\end{array}}\right) <l^2\) transpositions in \(\mathfrak {S}(l)\), this concludes the proof. \(\square \)
We revisit Sect. 3.8.2. In the following we will need a convenient way of parametrizing the equivalence classes in \(\mathcal {X}_l/\sim \); for this purpose we note that in each equivalence class one can choose a representative (which is not necessarily unique) \((\sigma _1,\sigma _2)\) with the property that the permutation \(\sigma _2\) has a particularly simple cycle structure, namely
for some increasing sequence \(1\le i_1<i_2<\cdots <i_\ell =l\). Note that for a fixed \(\ell =|C(\sigma _2)|\)
4.4 Growth of free cumulants
Proposition 4.4
We use the notations and assumptions of Theorem 1.3. For the random variable \(\mathcal {R}_l=\mathcal {R}_l(\lambda _n)\) we define
Then there exists some constant C such that
holds true for each integer \(l\ge 2\), where m is given by (1.13).
Proof
For a given value of n we will investigate the collection of random variables
Approximate factorization property, by Theorem 2.3(a)(C), implies (for \(\ell =1\)) that the limit (4.7) exists and is finite for each integer \(l \ge 2\). Furthermore, it implies that each cumulant \(\kappa _{\ell }\) for \(\ell \ge 2\) of the random variables (4.9) converges to zero as \(n\rightarrow \infty \).
Each moment (i.e. the mean value of a product of some random variables) can be expressed as a polynomial in the cumulants of the individual random variables via “moment-cumulant formula”. Thus by vanishing of the higher cumulants which correspond to \(\ell \ge 2\), the expected value of a product of free cumulants approximately factorizes:
We consider first the case \(g=0\), \(m=1\). Let us divide both sides of (3.17) by \(n^{\frac{l+1}{2}}\) and take the mean value \(\mathbb {E}_{\chi _n}\). By taking the limit \(n\rightarrow \infty \) and using (4.10) we obtain in this way
and the claim follows immediately.
From the following on we consider the generic case \(g\ne 0\) and \(m=2\). Analogously as above, let us divide both sides of (3.18) by \(n^{\frac{l+1}{2}}\) and take the mean value \(\mathbb {E}_{\chi _n}\). By taking the limit \(n\rightarrow \infty \) and using (4.10) we obtain in this way
We shall cluster the summands according to the parameters \(u\) and \(v\) given by
In the following we will show that from the transitivity requirement in the definition of \(\mathcal {X}_l\) it follows that
Indeed, let us construct a bipartite graph \(G = (V_\circ \sqcup V_\bullet ,E)\) with the vertices corresponding to the cycles of \(\sigma _1\) and the cycles of \(\sigma _2\): \(V_\circ = C(\sigma _1), V_\bullet = C(\sigma _2)\); we connect two vertices by an edge if the corresponding cycles are not disjoint, that is \(e = (c_1,c_2)\in E\) if \(c_1 \cap c_2 \ne \emptyset \). Then, the transitivity of the action of the group generated by \(\sigma _1,\sigma _2\in \mathfrak {S}(l)\) means precisely that the graph G is connected. Since the number of edges of G is bounded from above by l it follows that the number of vertices of G, which is equal to \(|C(\sigma _1)|+|C(\sigma _2)|\), cannot exceed \(l+1\), which gives the required inequality.
Furthermore, the contribution of the terms for which the equality \(v=0\) holds true corresponds to the specialization \(g=0\); by revisiting (3.17) it follows that this contribution is equal to \(r_{l+1}\) which corresponds to the unique equivalence class
for which \(u=0\) and \(v=0\). It is easy to check that it is the unique summand for which \(u=0\) (since the latter condition is equivalent to \(\sigma _1={\text {id}}\)). By singling out this particular summand, (4.11) can be transformed to
With the notations used in Eq. 4.12
which implies that for each \(C>0\) we have that
By Lemma 4.3 and (4.6), for each pair of integers \(u,v\ge 1\) the number of equivalence classes \([(\sigma _1,\sigma _2)]\) which could possibly contribute to the above sum is bounded from above by
For each representative \((\sigma _1,\sigma _2)\) of an equivalence class the number of functions \(q:C(\sigma _2)\rightarrow \{2,3,\ldots \}\) which fulfill (4.13) is bounded from above by
Our strategy is to prove (4.8) for \(m=2\) by induction over \(l\ge 2\). It is trivial to check that \(r_2 = 1\) always holds true and thus the induction base \(l=2\) is valid if \(C\ge 1\). We shall assume that that (4.8) holds true for \(2\le k\le l\). The value of the constant C will be specified at the end of the proof in such a way that each induction step can be justified. The induction hypothesis implies that
We claim that the following inequality holds true:
Indeed, the logarithm of the left-hand side is a convex function
its supremum over the simplex given by inequalities \(q(c)\ge 2\) and the equality (4.13) is attained in one of the simplex vertices which corresponds to
this concludes the proof of (4.15).
In this way we proved that
It follows that the right-hand side of (4.14) is bounded from above by
for \(\frac{|g|}{2^4 C}<1\). The right-hand side tends to zero uniformly over l as \(C\rightarrow \infty \); there exists therefore some C such that the right-hand side is smaller than 1. Such a choice of C assures that each inductive step is justified. This concludes the proof. \(\square \)
5 Law of large numbers: Proof of Theorem 1.3
For Reader’s convenience the proof of Theorem 1.3 was split into several subsections which consitute the current section.
5.1 Measure associated with a Young diagram
Suppose an anisotropic Young diagram \(\Lambda \subseteq \mathbb {R}\times \mathbb {R}\) (viewed in the French coordinate system) is given. We will assume that the area of \(\Lambda \) is equal to 1. Let \((x,y)\in \Lambda \) be a random point in \(\Lambda \), sampled with the uniform probability. We denote by \(P_{\Lambda }\) the probability distribution of its Russian coordinate
It is a probability measure on \(\mathbb {R}\) with the probability density
This density is a Lipschitz function with the Lipschitz constant equal to 1. Such probability measures \(P_{\Lambda }\) will be our main tool for investigation of asymptotics of Young diagrams \(\Lambda \). The Reader should be advised that this is not Kerov’s transition measure which is also a probability measure on the real line associated with a Young diagram [13] for similar purposes.
Any anisotropic Young diagram \(\Lambda \) with unit area which contains some point \((x_0,y_0)\), contains also the whole rectangle \(\{ (x,y) : 0\le x \le x_0, 0\le y\le y_0 \}\); by comparison of the areas it follows that \(x_0 y_0\le 1\). The latter inequality written in the Russian coordinate system gives the following restriction on the possible values of the corresponding profile \(\omega \):
and for the corresponding density
A simple change of variables in the integrals shows that for a Young diagram \(\lambda _n\) with n boxes and the corresponding anisotropic Young diagram \(\Lambda _n\) given by (1.16) the moments of the measure \(P_{\Lambda _n}\) are given by
5.2 Random variables \(S^{[n]}_k\) and their convergence in probability
We start the proof of Theorem 1.3. For \(k\ge 2\) consider the random variable
By aproximate factorization property, the condition (A) from Theorem 2.3 is fulfilled; it follows that the condition (C) is fulfilled as well. In the special case \(\ell =1\) and \(x_1=\mathcal {S}_k\) it follows that the limit
exists; in the special case \(\ell =2\) and \(x_1=x_2=\mathcal {S}_k\) it follows that the variance
converges to zero. Chebyshev’s inequality implies that for each \(k\ge 2\) the sequence of random variables \((S_k^{[n]})_n\) converges (as \(n\rightarrow \infty \)) to \(s_k\) in probability.
5.3 The limiting probability measure \(P_{\Lambda _\infty }\)
By (5.2), for each n the mean value
exists, is finite, and fulfills analogous bounds to (5.2). It is the density of the probability measure \(\mathbb {E}P_{\Lambda _n}\); the moments of this measure are given by
The topology on the set of probability measures (with all moments finite) given by convergence of moments can be metrized; we denote by d the corresponding distance. Equation (5.3) implies that the sequence of measures \(\left( \mathbb {E}P_{\Lambda _n} \right) \) is a Cauchy sequence in the metric space given by d; this sequence converges therefore in moments to some probability measure which will be denoted by \(P_{\Lambda _\infty }\), in particular
In general, it might happen that the measure \(P_{\Lambda _\infty }\) is not unique; it turns out, however, that in the setup which we consider the measure\(P_{\Lambda _\infty }\)is uniquely determined by its moments; we shall prove it in the following.
5.4 The measure \(P_{\Lambda _\infty }\) is determined by its moments
By a minor modification of the proof of (4.10) we have
It follows that the relation between the families of real numbers \((s_k)_{k\ge 2}\) and \((r_k)_{k \ge 2}\) (given by (4.7)) is given by an analogue of (3.7).
Proposition 4.4 states that there exists some constant C such that
for all positive integers \(k \ge 2\), where m is given by (1.13). Thus Lemma 4.2 gives us the following estimates for the moments of \(P_{\Lambda _\infty }\):
for some constants \(C',C''\).
We consider first the case \(g=0\). Lemma 4.1 implies immediately that the measure \(P_{\Lambda _\infty }\) is uniquely determined by its moments which concludes the proof.
In the case \(g>0\) the height of each box constituting the anisotropic Young diagram \(\Lambda _n\) is equal to \(g+o(1)>c\) for some constant \(c>0\), uniformly over n, cf. Sect. 1.11. By comparison of the areas it follows that the length l of the bottom rectangle constituting \(\Lambda _n\) fulfills \( l c \le 1 \); in particular it follows that the support of the measure \(P_{\Lambda _n}\) is contained in the interval \(\left( -\infty , \frac{1}{c} \right] \). It follows that an analogous inclusion holds true for the support of the mean value \(\mathbb {E}P_{\Lambda _n}\); by passing to the limit the same is true for \(P_{\Lambda _\infty }\). It follows that Lemma 4.1 can be applied which concludes the proof.
The case \(g<0\) is fully analogous.
5.5 Weak convergence of probability measures implies uniform convergence of densities
For \(\epsilon >0\) and \(u_0\in \mathbb {R}\) let \(\phi _\epsilon :\mathbb {R}\rightarrow \mathbb {R}_+\) be a function on the real line such that \(\phi _\epsilon \) is supported on an \(\epsilon \)-neighborhood of \(u_0\) and \(\int \phi _\epsilon (u) \hbox {d}u = 1\). Since \(\mathbb {E}f_{\Lambda _n}\) is Lipschitz with constant 1, it follows that
By weak convergence of probability measures, the integral on the left-hand side converges, as \(n\rightarrow \infty \), to \(\int \ \phi _\epsilon (u)\ \hbox {d}P_{\Lambda _\infty }(u)\). By passing to the limit, the above inequality implies therefore that
Since this inequality holds true for arbitrary \(\epsilon >0\), it follows that the sequence \(\mathbb {E}f_{\Lambda _n}(u_0)\) is a Cauchy sequence, hence it converges to a finite limit which will be denoted by \(f_{\Lambda _\infty }(u_0)\). In other words, we have proved that the functions \(\mathbb {E}f_{\Lambda _n}\) converge pointwise to the function \(f_{\Lambda _\infty }\); since all functions \(\mathbb {E}f_{\Lambda _n}\) are Lipschitz with the same constant, the convergence is uniform on a compact set\(K=[-R,R]\)for arbitrary value ofR.
On the other hand, inequalities (5.2) show that the distance between \(\mathbb {E}f_{\Lambda _n}\) and \(f_{\Lambda _\infty }\) with respect to the supremum norm on the set \(K^c=\mathbb {R}\setminus K\) is bounded by
Since the right-hand side converges to zero as \(R\rightarrow \infty \), it follows that the sequence of functions\(\mathbb {E}f_{\Lambda _n}\)converges to\(f_{\Lambda _\infty }\)uniformly on the whole real line\(\mathbb {R}\).
To conclude, we proved the following theorem which might be of independent interest.
Theorem 5.1
Let \((\Lambda _n)\) be a sequence of random anisotropic Young diagrams, each with the unit area. Let \((P_{\Lambda _n})\) be the corresponding sequence of random probability measures on \(\mathbb {R}\) with densities \((f_{\Lambda _n})\) as in Sect. 5.1. Assume that the sequence of probability measures \((\mathbb {E}P_{\Lambda _n})\) converges to some limit in the weak topology.
Then there exists a function \(f_{\Lambda _\infty }\) such that \(\mathbb {E}f_{\Lambda _n} \rightarrow f_{\Lambda _\infty }\) uniformly on \(\mathbb {R}\).
5.6 Convergence of densities, in probability
We have proved that the sequence of random variables \((S_k^{[n]})_n\) converges (as \(n\rightarrow \infty \)) to \(s_k\) in probability; in other words for each \(\epsilon >0\) and each integer \(k\ge 0\)
in other words the sequence of random probability measures \(P_{\Lambda _n}\) converges to the measure \(P_{\Lambda _\infty }\)in moments, in probability.
The weak topology of probability measures can be metrized, for example by Lévy–Prokhorov distance \(\pi \). Since the measure \(P_{\Lambda _\infty }\) is uniquely determined by its moments, convergence to \(P_{\Lambda _\infty }\)in moments implies convergence to the same limit in the weak topology of probability measures. With the help of the distances d (cf. Sect. 5.3) and \(\pi \), the latter statement can be rephrased as follows: for each \(\varepsilon >0\) there exists \(\delta >0\) such that for any probability measure \(\mu \)
It follows that the sequence of random probability measures \(P_{\Lambda _n}\) converges to the measure \(P_{\Lambda _\infty }\)in the weak topology of probability measures, in probability, i.e. for each \(\varepsilon >0\)
Let \(\epsilon >0\); by adapting the proof of (5.6), we get that
Lévy–Prokhorov distance \(\pi \) metrizes the weak convergence of probability measures; it follows that we can choose sufficiently small \(\varepsilon >0\) with the property that for any probability measure \(\mu \) on \(\mathbb {R}\)
Equation (5.9) combined with (5.11) as well as (5.10) imply therefore that
As \(\epsilon \searrow 0\), the integral \(\int \phi _\epsilon (u) \hbox {d}P_{\Lambda _\infty }(u) \) converges to the density \(f_{\Lambda _\infty }(u_0)\) by an analogue of (5.6). In this way we proved that for each\(u_0\)the sequence\(f_{\Lambda _n}(u_0)\)converges to\(f_{\Lambda _\infty }(u_0)\)in probability.
By the same type of argument as in (5.7) it follows that the sequence of functions\(f_{\Lambda _n}\)converges uniformly to\(f_{\Lambda _\infty }\)in probability, i.e. for each \(\epsilon >0\)
with respect to the supremum norm.
5.7 Back to Young diagrams
The function \(\omega _{\Lambda _\infty }\) which was promised in the formulation of Theorem 1.3 is simply given by the relationship (5.1) for the specific choice of \(f_{\Lambda }:=f_{\Lambda _\infty }\), namely
We just finished the proof of the fact that \(\omega _{\Lambda _n}\) converges to \(\omega _{\Lambda _\infty }\) in the supremum norm as \(n \rightarrow \infty \), in probability, thus the proof of Theorem 1.3 is completed.
6 Central Limit Theorem: Proof of Theorem 1.5
Proof of Theorem 1.5
In the light of Remark 1.6 we shall investigate the cumulants of the form
for the random variables \((Y_k)\) given by (1.18).
We start with the case \(\ell \ge 2\). By (1.17), each \(Y_k\) is equal (up to a deterministic shift) to the random variable
For \(\ell \ge 2\) the cumulant \(\kappa _\ell \) is translation-invariant; it follows therefore that
By Theorem 2.3(a) the approximate factorization property of \((\chi _n)\) is equivalent to condition (C) which we apply in the special case when \((x_1,\ldots ,x_{\ell }):=(\mathcal {S}_{i_1},\ldots ,\mathcal {S}_{i_\ell })\). The latter implies that the right-hand side of (6.1) is of order
\(O\left( {n}^{\frac{2-\ell }{2}} \right) \). This implies that for each \(\ell \ge 3\)
Consider now the case \(\ell =2\). If we adapt the above reasoning, we get that the limit
exists and is finite.
We consider now the case \(\ell =1\). By Theorem 2.3(b), enhanced approximate factorization property implies that for each \(k\ge 2\) there exist constants \(a_k'', b_k''\) such that
as \(n\rightarrow \infty \). It follows that the cumulant
converges as \(n\rightarrow \infty \) to \(b_k''\) (given explicitly by (3.24)).
Let us summarize the above discussion. We have proved that the limit
exists and is finite for any choice of \(\ell \ge 1\) and \(i_1,\ldots ,i_\ell \ge 2\). In other words: the joint distribution of the random variables \((Y_i)\) converges in moments as \(n\rightarrow \infty \) to the joint distribution of an abstract family of random variables \((Z_i)\) with the property that all cumulants vanish: \(\kappa _\ell \left( Z_{i_1},\ldots , Z_{i_\ell } \right) =0\), except for \(\ell \le 2\). The latter is the defining property of the Gaussian distribution. Since the Gaussian distribution is uniquely determined by its moments, it follows that \((Y_i)\) converges to \((Z_i)\) not only in moments but also in the weak topology of probability measures, as required. \(\square \)
References
Baik, J., Deift, P., Johansson, K.: On the distribution of the length of the longest increasing subsequence of random permutations. J. Am. Math. Soc. 12(4), 1119–1178 (1999)
Borodin, A., Gorin, V., Guionnet, A.: Gaussian asymptotics of discrete \(\beta \)-ensembles. Publ. Math. Inst. Hautes Études Sci. 125, 1–78 (2017)
Biane, P.: Representations of symmetric groups and free probability. Adv. Math. 138(1), 126–181 (1998)
Biane, P.: Approximate factorization and concentration for characters of symmetric groups. Int. Math. Res. Not. 4, 179–192 (2001)
Dołęga, M., Féray, V.: Gaussian fluctuations of Young diagrams and structure constants of Jack characters. Duke Math. J. 165(7), 1193–1282 (2016)
Dołęga, M., Féray, V., Śniady, P.: Explicit combinatorial interpretation of Kerov character polynomials as numbers of permutation factorizations. Adv. Math. 225(1), 81–120 (2010)
Dołęga, M., Śniady, P.: Examples of Jack-deformed random Young diagrams. In preparation (2018)
Forrester, P.J.: Log-Gases and Random Matrices, Volume 34 of London Mathematical Society Monographs Series. Princeton University Press, Princeton (2010)
Fulman, J.: Stein’s method, Jack measure, and the Metropolis algorithm. J. Comb. Theory Ser. A 108(2), 275–296 (2004)
Ivanov, V., Olshanski, G.: Kerov’s central limit theorem for the Plancherel measure on Young diagrams. In: Symmetric Functions 2001: Surveys of Developments and Perspectives, Volume 74 of NATO Sci. Ser. II Math. Phys. Chem., pp. 93–151. Kluwer, Dordrecht (2002)
Jack, H.: A class of symmetric polynomials with a parameter. Proc. Roy. Soc. Edinburgh Sect. A 69:1–18 (1970/1971)
Kerov, S.: Gaussian limit for the Plancherel measure of the symmetric group. C. R. Acad. Sci. Paris Sér. I Math. 316(4), 303–308 (1993)
Kerov, S.: Transition probabilities of continual Young diagrams and the Markov moment problem. Funct. Anal. Appl. 27(3), 104–117 (1993)
Kerov, S.: The boundary of Young lattice and random Young tableaux. In: Formal Power Series and Algebraic Combinatorics (New Brunswick, NJ, 1994), Volume 24 of DIMACS Ser. Discrete Math. Theor. Comput. Sci., pp. 133–158. Amer. Math. Soc., Providence (1996)
Kerov, S.: Anisotropic Young diagrams and Jack symmetric functions. Funct. Anal. Appl. 34, 41–51 (2000)
Kerov, S., Olshanski, G.: Polynomial functions on the set of Young diagrams. C. R. Acad. Sci. Paris Sér. I Math. 319(2), 121–126 (1994)
Kerov, S., Okounkov, A., Olshanski, G.: The boundary of the Young graph with Jack edge multiplicities. Int. Math. Res. Not. 4, 173–199 (1998)
Lassalle, M.: A positivity conjecture for Jack polynomials. Math. Res. Lett. 15(4), 661–681 (2008)
Lassalle, M.: Jack polynomials and free cumulants. Adv. Math. 222(6), 2227–2269 (2009)
Logan, B.F., Shepp, L.A.: A variational problem for random Young tableaux. Adv. Math. 26(2), 206–222 (1977)
Macdonald, I.G.: Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (1995). (With contributions by A. Oxford Science Publications)
Matsumoto, S.: Jack deformations of Plancherel measures and traceless Gaussian random matrices. Electron. J. Comb. 15(R149), 1 (2008)
Moll, A.: Random partitions and the quantum Benjamin–Ono hierarchy. Preprint arXiv:1508.03063 (2015)
Okounkov, A.: The uses of random partitions. In: 14th International Congress on Mathematical Physics, pp. 379–403. Word Scientists (2003)
Sagan, B.E.: The symmetric group, volume 203 of Graduate Texts in Mathematics. In: Representations, Combinatorial Algorithms, and Symmetric Functions, 2nd edn. Springer, New York (2001)
Śniady, P.: Gaussian fluctuations of characters of symmetric groups and of Young diagrams. Probab. Theory Rel. Fields 136(2), 263–297 (2006)
Śniady, P.: Asymptotics of Jack characters. Preprint arXiv:1506.06361v3 (2018)
Stanley, R.P.: Some combinatorial properties of Jack symmetric functions. Adv. Math. 77(1), 76–115 (1989)
Thoma, E.: Die unzerlegbaren, positiv-definiten Klassenfunktionen der abzählbar unendlichen, symmetrischen Gruppe. Math. Z. 85, 40–61 (1964)
Vershik, A.M: Asymptotic combinatorics and algebraic analysis. In Proceedings of the International Congress of Mathematicians, vol. 1, 2 (Zürich, 1994), pp. 1384–1394. Birkhäuser, Basel (1995)
Vershik, A.M., Kerov, S.V.: Asymptotic behavior of the Plancherel measure of the symmetric group and the limit form of Young tableaux. Dokl. Akad. Nauk SSSR 233(6), 1024–1027 (1977)
Vershik, A.M., Kerov, S.V.: Asymptotic theory of the characters of a symmetric group. Funktsional. Anal. i Prilozhen. 15(4), 15–27 (1981). 96
Acknowledgements
Research supported by Narodowe Centrum Nauki, Grant No. 2014/15/B/ST1/00064.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dołęga, M., Śniady, P. Gaussian fluctuations of Jack-deformed random Young diagrams. Probab. Theory Relat. Fields 174, 133–176 (2019). https://doi.org/10.1007/s00440-018-0854-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-018-0854-9