Abstract
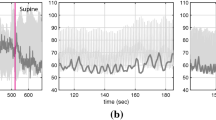
Mathematical models can provide useful insights explaining behavior observed in experimental data; however, rigorous analysis is needed to select a subset of model parameters that can be informed by available data. Here we present a method to estimate an identifiable set of parameters based on baseline left ventricular pressure and volume time series data. From this identifiable subset, we then select, based on current understanding of cardiovascular control, parameters that vary in time in response to blood withdrawal, and estimate these parameters over a series of blood withdrawals. These time-varying parameters are first estimated using piecewise linear splines minimizing the mean squared error between measured and computed left ventricular pressure and volume data over four consecutive blood withdrawals. As a final step, the trends in these splines are fit with empirical functional expressions selected to describe cardiovascular regulation during blood withdrawal. Our analysis at baseline found parameters representing timing of cardiac contraction, systemic vascular resistance, and cardiac contractility to be identifiable. Of these parameters, vascular resistance and cardiac contractility were varied in time. Data used for this study were measured in a control Sprague-Dawley rat. To our knowledge, this is the first study to analyze the response to multiple blood withdrawals both experimentally and theoretically, as most previous studies focus on analyzing the response to one large blood withdrawal. Results show that during each blood withdrawal both systemic vascular resistance and contractility decrease acutely and partially recover, and they decrease chronically across the series of blood withdrawals.







Similar content being viewed by others
References
Balsa-Canto E, Alonso AA, Banga JR (2010) An iterative identification procedure for dynamic modeling of biochemical networks. BMC Syst Biol 4:11
Beard DA, Mescam M (2012) Mechanisms of pressure-diuresis and pressure-natriuresis in Dahl salt-resistant and Dahl salt-sensitive rats. BMC Physiol 12:6
Boron W, Boulpaep E (2017) Textbook of medical physiology. Elsevier, Philadelphia
Brizzee BL, Russ RD, Walker BR (1991) Role of vasopressin in acutely altered baroreflex sensitivity during hemorrhage in rats. Am J Physiol 261:R677–R685
Bugenhagen SM, Cowley AW Jr, Beard DA (2010) Identifying physiological origins of baroreflex dysfunction in salt-sensitive hypertension in the Dahl SS rat. Physiol Genom 42:23–41
Chis O-T, Banga JR, Balsa-Canto E (2011) Structural identifiability of systems biology models: a critical comparison of methods. PLoS ONE 6:e27755
Cintrón-Arias A, Banks HT, Capaldi A, Lloyd AL (2009) A sensitivity matrix based methodology for inverse problem formulation. J Inverse Ill posed Prob 17:545–564
Cowley AW Jr (1992) Long-term control of arterial blood pressure. Physiol Rev 72:231–300
Di Rienzo M, Parati G, Radaelli A, Castiglioni P (2009) Baroreflex contribution to blood pressure and heart rate oscillations: time scales, time-variant characteristics and nonlinearities. Phil Trans R Soc A 367:1301–1318
Ellwein LM (2008) Cardiovascular and respiratory regulation, modeling and parameter estimation. PhD Thesis, Applied Math, NC State University, Raleigh, NC
Forsyth RP, Hoffbrand BI, Melmon KL (1970) Redistribution of cardiac output during hemorrhage in unanesthetized monkey. Circ Res 27:311–320
Gelman S (2008) Venous function and central venous pressure: a physiologic story. Anesthesiology 108:735–748
Greenway CV, Lautt WW (1986) Blood volume, the venous system, preload, and cardiac output. Can J Physiol Pharmacol 64:383–387
Hinojosa-Laborde C, Greene AS, Cowley AW (1988) Autoregulation of the systemic circulation in conscious rats. Hypertension 11:685–691
Johnson PC (1980) The myogenic response. In: Bohr DF, Somlyo AP, Sparks HV (eds) The handbook of physiology. The cardiovascular system. Vascular smooth muscle. American Physiological Society, Bethesda, MD, Chapter 15, pp 409–442
Kapela A, Bezerianos A, Tsoukias NM (2008) A mathematical model of Ca2+ dynamics in rat mesenteric smooth muscle cell: agonist and NO stimulation. J Theor Biol 253:238–260
Kim T, Hendrich KS, Masamoto K, Kim SG (2007) Arterial versus total blood volume changes during neural activity-induced cerebral blood flow change: implication for BOLD fMRI. J Cereb Blood Flow Metab 27:1235–1247
Krames BB, Vanliere EJ (1966) Heart weight and ventricular weights of normal adult albino rats. Anat Rec 156:461–464
Leggett RW, Williams LR (1995) A proposed blood circulation model for reference man. Health Phys 69:187–201
Magder S, de Varennes B (1998) Clinical death and the measurement of stressed vascular volume. Crit Care Med 26:1061–1064
Marquis AD, Arnold A, Dean C, Carlson BE, Olufsen MS (2018) Practical identifiability and uncertainty quantification of a pulsatile cardiovascular model. Math Biosci. https://doi.org/10.1016/j.mbs.2018.07.001
Matzuka B, Mehlsen J, Tran H, Olufsen MS (2015) Using Kalman filtering to predict time-varying parameters in a model predicting baroreflex regulation during head-up tilt. IEEE Trans Biomed Eng 62:1992–2000
Miao H, Xia X, Perelson AS, Wu H (2011) On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev 53:3–39
Oosting J, StruijkerBoudier HAJ, Janssen BJA (1997) Validation of a continuous baroreceptor reflex sensitivity index calculated from spontaneous fluctuations of blood pressure and pulse interval in rats. J Hypertens 15:391–399
Ottesen JT, Mehlsen J, Olufsen MS (2014) Structural correlation method for model reduction and practical estimation of patient specific parameters illustrated on heart rate regulation. Math Biosci 257:50–59
Patterson SW, Piper H, Starling EH (1914) The regulation of the heart beat. J Physiol 48:465–513
Pope SR, Ellwein LM, Zapata CL, Novak V, Kelley CT, Olufsen MS (2009) Estimation and identification of parameters in a lumped cerebrovascular model. Math Biosci Eng 6:93–115
Raue A, Kreutz C, Maiwald T, Bachmann J, Schilling M, Klingmüller U, Timmer J (2009) Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 25:1923–1929
Skrajnar S, Cerne M, Bozic M, Peternel L (2009) Effect of replacement fluids saline, gelofusine, and blood on biochemical and hematological parameters in rats subjected to repeated blood sampling. Med Sci Monit 15:BR293–BR300
Smith JJ, Forth CM, Erickson M (1994) Hemodynamic response to the upright posture. J Clin Pharmacol 34:375–386
Smith BW, Chase JG, Nokes RI, Shaw GM, Wake G (2004) Minimal haemodynamic system model including ventricular interaction and valve dynamics. Med Eng Phys 26:131–139
Transtrum MK, Machta BB, Sethna JP (2011) Geometry of nonlinear least squares with applications to sloppy models and optimization. Phys Rev E 83:036701
Trippodo NC (1981) Total circulatory capacity in the rat. Effects of epinephrine and vasopressin on compliance and unstressed volume. Circ Res 49:923–931
Williams ND, Wind-Willassen Ø, Wright AA, Program REU, Mehlsen J, Ottesen JT, Olufsen MS (2014) Patient-specific modelling of head-up tilt. Math Med Biol 31:365–392
Wu F, Yang F, Vinnakota KC, Beard DA (2007) Computer modeling of mitochondrial tricarboxylic acid cycle, oxidative phosphorylation, metabolite transport, and electrophysiology. J Biol Chem 282:24525–24537
Young DB (2010) Control of cardiac output. In: Granger DN, Granger JP (eds) Colloquium series on integrated systems physiology: from molecule to function to disease. Morgan and Claypool Life Sciences, San Rafael
Funding
This material is based upon work supported by the Mathematics Research Communities of the American Mathematical Society, under National Science Foundation Grant Number DMS 1321794. The project was initiated during the Mathematics Research Community on Mathematics in Physiology and Medicine workshop (2016). Follow-up visits and workshops were supported by the John N. Mordeson Endowed Chair in Mathematics at Creighton University and by the Mathematical Biosciences Institute. In addition, MVC was supported in part by the Mathematical Biosciences Institute and the National Science Foundation under Grant Number DMS 1440386, and by NSF Grant Number DMS 1408742. SSD was supported by a Joint University of California Davis and Lawrence Livermore National Laboratory Graduate Mentorship Award. CD, BEC and MSO were been supported in part by NIH NIGMS Grant Number P50-GM094503-02, and CD was supported by was supported by the U.S. Department of Veterans Affairs BLR&D program by a Merit Review Award # BX001863. CD and BEC were also supported by NIH NHLBI Grant Number U01 HL109505-01.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Ethical approval
All applicable international, national, and/or institutional guidelines for the care and use of animals were followed. All procedures performed in studies involving animals were in accordance with the ethical standards of the institution at which the studies were conducted.
Data
The datasets generated during and/or analyzed during the current study are available on request from the corresponding author.
Additional information
Communicated by Peter J. Thomas.
This article belongs to the Special Issue on Control Theory in Biology and Medicine. It derived from a workshop at the Mathematical Biosciences Institute, Ohio State University, Columbus, OH, USA.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: Cardiovascular model equations
Appendix: Cardiovascular model equations
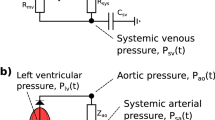
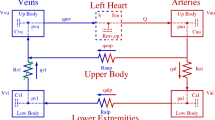
We provide here the complete set of equations for the five-compartment cardiovascular model proposed above and summarized in Fig. 2. The evolution of each compartment’s volume is given by:
Note that this corresponds to the blood withdrawal simulations where the withdrawal rate is \(q_{\mathrm{out}}\). The flow between compartments is given by:
(The expressions for \(q_{\mathrm{av}}\) and \(q_{\mathrm{mv}}\) are provided again for completeness.)
The pressures in each compartment are given by:
where variables \(C_i\) correspond to the compliance in compartment i (see Table 3 for nominal values) and \(E_{\mathrm{lv}}(t)\) denotes the time-varying elastance described in Eq. (4).
Rights and permissions
About this article
Cite this article
Ciocanel, MV., Docken, S.S., Gasper, R.E. et al. Cardiovascular regulation in response to multiple hemorrhages: analysis and parameter estimation. Biol Cybern 113, 105–120 (2019). https://doi.org/10.1007/s00422-018-0781-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-018-0781-y