Closed-loop firing rate regulation of two interacting excitatory and inhibitory neural populations of the basal ganglia

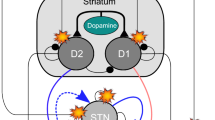
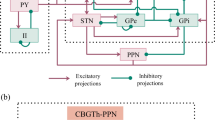
Abstract

This paper develops a new closed-loop firing rate regulation strategy for a population of neurons in the subthalamic nucleus, derived using a model-based analysis of the basal ganglia. The system is described using a firing rate model, in order to analyse the generation of beta-band oscillations. On this system, a proportional regulation of the firing rate reduces the gain of the subthalamo-pallidal loop in the parkinsonian case, thus impeding pathological oscillation generation. A filter with a well-chosen frequency is added to this proportional scheme, in order to avoid a potential instability of the feedback loop due to actuation and measurement delays. Our main result is a set of conditions on the parameters of the stimulation strategy that guarantee both its stability and a prescribed delay margin. A discussion on the applicability of the proposed method and a complete set of mathematical proofs is included.

Appendices

Appendix 1: The Nyquist criterion

Consider a transfer function G(s), and in order to keep the discussion simple, assume that it is rational and that it has no poles on the imaginary axis. Note that the poles of a rational transfer function are the roots of its denominator, while its zeros are the roots of its numerator, and that such a transfer function is stable if all its poles have a strictly negative real part. A pole with strictly positive real part is called unstable. A standard question, in control theory, is to determine whether the closed-loop transfer function

$$\begin{aligned} H(s) = \dfrac{G(s)}{1 + G(s)}, \end{aligned}$$

associated with the feedback interconnection in Fig. 6, is stable. Observe that $y(s) = H(s) u(s)$.

Fig. 6

Block diagram associated with the Nyquist criterion

An answer to this question is given by Nyquist’s stability theorem. Consider the Nyquist contour $\varGamma$ (see Fig. 7), composed of a straight line on the imaginary axis, going from $-iR$ to $+iR$, and a half-circle of radius R. It is assumed that R is big enough so that all unstable poles of G(s) are contained in the interior of $\varGamma$. The Nyquist plot of the open-loop transfer G(s) is the image of $\varGamma$ under the complex function G (see Fig. 8).

Fig. 7

Parameter R of the Nyquist contour must be chosen in such a way that all the unstable poles of G(s) are contained in its interior

Fig. 8

Nyquist plots of the open-loop transfer $G(s) = 1/\left( (s+1) ( s^2 + 2 \zeta s + 1 ) \right)$. The solid and dashed parts of the plot correspond, respectively, to the positive and negative frequencies on the imaginary axis of the Nyquist contour. The dotted part of the contour does not appear in the plot, when R is big enough, because the image of the circle at infinity by a strictly proper rational function is a single point at the origin. Left when $\zeta =1/2$, the Nyquist locus does not encircle the critical point $-1$. Since G(s) is stable ($P=0$), the closed-loop transfer H(s) is then also stable. Right when $\zeta =1/6$, the Nyquist locus encircles $-1$, and thus H(s) is unstable

Theorem 1

(Nyquist’s stability theorem) Assume that the open-loop transfer function G(s) has P unstable poles and that they are all contained in the interior of the Nyquist contour $\varGamma$. The closed-loop transfer function H(s) is stable if and only if the total number of clockwise encirclements of the critical point $-1$ by G(s), when s follows $\varGamma$ in the clockwise direction, is equal to $-P$. In particular, if G(s) is stable, then H(s) is stable if and only if the Nyquist plot of G(s) does not encircle the critical point.

In fact, this result is directly related to the argument principle of Cauchy, which applies to any meromorphic function. For this reason, the assumption that G(s) is rational is not essential and this result can also be applied to transfer functions that contain delays. We refer the reader to Curtain and Zwart (1995) for a detailed account on this question, and to Haidar et al. (2014) for an example on how such extended results can be applied in the case of the basal ganglia dynamics. A particularly interesting case, for which the application of the previous criterion is trivial, is the small-gain case.

Corollary 1

(Small-gain theorem) Assuming that the open-loop transfer function G(s) is stable and that $\Vert G \Vert _\infty < 1$, then the closed-loop transfer function H(s) is also stable.

Indeed, when the gain of G is smaller than 1, the Nyquist locus is contained inside the unit circle and thus cannot encircle the critical point. The interested reader will find in (Aström and Murray 2010, Chap. 9) an accessible introduction to the two previous classical results of control theory, and in Curtain and Zwart (1995) a detail mathematical account that in particular, covers the case of non-rational transfer functions. In order to illustrate them with a simple example, we consider the following transfer function

$$\begin{aligned} G(s) = \frac{1}{\left( s+1 \right) \left( s^2 + 2 \zeta s + 1 \right) }. \end{aligned}$$

(12)

When $\zeta >0$, this transfer function does not have any unstable pole. Since $P=0$, the closed-loop function H(s) will be stable if and only if the Nyquist plot of G(s) does not encircle the critical point. The curves obtained for $\zeta =1/2$ and $\zeta =1/6$ are shown in Fig. 8. In the first case H(s) is stable, while in the second it is unstable.

One of the main strengths of the Nyquist criterion is that in addition to the information it provides about whether a system is stable, it also gives an indication on the robustness of the stability, with respect to different perturbations. In order to explain this point, one has to introduce two additional concepts. To any transfer function G, one can associate its gain $\gamma _G(\omega )$ and phase $\varphi _G(\omega )$, at a given frequency $\omega \ge 0$, which are defined by the relations

$$\begin{aligned} \gamma _G(\omega )=20\log _{10}\left| G(j\omega )\right| \quad \text{ and } \quad \varphi _G(\omega )= \arg \left( G(j\omega ) \right) . \end{aligned}$$

(13)

In control theory, the gain and phase of the system are often represented graphically either as a Bode diagram (the gain and the phase are plotted using a logarithmic scale for the frequencies) or as a Nyquist diagram (the gain and the phase are represented in polar coordinates, like in Fig. 8). In our approach, the case where the function $\gamma _G$ is strictly decreasing is of a particular interest. Indeed, in this case, to any strictly proper transfer function G such that $\gamma _G(0) > 0$ we can associate its (gain) crossover frequency $\omega _G$, which is defined as the only frequency such that

$$\begin{aligned} \gamma _G(\omega _G)=0. \end{aligned}$$

(14)

This frequency can be used to define the delay margin $\varDelta (G)$ by the relation

$$\begin{aligned} \varDelta (G) = \dfrac{\pi +\varphi _G\left( \omega _G\right) }{\omega _G}. \end{aligned}$$

(15)

If $\gamma _G$ is strictly decreasing but $\gamma _G(0) \le 0$, if G is stable, then we can still define $\omega _G = +\infty$. The case of non-monotonic gains is more complicated. Indeed, in this case, the delay margin might not be unique. We refer the interested reader the survey paper of Sipahi et al. (2011) for a more detailed introduction to systems with time-delays.

In order to illustrate the application of the Nyquist criterion for quantifying the robustness of stability, we consider again the transfer function G(s) of Eq. (12) but, this time, with a delay d in the loop (see Fig. 9). When $\zeta =1/3$, the system is stable when $d=0$. Nevertheless, there is a single strictly positive frequency $\omega _G$ such that $\gamma _G(\omega _G)=0$. This frequency defines the phase margin $\pi +\varphi _G\left( \omega _G\right)$ and the delay margin $\varDelta (G)$ defined above. When the delay is such that $d \ge \varDelta (G)$, the system becomes unstable (see Fig. 10).

Fig. 9

Block diagram for the Nyquist stability criterion, with a delay

Fig. 10

Nyquist plots for $\zeta = 1/3$, for $d=0$ and $d=\varDelta (G)$

Appendix 2: Mathematical proofs

Proof of Proposition 1

We recall that the transfer function $H_s$ is given by

$$\begin{aligned} H_s(s)=\dfrac{\sigma _s^{\star }}{\tau _s s+1+\sigma _s^{\star }C(s)e^{-ds}}=\dfrac{\sigma _s^{\star }}{D(s)}, \end{aligned}$$

where

$$\begin{aligned} C(s)=\frac{k_p}{1+\frac{s}{\omega _p}} \quad \hbox {and} \quad D(s):=1+\tau _s s+\sigma _s^{\star }C(s)\hbox {e}^{-ds}. \end{aligned}$$

Remark that reducing $\Vert H_s\Vert _{\infty }$ amounts to increasing $\Vert D\Vert _{\infty }$. The computation of $\Vert D\Vert _{\infty }$ is complicated because of the presence of delay in D(s). For this reason, we introduce the function

$$\begin{aligned} D_0(s):=1+\tau _s s+\sigma _s^{\star }C(s). \end{aligned}$$

The proof is decomposed in five steps. The first step consists in comparing the magnitude of the transfer functions D and $D_0$. This is done with the help of a function $D_1$, introduced below. In the second step, we compute the magnitudes of $D_0$ and $D_1$. The third step consists in providing a lower bound and an upper bound on $\left| D_0(s)\right|$ and $\left| D_1(s)\right|$, respectively. In the fourth step, we give an estimate of $\Vert D\Vert _{\infty }$ when the filter frequency $\omega _p$ is sufficiently close to zero. By the last step, we conclude the proof.

Step i Let $s=j\omega$, where $\omega \in \mathbb {R}$. Using the triangle inequality, we have

$$\begin{aligned} \left| D_0(j\omega )\right| -\left| D(j\omega )\right|\le & {} \Big |\left| D_0(j\omega )\right| -\left| D(j\omega )\right| \Big |\\\le & {} \left| D(j\omega )-D_0(j\omega )\right| \\\le & {} \sigma _s^{\star }\left| C(j\omega )\right| \left| \hbox {e}^{-jd\omega }-1\right| , \end{aligned}$$

from which we obtain that

$$\begin{aligned} \left| D(j\omega )\right| \ge \left| D_0(j\omega )\right| -\sigma _s^{\star }\left| C(j\omega )\right| \left| \hbox {e}^{-jd\omega }-1\right| . \end{aligned}$$

(16)

From (Doyle et al. 1990, Sect. 4), we know that for each $d>0$, there exist two real positive numbers $\alpha$ and $\beta$, such that the following inequality holds

$$\begin{aligned} \left| e^{-jd\omega }-1\right| <\left| \dfrac{j\alpha \omega }{1+j\beta \omega }\right| , \end{aligned}$$

for all $\omega \in \mathbb {R}$. Thanks to this property, the delay d will not be involved in our estimation of $\Vert H_s\Vert _{\infty }$. Now, introduce the function

$$\begin{aligned} D_1(s):=\sigma _s^{\star }C(s)\dfrac{\alpha s}{1+\beta s}. \end{aligned}$$

Inequality (16) then implies that

$$\begin{aligned} \left| D(j\omega )\right| \ge \left| D_0(j\omega )\right| -\left| D_1(j\omega )\right| . \end{aligned}$$

(17)

Step ii A direct computation shows that the magnitude of $D_0(j\omega )$ and $D_1(j\omega )$ are given by

$$\begin{aligned} \left| D_0(j\omega )\right| ^2 =&\left[ \tau _s^2\omega ^4+\left( \omega _p^2\tau _s^2+1-2 \omega _p\sigma _s^{\star }k_p\tau _s\right) \omega ^2\right. \\&+\left. \omega _p^2\left( 1+\sigma _s^{\star }k_p\right) ^2 \right] \Big / \left( \omega _p^2+\omega ^2\right) \end{aligned}$$

and

$$\begin{aligned} \left| D_1(j\omega )\right| ^2 =\dfrac{\left( \alpha \omega _p\sigma _s^{\star }k_p\right) ^2}{\beta ^2 \omega ^4+\left( 1+\beta ^2\omega _p^2\right) \omega ^2+\omega _p^2}. \end{aligned}$$

Thus, the expressions of $|D_0(j\omega )|^2$ and $|D_1(j\omega )|^2$ can be rewritten as

$$\begin{aligned} |D_0(j\omega )|^2=\dfrac{1}{h_0(\omega ^2)} \quad \text{ and } \quad |D_1(j\omega )|^2=h_1(\omega ^2), \end{aligned}$$

(18)

where $h_0(\cdot )$ and $h_1(\cdot )$ are given by

$$\begin{aligned} h_0(x)&=\dfrac{x+\omega _p^2}{\tau _s^2x^2+\left( \omega _p^2\tau _s^2+1-2 \omega _p\sigma _s^{\star }k_p\tau _s\right) x+\omega _p^2\left( 1+\sigma _s^{\star } k_p\right) ^2}\\ h_1(x)&=\dfrac{(\alpha \omega _p\sigma _s^{\star }k_p)^2x}{\beta ^2x^2+(\beta ^2 \omega _p^2+1)x+\omega _p^2}. \end{aligned}$$

Step iii The functions $h_0$ and $h_1$ have the same expression of h, with parameters summarized in Table 2. To compute their extrema, we rely on the following fact:

Consider a rational function $h:\mathbb {R}^+\rightarrow \mathbb {R}^+$, defined as

$$\begin{aligned} h(x):=\dfrac{a_1x+a_2}{a_3x^2+a_4x+a_5}, \end{aligned}$$

where $a_1,a_3, a_4$ and $a_5$ are positive constants and $a_2\ge 0$. If $a_2a_4<a_1a_5$ then $\max _{x\ge 0}h(x)=h(\bar{x})$ with

$$\begin{aligned} \bar{x}:=-\dfrac{a_2}{a_1}+\sqrt{\left( \dfrac{a_2}{a_1}\right) ^2 +\dfrac{a_1a_5-a_2a_4}{a_1a_3}}. \end{aligned}$$

(19)

Now, let

$$\begin{aligned} \omega _a:=\dfrac{\sigma _s^{\star }k_p+\sqrt{2\sigma _s^{\star }k_p \left( 1+\sigma _s^{\star }k_p\right) }}{\tau _s}. \end{aligned}$$

(20)

One can verify that if $\omega _p<\omega _a$, then the condition $a_2a_4<a_1a_5$ is well satisfied in each case. This implies that we have $\max _{x\ge 0} h_0(x)=h_0(\bar{x}_0)$ and $\max _{x\ge 0} h_1(x)=h_1(\bar{x}_1)$, where $\bar{x}_0$ and $\bar{x}_1$ are calculated using formula (19), and they are given by

$$\begin{aligned} \bar{x}_0=\omega _p \dfrac{\sqrt{2\sigma _s^{\star } k_p\tau _s\omega _p+\left( \sigma _s^{\star }k_p\right) ^2+2\sigma _s^{\star }k_p}}{\tau _s}-\omega _p^2\quad \end{aligned}$$

and

$$\begin{aligned} \bar{x}_1=\dfrac{\omega _p}{\beta }. \end{aligned}$$

By replacing $\bar{x}_0$ and $\bar{x}_1$ by their values in $h_0(\cdot )$ and $h_1(\cdot )$, we obtain

$$\begin{aligned} h_0(\bar{x}_0)&=\dfrac{\bar{x}_0+\omega _p^2}{\tau _s^2\bar{x}_0^2+ \left( \omega _p^2\tau _s^2+1-2\omega _p\sigma _s^{\star }k_p\tau _s\right) \bar{x}_0 +\omega _p^2\left( 1+\sigma _s^{\star }k_p\right) ^2}\nonumber \\&=\omega _p Q_0(\omega _p)\Big /\left[ \tau _s^2\omega _p^2\left( Q_0(\omega _p) -\omega _p\right) ^2\right. \nonumber \\&+\left( \omega _p^2\tau _s^2+1-2\omega _p\sigma _s^{\star }k_p\tau _s\right) \omega _p\left( Q_0(\omega _p)-\omega _p\right) \nonumber \\&\left. +\omega _p^2\left( 1+\sigma _s^{\star }k_p\right) ^2\right] \nonumber \\ \end{aligned}$$

(21)

and

$$\begin{aligned} h_1(\bar{x}_1)&=\dfrac{(\alpha \omega _p\sigma _s^{\star }k_p)^2\bar{x}_1}{\beta ^2\bar{x}_1^2+(\beta ^2\omega _p^2+1)\bar{x}_1+ \omega _p^2}\nonumber \\&=\dfrac{\left( \alpha \omega _p\sigma _s^{\star }k_p\right) ^2}{\left( 1+\omega _p\beta \right) ^2}, \end{aligned}$$

(22)

where

$$\begin{aligned} Q_0(\omega _p):=\dfrac{1}{\tau _s}\sqrt{2\sigma _s^{\star }k_p\tau _s\omega _p +\left( \sigma _s^{\star }k_p\right) ^2+2\sigma _s^{\star }k_p}. \end{aligned}$$

Therefore, from Eq. (18), we have

$$\begin{aligned} \left| D_0(j\omega )\right| \ge \dfrac{1}{\sqrt{h_0(\bar{x}_0)}} \quad \text{ and } \quad \left| D_1(j\omega )\right| \le \sqrt{h_1(\bar{x}_1)}. \end{aligned}$$

(23)

Step iv Let

$$\begin{aligned} Q(\omega _p):= \dfrac{\sqrt{h_0(\bar{x}_0)}}{1-\sqrt{h_0(\bar{x}_0)h_1(\bar{x}_1)}}. \end{aligned}$$

(24)

Equation (17) together with (23) implies that

$$\begin{aligned} \left| D(j\omega )\right| \ge \dfrac{1}{Q(\omega _p)}. \end{aligned}$$

One can check that

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}h_0(\bar{x}_0(\omega _p))=1 \quad \text{ and } \quad \lim _{\omega _p\rightarrow 0}h_1(\bar{x}_1(\omega _p))=0, \end{aligned}$$

which imply that

$$\begin{aligned} \Vert D\Vert _{\infty }\ge \dfrac{1}{Q(\omega _p)}, \quad \hbox { with } \lim _{\omega _p \rightarrow 0}Q(\omega _p)=1. \end{aligned}$$

Step v Recalling that $\Vert H_s\Vert _{\infty }=\dfrac{\sigma _s^{\star }}{\Vert D\Vert _{\infty }}$, we deduce that for each delay $d>0$, each firing rate reference $\bar{x}_s \in [0,M_s]$, and each gain $k_p>0$, there exists $\omega _a>0$ such that for every $\omega _p<\omega _a$, Eq. (9) holds, which concludes the proof.$\square$

Table 2 Parameters of $h_0(\cdot )$ and $h_1(\cdot )$

Proof of Proposition 2

We recall that the transfer function $H_g$ is given by

$$\begin{aligned} H_g(s)=\dfrac{\sigma _g^{\star }}{1+\tau _g s+\sigma _g^{\star }w_{gg}e^{-\delta _{gg}s}}=\dfrac{\sigma _g^{\star }}{E(s)}, \end{aligned}$$

where

$$\begin{aligned} E(s):=1+\tau _g s+\sigma _g^{\star }w_{gg}\hbox {e}^{-\delta _{gg}s}. \end{aligned}$$

We want to estimate $\Vert H_g\Vert _{\infty }$. Remark that reducing $\Vert H_g\Vert _{\infty }$ amounts to increasing $\Vert E\Vert _{\infty }$. As in Proposition 1, we introduce the auxiliary function

$$\begin{aligned} E_{0}(s):=1+\tau _g s. \end{aligned}$$

Let $s=j\omega$, where $\omega \in \mathbb {R}$. Using the triangle inequality, we have

$$\begin{aligned} \left| E_0(j\omega )\right| -\left| E(j\omega )\right| \le \left| E(j\omega ) -E_0(j\omega )\right| = \sigma _g^{\star }w_{gg}. \end{aligned}$$

(25)

One can check that for all $\omega \in \mathbb {R}$, we have $\left| E_0(j\omega )\right| \ge 1$. Equation (25) together with the fact that $\sigma _g$ is the maximal slope of the activation function $F_g$ leads to the following

$$\begin{aligned} \left| E(j\omega )\right| \ge 1-\sigma _g^{\star } w_{gg}\ge 1-\sigma _g w_{gg}, \quad \quad \forall \omega \in \mathbb {R}. \end{aligned}$$

This implies that $\Vert E\Vert _{\infty }\ge 1-\sigma _g w_{gg}$. Recalling that $\Vert H_g\Vert _{\infty }=\dfrac{\sigma _g^{\star }}{\Vert E\Vert _{\infty }} \le \dfrac{\sigma _g}{\Vert E\Vert _{\infty }}$, we deduce that for each firing rate reference $\bar{x}_s \in [0,M_s]$ and each gain $k_p>0$, Eq. (10) holds if $\sigma _g w_{gg}<1$, which concludes the proof.$\square$

Proof of Proposition 3

The proof is split into two steps. In the first step, we prove that for sufficiently large values of $k_p$, the equilibrium point $x_s^\star$ is close to the reference $\bar{x}_s$. The second step consists in showing that reducing the value of $\sigma ^{\star }_s$ can be made as small as we want by picking $\bar{x}_s$ near to 0 or $M_s$, provided that $k_p$ is sufficiently large.

Step i Following the lines of the proof of [Pasillas-Lépine 2013, Theorem 1], we affirm that system (1) has a unique equilibrium point $(x^{\star }_s,x^{\star }_g)\in [0,M_s]\times [0,M_g]$ solution of

$$\begin{aligned} x^{\star }_s= & {} F_{s}\left( -w_{gs}x^{\star }_g+w_{cs}\nu _s+k_p (\bar{x}_s-x^{\star }_s)\right) \end{aligned}$$

(26)

$$\begin{aligned} x^{\star }_g= & {} F_{g}\left( w_{sg}x^{\star }_s-w_{gg}x^{\star }_g-w_{xg}\nu _g\right) . \end{aligned}$$

(27)

We see clearly, from Eq. (26), that this equilibrium depends on $k_p$. Let $\bar{x}_s\in [0,M_s]$. We have that $\lim \nolimits _{k_p\rightarrow +\infty }x_s^{\star }(k_p)=\bar{x}_s.$ To see this, it is sufficient to prove that $\limsup \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)=\liminf \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)=\bar{x}_s$.

Suppose, by contradiction, that $\limsup \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)<\bar{x}_s$, i.e. $\limsup \nolimits _{k_p \rightarrow {+\infty }}k_p(\bar{x}_s-x_s^{\star }(k_p))=+\infty$.

Recalling that the activation function $F_s$ is increasing with a supremum equal to $M_s$, we obtain, from (26), that $\limsup \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)=M_s$. This leads to conclude that $\bar{x}_s>M_s$. In a similar way, if we suppose that $\limsup \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)>\bar{x}_s$, we obtain that $\bar{x}_s<0$, which leads to a contradiction.

Thus, we have $\lim \nolimits _{k_p \rightarrow {+\infty }}x_s^{\star }(k_p)=\bar{x}_s$, as claimed.

Step ii In view of (7), the expression of $\sigma ^{\star }_s$ is given by

$$\begin{aligned} \sigma ^{\star }_s = F_s^\prime \left( -w_{gs} x_g^\star + \underbrace{k_p (\bar{x}_s - x_s^\star )}_{u^{\star }} + w_{cs} v_s \right) . \end{aligned}$$

(28)

We are going to show that if $\bar{x}_s$ is sufficiently close to either 0 or $M_s$, then $\left| u^{\star }\right|$ tends to $+\infty$ when $k_p$ tends to $+\infty$. This will imply that $\sigma ^{\star }_s$ tends to zero since (2) guaranties that

$$\begin{aligned} \lim _{x\rightarrow -\infty }F_s(x)=0, \lim _{x\rightarrow +\infty }F_s(x)=M_s \quad \text{ and } \quad \lim _{|x|\rightarrow +\infty }F_s^{\prime }(x)=0. \end{aligned}$$

(29)

From Eq. (26), we have

$$\begin{aligned} u^{\star }=F^{-1}_s(x_s^{\star })+w_{gs}x_g^{\star }-w_{cs}\nu _s, \end{aligned}$$

(30)

where $F^{-1}_s$ denotes the inverse function of $F_s$. Adding and subtracting $F^{-1}_s(\bar{x}_s)$ to Eq. (30) and applying the triangle inequality, we obtain that

$$\begin{aligned} \left| u^{\star }\right| \ge \underbrace{\left| F^{-1}_s(\bar{x}_s)\right| }_{u_1}-\underbrace{\left| F^{-1}_s (x_s^{\star })-F^{-1}_s(\bar{x}_s)\right| }_{u_2}-\underbrace{\left| w_{gs}x_g^{\star } -w_{cs}\nu _s\right| }_{u_3}. \end{aligned}$$

In view of (29), for every $\epsilon >0$ there exists a $\delta _\epsilon >0$ such that $u_1>\dfrac{1}{\epsilon }$ as soon as either $0 < \bar{x}_s < \delta _\epsilon$ or $M_s-\delta _\epsilon < \bar{x}_s < M_s$. Furthermore, knowing that $F^{-1}_s$ is continuous and using Step (i), we state that for this $\epsilon >0$, there exists $k_{\epsilon }>0$ such that if $k_p>k_\epsilon$, then $u_2<\epsilon .$ Noticing that $u_3$ is bounded, we conclude [in view of (28)] that for every $\epsilon >0$, there exist $\bar{x}_\epsilon >0$ and $k_{\epsilon }>0$ such that if $k_p>k_\epsilon$ and $\bar{x}_s\in \left( 0,\bar{x}_\epsilon \right) \cup \left( M_s-\bar{x}_\epsilon ,M_s\right)$, then $\sigma _s^\star <\epsilon$, which concludes the proof.$\square$

Proof of Proposition 4

The proof is split into two steps. In the first step, we give explicitly the delay margin of stability of the transfer function $H_s$. In the second step, we prove that this delay margin is near $+\infty$ when $\omega _p$ is close to zero.

Step i The transfer function $H_s$ can be reformulated as

$$\begin{aligned} H_s(s)=\dfrac{G_s(s)}{1+C(s)G_s(s)}, \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{array}{lll} G_s(s):=\dfrac{\sigma ^{\star }_s}{1+\tau _{s}s}. \end{array} \end{aligned}$$

The stability of the closed-loop transfer function $H_s(s)$ can be determined from the characteristics of its open-loop transfer function $G(s):=C(s)G_s(s)$ (see, for example, Curtain and Zwart 1995). Considering the expression of G(s), which is given by

$$\begin{aligned} \begin{array}{lll} G(s)=\dfrac{k_p\sigma ^{\star }_s}{\left( 1+s/\omega _p\right) \left( 1+\tau _{s}s\right) }, \end{array} \end{aligned}$$

we see clearly that its gain is strictly decreasing. The latter means that for each firing rate reference $\bar{x}_s$, each constant $k_p$, and each filter frequency $\omega _p$, there exists a unique delay margin $\varDelta$ (calculated from the expression of G) such that $H_s$ is stable if and only if $d<\varDelta$ (see, for example, Middleton and Miller 2007). This delay margin can be computed analytically.

For simplicity of further calculations, we introduce the following notations:

$$\begin{aligned} a_0:=\left( \dfrac{\tau _s}{\sigma _s^{\star }k_p\omega _p}\right) ^2,\quad b_0:=\left( \dfrac{1}{\sigma _s^{\star }k_p\omega _p}\right) ^2+\left( \dfrac{\tau _s}{\sigma _s^{\star }k_p}\right) ^2 \end{aligned}$$

and

$$\begin{aligned} c_0:=\left( \dfrac{1}{\sigma _s^{\star }k_p}\right) ^2-1. \end{aligned}$$

We can distinguish, from (Pasillas-Lépine 2013, Corollary 1), two different cases:

• If $k_p\sigma _s^{\star }<1$, then $\varDelta =+\infty$.

• If $k_p\sigma _s^{\star }\ge 1$, then the delay margin of the transfer function $H_s$ is given by

  $$\begin{aligned} \varDelta =\dfrac{\pi +\phi _0}{\omega _0}, \end{aligned}$$

  with (observe that $c_0\le 0$)

  $$\begin{aligned} \omega _0=\sqrt{\dfrac{-b_0+\sqrt{b_0^2-4a_0c_0}}{2a_0}}, \end{aligned}$$

  and

  $$\begin{aligned} \phi _0=\arctan (-\tau _s\omega _0)+\arctan \left( -\dfrac{\omega _0}{\omega _p}\right) . \end{aligned}$$

  (32)

Step ii In the case when $k_p\sigma _s^{\star }\ge 1$, one can show that

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}\varDelta =+\infty . \end{aligned}$$

(33)

To see this, it is enough to estimate the limit when $\omega _p$ tends to $+\infty$ of $\omega _0$ and $\dfrac{\omega _0}{\omega _p}$. We have

$$\begin{aligned} \omega _0^2= & {} \dfrac{-b_0+\sqrt{b_0^2-4a_0c_0}}{2a_0}\\= & {} \dfrac{-b_0+\sqrt{b_0^2-4a_0c_0}}{2a_0}\dfrac{b_0+\sqrt{b_0^2-4a_0c_0}}{b_0+\sqrt{b_0^2-4a_0c_0}}\\= & {} \dfrac{-2c_0}{b_0+\sqrt{b_0^2-4a_0c_0}}\\\le & {} \dfrac{-2c_0}{b_0}. \end{aligned}$$

Noticing that $\lim \nolimits _{\omega _p\rightarrow 0}b_0=+\infty$ and that $c_0$ does not depend on $\omega _p$, we obtain that

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}\omega _0=0. \end{aligned}$$

(34)

On the other hand, we have

$$\begin{aligned} \left( \dfrac{\omega _0}{\omega _p}\right) ^2= & {} \dfrac{1}{\omega _p^2}\dfrac{-b_0+\sqrt{b_0^2-4a_0c_0}}{2a_0}\\= & {} \dfrac{-2c_0}{b_0\omega _p^2+\sqrt{\left( b_0\omega _p^2\right) ^2-4a_0c_0\omega _p^4}}. \end{aligned}$$

Observing that

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}b_0\omega _p^2=\dfrac{1}{\left( \sigma _s^{\star }k_p\right) ^2} \quad \text {and} \quad \lim _{\omega _p\rightarrow 0}a_0\omega _p^4=0, \end{aligned}$$

we thus have

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}\left( \dfrac{\omega _0}{\omega _p}\right) ^2= & {} \lim _{\omega _p\rightarrow 0}\dfrac{-2c_0}{b_0\omega _p^2+\sqrt{\left( b_0\omega _p^2\right) ^2-4a_0c_0\omega _p^4}}\\= & {} \lim _{\omega _p\rightarrow 0}\dfrac{-c_0}{b_0\omega _p^2}\\= & {} \left( \sigma _s^{\star }k_p\right) ^2-1\\\ge & {} 0, \end{aligned}$$

from which we conclude that

$$\begin{aligned} \lim _{\omega _p\rightarrow 0}\dfrac{\omega _0}{\omega _p}=\sqrt{\left( \sigma _s^{\star }k_p\right) ^2-1}. \end{aligned}$$

(35)

Thus, in view of (32), (34), and (35), we conclude that Eq. (33) is satisfied. Then, for each delay $d>0$, each firing rate reference $\bar{x}_s$, and each gain $k_p>0$, there exists a frequency $\omega _b>0$ such that the transfer function $H_{s}$ is stable for every filter frequency $\omega _p>0$ such that $\omega _p<\omega _b$, which concludes the proof.$\square$