Abstract
We investigated induction of chromosome aberrations (CA) in human lymphocytes when exposed to 150 MeV and spread out Bragg peak (SOBP) proton beams, and 199 MeV/u carbon beam which are currently widely used for cancer treatment and simultaneously are important components of cosmic radiation. For a comparison, the boron ions of much lower energy 22 MeV/u and a 60Co γ rays were used. Dose–effect curves as well as the distributions of CA were studied using Poisson and Neyman type A statistics. Systematics of experimentally determined parameters, their dependence on applied doses and irradiation quality are presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The study of biological efficiency of accelerated particle beams is of great interest in medicine due to the increasing use of hadron therapy for cancer treatment (Schulz-Ertner et al. 2007; Nikoghosyan et al. 2004). Furthermore, protons, carbon and other high energetic light ions are known to dominate in the space radiation flux (unlike terrestrial background radiation, dominated by γ radiation) and mainly determine the radiation hazard and health risks to astronauts during long space missions (Cucinotta and Durante 2006).
Chromosome aberrations (CA) are considered to be sensitive and reliable indicators of radiation action in humans and their assessment is a valuable method in biodosimetry. Induction of CA in human peripheral blood lymphocytes (PBL) was chosen as an endpoint of radiation exposure due to several reasons: (1) blood probes are the most simple and available samples of human tissues; (2) the fact that quiescent PBLs represent a population naturally synchronized in G0 facilitates the data interpretation; (3) PBL are actually used as a model of bone marrow cells (BMC) which are known to be the most sensitive cells of human organisms and are used as the limitation factor in health risk estimations.
Experimental studies devoted to CA as a response to ionizing radiation are often performed by means of dose–effect curves, which usually have a linear-quadratic shape (Lea 1955) and can be easily used for estimation of the clinically important relative biological effectiveness (RBE). The quadratic term, like to the nonlinear term in the survival curves, can result from two different effects. The first one is of a physical origin and arises from overlapping ion tracks at high ion fluencies, which locally lead to higher doses and a stronger biological response (Scholz 2006; Loucas et al. 2013). Generally, it is assumed that the spatially localized dose distribution within the ion tracks induced by heavy charged particles follows the distribution of fast electrons of the ionization process and, therefore, can be in principle calculated analytically. Otherwise, the quadratic term in the dose–effect curve can also result from the repair mechanisms of the DNA damage leading to CA, which also depends on the local ionization density and thus on the radiation quality (Scholz and Kraft 1996; Loucas et al. 2013).
Another effect that can be observed in radiobiological experiments is a considerable difference in frequency distributions of CA obtained for low and high LET radiations (Gudowska-Nowak et al. 2007). This is caused once again by differences in microscopic energy deposition of both radiation qualities. Uniform dose deposition of low-LET radiations (i.e., X-rays or γ quanta) results in a simple random damage distribution, well described by Poisson statistics. In comparison, microscopically inhomogeneous pattern of energy deposition characteristic for high-LET particles leads to clusters of damages randomly distributed along paths of ionizing particles (i.e., ion tracks). Since ions are also randomly distributed within the cell nucleus, the aberration frequency is well described by the Neyman type A statistics, which folds these two stochastic processes (Gudowska-Nowak et al. 2005, 2007; Deperas-Standyło et al. 2012). Such variable energy deposition results in higher frequency of cells carrying multiple aberrations, but also higher frequency of non-hit cells.
Generally, both kinds of studies can help us to separate physical and biological contributions to observed effects. However, there are as yet no ab initio calculations which could do it and, therefore, some phenomenological models have been developed concerning the highly inhomogeneous distribution of the dose deposited by heavy particle irradiation. One of the most used is the Local Effect Model (LEM) predicting the biological effect of ions from the response of cells and tissues to photon radiation (Scholz and Kraft 1996). Nevertheless, experimental data have shown some overestimation of the dose calculated for light ions, especially for protons (Scholz et al. 1997). The last version of the model, LEM IV (Friedrich et al. 2012) includes a microscopic double-strand distribution of DNA, including a giant loop structure. It allows to calculate the RBE values much more precisely but at the cost of introducing an additional free parameter. Some problems with understanding of the proton interaction with biological samples in terms of the low RBE values have been previously discussed (Kowalska et al. 2015) and it was suggested that the local dose is possibly distributed in a larger region than only within the standard ion track. Another model, which assumes the amorphous track structure of heavy ions, has been developed by Katz (Katz et al. 1971). The model distinguishes between two action modalities “ion-kill” and “γ-kill”. There is an additional contribution at high fluencies where δ-electrons of several ions can overlap in space and determine the additional effect (γ-kill). The model of Katz is well suited to reproduce the cell-survival curves and the Z-dependence of the RBE-LET function including the overkill effects; therefore, both physical and biological processes might be simultaneously described.
The purpose of our work is to propose a new analytical model that could use experimentally determined dose–effect curves and CA statistical distributions to conclude the effective biological interaction radius within the ion tracks and compare the obtained values with physical predictions. For our study, we collected experimental data using several particle species of different LET values which are of great importance in the space research and therapy: the 150 MeV proton beam and the SOBP (spread out Bragg Peak) protons as well as the 199 MeV/u 12C and 22 MeV/u 11B beams.
Here, we will focus on a more detailed analysis of experimental results and on determining values of representative parameters of the dose–effect curves and of aberration frequency distributions. We would like to demonstrate the differences in experimentally determined parameters for different radiation qualities and also arrive at a data set suitable for a modelling study that we plan to perform.
Materials and methods
Blood samples and irradiation
The blood used for the study was obtained by venipuncture into heparinized vacuum containers. The samples were collected from informed, healthy volunteers, in accordance with local ethical regulations. The whole blood was irradiated in 0.5 ml Eppendorf tubes; whereas isolated lymphocytes used for the boron irradiation were placed in special Plexiglas vessels. All exposures were done at room temperature and controls were sham-irradiated. The scoring and recording criteria followed those given in IAEA Manuals (2001, 2011). Irradiation experiments were performed for each quality separately.
Proton beam
Proton exposure was performed at the clinical proton beam facility of the Medico-technical complex of Dzhelepov Laboratory of Nuclear Problems, JINR, Dubna, Russia (for more details see Pachnerova Brabcova et al., 2014; Racjan et al., 2015). Blood samples were irradiated with unmodified 150 MeV proton beams (LET 0.57 keV/µm) and with slowed down protons at the central region of the 10 mm wide SOBP plateau at an experimentally determined average LET 1.4 keV/µm (Kubancak and Molokanov 2013). Dose rate in the target volume amounted to 0.7 Gy/min for high energy protons and 1.3 Gy/min in the SOBP. As a reference, the 60Co γ radiation source of the radiation therapy unit ROKUS-M was used. Dose rate at irradiation point was 0.82 Gy/min. Doses ranged between 1 and 5 Gy for protons and 0.5–3 for 60Co γ-rays.
Carbon beam
Irradiation with 199 MeV/u 12C ions (LET 16 keV/µm) was done at the ITEP-TWAC accelerator (Russia, Moscow). Special features of the beam extraction from the synchrotron enabled us to use short ion pulses with duration of 500 ns. Irradiation was carried out in the plateau region of the Bragg curve, where the LET of the particles did not change significantly (Markov et al. 2014). Doses were ranging between 0.8 and 6.37 Gy.
Boron beam
The PBL were irradiated with doses of 0.05–2 Gy applying the monoenergetic 11B beam of energy 22.1 MeV/u (average LET 76 keV/µm) generated in the MC-400 cyclotron at Flerov Laboratory of Nuclear Reactions, JINR, Dubna, Russia. The isolated lymphocytes were highly concentrated in nutrient medium and irradiated as 1.5 mm layer in specially designed Plexiglas chambers sealed by 8 µm polycarbonate foils so that all ions passed the sample and stopped behind it. The chambers were exposed using automatic irradiation facility Genom-M (Bezbakh et al. 2013).
Cell cultivation and metaphase analysis
Immediately after 11B irradiation, isolated lymphocytes were seeded with a density of 0.5 × 106/ml in RPMI medium supplemented by 20% 6. fetal calf serum, 2 mM l-glutamine, 100 U/ml penicillin, 100 µg/ml streptomycin and 1.5% phytohaemagglutinin (PHA).
After exposure to proton, carbon and 60Co γ rays, the blood samples were diluted in 4.5 ml of the same medium. All samples were incubated at 37 °C and 5% CO2. Cells were fixed at 48 h after PHA stimulation proceeded by 3 h colcemid treatment (200 ng/ml) for metaphase accumulation and stained in 3% Giemsa. Typically, 100–300 metaphases were analyzed for every data point. Chromosomal aberrations were classified according to (Savage 1975). All aberrations of the chromosome and chromatid types visible without karyotyping were recorded. The chromosome-type aberrations comprise paired fragments, dicentrics, centric and acentric rings (the latter also includes double minutes) and translocations visible without karyotyping. The minor fraction of chromatid-type aberrations includes the chromatid-type breaks and chromatid-type exchanges. The gaps were not scored as aberrations.
Statistical analysis, distribution of aberrations
Statistical distribution of the number of observed CA can be described by two different stochastic distributions: Poisson and Neyman A. The Neyman A distribution is a folding of two independent Poisson distributions. One of them \({P_{{\lambda _{\text{N}}}}}\)(n) describes the probability that the cell nucleus will be hit by n ions. The other Poisson probability \({P_{n\mu }}\)(k) assess the number of aberrations k produced by each hit (Gudowska-Nowak et al. 2007):
Here λN and µ reflect the mean number of particle traversals per cell and mean number of CA induced by a single hit, respectively. Parameter λN can be calculated from the particle fluence and the cross section of human lymphocytes of ~ 25 µm2 (Anderson et al. 2000), which leads to the fluence of 4 × 106 particles/cm2 corresponding to one hit per cell. The variance of the Neyman A distribution is larger than its mean value and can be expressed as: \(\sigma _{{\text{N}}}^{2}={\lambda _{\text{N}}}~\mu \left( {1+\mu } \right)\) (Gudowska-Nowak et al. 2007).
In the case of low-LET radiation, when µ is very low, the variance corresponds to that of a Poisson distribution as for γ radiation. Nevertheless, the energy distribution imparted by many low-LET particles due to their ion track structure still differs from that of γ quanta, which is almost homogenously distributed. For the simple Poisson statistics, the aberration frequency can be calculated as follows:
Here m stands for the number of aberrations per individual cell and λP is the average number of CA observed in the whole cell population exposed to a given dose of a given radiation. Parameters λP, µ and λN are linked by a simple relation: \({\lambda _{\text{P}}}={\lambda _{\text{N}}} \cdot \mu\). Mean numbers of hits per nucleus for a given dose of a given ion irradiation are presented in Table 2.
Cytogenetic data are distributed according to Poisson statistics when relative variance \({\sigma ^2}/\left\langle X \right\rangle\) is equal to one (Edwards et al. 1979) where \(\left\langle X \right\rangle\) denotes the experimentally determined mean number of CA per cell. It results from the fact that for the Poisson distribution \(\left\langle X \right\rangle\) is equal to λP and \(\left\langle {{X^2}} \right\rangle =~\lambda _{{\text{P}}}^{2}+{\lambda _{\text{P}}}\), thus the variance \(\sigma _{{\text{P}}}^{2}\) is equal to the mean value:
To judge whether a deviation from the Poisson statistics is significant, the so-called U test has been used (Edwards et al. 1979). The U test gives a normalized comparison of the relative variance with the expected Poisson value at the 95% confidence level. Distributions for which the U test values are smaller than − 1.96 or larger than + 1.96 are under- or over-dispersed compared to the Poison distribution, respectively.
The formula to assess values of the U test reads as follows:
where N is the number of analyzed metaphases, d represents the coefficient of dispersion which provides an indicator of how well the variance of a given sample corresponds to the Poisson distribution. The coefficient of dispersion and its corresponding variance can be calculated according to the following equations:
Results
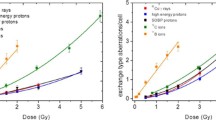
The percentage of aberrant cells, total CA yield and CA spectra produced by all radiation species used are listed in Table 2, and the dose-dependence of CA frequencies is depicted in Fig. 1. The total CA numbers have been fitted by a linear-quadratic function with exception of those induced by boron ions, which were fitted by a linear relation. Parameters of the least squares fits are presented in Table 1.
Dose–effect curves plotted for chromosome aberrations produced by all radiation species listed in Table 2: (filled triangle) 60Co γ rays, LET 0.2 keV/µm; (open circle) high energy protons 150 MeV, LET 0.57 keV/µm; (filled circle) SOBP protons, LET 1.4 keV/µm; (open square—donor 1, filled square—donor 2, open diamond—donor 3) 12 C ions 199 MeV/u, LET 16.3 keV/µm; (filled diamond) 11B ions 22.1 MeV/u, LET 76 keV/µm. Error bars are calculated according to Poisson statistics: \(\Delta y=\sqrt Y /N\), where Y is the total aberration number and N is the number of cells scored for each point
The spectra of CA are very similar for all low-LET radiations (photons and both proton beams) where exchange-type aberrations comprise 75–85% of total CA yield while these values decrease down to 64–70% for carbon and boron ions.
Distributions of CA frequencies have been analyzed for radiation of different quality. Data obtained for 60Co γ - rays, high energy protons, SOBP protons and carbon ions could be fitted either by the Poisson or by the Neyman A distribution whereas the data obtained for 11B irradiation could be analyzed only by means of the Neyman A distribution. Accordingly, experimentally determined CA distributions and corresponding fits for chosen doses of each irradiation type are shown in Fig. 2. For comparison, CA spectra obtained for carbon irradiation were fitted by means of both statistical models (Fig. 3). The dose-dependence of the parameters λN and µ, describing the mean number of hits per cell and of aberrations induced by single ion hit, respectively, obtained for high energy and SOBP protons, 12C ions and 11B ions are depicted in Fig. 4a, b.
a Dose-dependence of the λN parameter (describing mean number of hits per cell) obtained for high energy protons, 12C ions and 11B ions. b Dependence of the parameter µ (describing the mean number of aberrations induced by single ion hit) on the radiation dose determined for high energy protons, 12C ions and 11B ions
We have also estimated the average number of particle hits λN per spherical G0 lymphocyte nucleus of diameter ~ 5 µm. At 1 Gy it amounts to 274 in case of 150 MeV protons and 126 in case of SOBP protons, while for carbon and boron ions, it amounts only to 10.2 and 2.15, respectively. In the last case, it means that according to the Poisson statistics, 12% of cells received no hit, 25%—1 hit, 27%—2 hit, 36%—3 and more hits/nucleus.
When comparing both distributions for the same mean number of aberrations per cell, Neyman A gives a higher number of non-hit cells and a higher number of cells with multiple aberrations. This statistical prediction can be demonstrated by a comparison between the Poisson distribution fitted for 3 Gy of high energy protons (λP = 1.32) and the Neyman A fitted for 0.5 Gy boron irradiation (λP = 1.13). In the case of 150 MeV protons, the frequency of “zero-class” cells is 0.33 ± 0.05 and for boron ions it amounts to 0.46 ± 0.03.
Differences between both distributions are also detectable in the number of cells carrying multiple aberrations. For example, for the 2 Gy boron irradiation with the mean number of aberrations per cell λP = 4.2, the frequency of cells carrying eight aberrations amounts to 0.08 ± 0.03. The dose of 5 Gy of fast protons (λP = 3.5) results in the much lower frequency of cells carrying eight aberrations of 0.01 ± 0.01. It means that among one hundred of scored cells (exposed to the dose leading to the mean number of ~ 4 aberrations per cell), eight cells carried eight aberrations in case of boron ions and only one cell in case of 150 MeV protons.
Evaluation of the degree of spread of experimental data has been also performed by assessing the variance to mean ratio \(({\sigma ^2}/\left\langle X \right\rangle )~\) and the U test (see Table 3). The relative dispersion has been found significantly higher than one in the case of 11B ions. In the case of 60Co γ-rays and high energy proton beam, the relative dispersion is lower than one; however, such under-dispersion is not significant according to the applied U test. Only for 0.84 Gy 12C ions, the relative variance amounting to 1.29 is at the edge of significance (see Table 3). The U test delivers, however, both negative and positive values for different doses.
According to the Neyman A distribution, we would expect a constant value of the parameter µ—independent of the dose. It is well fulfilled for boron ions, having relatively high ionization density. Values of the µ parameter obtained for boron ions are scattered around its mean 0.94 ± 0.06, i.e., every particle hit induced a chromosome aberration. An increase of the µ value with the dose is, however, observed for particles with lower LET: carbon ions, SOBP and high energy protons for which is the most pronounced (see Table 4).
The second parameter λN, corresponding to the mean number of hits per single cell, is determined from the projectile fluence F applying the simple relation \({\lambda _{\text{N}}}=\sigma ~ \times F,\) where \(\sigma\) corresponds to the cross section area of our target (25 µm2), and the fluence is related to the dose: \(D=1.602 \times {10^{ - 9}} \times LET \times F \times {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \rho }}\right.\kern-0pt}\!\lower0.7ex\hbox{$\rho $}}\) where ρ is the target mass density. As expected, the dose-dependence of λN is linear (see Fig. 4a; Table 4).
Discussion and conclusions
Chromosome aberrations (CA) are considered to be the most sensitive and reliable bioindicator of radiation action. The detailed analysis of chromosome aberrations as an endpoint of radiation exposure is thus essential for biodosimetric considerations and for risk of carcinogenesis assessment (Bonassi et al. 2004). The importance of such studies is forced not only by the wide use of hadron therapy for cancer treatment, but also by the necessity of the astronaut protection during space missions (Schulz-Ertner et al. 2007; Cuccinotta and Durante 2006).
In this study, we investigated CA induction in human lymphocytes by different heavy charged projectiles (protons, 12C and 11B ions) and compared it with the results obtained for 60Co γ rays. The data with the exception of those obtained for boron ions were collected for different patients in relation to our previously published study (Kowalska et al. 2015) to reduce experimental uncertainties. Both, dose–effect curves and statistical distributions of CA were used to analyze the dependence of experimentally determined parameters on the radiation quality which will be compared with predictions of different radiobiological models in the second part of the work.
The experimental dose–effect curves have a linear-quadratic shape for all radiations applied with exclusion of 11B ions for which a linear dependence is observed (see Table 1). This simple linear behavior is usually found for high-LET radiation qualities (Lee et al. 2005) and should not be interpreted as a vanishing of the quadratic parameter β. It is rather the result of a strong increase of the linear parameter α for high-LET values corresponding to a higher ionization density. Since our LET values are still below the maximum of the biological effectiveness expected for LET of about 100 keV/µm, the α parameter increases almost linearly (Ando and Goodhead 2016). Therefore, the linear part of the dose–effect curve for 11B ions should dominate the quadratic term and reduces the curvature of the response function.
On the other hand, the quadratic parameter reflects, as mentioned before, radiobiological repair mechanisms and physical effects of overlapping ionization areas of individual projectiles at higher fluencies. Thus, the study of LET dependence of the β parameter can contribute to understanding of both processes. In the present work, we have observed for the first time that the β values within the experimental uncertainties do not change significantly for different radiation qualities and LET values. Similar results, but obtained only for proton beams of different energies, has been recently reported (Wilkens and Oelfke 2004).
Differences in acting of ions of low- and high-LET ions can be also observed in the statistical distributions of CA. Neglecting the fact that the high-LET radiations produce more complex chromosome aberrations (Kowalska et al. 2017) and treating all aberration types similarly, the frequency of CA can be described by the Poisson as well as by Neyman type A distributions. The latter one includes effects of limited ionization area induced by heavy charged particles in the biological materials (so-called ion tracks). Whereas the Neyman A distribution parameter λN can be directly determined from the fluence of the applied radiation, the second one, µ, corresponds to the probability of CA production and is important for modelling of the interaction process. We have found that the differences between the Poisson and Neyman A distributions for low-LET radiation are very small. This result can be easily understood in terms of relation between the Poisson \(\sigma _{{\text{P}}}^{2}\) and Neyman A \(\sigma _{{\text{N}}}^{2}\) variances
For a small value of the µ parameter (µ << 1), both distributions have similar variances. In our case, only 11B ions deliver µ values close to unity. Thus, the Poisson and Neyman A statistics strongly differ and give different shapes of the CA frequency distributions.
Another of our finding is related to the beam energy dependence of the determined µ parameter. Its value increases linearly with the energy of ions, and this increase is weaker for particles with higher LET values, vanishing finally for 11B ions (see Fig. 4 b; Table 4). Comprehensive model calculations including physical and radiobiological effects should certainly explain this finding.
To compare experimental CA frequencies with the Poisson statistics, we additionally applied the U test introduced by Edwards et al. (1979). It can be used to answer the question whether the frequency number of multiple aberrations is under- or overestimated compared to the Poisson distribution. Whereas a sign of underestimation can be found for γ rays and high energy protons (however, with a confidence level lower than 95%), only a significant overestimation can be observed for boron ions. The overestimation certainly comprises the main feature of the Neyman A distribution which increases the number of multiple aberrations. On the other hand, the underestimation can be explained by a contribution of repair effects (Kowalska et al. 2015), which is, however, very difficult to observe in the distribution of CA frequencies. It seems that the underestimation effect can be determined much more easily by the so-called Fano factor applying a Chi-square analysis as proposed in (Kowalska et al. 2015).
Summarizing, the present experimental study of the CA frequencies and resulting dose–effect curves obtained for different radiation qualities have demonstrated applicability of the Neyman A statistics even to low-LET irradiations. We have found some LET dependences of experimentally determined parameters of the dose effect curves and the Neyman A distributions which can be used for comparison with the radiobiological models.
References
Anderson R, Marsden S, Wright E, Kadhim M, Goodhead D, Griffin C (2000) Complex chromosome aberrations in peripheral blood lymphocytes as a potential biomarker of exposure to high-LET α-particles. Int J Radiat Biol 76:31–42
Ando K, Goodhead DT (2016) Dependence and independence of survival parameters on linear energy transfer in cells and tissues. J Radiat Res 57:596–606
Bezbakh AA, Zager VB, Kamiński G, Krylov AI, Teterev YG, Timoshenko GN (2013) Upgrading the genome facility for radiobiological experiments with heavy-ion beams. Phys Part Nuclei Lett 10:175–178
Bonassi S, Znaor A, Norppa H, Hagmar L (2004) Chromosomal aberrations and risk of cancer in humans: an epidemiological perspective. Cytogenet Genome Res 104:376–382
Cucinotta FA, Durante M (2006) Cancer risk from exposure to galactic cosmic rays: implications for space exploration by human beings. Lancet Oncol 7:431–435
Deperas-Standyło J, Lee R, Nasonova E, Ritter S, Gudowska-Nowak E (2012) Production and distribution of aberrations in resting or cycling human lymphocytes following Fe-ion or Cr-ion irradiation: emphasis on single track effects. Adv Space Res 50:584–597
Edwards AA, Lloyd DC, Purrott RJ (1979) Radiation induced chromosome aberrations and the Poisson distribution. Radiat Environ Biophys 16:89–100
Friedrich T, Scholz U, Elsässer T, Durante M, Scholz M (2012) Calculation of the biological effects of ion beams based on the microscopic spatial damage distribution pattern. Int J Radiat Biol 88:103–107
Gudowska-Nowak E, Kleczkowski A, Nasonova E, Scholz M, Ritter S (2005) Correlation between mitotic delay and aberration burden, and their role for the analysis of chromosome damage. Int J Radiat Biol 81:23–32
Gudowska-Nowak E, Lee R, Nasonova E, Ritter S, Scholz M (2007) Effect of LET and track structure on the statistical distribution of chromosome aberrations. Adv Space Res 39:1070–1075
IAEA (2011) Cytogenetic dosimetry: application in preparedness for and response to radiation emergencies. IAEA, Vienna
IAEA Technical series No 405 (2001) Cytogenetic analysis for radiation dose assessment. A manual. IAEA, Vienna
Katz R, Ackerson B, Homayoonfar M, Sharma SC (1971) Inactivation of cells by heavy ion bombardment. Radiat Res 47:402–425
Kowalska A, Czerski K, Kaczmarski M, Lewocki M, Masojć B, Łukowiak A (2015) Comparison of cell rep air mechanisms by means of chromosome aberrations induced by proton and gamma irradiation—preliminary results. Eur Phys J D 69:79
Kowalska A, Czerski K, Nasonova E, Kutsalo P, Krasavin E (2017) Radiation dose-response curves—cell repair mechanisms vs. probability of ion track overlapping. Eur Phys J D 71:332
Kubancak J, Molokanov AG (2013) Measurements of LET spectra of the JINR phasotron radiotherapy proton beam JINR Report. http://www1.jinr.ru/Preprints/2013/077(P16-2013-77).pdf
Lea DE (1955) Actions of radiations on living cells. Cambridge University Press, Cambridge
Lee R, Nasonova E, Ritter S (2005) Chromosome aberration yields and apoptosis in human lymphocytes irradiated with Fe-ions of differing LET. Adv Space Res 35:268–275
Loucas BD, Durante M, Bailey SM, Cornforth MN (2013) Chromosome damage in human cells by γ rays, α particles and heavy ions: track interactions in basic dose-response relationships. Rad Res 179:9–20
Markov NV, Bakhmutova AV, Golubev AA, Kantsyrev AV, Luckjashin VE, Rudskoi IV, Smirnov GN, Fertman AD, Khudomyasov AV (2014) A procedure of determining the absorbed dose in a substance exposed to pulsed heavy ion beams. Instrum Exp Tech 57:55–61
Nikoghosyan A et al (2004) Evaluation of therapeutical potential of heavy ion therapy for patients with locally advanced prostate cancer. Int J Radiat Oncol Biol Phys 58:89–97
Pachnerová Brabcová K, Ambrožová I, Kubančak J, Puchalska M, Vondráček V, Molokanov AG, Sihver L, Davidková M (2014) Dose distribution outside the target volume for 170 MeV proton beam. Radiat Prot Dosimetry 161:410–416
Racjan M, Molokanov AG, Mumot M (2007) Simulations of proton beam depth-dose distributions Communication of the Joint Institute for Nuclear Research, E18-2007-91
Savage JRK (1975) Classification and relationships of induced chromosomal structural changes. J Med Genetics 12:103–122
Scholz M (2006) Dose response of Biological Systems to Low- and High-LET Radiation. In: Horowitz Y (ed) Microdosimetric response of physical and biological systems to low- and high- LET radiations: theory and applications to dosimetry, 1st edn. Elsevier, Amsterdam, pp 3–68
Scholz M, Kraft G (1996) track structure and the calculations of biological effects of heavy charged particles. Adv Space Res 18:5–14
Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G (1997) Computation of cell survival in heavy ion beams for therapy. The model and its approximation. Radiat Environ Biophys 36:59–66
Schulz-Ertner D, Karger CP, Feuerhake A et al (2007) Effectiveness of carbon ion radiotherapy in the treatment of skull-base chordomas. IntJRadiatOncolBiolPhys 68:449–457
Wilkens JJ, Oelfke U (2004) A phenomenological model for the relative biological effectiveness in therapeutic proton beams. Phys Med Biol 49:2811–2825
Acknowledgements
We thank the staff of the Medical Centre of JINR and Flerov Laboratory of Nuclear Reactions, JINR for supporting the accelerator studies, as well as Golubev A.A. and Markov N.V. (ITEP, Moscow, Russia) for providing the opportunity of carbon irradiation at the ITEP-TWAC accelerator.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kowalska, A., Nasonova, E., Czerski, K. et al. Production and distribution of chromosome aberrations in human lymphocytes by particle beams with different LET. Radiat Environ Biophys 58, 99–108 (2019). https://doi.org/10.1007/s00411-018-0771-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00411-018-0771-4