Abstract
A commonly-used model of the global radiative budget assumes that the radiative response to forcing, R, is proportional to global surface air temperature T, \(R=\lambda T\). Previous studies have highlighted two unresolved issues with this model: first, the feedback parameter \(\lambda\) depends on the forcing agent; second, \(\lambda\) varies with time. Here, we investigate the factors controlling R in two atmosphere–slab ocean climate models subjected to a wide range of abrupt climate forcings. It is found that R scales not only with T, but also with the large-scale tropospheric stability S (defined here as the estimated inversion strength area-averaged over ocean regions equatorward of 50\(^\circ {}\)). Positive S promotes negative R, mainly through shortwave cloud and lapse-rate changes. A refined model of the global energy balance is proposed that accounts for both temperature and stability effects. This refined model quantitatively explains (1) the dependence of climate feedbacks on forcing agent (or equivalently, differences in forcing efficacy), and (2) the time evolution of feedbacks in coupled climate model experiments. Furthermore, a similar relationship between R and S is found in observations compared with models, lending confidence that the refined energy balance model is applicable to the real world.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The response of the climate system to external forcing is often interpreted using the global top-of-atmosphere energy balance framework
(Gregory et al. 2002), which states that the net radiative imbalance N equals the sum of the effective radiative forcing F (Sherwood et al. 2015) and the radiative response R, which is assumed to scale with the global surface air temperature anomaly T. We define downward fluxes as positive, and the anomalies are relative to an unperturbed equilibrium state with \(N=F=0\). Our sign convention implies that the proportionality constant \(\lambda\), denoted the feedback parameter, must be negative in a stable climate system, so that R opposes F.
The global energy balance (1) is widely used to quantify forcing, feedbacks, and climate sensitivity in climate model experiments, historical observations, and paleoclimate data (see Knutti et al. 2017, and references therein). While simple and powerful, the relationship (1) also suffers from known limitations. First, the value of \(\lambda\) (i.e., the magnitude of the climate feedbacks) depends on the forcing agent (Joshi et al. 2003; Hansen et al. 2005; Forster et al. 2007; Modak et al. 2016), leading to difficulties in interpreting the energy budget in the historical period, where multiple forcing agents drove climate change (e.g., Marvel et al. 2016; Medhaug et al. 2017). Second, \(\lambda\) can also vary in time; large variations in \(\lambda\) occurred during the historical period (Gregory and Andrews 2016; Zhou et al. 2016; Andrews et al. 2018), and in most coupled climate models, climate feedbacks evolve towards more positive values over time under \(\hbox {CO}_2\) forcing (e.g., Murphy 1995; Senior and Mitchell 2000; Winton et al. 2010; Andrews et al. 2012; Armour et al. 2013; Andrews et al. 2015; Proistosescu and Huybers 2017; Ceppi and Gregory 2017). These issues suggest that the radiative response may depend on variables other than just global surface temperature.
Recent studies have explained the time dependence of \(\lambda\) in terms of sea surface temperature (SST) patterns and their impacts on tropospheric stability, with increasing stability favoring more negative cloud and lapse-rate feedbacks (Zhou et al. 2016; Ceppi and Gregory 2017; Andrews and Webb 2018). Tropospheric stability has long been recognized as a key control on low cloud amount (e.g., Klein and Hartmann 1993; Wood and Bretherton 2006), and has been used to make quantitative predictions of low cloud responses to external forcing (e.g., Qu et al. 2015b; Myers and Norris 2016; Brient et al. 2016). Such predictions have generally been restricted to low-cloud subsidence regions, however, and in the absence of a quantitative understanding of how large-scale stability changes affect the global energy budget, we are unable to account for the “pattern effect” in the energy balance relationship (1). Furthermore, it is unclear whether SST patterns can also be invoked to explain the dependence of \(\lambda\) on forcing agent.
Here we propose an improved energy balance relationship that helps interpret the two aforementioned issues in a consistent way. We perform experiments with two global climate models to demonstrate that the dependence of \(\lambda\) on forcing agent and time can be explained by a common dependence of the radiative response on the large-scale stability of the troposphere, independent of the forcing agent or time scale. This allows us to quantitatively account for the radiative impact of SST patterns, via changes in stability, in the energy balance relationship.
2 The equilibrium radiative response to a range of forcing agents
In this section we demonstrate the dependence of the climate feedback parameter on the forcing agent in the perturbed equilibrium that is reached by the climate system if there is no change in ocean heat transport. We use two atmospheric models, CAM4 (Neale et al. 2010) and HadAM3 (Pope et al. 2000). These models are run either with prescribed SSTs and sea ice concentration, or coupled to a mixed-layer “slab” ocean, which simulates sea surface conditions. Where necessary, we refer to the atmosphere–slab ocean models as CAM4-SOM and HadSM3, respectively. For brevity, we will refer to the experiments with prescribed sea surface conditions as “atmosphere-only”, while the atmosphere–slab ocean experiments will be denoted “slab” for brevity.
2.1 Models
CAM4 is run at a latitude/longitude resolution of \(1.9^\circ {} \times 2.5^\circ {}\) with 24 vertical levels, while HadAM3’s horizontal resolution is \(2.5^\circ {} \times 3.75^\circ {}\) with 19 levels. The slab ocean models’ energy budget includes a prescribed monthly climatology of ocean heat flux convergence, mimicking the effect of ocean heat transport, to maintain a realistic spatiotemporal distribution of SST. The depth of the slab is set to 50 m everywhere in HadSM3, whereas it varies spatially in CAM4-SOM, being determined from a reference coupled atmosphere-ocean simulation.
2.2 Control parameter values and aerosol treatment
The default parameter values used in our simulations are summarized in Table 1. CAM4 uses prescribed aerosol mixing ratios, set to an 1850 monthly climatology (Neale et al. 2010); the aerosol forcing experiments described in the next section use perturbations relative to this climatology. HadAM3 uses an idealized representation of aerosols, with prescribed uniform vertical distributions over land and ocean (Cusack et al. 1998).
2.3 Forcing agents
The slab models are subjected to a variety of forcing agents, including greenhouse gases (\(\hbox {CO}_2\), \(\hbox {CH}_4\)), solar irradiance (\(\hbox {S}_0\)), tropospheric sulphate aerosol (\(\hbox {SO}_4\)), black carbon aerosol (BC), volcanic aerosol (VOLC), ocean heat uptake (OHU), and idealized, uniform surface forcings (UNIF). The forcing agents and magnitudes, as well as the experiment names, are listed in Table 2. Additional details are listed below for the VOLC, OHU, and UNIF experiments.
-
For VOLC we use the January 1992 aerosol loading, near its peak following the Pinatubo eruption in June 1991. Because volcanic forcing typically lasts for a few years only, we assess the response to volcanic forcing using a 20-member ensemble of 2-year simulations, with the ensemble members initialized from successive years of the respective control simulations.
-
The OHU forcings are taken from the multi-model mean of the CMIP5 abrupt4xCO2 experiment, averaged over years 1–20 and 21–150. For practical reasons, they are applied jointly with a \(4\times \hbox {CO}_2\) forcing; we find that OHU in isolation causes a runaway “snowball earth” response in CAM4 (Rugenstein et al. 2016a), owing to the large negative forcings near the sea ice margins. The details of the OHU calculation are provided in “Appendix”.
-
Finally, the uniform surface forcings are prescribed as extra terms in the surface energy budget. These “ghost” forcings (Hansen et al. 1997; Alexeev et al. 2005; Ceppi and Shepherd 2017) are applied separately in the tropics (equatorward of 30\(^\circ {}\); \(\hbox {UNIF}_\mathrm {T}\), Table 2) and in the extratropics (poleward of 30\(^\circ {}\); \(\hbox {UNIF}_\mathrm {ET}\)), covering half of the Earth’s area in each case. The local forcing magnitude is set to \(\pm 7\)\(\hbox {W} \hbox { m}^{-2}\), yielding a global effective forcing comparable to that of a doubling of \(\hbox {CO}_2\) (Table 2).
Note that some forcing cases have not been run for both models (Table 2). Namely, the representation of aerosol in HadAM3 is too limited to allow us to run the \(\hbox {SO}_4\) and BC cases, and we found that CAM4-SOM quickly enters a snowball Earth–type runaway response in negative forcing experiments such as \(0.5\times \hbox {CO}_2\), \(-1.5\)%\(\hbox {S}_0\) or \(-\mathrm {UNIF}_\mathrm {ET}\).
2.4 Experimental design
All forced slab simulations are branched from the same date in the reference control experiment with the forcing switched on at the start of the simulations and held constant thereafter. The simulations are run to steady state, which is typically reached within 20 years (Fig. 1). These simulations are run for 50 years in total, and the new equilibrium climate is calculated as the climatology of years 31–50, except for VOLC where the response is calculated from the ensemble-mean year 2 climate. The control climatology is also based on a 20-year average.
Evolution of global-mean surface air temperature anomalies T relative to the control climatology in the slab experiments. The symbols at year 50 denote averages over the last 20 years, the period we use to calculate responses. For VOLC, the circles denote the 20-member ensemble average in year 2 (Sect. 2.4). Here and in subsequent figures, open symbols indicate CAM4-SOM results, while filled symbols correspond to HadSM3
For any variable X, we denote the slab control climatology as \(X_\mathrm {ctl}\), while the perturbed climatology is \(X_\mathrm {pert}\). The total response of that variable in the forced slab runs is then \({\Delta } X_\mathrm {cpl} = X_\mathrm {pert} - X_\mathrm {ctl}\). This total response can be decomposed into an SST-mediated component, \({\Delta } X_\mathrm {SST}\), and a fast adjustment, \({\Delta } X_\mathrm {adj}\) (Hansen et al. 1997). The adjustment is regarded as part of the forcing (Gregory and Webb 2008; Sherwood et al. 2015), whereas we are interested in the SST-mediated component, which drives the radiative response.
We therefore perform additional atmosphere-only simulations to separate the fast adjustments from the SST-mediated response. These atmosphere-only simulations are run for a minimum of 20 years with the same set of forcings as the slab runs, but keeping SSTs and sea ice fixed to their slab control climatologies. Although the sea surface conditions are the same as for the slab control, the removal of coupled feedback means that the atmosphere-only control state (without forcing agents) differs slightly from the slab control. Therefore we also run an atmosphere-only control experiment.
Denoting the atmosphere-only perturbed climatology as \(X_\mathrm {atm,pert}\) and its control as \(X_\mathrm {atm,ctl}\), we can then write
Note that if X is the net TOA radiative flux N, then Eq. 2 gives the effective radiative forcing F, while Eq. 3 gives the radiative response R. In the remainder of the paper, the results will be calculated following Eq. 3 unless otherwise noted, and we will drop the subscript SST when referring to the SST-mediated responses.
Additional atmosphere-only simulations are performed to assess the responses to uniform and patterned SST changes. These simulations are based on the atmosphere-only control described above and are also run for 20 years. Further details on these simulations are provided in Sect. 3 where these results are discussed.
2.5 Results
In the energy balance relationship of Eq. 1, the climate feedback parameter is \(\lambda = R/T\) i.e. the radiative response normalized by warming. In both models, there is a wide range of R/T in the slab experiments, contradicting the assumption that \(\lambda\) is a constant of the climate system (Fig. 2). Although HadSM3 produces less negative R/T than CAM4-SOM, the two models are generally very similar in terms of the dependence of R/T on the forcing agent: for example, the \(\hbox {UNIF}_\mathrm {T}\) and VOLC experiments yield more negative R/T, whereas \(\hbox {UNIF}_\mathrm {ET}\) gives less negative values; and \(4\times \hbox {CO}_2+\hbox {OHU}\) yields more negative R/T than \(4\times \hbox {CO}_2\) without OHU. An interpretation for the dependence of R/T on forcing agent will be provided in Sect. 5.1.
R/T in CAM4-SOM and HadSM3 slab experiments. The black line represents the one-to-one relationship. Because some of the experiments were run with only one of the models (Table 2), the full set of results is shown in the plot margins for each model
3 Equilibrium radiative response to uniform and patterned SST change
3.1 Radiative response to globally-uniform SST change
The range of R/T that we find in equilibrium climate change for a range of forcing agents indicates that the assumption of proportionality \(R\propto T\) is not accurate. However, it explains most of the variation of R across the slab experiments (Fig. 3a, b; colored symbols). The correlation coefficients between R and T are \(-\,0.95\) in both CAM4-SOM and HadSM3.
Top row: R versus T in a CAM4 and b HadAM3. Bottom row: R/T versus T in c CAM4 and d HadAM3. Colored circles denote results from the slab simulations, while the black circles are from atmosphere-only simulations with uniform SST changes in 2-K increments. The black lines represent linear or quadratic fits to the uniform-\({\Delta }\)SST results
The results from a set of atmosphere-only experiments with globally uniform SST changes are also included in Fig. 3 (black dots), in which global SST perturbations ranging between \(-\,4\) and \(+\,10\) K in 2-K increments are added to the control state while keeping sea ice fixed. The relationship between R and T in these simulations is overall consistent with the results from the slab experiments. (Note that the uniform-\({\Delta }\)SST experiment results were corrected for the lack of an ice-albedo feedback, for consistency with the slab experiments; see the “Appendix”) The uniform-\({\Delta }\)SST experiments predict that R/T is roughly constant in CAM4, and linearly dependent on temperature in HadAM3 (Fig. 3c, d). Thus, the atmosphere-only experiments reveal that even for idealized, uniform, SST perturbations, the relationship between R and T can be nonlinear (black curve in Fig. 3b). A kernel decomposition of the radiative changes, following Soden et al. (2008), indicates that the nonlinearity is primarily associated with the cloud response (not shown). This nonlinearity constitutes one limitation of the classical energy balance framework in Eq. 1.
3.2 Radiative response to SST patterns of change
The radiative responses in some of the slab experiments depart substantially from the relationship expected from the uniform-\({\Delta }\)SST experiments; for a given T, the deviations amount to several \(\hbox {W} \hbox { m}^{-2}\) in some experiments. The differences between the slab and uniform-\({\Delta }\)SST experiments are much more striking when considering R/T (Fig. 3c, d). In the slab experiments, R/T is not constant but shows no obvious monotonic dependence on T. To the extent that the radiative responses can be linearly decomposed into mean and pattern components of the SST change (as will be demonstrated later, Sect. 3.3), the deviations must be associated with the SST pattern (Andrews et al. 2015; Gregory and Andrews 2016; Zhou et al. 2016; Ceppi and Gregory 2017). Since the classical energy balance framework (Eq. 1) assumes that the radiative response scales with mean temperature only, this “pattern effect” constitutes a second, arguably more fundamental, limitation of the classical framework.
3.3 Combination of the radiative responses to uniform and patterned SST change
We will next demonstrate that the radiative responses in the slab experiments can be partitioned into mean and pattern components of the SST response, and that these components of the radiative response are governed by distinct physical processes. In Fig. 4a we compare the actual R from the slab experiments with \(R_\mathrm {m}+R_\mathrm {p}\), which is the sum of the mean SST-driven component \(R_\mathrm {m}\) (predicted from the linear or quadratic fits in Fig. 3a, b) and the pattern component \(R_\mathrm {p}\), obtained from a separate set of atmosphere-only experiments. For these experiments, we calculate the SST anomalies in the equilibrium slab climatology for each month and gridpoint, subtract the global-mean SST anomaly to form a pattern which has zero global mean by construction, and add this pattern to the control atmosphere-only climatology, keeping sea ice fixed.
The relationship in Fig. 4a is generally close to the one-to-one line, although errors are larger in HadAM3, which tends to produce SST patterns of larger amplitude compared with CAM4. In Fig. 4b, the results from panel (a) are normalized by the total temperature anomalies taken from the slab experiments. The predicted R/T values are within 15% of the actual values, with the exception of the \(-\mathrm {UNIF}_\mathrm {ET}\) case in HadAM3, which features an anomalously positive albedo feedback (not shown). Overall, however, the sum of the mean and pattern responses accurately predicts R and R/T. Similar linearity of the responses was documented in previous work with the CAM5 model (Zhou et al. 2016, 2017). We can therefore separately investigate the responses to mean and pattern SST changes in order to understand the full radiative responses.
We have already explained the radiative responses to changes in mean SST, \(R_\mathrm {m}\), in terms of global-mean temperature (Fig. 3). In the pattern experiments, the global-mean temperature changes are small by construction (the standard deviations across experiments are 0.04 and 0.26 K in CAM4 and HadAM3, respectively), so \(R_\mathrm {p}\) cannot be explained in terms of \(T_\mathrm {p}\). Instead, we propose that the radiative impact of the SST patterns comes through changes in near-global tropospheric stability, S (in K). Here we define S as the area-average change in estimated inversion strength (EIS; Wood and Bretherton 2006) over ocean areas between 50\(^\circ {}\) S and 50\(^\circ {}\) N. S in our definition is therefore not strictly global, but we find a stronger relationship between S and R if the high latitudes are excluded. We speculate this is because large stability changes occur at high latitudes in association with changes in sea ice extent, but these changes are not reflected in the processes controlling radiation—primarily cloud cover, as discussed below.
The relationship between radiative response and stability is demonstrated in Fig. 5 for the pattern experiments (colored symbols). In both models, the relationship is negative, and remarkably linear. That increasing stability promotes a negative radiative response is consistent with the findings of Zhou et al. (2016), Ceppi and Gregory (2017), and Andrews and Webb (2018), who ascribed the stability effect to the cloud and (to a lesser extent) lapse-rate feedbacks. We confirm these findings by performing a kernel decomposition of \(R_\mathrm {p}\) (Fig. 6), which reveals that the stability effect is dominated by shortwave (SW) cloud feedback, with some cancellation by the longwave (LW) cloud feedback, and a smaller contribution from the lapse-rate feedback. SW cloud feedback also explains the stronger sensitivity of R to S in CAM4 relative to HadAM3, likely a consequence of different cloud parameterizations. It is worth noting here that low cloud amount in CAM4 is an explicit function of lower-tropospheric stability (Neale et al. 2010).
As in Fig. 5, but \(R_\mathrm {p}\) is decomposed into contributions from a the Planck response, b the lapse rate, c relative humidity, d surface albedo, e longwave cloud-radiative effects, f shortwave cloud-radiative effects, g net cloud-radiative effects, and h the sum of all contributions. The decomposition is calculated with CAM5 radiative kernels (Pendergrass et al. 2017) following the method of Soden et al. (2008). The lines denote least-squares fits to the CAM4 (solid) and HadAM3 (dashed) results. The corresponding slopes (in \(\hbox {W} \hbox { m}^{-2} \hbox { K}^{-1}\)) are shown in the bottom left corner of each panel
The negative cloud-radiative response occurs primarily because increased stability favors more low cloud in the global mean (Fig. 7). On local scales, this relationship between low cloud fraction and tropospheric stability is very well established observationally (Klein and Hartmann 1993; Wood and Bretherton 2006), and is present in most global climate models, even though models tend to underestimate the magnitude of the cloud response (Qu et al. 2015b; Myers and Norris 2016). A novel aspect of our results is to relate the global responses of tropospheric stability and radiation in a quantitative way; to our knowledge, so far this had only been done locally. The relatively large radiative responses to stability variations (Fig. 5) reflect the key importance of low clouds for the global radiative budget and climate sensitivity (Bony and Dufresne 2005; Webb et al. 2013).
In principle, we do not expect the radiative responses to stability variations to be spatially uniform. For example, the latitudinal dependence of insolation means that even under the assumption of a uniform dependence of cloud cover on S, the radiative response would be largest in the tropics. We therefore expect that spatial variations in the dependence of R on stability are implicit in the regression slope in Fig. 5.
4 A refined energy balance model
Motivated by our findings, we propose a simple refinement of the energy balance relationship (1) to address both the deficiencies that we have demonstrated. We postulate that the radiative response can be formulated as
where \(\tau\) and \(\sigma\) are both in units of \(\hbox {W} \hbox { m}^{-2} \hbox { K}^{-1}\). If \(\tau\) and \(\sigma\) are constants, R depends linearly on T and S, but in general \(\tau = \tau (T)\) and \(\sigma = \sigma (S)\), as discussed later in this section.
The decomposition of the radiative response into temperature and stability components is not equivalent to decomposing into mean SST and SST pattern components. This is because uniform SST perturbations cause changes in both T and S (Fig. 8; see also Qu et al. 2015a). However, the relationship (4) can be used to interpret the radiative impacts of mean and pattern SST changes, as follows. We have shown that \(R = R_\mathrm {m} + R_\mathrm {p}\), to a good approximation, so we formulate both components in terms of temperature and stability:
where \(S_\mathrm {m}\) is the stability change induced by the uniform change in SST. Note that since the SST pattern in isolation causes negligible changes in global-mean temperature, T is included only in Eq. 5 and is not subscripted. We parameterize the stability response to mean SST changes as a linear function of temperature:
The relationship seems closer to quadratic in the case of CAM4 (Fig. 8), but the linear approximation suffices for our purposes: the correlation coefficient between \(S_\mathrm {m}+S_\mathrm {p}\) and S (combining all experiments and models) is 0.96. We can then rewrite (5) as
and defining
we obtain
By taking the sum of (6) and (8), we obtain an alternative formulation of (4) which allows us to directly relate R to the decomposition into mean SST change and SST pattern discussed in Sect. 3.3:
We calculated \(\tau _\mathrm {m}\), \(\sigma\), and \(\zeta\) from our mean and pattern experiments using the fits in Figs. 3, 5, and 8. We then derived \(\tau\) using Eq. 7. The values of these parameters are listed in Table 3. Note that the quadratic fit in Fig. 3b suggests that \(\tau _\mathrm {m}\) (and hence also \(\tau\)) is itself a linear function of T in HadAM3.
As a simple test of the refined energy balance model, we plot the actual radiative responses in the slab experiments against those predicted by Eq. 9 (Fig. 9). Consistent with the results in Fig. 4, the prediction tends to be slightly less accurate for HadAM3, but overall the relationship accurately predicts the range of R and R/T values in our experiments for both models. Note that the \(\tau\) and \(\sigma\) parameters are independent of the results we are predicting, since they are derived from the atmosphere-only mean and pattern SST experiments, while the predicted values are from slab runs. Although not shown, the prediction based on Eq. 4 performs equally well.
Our revised energy balance model helps to interpret the results of Dessler et al. (2018), who proposed a variant of the classic model where the radiative response scales with 500 hPa temperature (\(T_{500}\)) rather than with surface air temperature T. Their finding that R correlates better with \(T_{500}\) than with T reflects the fact that mid-tropospheric temperature responds to changes in both T and S. An advantage of the model proposed here is that the relationship between R and climate sensitivity is straightforward (since the model is based on global surface temperature), and furthermore additional physical insight is gained by considering the distinct processes associated with mean warming versus stability changes.
5 Implications of the refined model
We now discuss the significance of our refined energy balance model for three issues: the dependence of the feedback parameter on the forcing agent, the time variation of the feedback parameter, and the interpretation of the observed global radiative budget. These issues are discussed in turn in the next three subsections.
5.1 Dependence of the feedback parameter on forcing agent
The value of the classical feedback parameter \(\lambda\) (Eq. 1) is known to depend on the forcing agent (cf. Fig. 3c, d); equivalently, this dependence can also be interpreted in terms of differences in forcing efficacy, the global temperature response per unit (effective) radiative forcing, T/F, relative to that of \(\hbox {CO}_2\)Footnote 1 (Joshi et al. 2003; Hansen et al. 2005; Forster et al. 2007; Winton et al. 2010; Rose et al. 2014; Marvel et al. 2016; Modak et al. 2016; Rugenstein et al. 2016a). Understanding the cause for differences in efficacy among forcing agents has been a long-standing question in climate dynamics.
Here we demonstrate that, at least for the climate models and forcing agents considered here, the forcing agent dependence of the feedback parameter can be explained in terms of the stability response to different forcings. Dividing Eq. 4 by T yields
indicating that the classical feedback parameter, \(\lambda =R/T\), should be a linear function of the stability response per unit warming. If \(\tau\) is a linear function of T rather than a constant, as is the case in HadAM3, we can substitute \(\tau = (\tau _1 T + \tau _0)T\) in Eq. 4 before diving by T, yielding
For HadAM3, \(\tau _1=0.06\)\(\hbox {W} \hbox { m}^{-2} \hbox { K}^{-2}\) and \(\tau _0=-0.91\)\(\hbox {W} \hbox { m}^{-2} \hbox { K}^{-1}\) (Fig. 3b).
We confirm this by plotting R/T (Fig. 10a) and \(R/T - \tau _1 T\) (Fig. 10b) against S/T for the slab experiments. In this representation, the intercept of the linear fit represents \(\tau\) (or \(\tau _0\)), while the slope corresponds to \(\sigma\). The points lie close to the predicted relationships based on Eqs. 10 and 11. Our results therefore suggest that forcing agents cause different feedbacks, i.e. vary in efficacy, because they induce different SST patterns, and hence different stability responses per unit warming.
Among the forcing agents studied here, a good predictor of the variation in \(\lambda =R/T\) is the ratio of tropical to global effective forcing (Fig. 11): forcings that are more focused on the tropics tend to yield more negative \(\lambda\), i.e. have lower efficacy (\(r=-\,0.92\) if excluding the two outlier CAM4 experiments \(\hbox {BC} \times 10\) and VOLC, discussed below). Compared with uniform forcings, tropical forcings tend to cause enhanced free-tropospheric warming per unit global surface warming (higher S/T), because the tropics are generally close to neutral moist stability, and therefore well coupled with the free troposphere through convection, relative to other parts of the world. This interpretation is consistent with Zhou et al. (2017) and Andrews and Webb (2018), who showed that increasing SSTs in tropical ascent regions excites a negative global radiative response (consistent with positive S), while warming away from ascent regions mostly causes positive radiative changes.
Values of R/T, taken from the slab runs, versus the ratio of tropical to global effective forcing, calculated from atmosphere-only simulations with fixed SST and sea ice. The forcing ratio is defined so that a value of 1 means that the forcing is entirely in the tropics, where the tropics include the area between 30\(^{\circ }\) S and 30\(^{\circ }\) N. The global effective forcing values are listed in Table 2
The results in Fig. 11 provide a physical basis to interpret the low efficacy of solar and volcanic forcings (Fig. 11; Hansen et al. 2005; Marvel et al. 2016; Modak et al. 2016; Gregory et al. 2016), which are more focused on the tropics relative to \(\hbox {CO}_2\). They also account for the high efficacy of ocean heat uptake and other extratropical forcings (Winton et al. 2010; Rose et al. 2014; Rose and Rayborn 2016; Rugenstein et al. 2016a; Liu et al. 2018). We note, however, that two CAM4 experiments, \(\hbox {BC} \times 10\) and VOLC, have substantially lower R/T than expected given the meridional structure of these forcings. The VOLC experiment is not run to equilibrium (Sect. 2.4), which likely affects the pattern of the SST response (and therefore the change in S), since the SST pattern is likely to evolve in time. The \(\hbox{BC}\times 10\) forcing is mainly characterized by a pattern of land-sea contrast, rather than by a meridional contrast (not shown), and we speculate that this land-sea contrast causes a large stability response that is not captured by our simple index. In support of this reasoning, Qu et al. (2015a) found that land warming could cause a decrease in coastal stratocumulus cloud via the stability mechanism. We therefore conclude that the meridional structure of the forcing is an important but not the sole factor controlling forcing efficacy.
5.2 Apparent time dependence of the feedback parameter
Previous studies have proposed that large-scale stability changes are responsible for time variations in \(\lambda\) in the historical period (Zhou et al. 2016) and in \(\hbox {CO}_2\)-forced model simulations (Ceppi and Gregory 2017; Andrews and Webb 2018). Here we demonstrate that these variations can be accounted for quantitatively by using the energy balance (4).
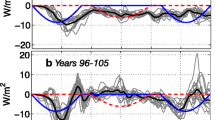
We begin with historical variations in \(\lambda\). Following Gregory and Andrews (2016) and Andrews et al. (2018), we define \(\lambda\) as the least-squares slope of R versus T, \(\lambda = \partial R/\partial T\). We assess the evolution of \(\lambda\) by calculating \(\partial R/\partial T\) over sliding 30-year windows in the amip-piForcing experiment, where our two atmosphere models are forced with historical observed SSTs from 1871 to 2012 while keeping forcing agents at pre-industrial levels. Note that for both models, the results are averages over four ensemble members. Since there is no forcing, in these runs we can readily diagnose R as \(R = N\). If the refined energy balance (4) holds, then we should be able to predict the time evolution of \(\partial R/\partial T\) using
and
which is Eqs. 10, 11 rewritten in differential form. Comparing the actual \(\partial R/\partial T\) with the predicted values, we find that Eqs. 12, 13 predict the time evolution well, despite an overall negative bias in CAM4 (Fig. 12). The results show that during the historical period, the stability response generally led to more negative feedbacks (more negative \(\lambda\), lower climate sensitivity) compared to a case with no stability changes (Fig. 12, dashed lines) or compared to the expected response to \(\hbox {CO}_2\)-only forcing (dotted lines).
Time evolution of \(\partial R/\partial T\), the regression slope of R versus T, calculated over 30-year sliding windows in amip-piForcing simulations (Andrews et al. 2018) with a CAM4 and b HadAM3. For both models, the results are averages over four ensemble members. Black curves are the actual \(\partial R/\partial T\) values; solid red curves denote the values predicted from Eqs. 12, 13 using the values in Table 3; dashed lines also indicate predictions based on Eqs. 12, 13, but omitting the stability term; and dotted lines show R/T obtained from the atmosphere–slab ocean \(4\times \mathrm {CO}_2\) simulations
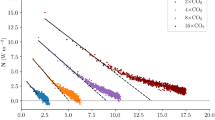
Next we turn to the problem of increasing climate sensitivity over time under \(\hbox {CO}_2\) forcing. Figure 13a, b shows N versus T in simulations with atmosphere–ocean general circulation models (including a three-dimensional dynamical ocean model rather than a slab model), where the models are subjected to an abrupt \(4\times \mathrm {CO}_2\) forcing. In this configuration, we refer to our models as CESM-CAM4 and HadCM3. The simulations are 250 years long and 100 years long in CESM-CAM4 and HadCM3 respectively. To minimize noise, we use ensemble averages. For CESM-CAM4 the experiment contains 12 ensemble members over the first 100 years, then 5 members over the remaining 150 years; for HadCM3 there are 7 members over the whole experiment. The CESM-CAM4 and HadCM3 abrupt\(4\times \mathrm {CO}_2\) ensembles are described in more detail in Rugenstein et al. (2016b) and Andrews et al. (2015), respectively.
Top: N versus T in fully-coupled atmosphere-dynamical ocean \(4\times \mathrm {CO}_2\) simulations. Black circles denote individual years. The simulations are 250 years long in CESM-CAM4 (a) and 100 years long in HadCM3 (b). For both models, the results are ensemble averages (see text). The red lines show the least-squares fits of N versus T over 1.2 K windows, for the first and last windows available in the time series. The lines are solid over the 1.2 K window used to calculate the fit and dotted elsewhere. Bottom: time evolution of \(\partial N/\partial T\), the regression slope of N versus T, calculated over 1.2 K sliding windows. The thick solid red curves show the actual \(\partial N/\partial T\) values, the thin solid red curves indicate the predicted \(\partial N/\partial T\) based on Eqs. 12, 13, and the dashed lines also correspond to predictions based on Eqs. 12, 13 but excluding the stability term
Since the forcing is abrupt and therefore constant, we can consider N instead of R, and we use \(\lambda = \partial N/\partial T\). As highlighted by the red least-squares fits in Fig. 13a, b, \(\partial N/\partial T\) becomes less negative as time passes. We calculate the \(\lambda\) evolution as above, except that we use a sliding 1.2 K window (as in Rugenstein et al. 2016b) rather than a fixed time window; this maintains an adequate signal-to-noise ratio throughout the time series and yields cleaner results towards the later part of the runs, where T and N evolve very slowly in time.
The sliding regressions over the \(4\times \mathrm {CO}_2\) simulations again indicate that the refined energy balance predicts the evolution of \(\lambda\) well (Fig. 13c, d). The predictions look noisier towards the beginning of the runs, possibly due to residual noise in the results despite the use of ensemble averages, because there are fewer years in a given T interval at the start of the experiment. In HadAM3, part of the increase in \(\lambda\) over time is associated with the temperature dependence of \(\tau\) (dashed line in Fig. 13d), but changes in stability mostly explain the \(\lambda\) evolution.
It is interesting to note that although CESM-CAM4 and HadCM3 produce similar feedback values under \(4\times \mathrm {CO}_2\) forcing, they achieve these values through very different combinations of the uniform-SST and pattern responses. In CESM-CAM4, the normalized stability response, \(\partial S/\partial T\), is near zero or negative, while it is substantially positive in HadCM3 (compare the thin solid and dashed lines in Fig. 13c, d, and recall \(\mathrm {R}\propto -\mathrm {S}\)). This indicates that the two models produce substantially different patterns of SST response to \(\hbox {CO}_2\) forcing, highlighting the need for constraints on future patterns of SST change in response to forcing.
5.3 Observations of the Earth’s radiation budget
Having demonstrated the relationship between stability and radiative budget in climate models, we now verify whether our findings apply to the real world. We use global satellite observations of net top-of-atmosphere radiative flux, N, based on the Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) version 4.0 data product (Loeb et al. 2018). We analyze deseasonalized monthly data for the period March 2000–February 2017. We estimate R as \(N-F\), where F is based on the IPCC AR5 forcing time series, revised and extended by Dessler and Forster (2018). Estimates of T and S are obtained from ERA5 reanalysis data (Hersbach and Dee 2016).
R is negatively correlated with S on monthly timescales, and this relationship is statistically significant (Fig. 14a). By comparison, T is a poor predictor of monthly variations in R (\(r=-0.14\), not statistically significant; not shown). Since T and S tend to covary in monthly observations (\(r=0.44\)), the relationship in Fig. 14a could include a response to T; however, we obtain a nearly identical result if the effect of T is regressed out from both S and R (Fig. 14b). Meanwhile, the relationship between R and T remains weak if S is regressed out (\(r=0.15\); not shown). It therefore appears that tropospheric stability is a key control on the global energy budget in the real world.
R versus S in observations (CERES-EBAF version 4.0) and reanalysis data (ERA5) during March 2000–February 2017. Black circles denote individual months; black lines are least-squares fits. The confidence intervals for the regression slopes (\(\sigma\)) are for a 95% confidence level. Following Santer et al. (2000), we account for the reduction in the number of degrees of freedom owing to autocorrelation in the time series before calculating confidence intervals. In panel b, the subscript “fixed T” indicates that T was regressed out from the respective variables, i.e. \(R_{\mathrm {fixed}\;T}\) is the residual of the regression of R onto T
An implication of this result is that previous observational estimates of \(\lambda\) based on Eq. 1 (e.g., Gregory et al. 2002; Forster and Gregory 2006; Roe and Armour 2011; Otto et al. 2013; Kummer and Dessler 2014; Lewis and Curry 2015, 2018; Resplandy et al. 2018) may have been biased by not accounting for the role of stability variations. Our results also support the findings of Andrews et al. (2018), who showed that accounting for the impact of SST patterns (which we show to be mediated by stability) increases previous observational estimates of climate sensitivity, making them consistent with model-based estimates.
6 Conclusions
The radiative response to forcing is commonly assumed to follow a simple linear dependence on global surface air temperature, \(R = \lambda T\). Using two global climate models, we demonstrate that a better model of the radiative response is obtained by including the effect of large-scale tropospheric stability S, quantified as the estimated inversion strength (EIS, in K): \(R = \tau T + \sigma S\). All other things being equal, positive S causes a negative R (a cooling effect), because of (a) increased low cloud cover (a negative shortwave cloud feedback), and (b) increased longwave emission to space from the upper troposphere (a negative lapse-rate feedback). The importance of the stability term in the refined energy balance model results from the fact that low clouds are a leading cause of differences in radiative feedback across climate models and forcing agents.
The stability term \(\sigma S\) quantitatively explains the impact of diverse SST patterns on the radiative response. By including this term, we show that differences in efficacy across a wide range of forcing agents are largely due to the associated SST patterns, which cause different stability responses. Forcings focused on the tropics tend to cause a more positive stability response, resulting in lower efficacy, compared with extratropical forcings. This helps to explain previous findings, e.g. the low efficacy of solar and volcanic forcing (Hansen et al. 2005; Marvel et al. 2016; Modak et al. 2016; Gregory et al. 2016), and the high efficacy of ocean heat uptake and other extratropical forcings (Winton et al. 2010; Rose et al. 2014; Rose and Rayborn 2016; Rugenstein et al. 2016a; Liu et al. 2018).
Furthermore, the impact of SST patterns on the time evolution of the feedback parameter (\(\lambda = \partial R/\partial T\)) can also be captured by the stability term in our refined model of the radiative response. In periods where the stability response per unit warming, \(\partial S/\partial T\), is more positive, the radiative response per unit warming \(\partial R/\partial T\) is more negative, and vice versa. This explains both the historical variations in \(\partial R/\partial T\) given the observed evolution of SSTs (Gregory and Andrews 2016; Zhou et al. 2016; Andrews et al. 2018), and the increase in \(\partial R/\partial T\) over time in coupled models under \(\hbox {CO}_2\) forcing (e.g., Murphy 1995; Senior and Mitchell 2000; Williams et al. 2008; Winton et al. 2010; Andrews et al. 2012; Armour et al. 2013; Andrews et al. 2015; Proistosescu and Huybers 2017; Ceppi and Gregory 2017).
Finally, we show that the relationship between S and R is qualitatively similar in the real world compared with climate models. In recent satellite observations of the radiative budget, most of the monthly variations in R are driven by S, and the two variables are well-correlated on monthly timescales (\(r=-0.57\)). Because the stability response will affect the estimate of \(\lambda = \partial R/\partial T\), this implies that the role of stability must be taken into account when quantifying climate sensitivity from historical observations. This could be done by diagnosing the two parameters in our refined energy balance model using multiple linear regression, an approach similar to that followed by low cloud observational studies (Klein et al. 2017, and references therein) but extended to global scales.
Notes
The link between \(\lambda\) and T/F can be understood by setting N to 0 in Eq. 1, and solving for T/F, yielding \(T/F=-1/\lambda\). Hence, more positive \(\lambda\) (in our sign convention) corresponds to higher efficacy.
References
Alexeev VA, Langen PL, Bates JR (2005) Polar amplification of surface warming on an aquaplanet in ghost forcing experiments without sea ice feedbacks. Clim Dyn 24(7–8):655–666. https://doi.org/10.1007/s00382-005-0018-3
Andrews T, Webb MJ (2018) The dependence of global cloud and lapse-rate feedbacks on the spatial structure of tropical Pacific warming. J Clim 31(2):641–654. https://doi.org/10.1175/JCLI-D-17-0087.1
Andrews T, Gregory JM, Webb MJ, Taylor KE (2012) Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere–ocean climate models. Geophys Res Lett 39(9):L09. https://doi.org/10.1029/2012GL051607
Andrews T, Gregory JM, Webb MJ (2015) The dependence of radiative forcing and feedback on evolving patterns of surface temperature change in climate models. J Clim 28(4):1630–1648. https://doi.org/10.1175/JCLI-D-14-00545.1
Andrews T, Gregory JM, Paynter D, Silvers LG, Zhou C, Mauritsen T, Webb MJ, Armour KC, Forster PM, Titchner H (2018) Accounting for changing temperature patterns increases historical estimates of climate sensitivity. Geophys Res Lett 45(16):8490–8499. https://doi.org/10.1029/2018GL078887
Armour KC, Bitz CM, Roe GH (2013) Time-varying climate sensitivity from regional feedbacks. J Clim 26(13):4518–4534. https://doi.org/10.1175/JCLI-D-12-00544.1
Bony S, Dufresne JL (2005) Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models. Geophys Res Lett 32(20):L20. https://doi.org/10.1029/2005GL023851
Brient F, Schneider T, Tan Z, Bony S, Qu X, Hall A (2016) Shallowness of tropical low clouds as a predictor of climate models’ response to warming. Clim Dyn 47(1–2):433–449. https://doi.org/10.1007/s00382-015-2846-0
Ceppi P, Gregory JM (2017) Relationship of tropospheric stability to climate sensitivity and Earth’s observed radiation budget. Proc Natl Acad Sci USA 114(50):13,126–13,131. https://doi.org/10.1073/pnas.1714308114
Ceppi P, Shepherd TG (2017) Contributions of climate feedbacks to changes in atmospheric circulation. J Clim JCLI–D–17–0189.1, https://doi.org/10.1175/JCLI-D-17-0189.1
Cusack S, Slingo A, Edwards JM, Wild M (1998) The radiative impact of a simple aerosol climatology on the Hadley Centre atmospheric GCM. Quart J R Meteorol Soc 124(551):2517–2526. https://doi.org/10.1002/qj.49712455117
Dessler AE, Forster PM (2018) An estimate of equilibrium climate sensitivity from interannual variability. J Geophys Res: Atmos 123(16):8634–8645. https://doi.org/10.1029/2018JD028481
Dessler AE, Mauritsen T, Stevens B (2018) The influence of internal variability on Earth’s energy balance framework and implications for estimating climate sensitivity. Atmospheric Chemistry and Physics 18(7):5147–5155. https://doi.org/10.5194/acp-18-5147-2018, https://www.atmos-chem-phys.net/18/5147/2018/
Forster P, Ramaswamy V, Artaxo P, Berntsen T, Betts R, Fahey D, Haywood J, Lean J, Lowe D, Myhre G, Nganga J, Prinn R, Raga G, Schulz M, Dorland RV (2007) Changes in Atmospheric Constituents and in Radiative Forcing. In: Solomon, S, D Qin, M Manning, Z Chen, M Marquis, KB Averyt M, Miller H (eds) Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, chap 2, pp 129–234
Forster PMdF, Gregory JM (2006) The climate sensitivity and its components diagnosed from earth radiation budget data. J Clim 19(1):39–52. https://doi.org/10.1175/JCLI3611.1
Gregory J, Webb M (2008) Tropospheric adjustment induces a cloud component in CO2 forcing. J Clim 21(1):58–71. https://doi.org/10.1175/2007JCLI1834.1
Gregory JM, Andrews T (2016) Variation in climate sensitivity and feedback parameters during the historical period. Geophys Res Lett 43(8):3911–3920. https://doi.org/10.1002/2016GL068406
Gregory JM, Stouffer RJ, Raper SCB, Stott PA, Rayner NA (2002) An observationally based estimate of the climate sensitivity. J Clim 15(22):3117–3121. https://doi.org/10.1175/1520-0442(2002)015<3117:AOBEOT>2.0.CO;2
Gregory JM, Andrews T, Good P, Mauritsen T, Forster PM (2016) Small global-mean cooling due to volcanic radiative forcing. Clim Dyn 47(12):3979–3991. https://doi.org/10.1007/s00382-016-3055-1
Hansen J, Sato M, Ruedy R (1997) Radiative forcing and climate response. J Geophys Res: Atmos 102(D6):6831–6864. https://doi.org/10.1029/96JD03436
Hansen J, Sato M, Ruedy R, Nazarenko L, Lacis A, Schmidt GA, Russell G, Aleinov I, Bauer M, Bauer S, Bell N, Cairns B, Canuto V, Chandler M, Cheng Y, Del Genio A, Faluvegi G, Fleming E, Friend A, Hall T, Jackman C, Kelley M, Kiang N, Koch D, Lean J, Lerner J, Lo K, Menon S, Miller R, Minnis P, Novakov T, Oinas V, Perlwitz J, Perlwitz J, Rind D, Romanou A, Shindell D, Stone P, Sun S, Tausnev N, Thresher D, Wielicki B, Wong T, Yao M, Zhang S (2005) Efficacy of climate forcings. J Geophys Res 110(D18):D18,104. https://doi.org/10.1029/2005JD005776
Hersbach H, Dee DP (2016) ERA5 reanalysis is in production. ECMWF Newslett 147(7):5–6
Joshi M, Shine K, Ponater M, Stuber N, Sausen R, Li L (2003) A comparison of climate response to different radiative forcings in three general circulation models: towards an improved metric of climate change. Clim Dyn 20(7–8):843–854. https://doi.org/10.1007/s00382-003-0305-9
Klein SA, Hartmann DL (1993) The Seasonal Cycle of Low Stratiform Clouds. Journal of Climate 6(8):1587–1606. https://doi.org/10.1175/1520-0442(1993)006<1587:TSCOLS>2.0.CO;2, http://journals.ametsoc.org/doi/abs/10.1175/1520-0442(1993) 006%3C1587:TSCOLS%3E2.0.CO;2
Klein SA, Hall A, Norris JR, Pincus R (2017) Low-cloud feedbacks from cloud-controlling factors: a review. Surveys Geophys 38(6):1–23. https://doi.org/10.1007/s10712-017-9433-3
Knutti R, Rugenstein MAA, Hegerl GC (2017) Beyond equilibrium climate sensitivity. Nature Geoscience 10(10):727–736. https://doi.org/10.1038/ngeo3017, http://www.nature.com/doifinder/10.1038/ngeo3017
Kummer JR, Dessler AE (2014) The impact of forcing efficacy on the equilibrium climate sensitivity. Geophys Res Lett 41(10):3565–3568. https://doi.org/10.1002/2014GL060046
Lewis N, Curry J (2018) The impact of recent forcing and ocean heat uptake data on estimates of climate sensitivity. J Clim 31(15):6051–6071. https://doi.org/10.1175/JCLI-D-17-0667.1
Lewis N, Curry JA (2015) The implications for climate sensitivity of AR5 forcing and heat uptake estimates. Clim Dyn 45(3–4):1009–1023. https://doi.org/10.1007/s00382-014-2342-y
Liu F, Lu J, Garuba OA, Huang Y, Leung LR, Harrop BE, Luo Y, Liu F (2018) Sensitivity of surface temperature to oceanic forcing via q-flux green’s function experiments. Part II: feedback decomposition and polar amplification. J Clim 31(17):6745–6761. https://doi.org/10.1175/JCLI-D-18-0042.1
Loeb NG, Doelling DR, Wang H, Su W, Nguyen C, Corbett JG, Liang L, Mitrescu C, Rose FG, Kato S (2018) Clouds and the earth’s radiant energy system (CERES) Energy balanced and filled (EBAF) Top-of-atmosphere (TOA) edition-4.0 data product. J Clim 31(2):895–918. https://doi.org/10.1175/JCLI-D-17-0208.1
Marvel K, Schmidt GA, Miller RL, Nazarenko LS (2016) Implications for climate sensitivity from the response to individual forcings. Nature Climate Change 6(4):386–389. https://doi.org/10.1038/nclimate2888, http://www.nature.com/articles/nclimate2888
Medhaug I, Stolpe MB, Fischer EM, Knutti R (2017) Reconciling controversies about the ‘global warming hiatus’. Nature 545(7652):41–47. https://doi.org/10.1038/nature22315
Modak A, Bala G, Cao L, Caldeira K (2016) Why must a solar forcing be larger than a CO<sub>2</sub> forcing to cause the same global mean surface temperature change? Environmental Research Letters 11(4):044,013, https://doi.org/10.1088/1748-9326/11/4/044013, http://stacks.iop.org/1748-9326/11/i=4/a=044013?key=crossref.943a9361d22b6838f2d46dae76b64290
Murphy JM (1995) Transient Response of the Hadley Centre Coupled Ocean-Atmosphere Model to Increasing Carbon Dioxide. Part I: Control Climate and Flux Adjustment. Journal of Climate 8(1):36–56, https://doi.org/10.1175/1520-0442(1995)008<0036:TROTHC>2.0.CO;2, http://journals.ametsoc.org/doi/abs/10.1175/1520-0442%281995%29008%3C0036%3ATROTHC%3E2.0.CO%3B2
Myers TA, Norris JR (2016) Reducing the uncertainty in subtropical cloud feedback. Geophys Res Lett 43(5):2144–2148. https://doi.org/10.1002/2015GL067416
Neale RB, Richter JH, Conley AJ, Park S, Lauritzen PH, Gettelman A, Williamson DL, Rasch PJ, Vavrus SJ, Taylor MA, Collins WD, Zhang M, Lin SJ (2010) Description of the NCAR Community Atmosphere Model (CAM 4.0). In: NCAR Tech. Note TN-485, NCAR, p 212
Otto A, Otto FEL, Boucher O, Church J, Hegerl G, Forster PM, Gillett NP, Gregory J, Johnson GC, Knutti R, Lewis N, Lohmann U, Marotzke J, Myhre G, Shindell D, Stevens B, Allen MR (2013) Energy budget constraints on climate response. Nature Geoscience 6(6):415–416. https://doi.org/10.1038/ngeo1836, http://www.nature.com/articles/ngeo1836
Pendergrass AG, Conley A, Vitt F (2017) Surface and top-of-atmosphere radiative feedback kernels for CESM-CAM5. Earth System Science Data Discussions pp 1–14, https://doi.org/10.5194/essd-2017-108, https://www.earth-syst-sci-data-discuss.net/essd-2017-108/
Pope VD, Gallani ML, Rowntree PR, Stratton RA (2000) The impact of new physical parametrizations in the Hadley Centre climate model: HadAM3. Clim Dyn 16(2–3):123–146. https://doi.org/10.1007/s003820050009
Proistosescu C, Huybers PJ (2017) Slow climate mode reconciles historical and model-based estimates of climate sensitivity. Sci Adv 3(7). http://advances.sciencemag.org/content/3/7/e1602821
Qu X, Hall A, Klein SA, Caldwell PM (2015a) The strength of the tropical inversion and its response to climate change in 18 CMIP5 models. Clim Dyn 45(1–2):375–396. https://doi.org/10.1007/s00382-014-2441-9
Qu X, Hall A, Klein SA, DeAngelis AM (2015b) Positive tropical marine low-cloud cover feedback inferred from cloud-controlling factors. Geophys Res Lett 42(18):7767–7775. https://doi.org/10.1002/2015GL065627
Resplandy L, Keeling RF, Eddebbar Y, Brooks MK, Wang R, Bopp L, Long MC, Dunne JP, Koeve W, Oschlies A (2018) Quantification of ocean heat uptake from changes in atmospheric O2 and CO2 composition. Nature 563(7729):105–108. https://doi.org/10.1038/s41586-018-0651-8
Roe GH, Armour KC (2011) How sensitive is climate sensitivity? Geophysical Research Letters 38(14):n/a–n/a, https://doi.org/10.1029/2011GL047913
Rose BEJ, Rayborn L (2016) The effects of ocean heat uptake on transient climate sensitivity. Curr Clim Change Rep 2(4):190–201. https://doi.org/10.1007/s40641-016-0048-4
Rose BEJ, Armour KC, Battisti DS, Feldl N, Koll DDB (2014) The dependence of transient climate sensitivity and radiative feedbacks on the spatial pattern of ocean heat uptake. Geophys Res Lett 41(3):1071–1078. https://doi.org/10.1002/2013GL058955
Rugenstein MAA, Caldeira K, Knutti R (2016a) Dependence of global radiative feedbacks on evolving patterns of surface heat fluxes. Geophys Res Lett 43(18):9877–9885. https://doi.org/10.1002/2016GL070907
Rugenstein MAA, Gregory JM, Schaller N, Sedláček J, Knutti R (2016b) Multi-annual ocean-atmosphere adjustments to radiative forcing. Journal of Climate pp JCLI–D–16–0312.1, https://doi.org/10.1175/JCLI-D-16-0312.1
Santer BD, Wigley TML, Boyle JS, Gaffen DJ, Hnilo JJ, Nychka D, Parker DE, Taylor KE (2000) Statistical significance of trends and trend differences in layer-average atmospheric temperature time series. J Geophys Res: Atmos 105(D6):7337–7356. https://doi.org/10.1029/1999JD901105
Senior CA, Mitchell JFB (2000) The time-dependence of climate sensitivity. Geophys Res Lett 27(17):2685–2688. https://doi.org/10.1029/2000GL011373
Sherwood SC, Bony S, Boucher O, Bretherton C, Forster PM, Gregory JM, Stevens B (2015) Adjustments in the forcing-feedback framework for understanding climate change. Bull Am Meteorol Soc 96(2):217–228. https://doi.org/10.1175/BAMS-D-13-00167.1
Soden BJ, Held IM, Colman R, Shell KM, Kiehl JT, Shields CA (2008) Quantifying climate feedbacks using radiative kernels. J Clim 21(14):3504–3520. https://doi.org/10.1175/2007JCLI2110.1
Webb MJ, Lambert FH, Gregory JM (2013) Origins of differences in climate sensitivity, forcing and feedback in climate models. Clim Dyn 40(3–4):677–707. https://doi.org/10.1007/s00382-012-1336-x
Williams KD, Ingram WJ, Gregory JM (2008) Time variation of effective climate sensitivity in GCMs. J Clim 21(19):5076–5090. https://doi.org/10.1175/2008JCLI2371.1
Winton M, Takahashi K, Held IM (2010) Importance of ocean heat uptake efficacy to transient climate change. J Clim 23(9):2333–2344. https://doi.org/10.1175/2009JCLI3139.1
Wood R, Bretherton CS (2006) On the relationship between stratiform low cloud cover and lower-tropospheric stability. J Clim 19(24):6425–6432. https://doi.org/10.1175/JCLI3988.1
Zhou C, Zelinka MD, Klein SA (2016) Impact of decadal cloud variations on the Earth’s energy budget. Nat Geosci 9(12):871–874. https://doi.org/10.1038/ngeo2828
Zhou C, Zelinka MD, Klein SA (2017) Analyzing the dependence of global cloud feedback on the spatial pattern of sea surface temperature change with a Green’s function approach. J Adv Model Earth Syst. https://doi.org/10.1002/2017MS001096
Acknowledgements
We are grateful to the reviewers (Andrew Dessler and Steve Klein) for their constructive comments. We thank Maria Rugenstein for providing the \(4\times \mathrm {CO}_2\) CESM-CAM4 ensemble, and Andrew Dessler and Piers Forster for making their updated AR5 forcing time series available. This work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). PC was supported by an Imperial College Research Fellowship. JMG was supported by the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 786427, project “Couplet”).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A. Calculation of the ocean heat uptake forcing
We assume that the mixed-layer energy budget follows
where \(\rho _w\) denotes the density of sea water, \(c_p\) is the heat capacity of water, \(h_\mathrm {ML}\) is the the mixed layer depth, \(F_\mathrm {net}\) is the the net surface energy flux (radiative, latent and sensible), \(\nabla \cdot {\mathbf {H}}\) is the horizontal ocean heat flux divergence, and Q is the flux of heat into the deep ocean. \(F_\mathrm {net}\) and Q are defined as positive downward.
We wish to determine the q-flux to be imposed in our slab model to sustain an SST evolution that is consistent with the multimodel-mean SST evolution in the CMIP5 abrupt4xCO2 experiment, using the terms in Eq. 14. To do this, it is convenient to define ocean heat uptake (OHU) as the sum of the horizontal heat flux divergence and flux into the deep ocean, \(\mathrm {OHU} = \nabla \cdot {\mathbf {H}} + Q\). This definition allows us to calculate OHU using only SST and surface flux data from the abrupt4xCO2 experiment, by rearranging Eq. 14:
We calculate OHU following Eq. 15, using multimodel-mean monthly surface fluxes and SSTs from the abrupt4xCO2 experiment in CMIP5. The mixed-layer depth \(h_\mathrm {ML}\) is a property of the slab model and differs between CAM4-SOM and HadSM3 (Sect. 2.1), so OHU is calculated separately for the two models. We then form monthly OHU climatologies for years 1–20 and 21–150, which we use in experiments \(4\times \hbox {CO}_2+\hbox {OHU}_{1-20}\) and \(4\times \hbox {CO}_2+\hbox {OHU}_{21-150}\). The following 14 models are used in the OHU calculation: ACCESS1.0, ACCESS1.3, BCC-CSM1.1, BCC-CSM1.1(m), CNRM-CM5, GFDL-ESM2G, GISS-E2-R, INMCM4, MIROC5, MIROC-ESM, MPI-ESM-LR, MPI-ESM-MR, MPI-ESM-P, MRI-CGCM3.
B. Albedo feedback in the uniform-\({\Delta }\)SST experiments
Owing to the constraint of fixed sea ice concentrations, the uniform-\({\Delta }\)SST experiments lack an ice-albedo feedback. Since we are interpreting the slab radiative responses as the sum of a uniform-\({\Delta }\)SST component and an SST pattern component, \(R = R_\mathrm {m} + R_\mathrm {p}\) (Fig. 4), we need to account for the missing ice-albedo feedback in the uniform warming simulations in order to explain the slab responses. We therefore use a modified radiative response \(R_\mathrm {m} + \alpha T\), where \(\alpha\) is a pseudo-ice-albedo feedback. \(\alpha\) is estimated by taking the difference between the mean albedo feedback in the slab runs, and the mean albedo feedback in the uniform SST runs, calculated in both cases using CAM5 radiative kernels (Soden et al. 2008; Pendergrass et al. 2017). We estimate \(\alpha\) to be \(0.30 \hbox { W} \hbox { m}^{-2} \hbox { K}^{-1}\) in CAM4 and \(0.20 \hbox { W} \hbox { m}^{-2} \hbox { K}^{-1}\) in HadAM3.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ceppi, P., Gregory, J.M. A refined model for the Earth’s global energy balance. Clim Dyn 53, 4781–4797 (2019). https://doi.org/10.1007/s00382-019-04825-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04825-x