1 Introduction

Arctic amplification, a stronger Arctic than global mean surface temperature trend, is one of the primary patterns of climate change as observed and simulated by climate models (e.g., Manabe and Stouffer 1980; Holland and Bitz 2003). Enhanced oceanic heat transport (OHT) towards the Arctic is one of the many factors linked to stronger future Arctic warming and polar amplification in fully coupled global climate models (Holland and Bitz 2003; Bitz et al. 2006; Mahlstein and Knutti 2011). Studies with an ocean-only model illustrate and confirm the central role of the ocean circulation in amplifying the warming signal in the Arctic (Marshall et al. 2014, 2015).

In simulations of the twentyfirst-century climate, most coupled models project only weak increases in total energy transport into the Arctic (Hwang et al. 2011). The contribution of atmospheric heat transport (AHT) to poleward energy transport consists of moisture and dry static energy transport. Atmospheric moisture transport increases due to the larger amount of water vapor in the atmosphere, although in high latitudes this effect is smaller because of the non-linear relation between water vapor pressure and air temperature (the Clausius–Clapeyron relation). On the other hand, transport of dry static energy decreases in a warming climate due to the smaller north–south temperature gradient induced by Arctic amplification, and dominates the net change in AHT at \(70^{\circ }\hbox {N}\). Moreover, most models project a decrease in poleward OHT in the midlatitudes and an increase in higher latitudes (Hwang et al. 2011). The decrease of OHT in the midlatitudes is mainly associated with a weakening of the Atlantic meridional overturning circulation (AMOC) (Cheng et al. 2013), which plays a key role in the Atlantic ocean heat redistribution by transporting heat northwards from the tropics and subtropics. This concurs with a paleoclimate model simulation of the Eocene climate (\(\sim 50\ \hbox {Ma}\))—with about four times modern \(\hbox {CO}_2\) values—in which the North Atlantic overturning reduces in intensity and depth relative to present-day values (Huber and Sloan 2001). Despite the consensus about the slowdown of the AMOC under climate warming, it is still not clear what mechanisms explain the projected increase in OHT at higher latitudes. Studies including several versions of the Geophysical Fluid Dynamics Laboratory (GFDL) model suggest that a large AMOC decline relates to less high-latitude transient warming (Rugenstein et al. 2013; Winton et al. 2013, 2014).

Several modeling studies found that the simulated high-latitude increase in OHT is primarily caused by increased temperatures of the incoming Atlantic water (Koenigk and Brodeau 2014; Jungclaus et al. 2014; Nummelin et al. 2017), which is consistent with a 2000-year record of ocean temperature variations derived from marine sediments (Spielhagen et al. 2011). Other model studies demonstrated the importance of ocean circulation changes in high latitude warming (Bitz et al. 2006; Rugenstein et al. 2013; Winton et al. 2013; Marshall et al. 2015). The observed ocean heat transport variability into the Arctic has been mainly associated with changes in circulation (volume transport) (Årthun et al. 2012; Orvik and Skagseth 2005). The enhanced OHT into the Arctic Ocean might thus well stem from a combination of (remote) circulation changes and increased water temperatures. The heat transport into the Arctic in colder-than-present climates has not been extensively studied thus far.

In this study, we systematically investigate differences in OHT into the Arctic between the current climate and for two colder and two warmer climate states, with atmospheric \(\hbox {CO}_2\) levels varying from one-fourth to four times modern levels. In contrast to most previous sensitivity studies of OHT, in which transient experiments are investigated, the climate states in the present study are all in quasi-equilibrium. The broad range of atmospheric \(\hbox {CO}_2\) concentrations allows us to test the sensitivity of OHT for equilibrium changes to constant \(\hbox {CO}_2\) forcings. To our knowledge, this is the first time that the OHT to the Arctic under both very high and very low \(\hbox {CO}_2\) conditions is systematically analyzed with a state-of-the-art global coupled climate model. Moreover, the \(\hbox {CO}_2\) concentrations in the extreme climate states are similar to typical values in paleoclimate model studies (e.g., \(\hbox {CO}_2\) levels in the LGM are about \(\sim 50\%\) and in the Eocene \(\sim 400\%\) modern values). In this way, climate states with \(\hbox {CO}_2\) levels similar to modern, Eocene, and LGM values are all included, and the sensitivity of ocean processes to \(\hbox {CO}_2\) concentration can be properly analyzed. In the present paper, we focus on the differences in Atlantic OHT at \(70^{\circ }\hbox {N}\) into the Arctic and the mechanisms behind these differences. Therefore, our main study area is the Nordic Seas, where in the current climate the largest heat inflow toward the Arctic occurs.

This paper is organized as follows. The model simulations and methods are presented in Sect. 2. Section 3 describes some general characteristics of the climate states, including climate sensitivity and Arctic amplification. The northern hemisphere meridional oceanic and atmospheric heat transports are presented in Sect. 4. Section 5 discusses changes in the volume and heat transports through the Arctic Straits. The mechanisms behind these changes are examined in detail in Sect. 5, by decomposing the heat transport in gyre and overturning components. Finally, Sect. 7 contains a summary and conclusions.

2 Model, simulations, and methods

2.1 Model description

The model simulations in this study are performed with the state-of-the-art global climate model EC-Earth (Hazeleger et al. 2012). Here, we use version 2.3, which has also been used in the Coupled Model Intercomparison Project phase 5 (CMIP5) (Taylor et al. 2012). EC-Earth is a fully coupled ocean-atmosphere global climate model. The atmospheric component is the Integrated Forecast System (IFS) of the European Center for Medium-range Weather Forecasts (ECMWF). It runs at T159 spectral resolution with 62 vertical levels. The ocean component is the Nucleus for European Modelling of the Ocean (NEMO) model (Madec 2008), developed by the Institute Pierre Simon Laplace (IPSL). NEMO uses a horizontal grid configuration which has a resolution of about 1\(^{\circ }\) and 42 vertical levels. NEMO incorporates the Louvain la Neuve sea ice model version 2 (LIM2) (Fichefet and Morales Maqueda 1997; Bouillon et al. 2009), which is a dynamic-thermodynamic sea ice model. The atmosphere and ocean/sea-ice model are coupled through the OASIS (Ocean, Atmosphere, Sea Ice, Soil) coupler (Valcke et al. 2003).

The performance of the ocean component in EC-Earth is described in detail by Sterl et al. (2012). Future projections of climate change and ocean heat transports in EC-Earth, focused specifically on the Arctic region, are analyzed in detail by Koenigk et al. (2013) and Koenigk and Brodeau (2014).

2.2 Simulations

We study five simulations performed with EC-Earth with different atmospheric \(\hbox {CO}_2\) concentrations (Table 1), which have also been used in van der Linden et al. (2017) to assess Arctic decadal variability. The first integration is the control climate which contains greenhouse gas concentrations, aerosol forcing, and land use of the year 2000 (present-day). The initial state for the control run is obtained from a spin-up of about thousand years with preindustrial (1850) forcing and a subsequent integration over 44 years with present-day forcing. Thereafter the integration is continued over 550 years with constant present-day forcing, producing the control simulation in this study. The other integrations all start from the initial state of the control climate. Their \(\hbox {CO}_2\) concentrations are instantaneously set at 0.25, 0.5, 2 and 4 times the present-day value and kept constant at that level for 550 years. Ocean temperatures show that after 450 years the upper ocean (0–200 m) almost reaches a quasi-equilibrium state, but the deep ocean is not yet in equilibrium (Fig. 1). Over the final 100 years, trends in the upper ocean range from \(-1.4 \times 10^{-3}\ ^{\circ }\hbox {C year}^{-1}\) in \(0.25 \times \hbox {CO}_2\) to \(2.8 \times 10^{-3}\ ^{\circ }\hbox {C year}^{-1}\) in \(4\times \hbox {CO}_2\) (Table 1). The deep ocean typically takes several thousands of years to reach equilibrium (Li et al. 2013). We use the final 100 years of the simulations in our analysis.

Table 1 Simulation name, \(\hbox {CO}_2\) concentration, trend in upper ocean (0–200 m) temperature over last 100 years (\(d\hbox {T}_{o}/ d\hbox {t}\)), the global equilibrium 2-m air temperature (\(\hbox {T}_{global}\)), the equilibrium climate sensitivity (ECS), the Arctic equilibrium 2-m air temperature (\(\hbox {T}_{arctic}\)), and Arctic amplification (AA)
Full size table
Fig. 1
figure 1

Timeseries of the global mean ocean temperature (\(^{\circ }\hbox {C}\)) averaged over the a upper (0–200 m), b middle (200–2000 m), and c deep (2000 m–bottom) ocean

Full size image

All changes or anomalies in the \(\hbox {CO}_2\) sensitivity experiments are defined relative to the control climate state. Note that the climate change simulations analyzed here do not account for possible changes in land ice extent or elevation (Greenland, Antarctica), changes in land use or aerosols, or ocean basin changes due to sea level variations.

2.3 Computation of transports

The transports are computed for the ocean and the atmosphere from monthly mean model output.

2.3.1 Atmospheric heat transports

The northward atmospheric heat transport (AHT) is approximated as:

$$\begin{aligned} \text {AHT} = \iint _{Arctic} ( \text {F}_{\text {sfc}} -\text {F}_{\text {toa}} ) d \phi d \lambda \end{aligned}$$
(1)

where \(\phi\) is latitude and \(\lambda\) is longitude. \(\hbox {F}_{\text {sfc}}\) and \(\hbox {F}_{\text {toa}}\) are the net surface and top-of-the-atmosphere fluxes, respectively, which are defined positive downward. \(\hbox {F}_{\text {toa}}\) is obtained from differencing net absorbed shortwave radiation and outgoing longwave radiation at the top of the atmosphere. \(\hbox {F}_{\text {sfc}}\) is computed as the sum of the net longwave and shortwave radiative fluxes, and the turbulent latent and sensible heat fluxes at the surface.

2.3.2 Ocean heat transports

For the ocean, we use two different ways to compute northward transport. First, the oceanic heat transport (OHT) is estimated as the residual of the surface fluxes and the ocean heat storage (\(d\hbox {E}/d\hbox {t}\)):

$$\begin{aligned} \text {OHT} = \iint _{Arctic} ( d\text {E}/d\text {t} -\text {F}_{\text {sfc}} ) d \phi d \lambda \end{aligned}$$
(2)

The ocean heat content (E) is calculated as the volume integral of \(\rho _0 c_p \theta\), where \(\rho _0\) is the reference density, \(c_p\) is the specific heat capacity for sea water, and \(\theta\) the potential temperature of the ocean water. This computation involves all ocean grid points, including those covered by sea ice. The ocean heat storage (\(d\hbox {E}/d\hbox {t}\)) is the time derivative of ocean heat content. Since the deep ocean is not yet in equilibrium after 450 years, there is some residual drift in E. Therefore, \(d\hbox {E}/d\hbox {t}\) is not equal to zero, but varies from \(-\,0.22\ \hbox {W m}^{-2}\) in the \(0.25\times \hbox {CO}_2\) climate to \(0.55\ \hbox {W m}^{-2}\) in the \(4\times \hbox {CO}_2\) climate.

Second, we computed the ocean heat transport through the three Arctic entrances (Nordic Seas, Bering Strait, and Canadian Archipelago) from the three-dimensional velocity (v) and temperature (T) fields:

$$\begin{aligned} OHT = \rho _0 c_p \int _{-H(\lambda )}^{0} \int _{\lambda _1(z)}^{\lambda _2(z)} v T \, \cos \phi \, a \, d \lambda \, dz \end{aligned}$$
(3)

where \(\rho _0\) is the density of seawater, \(c_p\) is the specific heat of seawater, H is the depth of the basin, a is the radius of the Earth, and \(\lambda _1\) and \(\lambda _2\) are the western and eastern boundaries, which are functions of ocean depth. In a similar way, we computed the ocean volume transport directly from the three-dimensional velocity (v) field:

$$\begin{aligned} OVT = \int _{-H(\lambda )}^{0} \int _{\lambda _1(z)}^{\lambda _2(z)} v \, \cos \phi \, a \, d \lambda \, dz \end{aligned}$$
(4)

In these computations, the monthly mean values of v and T are used, where the temperature is taken compared to a reference temperature of \(0\ ^{\circ }\hbox {C}\). A reference temperature is required since the mass budget of the ocean is not necessarily closed, making it impossible to compute the absolute value of ocean heat (i.e. work must be done by or on the mass that enters or exits the ocean). To calculate the Arctic energy balance, however, only the change in ocean heat is required.

2.3.3 Relative contribution of temperature and volume

To further unravel the changes in ocean heat inflow, we have quantified the relative contribution of temperature and volume to the total changes in ocean heat transport. For this purpose, velocity and temperature in the \(\hbox {CO}_2\) sensitivity experiments (\(v_s\) and \(T_s\), respectively) are defined as the corresponding values in the control climate state (\(v_c\) and \(T_c\)) plus a perturbation value (\(v'\) and \(T'\)). In other words, for velocity we take \(v_s = v_c + v'\) and for temperature \(T_s = T _c + T'\). Using this decomposition, the changes in ocean heat transport can be split into three components: (1) the advection by velocity perturbations operating on control climate temperatures (\(v' T_c\)), (2) advection by control climate velocities acting on temperature perturbations (\(v_c T'\)), and (3) their covariance (\(v' T'\)):

$$\begin{aligned} v_s T_s - v_c T_c = v_c T' + v'T_c + v'T' \end{aligned}$$
(5)

2.3.4 Overturning and gyre components

The total Atlantic OHT can also be dynamically decomposed into contributions by the mean meridional overturning circulation and by horizontal gyre motions following Bryan (1982). The gyre component is composed mostly of the subpolar gyre south of Greenland and a (weaker) gyre circulation in the Nordic Seas. This decomposition is based on a closed ocean basin. Therefore, we correct the overturning circulation for the effect of the volume transport through Bering Strait. Ignoring river input, evaporation, and precipitation, there will be a constant net volume transport in the Arctic and Atlantic that is equal to the Bering Strait volume transport (\(OVT_{Bering}\)). The associated OHT contribution of the Bering Strait traversing a section in the Atlantic–Arctic is

$$\begin{aligned} OHT_{Bering}(\phi ) = \rho _0 c_p OVT_{Bering} T_A(\phi ), \end{aligned}$$
(6)

where \(\hbox {T}_A\) is the mean temperature in the Atlantic–Arctic zonal section.

The overturning heat transport is quantified as the integral of the product \(\rho _0 c_p \langle v \rangle \langle T \rangle\), where \(\langle \rangle\) denotes the zonal average:

$$\begin{aligned}&OHT_{overturning} \nonumber \\&\quad = \rho _0 c_p \int _{-H(\lambda )}^{0} \int _{\lambda _1(z)}^{\lambda _2(z)} \langle v \rangle \langle T \rangle \, \cos \phi \, a \, d \lambda \, dz - OHT_{Bering}(\phi ), \end{aligned}$$
(7)

Here, the last term is the correction for the Bering Strait throughflow (Eq. 6). The gyre component is calculated as the integral of the product \(\rho _0 c_p \langle v^{*} T^{*} \rangle\), where \(^{*}\) denotes the departure from the zonal average:

$$\begin{aligned} OHT_{gyre} = \rho _0 c_p \int _{-H(\lambda )}^{0} \int _{\lambda _1(z)}^{\lambda _2(z)} \langle v^{*} T^{*} \rangle \, \cos \phi \, a \, d \lambda \, dz \end{aligned}$$
(8)

3 Global characteristics

3.1 Equilibrium climate sensitivity

The equilibrium climate sensitivity (ECS) in EC-Earth is 3.0 ºC (for \(\hbox {CO}_2\) doubling relative to present day), which is close to the median of global coupled models participating in CMIP5 (Rogelj et al. 2012). The EC-Earth model shows a slight asymmetry in climate sensitivity with respect to atmospheric \(\hbox {CO}_2\) concentration: ECS is 2.5 ºC for \(0.25\times \hbox {CO}_2\) and 3.3 ºC for \(4\times \hbox {CO}_2\) (Table 1). This is consistent with other CMIP5-models that exhibit increasing values of ECS in warmer climates due to a strengthening of the water-vapor feedback (Meraner et al. 2013). There are also opposing effects through which ECS is enhanced in cold climate states and reduced in warm ones, which vary between models (Kutzbach et al. 2013). The climate sensitivity to changing greenhouse gas concentrations is thus model-dependent. In any case, the changing ECS with climate states suggests that the simulated climate feedbacks change with the mean climate state.

3.2 Arctic amplification

Figure 2 shows the change in annual mean 2-m air temperature and the Arctic sea ice edge in March and September for the different climate states. The average 2-m temperature over the Arctic (70–\(90^{\circ }\hbox {N}\)) varies from \(3.6\ ^{\circ }\hbox {C}\) in \(4\times \hbox {CO}_2\) to \(-29.1\ ^{\circ }\hbox {C}\) in \(0.25 \times \hbox {CO}_2\) (Table 1). For each \(\hbox {CO}_2\) doubling, the increase in global mean 2-m temperature becomes slightly larger, corresponding to the larger ECS in warmer climates. Also the increment in Arctic temperature increases with \(\hbox {CO}_2\) from 8.2 ºC for \(0.25\times \hbox {CO}_2\)–\(0.5\times \hbox {CO}_2\) up to 9.0 ºC for control–\(2\times \hbox {CO}_2\), but suddenly drops to 6.7 ºC for 2–\(4\times \hbox {CO}_2\). As a consequence, the degree of Arctic amplification (AA) is smaller in the warmest climate state (Table 1), but still considerable. Here, AA is defined as the equilibrium change in Arctic surface air temperature relative to the global mean surface air temperature change. A reason for the reduced Arctic warming could be that in \(2\times \hbox {CO}_2\) a large part of the 70–\(90^{\circ }\hbox {N}\) area is ice free year-round and the Arctic is almost completely ice free in summer. Consequently, feedbacks such as the ice-albedo or water vapor feedback will be less active between \(2\times \hbox {CO}_2\) and \(4\times \hbox {CO}_2\) compared to doubling of \(\hbox {CO}_2\) concentrations at lower \(\hbox {CO}_2\) levels. On average, the Arctic temperature change is about three times larger than the global mean. This value is somewhat larger than that of the multimodel mean AA (2.6) for transient \(\hbox {CO}_2\) quadrupling in an ensemble of CMIP5 simulations (van der Linden et al. 2014), but similar to the transient value of AA in EC-Earth. Arctic amplification thus occurs in both colder and warmer climates, as was also found for a broad range of summer paleoclimate data (Miller et al. 2010) as well as in LGM and future climate model simulations (Masson-Delmotte et al. 2006).

Fig. 2
figure 2

The annual mean change in 2-m air temperature (K) in  a \(0.25\times \hbox {CO}_2\), b \(0.5\times \hbox {CO}_2\), c\(2\times \hbox {CO}_2\), and d \(4\times \hbox {CO}_2\) relative to the control climate at 40–\(90^{\circ }\hbox {N}\). The thick black lines represent the sea ice edge in March (solid) and September (dashed), which is defined as the 15% sea ice concentration isopleth

Full size image

Many factors within the climate system, including changes in sea ice (Serreze et al. 2009; Screen and Simmonds 2010), changes in clouds and water vapor content (Francis and Hunter 2006; Graversen and Wang 2009; Pithan and Mauritsen 2014), and changes in meridional energy transports (Graversen et al. 2008; Chylek et al. 2009; Yang et al. 2010; Graversen and Burtu 2016), have been shown to contribute to AA. Although changes in northward heat transport are relatively small, the tight coupling between local feedbacks and poleward energy transport makes the latter a potentially important contributor to Arctic amplification. For example, northward ocean heat transport plays an important role in local sea ice melt and heat release to the atmosphere (Koenigk et al. 2009; van der Linden et al. 2016). In the following, we therefore focus on quantifying and understanding the changes in poleward heat transport toward the Arctic, a prerequisite to quantify its impact on amplified Arctic temperature change.

4 Meridional heat transport by ocean and atmosphere

In this section, we examine the deviations in meridional heat transport (MHT) toward the Arctic for modified \(\hbox {CO}_2\) concentrations. OHT and AHT are computed using Eqs. 1 and 2.

4.1 Validation of heat transports

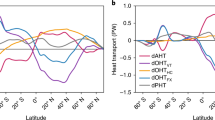
First, we compare the simulated transports to the observation-based estimates of meridional heat transports of Fasullo and Trenberth (2008) (hereinafter referred to as FT08). For each climate state, the total transport of about 5.3 PW peaks around \(37^{\circ }\hbox {N}\) (not shown), which is somewhat smaller than the estimate of 5.9 PW at \(35^{\circ }\hbox {N}\) in FT08. The total (\(\hbox {ocean} + \hbox {atmosphere}\)) poleward heat transport in the northern hemisphere is nearly identical in each climate state since the poleward heat transport must compensate the latitudinal gradient in the radiation balance at the top of the atmosphere. Following energy conservation, the top-of-atmosphere radiation balance, which governs the total transport, hardly changes between climates and is only slightly perturbed by changes in albedo, e.g., by sea ice. Figure 3a, b depict the northern hemisphere oceanic and atmospheric heat transports, respectively. In the control climate, the ocean component dominates the total MHT in the deep tropics and peaks at 1.6 PW at \(19^{\circ }\hbox {N}\), which is compatible with the observation-based estimate of 1.7 PW at \(15^{\circ }\hbox {N}\) in FT08. The atmosphere dominates in the regions poleward of about \(10^{\circ }\hbox {N}\). Maximum atmospheric heat transport is about three times larger (4.6 PW) than the peak value in OHT and is located more northerly (near \(43^{\circ }\hbox {N}\)) compared to the 5.1 PW at \(41^{\circ }\hbox {N}\) in FT08.

Fig. 3
figure 3

Zonally averaged a OHT and b AHT, c, d their respective changes relative to the control simulation, and e the Bjerknes compensation rate. The grey shaded area represents two standard deviations of interannual variability in the control simulation

Full size image

4.2 Bjerknes compensation

The meridional distribution of the total MHT, i.e. the atmosphere plus ocean heat transport, is almost identical for all five climate states (shown in Table 2 at \(70^{\circ }\hbox {N}\)). Although the total MHT is rather constant, the individual components are not. The zonal mean deviations in OHT and AHT relative to the control climate are almost equal in magnitude, but opposite in sign (Fig. 3). In the tropics and polar latitudes, changes in Northern Hemisphere OHT and AHT vary more or less monotonically with increasing atmospheric \(\hbox {CO}_2\) concentration. In warmer climates, the OHT increases in high latitudes whereas it decreases in low latitudes (Fig. 3c). Conversely, in warmer climates, AHT decreases in high latitudes and increases in low latitudes (Fig. 3d). There is a transition region between \(40^{\circ }\hbox {N}\) and \(65^{\circ }\hbox {N}\) where OHT and AHT do not change monotonically with \(\hbox {CO}_2\) concentration. The compensation mechanism between oceanic and atmospheric heat transports is generally known as Bjerknes compensation (Bjerknes 1964). Here, we assess its applicability on longer, equilibrium time scales by comparing the last 100 years of our 550-year long simulations. To quantify the ocean-atmosphere compensation, we compute the compensation rate (CR) as the residual of the ratio of the net MHT changes to the maximum changes in OHT and AHT following van der Swaluw et al. (2007):

$$\begin{aligned} |d\text {MHT}|&= |d\text {AHT} + d\text {OHT}|, \nonumber \\ W&\equiv \text {max}(|d\text {AHT}|,|d\text {OHT}|) \nonumber \\ V&\equiv |d\text {MHT}|/W, \text {and} \nonumber \\ \text {CR}&\equiv (1 - V) \times 100 \%. \end{aligned}$$
(9)

In this computation, \(d\hbox {MHT}\), \(d\hbox {AHT}\), and \(d\hbox {OHT}\) denote the change in the considered heat transport with respect to the control climate. The compensation mechanism is clearly operating at all latitudes for each \(\hbox {CO}_2\) concentration: the compensation rate is larger than 75% for all climate states and latitudes in the northern hemisphere, except for \(2\times \hbox {CO}_2\) near the equator and between \(20^{\circ }\hbox {N}\) and \(47^{\circ }\hbox {N}\) (Fig. 3e). Our results show that Bjerknes compensation is applicable for equilibrium climate states as well. The forcing causing the different climate states may not be relevant for the response: Enderton and Marshall (2009) show that meridional oceanic and atmospheric heat transport largely compensate one another in different climate states that were created through geometrical constraints on ocean circulation on an aquaplanet. They found that the distribution of incoming solar radiation and meridional gradients in albedo are the most important constraints on the total meridional heat transport. We found comparable results in our simulations.

Table 2 Total meridional heat transport (MHT), oceanic heat transport (OHT), and atmospheric heat transport (AHT) in \(\hbox {PW} (= 10^{15}\ \hbox {W})\) across \(70^{\circ }\hbox {N}\), as computed with Eqs. 1 and 2
Full size table

At the entrance of the Arctic, at \(70^{\circ }\hbox {N}\), the compensation rate between OHT and AHT is nearly complete with values between 79 and 93% at \(70^{\circ }\hbox {N}\), as compared to a maximum compensation rate of \(\sim 55\%\) in HadCM3, 28% in ECHAM5, and 36% in BCM on decadal time scales (van der Swaluw et al. 2007; Jungclaus and Koenigk 2010; Outten and Esau 2016). The poleward OHT at \(70^{\circ }\hbox {N}\) is stronger in warmer climates, and, consistent with Bjerknes compensation, the atmosphere transports less heat toward the Arctic in warmer climates (Table 2). The opposite is the case for the colder climate states.

The importance of the ocean in Arctic amplification is evident, since it is also found in ocean-only simulations (Marshall et al. 2014, 2015). From now on, we will focus on OHT adjustment in coupled models and the physical role of ocean heat transport and coupled processes in AA, which is not yet fully understood.

5 Ocean volume and heat transport through Arctic entrances

The Arctic Ocean is connected to the North Atlantic Ocean via (1) the Greenland–Iceland–Norwegian (Nordic) Seas and (2) the Canadian Archipelago, and to the Pacific Ocean through (3) the Bering Strait. This section unravels the ocean volume (Eq. 3) and heat transports (Eq. 4) through these Arctic entrances across the five climate states.

5.1 Total transports

Figure 4 depicts OVT and OHT through the Bering Strait, Nordic Seas, and Canadian Archipelago, and the sum of the three components. In addition, it shows OVT and OHT through the Barents Sea Opening between Norway and Svalbard and through Fram Strait between Greenland and Svalbard. The total ocean volume transport into the Arctic (black line) (Fig. 4a) is slightly negative for all five climate states. These negative values are largely compensated by positive surface water fluxes in the Arctic region (Fig. 5). Precipitation and runoff are sources of volume fluxes into the Arctic, whereas evaporation acts as a sink of fresh water. In a warming climate, increases in water supply by precipitation and runoff exceed the enhanced water loss through evaporation, compensating the increasingly negative net volume transport with increasing \(\hbox {CO}_2\) values. Other potential sources for the imbalance are transports of sea ice and snow on ice, which are not included in the volume transport calculation.

Fig. 4
figure 4

a Ocean volume transport (\(1\ \hbox {Sv} = 10^6\ \hbox {m}^3\ \hbox {s}^{-1}\)) and b ocean heat transport through the Bering Strait (blue), the Nordic Seas (orange) and the Canadian Archipelago (red) at \(70^{\circ }\hbox {N}\), and their sum (black). c, d As in a, b but for the Nordic Seas (orange), Barents Sea Opening (dark red), and Fram Strait (green)

Full size image
Fig. 5
figure 5

Precipitation (dark blue), evaporation (red), and runoff (cyan) fluxes into the Arctic region (north of \(70^{\circ }\hbox {N}\)) in \(10^6\ \hbox {m}^3\ \hbox {s}^{-1}\) (\(= 1\ \hbox {Sv}\)), and their sum (black)

Full size image

In all five climates, there is a net inflow of Pacific water through the Bering Strait (blue line). In the Canadian Archipelago (red line), a net outflow of Arctic Ocean water occurs, except in the coldest climate state in which there is no volume exchange. In the Nordic Seas (orange line), the inflow of Atlantic water on the Norwegian side through the Barents Sea Opening (dark red line) compensates the outflow of Arctic Ocean water on the Greenland side through Fram Strait (green line) for the three middle climates, resulting in zero net transport (Fig. 4c). However, in the coldest climate there is a net volume outflow and in the warmest climate a net volume inflow. The simulated eastward volume transport through the Barents Sea Opening and southward flow through Fram Strait of roughly 4 Sv are both on the high side compared to observations (2–4 Sv; Schauer et al. 2004; Skagseth 2008).

Total ocean heat transport across \(70^{\circ }\hbox {N}\) increases towards warmer climates (Fig. 4b). In all five climate states, the Nordic Seas component dominates ocean heat transport into the Arctic Ocean. In the control climate simulation, the simulated heat transport across \(70^{\circ }\hbox {N}\) through the Nordic Seas is 0.17 PW, which is compatible with the observation-based estimate of Oliver and Heywood (2003). The transports through the Bering Strait (0.01 PW) and Canadian Archipelago (0.01 PW) are much smaller than the Nordic Seas component. Observation-based estimates show that Bering Strait heat transports (0.003–0.01 PW between 1991 and 2004) are comparably small (Woodgate et al. 2006). Furthermore, the heat transport through the Nordic Seas includes both the eastern heat inflow into the Barents Sea and the western heat outflow through Fram Strait (Fig. 4d).

The changes in ocean heat transport compared to the control climate are also largest in the Nordic Seas. However, for the \(4\times \hbox {CO}_2\) climate, the increase in heat transport through the Bering Strait (\(+\,0.05\ \hbox {PW}\)) almost equals the increase in the Nordic Seas (\(+\,0.06\ \hbox {PW}\)) (Fig. 4b). Such an increase is relatively large compared to the total heat inflow through the Bering Strait in the control climate (0.01 PW), but it should be noted that the volume transport through Bering Strait is larger than the net volume transport through the Nordic Seas. Thus, small temperature changes have large impact on the heat transport. The increase through the Barents Sea Opening from the control to the \(4\times \hbox {CO}_2\) climate (\(+0.17\ \hbox {PW}\)) is more than three times larger than the increase through the Bering Strait (Fig. 4d). For the same GCM, Koenigk and Brodeau (2014) have shown that the projected twentyfirst-century increase in OHT through the Barents Sea Opening is one order of magnitude larger than that through the Bering Strait. The heat transport changes through the Barents Sea Opening thus play the most important role in the increase in heat transport towards the Arctic under enhanced \(\hbox {CO}_2\) forcing.

5.2 Relative contribution of temperature and volume

As a next step, we quantify the relative contribution of temperature and volume to the total changes in ocean heat transport (Eq. 5). In the two warmer-than-present climates, velocity anomalies in the Nordic Seas act to increase the heat transport into the Arctic region compared to the control climate (Fig. 6b). Temperature anomalies indicate a non-monotonic response to \(\hbox {CO}_2\) forcing, with increased heat inflow in the Nordic Seas for the \(2\times \hbox {CO}_2\) climate and reduced northward heat transport into the Arctic for the \(4\times \hbox {CO}_2\) climate (Fig. 6c). A decomposition of the heat flow through the Barents Sea Opening and Fram Strait (Fig. 7) shows that in the warmer climates temperature anomalies dominate heat transport changes. There is a large divergence between increasing heat transport through the Barents Sea Opening and decreasing heat transport through Fram Strait. Although the Arctic imports warmer-than-present ocean water on the Norwegian side, there is enhanced outflow of relatively warm water (i.e. reduced heat import) on the Greenland side due to warmer ocean water temperatures and stronger currents. The negative contribution to northward heat transport of the temperature anomalies in the \(4\times \hbox {CO}_2\) climate in the Nordic Seas (Fig. 7c) are thus mainly due to the warmer temperature of the outflowing water (\(> 0\,^{\circ }\hbox {C}\)). The combined effect of volume and temperature increases the net heat inflow into the Arctic in the Nordic Seas in a warming climate. For cold climates, both temperature anomalies and the anomaly product are important for the Nordic Seas heat transport, with the warm Norwegian inflow being more important than the outflow on the Greenland side.

Fig. 6
figure 6

Decomposition of ocean heat transport anomalies (compared to the control climate) for the Bering Strait (blue), the Nordic Seas (orange) and the Canadian Archipelago (red) through \(70^{\circ }\hbox {N}\), and their sum (black). a Changes compared to the control climate, b advection by velocity perturbations operating on control climate temperatures, c advection by control climate velocities acting on temperature perturbations, and d their covariance

Full size image
Fig. 7
figure 7

Decomposition of ocean heat transport anomalies (compared to the control climate) for the Nordic Seas (orange) and the Barents Sea Opening (brown) and Fram Strait (green). a Changes compared to the control climate, b advection by velocity perturbations operating on control climate temperatures, c advection by control climate velocities acting on temperature perturbations, and d their covariance

Full size image

Apart from the changes in the Nordic Seas, the heat transport changes through the Bering Strait and Canadian Archipelago become more and more important in the warmer climates (Fig. 6a). The Bering Strait component enhances OHT into the Arctic, which is mainly associated with higher ocean temperatures. On the other hand, temperature anomalies in the Canadian Archipelago act to decrease OHT into the Arctic compared to the control climate (Fig. 6c). This negative contribution of temperature anomalies is associated with the warming of the Arctic Ocean, which leads to an export of warmer sea water, thus, to a decrease in the net import of heat.

In the two colder-than-present climates, the heat transport into the Arctic decreases, which is mainly associated with a heat transport reduction in the Nordic Seas. The reduction is dominated by the covariance of heat and volume perturbations (Fig. 6d). Especially for the coldest climate, the covariance plays a major role, with advection of temperature anomalies being of secondary importance. The cold climate heat transport anomalies in the Bering Strait inflow are negligible compared to the other changes in the heat transports (Fig. 6a).

Since changes in the Nordic Seas obviously dominate the heat transport changes into the Arctic across the five climate states, in the next section we will concentrate our analysis on the underlying mechanisms in the Atlantic-Arctic domain.

6 Mechanisms driving transport changes in the Nordic Seas

In this section, we will investigate how the quantified changes in the volume and heat transports at the Arctic entrances relate to physical adjustments in the Atlantic-Arctic climate system.

Figure 8 shows the meridional profiles of the total northward heat transport in the Atlantic-Arctic Ocean, as well as its overturning, gyre, and Bering Strait components as described by Eqs. 6–8 in Sect. 2.3.4. The northward heat transport contributions of the overturning, gyre, and Bering Strait components at \(70^{\circ }\hbox {N}\) are listed in Table 3.

Fig. 8
figure 8

Meridional profiles of the zonal- and vertical-mean northward heat transport in the Atlantic Ocean: a the total heat transport, b the stationary meridional overturning component, c the stationary eddy (gyre) component, and d the Bering Strait contribution

Full size image
Table 3 Atlantic meridional oceanic heat transport through \(70^{\circ }\hbox {N}\): total OHT and its overturning, gyre, and Bering Strait components (\(10^{14}\ \hbox {W}\))
Full size table

6.1 Gyre component

The Atlantic gyre component dominates the poleward ocean energy flux at \(70^{\circ }\hbox {N}\), except for the coldest climate state in which it almost disappears (Table 3). A measure of the strength of the gyre circulation is the barotropic streamfunction (Fig. 9). At polar latitudes (north of \(65^{\circ }\hbox {N}\)), the Atlantic gyre heat transport strengthens monotonically with climate warming (Fig. 8c). This coincides with a strengthening of the gyre circulation in the Nordic Seas in a warming climate (Fig. 9). However, the gyre strength at \(70^{\circ }\hbox {N}\) is not linearly related to the gyre strength at subpolar latitudes south of Greenland. In the subpolar region (50–\(65^{\circ }\hbox {N}\)), the contribution of the gyre component to the total northward heat transport peaks in the control climate, and reduces towards warmer and colder climate states (Fig. 8c). This is consistent with the strength of the subpolar North Atlantic gyre, which is strongest in the control and \(0.5\times \hbox {CO}_2\) climate and weakens towards the more extreme climate states (Table 4). Clearly, subpolar changes in ocean heat transport and gyre strength are not representative for their respective changes at \(70^{\circ }\hbox {N}\). To understand the changes at \(70^{\circ }\hbox {N}\), we will first explore the circulation changes in the Nordic Seas, where the ocean heat transport across \(70^{\circ }\hbox {N}\) mainly occurs. Thereafter, we will explore how the nonlinear response to \(\hbox {CO}_2\) of the subpolar gyre affects temperature anomalies—and thus the heat transport—in the Nordic Seas.

Fig. 9
figure 9

The annual mean streamfunction (Sv) of the vertically integrated volume transport for a the control, b\(0.25\times \hbox {CO}_2\), and c\(4\times \hbox {CO}_2\) climates in the Nordic Seas, with a positive values meaning clockwise circulation. The contour lines (spacing: 5 Sv) represent the streamfunction in the control climate

Full size image
Table 4 AMOC index: maximum overturning streamfunction between \(20^{\circ }\hbox {N}\) and \(65^{\circ }\hbox {N}\) and below 500 m depth in Sv
Full size table

The gyre heat transport in the Nordic Seas is strongly reduced in the two cold climates. In these climates, the extended sea ice cover plays a prominent role in modulating the surface heat fluxes and the impact of wind stresses on ocean currents. The sea ice cover is expanded over the Barents–Norwegian and Labrador Seas, which significantly reduces the ocean heat losses towards the atmosphere (Fig. 10a, b). The reduced surface heat loss increases the stability of the overlying atmosphere, which is consistent with considerable positive anomalies in sea level pressure over the Barents-Norwegian and Labrador Seas in the two cold climates (Fig. 11a, b). The positive pressure anomalies, in turn, cause an anticyclonic wind anomaly over the Nordic Seas with southwestward wind anomalies along the Norwegian coast and northward wind anomalies along the east coast of Greenland. In this way, the atmospheric pressure anomaly reduces the barotropic ocean circulation in the Nordic Seas over the regions that are not covered with sea ice (Fig. 9b), which are typically located along the Norwegian coast. The atmospheric circulation anomaly over the Nordic Seas thus contributes to the decline in Arctic heat inflow on the Norwegian side of the Atlantic in the cold climate states.

Fig. 10
figure 10

Surface heat flux anomalies (\(\hbox {W m}^{-2}\)) with respect to the control climate at 40–\(90^{\circ }\hbox {N}\). The thick lines represent the sea ice edge in March for the perturbed (black) and control (green) climate states, which is defined as the 15% sea ice concentration isoline

Full size image
Fig. 11
figure 11

Mean sea level pressure anomalies (Pa) with respect to the control climate at 40–\(90^{\circ }\hbox {N}\)

Full size image

In contrast, in the warm climate states, a low pressure anomaly sits over regions that are sea-ice covered in the control climate, but ice-free in the warm climates (Fig. 11c, d). This signal is consistent with a direct thermal response to ice changes, but may also be related to changes in the large-scale circulation due to greenhouse gas forcing. Moreover, in combination with a high pressure anomaly off the coast of Ireland, this anomalous low pressure area induces a cyclonic wind stress anomaly over the Nordic Seas. In the warm climates, wind anomalies can directly influence the ocean over the Nordic Seas because the sea ice cover disappeared over this region. The wind-induced strengthening of the cyclonic circulation in the Nordic Seas (Fig. 9b) therefore enhances the northward propagation of anomalous warm water along the Norwegian coast and southward export of Arctic Ocean water.

Nonlinear behavior of the subpolar gyre has also been observed in other coupled climate models (Born and Stocker 2014). Although the nonlinear response of the subpolar gyre to the increase in \(\hbox {CO}_2\) concentration does not have a direct relation to the heat transport across \(70^{\circ }\hbox {N}\), it could contribute to the temperature anomalies at this more northerly location. For example, similar coupled atmosphere-sea ice-ocean mechanisms over the subpolar region have been associated with abrupt climate cooling over the North Atlantic in Drijfhout et al. (2013) and Sgubin et al. (2017). However, in our simulations, the strength of the subpolar gyre in \(0.5\times \hbox {CO}_2\) is similar to the control climate (Table 4), whereas Atlantic heat transport in \(0.5\times \hbox {CO}_2\) is roughly equal to the \(0.25\times \hbox {CO}_2\) climate (Fig. 8), pointing at (a complex interplay with) other mechanisms dominating the temperature response in the Nordic Seas.

6.2 Overturning component

The time series of the AMOC index, defined as the maximum AMOC strength between \(20^{\circ }\hbox {N}\) and \(65^{\circ }\hbox {N}\) and below 500 m depth, has stabilized for most climate states after several hundreds of years (not shown). Averaged over the last 100 years of the simulations, the AMOC index is highest in the control and \(0.5\times \hbox {CO}_2\) climates and decreases towards the two warmest and the coldest climate states, describing a non-linear response to atmospheric \(\hbox {CO}_2\) forcing (Table 4). The maximum AMOC strength is not linearly related to the overturning heat transport at \(70^{\circ }\hbox {N}\) (Table 3). The \(0.25\times \hbox {CO}_2\) climate is the only climate state in which the overturning component dominates OHT at \(70^{\circ }\hbox {N}\). For this coldest climate, a stronger AMOC is correlated with colder water in the Barents Sea Opening and warmer water in Fram Strait (not shown), corresponding with reduced OHT into the Arctic in this climate. It should be noted that, except for the coldest climate (in which the gyre component vanishes), the overturning contributes less than 20% to the total Atlantic northward heat transport across \(70^{\circ }\hbox {N}\) for all climate states and even has a negative contribution in the \(4\times \hbox {CO}_2\) climate (Table 3). This negative contribution of the overturning component is caused by strong southward export of ‘warm’ water (\(>0\,^{\circ }\hbox {C}\); net outflow of heat) at about 800 m depth along the east coast of Greenland. Apart from the coldest climate state, at \(70^{\circ }\hbox {N}\), the Atlantic ocean heat transport associated with the overturning component turns out to be subordinate to changes in the gyre component (Table 3). We conclude that changes in the gyre component are most important to understand the changes in the Atlantic OHT toward the Arctic and its contribution to Arctic amplification.

7 Summary and conclusions

In this study, we have investigated quasi-equilibrium changes in ocean heat transport toward the Arctic using the state-of-the-art coupled climate model EC-Earth. Our results are based on five model integrations with a wide range of atmospheric \(\hbox {CO}_2\) levels, varying from one-fourth to four times modern levels. At first sight, our results reveal that climate sensitivity and Arctic amplification are quite robust under these extreme forcing conditions, as we find many similarities between the simulated climate states. For instance, even in climates with extreme warming, in which sea ice almost totally disappears, or extreme cooling, where it expands as far southward as \(45^{\circ }\hbox {N}\), the magnitudes of climate sensitivity and Arctic amplification do not change substantially.

In this study, we focused on the ocean heat transport through the Arctic entrances (Bering Strait, Canadian Archipelago, and Nordic Seas) and identified the relative contributions of volume and temperature to the OHT changes. We found that changes in the Nordic Seas dominate ocean heat transport changes toward the Arctic and therefore concentrated on mechanisms in the Atlantic-Arctic sector. Over the Nordic Seas, the cyclonic circulation strengthens with climate warming due to the presence of a low pressure anomaly. This anomalous circulation pattern promotes OHT into the Arctic Ocean through inflow of warm Atlantic water on the eastern boundary and outflow of cool Arctic water on the western boundary. In addition, in the warmer climates, the waters that are transported northwards have warmed significantly compared to the control climate. The net effect of these changes is that the poleward OHT at \(70^{\circ }\hbox {N}\) is enhanced in warmer climate states.

Our results demonstrate that Bjerknes compensation—opposing changes in oceanic and atmospheric heat transports—is a governing mechanism in equilibrium climate states, with compensation rates between 79% and 93% at \(70^{\circ }\hbox {N}\). In earlier studies, the importance of Bjerknes compensation was already demonstrated for climate variations on decadal time scales (Shaffrey and Sutton 2006; van der Swaluw et al. 2007; Jungclaus and Koenigk 2010; Outten and Esau 2016); on interannual time scales the compensation mechanism was found to be negligible (Shaffrey and Sutton 2004). This implies that the degree of compensation increases for longer time scales. Changes in ocean heat transport act to enhance Arctic amplification but are counteracted by adjustments in the atmospheric heat transport. Although the resulting anomalies in net northward heat transport are small, this compensation might still lead to changes in the Arctic climate system owing to differing responses to changes in oceanic and atmospheric heat transports.

Another interesting area of research is whether the anomalous pressure patterns can be detected in observations. We find a change in sea level pressure over former sea-ice-covered areas in warmer climates (e.g., the Greenland Sea) and over newly-formed sea-ice-covered areas in colder climates (the Norwegian-Barents Seas and the Labrador Sea), which could be a direct thermal response, although this cannot be assessed in our quasi-equilibrium simulations. The high pressure in the eastern Atlantic is likely a response to tropical and midlatitude changes rather than to Arctic changes (Haarsma et al. 2015).

We must stress that our model, although state-of-the-art in resolution for a coupled model, has a relatively coarse ocean resolution. Details of the boundary current structure, important for accurately determining OHT, cannot be resolved at these resolutions. Hence, models with higher ocean resolution may exhibit a different OHT response. Nevertheless, this is the first systematic study of the effect of \(\hbox {CO}_2\) forcing in quasi-equilibrium climate states; as such our results point at important and intricate OHT sensitivity to changes in climate.

To conclude, we find distinctly different \(\hbox {CO}_2\)-induced equilibrium changes in ocean heat transport toward the Arctic between warm and cold climates. Our results show that ocean heat transport contributes to Arctic amplification mainly through changes in gyre heat transport. However, since this paper presents the results of only one coupled model, it remains to be seen how robust these findings are. Further research on these mechanisms with other coupled models and observations is therefore necessary.