Prediction and predictability of tropical intraseasonal convection: seasonal dependence and the Maritime Continent prediction barrier

Abstract

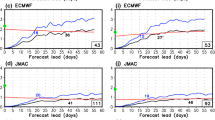
Prediction and predictability of tropical intraseasonal convection in the WMO subseasonal to seasonal (S2S) forecast database is assessed using the real-time OLR based MJO (ROMI) index. ROMI prediction skill in the S2S models, as measured by the maximum lead time at which the bivariate correlation coefficient between forecasts and observations exceeds 0.6, ranges from ~ 15 to ~ 36 days in boreal winter, which is 5–10 days higher than the MJO circulation prediction skill based on the MJO RMM index. ROMI prediction skill is systematically lower by 5–10 days in summer than in winter. Predictability measures show similar seasonal contrast in the two seasons. These results indicate that intraseasonal convection is inherently less predictable in summer than in winter. Further evaluation of correlation skill assuming either perfect amplitude or perfect phase forecasts indicates that phase bias is the main contributor to skill degradation at longer forecast lead times. Nearly all the S2S models have lesser skill for target dates in which the MJO convection is centered over the Maritime Continent (MC) in boreal winter, and phase bias contributes to this MC prediction barrier. This issue is less prevalent in boreal summer. Many S2S models significantly underestimate ROMI amplitudes at longer forecast leads. Probabilistic evaluation of the S2S model skills in forecasting ROMI amplitude is further assessed using the ranked probability skill score (RPSS). RPSS varies significantly across models, from no skill to more than 30 days, which is partly due to model configuration and partly due to amplitude bias. Accounting for the systematic underestimates of the amplitude improves RPSS.