Abstract
The impact of climate change on Sahel precipitation is uncertain and has to be widely documented. Recently, it has been shown that Arctic sea ice loss leverages the global warming effects worldwide, suggesting a potential impact of Arctic sea ice decline on tropical regions. However, defining the specific roles of increasing greenhouse gases (GHG) concentration and declining Arctic sea ice extent on Sahel climate is not straightforward since the former impacts the latter. We avoid this dependency by analysing idealized experiments performed with the CNRM-CM5 coupled model. Results show that the increase in GHG concentration explains most of the Sahel precipitation change. We found that the impact due to Arctic sea ice loss depends on the level of atmospheric GHG concentration. When the GHG concentration is relatively low (values representative of 1980s), then the impact is moderate over the Sahel. However, when the concentration in GHG is levelled up, then Arctic sea ice loss leads to increased Sahel precipitation. In this particular case the ocean-land meridional gradient of temperature strengthens, allowing a more intense monsoon circulation. We linked the non-linearity of Arctic sea ice decline impact with differences in temperature and sea level pressure changes over the North Atlantic Ocean. We argue that the impact of the Arctic sea ice loss will become more relevant with time, in the context of climate change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As a consequence of climate change induced by human activities, Arctic sea ice is projected to disappear in summer at the end of the twenty-first century (Massonnet et al. 2012; Stroeve et al. 2012) leaving an ice-free ocean. At high latitudes the surface albedo is then projected to decrease, allowing a strong surface warming (Chiang and Bitz 2005; Kang et al. 2008; Deser et al. 2010, 2015; Screen and Simmonds 2010; Peings and Magnusdottir 2014; Smith et al. 2017; Oudar et al. 2017). The impact of sea ice decline is not bounded to only mid and high latitudes and is associated with an increase in precipitation over the equator, in Deser et al. (2015), and with a shift in the location of the Intertropical Convergence Zone (ITCZ) in Chiang and Bitz (2005) and Kang et al. (2008). Recently Smith et al. (2017) have shown that sea ice loss can also conduct to increased precipitation over West Africa through impacting sea surface temperatures (SSTs) over the North and subtropical Atlantic Ocean.
There is thus a rationale to link the Arctic sea ice decline with a change in the West African Monsoon (WAM) dynamics. The mechanism proposed by Smith et al. (2017) involves a warming of the North Atlantic Ocean leading to a reinforced atmospheric circulation. This is illustrated by Talento and Barreiro (2017) that have performed idealised numerical experiments in which a temperature increase of several degrees was prescribed at high latitudes to the model. In particular, they found a response consisting of a warming over the subtropical Atlantic Ocean, the Mediterranean Sea and northern Africa, leading to a northward shift of the ITCZ and to an increase in Sahel precipitation. A modulation of the WAM due to a warming of the North Atlantic Ocean (Knight et al. 2006; Zhang and Delworth 2006; Ting et al. 2009; Mohino et al. 2011; Liu et al. 2014; Martin et al. 2014) and of the Mediterranean Sea (Rowell 2003; Fontaine et al. 2010; Gaetani et al. 2010) is widely documented, both contributing to enhanced Sahel precipitation through increased moisture transport. Besides the role of the moisture transport, additional heat is advected to northern Africa from the anomalously warm North Atlantic Ocean and Mediterranean Sea, allowing a deepening of the Saharan Heat Low (SHL) (Roehrig et al. 2011; Liu et al. 2014; Martin et al. 2014), hence strengthening the wind convergence over the Sahel (Lavaysse et al. 2009, 2010; Pu and Cook 2010; Evan et al. 2015). Changes that occur at subtropical latitudes are thus primordial to explain a remote impact of the Arctic sea ice decline on the WAM. It is also important to keep in mind that the increased temperature over the North Atlantic Ocean could in turn impact Arctic sea ice extent, and hence affecting the atmospheric circulation (Luo et al. 2016, 2017).
Arctic sea ice loss is associated with an increase in surface air temperature (SAT), larger in autumn and early winter than during the preceding summer (Screen et al. 2013; Deser et al. 2015), resulting in a delay in phase of the SAT annual cycle at high latitudes (Mann and Park 1996; Dwyer et al. 2012). This delay is also found at lower latitudes (Dwyer et al. 2012), impacting then the seasonality (e.g. phase) of tropical precipitation (Dwyer et al. 2014). We can hypothesize that a projected decline in Arctic sea ice could also induce changes on the magnitude and the phase of the Sahel precipitation seasonal cycle (as proposed in Biasutti and Sobel 2009).
A robust response of climate change stands out: an increase in precipitation over the central Sahel along with a decrease in precipitation over the western Sahel (Monerie et al. 2012, 2013, 2016b; Biasutti 2013; James et al. 2015), with the strongest precipitation increase found from September to October, i.e. during the late rainy season (Wang and Alo 2012; Biasutti 2013; Seth et al. 2013; Monerie et al. 2016a, b). However a lot of uncertainties regarding the WAM future evolution remain, as shown from studies using CMIP3 (Coupled Model Intercomparison Phase 3) and CMIP5 (Coupled Model Intercomparison Phase 5) experiments (Druyan 2011; Monerie et al. 2016b). A deeper understanding of the mechanisms leading to Sahel precipitation change is therefore crucial. There is a rationale that Arctic sea ice decline, induced by increasing GHG concentration, can potentially lead to changes in the mean state and seasonal cycle of the Sahel precipitation. However, the mechanisms at play are not fully understood. Addressing the respective impact of an increased GHG concentration and a decreased Arctic sea ice extent is however not straightforward from historical climate simulations (CMIP5-type), since the direct radiative forcing due to GHG concentration increase leads to Artic sea ice melting, which in turn could indirectly affect the climate. This is a complicated feedback mechanism that make difficult the understanding of the specific role of the Arctic sea ice loss outside polar latitudes.
In this study, we analyse separately the impact of changes due to both the GHG concentration increase and the Arctic sea ice decline, by using a set of idealised sensitivity experiments performed with a coupled model. In particular, we assess the relevance of the mechanisms that may link Arctic sea ice change with Sahel precipitation, which are: (1) a change in SAT at high and subtropical latitudes and (2) a reduced poleward heat transport that can impact meridional temperature gradients. Since the concentration in atmospheric GHG is projected to increase with time, we assess the impact of Arctic sea ice loss on different time-horizons (i.e. GHG concentration levels). A focus is therefore made on the linearity of the Arctic sea ice impact over West Africa.
The main questions addressed in this study can be summarized as follows:
-
Is the Arctic sea ice loss able to impact the WAM mean state and seasonal cycle?
-
What are the mechanisms involved in this relation?
-
Is the impact of Arctic sea ice loss depending on the level of GHG concentration?
2 Data and methods
2.1 The CNRM-CM5 coupled climate model
We use the CNRM-CM5 coupled ocean–atmosphere climate model developed by the CNRM-CERFACS modeling group (Voldoire et al. 2013). The atmosphere model is ARPEGE-Climat v5.2 that operates at a horizontal resolution of 1.4° and 31 vertical levels (T127L31; in a “low-top” configuration). The surface module is the SURFEX (SURface Externalisé) modelling system, embedded in ARPEGE. It includes three surface schemes of natural land, inland water and sea/ocean areas based on the Soil Biosphere and Atmosphere (ISBA) model (Noilhan and Planton 1989; Noilhan and Mahfouf 1996). The ocean model is the Nucleus for European Models of the Ocean (NEMO) v3.2 (Madec 2008) platform. NEMO runs on an ORCA1 triangular grid (horizontal resolution of ~ 1°) with 42 vertical levels (Hewitt et al. 2011). The sea ice GELATO v5.7 (Global Experimental Leads and sea ice for Atmosphere and Ocean) model developed at CNRM is embedded in NEMO (Salas-Mélia, 2002). The atmospheric and oceanic components are coupled with the OASIS software version 3.3 (Valcke et al. 2013). The CNRM-CM5 model has participated to the CMIP5 exercise (Taylor et al. 2012).
2.2 Idealized coupled experiments
Following Oudar et al. (2017; hereafter noted OU17) the relative impacts of a decline in Arctic sea ice extent and an increase in GHG concentration are isolated by performing a set of four idealized experiments. A given GHG concentration (representative of the 1980s and the 2080s, respectively) is maintained constant, while a flux correction (non-solar flux) is applied over the Arctic domain in order to create or melt sea ice under different GHG backgrounds. The experimental protocol is quite similar to the one implemented previously in Deser et al. (2015). First of all, the sea ice concentration differences between the RCP8.5 simulations (for the period 2070–2099) and the historical simulations (for the period 1970–1999) are computed. Then, a spatial mask is built considering those grid points for which sea ice loss between these two periods is larger than 10%. The heat flux correction is only applied over the masked points. Second, a first guess for heat flux correction values is determined by computing the non-solar heat flux differences between the RCP8.5 and the historical ensemble.
The first flux corrected simulation is called ICE21. In this experiment the GHG concentration is maintained constant to the level of 1985, and a positive heat flux correction term (fluxes are counted positively downwards) is added over the masked Arctic sea ice points to melt sea ice and approximate sea ice conditions of the RCP8.5 period 2070–2099. In this way, we obtain a GHG background state representative of present climate with Arctic sea ice values corresponding to the end of twenty-first century. The second flux corrected experiment is named ICE20. We proceed in the same way as for ICE21, but in this case GHG concentration is fixed to the level of 2085, and a negative heat flux correction term (artificial cooling of the ocean) is applied to create sea ice. The first guess of flux correction values (determined from the RCP8.5-historical differences) is not used directly. Similar to Deser et al. (2015) a number of simulations are necessary to perform a linear adjustment in order to determine a multiplying factor that allows to fit the best the targeted sea ice conditions (see OU17 for a detailed description of the method). As stated in OU17, it is important to mention that the methodology is not conservative in terms of energy.
Finally two control experiments are performed. CTL20 consists of a stabilised climate simulation in which GHG concentration and other external forcings are maintained to their 1985 values. A similar CTL21 is conducted, but in this case external forcings are maintained to the value of 2085. Table 1 summarized the characteristics of the four experiments described above.
The impact of Arctic sea ice change under the twentieth century GHG conditions is isolated by computing the ICE21-CTL20 difference (hereafter noted ΔICE_hist) whereas the effect of Arctic sea ice loss at the end of the twenty-first century is obtained by computing the CTL21-ICE20 difference (hereafter noted ΔICE_rcp). Then, the impact of the GHG concentration background is analysed by computing the ΔICE_rcp-ΔICE_hist difference (hereafter noted ΔICE_back). To isolate the effect of increasing GHG concentration under present Arctic sea ice conditions, the ICE20-CTL20 difference (called ΔGHG_hist) is computed. Similarly, the CTL21-ICE21 difference (hereafter noted ΔGHG_rcp) is used to determine the role of an increase in GHG concentration under the late twenty-first century Arctic sea ice conditions. Finally, the impact of changes in both GHG concentration increase and Arctic sea ice decline is obtained from CTL21-CTL20 (hereafter noted ΔICE + GHG). Table 2 summarizes the different analysis and usage of the experiments as explained above.
All the simulations are run for 200 years. Sahel climate stabilises after the first 50 years (not shown) and only the 150 last years of the simulations are therefore analysed here (i.e. a spin-up of 50 years is considered). Sahel precipitation undergoes a decadal to multidecadal variability, in association with the Atlantic Multidecadal Variability (AMV; Mohino et al. 2011; Martin et al. 2014) and the Interdecadal Pacific Variability (IPV; Villamayor and Mohino 2015). An average over a long-time period removes thus the natural climate variability effects due to IPV or AMV. Nevertheless we tested the sensitivity to the period length by using a 100 years spin-up instead. Results are very similar to the one obtained with the 50 years spin-up (not shown).
2.3 Validation of the experimental protocol
The seasonal cycle of the Arctic sea ice extent is analysed for the four idealized experiments (Fig. 1). For comparison, the current (historical scenario, averaged over the 1970–1999 period) and future (RCP8.5 emission scenario, averaged over the 2070–2099 period) Artic sea ice extent simulated by CNRM-CM5 are included. ICE20 and CTL20 show a similar extent in Arctic sea ice, of ~ 15 million km2 in March and of ~ 6 million km2 in September. The latter values are close to the observed sea ice extent (see Simmonds 2015). ICE21 and CTL21 simulate also a similar Arctic sea ice extent, ranging from ~ 11 million km2 in March to an ice-free ocean in late boreal summer and early autumn (August–September–October). Thus, ICE20 (ICE21) and CTL20 (CTL21) simulate similar Arctic sea ice extent values and thus only differ by their GHG concentration. We also verified that values of sea ice concentration are similar when the Arctic sea ice extent is at its maximum (i.e. in March) and minimum (i.e. in September). In spite of several differences, patterns of sea ice cover are very similar between CTL20 and ICE20, and between CTL21 and ICE21 (Figure S1 and S2). Therefore, Fig. 1 shows that the experimental protocol has been successful in reproducing the respective targeted Arctic sea ice conditions.
Seasonal cycle of the Arctic sea ice extent (106 km2) for CTL20 (blue line), CTL21 (red line), ICE20 (yellow line), ICE21 (green line), the ensemble mean of the historical run (1970–1999) (continuous black line) and the ensemble mean of the RCP85 (2070–2099) (discontinuous black line). Historical and RCP8.5 ensembles mean are shown and computed from five members. The gray shading indicates the inter-member spread, defined as the minimum and maximum value of Arctic sea ice extent
We analyse Sahel precipitation change to complete the validation of the experimental protocol. Changes in Sahel precipitation, i.e. the RCP8.5-historical differences (noted ΔRCP hereinafter), estimated from a set of 32 CMIP5 models are shown in Fig. 2. The goal is to ensure that CNRM-CM5 is not an outlier model. Precipitation change ranges from a decrease to an increase, in consistency with previous results obtained with CMIP3 (Druyan 2011) and CMIP5 simulations (Monerie et al. 2016b). Here, several models produce a strong decrease in precipitation (e.g. gfdl-esm2m and csiro-mk3-6-0) and other models project a strong increase in precipitation (e.g. miroc models). Both ΔRCP and ΔICE + GHG consist of an increase in Sahel precipitation close to the CMIP5 multi-model ensemble mean, since included between the lower and upper bounds of the precipitation change (defined by 1 standard deviation). The moderate difference found between ΔICE + GHG and ΔRCP (~ 0.2 mm day− 1) can partially be explained by the fact that ΔICE + GHG is computed from two stabilised simulations with constant GHG concentration, whereas in ΔRCP the GHG forcing is varying with time. This slight difference was also reported at global scale in OU17, which provides a more extended validation confirming that ΔICE + GHG successfully simulates a similar result (in terms of pattern and intensity) than ΔRCP. It has also been shown that the impact of climate change is complex in terms of spatial pattern and seasonality (Biasutti 2013; Monerie et al. 2016a, b). Contrarily to most of the CMIP5 models, CNRM-CM5 does not project a decrease in precipitation over the Western Sahel (Fig. 3a; see Monerie et al. 2016a, b).
Summer (JAS) Sahel precipitation responses (mm day− 1), computed as the differences between RCP8.5 (2060–2099) and historical (1960–1999) ensembles mean. The Sahel box is defined here as 10°W to 10°E and 10°N to 20°N. Sahel precipitation changes are shown for 32 CMIP5 simulations (gray bars), the CNRM-CM5 response (orange) and ΔICE + GHG response (red). For CNRM-CM5 the vertical bar represents the distance between the minimum and maximum value of the Sahel precipitation change. The horizontal dashed lines represent the one standard deviation envelope estimated from the 32 CMIP5 simulations. The horizontal dotted line represents the multi-model mean of the 32 Sahel precipitation changes
Precipitation response (mm day− 1) in JAS for a ΔICE + GHG, b ΔGHG_hist, c ΔGHG_rcp, d ΔICE_hist and e ΔICE_rcp. Stippling indicates where the differences are statistically significant at the 90% confidence level according to a Student t test. The red line indicates the JAS climatology (from 0 to 16 mm day− 1, every 2 mm day− 1), for a, b and d CTL20, c ICE21 and e ICE20
2.4 Moisture flux decomposition
In this study we decompose the moisture flux into its mean circulation dynamic (MCD) and thermodynamic (TH) components:
where,
a and b refer to the two simulations being considered. For example, to compute the moisture flux decomposition associated with ΔICE + GHG (that is CTL21-CTL20), a is CTL20 and b is CTL21. Bars denote the monthly means. The decomposition is performed on the zonal (u) and meridional (v) wind components (\(\vec {u}\)). This decomposition is based on Seager et al. (2010), and is here applied to low atmospheric levels, since the monsoon flow is strongest at 925 hPa. The MCD component indicates the part of moisture flux change that is due only to wind changes. The TH component allows highlighting the role of moisture increase in moisture flux changes. It is worth noting to mention that we also computed changes due to the transient eddies (TE), but we found a negligible impact due to the GHG and ICE effects on the moisture transport associated with TE (not shown). We thus decided to focus the analysis on only the MCD and TH components.
3 Impacts on Sahel precipitation in July–August–September
3.1 Precipitation
The impact of both effects, that is sea ice decline and GHG concentration increase, consist of a large precipitation increase over West Africa and over the maritime ITCZ (Fig. 3a). This precipitation change is consistent with ΔRCP as simulated by CNRM-CM5, which projects a homogeneous increase in Sahel precipitation throughout the Sahel (Fig. 2). This is also consistent with the CMIP5 ensemble since most of the models project an increase in precipitation over the central Sahel at the end of the twenty-first century (Monerie et al. 2012, 2016b; Biasutti 2013; James et al. 2015; Fig. 2).
The isolated GHG effect depicts a similar pattern under both present (Fig. 3b) and future (Fig. 3c) Arctic sea ice conditions: a negative anomaly of precipitation, located between 10°S and the equator, and a positive anomaly north of the equator, indicate that the rain belt is projected to shift northward. It is worth noting that climatological value in Arctic sea ice extent slightly modulates the impact of the increased GHG concentration since precipitation increase is larger in ΔGHG_rcp (Fig. 3c) than in ΔGHG_hist (Fig. 3b).
The influence of the isolated Arctic sea ice effect on Sahel precipitation, under present (ΔICE_hist ; Fig. 3d) GHG concentration, is weak, and only statistically significant over several grid points. Under future (ΔICE_rcp; Fig. 3e) GHG concentration, the Artic sea ice effect is stronger and comparable to ΔGHG_hist over the Sahel (figure S3). In ΔICE_hist precipitation increases over the Gulf of Guinea and decreases over the Sahel, from 5°W to 25°E, denoting a southward shift of the rain belt. In ΔICE_rcp, precipitation increases between 5°N and 15°N and decreases over the Gulf of Guinea, due to a northward shift of the rain belt. Here, results are clearly different since exhibiting an opposite sign, highlighting a non-linearity of the sea ice effect.
Thus, Fig. 3 shows that (1) the GHG effect (ΔGHG) is stronger than the sea ice loss effect (ΔICE) and dominates the impact of climate change on Sahel precipitation; (2) sea ice decline leads to different impacts on precipitation, depending on the GHG concentration. This issue will be discussed in Sect. 5. (3) ΔICE_hist represents the response to sea ice decline for a near-term horizon whereas ΔICE_rcp represents the response to sea ice loss for a long-term horizon. Hence, the sea ice effect is projected to become stronger with time and to push the WAM cell more northward.
In the next section we analyse the physical mechanisms that explain the different effects of GHG concentration increase and Arctic sea ice decline.
3.2 Atmospheric circulation changes at low-level
ΔICE + GHG, ΔGHG_hist and ΔGHG_rcp depict a stronger warming over the Sahara (of up to + 5 °C) and over the subtropical North Atlantic Ocean (of up to + 3.5 °C) than over the Gulf of Guinea (of up to + 2.5 °C), (Fig. 4a–c) hence strengthening the land-sea and North Atlantic–Equatorial Atlantic thermal contrasts (as seen in Haarsma et al. 2005; Skinner et al. 2012; Lee and Wang 2014). Moreover, the SAT increase is associated with a deepening of the Saharan heat low, as shown by the decrease in sea level pressure over northern Africa, favouring the strengthening of the south-westerlies and of the moisture flux over the Sahel (Fig. S4acd). The moisture flux strengthening is mostly due to the increase in air moisture content (TH term, i.e. advection of moisture by the mean flux) (Fig. S4bde). The strong warming of the sea over the tropical region, the North Atlantic Ocean and of the Mediterranean Sea allows feeding the low-atmosphere in moisture, following the Clausius–Clapeyron relation. This is consistent with Kitoh et al. (2013) that have shown that climate change mainly impacts the WAM by strengthening evaporation over the ocean and strengthening the moisture convergence. Although the magnitude of the warming is stronger in ΔGHG_rcp (Fig. 4c) than in ΔGHG_hist (Fig. 4b) the physical mechanism at play is the same.
Responses of 925 hPa moisture flux (g kg− 1 * m s− 1; green arrow), surface air temperature (°C; shading) and sea level pressure (Pa; blue lines) in JAS for a ΔICE + GHG, b ΔGHG_hist, c ΔGHG_rcp, d ΔICE_hist and e ΔICE_rcp. Only statistically significant differences in temperature and moisture fluxes are shaded, according to a Student t test at the 95% confidence level
ΔICE_hist (Fig. 4d) and ΔICE_rcp (Fig. 4e) responses exhibit different patterns. ΔICE_hist shows a homogeneous warming of up to 0.5 °C over Africa and over the tropical Atlantic Ocean. ΔICE_hist shows a decrease in moisture flux (Fig. 4d) due to a weakening of the low-level westerlies (i.e. the MCD component; Fig. S4g), explaining the increase in precipitation over the Equatorial Atlantic Ocean, and the decrease in precipitation over central Sahel (Fig. 3d). In ΔICE_rcp the warming is stronger north of 30°N than south of 30°N, leading to a strengthening in moisture flux from the Tropical Atlantic Ocean and from the Mediterranean Sea to the Sahel (Fig. 4e). Here, the moisture flux change is mainly due to the strengthened evaporation (i.e. the TH component; Fig. S4j). ΔICE_rcp exhibits a similar mechanism as ΔGHG_hist and ΔGHG_rcp, with however a much weaker magnitude.
Therefore, the main discrepancy among the different effects lies on the magnitude and pattern of SAT change due to a different balance of the excess heat generated by the perturbation of the Arctic sea ice extent and GHG concentration. This is investigated in the next section.
3.3 Poleward heat transport
In this section we analyse the meridional poleward heat transport (PHT), which plays a fundamental role in governing the response of the climate system to changes in GHG concentration and Arctic sea ice extent. PHT is estimated following the method described in Trenberth and Caron (2001) and Trenberth and Fasullo (2007), and also used in Deser et al. (2015) and Sanchez-Gomez et al. (2016), to characterize the redistribution of energy between and within each component of the climate system (ocean, atmosphere) due to an imposed change in the radiative imbalance.
The poleward heat transport of the atmosphere (TA) is estimated as the difference between the net heat budget at the top of the atmosphere and the net heat budget at the surface. The poleward oceanic heat transport (TO) is estimated by computing the net heat budget at the surface by only considering the ocean points. Both TA and TO are then zonally integrated and the cumulative sum from South to North is computed. Following Magnusdottir and Saravanan (1999) the global average fluxes is subtracted to TO, TA and TO+A, but using the simulation used as reference when computing the PHT anomalies. Decreasing values indicate a weakening in PHT and increasing values indicate a strengthening in PHT. The total heat transport (TO+A) is then estimated as the sum TO + TA.
Figure 5 depicts the total (TA+O, Fig. 5a), atmospheric (TA, Fig. 5b) and oceanic (TO, Fig. 5c) PHT during the rainy season (JAS). The total response (ΔICE + GHG) consists of a strengthening in PHT from the equator to Arctic latitudes, which is mainly associated with the GHG effect (ΔGHG_hist and ΔGHG_rcp). Here, an enhanced PHT is associated with a warming, stronger over the northern subtropical latitudes than over the tropics, hence strengthening the land-sea thermal contrast over Africa (Fig. S5bc). The increase in PHT consists of a re-balancing of heat (Fig. 5a) through an increase in TA, from 30°S to 60°N (Fig. 5b), and in TO, from 10°N to the Arctic region (Fig. 5c). PHT increase is stronger in ΔGHG_hist than in ΔGHG_rcp due to a tropical/polar thermal contrast stronger in the former than in the latter, because of a wider sea ice extent in ΔGHG_hist than in ΔGHG_rcp.
ΔICE_hist and ΔICE_rcp are characterized by a global weakening in PHT, due to the strong warming of the Arctic (i.e. the Arctic Amplification, Serreze and Barry 2011) (Fig. S5). The meridional tropic/arctic thermal gradient then weakens, in association with a reduced PHT, and with a warming of the tropical and subtropical regions, since less heat is exported towards North (Fig. 4d, e). The oceanic PHT weakens globally, with differences according to latitudes: PHT strengthens between the equator and 40°N and between 75°N and 90°N. On the other hand, PHT weakens between 40°N and 70°N, indicating that less heat is transported poleward in the midlatitudes, favouring a temperature increase of the North Atlantic Ocean (as in the Fig. 4d, e). We note that for the ICE effect, TO is much stronger than TA between 60°S and 90°N, indicating that the role of the ocean is here primordial in modulating the heat at low-latitudes after a perturbation occurring at high latitudes. This is consistent with Deser et al. (2015) that show larger changes at low-latitudes from coupled than from uncoupled simulations in response to a change in Arctic sea ice extent. This is also consistent with the surface warming, stronger over the equator than over the subtropical Atlantic Ocean in ΔICE_hist, leading to weakened westerlies (Fig. 4d).
As TA cannot be computed considering only the Atlantic Ocean and Africa regions, we only show the change in globally averaged PHT. We assume that this result is relevant for West Africa since the change in SAT is roughly zonally homogeneous over the globe (i.e. stronger over the subtropics than over the tropics for both the GHG and ICE effect).
We show here that the perturbation of the climate system leads to a heat re-balancing through changes in PHT. Different mechanisms seem to be at play in response to a change in the GHG concentration and Arctic sea ice loss. However, both effects impact the global-scale and West African climates. The regional consequences of the PHT response on the atmospheric dynamics are analysed in the next section.
3.4 Changes throughout the atmospheric column
Figure 6 shows cross-sections of omega throughout the atmospheric column, zonally averaged between 10°W and 10°E in JAS. The climatological WAM cell extends from the equator to 25°N with a maximum of air ascent located around 10°N where the strongest convection occurs (see the climatology represented with contours in Fig. 6a–e). North of 20°N the shallow circulation cell is associated with dry convection (Peyrillé et al. 2007; Thorncroft et al. 2011).
Cross section, latitude-pressure levels of omega (Pa s− 1) in JAS for a ΔICE + GHG, b ΔGHG_hist, c ΔGHG_rcp, d ΔICE_hist and e ΔICE_rcp. Stippling indicates where the differences are statistically significant at the 95% confidence level according to a Student t test. The black contour indicates the JAS climatology, for a, b and d CTL20, c ICE21 and e ICE20. Solid (dashed) lines indicate downward (upward) motion. The cross-section is defined as the average between 10°W and 10°E
ΔICE + GHG (Fig. 6a), ΔGHG_hist (Fig. 6b) and ΔGHG_rcp (Fig. 6c) simulate an anomalously wet Sahel, in association with a northward extent of the monsoon system, as indicated by the anomalously strong air ascent (negative omega anomalies) obtained between 15°N and 20°N and between the surface and the mid-troposphere (400 hPa; colors), as well as by a decrease in air ascent (positive anomalies) obtained South of 15°N. A northward shift of the monsoon system was also reported during anomalously wet period, using reanalysis (Grist and Nicholson 2001; Nicholson 2013). Between 15°N and 20°N the anomalously ascent is stronger at mid-level in ΔGHG_rcp than in ΔGHG_hist, indicating a more intense circulation change in the latter than in the former.
As for precipitation, the magnitude of the Arctic sea ice effect on omega is weaker than the one exerted by the GHG concentration change. In ΔICE_hist the positive anomaly of omega obtained at around 15°N along with the negative anomaly around the equator indicate a southward displacement of the monsoon cell (Fig. 6d) in consistency with reduced Sahel precipitation (Figs. 3d, 6). In ΔICE_rcp the negative anomaly at mid-level and north of 10°N, and the positive anomaly south of 10°N, indicate a northward shift of the monsoon-cell. Anomalies are however moderate over the Sahel (Fig. 6e).
To further investigate the WAM dynamics response, the zonal wind component is analysed throughout the atmospheric column, zonally averaged between 10°W and 10°E (Fig. 7). The climatological westerly winds are located between the equator and 20°N below 700 hPa (see the climatology contours in Fig. 7). ΔICE + GHG, ΔGHG_hist and ΔGHG_rcp responses exhibit a strengthening and a northward shift of the low-level westerlies over the Sahel (Fig. 7a–c). This is consistent with a strengthening of the low-level moisture flux (Fig. 4a–c). The core of the African Easterly Jet (AEJ) is located at 15°N and at 600 hPa. In ΔICE + GHG (Fig. 7a) and ΔGHG_rcp (Fig. 7c) negative anomalies of zonal wind are located northward and southward of the AEJ core and a change in the AEJ location is therefore not clear. The AEJ moves southward in ΔGHG_hist (Fig. 7b), as indicated by the strong increase in zonal wind speed between Equator and 15°N and between 850 and 500 hPa. Here the strengthening of the low-level southerlies together with the southward shift of the AEJ suggest that two opposite mechanisms are at play: the former acting to bring moisture to the Sahel and the latter exporting moisture from the Sahel.
Cross section, latitude-pressure levels of the zonal wind response (m s− 1) in JAS for a ΔICE + GHG, b ΔGHG_hist, c ΔGHG_rcp, d ΔICE_hist and e ΔICE_rcp. Stippling indicates where the differences are statistically significant at the 95% confidence level according to a Student t test. The black contour indicates the JAS climatology, for a, b and d CTL20, c ICE21 and e ICE20. Solid (dashed) lines indicate downward (upward) motion. The cross-section is defined as the average between 10°W and 10°E
ΔICE_hist and ΔICE_rcp show contrasted results (Fig. 7d, e): low-level winds weaken in ΔICE_hist and strengthen in ΔICE_rcp. Besides, ΔICE_hist shows a strengthening of the zonal winds south of 15°N and from the surface to 500 hPa, indicating a southward shift of the AEJ core. At the opposite, the AEJ moves northward in ΔICE_rcp, as shown by the increase in zonal wind speed north of 20°N.
A southward displacement of the AEJ is obtained in ΔICE_hist (Fig. 7b, d). An anomalously strong AEJ was associated with a decrease in precipitation by exporting moisture at mid-levels (Cook 1999). It is here important to note that the impact of the AEJ location on Sahel precipitation is not straightforward, because of the existence of precipitation-AEJ speed feedbacks (Thorncroft and Blackburn 1999; Cook 1999).
4 Impact on the seasonal cycle of the Sahel precipitation
One consequence of an ice-free Arctic Ocean is a reduction of surface albedo, which acts to enhance the warming over the Arctic (Fig. S5de). The maximum of sea ice decline occurs in late summer and early autumn (Fig. 1), but the net upward heat flux response (i.e. positive from the ocean to the atmosphere) is largest in December-January (Fig. S6). This delay is due to a stronger climatological air-sea thermal contrast in winter than in summer, which leverages the efficiency of the turbulent energy flux (as also discussed in Deser et al. 2010, 2015; Screen and Simmonds 2010; Peings and Magnusdottir 2014). Arctic sea ice loss is therefore associated with a delay in phase of the seasonal cycle of SAT at high latitudes (Mann and Park 1996; Dwyer et al. 2012; Stine and Huybers 2012). The simulations performed in OU17 confirm this behaviour since a delay in phase (of up to 1 month) of the SAT seasonal cycle is obtained at high latitudes in ΔICE + GHG and can only be explained by the replacement of sea ice by an ice-free ocean (ΔICE_hist and ΔICE_rcp) (Fig. S7ade). Over subtropical latitudes the phase of SAT seasonal cycle undergoes also a delay, but it is only due to the GHG effect (Fig. S7bc). This does not support the idea of an impact of Arctic sea ice decline on the phase of the subtropical Atlantic SAT seasonal cycle.
The respective impacts of GHG and sea ice effects on the Sahel precipitation seasonal cycle is assessed by analysing the responses in precipitation (ΔP), evaporation (ΔE) and moisture flux convergence (Δ(P − E)) (Fig. 8). ΔICE + GHG and ΔGHG_rcp project an increase in precipitation from July to November, which is due to changes in both moisture convergence Δ(P − E) and local recycling ΔE (Fig. 8a, c). ΔGHG_rcp and ΔICE + GHG responses are particularly strong in August, that is the peak of the rainy season, and in September–October, that is the end of the rainy season, in consistency with CMIP5 multi-model analyses (Monerie et al. 2016a; among others). ΔGHG_hist effect exhibits a decrease in Sahel precipitation in May–June, due to a weakened moisture flux convergence (Fig. 8b). Sahel precipitation increases from July to October, because of a strengthened evaporation (ΔE > Δ(P − E)) indicating a prominent role of local water recycling in precipitation change.
Results indicate a profound difference in terms of dynamical processes between ΔGHG_hist and ΔGHG_rcp, with more moisture transport and convergence in the latter than in the former. The SAT increase is stronger in ΔGHG_rcp than in ΔGHG_hist, especially over the Arctic, the North Atlantic Ocean and around the Mediterranean Sea (Fig. S5bc). Hence, we hypothesize that their differences are simply due to a stronger warming in ΔGHG_rcp than in ΔGHG_hist. We assess this issue by analysing the projected response simulated by CNRM-CM5 using a medium–low emission scenario (RCP4.5; the response noted as ΔRCP4.5) and a high emission scenario (RCP8.5; ΔRCP8.5) (Fig. S8). ΔRCP4.5 shows a similar response than ΔGHG_hist with a decrease in precipitation in May–June and a moderate precipitation increase from July to November (Fig. S8a). Changes are larger in ΔRCP8.5 due to a strengthening in moisture flux convergence and local water recycling. Hence, the GHG impact on the Sahelian hydrological cycle strongly depends on the global mean temperature increase, which explains the difference between ΔGHG_hist and ΔGHG_rcp.
In ΔICE_hist, precipitation decreases throughout the year due to a weakened moisture flux convergence (Fig. 8d). This is consistent with the weakening of the low-level southerlies (Fig. 4d). When sea ice loss is associated with a higher GHG concentration (ΔICE_rcp), precipitation increases due to strengthened water vapour recycling and moisture convergence.
ΔP response is particularly strong in ASO (August–September–October) in ΔICE + GHG, ΔGHG_rcp and ΔICE_rcp, indicating an increase in precipitation at the core and during the late rainy season. These changes are however not associated with a decrease in precipitation at the beginning of the Sahel rainy season (June–July) and we cannot conclude on a delay in phase of the Sahel precipitation seasonal cycle. However, the positive value of ΔP in ASO clearly indicates a stronger increase in precipitation during the late than during the early rainy season. A wetter Sahel in SO does not necessary denotes a delay of the demise date of the rainy season, since this has to be addressed using daily precipitation values.
It is worth to mention that the Arctic sea ice effect is only associated with more SO precipitation under a high GHG background, suggesting again a non-linearity in the response to Arctic sea ice loss. This question is investigated in the next section.
5 Linearity of the Arctic sea ice effect
To investigate the sensitivity of the sea ice effect according to the concentration in GHG we define the ΔICE_back response, as the difference between ΔICE_rcp (the sea ice decline impact for a long-term horizon) and ΔICE_hist (the sea ice loss impact at a near-term horizon). The non-linearity in the sea ice effect is associated with a strong increase in precipitation from August to October due to increased moisture flux convergence (ΔP − E; Fig. 9a). Moisture flux strengthens from both the Tropical Atlantic Ocean and the Mediterranean Sea to the Sahel, due to the SAT increase and the sea level pressure decrease north of 10°N, which modulates the meridional land-sea and tropical North Atlantic/Tropical South Atlantic gradients in temperature and pressure (Fig. 9b). The ΔICE_back response is SAT is associated with a stronger forcing in ΔICE_rcp than in ΔICE_hist because of a stronger concentration in greenhouse gases.
ΔICE_rcp—ΔICE_hist difference in a precipitation (ΔP in mm day− 1; white bar), evaporation (ΔE in mm day− 1; gray bar) and moisture flux convergence (ΔP-E in mm day− 1; red line) and in b 925 hPa moisture flux (g kg− 1 * m s− 1; green arrow), surface air temperature (°C; shading) and sea level pressure (Pa; blue lines). The moisture fluxes are broken into its c mean circulation dynamic and d thermodynamic component (g kg− 1 * m s− 1)
The strengthening of the zonal moisture flux is due to the MCD component (Fig. 9c), whereas the meridional flux strengthening is due to the TH component (Fig. 9d). This is consistent with a warmer ocean north of 20°N, allowing more evaporation and a feeding of the low-level atmosphere in water vapour. Over the subtropical North Atlantic Ocean, sea level pressure decreases leading to an anomalously strong cyclonic circulation. Moisture flux differences are however not significant, due to opposite responses in the MCD (i.e. a cyclonic anomaly) and TH (i.e. an anticyclonic anomaly) components. A strong increase in the westerlies is consistent with Lélé et al. (2015), which have shown that anomalously wet periods in the Sahel are more associated with a strengthening of the zonal flux than of the meridional flux. ΔICE_back also displays a northward shift of the WAM, as indicated by omega anomalies (Fig. S9a) and zonal wind anomalies at low and mid-levels (Fig. S9b).
Following our results, the surface wind dynamic and sea level pressure anomalies are therefore crucial to understand the precipitation response in ΔICE_back. In fact, in ASO the pattern of sea level pressure change is different in ΔICE_hist and in ΔICE_rcp (Fig. S10de), resulting in a negative sea level pressure anomaly over the subtropical Atlantic Ocean, North Atlantic Ocean and Europe in ΔICE_back. We can thus hypothesize that the warming of the Arctic can impact the subtropical and the tropical climates through modifications of the polar/subtropical sea level pressure systems. Nevertheless, a consistent and significant change of the North Atlantic Oscillation is not distinguishable in ΔICE_back (Fig. S11).
As shown in Martin et al. (2014), a negative anomaly of sea level pressure and a positive anomaly of SAT over the subtropical North Atlantic Ocean are also observed during the positive phase of the AMV. ΔICE_back is thus associated with a change in the North Atlantic temperature, similarly as the AMV impact on Sahel precipitation. However, the sea ice effect does not lead to changes in the seasonal cycle of subtropical SAT (Fig. S7bc and Fig. S13) and changes in sea level pressure and SAT are therefore constant during the June to October period (Figs. S11 and S12).
6 Conclusion
The GHG concentration is projected to increase leading to a dramatic decline of the Arctic sea ice, and even to its almost complete melting in late summer and early autumn by the end of twenty-first century. Recent studies based on coupled simulations have reported that Arctic sea ice decline could impact not only high and mid-latitudes, but also tropical areas, such as the Sahel (Chiang and Bitz 2005; Kang et al. 2008; Deser et al. 2015; Blackport and Kushner 2016; OU17; Smith et al. 2017). Both increase in GHG concentration and decline in Arctic sea ice extent are expected to impact the climate at regional and global scale. Assessing the relative impacts of the GHG concentration and the Arctic sea ice decline over the climate is however not straightforward in state-of-the-art simulations (i.e. CMIP-like), where both effects are embedded.
In this study we investigate the respective impacts of GHG concentration increase and Arctic sea ice decline on Sahel precipitation. On this purpose, we used a set of idealised simulations performed in OU17 that allow to isolate the relative roles of both GHG concentration increase and Arctic sea ice decline. We applied a flux correction technique to obtain different (present and future) Arctic sea ice conditions along with fixed GHG concentration (maintained constant to the 1985 and 2085 values). Computed differences among the simulations allow to artificially isolate the different impacts of GHG concentration increase and sea ice decline (see Table 2).
First of all, the total response, that is the impact of global warming, as simulated by CNRM-CM5 coupled climate model consists of an increase in Sahel precipitation at the end of the twenty-first century (Figs. 2, 3a). Such a result is obtained in most of the CMIP5 simulations (Monerie et al. 2016b) and is mainly explained by an enhancement of the moisture flux over the Sahel due to increased evaporation (the thermodynamic part; as shown in Kitoh et al. 2013), and to strengthened sea-land thermal contrasts (the dynamic part; as also reported in Haarsma et al. 2005; Skinner et al. 2012; Lee and Wang 2014) (Fig. S3). Our analyses show that the total response and the mechanism explained above are largely dominated by the GHG concentration increase and that the impact of sea ice decline is much weaker (Fig. 3b–e).
Arctic sea ice decline leads to a weakening of the poleward heat transport (Fig. 5), allowing a warming of the tropical and subtropical latitudes (Fig. 4d, e). In ΔICE_hist, the warming is stronger over the tropical than over the subtropical Atlantic Ocean, leading to a weakening of the monsoon circulation (Figs. 6d, 7d) and to a weak (i.e. not significant) decrease in Sahel precipitation (Fig. 3d). The response observed in ΔICE_hist (decrease in Sahel precipitation) is contrarious to the ones induced by GHG concentration increase (increasing Sahel precipitation) in the model. However, the response under a high level of GHG (ΔICE_rcp) is the most probable picture at the end of twenty-first century. ΔICE_rcp shows that Arctic sea ice loss leads to a strengthening of the tropical/subtropical temperature gradient over land and a weakening of the tropical/subtropical temperature gradient over the Atlantic Ocean (Fig. 4e). Sea level pressure decreases over the subtropical and North Atlantic Ocean allowing then a northward shift of the ITCZ (Fig. 6e) and a strengthening of the West African Monsoon (WAM) (Fig. 3e). The Arctic sea ice effect on Sahel precipitation depends therefore on the atmospheric GHG concentration. We thus argue that the global warming impact on the Sahel could become stronger with time, leading to a reinforced WAM circulation at the end of the twenty-first century due to both GHG concentration increase and Arctic sea ice decline.
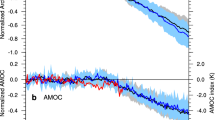
Unlike ΔICE_rcp, sea surface temperature becomes colder and surface air temperature does not increase from 30 to 60°N in ΔICE_hist (Fig. S14). The non-linearity of the Arctic sea ice effect shown here may thus be due to the difference in the amplitude of the surface warming of the North Atlantic Ocean (stronger in ΔICE_rcp than in ΔICE_hist) and to the strengthening of the Atlantic northward heat transport (Fig. S15). It is for instance found that the weakening of the Atlantic Multidecadal Overturning Circulation (AMOC) is stronger in ΔICE_hist than in ΔICE_rcp (Fig. S16), since the departure occurs from a colder mean state in the former than in the latter case. The mechanism involved to explain the response of Sahel precipitation to this warming is very similar to the one identified for the AMV (as shown in Knight et al. 2006; among others). Indeed, the temperature and sea level pressure changes over the North Atlantic Ocean and Northern Tropical Atlantic Ocean and northern Africa (Fig. 9b) lead to a strengthening of the westerlies (Fig. 9c) that in turn enhance the moisture convergence over the Sahel and increase precipitation (Fig. 9a, b). We conclude that the role of the North and Subtropical Atlantic Ocean is relevant to explain the link between the Arctic sea ice and the Sahel (as previously suggested in Smith et al. 2017).
Arctic sea ice decline is associated with a strong warming over the polar region (Fig. S5de) and locally, with a delay in phase of SAT seasonal cycle of up to 1 month (Fig. S7de). However, the seasonal cycle of SAT over the North and Subtropical Atlantic Ocean is not impacted (Fig. S7de). Hence from our study, sea ice loss does not seem to alter the phase of Sahel precipitation (Fig. 8e).
Since this study is based on one model simulation, uncertainties due to the model or even the experimental setup are not taken into account. As the response of the Sahel precipitation is strongly model dependent (Druyan 2011; Monerie et al. 2016b), we argue that a multi-model analysis using similar idealised experimental setups (Deser et al. 2015; Blackport and Kushner 2016; McCusker et al. 2017) should be undertook to provide more robustness to the Arctic sea ice changes on the Sahel climate. The background state is of primordial importance and has strong impacts on the results (see also Smith et al. 2017; Screen et al. 2018 for instance), a range of simulations should also be performed using different initial conditions, using both micro and macro permutations, as in Hawkins et al. (2016).
References
Biasutti M (2013) Forced Sahel rainfall trends in the CMIP5 archive. J Geophys Res Atmos 118:1613–1623. https://doi.org/10.1002/jgrd.50206
Biasutti M, Sobel AH (2009) Delayed Sahel rainfall and global seasonal cycle in a warmer climate. Geophys Res Lett 36:L23707. https://doi.org/10.1029/2009gl041303
Blackport R, Kushner PJ (2016) The transient and equilibrium climate response to rapid summertimes sea ice loss in CCSM4. J Clim 29:401–417. https://doi.org/10.1175/JCLI-D-15-0284.1
Chiang JCH, Bitz CM (2005) Influence of high latitude ice cover on the marine Intertropical convergence zone. Clim Dyn 25:477–496. https://doi.org/10.1007/s00382-005-0040-5
Cook KH (1999) Generation of the African easterly Jet and its role in determining west African precipitation. J Clim 12:1165–1184. https://doi.org/10.1175/1520-0442(1999)012%3C1165:gotaej%3E2.0.co;2
Deser C, Tomas R, Alexander M, Lawrence D (2010) The seasonal atmospheric response to projected arctic sea ice loss in the late twenty-first century. J Clim 23:333–351. https://doi.org/10.1175/2009JCLI3053.1
Deser C, Tomas RA, Sun L (2015) The role of ocean–atmosphere coupling in the zonal-mean atmospheric response to Arctic Sea ice loss. J Clim 28:2168–2186. https://doi.org/10.1175/jcli-d-14-00325.1
Druyan LM (2011) Studies of 21st-century precipitation trends over West Africa. Int J Climatol 31:1415–1424. https://doi.org/10.1002/joc.2180
Dwyer JG, Biasutti M, Sobel AH (2012) Projected changes in the seasonal cycle of surface temperature. J Clim 25:6359–6374. https://doi.org/10.1175/jcli-d-11-00741.1
Dwyer JG, Biasutti M, Sobel AH (2014) The effect of greenhouse gas–induced changes in SST on the annual cycle of zonal mean tropical precipitation. J Clim 27:4544–4565. https://doi.org/10.1175/JCLI-D-13-00216.1
Evan AT, Flamant C, Lavaysse C, Kocha C, Saci A (2015) Water vapor–forced greenhouse warming over the sahara desert and the recent recovery from the Sahelian drought. J Clim 28:108–123. https://doi.org/10.1175/JCLI-D-14-00039.1
Fontaine B et al (2010) Impacts of warm and cold situations in the Mediterranean basins on the West African monsoon: observed connection patterns (1979–2006) and climate simulations. Clim Dyn 35:95–114. https://doi.org/10.1007/s00382-009-0599-3
Gaetani M, Fontaine B, Roucou P, Baldi M (2010) Influence of the Mediterranean Sea on the West African monsoon: Intraseasonal variability in numerical simulations. J Geophys Res 115:D24115. https://doi.org/10.1029/2010jd014436
Grist JP, Nicholson SE (2001) A study of the dynamic factors influencing the rainfall variability in the West African Sahel. J Clim 14:1337–1359. https://doi.org/10.1175/1520-0442(2001)014%3C1337:asotdf%3E2.0.co;2
Haarsma RJ, Selten FM, Weber SL, Kliphuis M (2005) Sahel rainfall variability and response to greenhouse warming. Geophys Res Lett 32:L17702. https://doi.org/10.1029/2005gl023232
Hawkins E, Smith RS, Gregory JM, Stainforth DA (2016) Irreducible uncertainty in near-term climate projections. Clim Dyn 46(11–12):3807–3819
Hewitt HT et al (2011) Design and implementation of the infrastructure of HadGEM3: the next-generation Met Office climate modelling system. Geosci Model Dev 4:223–253. https://doi.org/10.5194/gmd-4-223-2011
James R, Washington R, Jones R (2015) Process-based assessment of an ensemble of climate projections for West Africa. J Geophys Res Atmos. https://doi.org/10.1002/2014JD022513
Kang SM, Held IM, Frierson DMW, Zhao M (2008) The response of the ITCZ to extratropical thermal forcing: idealized slab-ocean experiments with a GCM. J Clim 21:3521–3532. https://doi.org/10.1175/2007jcli2146.1
Kitoh A, Endo H, Krishna Kumar K, Cavalcanti IFA, Goswami P, Zhou T (2013) Monsoons in a changing world: a regional perspective in a global context. J Geophys Res Atmos 118:3053–3065. https://doi.org/10.1002/jgrd.50258
Knight JR, Folland CK, Scaife AA (2006) Climate impacts of the Atlantic Multidecadal Oscillation. Geophys Res Lett 33:L17706. https://doi.org/10.1029/2006gl026242
Lavaysse C, Flamant C, Janicot S, Parker DJ, Lafore J-P, Sultan B, Pelon J (2009) Seasonal evolution of the West African heat low: a climatological perspective. Clim Dyn 33:313–330. https://doi.org/10.1007/s00382-009-0553-4
Lavaysse C, Flamant C, Janicot S (2010) Regional-scale convection patterns during strong and weak phases of the Saharan heat low. Atmos Sci Lett 11:255–264. https://doi.org/10.1002/asl.284
Lee J-Y, Wang B (2014) Future change of global monsoon in the CMIP5. Clim Dyn 42:101–119. https://doi.org/10.1007/s00382-012-1564-0
Lélé MI, Leslie LM, Lamb PJ (2015) Analysis of low-level atmospheric moisture transport associated with the west African Monsoon. J Clim 28:4414–4430. https://doi.org/10.1175/JCLI-D-14-00746.1
Liu Y, Chiang JCH, Chou C, Patricola CM (2014) Atmospheric teleconnection mechanisms of extratropical North Atlantic SST influence on Sahel rainfall. Clim Dyn 43:2797–2811. https://doi.org/10.1007/s00382-014-2094-8
Luo D, Xiao Y, Diao Y, Dai A, Franzke CLE, Simmonds I (2016) Impact of ural blocking on winter warm Arctic-Cold Eurasian Anomalies. Part II: the link to the north Atlantic Oscillation. J Clim 29:3949–3971
Luo B, Luo D, Wu L, Zhong L, Simmonds I (2017) Atmospheric circulation patterns which promote winter Arctic sea ice decline. Env Res Lett 12:054017
Madec G (2008) NEMO ocean engine. Note du Pole de modélisation, Institut Pierre-Simon Laplace (IPSL), France No 27, ISSN No 1288–1619. https://www.nemo-ocean.eu/wp-content/uploads/NEMO_book.pdf
Magnusdottir G, Saravanan R (1999) The response of atmospheric heat transport to zonally averaged SST trends. Tellus 51A:815–832
Mann ME, Park J (1996) Greenhouse warming and changes in the seasonal cycle of temperature: model versus observations. Geophys Res Lett 23:1111–1114. https://doi.org/10.1029/96gl01066
Mann ME, Cane MA, Zebiak SE, Clement A (2005) Volcanic and solar forcing of the tropical pacific over the past 1000 years. J Clim 18:447–456. https://doi.org/10.1175/jcli-3276.1
Martin ER, Thorncroft C, Booth BB (2014) The multidecadal Atlantic SST—Sahel rainfall teleconnection in CMIP5 simulations. J Clim 27:784–806. https://doi.org/10.1175/JCLI-D-13-00242.1
Massonnet F, Fichefet T, Goosse H, Bitz CM, Philippon-Berthier G, Holland MM, Barriat PY (2012) Constraining projections of summer Arctic sea ice. Cryosphere 6:1383–1394. https://doi.org/10.5194/tc-6-1383-2012
McCusker KE, Kushner PJ, Fyfe JC, Sigmond M, Kharin VV, Bitz CM (2017) Remarkable separability of circulation response to Arctic sea ice loss and greenhouse gas forcing. Geophys Res Lett 44:7955–7964. https://doi.org/10.1002/2017GL074327
Mohino E, Janicot S, Bader J (2011) Sahel rainfall and decadal to multi-decadal sea surface temperature variability. Clim Dyn 37:419–440. https://doi.org/10.1007/s00382-010-0867-2
Monerie P-A, Fontaine B, Roucou P (2012) Expected future changes in the African monsoon between 2030 and 2070 using some CMIP3 and CMIP5 models under a medium-low RCP scenario. J Geophys Res Atmos. https://doi.org/10.1029/2012JD017510 (D16111)
Monerie P-A, Roucou P, Fontaine B (2013) Mid-century effects of climate change on African monsoon dynamics using the A1B emission scenario. Int J Climatol 33:881–896. https://doi.org/10.1002/joc.3476
Monerie P-A, Biasutti M, Roucou P (2016a) On the projected increase of Sahel rainfall during the late rainy season. Int J Climatol. https://doi.org/10.1002/joc.4638
Monerie P-A, Sanchez-Gomez E, Boé J (2016b) On the range of future Sahel precipitation projections and the selection of a sub-sample of CMIP5 models for impact studies. Clim Dyn. https://doi.org/10.1007/s00382-016-3236-y
Nicholson SE (2013) The West African Sahel: a review of recent studies on the rainfall regime and its interannual variability. ISRN Meteorol 2013:32. https://doi.org/10.1155/2013/453521
Noilhan J, Mahfouf J-F (1996) The ISBA land surface parameterisation scheme. Global Planet Change 13:145–159
Noilhan J, Planton S (1989) A simple parameterization of land surface processes for meteorological models. Mon Weather Rev 117:536–549
Oudar T, Sanchez-Gomez E, Chauvin F, Cattiaux J, Terray L, Cassou C (2017) Respective roles of direct GHG radiative forcing and induced Arctic sea ice loss on the Northern Hemisphere atmospheric circulation. Clim Dyn 1–21. https://doi.org/10.1007/s00382-017-3541-0
Oudar T, Sanchez-Gomez E, Chauvin F. Intense wintertime Northern Hemisphere storm tracks response in the future climate: role of Arctic sea ice loss versus GHG increase. In preparation
Peings Y, Magnusdottir G (2014) Response of the wintertime northern hemisphere atmospheric circulation to current and projected Arctic Sea ice decline: a numerical study with CAM5. J Clim 27:244–264. https://doi.org/10.1175/JCLI-D-13-00272.1
Peyrillé P, Lafore J-P, Redelsperger J-L (2007) An idealized two-dimensional framework to study the west African monsoon. Part I: validation and key controlling factors. J Atmos Sci 64:2765–2782. https://doi.org/10.1175/JAS3919.1
Polo I, Ullmann A, Roucou P, Fontaine B (2011) Weather regimes in the Euro-Atlantic and Mediterranean sector, and relationship with West African rainfall over the 1989–2008 period from a self-organizing maps approach. J Clim 24:3423–3432. https://doi.org/10.1175/2011JCLI3622.1
Pu B, Cook KH (2010) Dynamics of the west African Westerly jet. J Clim 23:6263–6276. https://doi.org/10.1175/2010jcli3648.1
Roehrig R, Chauvin F, Lafore J-P (2011) 10-25-day intraseasonal variability of convection over the Sahel: A role of the Saharan heat low and midlatitudes. J Clim 24:5863–5878. https://doi.org/10.1175/2011JCLI3960.1
Rowell DP (2003) The impact of mediterranean SSTs on the Sahelian Rainfall Season. J Clim 16:849–862. https://doi.org/10.1175/1520-0442(2003)016%3C0849:tiomso%3E2.0.co;2
Salas Mélia D (2002) A global coupled sea ice–ocean model. Ocean Model 4:137–172. https://doi.org/10.1016/S1463-5003(01)00015-4
Sanchez-Gomez E, Cassou C, Ruprich-Robert Y, Fernandez E, Terray L (2016) Drift dynamics in a coupled model initialized for decadal forecasts. Clim Dyn 46:1819–1840. https://doi.org/10.1007/s00382-015-2678-y
Screen JA, Simmonds I (2010) The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 464:1334–1337. http://www.nature.com/nature/journal/v464/n7293/suppinfo/nature09051_S1.html
Screen JA, Simmonds I, Deser C, Tomas R (2013) The atmospheric response to three decades of observed Arctic sea ice loss. J Clim 26:1230–1248. https://doi.org/10.1175/JCLI-D-12-00063.1
Screen JA, Deser C, Smith D et al (2018) Consistency and discrepancy in the atmospheric response to Artic sea-ice loss across climate models. Nat Geosci 11:pages155–163 (2018). https://doi.org/10.1038/s41561-018-0059-y
Seager R, Naik N, Vecchi GA (2010) Thermodynamic and dynamic mechanisms for large-scale changes in the hydrological cycle in response to global warming. J Clim 23:4651–4668. https://doi.org/10.1175/2010JCLI3655.1
Serreze MC, Barry RG (2011) Processes and impacts of Arctic amplification: a research synthesis. Global Planet Change 77(1):85–96
Seth A, Rauscher SA, Biasutti M, Giannini A, Camargo SJ, Rojas M (2013) CMIP5 projected changes in the annual cycle of precipitation in monsoon regions. J Clim 26:7328–7351. https://doi.org/10.1175/JCLI-D-12-00726.1
Simmonds I (2015) Comparing and contrasting the behaviour of Arctic and Antarctic sea ice over the 35-year period 1979–2013. Ann Glaciol 56(69):18–28
Skinner CB, Ashfaq M, Diffenbaugh NS (2012) Influence of twentyfirst-century atmospheric and sea surface temperature forcing on West African climate. J Clim 25:527–542
Smith DM, Dunstone NJ, Scaife AA, Fiedler EK, Copsey D, Hardiman SC (2017) Atmospheric response to Arctic and Antarctic sea ice: the importance of ocean-atmosphere coupling and the background state. J Clim 30:4547–4565. https://doi.org/10.1175/JCLI-D-16-0564.1
Stine AR, Huybers P (2012) Changes in the seasonal cycle of temperature and atmospheric circulation. J Clim 25:7362–7380. https://doi.org/10.1175/JCLI-D-11-00470.1
Stroeve JC, Serreze MC, Holland MM, Kay JE, Malanik J, Barrett AP (2012) The Arctic’s rapidly shrinking sea ice cover: a research synthesis. Clim Change 110:1005–1027
Talento S, Barreiro M (2017) Control of the South Atlantic convergence zone by extratropical thermal forcing. Clim Dyn. https://doi.org/10.1007/s00382-017-3647-4
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteor Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Thorncroft CD, Blackburn M (1999) Maintenance of the African easterly jet. Q J R Meteorol Soc 125:763–786. https://doi.org/10.1002/qj.49712555502
Thorncroft CD, Nguyen H, Zhang C, Peyrillé P (2011) Annual cycle of the West African monsoon: regional circulations and associated water vapour transport. Q J R Meteorol Soc 137:129–147. https://doi.org/10.1002/qj.728
Ting M, Kushnir Y, Seager R, Li C (2009) Forced and internal twentieth-century sst trends in the north Atlantic. J Clim 22:1469–1481. https://doi.org/10.1175/2008jcli2561.1
Trenberth KE, Caron JM (2001) Estimates of meridional atmosphere and ocean heat transports. J Clim 14:3433–3443. https://doi.org/10.1175/1520-0442(2001)014%3C3433:EOMAAO%3E2.0.CO;2
Trenberth KE, Fasullo J (2007) Water and energy budgets of hurricanes and implications for climate change. J Geophys Res Atmos. https://doi.org/10.1029/2006jd008304
Valcke S, Craig T, Coquart L (2013) OASIS3-MCT User Guide OASIS3-MCT 2.0. CERFACS/CNRS SUC URA. https://oasis3mct.cerfacs.fr/svn/branches/OASIS3-MCT_3.0_branch/oasis3-mct/doc/oasis3mct_UserGuide.pdf
Villamayor J, Mohino E (2015) Robust Sahel drought due to the Interdecadal Pacific oscillation in CMIP5 simulations. Geophys Res Lett 42:1214–1222. https://doi.org/10.1002/2014gl062473
Voldoire A et al (2013) The CNRM-CM5. 1 global climate model: description and basic evaluation. Clim Dyn 40:2091–2121. https://doi.org/10.1007/s00382-011-1259-y
Wang G, Alo CA (2012) Changes in precipitation seasonality in West Africa predicted by RegCM3 and the impact of dynamic vegetation feedback. Int J Geophys. https://doi.org/10.1155/2012/597205
Zhang R, Delworth TL (2006) Impact of Atlantic multidecadal oscillations on India/Sahel rainfall and Atlantic hurricanes. Geophys Res Lett. https://doi.org/10.1029/2006gl026267
Acknowledgements
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modelling groups for producing and making available their model output. For CMIP the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. This work was supported by the EU-funded PREFACE (grant agreement 603521) project. We thanks Laure Coquart, Marie-Pierre Moine and Christophe Cassou from the Centre Européen de Recherche et de Formation Avancée en Calcul Scientifique (CERFACS), and Fabrice Chauvin from CNRM (Centre National de Recherches Météorologiques), which helped in the design of the experimental setup, experiments performing and data post-processing. We thank our two anonymous reviewers for their comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Monerie, PA., Oudar, T. & Sanchez-Gomez, E. Respective impacts of Arctic sea ice decline and increasing greenhouse gases concentration on Sahel precipitation. Clim Dyn 52, 5947–5964 (2019). https://doi.org/10.1007/s00382-018-4488-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4488-5