Abstract
The Hadley circulation (HC) has conventionally been considered as thermally direct with uniform zonal distribution. However, the meridional circulation in the tropics is far from uniform, including the thermally direct cells associated with the global monsoon heating and indirect cells in the absence of diabatic heating. This study aims at assessing the thermally direct and indirect cells in different regions, identifying the geographic sectors responsible for interannual variability of HC strength and boundaries, and unraveling the underlying mechanism for the interannual variability of HC edges and intensity. Results derived from ERA-Interim reanalysis and climate models show that the climatological HC in wintertime (December–January–February) obscures longitudinal diversity of regional meridional cells (RMC), including thermally direct RMCs over Eurasia and the Eastern Pacific, thermally direct southern limbs of RMCs over the Central Pacific and Western Atlantic with opposite circulation. For each of the regions, El Niño-South Oscillation and mid-latitude eddies are assessed in terms of their relative contributions to the interannual variability of HC intensity and extent. Their underneath physical mechanisms are thoroughly investigated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Hadley circulation (hereafter HC) is conventionally depicted as the dominant large-scale atmospheric circulation in the Earth’s tropics and subtropics, as described by a conceptual model with zonal average over the globe (Hadley 1735). It plays an important role in the transport and balance of fundamental climate variables, such as moisture, energy, and momentum. The intensity and extent of the HC have varied significantly over recent decades (Quan et al. 2004; Hu and Fu 2007; Gastineau et al. 2011; Sun et al. 2013), with very pronounced interannual variability.
An early attempt to understand the interannual variability of HC was reported in Oort and Yienger 1996 who used radiosonde data and pinpointed a strong connection to ENSO. Most recent studies have used reanalysis datasets to examine the seasonal cycle and interannual variability of the HC. For instance, a good agreement on the interannual variability of the annual mean HC was reported among multi-reanalysis datasets (Nguyen et al. 2013). But HC has pronounced seasonality (Dima and Wallace 2003), annual mean does not reveal its complete picture. A few other studies were reported to examine the interannual variability of a specific season (Tanaka et al. 2004; Stachnik and Schumacher 2011).
Sun et al. (2013) showed that there is a mode of HC interannual variability that is driven by ENSO, and this mode is thought to be linked with the interannual variability of HC strength associated with HC anomalies that are similar (opposite) to its mean state in the tropics (subtropics). Furthermore, Sun and Zhou (2014) investigated the behavior of HC in boreal summer. There are two prominent variability modes for the developing and decaying phases of El Niño, respectively. The interannual variabilities of its northern branch in both modes are largely under the control of the East Asian summer monsoon (EASM) variability, while that of its southern branch results from the atmospheric response to meridional shift of diabatic heating from the developing to decaying phases of El Niño (Sun and Zhou 2014). A series of recent studies have decomposed the HC variability into an equatorially asymmetric mode (ASM) and a symmetric mode (SM) in terms of variability of annual mean (Feng et al. 2015), boreal winter (Ma and Li 2008) and boreal summer HC (Feng et al. 2011). The ASM mainly responds to the SST warming over the Indo-Pacific warm pool and thus explains the long-term variability of HC (Feng et al. 2013), while the SM linked to ENSO is responsible for the interannual variability of HC (Ma and Li 2008).
By comparing the impacts of different meridional structure of tropical SST on annual mean HC, ASM and SM have been identified as the contrasting responses to equatorially asymmetric and symmetric meridional SST structures (Feng et al. 2016). It is also true when the responses of the HC to different meridional SST structures in the seasonal cycle are taken into account (Feng et al. 2017). A recent case study was reported in Feng and Li (2013) who investigated different impacts of two ENSO types (canonical ENSO and ENSO Modoki) on the interannual variability of HC in boreal spring. They revealed the important role of the meridional structure of sea surface temperature (SST) on the variation of HC. It has been reported that SST changes can also explain part of variability in HC strength and extent (Corvec and Fletcher 2017). The intensity of HC is proportional to SST gradient between the tropics and subtropics (Williamson et al. 2013), while the edges of HC are inversely proportional to meridional SST gradient (Adam et al. 2014).
A rich literature can also be found in developing theories and mechanisms to understand the dynamics of HC. Under the assumption of angular momentum conservation, Held and Hou (1980) provided a thermal model to explain successfully the HC behavior. But this early theory neglected completely the role of mid-latitude eddies in the dynamics of HC. The effect of eddies has been highlighted in the subsequent work (Held 2000), together with local Rossby number R0 used to measure the relative importance of thermal forcing and eddy forcing on HC (Schneider 2006).
ENSO and mid-latitude eddies both affect the HC strength (Oort and Yienger 1996; Walker and Schneider 2006), but a larger role is attributed to mid-latitude eddies for the interannual variability of HC strength in boreal winter (Caballero 2007; Caballero and Anderson 2009). ENSO can however strongly affect the interannual variability of the extent and boundaries of the HC in boreal winter, suggesting that the ENSO-induced meridional temperature gradient plays a key role in setting the edges of the HC. There is also an indirect effect of ENSO through ENSO-induced changes in mid-latitude eddies, as demonstrated by Guo and Li (2016) on the interannual variability of the northern HC edge.
After an overview of numerous studies on global-scale HC, it is necessary to emphasize that HC is decomposed of regional meridional cells (RMC) over a few geographic sectors. They are collectively responsible for HC strength and extents, and there is a rich longitudinal diversity in the tropics. We want to study the contributions from RMC of different sectors to HC. We should point out that the lack of adequate metrics to gauge the regional characteristics of HC increases the complexity and challenges to study the relationship between HC and RMC.
The thermally direct summer monsoon cells in some geographic sectors (e.g. East Asia) are of inverse sense to the climatological HC in the summer hemisphere (Northern Hemisphere) (Riehl et al. 1950). The interannual variability of RMC over EASM sector plays a dominant role in the interannual variability of the northern branch of the HC in boreal summer (Sun and Zhou 2014). However, there are no studies to assess the direct linkage between HC and the global monsoon circulation. Additionally, it remains unknown whether the thermal direct circulation in association with the southern hemispheric monsoon regimes also makes a reverse contribution to the southern Hadley cell in austral summer.
Most of these previous studies are based on the mass stream function (MSF) that strictly satisfies the mass conservation constraint. This is a powerful tool for diagnosing the zonally-averaged HC. However, it neglects the regional diversity of the tropical atmospheric circulation. The vertical shear of the meridional wind between 200 and 850 hPa (V200–V850) is also a good indicator for HC and to some extent can remedy the shortcomings of MSF. It has been widely used as an alternative measure of boreal winter HC in earlier studies to depict the climatology of zonal HC (Oort and Yienger 1996; Quan et al. 2004), the interannual variation of HC related to ENSO (Oort and Yienger 1996; Sun et al. 2013), and the strengthening trend of HC related to the interdecadal intensification of ENSO amplitude (Quan et al. 2004). A recent study has used V200-V850 to separate regions where the HC is reinforced (i.e., the features are “Hadleywise”) from those where the HC is weakened (i.e., they are “anti-Hadleywise”) and highlighted the dynamics of the HC and its inextricable linkage to subtropical drying in a future scenario (Karnauskas and Ummenhofer 2014). In addition, a very recent study has attempted to investigate the regional variability of the extent of the HC in the Southern Hemisphere by calculating the stream function via the vertical integral of the divergent meridional wind (Nguyen et al. 2017). The strengthening trend of the HC in boreal winter has also been validated from the perspective of the velocity potential (Zhou et al. 2016). However, the stream function and velocity potential are obtained from the incompressible and irrotational components of air flow, respectively. Obviously, neither includes full details of the horizontal wind and may not give a complete description of the regional diversity of the HC (Sun et al. 2017). Moreover, there are increasing attempts to depict features of monsoon circulation using regional MSF via a direct integral of zonally averaged meridional wind over the specific monsoon sector (Bordoni and Schneider 2008; Toma and Webster 2010; Jayakumar et al. 2013; Walker et al. 2015). Out of consideration above, in the present paper we attempt to study the longitudinal diversity of RMC within global monsoon domains by calculating the MSF over specific sectors from the original wind fields and scaled by multiplying the coefficient \(\frac{{\Delta \theta }}{{2\pi }}\) (Δθ is longitudinal range of each sector) (Zhang and Wang 2015).
Given the general context and state-of-the-art for HC, firstly we would like in the present study to focalize on the longitudinal diversity of RMCs within different monsoon domains. We are not only interested in long-term mean climatology, but also the interannual variability of HC (intensity and its southern and northern edges) and the associated RMC in each sector. Secondly, we would like to qualitatively assess the relative contribution of ENSO and mid-latitude eddies in each sector on HC edges and intensity at interannual time scale. Finally, our aim is also to assess the performance of models forced by realistic SST in reproducing the interannual variability of HC and its connection to that of RMC within each global monsoon sector.
Due to the expected strong influence of monsoon on HC, transition seasons (spring and autumn) are not our ideal choice. But the boreal winter provides a good case. Moreover, ENSO usually reaches its strongest amplitude during boreal winter (December–January–February, DJF). Finally selecting boreal winter also offers us the possibility of comparison with previous work (Caballero 2007; Ma and Li 2008; Caballero and Anderson 2009).
This paper is organized as follows. Descriptions of the data and methodology are presented in Sect. 2. Section 3 gives the main results and a summary and conclusions are provided in Sect. 4.
2 Data and methodology
2.1 Reanalysis datasets and model simulation
We first evaluate the consistency of four reanalysis datasets in depicting the climatology of HC and its interannual variability. They are (1) the NCEP/NCAR Reanalysis (NCEP1) (Kalnay et al. 1996), (2) the NCEP–DOE AMIP-II Reanalysis (NCEP2) (Kanamitsu et al. 2002), (3) ERA-Interim, one of the latest generation of atmospheric reanalyses produced by the European Centre for Medium-Range Weather Forecasts (ECMWF), with a higher horizontal resolution of 1.25° × 1.25° (Dee et al. 2011), and (4) the Japanese 25-year Reanalysis (JRA25) obtained from the Japan Meteorological Agency (JMA) (Onogi et al. 2007).
In general, the four reanalyses are consistent. Throughout the paper, we use the ERA-Interim reanalysis to demonstrate the diversity of HC climatology and the implications for HC intensity and edges, except where multi-reanalyses are used to confirm the differences in the HC strength and extent in each of the four geographic sectors (Table 2).
We also examine model performance on simulating HC behavior using the Atmospheric Model Intercomparison Project (AMIP) simulations involved in the Coupled Model Intercomparison Project phase 5 (CMIP5) (Table 1). The multi-model ensemble (MME) is used to evaluate model performance, despite the fact that MME tends to reduce the variance and overestimate correlation, compared with each single model (Knutti et al. 2009).
2.2 Methodology
2.2.1 Mass stream function
The meridional–vertical MSF is an important metric of the HC (Oort and Yienger 1996). The MSF can be easily obtained via a mass-weighted vertical integral of the zonal mean meridional velocity. In spherical coordinates, the MSF, Ψ, at each pressure level, p, and latitude, \(\theta\), can be expressed as:
where a is the Earth’s radius, g the gravitational acceleration, and \(\bar {V}\) the zonal mean meridional velocity. For mass conservation, the zonal mean meridional velocity and vertical motion (\(\bar {\omega }\)) must satisfy:
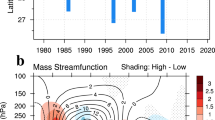
We should keep in mind that \(\bar {V}\) (\(\bar {\omega }\)) has the same (opposite) sign as \(\frac{{\partial {{\Psi}}}}{{\partial p}}\)\(\left( {\frac{{\partial {{\Psi}}}}{{\partial \theta }}} \right)\). By examining the climatology of the MSF (Fig. 1), it is clear that the MSF can depict the thermodynamic circulation, characterized by ascending motion near the equator \(\left( {\bar {\omega }\sim - \frac{{\partial {{\Psi}}}}{{\partial \theta }}<0} \right)\) and descending motion in the subtropics \(\left( {\bar {\omega }\sim - \frac{{\partial {{\Psi}}}}{{\partial \theta }}>0} \right)\) as well as poleward flow \(\left( {{\text{southerlies}}{:}\,\bar {V}\sim \frac{{\partial {{\Psi}}}}{{\partial p}}>0\;\;{\text{or}}\;\;{\text{northerlies}}{:}\,\bar {V}\sim \frac{{\partial {{\Psi}}}}{{\partial p}}<0} \right)\) at upper levels and equatorward flow \(\left( {{\text{northerlies}}{:}\,\bar {V}\sim \frac{{\partial {{\Psi}}}}{{\partial p}}<0\;\;{\text{or}}\;\;{\text{southerlies}}:\bar {V}\sim \frac{{\partial {{\Psi}}}}{{\partial p}}>0} \right)\) near the surface. The strength of the HC is defined by the maximum MSF between 30°S and 30°N (Oort and Yienger 1996). The edge of the HC in each hemisphere is defined as the latitudinal position where the value of MSF at 500 hPa is zero in the subtropics.
Climatological boreal winter (December–January–February, DJF) mass stream function (MSF, units: 1010 kg s−1, contour interval 2 × 1010 kg s−1) and vertical shear of meridional velocity between 200 and 850 hPa (i.e., V200 minus V850, units: m s−1) in ERA-Interim reanalysis (upper panels) and the multi-model ensemble mean (MME, lower panels) of AMIP-type simulations. The green arrows indicate the air flow direction of the HC in each hemisphere
2.2.2 Decomposition of the variability in HC strength and extent
Caballero (2007) emphasized the dominant role of mid-latitude eddies in driving the interannual variability of HC in boreal winter, by assessing the relative contributions of ENSO and non-ENSO variability to the total variance of winter hemisphere HC intensity (\(\Psi\)) over the period 1959–2001. He partitioned the detrended \(~{\Psi ^N}\) (N denotes Northern Hemisphere) into two components:
where \(\Psi _{e}^{N}\)is the linear regression of \(~{\Psi ^N}~\) on the El Niño 3.4 index (ENSO variability) and \(\Psi _{r}^{N}\) is an uncorrelated residual (non-ENSO variability referred to as mid-latitude eddy activity). Here we use the same method to evaluate the relative importance of ENSO and mid-latitude eddies in the interannual variability of HC intensity in the Northern Hemisphere and of the HC edge in each hemisphere over 30 years (1979–2008).
2.2.3 Wave activity flux and diabatic heating
Wave activity flux is used to track the source of mid-latitude eddies and their propagation from sources to sinks, which is a powerful tool (e.g. see Plumb 1985) to diagnose the impact of mid-latitude stationary waves on regional Hadley cells (Caballero and Anderson 2009). We calculate wave activity flux based on 6-hourly output of ERA-Interim reanalysis. This procedure is repeated for individual model simulations based on daily data before taking the MME average.
To understand thermal control of ENSO on HC intensity, diabatic heating estimated as a residual in the thermodynamic equation (Nigam et al. 2000) is calculated based on 6-hourly frequency of ERA-Interim reanalysis, and daily output for each model before MME average.
3 Results
3.1 Climatology of HC and inhomogeneous distribution of RMCs
We first examine the climatology of the HC in boreal winter and how its structure varies with longitude. Figure 1a, b depict the mean state of the HC in the ERA-Interim reanalysis based on the MSF and the vertical shear of meridional velocity (defined as V200 minus V850, V200–V850). The positive (negative) contours in Fig. 1a indicate clockwise (anticlockwise) circulation in the Northern (Southern) Hemisphere. Likewise, the positive and negative values of V200–V850 can distinguish clockwise motion in the Northern Hemisphere from anticlockwise in the Southern Hemisphere (Fig. 1b). Both panels reveal an obvious asymmetry of HC between the summer and winter hemispheres (Fig. 1a, b). The Hadley cell in the Northern Hemisphere (NHC) is much stronger and wider than that in the Southern Hemisphere (SHC).
Similarly, we can use MSF and V200–V850 to evaluate the performance of state-of-the-art climate models in simulating the HC in boreal winter. Under realistic SST forcing, the MME can reproduce reasonably well the hemispheric asymmetry of the strength and extent of HC (e.g., a much stronger and “fatter” NHC in the winter hemisphere than SHC in the summer hemisphere) (Fig. 1c, d).
It is important to keep in mind that the MSF is deduced from the vertical integral of zonal mean meridional velocity, and thus limits further insight into the horizontal distribution of the HC. Fortunately, V200–V850 performs well in representing the climatology of zonal HC and offers an opportunity to investigate longitudinal distributions of RMC and resultant climatology of HC (Fig. 2). Obviously, the RMC (Fig. 2a, contours) is far from zonally uniform as demonstrated by a comparison of the zonal mean V200–V850 with its horizontal distribution (Fig. 2b). The inhomogeneous RMCs across longitudes are of two types: one has almost the same features as the climatological zonal-mean HC in each hemisphere, as seen in the RMC over Eurasia (30°S–30°N, 30°W–155°E; RMC-EA) and the Eastern Pacific (30°S–30°N, 130°W–70°W; RMC-EP); the other has a spatial pattern in the Northern and Southern hemispheres almost opposite to the climatology of NHC and SHC, as in the RMCs over the Central Pacific (30°S–30°N, 155°E–130°W; RMC-CP) and the Western Atlantic (30°S–30°N, 70°W–30°W; RMC-WA). Therefore, the RMC-EA and RMC-EP both play a fundamental role in maintaining the climatological zonal-mean HC in boreal winter, while RMC-CP and RMC-WA act to oppose the climatology.
Interannual standard deviation of the HC in the ERA-Interim reanalysis and MME simulation (color shading), illustrated by the MSF (units: 1010 kg s−1) and V200–V850 (units: m s−1, contour interval: 0.25 m s−1) in comparison with the corresponding climatological distributions (contours). Rectangles in b indicate the different regional meridional cells (RMCs) along the geographic sectors, including RMCs with appearance similar to HC (red solid rectangles) and opposite to that of HC (blue dashed rectangles). The extent of each rectangle in the following plots is same as that presented here
Examining the spatial patterns of MSF and V200–V850 in the MME simulation reveals that the longitudinal diversity of RMCs presented in ERA-Interim and their associated distinct roles in the climatology of HC can be captured by state-of-the-art climate models (contours, Fig. 2c, d).
3.2 Decomposition of RMCs into thermally direct and indirect cells
The RMCs in the four geographic sectors show different contributions to the climatology of the HC. Traditionally the HC has been thought of as a thermally direct zonal-mean circulation. Here it may raise a question whether the RMCs are thermally direct cells with uniform distribution. The longitudinal diversity of RMCs consists of thermally direct monsoon cells and thermally indirect meridional cells. Figure 3a shows the spatial distributions of RMCs and diabatic heating in global monsoon (GM) domains. RMCs within GM domains are associated with monsoonal heating and thus they are thermally direct cells, including large resemblance of RMC over the African–Asian–Australian monsoon (RMC-EA) and the North American monsoon (RMC-EP) as the climatological HC, and RMC of signs opposite to climatological SHC over the South American monsoon (the southern limb of RMC-WA) and the pure oceanic monsoon-like region (OM) where there is no land–sea thermal contrast (southern limb of RMC-CP) (Liu et al. 2009). In contrast, the northern limbs of RMC-CP and RMC-WA in the absence of monsoon like heating are thermally indirect cells (counterclockwise circulation).
a A simple diagram drawn to reveal the relationship between the spatial distributions of RMCs over four geographic sectors and global monsoon (GM) domains (black dots) based on GPCP precipitation data. The vectors show the climatological wintertime atmospheric circulation at 850 hPa derived from ERA-Interim reanalysis data. The shaded areas indicate summertime diabatic heating (units: K day−1) in each hemisphere (boreal summer: May to September; austral summer: November to March); b Taylor diagram to evaluate the performance of climate models participating in CMIP5 and the consistency of the HC in three widely used reanalyses with the HC in ERA-Interim (REF)
RMCs in ERA-Interim show a longitudinal diversity within the meridional sectors of GM domains. By examining the horizontal distributions of V200–V850 in the MME simulation (contours, Fig. 2c, d), we can see that MME captures the decomposition of RMCs into thermally direct and indirect cells associated with the presence and absence of monsoonal heating within the different meridional sectors of the GM domains.
3.3 Interannual variability of HC and longitudinal diversity of RMCs variability
If we examine the interannual standard deviation of the MSF in ERA-Interim (Fig. 2a, shading), HC exhibits prominent variability in the tropics (15°S–10°N) with a larger standard deviation for NHC than for SHC. The interannual variability of RMCs is not zonally uniform as shown by the interannual standard deviation of V200–V850 in ERA-Interim (Fig. 2b, shading). RMC-CP has much stronger variability in the tropics of both the Northern and Southern hemispheres. The RMC shows strong interannual variability extending from the northern subtropics of WA sector to that of EA. Besides, the relatively weak variability of RMC also can be seen in the southern subtropics of geographic sectors extending from EP to EA.
The MME has the capability of reproducing interannual variations of HC and longitudinal diversity of RMC (Fig. 2c, d, shading). For instance, the simulated prominent variability of HC in the tropics (15°S–10°N) (Fig. 2c, shading), and the remarkable variability of RMC at the poleward limit of NHC and SHC are all comparable to ERA-Interim (Fig. 2d, shading). Nevertheless, there is an evident inter-model spread in the magnitude of HC variability, with a systematic weaker variability of HC in CMIP5 models than in ERA-Interim (Fig. 3b).
3.4 Inhomogeneity of climatological RMC and its variability: results from regional MSF
The interannual standard deviation of V200–V850 is helpful to obtain a qualitative understanding of the inhomogeneity of RMC and its variability. It is necessary to further validate those results by calculating the MSF over the meridional sectors of GM domains. Figure 4 shows the climatology of MSF in each sector and its interannual standard deviation in ERA-Interim and MME simulation. The climatological features of RMC-EA and RMC-EP have a large resemblance to the climatology of HC (Fig. 4a, b, contours). In contrast, the spatial patterns of RMC-CP and RMC-WA are almost inverse, compared to the climatology of HC, associated with a clockwise circulation in the Southern Hemisphere and a counterclockwise one in the Northern Hemisphere (Fig. 4c, d, contours). These features are well consistent with the results derived from V200–V850 (Fig. 2a, b, contours). Besides, the thermally direct and indirect cells of RMCs can be seen more clearly from regional MSF. The thermally direct cells associated with monsoonal heating are “Hadleywise” over EA and EP sectors and “anti-Hadleywise” in the southern parts of CP and WA sectors. The “anti-Hadleywise” features in the northern parts of CP and WA sectors are thermally indirect cells due to the absence of monsoon like heating.
Regional characteristics of the HC during boreal winter in ERA-Interim reanalysis data (left panels) and the MME simulation (right panels), as demonstrated by interannual standard deviations of RMCs over four geographic sectors (color shading, units: 1010 kg s−1). Contours (units: 1010 kg s−1) indicate the corresponding climatological mean RMC in each sector
As for the interannual variation of RMCs, the standard deviations of MSF in the four sectors are of distinct spatial patterns in terms of magnitude and position of RMC variability (Fig. 4a–d, shading). The RMC-EA has strong variability at the poleward limit of the NHC, and weaker variability in the northern tropics and at the poleward limit of the SHC (Fig. 4a, shaded areas). Compared with other RMCs (Fig. 4a, b, d, shaded areas), RMC-CP has the strongest variability in the tropics of both hemispheres (Fig. 4c, shaded areas). Meanwhile, RMC-EP also exhibits remarkable variability in the tropics of both hemispheres (Fig. 4b, shaded areas). Unlike the symmetric distributions of RMC-EA and RMC-CP variability, RMC-WA has one center of variability in the Northern Hemisphere [10°N–20°N], and two in the Southern Hemisphere [35°S–20°S and 15°S–5°S] (Fig. 4d, brown and yellow shading).
In MME simulation, the thermally direct cells calculated as MSF over EA and EP sectors have the typical features of the climatological HC (Fig. 4e, f, contours). The meridional stream function obtained from the CP (WA) sector is almost opposite to the typical distribution of HC climatology, associated with a thermally direct (indirect) cell in the Southern (Northern) Hemisphere of each sector (Fig. 4g, h, contours). The different features of climatological RMCs over the four sectors are in good agreement with ERA-Interim. Besides, the variability pattern of each RMC in MME simulation has a comparable distribution in ERA-Interim (Fig. 4e–h, shading), despite a much weaker magnitude of each RMC variability in MME simulation than in ERA-Interim. This is partly due to the reduction in MME variance caused by the averaging operation.
3.5 Links in interannual variability of the HC and RMCs
3.5.1 Dominant modes of HC and RMCs
In the previous section the interannual variability of HC and longitudinal diversity of RMCs were examined in ERA-Interim and MME. To further demonstrate the variability of HC and its links to RMC, an empirical orthogonal function (EOF) analysis is applied to both the zonal-mean MSF and to the regional MSF (Zhang and Wang 2015). The leading modes (EOF-1) of the HC and of the four RMCs are shown in Figs. 5 and 6, respectively. Time series of the principal component (i.e., PC-1) of HC and RMCs are also shown in Fig. 5c (ERA-Interim) and Fig. 5d (MME). We choose the sign convention for the EOF so that the patterns are similar for ERA-Interim and MME (Figs. 5, 6). For the sake of convenience, we only depict the spatial structures of HC and RMCs and their relationship during the positive phase.
(Left panels) The leading mode (EOF-1) of interannual variation of the zonal-mean HC meridional stream function in DJF (shading, arbitrary units), superimposed over the mean HC (contours, units: 1010 kg s−1). (Right panels) Time series of the corresponding principal component (PC-1) derived from ERA-Interim reanalysis and the MME simulation, together with time series of EOF-1 in each RMC sector
As the left panels in Fig. 5, but for the leading EOF patterns for the RMCs in the four geographic sectors
In both ERA-Interim (Fig. 5a) and MME (Fig. 5b), there is one thermally direct anomalous cell in the tropics and one indirect anomalous cell in the subtropics of the Northern Hemisphere, which correspond to the ascending and descending motions of the NHC in the tropics and subtropics. The thermally direct cell in the northern tropics is of similar pattern as shown in the recent work of Guo and Li (2016) and of intermediate pattern between ASM and SM (Ma and Li 2008). For instance, the southern extent of this anomalous cell (approximately at 5°S) in Fig. 5a is narrower than ASM (approximately at 10°S) and wider than SM (near the equator). The differences between the present and previous works largely result from the different influences of mid-latitude eddies and ENSO on the behaviors of HC. The spatial pattern associated with mid-latitude eddies is asymmetric about the equator and shows typical features of climatological HC (approximately at 10°S, see Caballero 2007). In contrast, the spatial pattern associated with ENSO is generally symmetric about the equator (Ma and Li 2008). Therefore, the combined constraints of mid-latitude eddies and ENSO on the interannual variability of HC could be responsible for the southern extent of this anomalous cell of the intermediate latitudinal position between mid-latitude eddies- and ENSO-related patterns.
In addition, there is one thermally direct anomalous cell in the southern tropics and a much weaker indirect cell in the southern subtropics. Following the MSF-based definitions of HC (Oort and Yienger 1996; Hu and Fu 2007), such anomalous cells in the tropics and subtropics directly affect the HC intensity and boundaries, resulting in a stronger and narrower HC during boreal winter.
The structure of the leading mode of RMC-EA variability is generally the reverse of its climatology (Fig. 6a). As a consequence, the thermally direct RMC is weakened over the EA sector, which tends to reduce the global HC. Furthermore, a pronounced counterclockwise anomalous cell in the northern subtropics stretches the NHC edge toward the equator. The leading mode of RMC-EP also opposes its climatology in both hemispheres. Therefore, the thermally direct RMC is also weakened over the EP sector (Fig. 6b). RMC-CP shows the most prominent mode, with a stronger anomalous cell in each hemisphere (Fig. 6c). This implies that RMC-CP contributes directly to the strength of the global HC. RMC-WA has a similar leading mode to RMC-EP, with slightly weaker cells in its spatial pattern (Fig. 6d).
By examining the temporal evolution of dominant HC and RMCs modes (Fig. 5c), we found that the interannual variability of HC is generally synchronous with that of RMCs. This result indicates that the leading mode of global HC is strongly linked to the modes of individual RMCs. In contrast to leading HC mode (Fig. 5a), the variability of the RMC in the CP sector plays a dominant role in modulating the thermally direct anomalous cells of the two hemispheres, contributing to a stronger global HC, while the variability modes in the other sectors play a dominant role in the anomalous subtropical cell that contributes to a narrower HC. The MME can reproduce the leading mode of HC (Fig. 5b) and the modes of RMCs in the four sectors (Fig. 6e–h). For instance, the MME can capture the reversed modes of RMC-EA and RMC-EP, which imply a reduction of global HC (Fig. 6e, f). The leading mode of RMC-CP in MME also exhibits a prominent variability similar to that of ERA-Interim (Fig. 6g). The leading mode of RMC-WA, which is close to its climatology in the tropics, is also well reproduced in MME (Fig. 6h).
3.5.2 Regional atmospheric circulation associated with leading modes of RMCs
In this section, we depict the regional atmospheric circulation directly relevant to the RMC variability. Figure 7 shows the regressions of the surface wind vector at 850 hPa onto the time series of each leading PC. A generally weakening of RMC-EA in ERA-Interim can be identified that is linked to an anomalous anticyclone over the Northwestern Pacific (NWPAC) and an anomalous anticyclone over the tropical Southern Indian Ocean (TSIOAC). The meridional components of wind anomalies on the left flank of the NWPAC and the TSIOAC reduce the northern and southern limbs of RMC-EA. The southerly winds in the Northern Hemisphere and northerly winds in the Southern Hemisphere result in a weakening of the North American winter monsoon and a reduction of the southern limb of the RMC-EP. In contrast, the southerly and northerly winds in the WA sector are different, which leads to an overall increase of RMC-WA, since there is a strengthening of the northern limb of RMC-WA and an increase of the South American summer monsoon circulation. The northerly winds in the Northern Hemisphere and southerly winds in the Southern Hemisphere meet near the equator in the CP sector, generating strong convergence and thus strengthens both the northern and southern limbs of the HC.
Regional circulation characteristics associated with the leading modes of RMCs (vectors) and their connections to ENSO (colors) in ERA-Interim (left panels) and MME (right panels). Plotted are the regressed surface wind vectors at 850 hPa (above the 5% significance level) and regressed SST pattern (above the 1% significance level)
The MME captures the overall decrease of RMC-EA, since there is a general weakening of the Asian–African–Australian monsoon circulation. However, there is a strong model bias of cyclonic anomalies over the mid-latitude ocean in the Southern Hemisphere. This model bias is largely associated with a general overestimate of diabatic heating in the southern mid-latitude of the EA sector (Fig. 12d). The MME also reproduces the weakened RMC-EP with a weaker limb in the Southern Hemisphere and a weakened North American winter monsoon in the Northern Hemisphere. The simulated strong convergence near the equator in the CP sector is comparable to that seen in ERA-Interim. The general increase of RMC-WA in ERA-Interim that results from southerly winds in the Northern Hemisphere and northerly winds in the Southern Hemisphere is also well reproduced in the MME.
3.5.3 Different roles of RMCs on HC strength and edges
As discussed above, the leading mode of the HC has a strong expression in both HC strength and extent, giving either a stronger and narrower HC or a weaker and broader HC. Moreover, the leading mode of HC is certainly associated with RMC variability over the four sectors. Here we calculate the correlation coefficients to further clarify the ties between each RMC and NHC intensity (NHCI) as well as the relationship between each RMC and the extent of the NHC and SHC (i.e., NHCE and SHCE).
As shown in Table 2a, the leading mode of HC is certainly a good indicator of NHCI variability, since positive correlation coefficients are obvious for the four reanalysis datasets and MME simulation (statistically significant at the 1% level). Meanwhile, NHCI also shows significant positive correlation with RMC-EP, RMC-CP and RMC-WA and generally insignificant correlation with RMC-EA (with the exception of NCEP2 and MME). Given that the temporal evolution of HC mode is generally synchronous with that of RMCs, the signs of the HC mode over the tropics with that of the four RMC modes are compared to identify the dominant sector responsible for NHCI (Figs. 5, 6). Result shows that only the positive correlation between NHCI and RMC-CP can ensure the leading role of the HC mode in NHCI. That is, RMC-CP plays a dominant role in the interannual variability of NHCI. Likewise, we can identify WA and EA as the dominant sectors whose RMCs determine the interannual variability of NHCE. EP, WA and EA are the geographic sectors whose RMCs are most related to the interannual variability of SHCE.
3.6 Mechanisms controlling the HC strength and extent
Two mechanisms are proposed to understand the variability of HC strength and extent. One is related to ENSO and the other to mid-latitude eddies. ENSO is the most prominent mode of tropical climate variability on interannual time scales. It exerts a significant impact on the atmospheric circulation at global and regional scales (Ropelewski and Halpert 1987). Atmospheric eddies are characterized by large-scale Rossby wave perturbations at mid-latitudes that may propagate into the tropics and affect the HC extent. In this section, we aim to assess the relative importance of these two proposed mechanisms on NHCI and extent of HC in each sector.
3.6.1 On the relative role of ENSO and mid-latitude eddies
To qualitatively assess the relative contribution of ENSO and mid-latitude eddies, we first calculate the regression of MSF and MSF in each sector onto \({{\Psi}}_{e}^{N}\) and \({{\Psi}}_{r}^{N}\), and then compare the regression patterns.
The regression pattern of NHCI for mid-latitude eddies (\({{\Psi}}_{r}^{N}\)) has a spatial structure comparable to its climatology (Fig. 8a), while that related to ENSO (\({{\Psi}}_{e}^{N}\)) has a structure close to the leading mode of HC (Fig. 8b). The mid-latitude eddies can explain a large fraction of the total variance of NHCI (74%). ENSO explains only 26%. Figure 8c, d display the regression patterns of the CP sector’s RMC onto \({{\Psi}}_{r}^{N}\) and \({{\Psi}}_{e}^{N}\). It is clear that both ENSO and mid-latitude eddies drive the interannual variability of NHCI in boreal winter.
Regression of MSF anomalies in ERA-Interim onto a\({{\Psi}}_{r}^{N}~\), b\({{\Psi}}_{e}^{N}~\)and regression of regional MSF anomalies (CP sector) in ERA-Interim onto c\(~{{\Psi}}_{r}^{N}\) and d\({{\Psi}}_{e}^{N}\). The right panels show results from MME. The dotted areas indicate where regression coefficients are significant at the 5% level (red: positive values and blue: negative values)
In addition, an eddy-relevant regression pattern over the EA sector is similar to the climatology of NHC (not shown), but with low significance. This result indicates a possible contribution from mid-latitude eddies via the EA sector into the NHCI. We still do not fully understand this behavior, but a composite analysis of V200–V850 (Fig. 9) can give us some hints. The composite of V200–V850 also shows dominant influences of both ENSO and mid-latitude eddies through the CP sector on NHCI (Fig. 9a, b), which is consistent with previous regression patterns shown in Fig. 8c, d. In contrast, the composite of V200–V850 over the EA sector has different features between ENSO and eddy cases. A significantly weakening of RMC during ENSO events is seen in both hemispheres [30°S–30°N, 60°–120°E], while a significant strengthening of RMC during eddy cases is seen in the Northern Hemisphere [0°–30°N, 0°–60°E], associated with a significant decrease of RMC over the Northwestern Pacific. The weakening of RMC over the Northwestern Pacific would, to some extent, counteract the strengthening of RMC in the Northern Hemisphere, which could be responsible for the regression pattern related to \({{~{\Psi}}}_{r}^{N}\) over the EA sector: resemblance to the climatology of NHC, but statistically insignificant.
Composite analysis of V200–V850 (units: m s−1) in ERA-Interim between a El Niño and La Niña events, b between strong and weak eddy cases. Dotted areas denote significance at 5% level. c, d Same as a, b, but for the MME simulation. The selected ENSO events follow the criterion of Welhouse et al. (2016). The criterion for strong-eddy cases is years with \({{\Psi}}_{r}^{N}>0.75~\sigma\) and \({{\Psi}}_{r}^{N}< - 0.75\sigma\) for weak-eddy cases. \({\varvec{\upsigma}}\) is the standard deviation of \({{\Psi}}_{r}^{N}\)
Figure 8e to h display the counterpart of ERA-Interim in MME simulation. The pattern related to mid-latitude eddies in the MME shows an overall increase of NHC like in ERA-Interim (Fig. 8e), while the simulated regression pattern related to ENSO has a symmetric structure about the equator as seen in ERA-Interim (Fig. 8f). Moreover, the predominance of the ENSO and mid-latitude eddy effect on NHCI are also seen in the CP sector in the regression patterns and the composite of V200-V850 (Figs. 8g, h, 9c, d). Nevertheless, ENSO explains a larger part of the total variance in NHCI (57%) than do the mid-latitude eddies (43%) in the MME. The proportion is reversed in ERA-Interim. The role of ENSO in driving NHCI is thus overestimated in MME. The underestimate of eddy’s role in NHCI in MME can also be seen in the composite of V200–V850 (Fig. 9d) showing especially a remarkable underestimate of the strengthening role of eddies in Northern Africa (0°–30°N, 0°–60°E).
A linear regression is also used to assess the relative role of ENSO and mid-latitude eddies on the extent of the HC in the two hemispheres. The time series of NHCE related to ENSO and to mid-latitude eddies are both positively correlated with NHCE in ERA-Interim, with correlation coefficients of 0.43 and 0.90 (significant at the 1% level), respectively. These statistically significant relations can also be seen in the northern subtropics for the regression patterns of HC against mid-latitude eddies and ENSO (Fig. 10a, b). Furthermore, the EA sector is identified as the main sector where mid-latitude eddies have significant influence on the interannual variability of wintertime NHCE (Fig. 10c), while WA is identified as the main sector where ENSO exerts its significant impact on the interannual variability of NHCE in boreal winter (Fig. 10d). Besides, it is important to note that mid-latitude eddies explain 82% of the total variance of NHCE and ENSO only 18%. Therefore, the meridional propagation of mid-latitude eddies through EA into the tropics plays a fundamental role in the interannual variability of NHCE, while ENSO plays a secondary role.
As Fig. 8, but for the regression patterns derived from the variation of NHCE, used to highlight the distinctive roles of ENSO and mid-latitude eddies in the variation of NHCE
In the MME, the ENSO-related regression pattern and that for mid-latitude eddies in the northern subtropics (Fig. 10e, f) are both comparable to those in ERA-Interim (Fig. 10a, b). However, in MME there is a general underestimation of the role of mid-latitude eddies in NHCE, with the fraction of total variance decreasing to 48%, smaller than that explained by ENSO (which increases to 52%). This reverse is largely associated with the dominant influence of ENSO on NHCE in the MME simulation evident through the EA sector (Fig. 10g). WA has been identified as one sector where ENSO plays the significant role on NHCE (Fig. 10h), and this is consistent with ERA-Interim.
Similarly, variability in SHCE also results from variations in both mid-latitude eddies and ENSO (Fig. 11a, b: ERA-Interim). Mid-latitude eddies and ENSO explain 61 and 39% of the total variance, respectively. Both EP and WA are identified as the main sectors where mid-latitude eddies in the Southern Hemisphere play the dominant role in the interannual variability of SHCE (Fig. 11c, d: ERA-Interim). If we compare the eddy-related regression pattern shown in Fig. 11a with that of the EP and WA sectors, the significant areas in the southern subtopics of the EP sector shift southward to south of 35°S. The regression pattern of the WA sector is generally insignificant with maximum shifting northward to north of 35°S. Nevertheless, the combined effects of regression patterns over EP and WA may contribute to the significant regression pattern in the southern subtropics (Fig. 11a).
As Fig. 10, but for regression patterns with SHCE, used to highlight the distinctive roles of ENSO and mid-latitude eddies in the variation of SHCE
It is important to note that SHCE, determined by the zero-MSF position at 500 hPa, is insignificantly correlated with RMC-EA (ERA-Interim: Fig. 11e) and its leading mode (Table 2). However, 500 hPa is not necessarily the correct pressure level on which to define the HC edge by the zero-MSF contour (Hu et al. 2011). Moreover, SHCE is significantly related to RMC-EA in most parts of the southern subtropics. In this sense, EA remains a sector where ENSO can exert an impact on SHCE (ERA-Interim: Fig. 11e). In general, SHCE varies in phase with RMC-EP and RMC-WA and EA.
In the MME simulation, mid-latitude eddies and ENSO contribute equally to the SHCE variance (Fig. 11f, g). The mid-latitude eddy-dominant sector EP (Fig. 11h) and the ENSO-dominant sector EA (Fig. 11j) show very similar regression patterns in the southern subtropics as those in ERA-Interim (Fig. 11c, e). However, the regression pattern of the WA sector related to mid-latitude eddies (Fig. 11i) does not match well its counterpart in ERA-Interim (Fig. 11d).
3.6.2 Mechanisms of ENSO and mid-latitude eddies on HC edges and its intensity
In previous section, by means of linear regression. we assessed the relative contribution of ENSO and mid-latitude eddies in each sector to the interannual variability of NHCI and HC edges. It remains necessary now to unravel their physical mechanisms.
We first discuss the physical processes of ENSO influence on NHCI and HC edges. A significant diabatic heating associated with ENSO is confined in the CP sector away from the equator (Fig. 12a). HC is sensitive to the latitudinal position of diabatic heating. The heating off the equator would strengthen the intensity of HC in the Northern Hemisphere as shown by Lindzen and Hou (1988). Therefore, the thermal control of ENSO on the interannual variability of NHCI is largely associated with CP diabatic heating off the equator.
As Fig. 9, but for composite analysis of the tropical diabatic heating (TDH) anomalies at 400 hPa (units: K/day, top), 250 hPa-zonal wind anomalies (shading, units: m s− 1) associated with its climatology (contours, intervals 10 m s−1, middle), HadISST anomalies (units: °C, bottom) during ENSO events
ENSO can further affect the interannual variation of the edges of HC in the Northern and Southern Hemispheres (Fig. 12b, c). Based on the zonal-mean concept, the impacts of ENSO on HC edges can be exerted through shifting the latitudinal position of subtropical Jets (Ceppi and Hartmann 2013) and altering the SST gradient between the tropics and midlatitudes (Adam et al. 2014). Here we highlight that the impact of ENSO on NHCE is largely associated with a southeastward shift of the North America jet in the WA sector (Fig. 12b). This result is also coherent with the fact that WA was identified as an ENSO-dominant factor for NHCE. The ENSO-induced meridional gradient of SST in the Southern Hemisphere can affect the interannual variability of SHCE. For instance, the increase of SST gradient between the tropics (0–20°S) and higher latitudes (20–45°S), consequence of warmer SST anomalies in the tropical Southern Indian Ocean and cooler SST anomalies in the mid-latitudes of the Southern Atlantic (Fig. 12c), results in a narrower SHC. The significant increase of ENSO-induced SST gradient in the EA sector is consistent with the fact that EA was identified as a responsible sector for ENSO’s control on SHCE in both ERA-Interim and MME.
The thermal control of ENSO via the CP sector off-equatorial diabatic heating on NHCI is reproduced in MME (Fig. 12d), but with a stronger magnitude, compared to ERA-Interim (Fig. 12a, d). In addition, ENSO affects NHCE through meridional shift of the North America jet, which is obvious in ERA-Interim, and well captured in MME (Fig. 12e).
Wave activity flux is presented to track the source areas of mid-latitude eddies and their propagation into the tropics. Caballero and Anderson (2009) showed that it is an efficient diagnostic tool for relating mid-latitude eddies and HC. It is complementary to the above linear regression methodology to identify privileged sectors where mid-latitude eddies exert impacts on NHCI and edges of HC. Figure 13 displays the wave propagation paths, we can identify the geographic sectors where mid-latitude eddies propagate into the tropics. We can compare them with those sectors responsible for NHCI and edges of HC in both hemispheres. As we can see in Fig. 13a, there are significant propagations of mid-latitude eddies through CP and North Africa into the northern tropics, which is consistent with what shown in Figs. 8c and 9b. Compared with ERA-Interim, the penetration of mid-latitude waves into tropical CP is overestimated in MME, while there are no significant mid-latitude eddies penetrating into tropical North Africa in MME (Fig. 13b). Similarly, wave penetrations into tropical EA are significant in ERA-Interim (Fig. 13c), but insignificant in MME (Fig. 13d). These results from the wave activity flux calculation coincide well with those shown in Fig. 10c, g. Significant equatorward propagations of mid-latitude eddies in the Southern Hemisphere hardly reach the EP sector (Fig. 13e), which may partly explain the southward shift of significant areas in Fig. 11c. Unlike EP, tropical WA (Fig. 13e) receives significant wave activity flux from the Southern mid-latitudes, which may contribute to the northward shift of the subtropical maximum in Fig. 11d.
As Fig. 12, but for wave activity flux (WAF, units: m2 s−2) anomalies associated with the eddy-related variability of NHCI and edges of HC in the Northern and Southern Hemispheres. Contours in each plot indicate the horizontal streamfunction anomalies (units: m2 s−1). Dotted areas in a–d indicate WAF of significance at the 5% level, while WAF of significance at the 10% level is shown in e, f
A direct but weak wave activity flux from mid-latitude eddies into EP is simulated in MME (Fig. 13f), which is consistent with what is shown from the regression pattern in Fig. 11h.
4 Summary and conclusions
HC is generally considered as a thermally direct circulation within the framework of zonal average in the tropics, sub-tropics and mid-latitudes of the globe. However, if we divide the tropical belt (30°S to 30°N) into 4 sub-domains, following roughly the global monsoon system, we obtain four RMCs including both thermally direct and indirect cells. A significant portion of this study was devoted to investigating roles of different geographic sectors in the interannual variability of NHCI and edges of HC in both the Northern and Southern Hemispheres, We paid a particular attention to the underlying physical mechanisms through statistical analyses and dynamic diagnostics. We used ERA-Interim and SST-driving climate models throughout the work. Our key findings are summarized as follows:
-
1.
Climatology of HC and inhomogeneity of climatological RMCs The thermally direct HC consists of a clockwise NHC and counterclockwise SHC (Fig. 1). The RMCs within the meridional sectors show a rich longitudinal diversity, including thermally direct RMCs over the EA and EP sectors with typical features as in the climatology of HC (i.e., “Hadleywise”) and the thermally direct southern limbs of RMC-CP and RMC-WA that oppose the SHC climatology (i.e., “anti-Hadleywise”), and the thermally indirect northern limbs of RMC-CP and RMC-WA that oppose the NHC climatology (i.e., “anti-Hadleywise”) (Figs. 2, 3a, 4).
-
2.
Interannual variability of HC linked to the variability of RMCs The leading mode of HC variability is associated with a stronger and narrower HC (Fig. 5) or the inverse. The mode of variability of HC is in phase with the principal components of the main variability modes of the four RMCs (Fig. 6). The meridional components of wind anomalies on the left flank of the NWPAC and the TSIOAC result in an overall decrease of RMC-EA. A reduction of the northern limb of RMC-EP largely is associated with a weakening of the North American winter monsoon. In contrast, a general increase of RMC-WA is associated with a strengthening of the northern limb of RMC-WA and an increase of the South American summer monsoon circulation. Strong convergence near the CP sector equator intensifies NHC and SHC (Fig. 7).
-
3.
Distinctive effects of the four RMCs on HC strength and extent By analyzing the spatial features of four RMC modes and diagnosing their correlation with NHCI and HC edges (Table 2), we found that CP and EA are identified as the dominant sectors where variabilities of RMCs determine the interannual variability of NHCI (Figs. 8, 9). RMC-EA and RMC-WA are the dominant contributors to the interannual variability of NHCE (Fig. 10). The combined effects of RMC-EP and RMC-WA and RMC-EA largely determine the interannual variability of SHCE (Fig. 11).
-
4.
The mechanism of ENSO and mid-latitudes eddies controlling NHCI and HC edges Both mid-latitude eddies and ENSO can influence the interannual variability of NHCI and extent in each hemisphere. The mid-latitude eddies explain a larger fraction of the total variance of HC strength and extent than does ENSO.
ENSO can impose its thermal control on the interannual variability of NHCI through CP diabatic heating off the equator (Fig. 12a). ENSO can affect the interannual variability of NHCE by shifting the North America jet southeastward in the WA sector (Fig. 12b). ENSO-induced SST gradient increases in the southern parts of EA leads to a narrower SHC (Fig. 12c). This is the consequence of warmer SST anomalies over the tropical Indian Ocean and Atlantic SST cooler in the subtropics and mid-latitude.
The penetration of mid-latitude eddies through CP and North Africa into the northern tropics can impact the interannual variability of NHCI (Fig. 13a). Mid-latitude eddies in the Northern Hemisphere propagate equatorward and penetrate into the northern subtropics of EA, and thus impose a signature on the interannual variability of NHCE (Fig. 13c). EP and WA are eddy-dominant sectors on the interannual variability of SHCE, with a stronger wave activity flux from the southern mid-latitude eddies into WA than into EP (Fig. 13e).
-
5.
Generally speaking, MME from the state-of-the-art climate models performs well in simulating HC behaviors, including the variability of HC, its climatology and the changes in HC strength and edges, despite a systematic underestimate of the magnitude of variability. However, there is an overestimate for ENSO contribution to the interannual variability of HC extent.
References
Adam O, Schneider T, Harnik N (2014) Role of changes in mean temperatures versus temperature gradients in the recent widening of the Hadley circulation. J Clim 27(19):7450–7461
Bordoni S, Schneider T (2008) Monsoons as eddy-mediated regime transitions of the tropical overturning circulation. Nat Geosci 1:515–519. https://doi.org/10.1038/ngeo248
Caballero R (2007) Role of eddies in the interannual variability of Hadley cell strength. Geophys Res Lett. https://doi.org/10.1029/2007GL030971
Caballero R, Anderson BT (2009) Impact of midlatitude stationary waves on regional Hadley cells and ENSO. Geophys Res Lett. https://doi.org/10.1029/2009GL039668
Ceppi P, Hartmann DL (2013) On the speed of the Eddy-Driven jet and the width of the Hadley cell in the southern hemisphere. J Clim 26:3450–3465. https://doi.org/10.1175/jcli-d-12-00414.1
Corvec S, Fletcher CG (2017) Changes to the tropical circulation in the mid-Pliocene and their implications for future climate. Clim Past 13:135–147. https://doi.org/10.5194/cp-13-135-2017
Dee DP et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Dima IM,Wallace JM (2003) On the seasonality of the Hadley cell. J Atmos Sci 60:1522–1527. https://doi.org/10.1175/1520-0469(2003)060<1522:OTSOTH>2.0.CO;2
Feng J, Li JP (2013) Contrasting Impacts of two types of ENSO on the Boreal Spring Hadley circulation. J Clim 26:4773–4789. https://doi.org/10.1175/jcli-d-12-00298.1
Feng R, Li JP, Wang JC (2011) Regime change of the boreal summer Hadley circulation and its connection with the tropical SST. J Clim 24:3867–3877
Feng J, Li JP, Xie F (2013) Long-term variation of the principal mode of boreal spring Hadley Circulation linked to SST over the Indo-Pacific Warm Pool. J Clim 26:532–544
Feng J et al (2015) Simulation of the equatorially asymmetric mode of the Hadley circulation in CMIP5 models. Adv Atmos Sci 32(8):1129–1142. https://doi.org/10.1007/s00376-015-4157-0
Feng J et al (2016) Contrasting responses of the hadley circulation to equatorially asymmetric and symmetric Meridional Sea surface temperature structures. J Clim 29:8949–8963. https://doi.org/10.1175/JCLI-D-16-0171.1
Feng J et al (2017) The responses of the Hadley circulation to different meridional SST structures in the seasonal cycle. J Geophys Res Atmos 122:7785–7799. https://doi.org/10.1002/2017JD026953
Gastineau G et al (2011) Some atmospheric processes governing the large-scale tropical circulation in idealized aquaplanet simulations. J Atmos Sci 68:553–575. https://doi.org/10.1175/2010jas3439.1
Guo Y-P, Li J-P (2016) Impact of ENSO events on the interannual variability of Hadley circulation extents in boreal winter. Adv Clim Change Res 7:46–53. https://doi.org/10.1016/j.accre.2016.05.001
Hadley G (1735) Concerning the cause of the general trade-winds: by Geo Hadley, Esq F. R. S. Philos Trans R Soc Lond 39:58–62. https://doi.org/10.1098/rstl.1735.0014
Held IM (2000) The general circulation of the atmosphere, paper presented at 2000 Woods Hole Oceanographic Institute Geophysical Fluid Dynamics Program, Woods Hole Oceanogr. Inst., Woods Hole, Mass. http://gfd.whoi.edu/proceedings/2000/PDFvol2000.html
Held IM, Hou AY (1980) Nonlinear axially symmetric circulations in a nearly inviscid atmosphere. J Atmos Sci 37:515–533
Hu Y, Fu Q (2007) Observed poleward expansion of the Hadley circulation since 1979. Atmos Chem Phys 7:5229–5236. https://doi.org/10.5194/acp-7-5229-2007
Hu Y, Zhou C, Liu J (2011) Observational evidence for poleward expansion of the Hadley circulation. Adv Atmos Sci 28(1):33–44. https://doi.org/10.1007/s00376-010-0032-1
Jayakumar A, Kumar V, Krishnamurti TN (2013) Lead time for medium range prediction of the dry spell of monsoon using multi-models. J Earth Syst Sci 122(4):991–1004
Kalnay E et al (1996) The NCEP/NCAR 40-Year reanalysis project. Bull Am Meteorol Soc 77:437–471. https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2
Kanamitsu M et al (2002) NCEP–DOE AMIP-II Reanalysis (R-2). Bull Am Meteor Soc 83:1631–1643. https://doi.org/10.1175/bams-83-11-1631
Karnauskas KB, Ummenhofer CC (2014) On the dynamics of the Hadley circulation and subtropical drying. Clim Dyn 42:2259–2269. https://doi.org/10.1007/s00382-014-2129-1
Knutti R et al (2009) Challenges in combining projections from multiple climate models. J Clim 23:2739–2758. https://doi.org/10.1175/2009JCLI3361.1
Lindzen RS, Hou AY (1988) Hadley circulations for zonally averaged heating centered off the equator. J Atmos Sci 45(17):2416–2427
Liu J et al (2009) Centennial variations of the global monsoon precipitation in the last millennium: results from ECHO-G model. J Clim 22:2356–2371. https://doi.org/10.1175/2008JCLI2353.1
Ma J, Li J (2008) The principal modes of variability of the boreal winter Hadley cell. Geophys Res Lett 35:L01808. https://doi.org/10.1029/2007GL031883
Nguyen H et al (2013) The Hadley circulation in reanalyses: climatology, variability, and change. J Clim 26:3357–3376. https://doi.org/10.1175/jcli-d-12-00224.1
Nguyen H et al (2017) Variability of the extent of the Hadley circulation in the southern hemisphere: a regional perspective. Clim Dyn. https://doi.org/10.1007/s00382-017-3592-2
Nigam S, Chung C, DeWeaver E (2000) ENSO diabatic heating in ECMWF and NCEP–NCAR reanalyses, and NCAR CCM3 simulation. J Clim 13:3152–3171
Onogi K et al (2007) The JRA-25 reanalysis. J Meteorol Soc Jpn Ser II 85:369–432. https://doi.org/10.2151/jmsj.85.369
Oort AH,Yienger JJ (1996) Observed interannual variability in the Hadley circulation and its connection to ENSO. J Clim 9:2751–2767. https://doi.org/10.1175/1520-0442(1996)009<2751:OIVITH>2.0.CO;2
Plumb RA (1985) On the three-dimensional propagation of stationary waves. J Atmos Sci 42:217–229
Quan XW, Diaz HF, Hoerling MP (2004) Change in the tropical Hadley cell since 1950. In: Diaz HF, Bradley RS (eds) Hadley circulation: present, past and future, vol 21. Springer, Dordrecht, pp 85–120
Riehl H et al (1950) The intensity of the net meridional circulation. Q J R Meteor Soc 76:182–188. https://doi.org/10.1002/qj.49707632808
Ropelewski CF, Halpert MS (1987) Global and regional scale precipitation patterns associated with the El Niño/Southern oscillation. Mon Weather Rev 115: 1606–1626. https://doi.org/10.1175/1520-0493(1987)115<1606:GARSPP>2.0.CO;2
Schneider T (2006) The general circulation of the atmosphere. Annu Rev Earth Planet Sci 34:655–688. https://doi.org/10.1146/annurev.earth.34.031405.125144
Stachnik JP, Schumacher C (2011) A comparison of the Hadley circulation in modern reanalyses. J Geophys Res Atmos. https://doi.org/10.1029/2011JD016677
Sun Y, Zhou T (2014) How does El Niño affect the interannual variability of the Boreal summer Hadley circulation? J Clim 27:2622–2642. https://doi.org/10.1175/jcli-d-13-00277.1
Sun Y et al (2013) Observational analysis and numerical simulation of the interannual variability of the boreal winter Hadley circulation over the recent 30 years. Sci China Earth Sci 56:647–661. https://doi.org/10.1007/s11430-012-4497-x
Sun Y et al (2017) Simulation of long-term trends in Hadley circulation during boreal winter using an ocean data assimilation scheme with the coupled general circulation model FGOALS-s2 (in Chinese). Chin Sci Bull 62:1–9. https://doi.org/10.1360/N972017-00409 (in press)
Tanaka HL et al (2004) Trend and interannual variability of Walker, monsoon and Hadley circulations defined by velocity potential in the upper troposphere. https://doi.org/10.3402/tellusa.v56i3.14410
Toma VE, Webster PJ (2010) Oscillations of the intertropical convergence zone and the genesis of easterly waves. Part I: diagnostics and theory. Clim Dyn 34(4):587–604
Walker CC, Schneider T (2006) Eddy influences on Hadley circulations: simulations with an idealized GCM. J Atmos Sci 63:3333–3350. https://doi.org/10.1175/JAS3821.1
Walker JM, Bordoni S, Schneider T (2015) Interannual variability in the large-scale dynamics of the South Asian summer monsoon. J Clim 28:3731–3750
Welhouse LJ et al (2016) Composite analysis of the effects of ENSO events on Antarctica. J Clim 29:1797–1808
Williamson DL et al (2013) The Aqua-Planet experiment (APE) response to changed meridional SST profile. J Meteor Soc Japan 91(A):57–89
Zhang G, Wang Z (2015) Interannual variability of tropical cyclone activity and regional Hadley circulation over the Northeastern Pacific. Geophys Res Lett 42:2473–2481. https://doi.org/10.1002/2015GL063318
Zhou BT, Shi Y, Xu Y (2016) CMIP5 simulated change in the intensity of the Hadley and Walker circulations from the perspective of velocity potential. Adv Atmos Sci 33:808–818
Acknowledgements
We acknowledge the World Climate Research Program’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups (listed in Table 1 of this paper) for producing and making available their model output. This work was jointly supported by National Natural Science Foundation of China (41661144009, 41505076), China Scholarship Council, and Chinese-French project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sun, Y., Li, L.Z.X., Ramstein, G. et al. Regional meridional cells governing the interannual variability of the Hadley circulation in boreal winter. Clim Dyn 52, 831–853 (2019). https://doi.org/10.1007/s00382-018-4263-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4263-7