1 Introduction

The discovery of dynamical chaos by Lorenz (1963) constitutes one of the most seminal contributions to twentieth century science. Lorenz’s lucid description of chaos and its implications for weather predictability have hardly been surpassed. Since Lorenz’s paper, various facets of predictability have been developed in numerous papers (see Palmer and Hagedorn 2006, for a review). In general, a variable is said to unpredictable from a set of observations if it is independent of those observations. This definition requires comparing two distributions: one that depends on observations and one that does not. These distributions are called the forecast and climatological distributions, respectively. When these two distributions are equal, then the variable is independent of the observations and therefore unpredictable. In principle, the forecast distribution can be derived from the governing dynamical equations using Liouville’s theorem or the Fokker–Planck equation. Whether the climatological distribution exists is a difficult question that is the subject of ergodic theory. In this paper, we assume the climatological distribution is equal to the forecast distribution initialized in the infinite past. In practice, these distributions can be estimated from an ensemble of forecasts, in which each member experiences the same time-dependent external forcing and evolves according to the governing physical laws, but with the forecast ensemble initialized at the present time and the climatological ensemble initialized long before the present time (Leith 1978). Although this framework provides a rigorous foundation for defining predictability, it has at least two unsatisfying elements.

The first unsatisfying element concerns externally forced variability. For instance, changes in solar insolation due to the earth’s orbit about the sun lead to a characteristic annual cycle in local climate. Because the climatological distribution is obtained from the same equations as the forecast distribution, it includes the annual cycle. As a result, the annual cycle is contained in both the forecast and climatological distributions and therefore does not contribute to predictability, which requires a difference in distributions. This formulation is often viewed as desirable since it implies a forecaster does not receive credit for predicting, say, that summer will be warmer than winter. However, an inescapable consequence of this formulation is that the response to other forms of external forcing also should be included in the climatological distribution, and therefore will not contribute to predictability. In particular, the response to changes in greenhouse gas concentration due to human activity should be included in the both the forecast and climatology, and therefore would not contribute to predictability. Such a framework is very unsatisfying given the importance of predicting climate change. Lorenz (1975) recognized this issue and introduced “predictability of the second kind,” or what is now called boundary-value predictability or forced predictability. A framework that accommodates externally forced climate changes has been discussed in several papers (Lorenz 1970, 1975; Leith 1978; Meehl et al. 2009; Branstator and Teng 2010). The present paper goes beyond these studies by giving a mathematically explicit treatment and by proposing a new measure, called total climate predictability, that can be decomposed as the sum of previously proposed measures of initial-value predictability and forced predictability. Part of this framework has appeared previously in DelSole (2017).

The above formulation of initial-value and forced predictability still has certain unsatisfying elements. Specifically, the climatological distribution derived from the above framework may be too broad for certain applications. For instance, paleo-climate records show that large climate changes can occur abruptly over periods as short as a decade (Alley and Clark 1999). This fact demonstrates that the climate system can display very different behavior under nearly identical external forcing. Consequently, the system’s climatological distribution may be much broader than the distribution that describes the past few decades. Under such a broad climatology, weather would be deemed predictable for as long as the associated forecast predicts no shift in climate (possibly for years). This particular issue does not arise often in predictability studies because climate models often are selected according to their ability to simulate the climate of the past century when given the corresponding forcing. Whether this criterion leads to an overly narrow climatological distribution is unclear. In any case, fundamentally similar issues arise even in seasonal predictability studies. For instance, some droughts can last a decade or longer (“mega-droughts”; Cook et al. 2010). To the extent that these droughts occur naturally, the climatological distribution should include them, which leads to the same unsatisfying conclusion: weather would be predictable for as long as the associated forecast predicts the mega-drought to continue. Similarly, other long time-scale processes, e.g., El Niño, ocean overturning circulations, and land-ice, broaden the climatological distribution. To resolve this issue, we propose generalized predictability, based on a conditional climatology, that effectively filters out predictability on long time scales so that the predictability on short time scales can be identified. This formalism can define a spectrum of predictability questions distinguished by time scale.

This paper is organized as follows. Section 2 reviews the standard framework of predictability. Section 3 discusses limitations of the standard framework and describes a generalized framework that resolves them. Specifically, we define forced predictability as changes in the climatology over time, and define a conditional climatology that allows predictability on different time scales to be isolated. Section 4 proposes a new measure of predictability called total climate predictability that captures both initial-value and forced predictability. Section 5 illustrates the above concepts in a forced AR(1) model, where all distributions required to evaluate predictability can be written in closed form. This paper concludes with a summary of our results.

2 What is predictability?

Most people agree that the outcome of a (fair) coin toss is unpredictable. Why? In other words, can you explain precisely what makes you say a coin toss is unpredictable? Is it because you cannot make a prediction about it? Actually, you can make a prediction about it. Here it is: the probability of heads is 50%. Moreover, this prediction correctly describes the outcomes. So there you have it—a falsifiable prediction about a coin toss! Now perhaps you believe a coin toss is unpredictable because you can make only probabilistic predictions about it, as opposed to making a prediction with certainty. This also is not true: all forecasts of nature are uncertain, and the most complete description of uncertainty is a probability distribution. Hence, all forecasts of nature should be probabilistic. Therefore, the mere probabilistic nature of the forecast does not make a coin toss unpredictable.

The reason a coin toss is considered unpredictable is because the outcome is independent of observations typically available to the forecaster prior to the toss.Footnote 1 The key word here is independent. More precisely, a variable is unpredictable from a given set of observations if it is independent of those observations. Any other definition of predictability would lead to situations that contradict the meaning of the term. For instance, if predictability were not defined based on statistical independence, then a variable might be declared predictable even though it is independent of observations, or be declared unpredictable even though there exists a dependence on observations.

To define predictability mathematically, let the observations available at time t be denoted as \(O_t\) (which includes observations before time t), and let the variable being predicted at future time \(t+\tau\) be denoted as Y. The variable t is called initial condition time, \(\tau\) is called lead time (usually positive), and \(t+\tau\) is called verification time. The most complete description of the future value of Y given observations \(O_t\) is the conditional distribution \(p_{t+\tau }(y|o_t)\). This distribution is called the forecast distribution.Footnote 2 The distribution of the future value of Y unconditional on observations is denoted \(p_{t+\tau }(y)\). This distribution is called the climatological distribution of Y. The variable Y is said to be unpredictable from \(O_t\), in an initial-value sense, if it is independent of \(O_t\):

$$\begin{aligned} \begin{array}{lll} p_{t+\tau }(y| o_t ) & = & p_{t+\tau }(y) \\ \text {forecast} && \text {climatological} \end{array} \qquad \left( \begin{array}{l} \text {for no initial} \\ \text {value predictability} \end{array} \right) . \end{aligned}$$
(1)

It follows that a necessary condition for predictability is \(p_{t+\tau }(y| o_t ) \ne p_{t+\tau }(y)\) for some \(o_t\). The term predictability is short for initial-value predictability.

Strictly speaking, predictability at \(t+\tau\) depends on the quality, type, and spatio-temporal distribution of observations at time t. Thus, a variable Y might be deemed predictable with respect to one set of observations but unpredictable with respect to a different set of observations. For instance, many hurricanes over the ocean were unobserved during the pre-satellite era and therefore land fall was difficult to predict. After satellite data became available, many hurricanes over the ocean that previously would have been unobserved could be identified and tracked to provide skillful predictions of land fall. Predictability also may be improved simply by reducing observational errors from the existing network. This dependence of predictability on observations raises questions about the best observing system for maximizing predictability, especially whether it is advantageous for the observational network to adapt to the synoptic situation (Lorenz and Emmanuel 1998).

If a variable has no initial-value predictability, there still exists meaningful information about its future value. Specifically, the climatological distribution describes the variable’s future value. For example, the weather a year from today cannot be predicted with precision, but the season will be the same and that knowledge allows us to predict that the temperature will be in a certain range characteristic for that season. A variable is unpredictable only in the sense that available observations do not tell us anything different than what we already knew from the climatological distribution. This point was illustrated by the coin flip: the unconditional distribution is “50% heads, 50% tails” and accurately describes the future coin flip. Because this distribution is not altered by conditioning on current observations, the event is unpredictable.

The basis of any prediction of the future is that variables change with time according to certain laws. In weather and climate, the relevant laws of physics are often modeled by governing equations of the form

$$\begin{aligned} \frac{d y_i}{dt} = N_i (y_1, y_2, \dots , y_S) , \end{aligned}$$
(2)

where \(y_1, \dots , y_S\) are a large but finite number of state variables and \(N_i\) are nonlinear functions of the state variables. For instance, all coupled atmosphere-ocean general circulation models are of this form. If the laws are such that the future state is specified uniquely by the present state, then the system is said to be deterministic, otherwise it is called stochastic.

Distributions derived from (2) satisfy the Markov property, which means that the distribution conditioned on a sequence of past states depends only on the most recent state. Accordingly, the dependence of the future state on the present is described by the transition kernel \(p_{t+\tau }(y|y_t)\) (also called a stochastic kernel or Markov kernel). The transition kernel is essentially a propagator obtained by integrating the governing equations. More precisely, the transition kernel is obtained from the governing equations (2) by solving the Chapman–Kolomogorov equation (Gardiner 1990, ch2). If the governing equations are deterministic and satisfy certain regularity conditions, then the Chapman–Kolomogorov equation can be written in a differential form called Liouville’s equation. If the governing equations are stochastic and of a certain class, then the Chapman–Kolomogorov equation can be written in a differential form called the Fokker–Planck equation. In either case, the transition kernel is derived by solving a partial differential equation under suitable boundary conditions and given initial condition. Alternatively, an approximate transition kernel might be estimated empirically from a long record of past observations.

The state of a real system is estimated from observations of that system. However, real observations contain random errors and gaps in spatial coverage. As a result, no unique state y can be inferred from observations—many different states Y are compatible with the observed realization of \(o_t\). The distribution of states that are compatible with the observations \(o_t\) is described by the analysis distribution, denoted \(p_t(y|o_t)\) (note that the lead time is zero). The derivation of this distribution is a central goal of data assimilation (Jazwinski 1970).

Fig. 1
figure 1

Schematic illustrating how initial conditions (from the analysis distribution) and dynamics contribute to the forecast distribution, as described in (5)

Full size image

The laws of probability imply that the forecast and analysis distributions are related as

$$\begin{aligned} p_{t+\tau }(y | o_t) = \int p_{t+\tau }(y | y_{t}, o_t) p_t(y_t | o_t) dy_t , \end{aligned}$$
(3)

where \(p_{t+\tau }(y | y_{t}, o_t)\) is the distribution of the future value of Y conditioned on the present value and conditioned on presently available observations. Note that the integration variable \(y_t\) is a vector, but for simplicity the multivariate nature of the integration is ignored. For Markov systems, observations do not add information about the future if the initial state is known, hence

$$\begin{aligned} p_{t+\tau }(y | y_{t}, o_t) = p_{t+\tau }(y | y_{t}) . \end{aligned}$$
(4)

Substituting this relation into (3) yields

$$\begin{aligned} \begin{matrix} p_{t+\tau }(y | o_t) & = \displaystyle \int & p_{t+\tau }(y | y_{t}) & p_t(y_t | o_t) & dy_t .\\ \text {forecast} & & \text {dynamics} & \text {analysis} \end{matrix} \end{aligned}$$
(5)

This equation defines how dynamics connects the analysis and forecast distributions. The solution is illustrated schematically in Fig. 1. The prediction process begins by observing the system, which constrains the distribution of states at time t. This distribution can be interpreted as a collection of initial states, called an ensemble, with relative frequencies proportional to the probability density. In weather and climate studies, this ensemble can be imagined as a theoretical collection of Earths, each subjected to the same external forcing. As time advances forward, each member of the ensemble evolves in accordance with the physical laws. The initial states may be visualized as a cloud of points in state space, each of which streams through state space as it follows a trajectory determined by physical laws. The distribution at any future time is obtained by integrating over all initial states.

Predictability of the climate system is limited by the fact that the atmosphere is chaotic. A chaotic system is one whose evolution is sensitive to small changes in the initial condition. This means that if the atmosphere were to come arbitrarily close to a state which it had assumed previously, the subsequent evolution would diverge wildly from the previous evolution after sufficient time. As a consequence, even the smallest uncertainties in the initial state translate into large uncertainties in the forecast after sufficient time.

For sufficiently small initial errors, predictability can be characterized by a set of Lyapunov exponents that measure error-growth rate. Atmospheric models based on the primitive equations suggest that small amplitude perturbations in the atmosphere amplify with an average doubling time of about 1.8 days, suggesting an upper limit of predictability of about two weeks (Simmons and Hollingsworth 2002). However, atmospheric predictability depends on spatial structure, with large-scale perturbations being more predictable than small-scale perturbations, so planetary-scale waves are found to be predictable even for averages over 16–46 days leads (Shukla 1981). Planetary waves may also interact with stratospheric waves to enhance their predictability (Tripathi et al. 2015). Beyond a few weeks, slowly varying components of the climate system, such as sea surface temperature, soil moisture, snow cover, or sea ice thickness, are still predictable owing to their slower time scale. These slower components can influence the atmosphere and hence give rise to predictability of atmospheric variables beyond a month (Charney and Shukla 1981; Shukla 1998). Because these slower components lie on the earth’s surface, this type of predictability is called boundary forced predictability. To the extent that atmospheric variables are independent of the slower components on long time scales, they can be treated as white noise stochastic forcing (Hasselmann 1976). In addition, coupled atmosphere-ocean systems support new mechanisms of predictability beyond those found in the separate uncoupled systems, the most well established of which is the El Niño Southern Oscillation (ENSO; Philander 1990), which has a doubling time of several months (Goswami and Shukla 1991) and can be predicted a few months in advance (Barnston et al. 2012).

Although small errors can grow exponentially in chaotic systems, the growth rate slackens when errors become large. The question arises as to when the errors become so large that all predictability is lost. The limit of predictability depends on how close the forecast distribution is to the climatological distribution. Defining this limit requires defining the climatological distribution.

The problem of deducing the climatological distribution from the nonlinear dynamical equations is difficult. In fluid mechanics, this is tantamount to the closure problem of turbulence, considered one of the great unsolved problems of classical physics (Nelkin 1992). Indeed, merely proving the existence of the climatological distribution is a difficult problem in ergodic theory. Nevertheless, probability laws assert that if it exists, then it must satisfy the equality

$$\begin{aligned} p_{t+\tau }(y) = \int p_{t+\tau }(y|o_t) p(o_t) do_t , \end{aligned}$$
(6)

where \(p(o_t)\) is the probability of the observations. We can make progress by assuming that the forecast distribution becomes independent of the initial observations in the limit of large lead time:

$$\begin{aligned} \lim _{s \rightarrow -\infty } p_{t+\tau }(y | o_{s} ) = \text {some distribution independent of }o_s . \end{aligned}$$
(7)

This assumption appears to hold for realistic climate models. If the observations are perfect, complete, and therefore indistinguishable from the state, the above identity is the defining property of a transitive system (Lorenz 1968). To understand the consequence of assumption (7), consider applying the transformation \(t \rightarrow t - \tau\) to (6) and taking the limit \(\tau \rightarrow \infty\):

$$\begin{aligned} p_t(y) \nonumber&= \lim _{\tau \rightarrow \infty } \int p_t(y|o_{t-\tau }) p(o_{t-\tau }) d o_{t-\tau } \\ \nonumber&= \int \left( \lim _{\tau \rightarrow \infty } p_t(y|o_{t-\tau }) \right) \left( \lim _{\tau \rightarrow \infty } p(o_{t-\tau }) d o_{t-\tau } \right) \\ \nonumber&= \left( \lim _{\tau \rightarrow \infty } p_t(y|o_{t-\tau }) \right) \left( \lim _{\tau \rightarrow \infty } \int p(o_{t-\tau }) d o_{t-\tau } \right) \\&= \lim _{\tau \rightarrow \infty } p_{t}(y| o_{t-\tau } ) , \end{aligned}$$
(8)

where we have used the fact that (7) implies that the forecast distribution \(p_t(y|o_{t-\tau })\) is independent of \(o_{t-\tau }\) for large \(\tau\), and therefore can be taken outside the integral. We have also invoked the theorem that the limit of a sum equals the sum of the limits, the limit of a product equals the product of the limits, and the integral of a probability distribution equals one. Identity (8) shows that if (7) is true, then the climatological distribution can be obtained by evaluating the forecast distribution at asymptotically long lead times. This result justifies the familiar rule of measuring initial-value predictability by the extent to which the forecast differs from its “saturation” distribution at long lead times (i.e., because the saturation distribution is the climatology).

If the climatological distribution \(p_t(y)\) is independent of time, then the system is said to be stationary. A stationary climatological distribution describes the relative frequency of states associated with sampling the system randomly in time. However, the observed climate system is clearly non-stationary owing to annual and diurnal cycles (e.g., winter and summer states clearly belong to different distributions). A more realistic assumption is that the climatological distribution is cyclostationary, i.e., it is a periodic function of time. For cyclostationary systems, the climatological distribution describes the relative frequency of states associated with sampling the system at random years but conditioned on calendar day and hour. A common approach to estimating the mean of the climatological distribution is to compute the mean of each calendar day and hour over a 30-year period (but see Narapusetty et al. 2009).

A representative schematic of the forecast and climatological distributions is shown in Fig. 2. Typically, the initial forecast is localized in state space and then spreads out with time. The spread is related to forecast uncertainty and often referred to as noise. The mean of the forecast often is called signal. As time advances, the forecast distribution typically approaches the climatological distribution. As a result, differences between the two distributions diminish with lead time, leading to decay of initial-value predictability. The predictability time scale is defined as the minimum lead time at which the difference between forecast and climatological distributions falls below some threshold.

Fig. 2
figure 2

Schematic of representative forecast and climatological distributions

Full size image

It should be recognized that the variable being predicted may be a state variable averaged over some period of time, rather than the instantaneous value of the state variable. For instance, weather predictability and seasonal predictability are both examples of initial-value predictability, but the former concerns variables averaged over hours or days while the latter concerns variables averaged over months or seasons. Decadal predictability concerns the predictability of multi-year averages of state variables. Other forms of predictability are discussed in the literature (e.g, “potential predictability”), but the definitions are not always consistent and so will not be defined here.

3 Climatology in a changing climate

The above framework is used in many predictability studies. In this section, we show that rigorous application of this framework leads to unsatisfying conclusions if the climatological distribution varies from year to year or is overly broad compared to the climate of the recent past. We then propose extensions of the above framework that resolves these limitations.

For illustration purposes, suppose the dynamical system (2) is modified as

$$\begin{aligned} \frac{d y_i}{dt} = N_i (y_1, y_2, \dots , y_S) + f_i , \end{aligned}$$
(9)

where \(f_i\) are time-dependent forcing terms that account for external forcing. The climatological distribution of this system requires solving (9) starting from the distant past, and would be expected to vary in time in response to changes in external forcing \(f_i\). Changes in climatological distribution from year to year are called climate changes. Thus, climate changes due to external forcing, such as that due to solar variability or human-cause changes in greenhouse gas concentrations, would be included in the climatological distribution. Because only differences relative to the climatological distribution contribute to predictability, it follows that climate changes do not contribute to initial-value predictability. In fact, climate change is treated the same as annual and diurnal cycles: they are each subsumed into the climatological distribution. However, changes in the climatological distribution relative to its distribution in different years, especially those due to global warming, are of considerable interest in themselves. To distinguish questions of this type from those of initial-value predictability, Lorenz (1975) suggested a new type of predictability called predictability of the second kind, or what is today called forced predictability or boundary-value predictability.Footnote 3 These terms are used even if the forcing itself is unpredictable (e.g., multi-decadal variations due to volcanic eruptions or solar variability). Assessing whether a climate forcing changes the climatological distribution of a variable is called climate change detection. Both kinds of predictability involve measuring differences in distributions, hence tools used to analyze one kind of predictability often are useful in the other.

The above framework for initial-value and forced predictability still may be unsatisfying. In particular, the climatological distribution derived from (7) may be much broader than is appropriate for certain problems. For instance, if the climatological distribution is obtained by initializing the system in the infinite past, then even orbital parameters would have a large uncertainty due to the impacts of random planetesimals over billions of years (indeed, this climatology may assign non-zero probability to a universe without Earth). Aside from this, the climate system may display a wide range of variability even for the same external forcing. For instance, geological evidence reveals that the climate can change drastically over short periods (e.g., as much as 10 \(^\circ\)C locally in 10 years; Alley et al. 2003). The existence of abrupt climate change demonstrates that the climate can have very different distributions over time periods subjected to nearly identical forcing. Because a climatological distribution describes all climates compatible with the physical laws, it can be much broader than the distribution that describes the recent past. Under a broad climatology, even weather could be deemed predictable for years, provided the associated forecast predicts no shift in climate. A framework that expunges weather predictability is unsatisfying. The above problem might seem esoteric because overly broad climatologies do not occur frequently in practice. However, this impression might be an artifact of assessing climate models on the basis of their ability to simulate the last few decades. In particular, the climatology of the past few decades may be unrealistically narrow. For instance, some models suggest that even El Niño can behave differently across multi-decadal epochs under fixed external forcing (Wittenberg 2009).

In any case, essentially the same issues occur in weather and seasonal predictability. Specifically, weather is affected by a variety of natural, long time-scale processes, e.g., El Niño, the Atlantic Meridional Overturning Circulation (AMOC) and mega-droughts. As a result, the climatological distribution that describes the joint behavior of weather and long time-scale processes is broader than the distribution that is conditioned on the state of a long time-scale process. Unfortunately, some attempts to define predictability conditioned on the state of a long time-scale process have been based on problematic modeling frameworks. For instance, one familiar approach is to run an atmospheric general circulation model (AGCM) with specified sea surface temperatures. However, the unphysical one-way forcing of an AGCM with prescribed lower boundary conditions raises questions about how results from such models relate to the fully coupled system (Barsugli and Battisti 1998). A similar criticism can be raised for any modeling framework in which one artificially constrains variables in a climate model that would ordinarily feedback to other variables (e.g., sea surface temperatures, land variables, sea ice).

Instead of conditioning explicitly on the state of a long time-scale process, we propose a formalism for filtering out the predictability of processes with long time scales, so that predictability on shorter time scales can be identified. The question arises as to whether this filtering can be done in a mathematically consistent way without constraining a dynamical model in an unphysical way. We propose such an approach by defining a conditional climatology, which is nothing more than a forecast initialized in the finite past, s, where \(s < t\):

$$\begin{aligned} p_{t+\tau }(y) \equiv p_{t+\tau }(y | o_s) = \int p_{t+\tau }(y | y_{s}) p_s(y_s | o_s) dy_s . \end{aligned}$$
(10)

Then, generalized predictability is measured by the degree to which the forecast \(p_{t+\tau }(y| o_t )\) differs from the conditional climatology \(p_{t+\tau }(y | o_s )\). For instance, if \(t-s = 30\) years, processes with time scales much longer than 30 years would be virtually identical in the forecast and climatology and therefore not contribute to predictability in our generalized sense. In this way, predictability of processes with time scales longer than 30 years are selectively attenuated. On the other hand, processes on shorter time scales, such as atmospheric weather and El Niño, would differ between the forecast and climatology and therefore contribute to predictability. As s increases, the climatology (10) is initialized further in the past and therefore broadens to describe a wider range of climate variability, increasing the generalized predictability due to processes with time scales longer than 30 years. The greater the value of \(t-s\), the greater the differences between forecast and conditional climatology, and the greater the predictability of long time-scale processes. Conversely, as s approaches t, the closer the forecast and climatology, and the smaller the predictability of long time-scale processes. The parameter s serves as a filter parameter that controls the time scale of processes that are included in generalized predictability.

Does the above proposal lead to a definition of predictability that is consistent with statistical independence? Yes, because generalized predictability is based on conditional independence. Here, conditional independence means

$$\begin{aligned} p_{t+\tau }(y| o_t, o_s ) = p_{t+\tau }(y | o_s ) , \end{aligned}$$
(11)

where \(p_{t+\tau }(y| o_t, o_s )\) denotes the conditional probability of Y given both \(O_t\) and \(O_s\). This identity differs from (1) only by \(o_s\) appearing as a conditional in both distributions. Formally, this identity expresses the fact that Y is conditionally independent of \(O_t\) given \(O_s = o_s\), for any value of \(o_s\). Recall that, by definition, \(O_t\) includes all observations up to and including time t, hence it includes \(O_s\). Thus, \(\{O_t, O_s\} = O_t\), and the identity (11) can be written equivalently as

$$\begin{aligned} p_{t+\tau }(y| o_t ) = p_{t+\tau }(y | o_s ) \qquad \text {for generalized unpredictability} , \end{aligned}$$
(12)

where the right hand side is the climatology (10). This is precisely the definition of generalized unpredictability proposed above. Thus, a climatology based on a forecast initialized in the finite past yields a definition of predictability that is consistent with the definition of conditional independence. Taking the limit \(s \rightarrow \infty\) recovers the traditional definition of predictability.

Generalized predictability offers a new way to identify regime-dependent predictability. To illustrate, consider mega-droughts. Presumably, weather behaves differently according to whether a drought is occurring or not. During the middle of a mega-drought, observations from one year ago effectively localize the climate in a mega-drought. Thus, for \(t-s = 1\) year, the forecast and conditional climatology both describe the same mega-drought, so predictability of the mega-drought itself is attenuated, allowing predictability of weather during the drought to be identified. In this way, regime-dependent weather predictability can be diagnosed by varying t while holding \(t-s\) constant: the parameter t controls the temporal location while \(t-s\) controls the time scales of interest. On the other hand, as \(s \rightarrow \infty\), the conditional climatology broadens to describe both droughts and non-droughts, thereby allowing us to quantify predictability of the drought itself. This approach to isolating short-period predictability differs fundamentally from time-filtering. The fact that defining a conditional climatology as (10) can act to filter predictability of processes on time scales beyond \(t-s\) does not seem to have been recognized previously.

In this paper, the current climate is understood to be the relevant climatology. Accordingly, in the remainder of this paper, we suppress the conditional \(o_s\) and adopt the implicit definition (10) for the climatological distribution.

4 Measures of predictability in a changing climate

By definition, a variable is unpredictable if the forecast and climatological distributions are identical. It is natural, then, to quantify predictability by some measure of the difference in distributions. However, no single measure can satisfy all purposes: some differences are more important than others, depending on the application. For instance, a civil engineer may be interested in the change in average rainfall while an emergency manager may be interested in the change in extreme rainfall. In choosing a measure, it is important to distinguish between predictability and utility (Palmer 2002). Utility is a measure of the benefit derived from a prediction. Because benefit depends on the arbitrary user, no universal measure of utility can be defined. Nevertheless, predictability and utility are related: if an event is unpredictable, then a forecast cannot add utility relative to that which is available from the climatological distribution. Thus, predictability analysis determines whether a forecast can add utility beyond the climatological distribution. Another nuance is that, technically, any difference in distribution constitutes predictability, but the difference may be so slight as to have no utility. These considerations imply that predictability is a necessary but not sufficient condition for utility.

Although no unique measure of predictability exists, an attractive measure is relative entropy (also called Kullback–Leibler Divergence), which is a central quantity in information theory and arises naturally in a number of disciplines, including communication, finance, statistical mechanics, and statistics (Kullback 1968; Cover and Thomas 1991; Mackay 2003). The relative entropy between two distributions p(x) and q(x) is defined as

$$\begin{aligned} R[p(x); \, q(x)] = \int p(x) \log \frac{p(x)}{q(x)} dx . \end{aligned}$$
(13)

A basic property of this measure is that it vanishes if and only if \(p= q\), otherwise it is positive. Additional reasons for preferring relative entropy will emerge below, but one particular application is worth mentioning here. A reasonable definition of the value of a forecast is the increase in wealth that results from knowing the forecast. In the absence of a credible forecast, an investor could use the climatological distribution inferred from past observations to devise a profitable investment strategy. This approach is very common in the insurance industry, for instance. The question arises as to how much can an investor increase his return by using the forecast distribution. A strikingly simple answer is that the difference in rate at which wealth is doubled by the best investment strategy equals the relative entropy between the forecast and climatological distributions (Cover and Thomas 1991).

Following the above reasoning, the cost of ignoring the climate forecast—i.e., the money you lose by not taking into account climate change and initial condition information—is measured by the relative entropy between the forecast and the initial climatology \(p_t(y)\):

$$\begin{aligned} R_T = R \left[ p_{t+\tau } (y|o_t); \, p_t(y) \right] . \end{aligned}$$
(14)

This measure depends on \(o_t\) and \(\tau\). Averaging \(R_T\) over observations yields a new measure, which we called total climate predictability \(M_T\),

$$\begin{aligned} M_T = \int R_T p(o_t) do_t. \end{aligned}$$
(15)

This measure depends only on lead time \(\tau\). We will show that total climate predictability \(M_T\) can be decomposed as

$$\begin{aligned} M_T = M_{IV} + M_F , \end{aligned}$$
(16)

where \(M_{IV}\) is a measure of initial-value predictability called mutual information, proposed by DelSole (2004), and \(M_F\) is a measure of forced predictability proposed by Branstator and Teng (2010). Thus, the previously proposed measures of predictability \(M_{IV}\) and \(M_F\) emerge naturally in our framework.

To show the above, it proves convenient to define the expectation operators

$$\begin{aligned} E_{Y|O} \left[ q(y) \right]&= \int p_{t+\tau } (y|o_t) q(y) dy \end{aligned}$$
(17)
$$\begin{aligned} E_O [ q(o) ]&= \int p(o_t) q(o_t) d o_t , \end{aligned}$$
(18)

where \(q(\cdot )\) is an arbitrary function. Then, total climate predictability (15) can be written equivalently as

$$\begin{aligned} M_T = E_O \left[ E_{Y|O} \left[ \log \frac{p_{t+\tau } (y|o_t)}{p_t(y)} \right] \right] . \end{aligned}$$
(19)

The logarithmic ratio can be partitioned as

$$\begin{aligned} \log \frac{p_{t+\tau } (y|o_t)}{p_t(y)} = \log \frac{p_{t+\tau } (y|o_t)}{p_{t+\tau } (y)} + \log \frac{p_{t+\tau } (y)}{p_t(y)} . \end{aligned}$$
(20)

Three distinct distributions appear in the above identity: the forecast distribution \(p_{t+\tau } (y|o_t)\), and the climatological distributions \(p_t(y)\) and \(p_{t+\tau } (y)\). These three distributions are illustrated schematically in Fig. 3a. Substituting (20) into (19) and using the fact that the expectation operator is linear yields

$$\begin{aligned} M_T = E_O \left[ E_{Y|O} \left[ \log \frac{p_{t+\tau } (y|o_t)}{p_{t+\tau } (y)} \right] \right] + E_O \left[ E_{Y|O} \left[ \log \frac{p_{t+\tau } (y)}{p_t(y)} \right] \right] . \end{aligned}$$
(21)

The two terms on the right correspond to the terms in the decomposition (16).

The first term on the right of (21) involves the quantity

$$\begin{aligned} R_{IV} = E_{Y|O} \left[ \log \frac{p_{t+\tau } (y|o_t)}{p_{t+\tau } (y)} \right] = \int p_{t+\tau }(y | o_t) \log \frac{p_{t+\tau }(y | o_t)}{p_{t+\tau }(y)} dy , \end{aligned}$$
(22)

which is the relative entropy between the forecast \(p_{t+\tau } (y|o_t)\) and climatology \(p_{t+\tau } (y)\). Kleeman (2002) proposed \(R_{IV}\) as a measure of initial-value predictability. This measure depends on lead time \(\tau\) and initial condition through \(o_t\). Averaging \(R_{IV}\) over \(p(o_t)\) yields a quantity called mutual information:

$$\begin{aligned} M_{IV} = \int R_{IV} p(o_t) do_t = \iint p_{t+\tau }(y,o_t) \log \frac{p_{t+\tau }(y,o_t)}{p_{t+\tau }(y)p(o_t)} dy do_t , \end{aligned}$$
(23)

where \(p_{t+\tau }(y,o_t) = p_{t+\tau }(y | o_t) p(o_t)\) has been used. DelSole (2004) proposed \(M_{IV}\) as a measure of average initial-value predictability. This measure depends on lead time \(\tau\) but not on \(o_t\) (because \(o_t\) has been integrated out).

The second term on the right of (21) can be written as

$$\begin{aligned} M_F = E_O \left[ E_{Y|O} \left[ \log \frac{p_{t+\tau } (y)}{p_t(y)} \right] \right] = R \left[ p_{t+\tau }(y); \, p_{t}(y) \right] , \end{aligned}$$
(24)

which is the relative entropy between the two climatologies \(p_{t+\tau }(y)\) and \(p_{t}(y)\). In deriving this equation, we make use of the fact that the forecast and climatological distribution are related through the probability law

$$\begin{aligned} \int p_{t+\tau }(y | o_t) p(o_t) do_t = p_{t+\tau }(y) , \end{aligned}$$
(25)

which effectively eliminates the initial condition variable \(o_t\) in the measure of forced predictability \(M_F\) (as we would expect).

Fig. 3
figure 3

Schematic of the spread of the three distributions relevant to quantifying decadal predictability (a) and the corresponding relative entropies (b). Schematics are based on results from Branstator and Teng (2010) for upper 300 m ocean temperature anomalies in model simulations. This figure is redrawn from DelSole (2017)

Full size image

The above measures are close to those proposed by Branstator and Teng (2010). Specifically, Branstator and Teng (2010) estimated the climatology from “an ensemble of realizations, each beginning long before \(t = 0\) and each experiencing the same time-dependent external forcing”. This procedure is tantamount to averaging over initial conditions and therefore is equivalent to our measure \(M_F\). On the other hand, Branstator and Teng measure initial value predictability using the relative entropy between the forecast and climatology without averaging over initial conditions, which is equivalent to our measure \(R_{IV}\). Branstator and Teng then add these two measures together to quantify total predictability. The sum \(M_F + R_{IV}\) quantifies the predictability due to changing climatology and the particular forecast. That is, this measure is a function of both lead time and initial condition, and hence is specific to a particular initial condition. In contrast, our proposed measure \(M_T = M_F + M_{IV}\) is independent of initial condition and quantifies predictability, or rate of increase in wealth, in an average sense over all initial conditions, and is therefore analogous to familiar skill measures that are averaged over initial conditions.

The above derivation clarifies that certain previously proposed measures of predictability can be summed together to produce a sensible measure of total climate predictability \(M_T\). Each term in the identity (16) is either a relative entropy, or an average of a relative entropy. Therefore, the attractive properties of relative entropy carry over to \(M_T\). Specifically, the individual terms in (16) possess the following attractive properties:

  1. 1.

    \(M_{IV}\) and \(M_F\) are non-negative.

  2. 2.

    \(M_{IV}\) vanishes if and only if Y at \(t+\tau\) is independent of \(O_t\).

  3. 3.

    \(M_F\) vanishes if and only if the climatologies at t and \(t+\tau\) are identical.

  4. 4.

    \(M_{IV}\) and \(M_F\) are invariant to invertible, nonlinear transformations of Y.

  5. 5.

    \(M_{IV}\) and \(M_F\) have natural generalizations to multivariate distributions.

The first three properties convey the notion of a “distance” between distributions: \(M_{IV}\) and \(M_F\) vanish if the two distributions in question are identical, and is positive otherwise. The fourth property implies the variable Y can be transformed nonlinearly without altering predictability. Any reasonable measure of predictability should possess this invariance property. The fifth property implies that the above measures can be generalized to an arbitrary number of variables. Remarkably, multivariate measures of predictability satisfy the same properties, including invariance to invertible, nonlinear cross-variable transformations among variables in the same random vector. Finally, each term has attractive interpretations in terms of investment strategies.

While our definition of initial-value predictability is clearly based on dependence (e.g., \(M_{IV}\) vanishes if and only if Y is independent of \(O_t\)), it might not be obvious that forced predictability also is based on dependence. To see that this is so, note that the concept of dependence applies not only to random variables, but also to parameters (Dawid 1979). Specifically, the distribution of Y may be derived from a statistical model involving a parameter \(\theta\). In this case, the distribution of Y may depend on \(\theta\), but the joint distribution between Y and \(\theta\) does not exist because \(\theta\) is not a random variable. The statement that Y is independent of \(\theta\) expresses the fact that the distribution of Y is the same for all values of \(\theta\). As a result of the properties discussed above, \(M_F\) is non-zero if and only if the climatological distribution depends on the parameter \(\tau\). Thus, \(M_F\) measures the degree to which the climatology changes in time. If the climatological distribution does not change when \(\tau\) is varied, then it is independent of \(\tau\). Thus, forced predictability can be interpreted as reflecting a (generalized) dependence of the climatological distribution on lead time \(\tau\).

Another indication that our proposed framework is sensible is that, based on the above measures, initial-value predictability of a Markov process decays with lead time under very general conditions. This property conforms with our intuition that a system should become less predictable as lead time advances. This property holds even for the conditional climatology (10), which is remarkable given that in the generalized case both forecast and climatology evolve in time. Our proof of this property follows that of Cover and Thomas (1991) (see Sect. 2.9). To prove this property, it is necessary to modify our notation slightly. Accordingly, let \(Y_t\) denote the random variable at time t, and let the joint distribution between \(Y_{t+\tau }\) and \(Y_t\) under different conditionals be

$$\begin{aligned} p(y_{t+\tau } , y_t | o_t ) \quad \text {and} \quad p(y_{t+\tau } , y_t | o_s ) . \end{aligned}$$
(26)

The relative entropy between the two joint distributions (26) can be decomposed in two different ways using the chain rule for relative entropy (Cover and Thomas 1991, Theorem 2.5.3). The first is

$$\begin{aligned} R[p(y_{t+\tau } , y_t | o_t );\, p(y_{t+\tau } , y_t | o_s ) ]&= R[p(y_{t} | o_t );\, p(y_{t} | o_s )] \nonumber \\&\quad + R[p(y_{t+\tau } | y_{t}, o_t );\, p(y_{t+\tau } | y_{t}, o_s ) ] . \end{aligned}$$
(27)

Focusing on the second line, the two distributions involved are identical owing to the Markov property (4), hence the relative entropy between them vanishes. The second decomposition is

$$\begin{aligned} R[p(y_{t+\tau } , y_t | o_t );\, p(y_{t+\tau } , y_t | o_s ) ]&= R[p(y_{t+\tau } | o_t );\, p(y_{t+\tau } | o_s )] \nonumber \\&\quad + R[p(y_{t} | y_{t+\tau }, o_t ); \,p(y_{t} | y_{t+\tau }, o_s ) ] \end{aligned}$$
(28)

There is no nice simplification of the second line, but we know that it is non-negative since relative entropy itself is always non-negative. Taking this fact into account after equating (27) and (28) yields the inequality

$$\begin{aligned} R[p(y_{t+\tau } | o_t );\, p(y_{t+\tau } | o_s )] \le R[p(y_{t} | o_t );\, p(y_{t} | o_s )] . \end{aligned}$$
(29)

This proves that the relative entropy between forecast and generalized climatological distribution (10) is a non-increasing function of lead time. This proof makes no assumption about time scales and therefore holds for arbitrary \(s < t\).

A schematic of the different predictability measures is shown in Fig. 3b. Initial-value predictability decays monotonically with lead time, but total climate predictability does not because external forcing can cause changes in the climatological distribution that increase with time.

For joint Gaussian distributions, the above measures depend only on the means and variances of the underlying distributions. To show this, let

$$\begin{aligned}&p_{t+\tau }(y|o_t) \sim \mathcal {N} \left( \mu _{Y|O}, \sigma _{Y|O}^2 \right) \quad \text {forecast} \end{aligned}$$
(30)
$$\begin{aligned}&p_{t+\tau }(y) \sim \mathcal {N} \left( \mu _Y, \sigma _Y^2 \right) \quad \text {climatology at } t + \tau \end{aligned}$$
(31)
$$\begin{aligned}&p_{t}(y) \sim \mathcal {N} \left( \mu _U, \sigma _U^2 \right) \quad \text {climatology at } t . \end{aligned}$$
(32)

We emphasize that \(\mu _{Y|O}\) generally is a function of \(o_t\). A standard result is that mutual information for joint normally distributed random variables is

$$\begin{aligned} M_{IV} = - \frac{1}{2} \log \left( \frac{\sigma _{Y|O}^2}{\sigma _Y^2 } \right) . \end{aligned}$$
(33)

This measure depends on the ratio of variances \(\sigma _{Y|O}^2 / \sigma _Y^2\), which is called the noise-to-total ratio because variance in the forecast distribution is associated with uncertainty or noise. Similarly, a standard result is that the relative entropy for normal distributions is

$$\begin{aligned} M_F = - \frac{1}{2} \log \left( \frac{\sigma _{Y}^2}{\sigma _{U}^2} \right) + \frac{1}{2} \frac{\sigma _{Y}^2}{ \sigma _U^2} + \frac{( \mu _{Y} -\mu _{U})^2}{2 \sigma _U^2} - \frac{1}{2} . \end{aligned}$$
(34)

This expression clearly vanishes when the two climatological distributions are equal. Finally, total predictability is derived from (16).

5 Predictability of a forced AR(1) processes

This section illustrates predictability in an exactly solvable model, namely a first order autoregressive model. Such models are called stochastic because they contain random variables as part of their dynamics. Stochastic models have limited predictability because the transition between two states is uncertain even if the initial state is known exactly. In contrast, nonlinear chaotic systems have limited predictability because of instability with respect to initial conditions. Nevertheless, stochastic models can be difficult to distinguish from chaotic deterministic systems, hence the predictability of simple stochastic models can give insight into the predictability of deterministic systems.

Consider a stochastic process \(Y_t\) governed by a forced AR(1) model

$$\begin{aligned} Y_t = \phi Y_{t-1} + W_t + f_t , \end{aligned}$$
(35)

where \(W_t\) is a stochastic process with zero mean and \(f_t\) is a deterministic function of time (e.g., it may be constant, vary periodically, or contain a long-term trend). The last assumption is made merely for simplicity—\(f_t\) could be a random variable, but this generalization would not change our conclusions regarding the predictability of \(Y_t\) because of the linearity of the model (35). In fact, we will show that the predictability of \(Y_t\) is independent of a deterministic \(f_t\).

We assume \(| \phi | < 1\), in which case the model (35) is stable. To compute distributions of \(Y_t\), the distribution of \(W_t\) needs to be specified. Here, \(W_t\) is assumed to be Gaussian white noise with zero mean and variance \(\sigma _W^2\).

In order to make a prediction, observations of the process must exist. Observations generally are imperfect. Accounting for errors in observation is not interesting for an AR(1) process because such processes are stable and hence initial condition errors are damped with lead time (in contrast to chaotic systems). Accordingly, only the case of perfect observations are considered. Suppose, then, that we have a set of perfect observations \(\{ y_0, y_{-1}, y_{-2}, \dots \}\).

To assess the predictability of \(Y_t\), the conditional distribution of \(Y_t\) given the observations needs to be computed. It is clear from (35) that

$$\begin{aligned} p_t(y | y_{t-1}, y_{t-2}, \dots ) = p_t(y | y_{t-1} ). \end{aligned}$$
(36)

This identity reflects the Markov property of an AR(1) process. One might question whether past observations are truly irrelevant given that \(Y_{t-2}\) and \(Y_t\) are autocorrelated. However, (35) shows that all information derivable from the past that is relevant to predicting \(Y_t\) is contained in \(Y_{t-1}\). Although \(Y_t\) and \(Y_{t-2}\) are correlated, all predictive information in \(Y_{t-2}\) is embedded in \(Y_{t-1}\). Thus, once \(Y_{t-1}\) is known, any observation prior to \(Y_{t-1}\) becomes irrelevant. \(Y_t\) and \(\{Y_{t-2}, Y_{t-3}, \dots \}\) are said to be conditionally independent given \(Y_{t-1}\).

Suppose the observed value at \(t=0\) is \(y_0\). What is the appropriate prediction for \(Y_1\)? First, the prediction should be probabilistic because the state at \(t=1\) is uncertain owing to the random process \(W_t\). Second, since \(Y_1 = \phi y_0 + W_1 + f_1\), the state at \(t=1\) is a constant (\(\phi y_0 + f_1\)) plus a Gaussian random variable \(W_t\), so the form of the distribution must be Gaussian. It is sufficient, therefore, to determine the mean and variance of \(Y_1\). This mean and variance should be conditioned on the initial condition \(Y_0 = y_o\). Specifically, the mean of Y conditioned on the observation \(y_0\) is

$$\begin{aligned} E[ Y_1 | y_o ] = E[ \phi Y_0 + W_1 + f_1 | y_0] = \phi y_0 + f_1 + E[W_1] = \phi y_0 + f_1, \end{aligned}$$
(37)

where we have used the fact that \(y_0\) and \(f_1\) are constant under the conditional distribution, and that \(W_t\) has zero mean regardless of the conditional. The conditional variance is

$$\begin{aligned} {{\rm{var}}}[Y_1 | y_0] = {{\rm{var}}}[ \phi y_0 + W_1 +f_ 1| y_0] = {{\rm{var}}}[ W_1 | y_0] = {{\rm{var}}}[W_1] = \sigma _W^2, \end{aligned}$$
(38)

where we have used the fact that adding a constant to a random variable does not alter variance. It follows that the forecast distribution after one step is

$$\begin{aligned} p_1(y | y_0 ) \sim \mathcal {N} \left( \phi y_0 + f_1 , \sigma _W^2 \right) . \end{aligned}$$
(39)

Note that the initial condition \(y_0\) and forcing \(f_1\) determine the mean of the forecast distribution, but play no role in forecast variance. This is a property of linear systems that may not carry over to nonlinear dynamical systems.

Fig. 4
figure 4

The distribution of \(Y_t\) at different times for an AR(1) process. The distributions have been offset in the vertical for clarity. The AR parameters are \(\phi = 0.99\), \(\sigma _W^2 = 1\), and \(f_t = 0\). The initial condition is chosen at the (unrealistically) large value of \(y_0 = -35\) to exaggerate changes in distribution. The axis labels have been omitted since only the qualitative behavior is important

Full size image

It is a standard exercise to show that the general solution to the forced AR(1) model (35) is

$$\begin{aligned} Y_t = \phi ^t y_0 + \sum _{j=0}^{t-1} \phi ^j W_{t-j} + \sum _{j=0}^{t-1} \phi ^j f_{t-j}. \end{aligned}$$
(40)

The conditional mean for arbitrary t is therefore

$$\begin{aligned} E[Y_t|y_0] = \phi ^t y_0 + \sum _{j=0}^{t-1} \phi ^j f_{t-j} , \end{aligned}$$
(41)

and the conditional variance is

$$\begin{aligned} {{\rm{var}}}[ Y_t |y_0 ] = {{\rm{var}}}\left[ \sum _{j=0}^{t-1} \phi ^j W_{t-j} \right] = \sum _{j=0}^{t-1} \sigma _W^2 \phi ^{2j} = \sigma _W^2 \frac{1 - \phi ^{2t}}{1-\phi ^2} , \end{aligned}$$
(42)

where we have used standard summation formulas for geometric series and the fact that the \(W_t\)’s are independent. Consolidating these results leads to the forecast distribution for general t:

$$\begin{aligned} p_t( y | y_0 ) \sim \mathcal {N} \left( \phi ^t y_0+ \sum _{j=0}^{t-1} \phi ^j f_{t-j}, \sigma _W^2 \frac{1 - \phi ^{2t}}{1-\phi ^2} \right) . \end{aligned}$$
(43)

As before, the initial condition and forcing affect only the mean of the forecast distribution. The behavior of the forecast distribution for \(f_t =\) constant is illustrated in Fig. 4. As time advances, the mean of the distribution travels toward the mean of the asymptotic (i.e., climatological) distribution. Also, the distribution spreads out. Initially, the distribution is narrow because the initial condition was perfectly known, but the distribution spreads out as time advances because of the constant addition of uncertainty with each time step.

Is \(Y_t\) predictable? To decide this, the forecast and climatological distributions must be compared. What is the climatological distribution in this example? As discussed in Sect. 2, the climatology is the asymptotic forecast distribution in the limit of large lead \(\tau\), as indicated in (8). It is a simple exercise to show that the forecast distribution can be written equivalently as

$$\begin{aligned} p_t( y | y_{t-s} ) \sim \mathcal {N} \left( \phi ^s y_{t-s}+ \sum _{j=0}^{s-1} \phi ^j f_{t-j}, \sigma _W^2 \frac{1 - \phi ^{2 s}}{1-\phi ^2} \right) . \end{aligned}$$
(44)

For instance, substituting \(s = t\) recovers (43). Taking the limit \(s \rightarrow \infty\) gives

$$\begin{aligned} \lim _{s \rightarrow \infty } p_t(y| y_{t-s}) \sim \mathcal {N} \left( \sum _{j=0}^{\infty } \phi ^j f_{t-j} , \frac{\sigma _W^2}{1-\phi ^2} \right) . \end{aligned}$$
(45)

Note that the above distribution is independent of the initial condition used in the infinite past. Also, the climatological distribution may be non-stationary because the mean of the distribution may depend on time through \(f_t\).

Predictability requires comparing (44) and (45). This comparison is facilitated by expressing means in terms of the (time-varying) climatological mean

$$\begin{aligned} \mu _Y (t) = \sum _{j=0}^{\infty } \phi ^j f_{t-j} . \end{aligned}$$
(46)

The mean of the forecast distribution (44) can be written in terms of \(\mu _Y(t)\) as

$$\begin{aligned} \mu _{Y|O} (t) \nonumber&= \phi ^s y_{t-s} + \sum _{j=0}^{s-1} \phi ^j f_{t-j} \\ \nonumber&= \phi ^s y_{t-s} + \sum _{j=0}^{\infty } \phi ^j f_{t-j} - \sum _{j=s}^{\infty } \phi ^j f_{t-j} \\ \nonumber&= \phi ^s y_{t-s} + \sum _{j=0}^{\infty } \phi ^j f_{t-j} - \sum _{j=0}^{\infty } \phi ^{j+s} f_{t-s-j} \\&= \phi ^s y_{t-s} + \mu _Y (t) - \phi ^s \mu _Y (t-s) \end{aligned}$$
(47)

We define the anomaly as the deviation from the climatological mean:

$$\begin{aligned} y_t ' = y_{t} - \mu _Y (t) . \end{aligned}$$
(48)

In this notation, the forecast mean (47) can be written as

$$\begin{aligned} \mu _{Y|O} (t) = \phi ^s y_{t-s}' + \mu _Y (t) . \end{aligned}$$
(49)

This equation shows that the mean of the forecast distribution corresponds to a damping of the initial anomaly plus the climatological mean \(\mu _Y(t)\). For future reference, the variance of the climatological distribution (45) is denoted

$$\begin{aligned} \sigma _Y^2 = \frac{\sigma _W^2}{1-\phi ^2} . \end{aligned}$$
(50)

Then the variance of the forecast distribution (44) is

$$\begin{aligned} \sigma _{Y|O}^2 = \sigma _Y^2 \left( 1 - \phi ^{2 \tau } \right) . \end{aligned}$$
(51)

Recall that predictability requires a difference between forecast and climatological distributions. For Gaussian distributions, this implies a difference between means or a difference between variances. The difference in means is

$$\begin{aligned} \mu _{Y|O}(t) - \mu _Y(t) = \phi ^\tau y_{t-\tau }' , \end{aligned}$$
(52)

and the ratio of variances is

$$\begin{aligned} \frac{\sigma _{Y|O}^2}{\sigma _Y^2} = 1 - \phi ^{2 \tau } . \end{aligned}$$
(53)

The two distributions differ when \(\phi \ne 0\) and \(\tau\) is finite. This result makes intuitive sense: if \(\phi = 0\), then \(Y_t\) is merely white noise, hence unpredictable; if \(\tau\) is infinite then an infinite amount of noise has been accumulated in the forecast. Although the two distributions differ in a mathematical sense for finite \(\tau\) (and \(\phi \ne 0\)), they may not differ in a practical sense if the difference is too small to detect with finite samples. The limit of predictability often is defined as the time after which some measure of the difference between the conditional and unconditional distributions exceed some (arbitrary) threshold.

Predictability as measured by mutual information (33) is

$$\begin{aligned} M_{IV} = - \frac{1}{2} \log \left( 1 - \phi ^{2 \tau } \right) , \end{aligned}$$
(54)

where (53) has been used for the noise-to-total ratio. Predictability is maximum at \(\tau =0\) and decays monotonically to zero with increasing \(\tau\). Importantly, this measure depends only on the parameter \(\phi\). That is, predictability is independent of initial condition, noise variance \(\sigma _W\), and forcing \(f_t\). Values of \(\phi\) close to one correspond to processes with “long memory” (i.e., their autocorrelation takes many steps to decay). Therefore, stochastic processes with longer memory have larger predictability, consistent with intuition.

Fig. 5
figure 5

Time series of the forecast and climatological means of a forced AR(1) process for \(f_t =\) constant (a) and \(f_t = \sin (2 \pi t / 8)\) (b). The AR parameters are \(\phi = 0.9\) and \(\sigma _W^2 = 1\). The y-axis label has been omitted since only the qualitative behavior is important

Full size image

Neither (52) nor (53) depend on the forcing term \(f_t\). Thus, the forcing term contributes no initial-value predictability in this model. To see how this works, consider constant forcing \(f_t = k\), for which the climatological mean (46) is

$$\begin{aligned} \mu _Y (t) = \sum _{j=0}^{\infty } \phi ^j f_{t-j} = k \sum _{j=0}^{\infty }\phi ^j = \frac{k}{1-\phi } , \end{aligned}$$
(55)

where we have used standard summation formulas for geometric series. The means of the forecast and climatological distributions [(44) and (45), respectively] for this choice of forcing are illustrated in Fig. 5a. As expected, the forecast mean relaxes monotonically toward the climatological mean. Note that the climatological distribution is constant, implying a stationary system. Now consider a time-dependent forcing, say \(f_t = \sin (\omega t)\), which may model an annual or diurnal cycle. It can be shown that

$$\begin{aligned} \mu _Y (t) = \sum _{j=0}^{\infty } \phi ^j \sin (\omega (t-j)) = \frac{\sin \omega t - \phi \sin \omega (t+1)}{1 - 2 \phi \cos \omega - \phi ^2} . \end{aligned}$$
(56)

In this case, the climatological distribution depends on time and is therefore non-stationary. The mean of the forecast and climatological distributions for this case, for the same initial condition used above, are shown in Fig. 5b. As in the stationary case, the forecast distribution relaxes toward the climatological distribution. Importantly, the rate of this relaxation is the same in both cases and determined by the parameter \(\phi\). Thus, in this model, predictability is independent of \(f_t\) and depends only on \(\phi\) and \(\tau\).

Fig. 6
figure 6

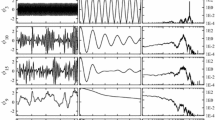
The 66% confidence intervals for forecast and climatological distributions for an AR1 process with exponential forcing (a), and the corresponding measures of initial-value, forced, and total climate predictability (b). The forcing is specified in (57) and the model parameters are \(\phi =0.6, \beta =0.1, k =1\), and \(\sigma _W =1\). The initial condition is at \(t=0\) and equal to four standard deviations above the climatological mean (a large initial perturbation was chosen so that the forecast can be distinguished from the climatologies). “Initial climatology” refers to the climatological distribution at time \(t=0\) and persisted forward in time

Full size image

To clarify the case of forced predictability, consider a forcing that is constant up to time \(t=0\), and is exponential thereafter:

$$\begin{aligned} f_t = \left\{ \begin{matrix} k & \quad t \le 0 \\ k \exp (\beta t) &\quad t> 0 \end{matrix} \right. . \end{aligned}$$
(57)

This forcing might model anthropogenic climate change. In this case, the climatological distribution is

$$\begin{aligned} \mu _Y (t) = \sum _{j=0}^{\infty } \phi ^j f_{t-j} = \left\{ \begin{array}{ll} \frac{k}{1-\phi } &\quad t \le 0 \\ k e^{\beta t} \left( \frac{1 - (\phi e^{-\beta })^t}{1 - \phi e^{-\beta }} + \frac{ \phi ^t}{1-\phi } \right) &\quad t> 0 . \end{array} \right. \end{aligned}$$
(58)

The relevant distributions are illustrated in Fig. 6a, where the forecast is initialized at time \(t=0\). The initial value predictability still is given by (54). Forced predictability is given by (34), which takes on a particularly simple form in the present example because the climatological variances are identical:

$$\begin{aligned} M_F = \frac{\left( \mu _Y(t)-\mu _Y(0) \right) ^2}{2 \sigma _Y^2} , \end{aligned}$$
(59)

where \(\mu _Y(t)\) is defined in (58). These measures are shown in Fig. 6b. Total climate predictability is the sum \(M_F\) and \(M_{IV}\). As discussed in Sect. 4, initial-value predictability decays with lead time, but total climate predictability can increase with lead time because of forced predictability.

The above analysis assumed a deterministic forcing \(f_t\). If, instead, \(f_t\) were a stochastic process with a predictable time scale much longer than that of \(Y_t\), then it would still be approximately a deterministic function on the short time scales relevant for \(Y_t\). Thus, the climatology could have been defined by evaluating (44) using a finite value of s, chosen such that \(t-s\) is short compared to the predictable time scale of \(f_t\), but long compared to the predictable time scale of \(Y_t\). An important point is that the model for the joint variable \((Y_t,f_t)\) would have two predictable time scales: a relatively short time scale for \(Y_t\) and a much longer time scale for \(f_t\). The above analysis illustrates how the short predictable time scale of \(Y_t\) can be defined even though it is dynamically coupled to a variable \(f_t\) with a much longer predictable time scale.

6 Conclusion

This paper discussed limitations of the standard framework of predictability and proposed a generalized framework for resolving these limitations. In the standard framework, an event is unpredictable from a given set of observations if it is independent of those observations. This definition requires comparing two distributions: one that is conditioned on observations and one that is not. These distribution are called the forecast and climatological distributions, respectively. For transitive systems, the climatological distribution is the forecast distribution initialized in the infinite past. The framework resulting from this definition is problematic if one is interested in climate changes due to external forcing, or if the climatological distribution dictated by the governing equations is too broad (i.e., describes the current climate and other climates that are very different from the present one). In the first case, an inevitable consequence of any sensible definition of predictability is that forced variability, such as that caused by human activities or annual cycles of solar insolation, must be subsumed in the specification of the climatological distribution. As a result, predictions of forced variability cannot constitute initial-value predictability because predictability requires a difference in distributions. Following Lorenz (1975), a new type of predictability, which we call forced predictability, is defined based on differences in climatological distribution between different times. We propose a general measure, called total climate predictability, that captures both forced and initial-value predictability. This new measure has a natural decomposition into measures that have been proposed previously. Specifically, it emerges naturally that forced predictability is measured by the relative entropy between the initial and final climatologies, as proposed by Branstator and Teng (2010), and initial-value predictability is measured by mutual information, as proposed by DelSole (2004). The new measure is invariant to nonlinear transformations of the variables and generalizes naturally to multivariate distributions. Most of these concepts are illustrated in a simple model in which all distributions can be expressed in closed form.

The above framework has many attractive features but still may be unsatisfying. In particular, it defines the climatological distribution as the forecast distribution initialized in the infinite past, which may be much broader than is appropriate for certain kinds of predictability questions. For instance, the existence of abrupt climate change in paleo-climate records demonstrates that very different climates can occur under nearly the same external forcing. This spectrum of climates should be described by the climatological distribution. However, if predictability studies were to use such a broad climatology, then weather would be deemed predictable for as long as the associated forecast predicts that the climate has not shifted, possibly for years. Many studies implicitly justify a narrower distribution by selecting a climate model that simulates the climate of the past few decades when given the present external forcing. Whether this criterion leads to overly narrow estimates of the climatological distributions is unclear. In any case, we propose a generalized predictability that provides a formalism for filtering out predictability due to long time scale processes so that predictability on short time scales can be identified. This framework is based on a conditional climatology, which is the forecast distribution initialized at a finite earlier time. Using such a conditional climatology filters out predictability contributions from long time-scale processes. This generalized framework follows naturally from the definition of conditional independence, and therefore retains consistency with the concept of dependence. Furthermore, generalized predictability retains the familiar property that initial-value predictability decays with lead time.