Abstract
This observational study during the 29-year period from 1979 to 2007 evaluates the potential role of Eurasian snow in modulating the North East-Indian Summer Monsoon Rainfall with a lead time of almost 6 months. This link is manifested by the changes in high-latitude atmospheric winter snow variability over Eurasia associated with Arctic Oscillation (AO). Excessive wintertime Eurasian snow leads to an anomalous cooling of the overlying atmosphere and is associated with the negative mode of AO, inducing a meridional wave-train descending over the tropical north Atlantic and is associated with cooling of this region. Once the cold anomalies are established over the tropical Atlantic, it persists up to the following summer leading to an anomalous zonal wave-train further inducing a descending branch over NE-India resulting in weak summer monsoon rainfall.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The North East Indian Summer Monsoon Rainfall (NEISMR) over the eastern-most part of the country (Fig. 1a), which is joined via a narrow belt clasped between Nepal and Bangladesh, is influenced by local and remote forces. In terms of geographical size, NE-India constitutes of about 8% of India’s total size. Its population is approximately 40 million, which represents around 3.1% of the total Indian population. This region has a predominantly humid sub-tropical climate with hot, humid summers, severe monsoons and mild winters. Along with the west coast of India, this region has some of the Indian sub-continent’s last remaining rain forests, which supports diverse flora and fauna and several crop species. Geographically, two-thirds of the area is a hilly terrain interspersed with valleys and plains. The mean summer monsoon rainfall over the NE-Indian region is around 1400 mm making for huge water and hydropower potential. However, this region has been exhibiting a declining trend in the summer monsoon rainfall since the last 4–5 decades (see Fig. 3, Fig. 4a in Preethi et al. 2016). Hence, it becomes imperative to examine the possible drivers of this variability.
Significance for long-term prediction of summer monsoon, considering its massive socio-economic impacts, have been widely attributed to the slowly varying boundary conditions such as sea surface temperature (SST) and snow cover (Shukla 1998). In general, rainfall distribution pattern over different regions of India is inhomogeneous due to influence of several local and remote factors. For instance, over the central Indian plain region, monsoon trough and the Himalayas along with local and external factors play a dominant role in its interannual rainfall variability. Likewise, the northwest region is influenced by the dry climates of the Thar Desert and the Western Himalayas. Apparently from the geographical features as described above, the rain producing mechanism of NE rainfall is a complex phenomenon and is largely dominated by an elevated orography of the Eastern Himalayas and large forests. The NE sector may be considered as a separate macro-region within the Indian landmass (Winstanley 1973; Parthasarathy et al. 1987). The most dominant mode of variability in summer monsoon rainfall over the Indian sub-continent clearly reveals that the summer monsoon rainfall over NE India and neighborhood is out-of-phase with rainfall over other parts of India (Kulkarni et al. 1992). Munot and Kothawale (2000) also suggest that seasonal and intraseasonal rainfall variability of NE-Indian regions is often out of phase with the central and peninsular India. Since local orography dominates the NE rainfall, its prediction is not at par with other regions of India (e.g. central-India). However, this region is close to the northern hemisphere (NH) mid latitude jet stream location. This implies that the large scale variability of mid and sub-polar latitudes may play an important role in modulating the NEISMR.
Previous studies have suggested about forcings, other than El Niño Southern Oscillation (ENSO), influencing the inter-annual variability of ISMR like Arctic seaice (Amita et al. 2012), winter climate anomalies over Europe (Rajeevan 2002; Pai 2004), Atlantic SST (Srivastava et al. 2002; Goswami et al. 2006) and Eurasian snow cover (e.g. Hahn and Shukla 1976; Bamzai and Kinter 1997; Kripalani and Kulkarni 1999) since it was first put forward by Blanford (1884). The NH snow cover is an integral component of the global climate system. Its inter-annual variability has an important climatic role to play, especially in influencing the summer monsoon rainfall over India (Kripalani et al. 1996). The albedo of fresh snow is around 90% (Hall and Martinec 1985). As a result of this, the cryospheric component work as an efficient insulator, reflecting most of incoming solar radiation and providing a positive feedback mechanism (Maykut 1978). This affects formation of cloud, stability of atmosphere and therefore, NH precipitation. The Eurasian snow cover too has a potential in shaping planetary scale features like the Arctic Oscillation (AO) (Cohen and Entekhabi 1999), which in turn influence the winter (Clark et al. 1999) and spring Eurasian snow cover extent (Bojariu and Gimeno 2003; Bamzai 2003). The AO is characterized by zonally symmetric structure of Sea Level Pressure (SLP) perturbations in the sub-polar regions located near 65°N and the surrounding zonal ring of opposing signs centered near 45°N latitude (Thompson and Wallace 1998). This high latitude modes explain more of the week-to-week, month-to-month, and year-to-year variance in the extratropical atmospheric flow than any other climate phenomenon (Thompson and Wallace 2000). Their study demonstrated that a high latitude mode explains more than 30% of the total variance in the Geopotential Height (GPH) and wind fields depending upon atmospheric pressure level and timescale considered. In the pressure field, the annular modes are characterized by north–south vacillations in atmospheric mass between sub-polar and mid-latitudes. By convention, the low (high) index polarity of AO is defined as higher (lower) than normal pressure over sub-polar latitudes and lower (higher) than normal pressure over the mid-latitudes. The AO features, which are zonally symmetric or “annular” exists year-round in troposphere with a maximum amplification in the NH midwinter (Thompson and Wallace 1998).
The mechanism of snow cover and Indian summer monsoon teleconnection through an atmospheric bridge linking this remote low frequency variability has been investigated in several studies. Raman and Maliekal (1985) analysed NH pressure anomalies in relation to contrasting ISMR and found that zonally integrated pressure anomalies across Eurasia during January to April between higher and subtropical latitudes to be associated with ISMR. Their study revealed that a steep poleward-directed pressure anomaly gradient during preceding winter to spring is associated with above-normal ISMR. This strong pressure gradient indicates a strong zonal flow in the circumpolar westerlies. On the other hand, when the pressure anomaly gradient reverses, the zonality is disturbed and the circumpolar flow becomes persistently meridional and the ISMR tends to be drier than normal.
Marked changes in the teleconnections of ISMR have been observed in the recent decades due to the atmospheric changes associated with climate shift post 1979 (Trenberth and Hurrell 1994; Graham 1994), wherein the traditional ISMR-ENSO relationship weakened (Krishna Kumar et al. 2006; Sabeerali et al. 2012). Fluctuation in the robustness of precursors, for instance the Equatorial Pacific ENSO being replaced by central Pacific warming in the recent decades, have been attributed to the changes in the large-scale circulations owing to global warming (Wang et al. 2015, Nature Communications). As such, the robustness of the predictors tend to change over a period a time. Subsequently, linkages associated with variability over the Atlantic Ocean and ISMR have received considerable attention. There have been studies involving the two phenomena on a multidecadal timescale (Zhang and Delworth 2006; Goswami et al. 2006; Krishnamurthy and Krishnamurthy 2015) with a positive or warm phase of Atlantic multidecadal oscillation leading to an increased rainfall activity over the Indian subcontinent. For interannual timescale too, the influence of Atlantic SSTs on ISMR have been extensively studied (Kucharski et al. 2009; Barimala et al. 2012). They focussed on the SST anomalies in the south tropical Atlantic with cold (warm) SST leading to low (high) surface pressure anomaly over India further leading to convergence (divergence) and consequently resulting in strong (weak) ISMR. A recent study by Yadav (2016) explained the mechanism connecting tropical Atlantic SSTs and summer monsoon rainfall over northwest and central India through the Eurasian wave. The link between the three entities, namely, Atlantic SST, Eurasian snow and summer monsoon, is manifested through Rossby waves that modulate the Tibetan High thereby influencing rainfall over the northwest and central India (Hoskins and Ambrizzi 1993; Ambrizzi et al. 1995). Hahn and Shukla (1976) reinforced the idea first put forward by Walker (Walker 1910) that boreal winters with excessive (less) snow cover over Eurasia tend to be followed by less (more) summer monsoon rainfall over India. While there have been ample of studies in finding the predictors for ISMR, not much effort has been vested in examining the potential predictors for foreshadowing the summer monsoon rainfall over the regions of NE-India. It is well known that mid-latitude Eurasian snow cover has a determining role in the interannual variability of Indian summer monsoon when we consider a large region over Indian subcontinent. Establishing a low frequency teleconnection, specifically for the NE Indian region, would thus be vital from the perspective of its potential seasonal prediction. Therefore, the present study explores a robust physical mechanism linking north Atlantic SSTs with NEISMR by examining the role of high-latitude Eurasian snow in bonding the two. Hence, in the present study, we have proposed a possible physical mechanism linking the winter Eurasian snow, AO and north tropical Atlantic SSTs with the NEISMR.
The outline of this paper is as follows: Sect. 2 describes the data sets used and methodologies adopted. Section 3 examines the NEISMR teleconnections with Eurasian SWE and Atlantic SST. Section 4 attempts to locate a common bridge and postulates a possible physical mechanism connecting the two. Finally, Sect. 5 summarizes the main results of this study.
2 Data and methodology
We have used several datasets to carry out this study and are listed below as follows:
-
1.
Snow Water Equivalent (SWE) is a measurement of the amount of water contained in snow pack. It can be considered as the depth of water that would hypothetically result if the whole snow pack instantaneously melts. It is given by the equation:
$${\text{SWE}}\left( {\text{m}} \right) = {\text{snow depth}}\;\left( {\text{m}} \right) \times {\text{snow density}}\;\left( {{\text{kg}}/{\text{m}}^{3} } \right)/{\text{water density}}\;\left( {{\text{kg}}/{\text{m}}^{3} } \right)$$The SWE dataset has been obtained from Scanning Multi-channel Microwave Radiometer and Special Sensor Microwave Imager sensors for the period November 1978 through May 2007 and is obtained from National Snow and Ice Data Center (NSIDC). The data is gridded to the Northern and Southern 25 km Equal-Area Scalable Earth Grids (EASE-Grids) and is found to be suitable for continental-scale time-series studies (Armstrong et al. 2007). So all the following datasets are archived for the period 1979–2007.
-
2.
The dataset for atmospheric parameters is employed from National Centers for Environmental Prediction (NCEP) and National Center for Atmospheric Research (NCAR) reanalysis (Kalnay et al. 1996).
-
3.
The optimally interpolated SST version 2 data set (Reynolds et al. 2002) having a spatial resolution of 1° × 1° latitude-longitude global grid is available from 1982 onwards. It is archived from National Oceanic and Atmospheric Administration (NOAA).
-
4.
NEISMR data (Parthasarathy et al. 1995) has been obtained from Indian Institute of Tropical Meteorology (ftp://www.tropmet.res.in/pub/data/rain/iitm-regionrf.txt). The time series of NEISMR is constructed from an area-weighted rainfall from June through September (JJAS) rainguage stations over this region.
-
5.
India Meteorological Department’s National Climate Centre (IMD-NCC) daily gridded rainfall data set at a spatial resolution of 0.25° × 0.25° (Pai et al. 2014), which is constructed from a network of 6955 rain gauge stations spread across the country (see Fig. 1 in Pai et al. 2014), is also used in this study. This high resolution data demonstrates that spatial distribution of rainfall over northeast regions are more realistic due to high density of rainfall stations over these areas. The seasonal June–September gridded rainfall data has been constructed using this product for evaluating the spatial response of summer monsoon rainfall over NE-India during the opposite phases of SSTs over the Atlantic.
-
6.
Teleconnections are determined using simple statistical techniques like composite and correlation analysis. The significance for correlation coefficients are tested using student’s T test method (Kendall and Stuart 1979) and the spatial maps by Bootstrap method (Efron and Tibshirani 1993). Normally, to test the significance of the correlation fields, the field significance test defined by Livezey and Chen (1983) for large samples or the bootstrapping method (Efron and Tibshirani 1993), especially for small sample size is utilized. While the Field significance as defined by Livezey and Chen (1983) accounts for spatial correlations in any geophysical variable field, there are certain limitations in the manner in which this is done. Specifically, the above test is based on ‘counts’ and therefore, does not account for ‘location’ of the significant correlations, i.e., the test does not account for the geographic dependence of the spatial correlations. Another shortcoming of the above test is that it does not account for the ‘magnitude’ of the significant correlations. Hence, we have opted for Bootstrapping method. Bootstrapping is a statistical method that uses data resampling with replacement to estimate the robust properties of nearly any statistic. Most commonly, these include standard errors and confidence intervals of a population parameter like a mean, median, correlation coefficient or regression coefficient. Bootstrapping statistics has two attractive attributes: (a) It is particularly useful when dealing with small sample sizes and (b) It makes no a priori assumption about the distribution of the sample data. The real strength of this method is sampling with replacement (Efron and Tibshirani 1993). Therefore, the combinations of samples (we have used 1000 samples) are limitless and are driven by random number generators from Monte Carlo. Further, since the number of observations we have used is small (29 years: 1979–2007), we have adopted this method. The level of significance is maintained at 95% confidence level throughout the analysis.
3 NEISMR teleconnections
NE-India is close to subtropics and is least explored in terms of evaluating prospective predictors pertaining to its summer monsoon rainfall. The NH subtropical variations, such as Atlantic SSTs and Eurasian snow cover, which are associated with low frequency surface forcings on interannual timescale in teleconnection patterns, have been comprehensively looked into for probable linkages. In general, SST and snow have the capability to exhibit the greatest tempo-spatial variability for different surface conditions (Varikoden and Babu 2014; Cohen 1994). Hence, to understand the proxies for summer monsoon variability over NE India, inter-relationships of NEISMR, NH-SST and NH-snow at various lag and lead times are examined.
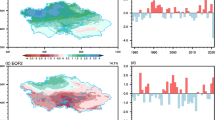
Correlation map of wintertime SWE (January) with the ensuing NEISMR (JJAS) carried out for a 29-year period spanning 1979–2007 reveals a robust inverse relationship between the two (Fig. 1b). Although correlation does not necessarily demonstrate causation but it provides an indication for the association between two components. Also, there is a physical basis for the teleconnection between Eurasian snow and summer monsoon rainfall over India as demonstrated by the earlier studies (Kripalani and Kulkarni 1999, Kripalani et al. 1996). Interestingly, during the same period, a similar spatial correlation map analysis carried out between SWE (January), which is averaged over the Eurasian region (50°–70°N, 70°–140°E), along with covarying NH-SSTs (January), reveal an out of phase relationship between the two, prominently over the tropical Atlantic (Fig. 1c). Furthermore, for the period 1979–2007, a simultaneous correlation map carried out between the NEISMR (JJAS) and the summertime NH-SST (JJAS) shows a significantly robust direct relationship between the two over the tropical Atlantic region (Fig. 1d). The above mentioned three relationships are prominent over the two regions of interest (ROI) namely the Eurasian region as defined over the area (50°–70°N, 70°–140°E; as shown in Fig. 2a) and the Atlantic Ocean region as defined over the area (0°–25°N, 60°W–10°E; as shown in Fig. 2b, c). From these three linkages we build up a hypothesis that states: An excess of snow over the Eurasian region in boreal winter cools down considerably the local temperature and is associated with the negative mode of Arctic Oscillation (AO) that brings cold dry winds into NH-Atlantic and induces a meridional wave train from sub-polar latitudes towards the equator having a descending branch over the tropical Atlantic, leading to a high pressure area. Once the cold anomalies are established over the north Atlantic, it persists up to the following summer further inducing a zonal wave-train that descend over NE-India subsequently resulting in weak monsoon rainfall. A schematic representation of the hypothesis as mentioned above linking NEISMR, tropical north Atlantic SST and Eurasian snow is shown in Fig. 3.
Correlation maps over the region of interest (ROI) for the relationship of a Eurasian SWE (January) with NEISMR (JJAS), b Eurasian SWE (January) with Atlantic SST (January) and c Atlantic SST (JJAS) with NESIMR (JJAS) as identified from Fig. 1b–d respectively. Statistical significance at 95% loc is shown as black slanting lines
4 Testing of hypothesis for a possible physical mechanism
To validate the hypothesis, we carry out a correlation analysis during the month of January between SWE and air temperature averaged over the Eurasian ROI (area shown in Fig. 2a) at 1000 hPa for the period 1979–2007. Figure 4a reveals an inverse relationship between the two with a correlation coefficient (cc) of −0.60 significant at 95% confidence level. This depicts that an anomalous increase in SWE leads to an anomalous cooling of surface temperatures over the Eurasian region. In the past, studies carried out using observations (Sankar-Rao et al. 1996) and general circulation models (Walland and Simmonds 1997) also revealed reduction in lower tropospheric temperature due to excessive snow anomaly. Bamzai and Shukla (1999) too have documented that there is a close relationship between snow cover extent and surface temperatures over Eurasia. Further, there have been studies in the past that accentuates on boreal autumn (winter) NH snow to be influencing the subsequent (simultaneous) winter AO (Saito et al. 2001; Cohen et al. 2002; Gong et al. 2002). Regional cooling due to excessive snow could potentially create atmospheric effects that propagate to other regions through atmospheric teleconnections (Namias 1985). It is well comprehended that global warming has a direct impact on the Arctic seaice decline leading to frequent occurrences of negative modes of AO causing more recurrent extreme heat and heavy rainfall events over the mid-latitide regions (Francis and Vavrus 2012). Apparently, the AO spring variability has been found to be associated with the subsequent East Asian summer monsoon (Gong and Ho 2003). But by far the cause has remained unclear for such remote teleconnections. Although, the AO is observed in all the seasons, it has a dominant mode of variability in winter (Thompson and Wallace 1998). Saito and Cohen (2003) demonstrate that continental-scale snow cover during boreal winter as a potential contributor to the interannual variability of the atmosphere. Next, we assess the simultaneous wintertime relationship between Eurasian snow and AO.
a Standardized time series of SWE and air temperature at 1000 hPa during the month of January over the Eurasian region of interest (ROI) as defined in Fig. 2a (50°–70°N, 70°–140°E). An inverse relationship having a correlation coefficient (cc) = −0.60, significant at 95% loc is observed between the two, b standardized time series of SWE over Eurasia as defined in Fig. 2a and the AO for the month of January depicting an inverse correlation (cc = −0.52, significant at 95% loc)
4.1 Effect of winter excess snow on AO
To comprehend the effect of near-surface cold temperature anomalies due to excessive Eurasian snow on the AO, we have constructed AO index (AOI) following Thompson and Wallace (1998) as the leading empirical orthogonal function of monthly values of wintertime (January) SLP anomalies poleward of 20°N. The primary mode of variability explains 41% of total variance associated with the NH-SLP. Figure 4b demonstrates interannual variability for the month of January between SWE over the Eurasian ROI (area shown in Fig. 2a) and the AOI during the period 1979–2007. An inverse relationship (cc = −0.52) significant at 95% confidence level is observed between the two. Consequently, an anomalous cooling over sub-polar latitudes in the month of January due to an excess snow is likely to influence the negative mode of AO.
Next, to understand the dominant atmospheric anomaly patterns prevailing during the negative mode of AO, we carry out the composite analysis of GPH anomalies for 10 strongest (Negative-minus-Positive) AO events. The years with standardized anomalies of AOI below and above 0 (as shown by orange line in Fig. 4b) are considered to be representing negative and positive AO events respectively. Accordingly, the ten strongest events of AOI considered for negative AO years are 1985, 1998, 1994, 2004, 1986, 1982, 1995, 2001, 1999 and 1996 while for positive AO years are 1993, 1989, 2007, 1992, 1983, 2002, 1997, 2000, 2006 and 1991. These years are arranged according to its decreasing strength of standard anomalies. Figure 5 shows distinctly the “annular” patterns of a negative phase of AO during the month of January (Fig. 5a) and also for the winter season from December through February (DJF) (Fig. 5b) at various atmospheric levels. Noticeably, the GPH anomalies in the month of January depict the pattern of negative phase of AO with an anomalous high over sub-polar latitudes (~65°N) and an anomalous low over the belt of mid-latitudes (~45°N). These anomaly patterns are more prominent at mid (500 hPa) and upper (200 hPa) atmospheric levels. Monahan et al. (2003) using nonlinear principal component technique revealed that while the positive mode of AO represent a strong polar vortex, the negative phase represents a breakdown of the polar vortex with more meridional and spatially variable flow patterns. Ding and Wang (2007) emphasized that anomalous GPH high over the northwest Europe followed by a low over the north of Caspian Sea and further a positive anomaly over northwest India infers to a Rossby wave propagation connecting these regions. In summary, the occurrence of wintertime excess snow over Eurasia cools down the regional surface considerably influencing the negative mode of AO. Next, we assess a robust pathway through meridional wave-train from sub-polar to tropical latitudes at different atmospheric levels during the existence of a negative phase of AO.
4.2 Meridional circulation during negative mode of AO
Mean meridional circulation, which is a zonally averaged meridional overturning motion connecting the tropics, mid- and sub-polar latitudes, is a key component of the global atmospheric general circulation having implications on changes in weather and climate patterns, particularly for the occurrence of severe floods and droughts around the world (Meehl and Bony 2011; Taylor et al. 2012). Figure 6 portrays anomalous Hadley/Ferrel circulation for the Atlantic longitudes averaged over 60°W–10°E, which is constructed by performing composite analysis for 10 strong (negative–minus–positive) AO events during the month of January as mentioned above. Although, AO associated with Eurasian wintertime snow (as seen in Fig. 5), is an annular mode covering over all the longitudes (Fig. 5), the Atlantic longitudes over 60°W–10°E are preferred for carrying out this analysis because of two factors, first one being, the Atlantic SSTs linkage to the Eurasian snow over ROI as shown in Fig. 2b during the month of January, and the second one, for its persistence effect, which means the Atlantic Ocean’s capability to retain the signal up to the subsequent summer monsoon season as demonstrated in the following section. Prevalence of cold belt over ~65°N and a warm belt over ~45°N from surface to 200 hPa is clearly observed implying a barotropic meridional wave-train associated with wintertime negative mode of AO. Manifestation of this pattern induces a descending branch over the northern tropical latitudes over the Atlantic making this region anomalously cooler. This pattern is similar to a Rossby-wave train propagating from Europe to Asia triggered by an excessive Eurasian snow anomaly during the spring season (March–May) as observed by Liu and Yanai (2002).
Meridional atmospheric circulation patterns for composites of 10 strongest (negative-positive) AO January events. The anomalous Hadley/Ferrel circulation pattern is shown for the Atlantic longitudes averaged over 60°W–10°E. The shaded plot is of vertical velocity in Pa/s (scaled by −0.01). It is superimposed by wind vectors in m/s. Statistical significance at 95% loc is shown as dot marks
4.3 Wintertime connection of snow-SST and SST Persistence
In the earlier section, we focused on the connection between Eurasian Snow and the AO, wherein an excess of wintertime snow leads to a negative mode of AO resulting in cooling over the tropical Atlantic through the meridional wave train. Further, to ascertain a possible role of excessive snow over Eurasia associated with cooling over the tropical Atlantic during the peak winter month of January, we carry out a lead-lag correlation between the two. The interannual time series of Atlantic SSTs in January is computed by averaging SSTs over the area as defined in Fig. 2b (0°–25°N, 60°W–10°E). This area over Atlantic is selected for generation of SST time series, as it is significantly correlated with Eurasian snow in the month of January (refer to Fig. 2b) and also with NEISMR during JJAS (refer to Fig. 2c). It may be noted that the selected box over Atlantic does not maximize the correlation, but is selected because of its clear physical meaning. As expected, a simultaneous inverse wintertime relationship (cc = −0.48, significant at 95% confidence level) between SWE over Eurasia and SSTs over tropical Atlantic is observed (Fig. 7a). A clear evolutionary feature is visible with correlation coefficients amplifying from the month of October in the previous year through to ensuing January and thereafter gradually decaying. Captivatingly, this relationship is seen to be dominant for the boreal winter month of January. Henderson et al. (2013) evaluated the atmospheric circulation response caused due to snow forcing using Atmospheric General Circulation Model with slab ocean model, wherein SST and sea ice concentration were used as the boundary conditions. Their study revealed that circulation response to maximum Eurasian snow cover in early winter led to significant Atlantic SST cooling, in agreement with our observational findings.
a Correlation analyses of Eurasian SWE [averaged over area as shown in Fig. 2a (50°–70°N, 70°–140°E)] during the month of January with Atlantic SSTs [averaged over area as shown in Fig. 2b (0°–25°N, 60°W–10°E)] where ‘−1’ represents month of previous year. b Auto-correlation analyses of January SST over the defined box with the SSTs over the same area for the subsequent months from February through December. Dashed line indicates the line of significance at 95% loc for the data period considered from 1982–2007
It is believed that major climatic memory on timescales of months to years is located in the tropical oceans (Webster et al. 1998). Hence, once cold anomalies are manifested over the tropical north Atlantic region in boreal winter (January), they tend to persist up to the following summer season. Due to high thermal inertia of sea, the anomalous SST is one of the most suitable variables to be used as a climatic predictor. The persistence of wintertime north Atlantic SST anomalies have been studied earlier by Watanabe and Kimoto (2000), de Coëtlogon and Frankignoul (2003) and the authors therein. Next, we assess how the north Atlantic SST cold anomalies during winter (January) act as an extended memory almost a season later. The persistence effect is examined by carrying out an autocorrelation analysis as shown in Fig. 7b. Again, a clear indication of persistence is noticed with magnitude of this relationship reducing gradually from January through to summer. Noticeably, Atlantic SST cold anomalies in the month of January sustain itself up to the following summer season (JJAS). Moreover, the cold imprints over the tropical Atlantic are also observed to be retained till the ensuing boreal autumn (October through November).
4.4 Linking SST-NEISMR through zonal circulation
Trenberth et al. (2000) emphasized that Hadley and Walker circulations are the strongest links to precipitation. The associated ocean–atmospheric feedback resulting from north Atlantic cold SST anomalies on the NE-Indian sector during summer monsoon season (JJAS) is evaluated through Walker circulation that demonstrates the behaviour of wind field zonally. Accordingly, Fig. 8 displays an anomalous zonal wave pattern associated with a significant cooling branch of the zonal wave located over the north Atlantic. Further, this zonal wave train is observed to have a descending branch over the NE-India sector eastward of 90°E. Furthermore, this pattern appears to be out of phase with central-India (west of 80°E). While the descending motion over the NE Indian longitudes is more apparent over the upper troposphere, the ascending motion over the central Indian longitudes is visible over the lower troposphere. Hence, the ascending and descending nodes over the Indian mainland and NE-India sector respectively may partly explain the diverse behavior between central- and NE-India. The consequence of such an atmospheric phenomenon on spatial distribution of summer monsoon rainfall during JJAS is evaluated next, exclusively over the regions of NE-India.
Zonal atmospheric circulation patterns for composites of (negative–positive) SST years for 10 strongest cases averaged over the latitudinal belt (0°–25°N) during the summer monsoon season (JJAS). The shaded plot is of vertical velocity in Pa/s (scaled by −0.01). It is superimposed by wind vectors in m/s. Statistical significance at 95% loc is shown as dot marks
4.5 Implication of cold SST anomalies on NEISMR
To examine the dominant spatial rainfall pattern over NE-India prevailing during anomalously cold SSTs over the Atlantic, we first construct a standardized SST index (SSTI) for the period 1982–2007 (as the SST data is available from December 1981 onwards) averaged over the Atlantic region as defined in Fig. 2c (0°–25°N, 60°W–10°E) during the summer monsoon season (JJAS). Years with standardized SSTI below and above 0 are considered as negative and positive SST events respectively. Accordingly, the ten strongest negative SSTI years are 1992, 1982, 1986, 1983, 1985, 1994, 1984, 2002, 1990 and 2001 while the positive SSTI years are 1987, 2003, 1999, 1995, 1998, 2005, 2007, 2004, 1989 and 1988. These years are arranged according to its decreasing strength of standard anomalies. Finally, the composites for ten strongest (negative minus positive) SST events are evaluated. Figure 9 clearly depicts a statistically significant below normal rainfall spread over NE India, barring a few intermittent areas of positive rainfall, thus proving the hypothesis using observational data.
Spatial pattern of NEISMR (mm) from IMD precipitation data obtained from composites of 10 strongest (negative–positive) SST events defined over the Atlantic region as shown in Fig. 2c (0°–25°N, 60°W–10°E) during the summer monsoon season (JJAS). Statistical significance at 95% loc is shown as dot marks
5 Summary
While there has been an extensive effort, over the past few decades, to investigate the predictors for All-India based summer monsoon rainfall, the NE-Indian sector comparatively has received much lesser attention in terms of establishing its plausible teleconnections. The rainfall variability over NE-India is often out of phase with that of central-India. Geographically being closer to the NH mid-latitude jet streams, the large scale variability of higher northern latitudes could play an important role in modulating the NEISMR.
Consequently, a possible connection between Eurasia, Atlantic and NE-India is proposed in this study. The study reveals that Eurasian snow variability significantly influences the summer monsoon rainfall over NE-India during the boreal winter month of January. An excessive wintertime snow over Eurasia leads to an anomalous surface cooling and is associated with the negative mode of AO. Prevalence of a cold belt over ~65°N and a warm belt over ~45°N from surface to 200 hPa leads to a barotropic meridional wave-train inducing a descending branch over the northern tropical latitudes centered over the Atlantic making this region anomalously cooler. Tropical oceans is believed to hold a major climatic memory on timescales of months to years. Hence, once cold anomalies are manifested over the Atlantic during boreal winter, it persists up to the following summer and zonally induces a descending motion over the regions of NE-India resulting in below normal rainfall.
In summary, through this study, the authors attempt to envisage an influence of low-frequency wintertime Eurasian snow forcing on NEISMR through the north Atlantic SST Bridge. However, it would be interesting to carry out sensitivity experiments using an appropriate SST forced atmospheric model to further ascertain the links as proposed in this study. In essence, while the summer monsoon rainfall over major parts of India (excluding the NE region) appears to be related with events in the Southern Hemisphere, namely the Southern Annular Mode through the Pacific SSTs (Amita et al. 2016), the variation of NEISMR appears to be related with events in the Northern Hemisphere through the AO, Eurasian snow and Atlantic SSTs.
References
Ambrizzi T, Hoskins BJ, Hsu HH (1995) Rossby wave propagation and teleconnection patterns in the austral winter. J Atmos Sci 52:3661–3672
Amita P, Mahajan PN, Khaladkar RM (2012) Association of the Indian summer monsoon rainfall variability with the geophysical parameters over the Arctic region. Int J Climatol 32:2042–2050. doi:10.1002/joc.2418
Amita P, Kripalani RH, Preethi B, Pandithurai G (2016) Potential role of the February–March Southern Annular Mode on the Indian summer monsoon rainfall: a new perspective. Clim Dyn 47(3):1161–1179
Armstrong RL, Brodzik MJ, Knowles K, Savoie M (2007) Global monthly EASE-grid snow water equivalent climatology. National Snow and Ice Data Center. Digital media, Boulder
Bamzai AS (2003) Relationship between snow cover variability and Arctic oscillation index on a hierarchy of time scales. Int J Climatol 23:131–142
Bamzai AS, Kinter JL III (1997) Climatology and interannual variability of Northern Hemisphere snow cover and depth based on satellite observations. Center for Ocean–Land–Atmosphere studies, Report 52, COLA, 4041 Powder Mill Road, Suite 302, Calverton, MD 20705, USA
Bamzai AS, Shukla J (1999) Relationship between Eurasian snow cover, snow depth, and the Indian summer monsoon: an observational study. J Clim 12:3117–3132
Barimala R, Bracco A, Kucharski F (2012) The representation of the south Tropical Atlantic teleconnection to the Indian Ocean in the AR4 coupled models. Clim Dyn 38:1147–1166. doi:10.1007/s00382-011-1082-5
Blanford HF (1884) On the connection of Himalayan snowfall with dry winds and seasons of drought in India. Proc R Soc Lond 37:3–22
Bojariu R, Gimeno L (2003) The role of snow cover fluctuations on multiannual NAO persistence. Geophys Res Lett 30:1156. doi:10.1029/2002GL015651a
Clark MP, Serreze MC, Robinson DA (1999) Atmospheric controls on Eurasian snow extent. Int J Climatol 19:27–40
Cohen J (1994) Snow cover and climate. Weather 49:150–156
Cohen J, Entekhabi D (1999) Eurasian snow cover variability and northern hemisphere climate predictability. Geophys Res Lett 26:345–348
Cohen J, Salstein D, Saito K (2002) A dynamical framework to understand and predict the major Northern Hemisphere mode. Geophys Res Lett 29(10):1412. doi:10.1029/2001GL014117
de Coëtlogon G, Frankignoul C (2003) The persistence of winter sea surface temperatures in the North Atlantic. J Clim 16:1364–1377
Ding Q-H, Wang B (2007) Intraseasonal teleconnection between the summer Eurasian wave train and the Indian Monsoon. J Clim 20:3751–3767
Efron B, Tibshirani RJ (1993) An introduction to the bootstrap. Chapman and Hall, New York
Francis JA, Vavrus SJ (2012) Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys Res Lett 39:L06801. doi:10.1029/2012GL051000
Gong D-Y, Ho C-H (2003) Arctic Oscillation signals in East Asian summer monsoon. J Geophys Res 108(D2):4066. doi:10.1029/2002JD002193
Gong G, Entekhabi D, Cohen J (2002) A large-ensemble model study of the wintertime AO–NAO and the role of interannual snow perturbations. J Clim 15:3488–3499
Goswami BN, Madhusoodanan MS, Neema CP, Segupta D (2006) A physical mechanism for North Atlantic SST influence on the Indian summer monsoon. Geophys Res Lett 33:L02706. doi:10.1029/2005GL024803
Graham NE (1994) Decadal-scale climate variability in the tropical and North Pacific during the 1970s and 1980s: observations and model results. Clim Dyn 10:135–162
Hahn DG, Shukla J (1976) An apparent relationship between Eurasian snow cover and Indian monsoon rainfall. J Atmos Sci 33:2461–2462
Hall DK, Martinec J (1985) Remote sensing of ice and snow. Chapman and Hall, New York
Henderson GR, Leathers DJ, Hanson B (2013) Circulation response to Eurasian versus North American anomalous snow scenarios in the northern hemisphere with an AGCM coupled to a slab ocean model. J Cli 26:1502–1515
Hoskins BJ, Ambrizzi T (1993) Rossby wave propagation on a realistic longitudinally varying flow. J Atmos Sci 50:1661–1671
Kalnay E et al (1996) The NCEP/NCAR 40-year re-analysis project. Bull Am Meteorol Soc 77:437–471
Kendall MG, Stuart A (1979) The advanced theory of statistics, vol 2: inference and relationship, 4th edn. Griffin. ISBN: 0852642555. Hodder Arnold, p 758
Kripalani RH, Kulkarni A (1999) Climatology and variability of historical Soviet snow depth data: some new perspectives in snow—Indian monsoon tele-connection. Clim Dyn 15:475–489
Kripalani RH, Singh SV, Vernekar AD, Thapliyal V (1996) Empirical study on Nimbus-7 snow mass and Indian summer monsoon rainfall. Int J Climatol 16:23–34
Krishna Kumar K, Rajagopalan B, Hoerting M, Bates G, Cane M (2006) Unraveling the mystery of Indian monsoon failure during El-Niño. Science 314:115–119
Krishnamurthy L, Krishnamurthy V (2015) Teleconnections of Indian monsoon rainfall with AMO and Atlantic tripole. Clim Dyn. doi:10.1007/s00382-015-2701-3
Kucharski F, Bracco A, Yoo JH, Tompkins AM, Feudale L, Ruti P, Dell’Aquila A (2009) A Gill–Matsuno-type mechanism explains the tropical Atlantic influence on African and Indian monsoon rainfall. Q J R Meteorol Soc 135:569–579
Kulkarni A, Kripalani RH, Singh SV (1992) Classification of summer monsoon rainfall patterns over India. Int J Climatol 12:269–280
Liu X, Yanai M (2002) Influence of Eurasian spring snow cover on Asian summer rainfall. Int J Climatol 22:1075–1089
Livezey RE, Chen WY (1983) Statistical field significance and its determination by Monte Carlo techniques. Mon Weather Rev 111:46–59
Maykut GA (1978) Energy exchange over young sea-ice in the central Arctic. J Geophys Res 83:3646–3658
Meehl GA, Bony S (2011) Introduction to CMIP5. CLIVAR Exch Newslett 16(2):4–5
Monahan AH, Fyfe JC, Pandolfo L (2003) The vertical structure of wintertime climate regimes of the northern hemisphere extratropical atmosphere. J Clim 16:2005–2021
Munot AA, Kothawale DR (2000) Intra-seasonal, inter-annual and decadal scale variability in summer monsoon rainfall over India. Int J Climatol 20:1387–1400
Namias J (1985) Some empirical evidence for the influence of snow cover on temperature and precipitation. Mon Weather Rev 113:1542–1553
Pai DS (2004) A possible mechanism for the weakening of El Niño monsoon relationship during the recent decade. Meteorol Atmos Phys 86:143–157
Pai DS, Sridhar L, Rajeevan M, Sreejith OP, Satbhai NS, Mukhopadhyay B (2014) Development of a new high spatial resolution (0.25 × 0.25 degree) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 65(1):1–18
Parthasarathy B, Sontakke NA, Munot AA, Kothawale DR (1987) Droughts/floods in the summer monsoon season over different meteorological subdivisions of India for the period 1871–1984. J Cimatol 7:57–70
Parthasarathy B, Munot AA, and DR Kothawale DR (1995) Monthly and seasonal rainfall series for all-India homogeneous regions and meteorological subdivisions: 1871–1994, Research Report, RR-65, IITM, Pune, India
Preethi B, Mujumdar M, Kripalani RH, Prabhu Amita, Krishnan R (2016) Recent trends and tele-connections among South and East Asian summer monsoons in a warming environment. Clim Dyn. doi:10.1007/s00382-016-3218-0
Rajeevan M (2002) Winter surface pressure anomalies over Eurasia and Indian summer monsoon. Geophys Res Lett 29(10):1454. doi:10.1029/2001GL014363
Raman CRV, Maliekal JA (1985) A ‘northern oscillation’ relating northern hemispheric pressure anomalies and the Indian summer monsoon? Nature 314:430–432
Reynolds RW, Rayner NA, Smith TM, Stokes DC, Wang W (2002) An improved in situ and satellite SST analysis for climate. J Clim 15:1609–1625
Sabeerali CT, Rao SA, Ajaymohan RS, Murtugudde R (2012) On the relationship between Indian summer monsoon withdrawal and Indo-Pacific SST anomalies before and after 1976/1977 climate shift. Clim Dyn 39:841–859. doi:10.1007/s00382-011-1269-9
Saito K, Cohen J (2003) The potential role of snow cover in forcing interannual variability of the major Northern Hemisphere mode. Geophys Res Lett 30(6):1302. doi:10.1029/2002GL016341
Saito K, Cohen J, Entekhabi D (2001) Evolution of atmospheric response to early-season Eurasian snow cover anomalies. Mon Weather Rev 129:2746–2760
Sankar-Rao M, Lau KM, Yang S (1996) On the relationship between Eurasian snow cover and the Asian summer monsoon. Int J Climatol 16:605–616
Shukla J (1998) Predictability in the midst of chaos: a scientific basis for climate forecasting. Science 282:728–731
Srivastava AK, Rajeevan M, Kulkarni R (2002) Teleconnection of OLR and SST anomalies over Atlantic Ocean with Indian summer monsoon. Geophys Res Lett 29(8):1284. doi:10.1029/2001GL013837
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. doi:10.1175/BAMS-D-11-00094.1
Thompson DWJ, Wallace JM (1998) The Arctic Oscillation signature in the wintertime geopotential height and temperature fields. Geophys Res Lett 25:1297–1300
Thompson DWJ, Wallace JM (2000) Annular modes in the extratropical circulation. Part I: month-to-month variability. J Clim 13:1000–1016
Trenberth KE, Hurrell JW (1994) Decadal atmosphere–ocean variations in the Pacific. Clim Dyn 9:303–319
Trenberth KE, Stepaniak JM, Caron JM (2000) The global monsoon as seen through the divergent atmospheric circulation. J Clim 13(22):3969–3993
Varikoden H, Babu CA (2014) Indian summer monsoon rainfall and its relation with SST in the equatorial Atlantic and Pacific Oceans. Int J Climatol. doi:10.1002/joc.4056
Walker GR (1910) Correlations in seasonal variations of weather II. Mem Indian Meteorol Dept 21:22–45
Walland DJ, Simmonds I (1997) Modelled atmospheric response to changes in Northern Hemisphere snow cover. Clim Dyn 13:25–34
Wang B, Xiang B, Li J, Webster PJ, Rajeevan MN, Liu J, Ha K-J (2015) Rethinking Indian monsoon rainfall prediction in the context of recent global warming. Nat Commun 6:7154. doi:10.1038/ncomm8154
Watanabe M, Kimoto M (2000) On the persistence of decadal SST anomalies in the North Atlantic. J Clim 13:3017–3028
Webster PJ, Magafia VO, Palmer TN, Shukla J, Tomas RA, Yanai M, Yasunari T (1998) Monsoons: processes, predictability, and the prospects for prediction. J Geophys Res 103(C7):14451–14510
Winstanley D (1973) Recent rainfall trends in Africa, the Middle East and India. Nature 243:464–465
Yadav RK (2016) On the relationship between east equatorial Atlantic SST and ISM through Eurasian wave. Clim Dyn. doi:10.1007/s00383-016-3074-y
Zhang R, Delworth TL (2006) Impact of Atlantic multidecadal oscillations on India/Sahel rainfall and Atlantic hurricanes. Geophys Res Lett 33:L17712. doi:10.1029/2006GL026267
Acknowledgements
Indian Institute of Tropical Meteorology (IITM) is fully supported by Ministry of Earth Sciences, Government of India. The authors wish to thank the Director, IITM for undertaking this study. The first author also wishes to acknowledge the support of Pukyong National University, Busan, South Korea for providing the necessary facilities in bringing the manuscript to its present state. Amita Prabhu was supported by the Korea Meteorological Administration Research and Development Program under the Grant KMIPA2015-6130 for her period of stay in Korea from January to December 2016. The first author also wishes to acknowledge useful discussions with S. Rao, R. Chattopadhyay and R.K. Yadav from IITM during the initial course of this work. Authors are also grateful to IMD-NCC, NCEP, NCAR, NOAA and NSIDC for freely providing their data products. We have used NCAR Command Language (NCL) script for computing correlation maps employing Bootstrapping method.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Prabhu, A., Oh, J., Kim, Iw. et al. Summer monsoon rainfall variability over North East regions of India and its association with Eurasian snow, Atlantic Sea Surface temperature and Arctic Oscillation. Clim Dyn 49, 2545–2556 (2017). https://doi.org/10.1007/s00382-016-3445-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3445-4