1 Introduction

Ocean reanalyses (ORAs) represent an important tool for understanding ocean variability and climate change (Lee et al. 2009) and underpin a number of forecast activities, such as operational oceanography and seasonal-to-decadal prediction (Rienecker et al. 2010). ORAs employ a variety of ocean general circulation models (OGCMs) and data assimilation schemes to synthesize a diverse network of available ocean observations in order to arrive at a dynamically consistent estimate of the historical ocean state. The nature of the underlying OGCM, data assimilation scheme and observations used varies, often according to the role for which the ORA is intended. For example, systems designed for near real-time forecasts of the ocean mesoscale tend to use higher resolution OGCMs and satellite altimeter data will feature strongly in the assimilation system. Conversely, systems that are used primarily for estimating the ocean state over the 20th Century will tend to use coarser resolution OGCMs and/or simpler assimilation schemes for reasons of computational expense. In addition, a number of products combine the available observations into spatially-complete gridded fields using purely statistical approaches, without the use of an OGCM.

Intercomparison of ORAs promotes insights into the performance of data assimilation systems, the underlying physical models, and adequacy of the ocean observing system to constrain key variables of interest, such as ocean heat content change (e.g. Carton and Santorelli 2008; Xue et al. 2012). Here we present a comparison of a number of state-of-the-art products as part of the Ocean Reanalysis Intercomparison Project (ORA-IP; Balmaseda et al. 2015), which is an international research collaboration led by the CLIVAR Global Synthesis and Observations Panel (GSOP) and the Global Ocean Data Assimilation Experiment (GODAE) community. The scope of ORA-IP includes various aspects of the ocean state, including the following: sea level; mixed layer depth; ocean salinity; surface fluxes and mass; heat and freshwater transports. The present work focuses on the representation of OHC variability and change as represented by an ensemble of ORAs (Table 1).

Table 1 Overview of the different ORAs used in this study
Full size table

OHC is a key variable for initialization of seasonal-to-decadal predictions (Balmaseda et al. 2010; Dunstone and Smith 2010) and the rate of ocean heat uptake under anthropogenic climate change plays an important part in determining future global surface temperature and sea level rise (Kuhlbrodt and Gregory 2012). Improved understanding the processes that control OHC variability and change may offer the potential to reduce uncertainties in future climate change projections through application of suitable observational constraints (e.g. Stott and Forest 2007). Thus ORAs have an important role to play in development of improved forecasts on a range of timescales and in refining our understanding of future global and regional climate change.

OHC variability and change is a particularly topical research area, given the strong scientific and wider media interest in the recent slowdown in surface temperature rise (e.g. Hawkins et al. 2014), often referred to as the global warming ‘hiatus’ (e.g. Trenberth and Fasullo 2013). Increased ocean heat uptake and the vertical re-arrangement of heat in the ocean have both been proposed as key mechanisms that have contributed to the ‘hiatus’. Heat re-arrangement has been linked primarily with the tropical Pacific (Meehl et al. 2011; England et al. 2014) but there is evidence that the higher latitudes may also have played a role (Chen and Tung 2014; Drijfhout et al. 2014; Roemmich et al. 2015).

ORAs provide an important resource for improving our understanding of the ocean’s role in modulating global surface temperature rise on interannual to decadal timescales. Analysis of climate model simulations has shown substantial vertical re-arrangement of ocean heat and highlighted the global ocean’s dominant role in Earth’s energy budget on annual-to-decadal timescales (Palmer et al. 2011; Palmer and McNeall 2014). Through combining the available ocean observations with OGCMs, ORAs may offer new insights into the processes of vertical heat re-arrangement and have also be used to derive estimates of Earth’s energy imbalance (Loeb et al. 2012; Trenberth et al. 2014; Smith et al. 2015).

Despite the recent development of the Argo network of profiling floats (Roemmich et al. 2009), historical observations of ocean temperature are sparse in time and space (Purkey and Johnson 2010; Desbruyères et al. 2014), often limited to a particular depth range, and may require correction for instrumental biases (Abraham et al. 2013). These issues mean that there are substantial—and difficult to quantify—uncertainties in our knowledge of ocean heat content change during the late twentieth and early twenty first centuries. One way to evaluate this uncertainty is using the spread of different reanalysis products that use ostensibly the same raw information, but different methodologies, to evaluate the same variable of interest. Previous studies have used similar ‘ensembles of opportunity’ to characterize the uncertainty in upper ocean heat content derived from statistical analyses (Lyman et al. 2010; Palmer et al. 2010; Abraham et al. 2013).

Estimates of the past ocean state are fundamentally limited by the availability of historical ocean profiles. Prior to the inception of the Argo array profiling floats in the early 2000s, reasonable ocean coverage is only afforded for the upper few hundred meters since the late 1960s (Roemmich et al. 2012; Lyman and Johnson 2014). As a result, many of the historical estimates of OHC variability and change have been limited to the upper 700 m or so (Lyman et al. 2010; Palmer et al. 2010; Abraham et al. 2013). In addition, the upper layers of the ocean are widely regarded to be the primary source of predictability for seasonal forecast systems, for example for initializing the tropical Pacific for ENSO forecasts (Xue et al. 2012). For these reasons, much of our analysis focuses ocean depth ≤700 m.

We present spatial patterns of depth-integrated temperature for the following: (i) the climatological time mean; (ii) the amplitude of the seasonal cycle; (iii) internannual variability; (iv) decadal and multi-decadal trends. We also compare zonal averages of (i) and (ii). The manuscript is organized as follows. In Sect. 2 we present an overview of the ORA datasets used. The pre-processing steps and analysis methods are presented in Sect. 3. The results are presented in Sects. 4–7 and cover the following aspects: the time-mean OHC and seasonal cycle; interannual variability; time series of OHC; and spatial trends of OHC. In Sect. 8 we present our closing discussion and summary.

2 Data

A total of 19 ORAs are used in the intercomparison presented here. These span a range of time periods and have a diverse set of data assimilation methods and underlying ocean model configurations (Table 1). While the majority of products include a dynamic OGCM, three of the products are based on statistical analysis of the observations (ARMOR3D, EN3 and NODC) and do not include a dynamic model component. Note that the ARMOR3D product only covers the upper 2000 m. For the purposes of this intercomparison the deeper levels use the NODC climatology and therefore the variability and change signals below 2000 m for ARMOR3D are very small, by construction. We use a version of the EN3 analysis that is based on profiles with expendable bathythermograph (XBT) corrections applied following table 1 of Wijffels et al. (2008). The NODC data have mechanical baythermograph (MBT) and XBT bias corrections applied as described in Levitus et al. (2012). All data providers carried out the computation of vertically-integrated temperature for a number of vertical layers (see Sect. 3) and interpolated the data onto a regular 1 × 1 degree latitude-longitude grid. To ensure consistency among the grids used, all data were subsequently post-processed using the Climate Data Operator bilinear re-mapping tool.

3 Methods

For the purposes of this intercomparison, the different production centers provided monthly-mean two-dimensional fields of depth-integrated potential temperature, 〈θ〉, from the surface to a number of fixed depths, defined as:

$$\left\langle\uptheta \right\rangle = \int {\uptheta\,({\text{x}},{\text{y}},{\text{z}})} \,{\text{dz}}$$

with units Celsius meters (Cm). Throughout much of the manuscript we use depth integrated temperature as basis of the intercomparison. An advantage of 〈θ〉 is that it has an intuitive physical interpretation. For example, a change in 〈θ〉 of 70 Cm over the 0–700 m layer is equivalent to a 0.1 C average change over the column. Annual time series of OHC are generated for each hemisphere and the globe by spatially integrating maps of 〈θ〉 and multiplying by reference values of seawater density (1025 kg m−3) and specific heat capacity (3985 J kg−1 K−1). These time series are converted to OHC anomalies by subtracting the mean value over a reference period. The integration depths specified for the intercomparison were: 0–100 m; 0–300 m; 0–700 m; 0–1500 m; 0–3000 m; 0–4000 m; and the full water column (0–bottom). For some products the closest model level was used for the integration, provided that this was within a few meters of the specified depth. The data are analyzed as a ‘true’ integral, meaning that the summation is inclusive of all ocean model grid boxes shallower than the lower bound of the integration. Thus the number of ocean grid points for each product is the same for all layer integrals and, for example, the 300–700 m layer can be reconstructed by simply subtracting the 0–300 m layer from the 0–700 m layer.

Monthly climatologies for each product are computed for the period 1993–2009, with the exception of MOVECORE (see Sect. 2), for which we use the period 1993–2007. These climatologies are used in two aspects of the intercomparison. Firstly, the time-average for each grid box is computed to provide a comparison of the mean state of the period 1993–2009. Secondly, the amplitude of the climatological seasonal cycle is computed for each grid box by simply subtracting the minimum monthly value from the maximum monthly value. The remainder of the analysis presented here is carried out using annual mean values of 〈θ〉.

Maps of interannual variability are computed for the period 1993–2009 (except MOVECORE, which uses 1993–2007). The variability for each ORA is computed as the standard deviation of annual values for each grid box after removing a linear trend. Lastly, spatial maps of 〈θ〉 change are computed by fitting a linear trend to each grid box over the periods 1970–2009 and 1997–2009, with the latter period intended to characterize ocean heat content changes during the surface warming ‘hiatus’ period.

In our analysis of interannual variability (calculated for each product following the removal of ORA-specific climatologies), we follow the ‘signal-to-noise’ definition of Xue et al. (2012). Here, the ‘signal’ (S) is defined as the temporal standard deviation of the ensemble mean over a specified period. The ‘noise’ (N) is defined as the temporal average of the standard deviation of ensemble spread over the same period. This definition of S/N is thus a measure of the average spread across the ensemble relative to the signal of the ensemble mean. Areas where S/N < 1 can be interpreted as regions where differences in the underlying ocean models tend to dominate over the ability of the available observations and data assimilation schemes to constrain the ORA solutions. In the other spatial map comparisons presented here we often show the ensemble mean (M), the ensemble standard devidation (SD) and the ratio of the two (M/SD) to provide an indication of the spread and level of agreement among ORAs.

4 Time-mean and amplitude of the seasonal cycle

The first aspect of our intercomparison is the time-mean 〈θ〉 over the 0–700 m layer for the period 1993–2009 (Figs. 1, 2). The largest differences across the ensemble are mostly associated with areas of high eddy kinetic energy (EKE), such as the Southern Ocean and boundary current regions. The representation of high EKE regions depends strongly on the resolution of the underlying OGCM and also the extent to which the ORA solution is constrained by satellite altimeter data, which can impact subsurface temperature and OHC (Lea et al. 2014). Not all ORAs assimilate satellite altimeter data (Table 1) and those that do may differ according to any errors in the mean dynamic topography (MDT) used in the assimilation (Haines et al. 2011). Differences in MDT and both hydrography and altimeter assimilation methods are particularly important in the Southern Ocean, and may explain the large spread and positive/negative dipoles exhibited in that region. Differences in the North Atlantic sector are likely associated with differing representation of the Atlantic meridional overturning circulation and the associated heat transport (Pohlmann et al. 2013; Valdivieso et al. 2015). While model resolution affects the simulation of the AMOC, studies have shown that the mean value can be reasonably well represented in ¼ degree models (Roberts et al. 2013), although the associated heat transports are too weak (Haines et al. 2013).

Fig. 1
figure 1

Anomaly of climatological depth-integrated temperature for the 0–700 m layer (Celsius meters) for each ORA relative to the ensemble mean. Also shown is the ensemble mean, standard deviation and signal-to-noise ratio. All values are computed for the period 1993–2009, except for MOVECORE (1993–2007)

Full size image
Fig. 2
figure 2

Zonally averaged anomaly of 0–700 m depth-integrated temperature, relative to the ensemble mean, for individual ORAs. All curves are shown in each panel and plotted in grey or according to the legend. A common data mask has been applied to all products. All values are computed for the period 1993–2009, except for MOVECORE (1993–2007)

Full size image

Many of the analyses show a widespread cool or warm bias, relative to the ensemble mean (e.g. SODA, GloSea). Disentangling the roles of differing ocean vertical mixing, ocean circulation and surface forcings in determining these biases is a challenging problem and requires further and detailed analysis. Errors in both momentum and heat fluxes have a role here (Lee et al. 2013; Valdivieso et al. 2015) and consideration of mixed layer depths may also offer additional insights (Toyoda et al. 2015). The representation of vertical mixing in ocean models remains an area that requires particular attention due to the different mixing schemes, related parameters and the often poorly quantified effects of numerical mixing (e.g. Buchard et al. 2008). Regionally, the departures from the ensemble mean can exceed ±500 Cm, or 0.7 C in terms of the depth-averaged temperature (Fig. 1). However, the zonal averages show that all analyses are generally within ±350 Cm (or 0.5 C) of the ensemble mean between 60S and 60N (Fig. 2). The increased spread north of 60N may be indicative of differing representation of the Arctic marginal ice zones and may be exacerbated by the reduction of ocean grid points at these latitudes.

The amplitude of the seasonal cycle of 〈θ〉 over the 0–700 m layer is well constrained by the ORA ensemble over the vast majority of the ocean (Fig. 3). The largest differences among the ORAs are often associated with areas of high EKE, as well as the North-west Pacific and central Indian Ocean. There is no obvious relationship between the individual ORAs representation of the ocean mean-state and the amplitude of the seasonal cycle, as seen by comparing Figs. 1 and 3. The zonal average plots show a similar morphology among the ORAs for the seasonal cycle amplitude (Fig. 4), with a characteristic off-equatorial double-peak and maxima around 40N/S—corresponding to the latitude of maximum wind stress curl and seasonal changes in Ekman divergence. Differences in the locations of the peaks at about 40N/S are therefore likely indicative of different wind-driven circulations among the ORAs. In addition, the MOVE products show another peak around 65–70N, in the region of the northern hemisphere marginal ice zone. Generally, the MOVE products show a larger amplitude seasonal cycle than the other ORAs and particularly pronounced peaks at 40N/S. Differences across the ensemble can arise from the representation of ocean vertical mixing, surface fluxes and also the data assimilation.

Fig. 3
figure 3

Top row ensemble mean (M); ensemble standard deviation (SD); and the ratio of the two (M/SD) for the amplitude of the seasonal cycle over the 0–700 m layer. Lower panels the difference between each ORA and the ensemble mean. All values are computed for the period 1993–2009, except for MOVECORE (1993–2007)

Full size image
Fig. 4
figure 4

Zonally averaged amplitude of the seasonal cycle in the 0–700 m layer for individual ORAs. All curves are shown in each panel and plotted in grey or according to the legend. A common data mask has been applied to all products. All values are computed for the period 1993–2009, except for MOVECORE (1993–2007)

Full size image

5 Interannual variability

ORA estimates of interannual variability over the 0–300 m layer (Fig. 5) show a S/N ratio >1 over most of the North Atlantic, Pacific and Indian Oceans. The South Atlantic and Southern Ocean typically show S/N values <1, due to weak signal and a combination of weak signal and relatively large ensemble noise, respectively. Again, areas of high EKE emerge as the regions of largest ensemble spread. Interannual variability in the products without an OGCM (i.e. ARMOR3D and EN3) is generally lower than the other ORAs, particularly in the Southern Ocean where observations are sparse and mesoscale variability is high.

Fig. 5
figure 5

Interannual variability of depth-integrated temperature for the 0–300 m layer (Celsius meters) for each ORA, computed as the temporal standard deviation of annual mean values for each grid box after removing a linear trend. White areas indicate where no data are available. Also shown is the ensemble average temporal standard deviation (‘signal’, S), the temporal average of the ensemble standard deviation (‘noise’, N), and the ratio of the two (S/N). The ensemble values (top row) are computed for each grid box based on all available data. All values computed for 1993–2009 except for MOVECORE (1993–2007)

Full size image

For the 300–700 m layer, we see a dramatic reduction in S/N ratio for the ensemble (Fig. 6). Areas where S/N > 1 are still found throughout large regions of the Pacific, but limited to isolated areas in the tropical Indian Ocean and the Northeast Atlantic. Compared to the 0–300 m layer, the change in S/N appears to be dominated by a reduction in the signal, with the noise having a similar spatial pattern and magnitude.

Fig. 6
figure 6

Same as Fig. 5, but for the 300–700 m layer

Full size image

The comparison of interannual variability for the 700–6000 m layer (Fig. 7) shows that there is very little agreement in the deep ocean such that S/N < 1 in almost all locations. We note that the products without an OGCM (ARMOR3D and EN3) generally have lower variability than the other ORAs. This is not surprising, as for the majority of this depth range, these products are unconstrained by observations and relax to climatology. In contrast, the ORAs that include an OGCM component are free to generate variability that is consistent with the model dynamics, even if it is not constrained by in situ observations. Some models show particularly large variability in the Southern Ocean and North Atlantic (e.g. GECCO, GODAS), but it is not clear whether this can be considered true interannual variability, or whether it is related to drift associated with long-timescale adjustments in the deep ocean. We also note that there appears to be a relationship between the regions of high signal and high noise for this depth range. The patterns show a strong resemblance to the distribution of mode waters (Hanawa and Talley 2001) and also include regions associated with open ocean convection and deep water formation (Marshall and Schott 1999). The implication is that the different ORAs vary in their representation of these water formation processes, owing to different surface forcings and representation of vertical mixing, as discussed in the previous section.

Fig. 7
figure 7

Same as Fig. 5, but for the 700–6000 m layer

Full size image

6 Time series of OHC change

Similar to previous studies (Lyman et al. 2010; Palmer et al. 2010; Abraham et al. 2013), ORA time series of OHC change for the 0–700 m vary in a number of aspects, including: interannual variations; the estimated response to the major volcanic eruptions in 1963, 1982 and 1991; decadal and multi-decadal trends (Fig. 8). The range of trends and spread among the analyses for the global ocean is similar to the statistical products presented in the IPCC 5th Assessment report (Rhein et al. 2013). A number of products appear to show large initialization or spin-up ‘shock’—i.e. an initial and rapid change in OHC in the first few years of the time series. Separating the time series by hemisphere illustrates the larger spread in the Southern Hemisphere—consistent with the lack of observations over this domain.

Fig. 8
figure 8

Time series of ocean heat content change, relative to a 1993–2007 baseline. All curves are shown in each panel and plotted in grey or according to the legend. To aid comparison the NODC product has been highlighted in black in all panels

Full size image

Many ORAs qualitatively support the findings of Balmaseda et al. (2013b); exhibiting enhanced ocean heat uptake below 300 m from the mid-1990s or early 2000s (Fig. 9a, b). This includes both of the statistical analyses (ARMOR3D and EN3), showing that an OGCM is not required to capture this behavior. Balmaseda et al. (2013b) suggested that the additional heat uptake below 300 m simulated by ORAS4 was associated with changes in the Pacific Decadal Oscillation and also a weakening of the AMOC. However, it remains unclear how much of this enhanced deep ocean heat uptake might be explained as a sampling artifact. Cheng and Zhu (2014) showed that the dramatic improvement in ocean sampling during the initiation of Argo resulted in an artificial jump in OHC over 0–700 m during 2001–2003. Given the lack of historical in situ ocean observations south of about 20S, it seems plausible that much of the increase in deep ocean heat uptake demonstrated by the ORAs during the 2000s may result from Argo suddenly ‘revealing’ a longer-term Southern Ocean warming signal (Roemmich et al. 2015).

Fig. 9
figure 9

Time series of ocean heat content change for a range of depth intervals, computed to a baseline period of 1948–1993 for illustrative purposes. The dashed grey lines indicate the equivalent heating rate (W m−2) computed for Earth’s surface area

Full size image

Some of the full depth OHC time series show very large rates of change—exceeding 3 W m−2 globally during some periods—and such changes cannot be reconciled with satellite-based reconstructions of Earth’s energy imbalance (Allan et al. 2014) or the global sea level budget (Church et al. 2011). CFSR (Fig. 9a) shows very some large, almost oscillatory, changes in OHC below 700 m that may be linked to previously documented discontinuities in deep ocean temperature and salinity (Xue et al. 2011). For the MOVE products (Fig. 9b), the large rates of OHC change are a known feature related to the use of vertical empirical orthogonal functions in those products.

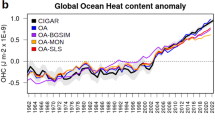
Since the rate of OHC change is the quantity of primary interest in the context of the understanding Earth’s energy imbalance, we fit rolling 5-year linear trends to each the ORA time series, following Smith et al. (2015). These time series are used to generate an ORA ensemble mean and standard deviation, for the various depth levels, integrated over the globe and each hemisphere with rates of OHC change expressed in W m−2 relative to the surface area of the Earth (Fig. 10). We omit CFSR and GODAS due to their large initialization ‘shock’ (Fig. 8) and also MOVECORE because the simulation terminates in 2007, resulting in a 15-member ORA ensemble for the period 1993–2009.

Fig. 10
figure 10

5-year rolling trends of ocean heat content change over various depth layers for: the Globe (black); Northern Hemisphere (red); and Southern Hemisphere (blue). The solid lines show the ensemble mean with shaded regions indicating ±1 standard deviation. Changes are expressed as equivalent heating rate, in W m−2, relative to Earth’s surface area. Trends plotted relative to the mid-point of each 5-year period. Results are based on 15 ORAs as described in the text

Full size image

As one would expect, the 0–300 m layer shows a relatively narrow spread, particularly for the Northern Hemisphere (Fig. 10). It is interesting to note that the Northern and Southern Hemisphere appear to be anti-correlated in these upper layers and this could be related to changes in the AMOC and associated changes in inter-hemispheric heat transport. The magnitude of mean global OHC change for the 0–300 m layer peaks at about 0.5 W m−2. The 300–700 m layer shows similar rates and sign of OHC change in both hemispheres, but a much larger spread in the Southern Hemisphere. Peak rates of the mean global OHC change are about 0.4 W m−2 for this layer. Below 700 m the mean global rate of OHC change is dominated by the Southern Hemisphere with the peak rate around 1997/1998. OHC integrated over the full column (Fig. 10, 0–6000 m) shows a fairly steady mean global rate of 0.9 ± 0.8 W m−2 for the period 1995–2002 that drops to 0.2 ± 0.6 W m−2 for the period 2004–2006 (error bars indicate 1 standard deviation of ensemble mean), in qualitative agreement with the findings of Smith et al. (2015). However, there is no evidence in our ORA ensemble mean of the ‘spike’ in OHC trends reported by Smith et al. in the early 2000s.

In terms of the ORA ensemble standard deviation, the spread in systematically less in the Northern Hemisphere than the Southern Hemisphere. This is probably a combination of both the better observational coverage and the lesser ocean volume north of the equator. There is a tendency towards reduced spread for all series over time, but this is not monotonic. Although the data here are limited to 2009, we appear to see the impact of Argo observations becoming available in the sharp reduction in ORA ensemble spread for the Southern Hemisphere below 300 m after about 2004 (Fig. 10).

7 Spatial patterns of OHC change

For the ORAs with data available back to 1970 (EN3, GECCO, ORAS4, SODA), we calculate linear trends in OHC for three layers (0–300, 300–700, and 700 m to bottom). For the upper 300 m (Fig. 11), the large scale pattern of warming is well-captured by the available ORAs, even in wide areas of the Southern Ocean, and there is agreement on the enhanced warmth of the North Atlantic sub-polar gyre relative to the global oceans. The equatorial Pacific and Indian oceans are areas where the ORA ensemble standard deviation exceeds the mean trend. This lack of agreement could be related to the large interannual variability in these regions associated with ENSO which will promote larger spread in the long-term trends through ‘end point’ effects. For 300–700 m (Fig. 12), the agreement across ORAs is substantially reduced, although there are some still some areas (e.g. North Atlantic) where the signals appear to be common across models. It is also surprising that some signals in the Southern Ocean appear to be consistent across products. However, the number of ORAs available for this comparison is limited (N = 4) so we should treat such evidence of ‘agreement’ across products with caution. For the 700 m-bottom layer (Fig. 13), the ensemble mean and spread across the ensemble is dominated by the very large signals in the GECCO product: this ORA exhibits a strong warming in the Atlantic and Sourthern Ocean and a cooling in the Indo-Pacific. Given the absence of strong observational constraints for this depth range during this period, it seems likely that these signals are unrepresentative of the real ocean and probably related to adjustment of the OGCM.

Fig. 11
figure 11

Trends in 0–300 m vertically-integrated temperature (Celsius meters per year) for the period 1970–2009. White areas indicate where no data are available. Also shown is the ensemble mean trend (M), the standard deviation of ensemble trends (SD), and the ratio of the two (M/SD). The ensemble values (top row) are computed for each grid box based on all available data

Full size image
Fig. 12
figure 12

Same as Fig. 11, but for the 300–700 m layer

Full size image
Fig. 13
figure 13

Same as Fig. 11, but for the 700–6000 m layer

Full size image

To evaluate the level of agreement in the spatial patterns of heat uptake and heat rearrangement by the ocean during the recent slow-down in global warming, we calculate spatial trends in OHC for the period 1997–2009. For the upper 300 m (Fig. 14), ORAs show agreement in a dipole pattern of warming in the West Pacific and cooling in the East Pacific. This is consistent with previous studies documenting increased sea surface heights and ocean temperatures in the West Pacific warm pool associated with the negative phase of the Pacific Decadal Oscillation (PDO) and a sustained increase in the Pacific trade winds (e.g. England et al. 2014). Although there is some agreement for a pattern of warming in the tropical and north Atlantic, there are large areas where the ORA ensemble spread exceeds the ensemble mean, which is perhaps surprising given that it is one of the best-observed regions of the global oceans. This may be indicative of the influence of dynamic processes, which are likely to vary among ORAs, as discussed in previous sections. Noise across the ensemble is largest in areas of ocean fronts, and there is very little agreement in the sign or magnitude trends in the Southern Ocean, likely reflecting the relative lack of observations in this region.

Fig. 14
figure 14

Trends in 0–300 m vertically-integrated temperature (Celsius meters per year) for the period 1997–2009. White areas indicate where no data are available. Also shown is the ensemble mean trend (M), the standard deviation of ensemble trends (SD), and the ratio of the two (M/SD). The ensemble values (top row) are computed for each grid box based on all available data

Full size image

For 300–700 m depth range (Fig. 15), agreement across the ensemble is limited to selected regions of sub-tropical convergence in the West Pacific and the North Atlantic sub-polar gyre. Ensemble spread is largest in the Southern Ocean, with products showing no agreement on whether there has been warming or cooling in this layer during this period.

Fig. 15
figure 15

Same as Fig. 14, but for the 300–700 m layer

Full size image

For the deepest layer (700 m to bottom, Fig. 16), there is virtually no agreement across ORAs for OHC trends during 1997–2009. Although the ensemble mean shows a particularly strong warming in the North Atlantic and more widespread warming in the Southern Ocean, there is no consensus on the magnitude of change. Perhaps notably, both ARMOR3D and EN3 (products that do not include a dynamical ocean model) exhibit warming signals in these regions. Warming of the North Atlantic sub-polar gyre is qualitatively consistent with previous studies that have linked such changes with a reduction in densities and a decline of the AMOC (e.g. Robson et al. 2014; Roberts et al. 2014).

Fig. 16
figure 16

Same as Fig. 14, but for the 700–6000 m layer

Full size image

8 Summary

We have presented a comparison of the representation of OHC variability and change as estimated by 16 state-of-the-art ORAs, focusing on five main aspects: (i) the time-mean state during 1993–2009; (ii) the amplitude of the seasonal cycle during 1993–2009; (iii) interannual variability during 1993–2009; (iv) global and hemispheric time series; (v) spatial patterns of change for 1970–2009 and 1997–2009.

The time-mean state and amplitude of the seasonal cycle for the 0–700 layer are generally well-constrained among the ensemble, but regional differences may warrant further investigation. We find that interannual variability for the 0–300 m can be resolved by the ORA ensemble over the majority of the Indo-Pacific and much of the Atlantic. However, the signal-to-noise ratio rapidly diminishes as one considers deeper layers.

Global time series of OHC show similar rates of change and ensemble spread to previous studies based only on statistical estimates. Comparison of the hemispheric OHC time series illustrates that the majority of the spread among analyses originates in the Southern Hemisphere. Several ORAs, including those that do not include an OGCM are in qualitative agreement about an increase in ocean heat uptake below 300 m from the mid 1990s or early 2000s. However, a number appear to suffer from large initialization shock and/or drifts in the deep ocean (where this is little observational constraint on the OGCM solution) so caution should be taken when using such products to estimate the global ocean heat inventory.

Spatial patterns of OHC change for the 0–300 m layer over the period 1970–2009 show large areas of agreement (ensemble mean trend > standard deviation of trends), based on the four analyses included here. While this area is reduced for the 300–700 m layer there remains some agreement on large-scale regions of warming in the Atlantic, Pacific and Southern Oceans. For the 700–6000 m layer only isolated regions of the Southern Ocean and central Atlantic show trends that are resolved by the ensemble spread.

The spatial trends of OHC for the 1997–2009 period generally show large areas of agreement for the 0–300 m, with the Pacific characterized by an east–west dipole. At deeper levels there is little or no agreement among the ensemble. However, the ensemble mean trends for the 700–6000 m layer show the largest warming trends in the North Atlantic sub-polar gyre, north Indian Ocean and Southern Ocean.