1 Introduction

Recent studies indicate that two types of El Niño (EN) have occurred over the last five decades, one with SST anomalies peaking in the eastern Pacific and the other peaking in the central equatorial Pacific (Larkin and Harrison 2005; Ashok et al. 2007; Kug et al. 2009). Whether the two types of events have distinct dynamics remains unclear, although ENSO positive skewness, a property arising from eastern Pacific events, could be associated with oceanic nonlinear advection (An and Jin 2004). Stochastically forced linear models fitted to observations are able to capture some aspects of the ENSO diversity (e.g. Newman et al. 2011b), but linear dynamics alone can not generate the nonlinear relation between the first two dominant statistical modes of equatorial Pacific SST anomalies, which has been proposed to emerge from dual EN regimes, with the 1982–1983 and 1997–1998 events corresponding to different dynamics from the other EN (Takahashi et al. 2011; Capotondi et al. 2015).

There have been various theories to explain the underlying physics of strong EN events, including oceanic nonlinear advection (Timmermann et al. 2003), nonlinear convective response to SST (Ohba and Ueda 2009; Dommenget et al. 2012; Choi et al. 2013), state dependent noise acting under EN favorable conditions (Lengaigne et al. 2004; Jin et al. 2007), all potentially producing asymmetric features of ENSO, like its skewness, the asymmetric time evolution of strong EN and La Niña (LN) event (Ohba and Ueda 2009; Okumura and Deser 2010) or the asymmetric pattern of the zonal wind stress along the equator (Kang and Kug 2002). Note that the study of ENSO nonlinearities has been mostly oriented towards explaining the aforementioned statistical features of ENSO, rather than focusing on the development phase of the strong warm events, which could convey other insights on their dynamics and predictability.

A major limitation to observationally study the strong EN is that only two of these events have been observed comprehensively, and even so only the 1997–1998 EN had subsurface temperature and surface winds fully observed by the TAO/TRITON array, while ocean analysis based on data assimilation suffer from model dependence (Su et al. 2010). From an empirical perspective, it would then be very difficult to propose generalizations purely based on observations. However, the synergistic analysis of observations and realistic numerical models could provide a way forward.

Here we expand on previous studies (Takahashi et al. 2011; Dommenget et al. 2012) by investigating the possible existence and the nonlinear processes responsible for the ENSO regimes associated to strong and moderate EN events, using available observations and long-term simulations with the GFDL CM2.1 model. In this paper, we first describe the datasets and basic processing (Sect. 2), then assess whether the results support the existence of distinct EN regimes (Sect. 3.1), analyze the roles of oceanic (3.2) and atmospheric (3.3) nonlinearities, and analyze the temporal evolution and predictor variables (3.4). Finally, we discuss some implications of the results (Sect. 4) and then summarize the main conclusions (Sect. 5).

2 Data

2.1 Observational data

The monthly HadISST v1.1 dataset (1870–2010) (Rayner et al. 2003) is used for calculating SST anomalies and the \(E\) and \(C\) indices, as in Takahashi et al. (2011). For this, we consider the first two normalized principal components (PC) of the equatorial Pacific (\(10^\circ \hbox {S}-10^\circ \hbox {N}\)) SST anomalies and calculate the indices as \(E=(\mathrm{PC}1-\mathrm{PC}2)/\sqrt{2}\) and \(C=(\mathrm{PC}1+\mathrm{PC}2)/\sqrt{2}\). These indices are uncorrelated by construction and describe the SST variability in the eastern and central equatorial Pacific, respectively (Fig. 1a, c).

Fig. 1
figure 1

Linear regression maps of SST (°C, shading), wind stress (\(10^{-2}\) Nm−2, only vectors with magnitude greater than \(5\times 10^{-3}\) Nm−2), and precipitation (blue contours for 0.5, 1, 1.5, 2, and 3 mm day−1, similar for negative values in red) onto the a, b \(E\) and c, d \(C\) indices, with data from a, c observations (HadISST, WASWIND, GPCP) and b, d the GFDL CM2.1 model (500-year PI control run). Also shown are equatorial (5°S–5°N) averaging boxes a \(u_E\) (160°W–120°W) and c \(u_C\) (160°E–160°W) for observations [b \(u_E\) (170°W–120°W) and d \(u_C\) (140°E–170°W) for CM2.1]

Full size image
Fig. 2
figure 2

Observed (HadISST, 1920–2013; solid circles) and CM2.1 (control and 20th century runs; open circles) EN peaks (\(E\) vs. \(C\)). \(k\)-means clusters, identified separately for the observations and model, are indicated in blue (moderate EN) and red (strong EN) with the centers of the clusters as triangles. The bivariate \(E\)–\(C\) probability density function for CM2.1 is contoured. The year corresponding to each observed EN peak is indicated

Full size image

Daily surface (4 m) wind observations from the TAO/TRITON buoy array (McPhaden et al. 1998) for 1993–2013, when temporal and spatial sampling is approximately homogeneous, are used to calculate monthly pseudo-stress anomalies from the climatology for the same period and wind stress is estimated using a neutral drag coefficient of \(1.2\times 10^{-3}\) (e.g. Harrison 1989). We also use the ship-based monthly wind stress anomalies from WASWind v.1.0 (Tokinaga and Xie 2011) for the 1950–2010 period (base period 1980–2009), which has best continuity along ship tracks. To represent atmospheric deep convection, we use the monthly NOAA interpolated outgoing longwave radiation (OLR) anomalies for 1974–2013 based on the 1980–2009 climatology (Liebmann and Smith 1996).

Subsurface ocean temperatures were obtained from the SODA 1.4.2 reanalysis (Carton and Giese 2008) for the 1958–2001 period. This dataset is based on the assimilation of ocean temperature and salinity measurements into a global ocean GCM forced by observationally-based surface fluxes. Monthly anomalies were calculated based on the 1979–2009 period (1979–2001 for SODA data). The linear trend was removed from the anomalies. The zonal tilt of the equatorial \(20\,^\circ \hbox {C}\) isotherm depth was estimated by fitting a linear relation to longitude between 120°E–80°W and reporting the corresponding east–west depth difference. The mean 20 °C isotherm depth or heat content was estimated by zonally averaging over the same longitudinal range.

We also use the Drakkar oceanic analysis over 1958–2007 for carrying out a heat budget analysis of the upper 50 m layer in the equatorial band. Drakkar is based on the NEMO 3.0 ocean general circulation model with observational surface boundary conditions based on ERA40 reanalysis, as detailed in (Brodeau et al. 2010). Details on the simulation and model validation results for the equatorial Pacific can be found in Lengaigne et al. (2012). In addition to its realism in this region, a motivation for using Drakkar, instead of a product with full ocean data assimilation, is that the heat budget is closed, whereas in other products, with subsurface data assimilation, energy is not necessarily conserved.

2.2 The GFDL CM2.1 model

Tropical climate and ENSO in CM2.1 was initially analyzed by Wittenberg et al. (2006) and they found it to be generally realistic although with some limitations. For instance, as many climate models, it has a mean cold bias along the equatorial Pacific and warm bias along the coast of South America, as well as a double ITCZ in the eastern Pacific. ENSO variability is substantially stronger than in the observations, presumably due to the weakness of damping by surface heat fluxes, in turn associated with mean biases in convection patterns related to the cold bias. The latter also results in a westward displacement of the SST variability by around 20–30° longitude. Additionally, the seasonal phase locking is not as strong as observed. Despite these limitations, CM2.1 simulates realistically many aspects of the ENSO, including its diversity (Kug et al. 2010) and decadal modulation (Wittenberg et al. 2014).

Here we use monthly data from the 500-year pre-industrial control run, with anomalies relative to this period. For the \(E\) and \(C\) statistics we additionally use the detrended SST anomalies from the 5-member 20th century ensemble 140-year runs (total of 1200 years).

Kug et al. (2010) analyzed ENSO events in this model according to the relative sizes of the anomalies in the (modified) Niño 3 and 4 regions and found the diversity of events to be reasonably realistic. Lengaigne and Vecchi (2009) identified this model as one of the few that reproduced the observed precipitation characteristics of the strongest EN. Takahashi et al. (2011) noted that this model reproduces qualitatively the nonlinear relation of the between the eastern (\(E\)) and central (\(C\)) Pacific SST indices seen in observations (see their Fig. 2). The spatial patterns linearly associated with the \(E\) and \(C\) indices are shown in Fig. 1 and are qualitatively similar between the observations and CM2.1, although there is a well documented westward shift in the model associated with a equatorial cold bias (Kug et al. 2010).

3 Regimes and nonlinearity

3.1 Bimodality and El Niño regimes

As Takahashi et al. (2011) pointed out, when the boreal winter anomalies EN are analyzed in the \(E\)–\(C\) space, the 1982–1983 and 1997–1998 EN stand out together separate from the rest, with a large \(E\). Here we do not assume that EN peaks can be identified in a single season, but rather take them as the maximum value of monthly 1-2-1-filtered PC1 = \((E+C)/\sqrt{2}\) that exceeds 0.6, the 75 % percentile of PC1 in CM2.1, within 2-year running windows, regardless of season.

The resulting 250 EN peaks in CM2.1 (PI control and 20th century runs) have a bimodal probability distribution function [PDF, estimated with locfit (Loader 1997)] in \(E\)–\(C\) phase space, with a mode corresponding to the strong EN, with high values of \(E\) and small positive \(C\), and the other mode corresponding to moderate EN with somewhat larger \(C\) but much smaller \(E\) (Fig. 2).

A \(k\)-means cluster analysis (Hartigan and Wong 1979) for both observations and CM2.1 with \(k=2\) yields clusters matching the modes in the CM2.1 PDF, with the boundary approximately at \(E=1.8\) and their centers near the modes of the PDF (Fig. 2). The correspondence between the model and observational regimes is surprisingly good considering the limitations of the model. In observations, only the 1982–1983 and 1997–1998 EN correspond to the strong regime (\(E>3\)), and the others to the moderate regime, although the 1972–1973 EN lies over the boundary (\(E=1.8\)). The two observed strong EN have somewhat larger \(E\) and \(C\) than the center of the CM2.1 mode, which could be a random fluctuation but could also reflect the larger nonlinearity in the Bjerknes feedback in the eastern Pacific in observations (see Sect. 3.3).

Fig. 3
figure 3

Similar to Fig. 2 for a all the EN peaks in CM2.1, and b–f dividing the EN peaks in CM2.1 into five disjoint subsets

Full size image
Fig. 4
figure 4

Monthly evolution during strong EN events of: a \(C\) and b \(E\) SST indices, equatorial c mean (HC) and d zonal tilt of the depth of the equatorial 20 °C isotherm, and zonal wind stress indices for the e eastern (\(u_E\)) and f central (\(u_C\)) equatorial regions. Each plot shows the median (lines with circles), the quartiles, and the 10 and 90 % percentiles for the events in the strong EN regime. The observational data for the 1982–1983 and 1997–1998 extraordinary strong EN events are shown in red and blue, respectively. The observational wind stress indices e, f are from WASWind (solid), ERA (dotted) and TAO (\(\times\), only for the 1997–1998 event)

Full size image

The robustness of the two regimes was tested in CM2.1 by dividing the set of 250 EN peaks into five disjoints subsets of 50 peaks each. They all reproduced the same clusters (Fig. 3) and, in four out of five subsets, the bimodal PDF. The relatively quiescent last 250 years of the preindustrial control run of CM2.1 (Fig. 3b; that includes period M1 in Wittenberg 2009) resembles the observational period in that it has few strong EN events, so the corresponding mode in the PDF of this subset could not be depicted, although the two clusters were identified similarly to the other subsets. We note that \(k=3\) does not consistently reproduce the same three clusters among the subsets.

For observations, statistical significance of the existence of a strong regime was assessed by taking as null hypothesis that only one regime (moderate EN) exists and that \(E\) is normally distributed within it, so the 1982–1983 and 1997–1998 EN events would have emerged from such a PDF. We verified that, after excluding the 1982–1983 and 1997–1998 EN, the \(E\) values have approximately a gaussian distribution, as indicated by a q–q plot (not shown) and the fact that the skewness is only 0.3 (this increases to 1.6 if the two extreme events are retained). Based on the fitted gaussian distribution, values of \(E>1.8\) would have a random probability of only 1.6 %, whereas the 1982–1983 and 1997–1998 values (\(E>3\)) would have effectively null probability. Thus, we reject the hypothesis that only one gaussian-distributed regime exists and that the two strong EN belong to it.

We also verify that the temporal evolution of the two observed strong EN is very consistent with the events in CM2.1 (Fig. 4). For instance, both observed and modelled strong EN feature weakly positive values of \(C\) and heat content during year (0) and strongly negative values in year (1) (Fig. 4a, c), whereas \(E\) and the thermocline tilt peak between years (0) and (1) (Fig. 4b, d). Additionally, the zonal wind stress indices associated to the \(E\) and \(C\) warming patterns (\(u_E\) and \(u_C\), respectively; see domain definition in caption of Fig. 1) are also consistent between the observations and the model (Fig. 4e, f). While \(u_E\) tends to peak near the end of year (0), consistent with \(E\), the evolution of the \(u_C\) wind stress anomaly in CM2.1 shows a double westerly peak in the most extreme cases, one around March–April of year (0) and the next around October–November (0) (Fig. 4e), similar to what was observed in 1997, whereas in 1982 there was only one peak in August-September, consistent with the lower end of the events in CM2.1. In both observations and CM2.1, the \(u_C\) anomaly becomes substantially negative during year (1), which has been explained in terms of the seasonality of deep convection and the meridional displacement of the westerly anomalies (Vecchi and Harrison 2006; McGregor et al. 2012). It is important to mention that the second westerly peak in 1997 is evident in the ERA Interim and the TAO/TRITON buoys (which had full spatial and temporal coverage for that period), but not in the WASWind data, apparently due to the gap between ship tracks around the dateline and the equator. The evolution of the \(u_E\) anomaly approximately follows that of \(E\), with positive \(u_E\) values in more than 90 % of the CM2.1 strong EN starting in September(0), at which time 90 % of the events show \(E\) values larger than \(\approx 0.7\) (Fig. 4f, b).

The existence of two distinct EN regimes, associated with different spatial patterns, and the strong nonlinear relation between E and C (Takahashi et al. 2011), suggests that nonlinearity in ENSO dynamics is responsible. Next we explore the possible roles that nonlinearities in ocean advection (e.g. Jin et al. 2003) and the atmospheric convective response to SST play in the origin of these regimes.

3.2 Ocean nonlinear advection as a positive feedback

To understand the oceanic processes that control the SST changes in the two EN regimes, we analyze the role of temperature advection in the heat budget of a 50 m-deep surface ocean layer (Jin et al. 2003; An and Jin 2004). The anomalous budget is formulated as:

$$\begin{aligned} \frac{\partial [T']}{\partial t} = \mathrm{ADV}_{XY}+\mathrm{ADV}_Z+\mathrm{NDH}+Q_\mathrm{net}'+R' \end{aligned}$$
(1)

where \(T'\) is the temperature anomaly. Square brackets indicate vertical averaging in the layer. The advective terms have been separated into horizontal and vertical linear terms:

$$\begin{aligned} \mathrm{ADV}_{XY}\equiv & {} \left[ -u'\frac{\partial \overline{T}}{\partial x} -v'\frac{\partial \overline{T}}{\partial y} -\overline{u}\frac{\partial T'}{\partial x} -\overline{v}\frac{\partial T'}{\partial y}\right] \end{aligned}$$
(2)
$$\begin{aligned} \mathrm{ADV}_{Z}\equiv & {} \left[ -w'\frac{\partial \overline{T}}{\partial z} -\overline{w}\frac{\partial T'}{\partial z}\right] , \end{aligned}$$
(3)

respectively, while the “non-linear dynamical heating” (NDH; Jin et al. 2003) is defined as:

$$\begin{aligned} \mathrm{NDH}\equiv & {} \left[ \,\,\,\,-u'\frac{\partial T'}{\partial x} -v'\frac{\partial T'}{\partial y} -w'\frac{\partial T'}{\partial z}\right. \nonumber \\&\left. \,+\,\overline{u'\frac{\partial T'}{\partial x}} +\overline{v'\frac{\partial T'}{\partial y}} +\overline{w'\frac{\partial T'}{\partial z}}\,\right] \end{aligned}$$
(4)

The bars and the primes indicate climatological values and anomalies, respectively. We should note that, in contrast to Jin et al. (2003) and An and Jin (2004), our calculation of NDH explictly removes the seasonality of the nonlinear advection (last three terms in Eq. 4).

The surface heat fluxes, distributed through the layer, are represented by \(Q_\mathrm{net}'\) and \(R'\) is the residual from Eq. 1, which includes mixing processes, not explicitly estimated here, and the errors associated with the calculations and approximations. It was verified that \(R'\) is small compared to the other terms during the EN development period, although it becomes more significant during the decaying phase.

The ocean heat budget for CM2.1 was calculated from monthly output for ocean temperatures, 3D velocities and surface heat fluxes. Spatial and temporal derivatives were calculated using a centered-difference scheme, except that advantage was taken of the vertical grid staggering to estimate the vertical advection by using the same numerical scheme as in the model. For Drakkar, the vertical velocity was estimated assuming mass conservation.

After computing the horizontal fields corresponding to the terms in Eq. 1, these were then projected onto the spatial patterns of the first two SST EOFs, taken between \(2^\circ \hbox {S}\) and \(2^\circ \hbox {N}\), and linearly combined as per the definition of \(E\) and \(C\), which is equivalent to averaging the tendency terms over the regions of main influence of the \(E\) and \(C\) patterns (Fig. 1). This provided an estimate of the contribution of each budget term to the changes in the principal components, which were then combined to estimate the contributions to the changes associated with \(E\) and \(C\). We verified that the heat content tendencies \(\partial [T']/\partial t\) projected in this way are comparable to the temporal derivative of the \(E\) and \(C\) indices, which allows using the heat budget analysis to assess the contributions of oceanic processes to the changes in \(E\) and \(C\).

Fig. 5
figure 5

Annual change (January–December) in upper 50 m ocean temperature anomalies associated with \(E\) contributed by a total, b linear, and c nonlinear advection, plotted against the total change. The linear contribution is further separated into d zonal, e meridional, and f vertical advection. The DRAKKAR reanalysis and CM2.1 from the PI control are shown in black and grey, respectively. The onset and decay (positive and negative \(\Delta T\), respectively) of the 1982–1983 and 1997–1998 EN are shown in red and blue, respectively

Full size image
Fig. 6
figure 6

Oceanic advective contributions to the rate of SST change in \(E\) between a January (0) and July (0) and b July (0) and January (1) of strong and moderate EN events in (left) Drakkar and (right) CM2.1. Unit is °C/month. The red bar accounts for the non-linear dynamical heating (NDH) whereas the green and blue bars represents the horizontal and vertical linear advection respectively. The orange vertical segment provides the standard error on the advection terms (14 moderate and 2 strong events for Drakkar). The percentage below the red bars corresponds to the ratio of the mean NDH over the considered period onto the mean of total advection (NDH + linear advection) over the preconditioning and development period (i.e. Jan(0)–Jan(1)). For Drakkar, the percentages are for the (top) 1982 and (bottom) 1997 El Niño events

Full size image

The analysis for \(E\), which shows the largest difference between strong and moderate EN, indicates that CM2.1 has a similar behaviour to the Drakkar reanalysis and that ocean advection explains most of the year-to-year variations in the upper ocean temperature anomalies (Fig. 5a), primarily by the linear contribution (Fig. 5b), which in turn is dominated by vertical advection (Fig. 5f). For the onset of the strong EN (high end of \(\Delta T\) in Fig. 5), the nonlinear advection (NDH) does not contribute with amplified warming, but plays a substantial role in weakening the cooling during the decay of the strong EN (low end of \(\Delta T\) in Fig. 5c; Su et al. 2010). On the other hand, the radiative feedback associated with clouds becomes negative for strong EN and reduces the net warming (see Sect. 3.3; Lloyd et al. 2012). In Drakkar, the decay of the strong EN in 1983 and 1998 (the two largest negative \(\Delta T\) in Fig. 5) is dominated by entrainment and surface heat fluxes (not shown), the latter of which would be associated with enhanced cloudiness response during the strong EN (Lloyd et al. 2012), although with the use of a deeper layer (e.g. 150 m) for the heat budget, linear zonal advection is the dominant term (not shown).

We now focus on the onset of the strong and moderate EN separately in two stages during year 0. Drakkar and CM2.1 show good correspondence, particularly for the individual components associated with strong EN (Fig. 6). For the moderate EN, the role of linear vertical advection differs between Drakkar and CM2.1, but is similar for the linear horizontal advection and NDH (Fig. 6). For the strong EN, we find that during the preconditioning and development period leading to the peak in E [i.e. January(year 0)–January(year 1)], the total advection is largely dominated by the linear vertical component, which accounts for around 74 and 82 % of the total advection in Drakkar and CM2.1, respectively. The horizontal linear advection has a small contribution (6 and 13 %), but varies substantially between the first and second halves of the year, switching from a positive to negative contributions, respectively (Fig. 6). In contrast, the contribution of nonlinear advection (NDH, Jin et al. 2003) to the total advective heating varies from slightly negative to positive after July(0) (Fig. 6) and ends up having a similar contribution as the linear horizontal advection for the full year (11 and 13 %).

Compared to the moderate events, the total advection for the development year is 8 (Drakkar) and 5 (CM2.1) times larger in strong events. But only 15 % (Drakkar) and 19 % (CM2.1) of the difference in total advection between moderate and strong is explained by NDH. The largest contribution to the difference is associated with linear vertical advection (55 % in Drakkar and 81 % in CM2.1).

For \(C\), NDH produces a cooling tendency over Jan(0)–Jan(1) during strong EN (not shown) and therefore acts against the development of strong warm events. NDH produces maximum heating in \(E\) in the decaying period of strong EN (Jan(1)–Jul(1)) so it therefore delays the transition from strong EN to LN conditions, as indicated above.

In summary, the onset of strong EN events takes place via linear oceanic advection. Nonlinear advection (NDH) only makes a contribution later on, by delaying the decay produced by entraiment, linear advection and nonlinearly enhanced damping from clouds. Explaining the existence of the regimes would require explaining why the linear advection is substantially larger during the onset of EN for strong events. This, as we propose in the next section, is associated with atmospheric nonlinearities.

3.3 Convective thresholds as origin of El Niño regimes

A well-known nonlinear ENSO process is associated with the existence of a threshold for SST to exceed in order for deep convection to take place (Graham and Barnett 1987), which in the eastern Pacific could be associated with the reversal of the meridional SST gradient required to bring the ITCZ to the equator (Lengaigne and Vecchi 2009; Cai et al. 2014). This simple approach has been used to model the eastern Pacific ITCZ (Xie and Philander 1994) and explain the asymmetry between EN and LN (Dommenget et al. 2012; Choi et al. 2013). Due to the predominantly cold conditions in the equatorial eastern Pacific, a substantial warm anomaly would be required to exceed the threshold and favor the development of EN in the eastern Pacific (Lengaigne and Vecchi 2009; Ham and Kug 2012), whereas in the central and western Pacific the mean state would be closer to the threshold and the convection would be easier to trigger by surface warming.

To characterize the nonlinearity in the atmospheric response to surface warming in the eastern and central equatorial Pacific, a piecewise linear relationship is assumed between the SST indices, \(E\) and \(C\), and the atmospheric variables. Although this may be oversimplified, it has the advantage of easing the interpretation of the results in terms of three key parameters: two linear regression slopes and the breakpoint. For this purpose, we use the piecewise linear (hereafter “nonlinear”) regression method based on the Multivariate Adaptive Regression Splines algorithm (Friedman 1991), as implemented by Jekabsons (2013), which detects the breakpoints (i.e. the “thresholds” in SST) and the regression slopes while maintaining continuity in the fitted function. We took the monthly equatorial (5°S–5°N mean) wind stress and convection variables (OLR for observations, precipitation for CM2.1) and calculated the nonlinear regressions separately with \(E\) and \(C\), restricting the number of thresholds to a maximum of one. If a threshold is detected, the nonlinear regression yields the linear slopes above and below this threshold (“high range” and “low range”, respectively).

Firstly, we consider the zonal wind stress and convective variables averaged in the \(u_E\) and \(u_C\) boxes (Fig. 1). This allows us to use the WASWind wind stress, that includes both extraordinary EN events but has heterogeneous spatial sampling. The results for both observations and CM2.1 show a generally larger response in the high range of both \(E\) and \(C\) (i.e. the “nonlinearity ratio”, the high range regression slope over the low range slope, is greater than one; Figs. 7 and 8).

Fig. 7
figure 7

Piecewise linear regression fit (red) and frequency distributions of observed a, b OLR and c, d zonal wind stress (WASWind) wind stress binned by a, c \(C\) and b, d \(E\) (shown as percentiles: 10, 90 % = dotted, 25, 75 % = dashed, 50 % = lines with circles every bin; with 1-2-1 smoothing across bins). The estimated threshold values for \(E\) and \(C\) and the nonlinearity ratio between the slopes for the high and low SST ranges are indicated in the corresponding panels. The averaging is done over the boxes indicated in Fig. 1a, c

Full size image
Fig. 8
figure 8

Similar to Fig. 7 but for the GFDL CM2.1 model (precipitation is shown instead of OLR) and with the averaging boxes indicated in Fig. 1b, d

Full size image

Particularly interesting is the response to \(E\) in observations (Fig. 7b, d), which is very consistent between OLR and zonal wind stress both in the amplification of the response in the high range of \(E\) (nonlinearity ratios of 3.7 and 3.3, respectively), as well as in the large positive value of the thresholds (E = 1.5 and 1.6 for OLR and stress, respectively). The good correspondence between the convective and wind stress response supports the conclusion that the nonlinearity in the Bjerknes feedback emerges from the triggering of deep convection. This is also consistent with the nonlinearity in the shortwave radiative feedback, that becomes negative as clouds transition from low to deep convective under strong surface warming (Lloyd et al. 2012).

In CM2.1 there is also a large nonlinearity ratio and a finite positive threshold for \(E\) (Fig. 8b, d). However, the nonlinearity ratio is less coherent between convection and wind stress, with a value of 5.2 for the precipitation response, but only a value of 2.0 for the wind stress. Additionally, the threshold for convection (\(E=0.8\)) is lower than for wind stress (\(E=1.9\)) (Fig. 8b, d). The fact that the convection response in CM2.1 is substantially more nonlinear for convection than for wind stress suggests that the linear forcing of wind stress by the zonal SST gradient (Lindzen and Nigam 1987) is larger than the convective forcing in the eastern Pacific in CM2.1.

The response to \(C\) in observations (Fig. 7a, c) is more linear than for \(E\) but still shows an nonlinearity ratio of 2.0 and 1.5 for OLR and wind stress, respectively. However, the threshold is very close to zero, so this nonlinearity would contribute to the EN–LN asymmetry but would not generate different EN regimes. In CM2.1 the threshold is also close to zero, but the nonlinearity ratio is much higher (5.7 and 5.5 for precipitation and wind stress, respectively) than in observations.

In order to understand better the east-west differences in the nonlinearity, as well as depicting their nonlocal character, we repeat a similar calculation but for the target variables at different longitudes, instead of a single box. In this case, we use observations of surface winds from the TAO/TRITON array data that has a shorter record (does not include the 1982–1983 EN) but has more homogeneous temporal and spatial sampling distribution than the ship-based WASWind.

Fig. 9
figure 9

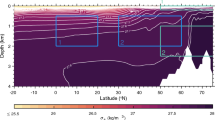
a–d High-range (solid) and low-range (dotted) piecewise linear and regular linear (dashed) regression coefficients onto \(C\) (blue) and \(E\) (red) for observations of equatorial (5°S–5°N) a TAO/TRITON zonal stress and c OLR, as well as for the CM2.1 (control run) b zonal stress and d precipitation. Also shown are the threshold values from the piecewise linear regression for e observations and f CM2.1. Piecewise regression parameters are only shown where a breakpoint was detected and the fit has \(R^2 > 0.45\) and 0.15 for CM2.1 and observations, respectively. The dashed lines in e, f indicate the values of C (blue) and E (red) required for the mean SST to locally reach 27.5 °C and 27 °C  for the observations and CM2.1, respectively

Full size image
Fig. 10
figure 10

Eastern Pacific SST index (\(E\)) in January(1) plotted against previous-year \(E\) (left column), equatorial mean 20 °C depth (m; central column) and equatorial central-western Pacific (\(u_C\) region) zonal wind stress anomaly (right column; \(10^{-2}\) Nm\(^{-2}\)), respectively, in January(0) (top row), June(0) (second row), August(0) (third row), and October(0) (bottom row). Observational data from HadISST, SODA, and WASWind is shown in red. The data for the GFDL CM2.1 pre-industrial control and 20th century runs is in grey (stress data for 140°E–170°W) and the 10, 50, and 90 % percentiles for \(E\) in Jan(0) binned by the predictor variables are shown in black. The horizontal and vertical lines indicate the threshold value of \(E=1.8\)

Full size image

The results for the observations are consistent with the previous analysis, but now we can see that the degree of nonlinearity in the response varies longitudinally (Fig. 9a, c). The convective response (Fig. 9c) in the low range is relatively uniform in longitude, but the high range response to \(E\) peaks between \(150^\circ \hbox {W}\) and \(130^\circ \hbox {W}\). Associated with this, the zonal wind response to \(E\) (Fig. 9a) suggests maximum values west of \(150^\circ \hbox {W}\) for the high range and east of \(130^\circ \hbox {W}\) in the low range, probably due to the latter being mainly a response to zonal SST gradients, whereas the former is mainly a response to convection.

With respect to \(C\), the observational convective response (Fig. 9c) maximizes between \(180^\circ\) and \(160^\circ \hbox {W}\) for the high range and west of \(170^\circ \hbox {E}\) for the low range, i.e. the convective response increases and shifts eastward with increasing \(C\). The zonal wind stress response to \(C\) (Fig. 9a) appears similar in both ranges, centered on the dateline and larger towards the west. However, if we consider that both response curves should merge into the linear response curve towards the west (the high/low range response should decrease/increase westward), this would suggest an eastward shift of the response of around \(10^\circ\) in the high range relative to the low range, consistent with the OLR results.

The results for CM2.1 (Fig. 9b, d) are broadly consistent to observations, except that the nonlinearity in the zonal wind stress response to \(C\) is much stronger, as noted earlier. Additionally, the maximum in the high range zonal wind stress response to \(E\) is shifted eastward relative to the low range, in contrast to the observations.

According to Graham and Barnett (1987), deep convection occurs in the tropics where SST exceeds \(27.5\,^\circ \hbox {C}\). So, if the thresholds in \(E\) and \(C\) for convection are physically linked to a critical absolute SST value, then these would depend on the local climatological SST and the values should be higher for \(E\) because the eastern Pacific is the coolest in the mean. To test this simple idea, we estimated the values of \(E\) and \(C\) that would bring the climatological mean SST at each longitude along the equator to this critical value. For this, we used the SST anomaly patterns associated with \(E\) and \(C\) as shown in Fig. 1. Considering critical SSTs of \(27.5\) and \(27\,^\circ \hbox {C}\) for observations and CM2.1, respectively, the results compare reasonably well, albeit not perfectly, with the thresholds in \(E\) and \(C\) obtained previously for the convective variables and the zonal wind stress (Fig. 9e, f). So, despite the crudity of the approximation, a first order explanation for the thresholds in \(E\) and \(C\) is that a critical absolute SST needs to be exceeded for deep convection.

3.4 Predictors and triggering of strong El Niño

In terms of EN forecasting, a key question is: what are the conditions that lead to an EN in the strong regime? In the idealized experiments by Lengaigne et al. (2004) with a coupled model initialized with same oceanic but different atmospheric conditions, the eastern Pacific SST anomalies for the different runs appear to evolve into two groups towards the end of the calendar year: one consisting in neutral conditions and moderate EN, and the other of strong EN (their Fig. 7). Prescribing a strong zonal wind forcing similar to that observed in March 1997, we estimate that the fraction of their runs producing a strong EN increased roughly from 10 to 40 %. Despite the large magnitude of this wind forcing, they concluded that it was insufficient to change the odds more radically because stochastic atmospheric variability during the subsequent development phase had a crucial role in determining the final outcome.

The question remains whether a state exists during the development of the system beyond which the evolution towards one or the other regime is deterministic, i.e. is there a point in phase space beyond which small stochastic perturbations cannot deviate the system trajectory from one regime to the other? We explore this by considering the degree to which the value of a state variable substantially affects the probability of the system evolving into a strong EN event. As an indicator of EN regime we use the January(1) value of the \(E\) index, while we analyze as potential predictor variables the equatorial ocean heat content (depth of \(20\,^\circ \hbox {C}\)), the zonal wind stress in the central-western Pacific (boxes in Fig. 1c, d), and the \(E\) index itself during the previous year (0). Additionally, we assess how the system evolves after a strong EN, particularly focusing on how the likelihood for another strong EN from occurring.

The statistics for strong EN events in both CM2.1 and observations agree that a necessary condition is that the ocean heat content is positive during April–May (0) (Fig. 4c). However, high positive heat content is neither sufficient nor necessary for a strong EN to take place. In CM2.1, even for heat content anomalies as high as observed in 1982 and 1997, the conditional probability of a strong event is on the order of only 10 % (Fig. 10b). From a predictability perspective, the heat content is mostly useful when its value is substantially negative (e.g. anomalies below \(-10\) m), as it then allows to rule out the occurrence of strong EN events (Fig. 10b).

Similarly, strong easterly wind stress anomalies in the central Pacific early in year (0) also appear to preclude a strong EN to develop in year (1), but otherwise, westerly anomalies are not very informative at this time. For instance, the weak westerly anomalies in early 1982 were not indicative of the strong magnitude of the EN later that year (Figs. 4e, 10c; Bergman et al. 2001). Additionally, it is unlikely that a strong EN in January(1) is preceded by a high value of \(E\) early in year (0) (Figs. 4b, 10a), which likely reflects the fact that a strong EN in CM2.1 tends to be followed by heat content discharge (Fig. 4c) and LN conditions in the central Pacific (Fig. 4a), so two consecutive strong EN are highly unlikely, at least in CM2.1. In fact, a strong EN event implies strong discharge and subsequent low heat content with high probability (Fig. 11), due to the meridional displacement of zonal wind anomalies (Vecchi and Harrison 2006; McGregor et al. 2012), which, together with zonal advection by reflected Rossby waves in the eastern equatorial Pacific (Picaut et al. 1997; Dewitte et al. 2003), leads to the termination of EN and the onset of a central Pacific LN (Fig. 4a; Vecchi and Harrison 2006; Kug et al. 2010). Additionally, both CM2.1 and observations indicate a very low probability of positive westerly wind stress anomaly in the central equatorial Pacific in August(1) after strong EN (Fig. 4e), which in turn indicates a low probability that high positive \(E\) (i.e. \(E>1.8\)) values develop towards year (2) (Fig. 4b).

Fig. 11
figure 11

Similar to Fig. 10 but for equatorial mean 20 °C depth anomaly (m) in August (1) versus \(E\) in January (1)

Full size image
Fig. 12
figure 12

a WASWind and b ERA40/Interim zonal wind stress (\(10^{-2}\) Nm−2; black circles) anomaly in August in the central-western equatorial Pacific (160°E–160°W, 5°S–5°N). The coupled component (blue triangles) is estimated with multiple linear regression against August \(E\) and \(C\) (fit over 1980–2007; regression equation is shown in the legend). The uncoupled component (green squares) is estimated by subtracting the coupled from the total anomalies (we assume additive stochastic forcing). Temporal 1-2-1 filtering was applied to the monthly data before the calculations. c Similar to above but for the central-eastern equatorial Pacific OLR index of Chiodi and Harrison (2010) (Wm−2, 170°W–100°W, 5°S–5°N). We note that nonlinearity has only a weak effect on the regression for August

Full size image

Towards the middle of year (0) the above is not substantially changed, except that the values of \(E\) preceding the strong EN become higher in CM2.1 (and 1997), although without increasing their predictive usefulness (Fig. 10d–f). However, around August(0) the relationship between the wind stress and the subsequent warming in the east is much stronger (Figs. 4e, 10i). In CM2.1, the probability of achieving \(E>1.8\) in the following January is higher than 90 % if the August(0) central Pacific stress anomaly (\(u_C\), \(160^\circ \hbox {E}-160^\circ \hbox {W}\)) exceeds \(3.4\times 10^{-2} \hbox {Nm}^{-2}\), whereas it is lower than 10 % for anomalies under \(1.5\times 10^{-2}\) Nm\(^{-2}\) (Fig. 10i). From another perspective, 90 % of the strong EN in CM2.1 had a stress anomaly higher than \(1\times 10^{-2}\) Nm−2 in August(0) (Fig. 4e). The observed evolution of \(u_C\) in 1982–1983 and 1997–1998, particularly the value around August, falls well within the envelope for CM2.1 (Figs. 4e, 10i). In the ERA data, which is closer to TAO/TRITON for August 1997 than WASWind for this region (Fig. 4e), the strong EN occured for stress anomalies above \(3\times 10^{-2}\) Nm−2, while all of the other years had lower values. The observed data seem to suggest that the separation between the strong EN regime and the rest is more abrupt than in CM2.1 (Fig. 10i), but with such a small sample it is not possible to assert this with confidence. This helps explain why the 1982–1983 and 1997–1998 EN were strong whereas the 1972–1973 remained moderate, since despite \(E\) was generally higher from February to September in 1972 than in 1982 (Fig. 10a, d, g), the wind stress index was higher for August 1982 and 1997 (Fig. 10i).

An important issue for predictability is whether this August westerly stress anomaly is part of the coupled response (Bjerknes feedback) or if it is externally forced. A simple approach adopted here is to empirically estimate the coupled stress anomaly using the August(0) \(E\) and \(C\) values as predictor variables with zero lead, for which we employed multiple linear regression (the piecewise linear approach produced very similar results for this month). The fit to the observations was very good (\(R^2=0.83\) and 0.87 for WASWind and ERA, respectively; Fig. 12a, b). The estimated coupled response fully describes the strong westerly stress observed in August 1972 and 1997, but is substantially smaller than the westerly anomaly in 1982 (around 40 and 60 %, respectively; Fig. 12a, b). We tentatively attribute the residual as the action of external forcing, which is consistent with the observation of a southerly jet east of Australia during 1982 that forced equatorial westerly anomalies (Harrison 1984). This southerly anomalies have also been more recently proposed by Hong et al. (2014) to play an important role for enhancing EN events. Since it is possible that issues with the observational sampling could have affected the wind stress estimation in 1982, we did a similar calculation using OLR data and found that the coupled estimation reproduced closely the observed August 1982 anomaly and that this OLR anomaly was much smaller than the one in August 1997 (Fig. 12c), supporting the hypothesis of a weak convective atmospheric coupling to SST in August 1982, so that external forcing at that time was key to trigger the 1982–1983 El Niño.

4 Discussion

4.1 Bjerknes feedback

The proposed threshold nonlinearity in atmospheric convection is proposed as a heuristic idealization, with practical applicability such as for comparing different climate models (e.g. Bellucci et al. 2010) or formulating a theoretical model (e.g. Xie and Philander 1994). However, what is essential is not that a sharp threshold exists, but rather that two regimes exist with sufficiently different feedbacks, even if their boundaries are fuzzy.

Several aspects could be involved in the Bjerknes feedback in realistic climate models such as GFDL CM2.1. For instance, as shown, the mean cold bias in CM2.1 shifts the nonlinearities farther westward than observed. With respect to the threshold value itself, the study of Bellucci et al. (2010) indicates that the corresponding absolute SST could vary by several degrees among models. Coupled to the different biases in mean SST, this would lead to diversity in the SST anomaly threshold and therefore to a likely diverse skill of these model to simulate two EN regimes (Kim and Yu 2012). Thus, the processes that lead to both the threshold and the mean SST, as well as the related biases, need to be understood. Additionally, the horizontal and vertical distribution of the convective heating should be assessed, as they will affect the response in the zonal wind stress (e.g. Wu 2003; Schumacher et al. 2004). Furthermore, the connection between the wind stress and SST in each regime will likely show different sensitivities to the physical parameterizations schemes in the atmospheric models, particularly the boundary layer and deep convection, so it could be valuable to analyze the regimes separately.

4.2 Ocean nonlinearity

It should be noted that our proposed conceptual model for nonlinear EN regimes includes specifically one nonlinearity: a SST threshold for enhanced Bjerknes feedback. Although nonlinear ocean advection also contributes, we believe that it is not essential for the existence of the regimes and the qualitative behavior of this system. However, from a quantitative perspective this process should also be considered as a factor that influences the relative probabilities, magnitudes and duration of the events (e.g. for El Niño prediction or assessment of its decadal-scale modulation), but uncertainty remains on how to estimate it observationally and how to take it into account in theoretical models.

A complicating issue is that ocean advection is a transient process that is associated with the past evolution of the event rather than with the instantaneous state, such as with atmospheric feedbacks. In particular, the details of Kelvin wave propagation and the reflection of Rossby waves from the eastern boundary are apparently highly influential. Thus, although it has been previously parametrized in simple models of the recharge-discharge family (Jin et al. 2003; Timmermann et al. 2003; An and Jin 2004), we believe that the neglect of wave dynamics could qualitatively affect the results (e.g. Su et al. 2010).

A practical issue with assessing the role of nonlinear ocean advection is the limitations in the observational data. Although the ocean analyses provide comprehensive datasets that are heavily used almost as equivalent to observations, it has to be kept in mind that these can be strongly influenced by the numerical models used in data sparse regions, such as the far eastern equatorial Pacific, and for weakly constrained variables such as vertical motions associated with wave dynamics (Su et al. 2010).

4.3 Nonlinear ENSO modeling

In general, it is probably not possible to show beyond doubt that strong EN in nature have intrinsically nonlinear dynamics due to the paucity of detailed observations of a sufficiently large sample of such events, but the results presented here are indicative that this hypothesis is plausible. Further work should be done to propose theoretical ENSO models that include explicitely the nonlinear Bjerknes feedback (e.g. Choi et al. 2013) but with a finite SST threshold, which our study suggests is the key process that explains the existence of strong and moderate EN events. Recent efforts have been dedicated to assess whether or not moderate EN events were driven by the recharge-discharge dynamics (Ren and Jin 2013; Mosquera-Vásquez et al. 2013) or if nonlinear processes could explain why central Pacific EN are confined to the warm pool region (Xiang et al. 2013; Mosquera-Vásquez et al. 2014). Our results rather calls for extending previous studies (Timmermann et al. 2003; Jin et al. 2003) to explain the bursting behavior of ENSO, which shall convey insights on the conditions favoring a regime over the other. Such models would allow the exploration of the influence of mean state changes onto the regime selection mechanism and statistics, extending previous works dedicated to the investigation of the change in stability of ENSO due to mean state changes (Fedorov and Philander 2001; An and Jin 2001; Thual et al. 2013).

From a broader dynamical system perspective, the existence of a threshold above which enhanced positive feedbacks can lead to a strong EN suggests that the ENSO system possesses stochastic excitable dynamics (Lindner et al. 2003), where excitable refers to the enhanced responsiveness above a threshold and stochastic refers to the key role that external processes (noise) can play in driving the system above the threshold. More specifically, the behavior of the proposed nonlinear ENSO system shares similarities to that of spiking neurons (e.g. Gerstner and Kistler 2002), where strong EN correspond to action potentials, whereas the subsequent heat content discharge and central Pacific LN event would characterize the refractory period in which triggering of new strong EN is unlikely. Although a mathematical model of this proposed nonlinear ENSO system is still lacking, it can be anticipated that the analysis methods developed for spiking neuron models (e.g. Gerstner and Kistler 2002) could be fruitfully applied to understand the strong EN events, the modulation of their statistics and their predictability.

On the other hand, although the limited sample of strong EN provides little challenge for empirical linear models to provide an adequate fit to the observational record (e.g. Penland 1996; Newman et al. 2011a, b), it would be illustrative to test whether such approach can reproduce the (apparent) nonlinearities in CM2.1 and whether it can provide a more parsimonious physical explanation than the nonlinear processes proposed here.

4.4 Predictability

Relatively few studies have explicitly addressed the predictability of different types of EN. For the POAMA system, Hendon et al. (2009) reported that predictions of SST patterns are limited to only one season lead. Xue et al. (2013) indicate that the CFS v2 system did not reproduce the decadal variance shift after 1998 between the eastern and central Pacific, whereas the onset of eastern Pacific EN in the 1982–1998 period was delayed in the forecasts (Xue et al. 2013). Ham and Kug (2012) determined that the suppression of convective response to warming in the eastern Pacific during EN due to cold biases in some models leads to only one type of EN, consistent with our results.

The high sensitivity of the EN regime selection to the zonal wind stress late in the onset phase of the EN events (\(\sim\)August(0)) suggests that the predictability of strong EN events is limited. On one hand, the initial development of the 1997–1998 event was so extreme that the likelihood of a strong EN was significantly increased (Lengaigne et al. 2004). On the other hand, little indication of a strong EN was observed in 1982 until the system experienced substantial external forcing in the latter half of the year. This seems inconsistent with the findings of Chen et al. (2004), who reported skillful (retrospective) forecasts of strong EN events with up to two-year lead. Although these authors indicate that these predictions were not severely plagued by false alarms, the fact that their two-year forecast substantially overestimated the magnitude of the 1972–1973 EN but substantially subestimated it at shorter leads (their Fig. 3) suggests that the internal dynamics of the model tends to generate large EN events, but also that the unresolved stochastic forcing can have a disruptive effect during the development phase (year (0)). In that sense, our study calls to further documenting the characteristics of both the high and low-frequency variability of wind stress in the equatorial Pacific and its imprints on the ocean dynamics.

5 Conclusions

In a previous study, Takahashi et al. (2011) proposed that the extraordinary EN events of 1982–1983 and 1997–1998 corresponded to a different dynamical regime from the other EN, presenting a much larger warming in the eastern Pacific than the others. However, by itself this observational sample is too small to establish the existence of these regimes conclusively.

In the present study, we analyzed 1200 years of simulations with the GFDL CM2.1 model and showed that it exhibits these two EN regimes: strong and moderate. This is made evident by the bimodal probability distribution of the states corresponding to EN peaks as seen in the phase space spanned by the linearly independent equatorial Pacific sea surface temperature (SST) indices \(E\) and \(C\), approximately corresponding to warming in the eastern and central Pacific, respectively. This is also supported by a \(k\)-means cluster analysis of these same indices of both model and observations, which yields similar results to the model probability distributions. The observed extraordinary EN events of 1982–1983 and 1997–1998 correspond well to the model strong EN regime, whereas the rest of the observed EN corresponds to the moderate regime. The probability of the null hypothesis that these two events correspond to a gaussian probability distribution that generated the other observed EN is close to zero.

In the phase-space of \(E\) and \(C\), the two regimes are separated by a high value of the eastern Pacific SST index (\(E\approx 1.8\)), i.e the regimes differ mainly in the magnitude of the eastern Pacific warming and not much in the central Pacific. Based on both observations and model data, we propose that this value is associated with a physical threshold in the SST anomaly above which deep convection and the westerly wind stress response to warming in the eastern Pacific is strongly enhanced. Such nonlinearity in the Bjerknes feedback increases the growth rate of EN events if the eastern Pacific warming reach sufficiently large amplitude and is very likely the essential mechanism that gives rise to the existence of the two EN regimes. Even though oceanic nonlinear advection is also found to contribute with additional positive feedback during the development phase of strong EN (10–15 % more warming), we do not believe that it is essential for the existence of the EN regimes, although it could contribute to their relative probabilities or magnitude.

The threshold nonlinearity could make statistics of EN regimes very sensitive to the characteristics of the stochastic forcing. The analysis of observations and the model suggest that a strong enough westerly wind stress anomaly in the central equatorial Pacific in late boreal summer (around August) is a necessary condition for the development of a strong EN in the following winter, although what constitutes “strong enough” is not as clear in observations as in the model due to the small sample and that this could in principle vary with the background climate state (e.g. decadally or with climate change). We however believe that a stochastic component during the austral summer of 1982 was instrumental for the development of the strong EN towards the end of 1982, whereas in 1997 this wind was a coupled response to the SST anomalies that occurred earlier in this year. Additionally, a well known necessary condition for EN, strong or moderate, is positive equatorial ocean heat content anomalies prior to its peak phase (Meinen and McPhaden 2000). Here we find that having both a positive heat content anomaly and a strong enough boreal summer westerly stress anomaly could be a necessary and sufficient condition for a strong EN in the following boreal winter.

Overall, our study suggests that atmospheric nonlinearity is a key process for the developement of strong EN events and that understanding the conditions that affects its occurence requires a better knowledge of the processes that control both the far eastern Pacific SST anomalies and mean state (see Takahashi et al. 2014), as well as the convective response. The analysis of retrospective forecasts of the observed strong EN events and their predictability would be also valuable for getting insights on their dynamics. This is planned as future work.