Aerodynamic performance of a bristled wing of a very small insect

Abstract

Aerodynamic force generation capacity of the wing of a miniature beetle Paratuposa placentis is evaluated using a combined experimental and numerical approach. The wing has a peculiar shape reminiscent of a bird feather, often found in the smallest insects. Aerodynamic force coefficients are determined from a dynamically scaled force measurement experiment with rotating bristled and membrane wing models in a glycerin tank. Subsequently, they are used as numerical validation data for computational fluid dynamics simulations using an adaptive Navier–Stokes solver. The latter provides access to important flow properties such as leakiness and permeability. It is found that, in the considered biologically relevant regimes, the bristled wing functions as a less than $50\%$ leaky paddle, and it produces between 66 and $96\%$ of the aerodynamic drag force of an equivalent membrane wing. The discrepancy increases with increasing Reynolds number. It is shown that about half of the aerodynamic normal force exerted on a bristled wing is due to viscous shear stress. The paddling effectiveness factor is proposed as a measure of aerodynamic efficiency.

Graphic abstract

1 Introduction

Some smallest insects have fringed wings with long bristles (setae) visually resembling bird feathers. They include representatives from different families such as, e.g., featherwing beetles Ptiliidae (Coleoptera), several families of parasitoid wasps (Hymenoptera), tiny flies Nymphomyia (Diptera) and thrips (Thysanoptera). They are active fliers, which implies that bristled wings produce enough force to support the animal body weight and propel it through the air (Yavorskaya et al. 2019; Cheng and Sun 2018; Zhao et al. 2019). Considering the bristled morphology as a biological adaptation, it is important to look into the potential benefits and penalties from the mechanical standpoint. The present study investigates into the aerodynamic aspect of this problem.

Horridge (1956) conjectured that the smallest insects may have forsaken their larger relatives’ airfoil action exploiting the lift force perpendicular to the direction of motion. Instead, they use a mechanism by which the drag on the upstroke is made less than that on the downstroke. Horridge’s analysis built upon earlier experiments with a ten percent thick airfoil (Thom and Swart 1940) having the drag at low Reynolds number independent of the angle of attack. Then logically, Horridge hypothesized that bending of the bristles could be critical for producing the necessary aerodynamic asymmetry. For instance, single cells with cilia such as Paramecium use asymmetric power- and recovery strokes based on bending. Kuethe (1975) extended upon the idea about the key role of elastic deformation. However, recent high-speed videography in free flight, e.g., of a featherwing beetle Nephanes titan (Yavorskaya et al. 2019), a chalcid wasp Encarsia formosa (Cheng and Sun 2018) and a thrips (Zhao et al. 2019; Lyu et al. 2019) shows large variation in the wing orientation during one stroke cycle, and relatively little bending of the setae.

It is, therefore, plausible that the aerodynamic asymmetry is primarily achieved by changing the angle of attack, instead of bristle bending deformation. An idealized two-dimensional computational study (Jones et al. 2015) demonstrated such possibility of drag-based mean force generation by a cyclic motion of a flat plate. Three-dimensional numerical simulations of Encarsia formosa (Cheng and Sun 2018) and thrips Frankliniella occidentalis (Lyu et al. 2019) with realistic wing kinematics also show cycle-average forces sufficient for body weight support, under the assumption that the wings are impermeable plates. However, until now, the force-generation capacity and aerodynamic function of the bristled wing morphology remains a largely open question.

Outwardly similar bristled appendages may function as virtually impermeable paddles or as leaky rakes, depending on the Reynolds number and on the geometrical parameters. This was pointed out in Cheer and Koehl’s theoretical study (Cheer and Koehl 1987) based on Umemura’s matched-asymptotic solution for a pair of cylinders (Umemura 1982), and confirmed in a recent numerical investigation of two-dimensional linear arrangements of multiple cylinders by Lee et al. (2020). Three-dimensional numerical computations of the forces of a bristled wing have been carried out by Barta and Weihs (2006) using the Stokes flow approximation for a linear array of slender ellipsoids. However, later Navier–Stokes simulations by Davidi and Weihs (2012) showed that, in the relevant for insects range of the Reynolds number between 10 and 100, the Stokes approximation is inaccurate by a factor greater than two. Despite that complication, both studies agreed that suitably spaced sparse arrays of rods can approach an impermeable wing in terms of aerodynamic force generation.

A linear array of cylindrical rods has been studied experimentally by Sunada et al. (2002). Their experimental apparatus implemented protocols of rectilinear translation and rotation about the vertical axis in a water-glycerin tank. The array of rods in all cases produced less force than a solid rectangular plate with the same external dimensions. However, the force per wing surface area was larger for the array of rods. Sato et al. (2013) downscaled this configuration to the size of one millimeter and tested it in a bench-top wind tunnel. Zhao et al. (2019) performed wind-tunnel force measurements on a thrips wing, paralleled by computational fluid dynamics (CFD) analysis.

A separate line of research focused on the bristled wing leakiness as a mechanism to facilitate the clap-and-fling interaction. Thus, Santhanakrishnan et al. (2014) and Jones et al. (2016b) concluded from two-dimensional Navier–Stokes simulations that bristles reduce the force to move the wings apart. Experiments with mechanical models in a glycerin solution by Kasoju et al. (2018) and Ford et al. (2019) showed that bristled wings can have higher lift to drag ratio during clap and fling than solid plate wings.

Virtually all previous computational and experimental estimates of the aerodynamic forces of bristled wings were based on highly simplified morphological representation. They covered a range of operating conditions and showed a variety of dynamical effects. However, it is not self-evident which effects are actually realized in the biological wings.

The objectives of our study are to implement and cross-validate an experimental facility and a numerical simulation software for studying the aerodynamics of bristles wings of bio-realistic shape. We constructed a dynamically scaled model that accurately matches the shape of a featherwing beetle Paratuposa placentis in terms of the bristle size and orientation, and the shape of the central membrane (blade). The diameter of the bristles was selected taking into consideration the secondary outgrowths on the setae measured in that species, see Appendix 1. Likewise, we implemented Navier–Stokes simulations of this wing.

We consider a revolving motion, which is a useful simplified kinematic protocol for studying the aerodynamics of biological flapping wings (Usherwood and Ellington 2002; Wolfinger and Rockwell 2015; Jones et al. 2016a). A revolving setup cannot replace a flapping setup as an aerodynamic test bed, but it offers a convenience of having a smaller kinematic parameter space while preserving the important spanwise gradient of the velocity that is also present in flapping (wing tip moves faster than the wing root). The two essential parameters are the angle of attack and the Reynolds number. Thus, a two-dimensional parameter sweep is performed with a bristled and with an equivalent membrane wing, the aerodynamic forces are measured and the flow properties are analyzed.

2 Materials and methods

This section describes, both, the mechanical apparatus for the dynamically scaled experiment and the numerical simulation setup.

2.1 Geometrical model and kinematics of the wing

The mechanical wing model and the CFD model share the same morphological features that mimic the real insect wing. Modelling artifacts such as the external boundaries of the fluid domain and attachment at the root of the wings are different in the experiment and in the simulation.

2.1.1 Geometrical model

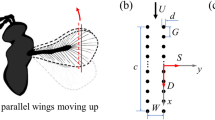
The wing is modelled after one of the tiniest beetles, Paratuposa placentis Deane, 1931. Adult individuals were collected in Vietnam in the Cát Tiên National Park. Morphological measurements were acquired using light microscopes (BX43, Olympus Corporation, Tokyo, Japan and SMZ168, Motic China group, Ltd., China) and a scanning electron microscope (SEM) JSM-6380 (JEOL, Tokyo, Japan), following the same protocol as described in an earlier study (Polilov et al. 2019). The external morphology of one of the samples is shown in Fig. 1a.

Fig. 1

a Wing of P. placentis. b Mechanical bristled wing model, with a dashed line showing the equivalent membrane outline. c Computer rendering of the wing model used in the numerical simulations

The samples were measured in AutoCAD (Autodesk, Inc., USA) using images taken with the light microscopes and SEM. Wing lengths and distances between tips and bases of setae (bristles) were measured using the light microscopic photographs. The wing length was measured as the distance between the base of the wing and the apex (the most distant point on the setae fringe). These measurements were made on ten wings. Then, diameters of setae were measured using SEM images. We measured both the diameters of the stems of the setae and the external diameters of the setae including the lengths of the outgrowths in middle regions of the setae. The diameter measurements were made on 20 setae.

The scaled mechanical model (Fig. 1b) and the CFD model (Fig. 1c) have similar major morphological features such as the number of long setae, their orientation, position on the wing blade, and the shape of the wing blade contour. The model wing length, defined as the distance from the axis of rotation to the apex, is scaled up to $R = {93}\,{\text {mm}}$.

The blade is approximated as a flat plate with a uniform thickness $h=1\,{\text {mm}}$, since the SEM measurements show that its out-of-plane deviation is less than 3% of the wing length. It is cut from a steel sheet using a printed photographic image of the insect wing as a template. Long setae are modelled as long and straight circular cylinders, all having the same diameter $b=0.36\,{\text {mm}}$, fabricated from hardened steel wire. Thus, the ratio $b/R = 0.00388$ is fixed equally in the experiment and in the simulation. Small setae near the wing base (root) are neglected in the experiment as they are unlikely to contribute to the fluid-dynamic forces. Note that the surface of each seta has a complex micro-relief composed of more-or-less regularly spaced outgrowths (Polilov et al. 2019). Therefore, the bristle diameter b in this study corresponds to an effective diameter, which is about two times as large as the diameter a seta having the outgrowths removed. The drag of a cylinder with the effective diameter b is the same as for a thinner cylinder covered with outgrowths. The value of the effective diameter used in this study is based on the results of a dedicated towing tank experiment described in Appendix 1.

In the mechanical model experiments and numerical simulations alike, the wing was flat. We did not have an objective to account for the wing deformation. No visually noticeable deformation has been observed during the experiment (also see static bending tests in the Supplementary material 1, section S1). In the simulation, the wing was perfectly rigid. However, there were some minor differences in the position of the bristles. They were soldered on one side of the blade in the experiment, but protruded along the mid-plane of the blade in the simulation. Besides that, in the experiment, the shape of the blade near the root was modified for the anchorage mechanism, and the root sections of the model were relatively wide to provide sufficient structural stiffness.

An equivalent membrane wing was fabricated from the bristled model by gluing adhesive tape sheets on either side and cutting the membrane out along the line connecting the bristle tips. Thus, the membrane only covers gaps between long bristles. The shape of the proximal part of the blade remains unchanged. The membrane wing outline is shown in Fig. 1b. This equivalent membrane wing shape definition is consistent with previous experiments (Sunada et al. 2002), but it is not the only one possible. The reader should keep in mind that the equivalent membrane wing is merely an analytical construct providing an intuitive reference for physical interpretation of the bristled wing data. It shows what happens when the gaps between bristles are perfectly sealed.

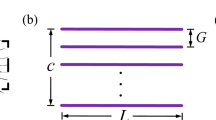
Since membrane wings are more common than bristled wings, they have received more attention in the previous research. In particular, it became customary to define the aerodynamic force coefficients using as reference quantities the projected area of the wing and the velocity at the radius of gyration determined from the second moment of area (Ellington 1984a, b), which is straightforward for a membrane wing. For a bristled wing, however, the projected area is extremely small, and using it for the force normalization can perplex the comparison with membrane wings (Sunada et al. 2002). In this study, therefore, we always use the geometrical parameters of the equivalent membrane wing non-dimensionalization. Thus, the reference area is equal to the projected area of the membrane wing, $S_{\text {ref}}=S_{\text {membrane}}=0.52R^2$. The mean chord length is then equal to $c_{\text {mean}} = S_{\text {ref}}/R = 0.52R$, hence the aspect ratio is as small as $R^2/S_{\text {ref}}=1.9$ (cf. Chen et al. (2018): $R^2/S_{\text {ref}}=3.28$ for a fruit fly, 3.64 for a bumblebee, 2.78 for a hawkmoth). The radius of the second moment of area (geometric radius of gyration) is calculated using the same outline as shown in Fig. 1b, yielding $r_{\text {g}} = 0.63R$. For comparison, the projected area of the bristled wing is equal to $S_{\text {bristled}}=0.08R^2$ (i.e., as small as $0.15 S_{\text {membrane}}$), and 27% of it belong to the blade.

2.1.2 Kinematic protocol

The spatial orientation of a rigid wing model is commonly described using three Euler angles. In the present setup, one of the angles—the one that describes the deviation of the spanwise axis from the horizontal plane—is identically equal to zero. Then, let $\alpha$ denote the angle of attack, which in our setup is the angle between the wing and the horizontal plane. Note that, in the present rotating wing setup, the geometrical angle of attack (i.e., relative to the horizontal plane) and the kinematic angle of attack (i.e., relative to the wing inflow direction) are equal. To vary $\alpha$, the wing is rotated about its longitudinal axis conventionally defined as a line connecting the root and one of the most distal bristle tips, see Fig. 1b. In every test, $\alpha$ is set before the beginning of motion, and remains constant during the test. Our tests are at $\alpha = 0^{\circ }, {15}^{\circ }, {30}^{\circ }, {45}^{\circ }, {60}^{\circ }, {75}^{\circ }$ and ${90}^{\circ }$.

The only angle that varies in time is the positional angle $\phi$, which determines the rotation with respect to the vertical axis. The motion starts from rest at $t=0$, $\phi =0$ and the wing accelerates until it reaches $\phi =\pi /8$, then continues rotation with its ultimate constant angular speed $\varOmega = 2 \pi f$. In the experiment, we tested at five different values of the frequency of rotation: $f = ~{0.04}\ {\text {rps}}$, ${0.08}\, {\text {rps}},\,{0.12}\, {\text {rps}}, {0.16}\, {\text {rps}},\,{0.2}\, {\text {rps}},\,{0.4}\, {\text {rps}},\,{0.7}\, {\text {rps}}.$ This corresponds to the range of the angular speed $\varOmega = ~0.25, \ldots ,~{4.40}\, {\text {s}}^{-1}$. The Reynolds number based on the wing length and the wing tip speed takes the values $Re_R = \varOmega R^2 / \nu = 6.0$, 12.1, 18.1, 24.2, 30.2, 60.4 and 105.7. Perhaps a more commonly used in studies on animal flight definition of the Reynolds number is based on the mean chord length $c_{\text {mean}}$ and the circumferential velocity of the wing at the radius of gyration $r_{\text {g}}$, yielding $Re = \varOmega r_{\text {g}} c_{\text {mean}} / \nu = 2.0$, 4.0, 5.9, 7.9, 9.9, 19.8 and 34.6, respectively. We will mainly use this definition through the paper, unless otherwise is stated. In the numerical simulations, we considered $Re = 2.0$, 9.9 and 39.6. See Section 4.1.2 in Shyy et al. (2007) for a discussion of the Reynolds number definitions in flapping-wing aerodynamics.

The time profiles of the instantaneous angular speed $\omega (t)$ are prescribed as

$$\begin{aligned} \omega (t)={\left\{ \begin{array}{ll} \displaystyle \frac{8}{\pi }\varOmega ^2 t, &{} {\text {if }} \, \varOmega t<\pi /8 .\\ \varOmega , &{} {\text {otherwise}}, \end{array}\right. } \end{aligned}$$

(1)

where t is the time from start in seconds. The positional angle $\phi (t)$ varies in time accordingly, in radians,

$$\begin{aligned} \phi (t)={\left\{ \begin{array}{ll} \displaystyle \frac{4}{\pi }\varOmega ^2 t^2, &{} {\text {if }} \, \varOmega t<\pi /8.\\ \varOmega t - \pi /16, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(2)

Supplementary material 2 contains a video that illustrates the wing motion.

2.1.3 Fluid-dynamic force normalization

The reference wing speed is obtained as $U_{\text {g}} = \varOmega r_{\text {g}} = 0.63 \varOmega R$. The force coefficients are determined as

$$\begin{aligned} c_{\text {L}} = \frac{L}{\frac{1}{2} \rho U_{\text {g}}^2 S_{\text {ref}}}, \quad c_{\text {D}} = \frac{D}{\frac{1}{2} \rho U_{\text {g}}^2 S_{\text {ref}}}, \end{aligned}$$

(3)

where L (lift) is the force in the vertical direction and D (drag) is the force in the direction opposite to the instantaneous velocity of the wing tip (apex).

2.2 Rotating wing experiment setup

2.2.1 Rotation mechanism

The dynamically scaled mechanical model of the wing (Fig. 1b) is mounted on a support holder as shown in Fig. 2a. An adjustable anchorage allows to set the geometrical angle of attack to any fixed value from $0^{\circ }$ to ${90}^{\circ }$ with $\pm \, {0.5}^{\circ }$ precision, using a digital angle finder. The support holder can rotate about the vertical axis, which passes through the wing root, and the rotation is driven by a NEMA 17 stepper motor 42HS60-1704A (Changzhou Jinsanshi Mechatronics Co., Ltd., Jiangsu, China), transmission belt and a gearbox with the transmission ratio that can be set as 2.5:1 or 12.5:1. The stepper motor is controlled using a TB6560 V2 driver connected to an Arduino Uno R3 controller, which enables gradual constant acceleration in the beginning of rotation. The control program is composed using the AccelStepper library and it allows prescribing the desired angular speed and acceleration of the stepper motor.

2.2.2 Fluid conditions

The wing model is fully immersed in the water-glycerin solution (which is a Newtonian fluid) filling a ${50}\, {\text {cm}} \times {80} \, {\text {cm}}\times {25}\,{\text {cm}}$ rectangular container (aquarium), see Fig. 2b. The volume fraction of water in the solution is small, and constant temperature is maintained to within $\pm \,{0.1}\,^{\circ }{\text {C}}$ from the target value corresponding to the kinematic viscosity of ${360}\,{\text {mm}}^{2} \, {\text {s}}^{-1}$, calibrated using a capillary viscometer (VPJ-2, Ecroskhim, Saint Petersburg, Russia).

2.2.3 Force measurement

The fluid-dynamic forces exerted on the model are measured using a strain gauge load cell (Beijing XNQ Electric Co., Ltd., Beijing, China; for specifications see Supplementary material 1, section S2) with ${0.0098}\,{\text {N}}$ accuracy. The sampling rate of the force measurement is ${1000}\,{\text {Hz}}$. The signal is processed using a custom-built amplifier, a resistor-capacitor circuit low-pass filer, and an L-Card E20-10 analog-to-digital converter (L-Card Ltd., Moscow, Russia). In addition, low-pass biquadratic digital filtering at 5 Hz is applied for denoising.

The drag and the lift are measured, respectively, in two different sets of experiments, using the load cell oriented as shown in Fig. 2a to measure the drag, or rotated by ${90}^{\circ }$ about the longitudinal axis to measure the lift. Each time series obtained for the model at any given $\alpha$ and Re is the average of three repetitions. In addition to that, calibration runs have been performed at equal Re, but with no wing model attached. To find the time evolution of the fluid dynamic force, calibration load cell voltage signal is then subtracted from the force measurement signals.

Fig. 2

Dynamically scaled experiment setup. a Zoom on the wing model on a rotating rig. b Model immersed in the glycerin tank

2.3 Computational setup

2.3.1 Navier–Stokes solver

The task of setting up a numerical simulation presents difficulties that are unique to bristled wings. The bristles are extremely thin in comparison with the wing length. A direct numerical simulation requires to resolve the fluid motion on these two different scales. This motivates us to employ an adaptive method. We use a wavelet-based incompressible Navier–Stokes solver for fully adaptive computations in time-varying geometries (Engels et al. 2020). It is an open-source software (https://github.com/adaptive-cfd/WABBIT) optimized for distributed-memory computer systems. The solver is based on Cartesian multi-block decomposition of the computational domain. Spatial derivatives in the governing equations are evaluated on locally uniform Cartesian grid blocks using second-order finite-difference schemes. The grid is adapted by adding or removing blocks of grid points, depending on the magnitude of wavelet coefficients used as refinement indicators. A Runge–Kutta–Chebyshev time marching scheme (Verwer et al. 2004) is employed, which allows explicit integration of all terms in the momentum equation with a reasonably large time step. The velocity–pressure coupling is enforced through the artificial compressibility method. No-slip boundaries are modelled using the volume penalization method.

2.3.2 Flow configuration in numerical simulations

The computational domain is an $8R \times 8R \times 8R$ periodic cube, it contains the fluid and the wing model excluding the attachment base and driving mechanism. The wing rotates about the vertical central axis of the domain. The computational domain is block-wise Cartesian. Each block contains $23 \times 23 \times 23$ grid points. The grid is dynamically adapted to the solution, with the limitation of maximum nine levels of refinement, which determines the minimum grid spacing as $\Delta x_{\text {min}} = 0.00071R$. The threshold value for thresholding wavelet coefficients is fixed as $\varepsilon =10^{-3}$. The time step $\Delta t$ is adapted according to the CFL condition with the Courant number equal to 1. The artificial speed of sound is set as $c_0 = 30.38 \varOmega R$ and the volume penalization parameter is $C_{\eta }=7.82 \times 10^{-6} \varOmega ^{-1}$.

3 Results and discussion

The experiment and the CFD results are presented together in this section in a topic-oriented manner focusing on different physical effects.

3.1 Time evolution of the forces

Figure 3 shows an example time profile of the two measured components of the force. This particular case corresponds to the angle of attack of $\alpha =60^{\circ }$, and the Reynolds number is $Re=9.9$, but the time evolution is similar in all cases (see the full data set in Supplementary material 3 and 4). Our choice of $\alpha =60^{\circ }$ for illustrative purposes instead of a more conventional $45^{\circ }$ angle is inspired by the large kinematic angle of attack during downstroke found in the smallest bristled-wing insects [e.g., thrips Frankliniella occidentalis (Lyu et al. 2019)].

The process begins with the acceleration reaction producing a peak of the force. As the acceleration ends, the force relaxes to what we call a quasi-steady value. The transient is slower at the higher Re than at the lower Re but, in all cases considered in this study, the force is nominally constant within the interval of $\varOmega t \in [\pi /3, \pi /2]$. The corresponding time interval is gray-shaded in Fig. 3. We exclude the later part of the sequence when the wing first encounters the wake of the rotating support holder and then its own wake. We are not interested neither in the transient effects in this study, which may be complicated by the inertia of the mechanical device and wake interactions. Even though the numerical simulation shows similar peaks as in the experiment, these peaks ultimately have little relevance to the forces on flapping wings of insects. Note that the large lift in the experiment during the first 0.2 s of the process is an artifact of low-pass filtering at 5 Hz. Also note that the forces in the numerical simulation show no oscillation after the angular acceleration discontinuity. Hereafter, let us focus on the quasi-steady values of the forces that can offer a crude approximation for a flapping wing in the mid downstroke and upstroke.

Fig. 3

Example time evolution of the lift and the drag of the bristled model. The angle of attack is $\alpha =60^{\circ }$ and the Reynolds number is $Re=9.9$. The gray shaded rectangle shows the time averaging interval for calculation of the quasi-steady forces

3.2 Time-average quasi-steady forces

The average force coefficients over the interval $\varOmega t \in [\pi /3, \pi /2]$ are displayed in Fig. 4 for a selected combination of Re and $\alpha$. Similar plots for all regimes realized in the experiment are provided in sections S4 and S5 of Supplementary material 1. Fig. 4a portrays a typical variation with respect to the angle of attack $\alpha$, while Fig. 4b elucidates the Reynolds number dependence. In the experiment, the bristled and the membrane models, both, show similar variation of $C_{\text {D}}$ and $C_{\text {L}}$ with $\alpha$ and Re. The values for the bristled wing are confirmed, in addition, by the results of the numerical simulation. The discrepancy between the experiment and the simulation is less than 5% of the maximum $C_{\text {D}}$ and 9% of the maximum $C_{\text {L}}$ at $Re=9.9$. It increases to 14% for $C_{\text {D}}$ at $Re=2.0$, probably because of the wall effect.

In all cases, $C_{\text {L}}$ is substantially less than $C_{\text {D}}$, which means that this wing, in the range of Re considered here, is better suited for drag-based flight (force in the opposite direction to the wing motion) than the lift-based (force perpendicular to the direction of wing motion). This is usual for the smallest fliers (Lyu et al. 2019; Jones et al. 2015). Low lift-to-drag ratio ($<1$) can be explained by a combination of factors including the low Reynolds number $<100$ and the small aspect ratio of the wing $<2$. The difference between the magnitudes of $C_{\text {D}}$ and $C_{\text {L}}$ increases as Re decreases.

The values of Re in the lower end are sufficiently small to observe transition to a Stokesian regime in which $C_{\text {D}}$ and $C_{\text {L}}$ are both decreasing functions of Re, which has been reported previously for nominally two-dimensional foils (Jones et al. 2015; Thom and Swart 1940). The values of Re in the higher end are sufficiently large to see the membrane wing $C_{\text {L}}$ increase with Re due to the leading-edge vortex, also in agreement with translating wing experiments and numerical simulations (Jones et al. 2015; Miller and Peskin 2004). In contrast, $C_{\text {L}}$ of the bristled wing continues to decrease with increasing Re, which means that the bristled wings does not benefit from the leading-edge pressure peak as much as the membrane wing does.

Fig. 4

Average force coefficients in the experiments and simulations a at the Reynolds number $Re=9.9$ and b at the angle of attack $\alpha =60^{\circ }$. Data for all Re and $\alpha$ tested in the experiment are provided in the Supplementary material 1, 3, 4, 5 and 6

It is instructive to see how large force the bristled wing can generate, in per cent of the membrane wing force. A color map of such quantity, ${C_{\text {D}}}_{\text {bristled}}/{C_{\text {D}}}_{\text {membrane}}$, is plotted in Fig. 5 versus $\alpha$ and Re. We focus on $C_{\text {D}}$ here, since we know from the previous discussion that $C_{\text {L}}$ is much smaller.

The bristled wing produces less drag than the membrane wing under equal conditions, but no less than $60\%$. This ratio consistently increases as $\alpha$ or Re decrease. At the lowest Reynolds number considered, $Re=2.0$, the ratio is above $90\%$ regardless of $\alpha$. It should be noted that the typical range of Re of P. placentis is supposedly below 20. For example, for a ptiliid beetle Nephanes titan that has the wing length $R=0.66\%$, which is only slightly larger than P. placentis, kinematic measurements (Yavorskaya et al. 2019) suggest that the flapping frequency is equal to $f=207\, {\text {Hz}}$ and the amplitude is $\Phi =195^{\circ }$. Taking the kinematic viscosity of air at the temperature ${25}\,^{\circ }{\text {C}}$ as $\nu =1.56 \times 10^{-5}{\text {m}}^{2}\,{\text {s}}^{-1}$, we find that $Re_R$ varies around $2 \Phi f R^2 / \nu = 39.3$ during one flapping cycle. A wing of N. titan has a similar outline shape to P. placentis, therefore, Re based on $r_{\text {g}} = 0.63R$ and $c_{\text {mean}}=0.52R$ varies around 12.9. This means that the bristled wings produce no less than $75\%$ of the force that the equivalent impermeable membrane wings could produce.

Fig. 5

Bristled-to-membrane drag force ratio. Circles mark the measurement points

3.3 Paddling effectiveness factor

The drag-based flight mode in insects (Jones et al. 2015) requires reciprocating motion of the wings: the drag should be larger when the wings move down than when they move up. It can be referred to as the “rowing mechanism” (Cheng and Sun 2018; Lyu et al. 2019), for its similarity with swimming or paddling action that was already noticed in an early work by Horridge (1956).

The present experiment focuses on steady rotation, but these force measurements can be used for quick estimation of the forces acting on flapping wings as well, under the quasi-steady assumption. As the Reynolds number decreases, viscous diffusion of the vorticity becomes more efficient. This means that the flow field adapts faster to the instantaneous position change of the boundary, and the aerodynamic forces depend less on the time history of the flow. Further, if the wing motion is periodic in time, the acceleration reaction makes zero net contribution to the time-average forces. Hence, at low Reynolds number, cycle-average forces can be expressed in terms of the force coefficients from the rotating wing experiment.

To make the quasi-steady calculation simple, let us consider an idealized “vertical stroke” (cf. Jones et al. (2015)). To maximize the net vertical force at a given Re, as the wings move down, the drag coefficient is held at its maximum ${C_{\text {D}}}_{\text {max}}$, but when the wings move up, it is kept at its minimum ${C_{\text {D}}}_{\text {min}}$. $C_{\text {D}}$ is controlled by changing the angle of attack using feathering rotation. The lift coefficient is zero in this scenario, $C_{\text {L}} = 0$. The real motions of insect wings are, in general, more complex. In the case of P. placentis, precise kinematic reconstruction is yet to be done. Nevertheless, in view of the known trend in the smallest insects to make deep U-shaped strokes to produce large upward pointing drag (Lyu et al. 2019), the simple vertical stroke model, which relies on the drag in a similar way, can provide useful insights.

Jones et al. (2015) introduced an aerodynamic performance metric suitable for wing kinematics that predominantly use drag for hovering: the ratio of the net vertical force to the net total force that the muscles have to produce: $\overline{C}_{\text {V}} / \overline{C}_{\text {T}}$, when written in terms of cycle-average force coefficients. Overlines denote time averaging over one wing beat cycle in this discussion. If the left and the right wings move symmetrically, the forces can be taken per wing.

Let us derive an approximate formula quantifying the effectiveness of the vertical stroke gait and analyze its Reynolds number dependence. For simplicity of calculation, we assume a triangle wave time profile of the up an down elevation angle,

$$\begin{aligned} \phi (t) = \Phi \times \left( 2 \left| f t + 1/4 - \lfloor f t + 3/4 \rfloor \right| - 1/2 \right) . \end{aligned}$$

(4)

The feathering angle is piecewise constant in time such that the kinematic angle of attack is equal to $90^{\circ }$ during the downstroke (flat-on) and 0 during the upstroke (edge-on). As Fig. 4a suggests, the maximum drag coefficient ${C_{\text {D}}}_{\text {max}}$ is attained at $\alpha =90^{\circ }$ and the minimum ${C_{\text {D}}}_{\text {min}}$ is at $\alpha =0$.

The total force on the wing is entirely due to drag, it acts in the direction perpendicular to the wing, its magnitude can be calculated as $F_{\text {T}}(t)=\frac{1}{2} C_{\text {D}}(t) \rho \dot{\phi }^2(t) r_{\text {g}}^2 S_{\text {ref}}$, and its vertical component is $F_{\text {V}}(t) = - F_{\text {T}}(t) \mathrm {sign}{\dot{\phi }(t)} \cos {\phi (t)}$. The time averaging yields

$$\begin{aligned} \overline{F}_{\text {T}} = \left( {C_{\text {D}}}_{\text {min}} + {C_{\text {D}}}_{\text {max}} \right) \times \Phi ^2 \rho f^2 r_{\text {g}}^2 S_{\text {ref}} \end{aligned}$$

(5)

for the total force perpendicular to the wing, and

$$\begin{aligned} \overline{F}_{\text {V}} = \left( {C_{\text {D}}}_{\text {max}} - {C_{\text {D}}}_{\text {min}} \right) \times 2 \Phi \sin (\Phi /2) \rho f^2 r_{\text {g}}^2 S_{\text {ref}} \end{aligned}$$

(6)

for the vertical force. A representative approximate value of the flapping amplitude is $\Phi = 2 \pi$ (cf. Yavorskaya et al. (2019) for N. titan, $195 \pm 4^{\circ }$ in the frontal and $187 \pm 3^{\circ }$ in the dorsal projection). We obtain

$$\begin{aligned} \frac{\overline{C}_{\text {V}}}{\overline{C}_{\text {T}}} = \frac{\overline{F}_{\text {V}}}{\overline{F}_{\text {T}}} = \frac{2}{\pi } \frac{{C_{\text {D}}}_{\text {max}}-{C_{\text {D}}}_{\text {min}}}{{C_{\text {D}}}_{\text {max}}+{C_{\text {D}}}_{\text {min}}}, \end{aligned}$$

(7)

which is a dimensionless quantity that we term the “paddling effectiveness factor” (PEF). It can be taken as a proxy for the efficiency of a wing as a drag-based propulsor, when precise kinematic information is not available. The numerator is approximately the time average useful vertical force carrying the insect aloft, and the denominator is approximately the time average parasite resistance force counteracted by muscles. In the high Reynolds number limit, ${C_{\text {D}}}_{\text {min}}$ is much smaller than ${C_{\text {D}}}_{\text {max}}$, therefore, PEF approaches $2/\pi$. In the range of Re considered in this study, PEF varies with Re as shown in Fig. 6. It agrees with the general trend for propulsors to lose efficiency at low Re. At $Re=2.0$, the useful vertical force of the flapping propulsor is only about $15\%$ of the total resistance force.

The bristled wing never outperforms the membrane one. At $Re=34.6$, the difference is about $13\%$. It reduces to $7\%$ as Re decreases to 2.0. It can be speculated from the Stokes flow considerations that this trend can be extrapolated, i.e., PEFs of the bristled wing and of the membrane wing should converge in the limit of $Re \ll 1$.

Fig. 6

Paddling effectiveness factor (7) as a function of the Reynolds number

3.4 Pressure force and shear force

For membrane wings on the fruit fly scale and above, it is known that pressure forces dominate the shear viscous forces (Roccia et al. 2013). An extreme illustrative example is the fluid-dynamic force acting on a thin flat plate in the normal direction to it. Even at a low Reynolds number, this force is practically due to the surface pressure only, for geometrical reasons.

Another useful idealized example is the Stokes drag on a sphere. In the low Reynolds number limit, the pressure forces account for 1/3 of the total drag on the sphere, and the shear resultant contribution is 2/3 of the total, respectively. Likewise, for a circular cylinder at any $Re<1$, the pressure and the shear stress components are practically equal in magnitude (Dennis and Shimshoni 1965). Even though the bristled wing in our study produces in total almost the same amount of aerodynamic force as the membrane wing, the force-generating structural elements are different. The bristles are circular cylinders, some parts of their surface is perpendicular to the flow direction and some part is parallel. It is, therefore, reasonable to expect the shear force be of the same order of magnitude as the pressure force.

Using the pressure distribution over the surface of the bristled wing model in the numerical simulations at $\alpha =60^{\circ }$, by numerical integration of the pressure gradient multiplied with the volume penalization mask function over the entire computational domain, we calculated the pressure component of the total force in the direction normal to the wing plane, $F_{Np}$, at time $t=2/\varOmega$. The shear component was evaluated as $F_{N\tau } = F_{N} - F_{Np}$, where $F_{N}$ is the total normal force. Table 1 contains the values of relative contributions $F_{Np}/F_{N}$ and $F_{N\tau }/F_{N}$, where the total normal force is related with the lift L and the drag D as $F_N = L \cos {\alpha } + D \sin {\alpha }$. In the range of Re between 2.0 and 39.6, the pressure force accounts for $44\%$ of the total normal force, and the shear accounts for $56\%$. This force breakdown reflects the fact that the bristles are bluff bodies. However, it should be interpreted with caution because, while the resolution of 15.14 grid points per blade thickness and 5.46 points per bristle diameter in our numerical simulations is sufficient for accurate evaluation of the total force, the relative contribution of the pressure force may be underestimated by as much as 30%, see Supplementary material 1, section S3.

3.5 Flow field and leakiness

Cheer and Koehl (1987) pointed out that bristled appendages can operate as highly permeable rakes or as virtually impermeable paddles. Which operational mode is realized depends on the combination or morphological parameters such as the bristle diameter and spacing, and on the Reynolds number of the flow. Our force measurements suggest that, in the range of Re considered, the bristled wing of P. placentis can produce aerodynamic forces of the same order of magnitude as membrane wings of the same size. To work as a paddle, the bristled rim must effectively block the air flow through the wing. Let us describe this flow.

In the following analysis, we consider the wing at a typical rowing angle of attack $\alpha =60^{\circ }$. Let us begin by depicting the flow velocity component in the direction normal to the wing plane, relative to the wing, at $Re=9.9$. Figure 7a shows its distribution over the wing plane, in the dimensionless form $u_n/\varOmega R$. The region occupied by the solid structure of the wing is masked with the white color. A black line connects the tips of the bristles, and the region exterior to it is also masked. The color map visualizes the velocity distribution. The velocity is very small, $u_n/\varOmega R<0.1$, close to the proximal side of the wing and near the blade where the bristles are densely packed. As the bristles extend radially, the gap increases and the flow velocity through the gap also increases to $u_n/\varOmega R \approx 0.5$. Further increase of the gap would entail larger throughflow velocity. The flux calculated as an integral of $u_n$ over the inter-bristle space $\Sigma$ evaluates as

$$\begin{aligned} Q_{\text {leak}} = \int _{\Sigma }u_n{\text {d}}x{\text {d}}y = 0.055 \varOmega R^3. \end{aligned}$$

(8)

Dividing it by the “ideal” flux based on the volume across which the wing sweeps

$$\begin{aligned} Q_{\text {sweep}} = \int _{\Sigma }\varOmega x \sin {\alpha } {\text {d}}x{\text {d}}y = 0.229 \varOmega R^3, \end{aligned}$$

(9)

we obtain the “leakiness” of the wing (cf. Cheer and Koehl (1987); Kasoju et al. (2018))

$$\begin{aligned} \varLambda = \frac{Q_{\text {leak}}}{Q_{\text {sweep}}}, \end{aligned}$$

(10)

which equals 0.24 at $Re=9.9$. As a matter of comparison with earlier related results (Cheer and Koehl 1987), the leakiness is also equal to 0.24 for a pair of ${1} \, \upmu {\text {m}}$ cylinders with ${15}\, \upmu {\text {m}}$ spacing at the diameter-based Reynolds number 0.01. These values are close to the typical parameters of setae in P. placentis.

Fig. 7

Flow across the wing plane. Reynolds number $Re=9.9$, angle of attack $\alpha =60^{\circ }$, time $t=2/\varOmega$. a Dimensionless normal velocity component $u_n / \varOmega R$; b dimensionless permeability $k \varOmega / \nu$

$\varLambda$ shows how effectively the viscous shear stresses block the flow through gaps between the bristles. It depends on Re. The values of $\varLambda$ obtained using the same procedure for different Re are shown in Table 1. $\varLambda$ increases with the Reynolds number, as expected (Cheer and Koehl 1987).

Table 1 Relative pressure normal force $F_{Np}/F_{N}$, relative shear normal force $F_{N\tau }/F_{N}$, leakiness $\varLambda$ (10) and average permeability $\kappa$ (12) of the bristled wing at $\alpha =60^{\circ }$, $\varOmega t=2$

An alternative measure to the leakiness is the permeability, as used in porous media flows. The Darcy law relates the fluid velocity $u_n$ and the pressure gradient $\nabla p$ driving the fluid flow through a permeable continuous medium with permeability k and dynamic viscosity $\mu$,

$$\begin{aligned} u_n = - \frac{k}{\mu } \frac{\partial p}{\partial n}, \end{aligned}$$

(11)

where $\partial p/ \partial n = \nabla p \cdot \mathbf {n}$, $\mathbf {n}$ is the flow direction unit vector. For a non-homogeneous anisotropic structure such as a bristled wing, the local permeability can be defined as $k = - \mu u_n / (\partial p / \partial n)$. The pressure gradient in the entire computational domain was calculated using the same finite-difference scheme and the same grid as in the CFD simulation. Then, it was sampled on the wing plane using linear interpolation in ParaView 5.8.0, and its scalar product with the normal vector of the wing plane was calculated. Thus obtained spatial distribution of k, normalized by $\nu /\varOmega$, is displayed in Fig. 7b. Similar to the throughflow velocity, it increases with the gap between the bristles, but it is less sensitive to the distance from the axis of rotation, because the increase of the velocity with x is compensated by a similar increase in the magnitude of $\nabla p$.

A convenient single-valued criterion of the permeability of the entire wing is the non-dimensionalized average permeability

$$\begin{aligned} \kappa = \frac{\varOmega }{\nu } \frac{\int _{\overline{\Sigma }} k {\text {d}}x {\text {d}}y}{\int _{\overline{\Sigma }} {\text {d}}x {\text {d}}y}, \end{aligned}$$

(12)

where $\overline{\Sigma }$ is the sub-region of the wing plane that includes the inter-bristle space and the interior of the wing, and it defines the virtual membrane area occupied by an equivalent porous medium. This expression evaluates to $\kappa = 4 \times 10^{-3}$ for the data in Fig. 7b. The values for other Re are provided in Table 1. Note that $\int _{\Sigma } {\text {d}}x {\text {d}}y / \int _{\overline{\Sigma }} {\text {d}}x {\text {d}}y = 1-S_{\text {bristled}}/S_{\text {membrane}} = 0.85$.

4 Conclusions and perspectives

The bristled wing model always produces less aerodynamic force than the equivalent membrane model although the difference varies with the Reynolds number. Thus, the drag differs between the two models by less than $10\%$ in the lower end of Re tested, but the discrepancy increases to $40\%$ for the highest Re. The lift shows a similar trend, except that the variation of $C_{\text {L}}$ with Re is smaller. The normal force of the bristled wing is evaluated as $44\%$ due to pressure and $56\%$ due to shear. However, our calculations of the those contributions separately are less accurate than the total force calculations.

Like many miniature insects, P. placentis may use drag-based “rowing” to fly. The effectiveness of this aerodynamic mechanism can be estimated knowing the minimum and the maximum drag coefficient. The paddling effectiveness factor obtained from such calculations is lower for the bristled wing than for the membrane one, but the difference is small when Re is in the typical range of the tiniest insects.

Although our study shows no net aerodynamic benefit for an isolated bristled wing model of P. placentis as compared with an equivalent membrane wing, the handicap is small. Positive effect of permeability during clap and fling of a pair of wings (Kasoju et al. 2018) may help equalize the aerodynamic performance. Thus, from the aerodynamic point of view and under the assumptions used in this study, the membrane appears merely unnecessary for flight at this low Re. Advantages of not having a membrane may be sought beyond the aerodynamics. For example, bristled wings are likely to be much lighter than their membrane counterparts and have lower cost of formation.

Our model does not account for the wing deformation, unsteady aerodynamic effects and aerodynamic interaction between two wings, though it is known that these factors can be important [e.g, flexible clap and fling (Miller and Peskin 2009)]. To include them in the model is a promising direction for the future work.

Appendix 1: Experimental determination of the effective diameter of bristles

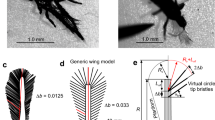
A dedicated dynamically scaled model experiment has been implemented to evaluate the fluid-dynamic drag force exerted on setae and to determine the effective diameter, i.e., the diameter of a circuar cylinder section producing equal drag. A three-dimensional geometrical model was designed based on the SEM images (Fig. 8a). The model consists of a cylinder bar covered with a regular helical pattern of outgrowths. A unit of 7 outgrowth elements makes two full spiral turns (Fig. 8b). Its length is equal to 3.75 times the diameter of the cylinder. The computer aided design (CAD) model shown in Fig. 8b consists of 3 units. The model enlarged to a scale 5747:1 was 3D printed (Anycubic Photon S, Shenzhen Anycubic Technology Co., Ltd., Shenzhen, China) from a photopolymer neutrally boyant in glycerin. Twelve identical pieces have been manufactured. Each two pieces were glued together. Thus, for the tested models, the cylinder bar was $b_{\text {base}}=5\, {\text {mm}}$ in diameter and 112.5 mm long.

Fig. 8

Modelling of setae. a SEM image of a seta; b CAD model consisting of a cylindrical body with outgrowths; c Assembly of six seta models in a dynamically scaled experiment; d Drag force measurements of different model assemblies. Points show averages and whiskers correspond to 95% confidence intervals of the measurements. The horizontal line corresponds to the drag magnitude obtained in the experiment with 3D printed seta models. The vertical line shows the effective cylinder diameter consequently used in the rotating wing experiment

An assembly of six parallel 3D printed models was mounted on a light alluminium frame, attached on a force sensor. The spacing between the bar axes was 82 mm, which corresponds to the typical spacing between setae in the distal part of P. placentis wing (Fig. 8c). During the experiment, the models were dipped in glycerin and the frame slided above the surface over the distance of 200 mm with constant velocity $U=3.37\, {\text { mm}} \, {\text {s}}^{-1}$ in the direction perpendicular to the bars. With the kinematic viscosity of glycerin $\nu = 360\,{\text {mm}}^{2} \, {\text {s}}^{-1}$, the Reynolds number based on the diameter was $Re_b = b_{\text {base}}V/\nu = 0.047$. The force sensor signal was recorded similarly as in the rotating wing experiment. The drag was time-averaged over the middle third of the time series.

Similarly, assemblies of cylindrical bars were tested under the same conditions. Circular cylinders were manufactured in an assortment of sizes from the same neutrally-buoyant polymer. The diameter varied from $b_{\text {base}}$ to the outer diameter of outgrowth: 5, 7, 9, 10, 11, 12, and 16.5 mm. It was found that the drag of the model with outgrowths is situated between the values corresponding to the 10 and 11 mm cylinder models, and it is significantly different from both. Figure 8d illustrates this point graphically. Thus, the effective diameter is evaluated as $b_{\text {eff}} = 2.1b_{\text {base}}$. Supplementary material 7 contains the underlying numerical data and statistical tests.