Abstract
We propose a new laser mode locking state in which the pulse disperses quickly and then revives after a certain time. This mechanism is based on the temporal Talbot effect and requires a large amount of intra-cavity group velocity dispersion. Similar to the usual mode locking it should be possible to employ the Kerr effect to force the laser into this mode, even when the cold cavity dispersion is not exactly matched. We show that the mode spectrum of such a laser is not equidistant but increases linearly with very high precision. This Talbot frequency comb can be self referenced. The beating with the adjacent modes uniquely defines the optical mode frequency, which means that the optical spectrum is directly mapped into the radio frequency domain. This is similar to the dual frequency comb technique, albeit without the limiting relative jitter between two combs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Talbot effect has been described for the first time in 1836 as a peculiar phenomenon observed in the near field of an optical grating. Summing over contributions of the individual rulings to the total field in the Fresnel approximation, a term of the form \(\exp(-ikl^2 a^2/2z)\) appears with the wave number k, the rulings numbered by l and spaced by a and the distance from the grating z. Summing over l generally yields a rather chaotic intensity distribution. Talbot noted though that all these terms reduce to \(\exp(-i2\pi l^2)=1\) at a distance of \(z=k a^2/4 \pi\). The remaining terms add up to the intensity at \(z=0\) provided that this intensity is periodic with a [1]. The same phenomenon can be observed in the time domain with a periodic pulse train signal that is subject to group velocity dispersion \(\phi ''\) that provides the quadratic phase evolution. The pulses first spread out in time, an then reassemble after propagation the distance \(t_r^2/2\pi \vert \phi '' \vert\), where \(t_r\) is the pulse repetition time [2, 3]. The same behaviour should be observable with a single pulse that is on a repetitive path in an optical cavity. In contrast to a free space pulse train, higher order dispersion is required as we will show below.
2 Talbot Comb
Consider the modes of a laser cavity with a mode spectrum
Here the modes are numbered around the optical carrier frequency \(\omega _0\) with integers \(n=0, \pm 1, \pm 2 \ldots\). Compared to the usual regularly spaced frequency comb [4] there is a quadratic term in n which leads to an equally spaced comb of radio frequency (RF) components:
Upper The optical spectrum of the Talbot-comb according to (1) for \(m=100\) assuming a Gaussian spectral envelope. With this rather small value it is possible to illustrate the linearly increasing mode spacing. Lower Equidistant radio frequency combs obtained with a photo detector. The left (blue) part is due to the first order (\(k=1\)) beating of adjacent modes \(\omega _{n+k}-\omega _{n}\) (Eq. (2)) which would be used for spectroscopy. The center (red) part are the second order (\(k=2\)) beatings and the right (green) part is the \(k=3\) radio frequency comb and so on. All of them have a uniform, equidistant spacing of \(2 k \omega _r/m\) (hence the name radio frequency comb). The width of the spectral envelopes are the same when measured by the number of components. Increasing m prevents the overlapping regions, at least for the lower orders. Even if the radio frequency combs would overlap, each component is still uniquely linked to a particular pair of optical modes
These RF components are the result of beating between adjacent optical modes and can be seen in the power spectrum of the laser output. Higher order mode beatings like \(\omega _{n+2}-\omega _n\) etc. are separated in the power spectrum by about \(\omega _r\). This is illustrated in Fig. 1 and similar to the harmonics of the repetition rate in a regular frequency comb. The optical mode spacing at the carrier frequency \(\omega _0\) is given approximately by \(\omega _r\) for large m. It becomes the spacing for all modes for \(m \rightarrow \infty\) for which (1) turns into a regular frequency comb [4]. Note however that \(\omega _r\) is not the usual repetition frequency. Nevertheless \(\omega _r\) and \(\omega _0\) can be measured in very much the same way as for a regular frequency comb (see Sect. 3). Besides representing an all new mode locking regime, the interesting aspect of (1) is that each mode beating uniquely belongs to on particular pair of modes. For example the RF signal at \(\Delta _0=\omega _r(1+1/m)\) belongs to the beating between \(\omega _0\) and \(\omega _1\) and so on. Hence a RF spectrum recorded with a photo detector and a radio frequency spectrum analyzer directly displays a scaled down version of the optical spectrum of the laser. By placing a sample between the laser and the photo detector and recording the change of the RF spectrum one gets the absorption spectrum of the sample. This is similar to a dual frequency comb setting with a linearly increasing spacing between the modes of the two frequency combs [5], albeit with a single laser avoiding problems due to the relative jitter of the combs.
To see how the laser spectrum might be forced to the modes defined by (1) it is instructive to compute the electric field at a fixed point inside the cavity. Assuming that the modes oscillate with some complex amplitudes \(a_n\) we get:
This can not represent a stable pulse in the time domain. Assuming that m is an exact integer however, the pulse will revive up to a carrier–envelope phase of \(\varphi _{ce}=2 \pi m \omega _0/\omega _r\) after the time \(T=2 \pi m/\omega _r\):
This is similar to the regular mode locking scheme, except that the pulse repetition rate is replaced by the much lower revival rate \(\omega _r/(2 \pi m)\). The revival time is the m multiple of the cavity round trip phase delay of the \(n=0\) mode at \(\omega _0\). Figure 2 shows an example of the resulting laser power for a special case as a function of time. Like in a regular mode locked laser, the peak power enhancement over the time averaged power is roughly given by the number of active modes. In contrast to the latter, the large peak power occurs not every cavity round trip but only every m-th cavity round trip. The usual Kerr lens mode locking mechanism might be used to enforce an integer m by reduced loss of the high peak intensity pulse. In the case of the Talbot comb, that large peak intensity occurs only every m-th round trip. We therefore expect that the self amplitude modulation of the Kerr effect has to be stronger for successful mode locking. The mode spacing nominally becomes negative for \(n<-m/2\) (see Fig. 3). Physically this means that the corresponding spectral region possesses a negative group velocity. While this is possible in principle we exclude this for a reasonable laser design and assume that the active modes of the laser are limited to \(n>-m/2\).
The power \(\propto \vert E(t) \vert ^2\) at a fixed point inside the laser cavity according to (3) normalized to the time averaged power. The recurrence coefficient is \(m=10,000\) and the amplitudes follow a Gaussian distribution \(a_n=e^{-(n/1000)^2}\) (which is not exactly a Gaussian spectral envelope). After m cavity round trips the original pulse revives. The plot looks very similar if one scales m and the number of modes up. The brute force computation using (3) with sufficient resolution for larger m is computational challenging
To find the required dispersion that results in the mode spectrum of (1), we first resolve it for n:
Like in any other laser with cavity length L, the round trip phase \(\phi (\omega )\) at frequency \(\omega\) has to fulfill the boundary condition:
Since \(\omega _0\) is the resonant mode with \(n=0\), the last term has to be added to obtain the total round trip phase. Without loss of generality we assumed in (1) that the parameter \(\omega _0\) is the center of the emitted spectrum (see Fig. 3). Using (7) and computing the derivatives at \(\omega _0\) we obtain the dispersion required to generate the mode spacing of (1):
Here !! represents the double factorial. For a real laser the requirements on the dispersion are quite extreme but not impossible (see Sect. 5 and Fig. 4). These requirements are mitigated by large values of m, i.e. a long pulse revival time (for a given \(\omega _r\)). However we expect that this would lead to a reduced Kerr effect and hence weakens the mode locking mechanism. We expect that once the laser is set up for a particular value of m, it will be reproduced every time it is put in the mode locked state.
Frequencies of the modes of the Talbot comb according to (1) shown as the red solid curve. The dashed part belongs to the negative mode spacing section (i.e. negative group velocity). We do not consider this possibility and therefore also discarded the other sign solution in (5). This curve defines the dispersion properties of the cavity whose expansion is shown in (11). The vertex of the curve at \([-m/2; \omega _0-m \omega _r/4]\) can be chosen without restriction by selecting m and \(\omega _r\). The active modes, i.e. the laser spectrum, is assumed to be centered at \(\omega _0\). It covers a certain range in \(\omega _n\) and n-space (grey area). The curvature of the parabola reflects the required group velocity dispersion which can be minimized by large values of m and \(\omega _r\) in accordance with (11)
Comparing the exact round trip phase given by (5) and (6) with the expansion given by (11) for different order with \(m=10^6\) and \(\omega _r=2 \pi \times 100\) MHz. Successively compensating dispersion up to the order \(\phi ^{(6)}(\omega )\), the phase mismatch reduces to 0.77 rad at the edges of the spectrum (width 10 THz), i.e. about 0.12 free spectral ranges. This mismatch has to be compensated by the Kerr effect like in a regular mode locked laser
3 Self-referencing
For self-referencing the two parameters of the Talbot comb, \(\omega _r\) and \(\omega _0\) need to be measured and ideally stabilized. We assume that the recurrence index m is known. One might get an estimate of it and then fix it to be an integer, by measuring the recurrence time and compare it to the cavity length. A more reliable method would be to measure a known optical frequency with a self-referenced Talbot comb and then identify the proper m compatible with that measurement. This is the same method often applied with regular combs to determine the correct mode number.
The parameter \(\omega _r\) can be determined by observing the mode beating dependence on n as expressed by (2), i.e. by the second order mode differences:
In practical terms this frequency is readily generated by mixing two adjacent RF modes \(\Delta _n\), say by driving something non-linear with the photo detector signal. The mixing result can then be locked to a precise reference frequency such as an atomic clock by feeding back on the cavity length and presumably also on the pump laser power. In that sense \(\omega _r\) is determined almost as simple as the repetition rate of a regular frequency comb.
The second parameters of the Talbot comb, \(\omega _0\) can be measured in very much the same way as done with the carrier envelope offset frequency of a regular comb [4], i.e. with an \(f-2f\) interferometer. A part from the red side of the Talbot comb with mode number \(n_1\) is frequency doubled and superimposed the blue part of mode number \(n_2\). According to (1) the generated beat notes have the frequencies:
The condition for a signal in the radio frequency domain is that out of the combinations of integers in the bracketed term there is one, that is large enough to multiply \(\omega _r\) all the way up to the optical frequency \(\omega _0\). For \(m \rightarrow \infty\) this condition is identical of the comb spanning an optical octave. If the combs bandwidth is sufficient there are many combinations of integers that fulfill this requirement, i.e. several radio frequency beat notes may be taken as \(\omega _0\). Again this is very similar to regular frequency combs where the offset frequency is only determined modulo the repetition rate. Which of the beat notes is taken for \(\omega _0\) does not matter as long as the mode numbering is adapted to that choice. Frequency doubling the Talbot comb however will generate even more frequencies as assumed in (13), as we will see in the next section. The challenge then might be to identify the correct beat note that determines \(\omega _0\).
4 Non-linear interactions
Both, frequency doubling for self-referencing and spectral broadening to obtain an octave spanning bandwidth require non-linear processes. Driving a \(\chi ^{(2)}\) non-linearity the resulting field can be written as
Just like (4), this field reproduces itself after the recurrence time \(T=2 \pi m/\omega _r\) by virtue of the same argument made in (3). This should not surprise because whatever the \(\chi ^{(2)}\) does in the time domain, a periodic input should result in an output of the same periodicity. The mode distribution of terms with \(n=n'\) belongs to a frequency doubled Talbot comb as used in (13). Since there is only one such combination in the sum for each n, the \(\chi ^{(2)}\) process is expected to be less efficient than for a regular frequency comb. Of course this can also be understood in the time domain where a short pulse is formed only after m cavity round trips. The mode combinations in (14) with \(n' \ne n\) do not belong to the doubled Talbot comb. This probably means that the frequency doubled Talbot comb are not good for the type of spectroscopy described above. However, the usual \(f-2f\) self referencing is possible using these processes if one finds ways for a more efficient non-linear interaction. Since the doubling process is expected to be weak, it might be advisable to work with an auxiliary frequency doubled cw laser beating the fundamental and second harmonic with the Talbot comb and the doubled Talbot comb respectively. It should be mentioned that even without self-referencing the Talbot comb could be a useful tool. One might instead reference one of its modes to a wavemeter or to a atomic or molecular line. In fact for the intended broad band spectroscopy referencing to an atomic clock is usually not necessary.
With a similar argument as above, driving a \(\chi ^{(3)}\) non-linearity for spectral broadening the combination of modes
are generated. In a regular frequency comb this process simply extends spectrum by adding new modes on the extended grid of original modes. In the case of the Talbot comb this does not take place. One can see this by requiring the modes in (15) to be a Talbot comb of the same m: \((n+n'-n'')^2=n^2+n'^2-n''^2\). Solving this equation yields two solution \(n''=n\) and \(n''=n'\). In neither case additional modes are added to the initial Talbot comb.
5 Example design
One of the possibilities to demonstrate the Talbot comb is to employ a fiber-laser-based design. Because of the small mode-volume and long interaction length, the fiber-laser could introduce strong nonlinear effects such as nonlinear polarization rotation which is often used for conventional mode-locked fiber lasers [6]. In the case of Talbot comb, the mode-locking mechanism is effectively m times smaller than the conventional lasers. Therefore either strong nonlinear effects or matching the overall dispersion to (6) with very good accuracy is required to enforce the Talbot mode-locking. Intracavity dispersion can be introduced through a fiber Bragg grating (FBG) that can be designed with very large values for the group velocity dispersion and precise values for the higher order dispersions. To manufacture a FBG a grating is written into a photo sensitive fiber with a UV laser. Up to the 6th order dispersion is commercially available.
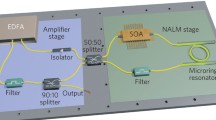
One or even several FBGs can be conveniently implemented into the fiber-laser cavity using an optical circulator. The cavity should include a gain fiber, a pump beam combiner, an optical isolator and an output coupler as shown in Fig. 5. An example for design parameters might be \(m=10^6\), \(\omega _r=2 \pi \times 100\) MHz assuming a spectral width of \(\delta \omega = 2 \pi \times 10\) THz and an optical carrier frequency of \(\omega _0=2 \pi \times 300\) THz (\(\lambda = 1~\upmu\)m) which is close to the Ytterbium gain maximum. With this we obtain from (11) \(\phi ''_{\omega _0}=-3.2\times 10^7\) fs\(^2\), \(\phi '''_{\omega _0}=3.0\times 10^8\) fs\(^3\) and \(\phi ^{(4)}_{\omega _0}=-4.8\times 10^9\) fs\(^4\) etc. Rather than this expansion one might use the first term in (7) to directly compute the required dispersion function.
To estimate the order of magnitude of the required length of the FBG \(\Delta z\) we calculate the difference of the round trip phase delay for the two ends of the spectrum (full width \(\Delta \omega)\) using (7): \(\Delta \phi =\phi (\omega _0+\Delta \omega /2)-\phi (\omega _0-\Delta \omega /2)\). This phase difference has to be divided by the wavenumber \(2\pi /\lambda\) to obtain the required path length difference between the two extreme colors. With the parameters above, dividing by the refractive index of 1.5 and taking into account that the light travels twice through the FBG we obtain \(\Delta z=3.3\) cm. The real length might then also depend on the requirements for the reflectivity. Fiber lasers generally come with a large optical gain so that it may be possible to compromise on that parameter. The first design may not be the rather optimistic one of this proposal but could be a trade off between large m (=low dispersion) and small m (=stronger mode locking). To start operation at a very large value of m it may also conceivable to include an intracavity modulator that mimics all or parts of the temporal envelope shown in Fig. 2.
6 Conclusions
This article is dedicated to Theodor Hänsch on the occasion of his 75th birthday. Among the many other laser tricks that he has invented is the optical frequency comb. Originally intended as a tool to measure laser frequencies, it has found several other applications for example in attosecond science and astronomy. Further it is used for large bandwidth direct comb spectroscopy. The current work tries to extends these possibilities, even though we have to admit that more ideas are required to turn it into a useful tool. Nevertheless we hope that this idea provides a new playground and entertainment for those who like curiosity driven research. In this spirit Theodor Hänsch has been our guide for many decades and we hope that there will be many more to follow. Happy Birthday!
References
S. Teng, J. Wang, F. Li, W. Zhang, Opt. Commun. 315, 103 (2014)
J. Azaña, M.A. Muriel, Appl. Opt. 38, 6700 (1999)
T. Suzuki, M. Katsuragawa, Opt. Expr. 18, 23088 (2010)
Th Udem, R. Holzwarth, T.W. Hänsch, Nature 416, 233 (2002)
T. Ideguchi et al., Nat. Commun. 5, 3375 (2014)
M. Hofer et al., Opt. Lett. 16, 502 (1991)
Acknowledgements
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the topical collection “Enlightening the World with the Laser” - Honoring T. W. Hänsch guest edited by Tilman Esslinger, Nathalie Picqué, and Thomas Udem.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Udem, T., Ozawa, A. Mode locking based on the temporal Talbot effect. Appl. Phys. B 123, 100 (2017). https://doi.org/10.1007/s00340-017-6676-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-017-6676-0